Abstract
The proliferation of classification-capable artificial intelligence (AI) across a wide range of domains (e.g., agriculture, construction, etc.) has been allowed to optimize and complement several tasks, typically operationalized by humans. The computational training that allows providing such support is frequently hindered by various challenges related to datasets, including the scarcity of examples and imbalanced class distributions, which have detrimental effects on the production of accurate models. For a proper approach to these challenges, strategies smarter than the traditional brute force-based K-fold cross-validation or the naivety of hold-out are required, with the following main goals in mind: (1) carrying out one-shot, close-to-optimal data arrangements, accelerating conventional training optimization; and (2) aiming at maximizing the capacity of inference models to its fullest extent while relieving computational burden. To that end, in this paper, two image-based feature-aware dataset splitting approaches are proposed, hypothesizing a contribution towards attaining classification models that are closer to their full inference potential. Both rely on strategic image harvesting: while one of them hinges on weighted random selection out of a feature-based clusters set, the other involves a balanced picking process from a sorted list that stores data features’ distances to the centroid of a whole feature space. Comparative tests on datasets related to grapevine leaves phenotyping and bridge defects showcase promising results, highlighting a viable alternative to K-fold cross-validation and hold-out methods.
1. Introduction
In recent years, the proliferation of classification-capable artificial intelligence (AI) across a wide range of domains (e.g., civil engineering [1], agriculture [2], medicine [3,4,5], aeronautics [6], footwear retail [7], etc.) has been of outstanding importance for the digitalization of knowledge among vanishing professionals with particular sets of relevant skills, leading to the automation of workflows, time-effective decision support, and the dynamization of business models, among many other benefits. Supporting the success of this family of computational approaches are several artificial neural network architectures of distinct complexities that have been proposed over time by the technical-scientific community—e.g., VGG [8], ResNet [9], Xception [10], within the scope of deep learning—with the goal of providing different strategies to reach inference models of increasingly better performances, which are typically assessed against unseen data [11]. Among the perceived challenges is the need to mitigate potential overfitting, which affects models of higher complexity more severely [12]. Therefore, employing best-practices to find the proper balance between generalization capabilities and biases contributes to the achievement of more suitable inference capabilities. One of these practices consists of finding adequate training data arrangements to ensure harmonization, configured by a balanced distribution of examples per class/label, representativeness, diversity, among other aspects. In that regard, the data splitting process for setting up datasets is crucial for the achievement of reliable and consistent models [13].
In the dataset splitting context, there are different techniques [14]. Currently, two methods are widely used for this purpose: K-fold cross-validation (KFCV) and hold-out validation (HO) [15,16,17,18]. These traditional approaches pose some issues, not only in terms of demanding both computational time and processing resources, but also because they do not always ensure the exploration of models’ full inference potential (or nearly close to that golden rate). Other eventual drawbacks include decompensations that may prevent the matching of features between training and validation examples, and even lead to unrepresentative performance assessments while testing the models against unseen data, especially in cases wherein heterogeneity is a prevalent characteristic—for example, with the inclusion of many classes and/or noisy backgrounds. In cases wherein the datasets are reduced, the division can result in subsets composed of only a few samples, impacting the effectiveness of training or evaluation. If the dataset is unbalanced, and if certain classes or categories are underrepresented in the training, validation, or testing subset, the model may not learn accurately. Design patterns [19] may not work in such scenarios either. While rebalancing by oversampling may induce bias for decompensated classes, doing it by underfitting can lead to a substantial loss of problem representation.
In this study, in contrast with conventional dataset split methodologies, two one-shot techniques are proposed and compared. Their primary focus is on achieving feature-based balanced datasets, aiming to mitigate the trial-and-error orientation underlying traditional subdivision approaches. More specifically, a lightweight feature-aware exploration strategy was conceptualized and developed to automatically and expeditiously organize data towards achieving uniform feature distribution, with the particular goal of assessing the impact of evenly distributing diversity in imagery characteristics on deep learning (DL) models’ convergence. Tests made to evaluate the proposed strategies, considering two datasets with distinct contexts (grapevine leaves for phenotyping determination and bridge defects for the identification of degradation factors) demonstrated very promising results in comparison to the KFCV and HO techniques.
Regarding the structure, besides this introductory section, the remainder of the paper is organized as follows: Section 2 will address the related work; Section 3 covers the material and methodology; Section 4 presents the experimental results, followed by Section 5, which provides a summary discussion, main conclusions and some future directions.
2. Related Work
Machine learning algorithms’ tasks include extracting features from data and constructing effective prediction models. Within this operational line, the primary objective is to create computational models that not only excel humans in making accurate predictions but also demonstrate a robust ability to generalize to new/unseen data. One of the factors that affect the model’s generalization performance is the binomial size/quality of the training, validation, and testing subsets; another one is the data arrangement, carried out through proper division. Highlighting the importance of appropriate data splitting, various statistical sampling methods for data splitting have been proposed [20].
Fox et. al [21] used both the KFCV and normal split techniques to divide the ITEC LapGyn4 Gynecologic Laparoscopy Image Dataset [22] and employed them to classify the images using a convolutional neural network (CNN) model and scale-invariant feature transform (SIFT) classification. Their results show better performance for the KFCV using a CNN. A feature-weighted sampling method was proposed in [23] to optimize the split of the dataset. In this work, firstly, a division of the full dataset into several subsets using the modified R-value-based sampling (RBS) [24] was carried out. Then, the distances of each set to the whole dataset were computed to obtain a similarity score, and the one with the smallest distance was chosen. Eliane [25] employed different methods to split the dataset into training/test sets, including KFCV, sample set partitioning based on joint x–y distance (SPXY), Kennard–Stone (KS), and a random sampling algorithm. The use of Pearson correlation scores (PCSs) for comparison allowed for ranking the performance of these approaches from best to worst, as follows: KFCV, SPXY, and KS. An algorithm for performing stratified KFCV with a focus on similarity-based sample splitting was developed by Farias et al. [26]. First, they select a pivot sample from each label group that is most similar to other samples within the same label group. Afterward, the algorithm identifies additional samples that are most similar to the “pivot” sample. They employed different similarity functions, including Cityblock, Chebyshev, Euclidean, cosine, and correlation, deploying different classifiers: nearest neighbors (KNN); random forest (RF) classifier with 100 trees; support vector machine (SVM); and multilayer perceptron (MLP). Their results showed the better performance of the proposed algorithm over the normal KFCV when using the correlation similarity function. It is worth mentioning that the difference between the accuracies of different similarity functions was almost 1%. Nurhopipah et al. [27] compared four dataset splitting techniques for face classification tasks: random sub-sampling validation, bootstrap validation, KFCV, and Moralis Lima Martin validation (MLMV). They concluded that KFCV provides a more stable performance, with higher accuracy. The KFCV method was, once again, employed in [28] to partition brain image samples for tumor diagnosis, using the SVM algorithm. In this work, different kernels of the SVM were used. In [29], KFCV, with K = 10, was applied to split a vegetation dataset into training and validation subsets and, subsequently, build different classifiers—k-nearest neighbors, Gaussian naive Bayes, random forests, SVM, and multilayer perceptron—capable of performing vegetation physiognomic classification. Inside the cross-validation loop, they performed a univariate statistical test (ANOVA F-value) between physiognomic classes and the features in the training set to select the best-scoring features from the training set. A higher accuracy (81%) was verified for random forests.
Varma and Simon [30] used both normal and nested KFCV and showed that the nested one can be considered a nearly bias-free method. Vabalas et al. [31] used the train/test split, normal, nested, and partially nested KFCV to split the dataset, as well as an SVM and a logistic regression classifier to distinguish autistic from non-autistic individuals. In their experiments, the train/test split and nested KFCV approaches produced robust performance. Kahloot et al. [32] developed a technique named “Algorithmic splitting”. They used, firstly, the Umap technique for dimension reduction and then two different clustering methods, including hierarchical density-based spatial clustering of applications with noise (HDBSCAN) [33] and gaussian mixture models (GMM) [34]. The distances of data points to the mean were computed using Chebyshev’s inequality bound [35]. For each cluster, they calculated the mean (μ) and standard deviation (σ) of the data points’ positions. Then, the algorithm defines different ranges based on μ and σ, which include a “median range” (within 1 standard deviation from μ), an “extreme range” (beyond 2 standard deviations from μ), and a “quantile range” (between median and extreme ranges). For each sub-dataset size (training, validation, testing with sizes of 70%, 20%, and 10%, respectively), the algorithm samples data points from the defined ranges according to specified percentages and experiments with different rates of selection for each range to train models based in VGG [8], ResNet [9], and Inception [36]. The optimal percentages were 55%, 35%, and 10% out of the median, extreme, and quantile ranges, respectively. For comparison purposes, they also split the dataset using random sampling. They concluded that the hierarchical density-based spatial clustering of applications with noise (HDBSCAN) outperforms the GMM with the algorithmic split.
To split the dataset, Doan et al. [37] first divided each class into clusters using HDBSCAN and then applied a stratification technique to select data from each cluster for the train/test set. They also used random sampling, stratified sampling, stratified cross-validation, and bootstrapping techniques as data splitting techniques and compared the results with their approach, which proved to outperform the others for all the trained models (MLP, SVM, RF, XGBoost).
Resampling, including normal, repeated, nested, leave-one-out KFCV, was used by [38] to split a dataset for training different ML algorithms (linear regression, Bayes ridge regression, ridge regression, LASSO regression, K-nearest neighbors, CART decision trees, support vector machines regression—SVMR, extreme gradient boosting, gradient boosting, random forests, and extra trees) to predict profits in olive farms. Their results presented a better performance for SVMR compared to the others, and the resampling technique outperformed the other splitting techniques. Huang et al. [39] split a dataset randomly, in a traditional fashion, with a ratio of 4:1 for training and validation, respectively, for their objective, which was using the U-Net for segmentation and AlexNet, VGG16, VGG19, ResNet-50, Inception V3, and Xception for classification.
In specific contexts, such as agriculture, traditional dataset splitting is the preferred option to be used [40,41,42], even in limited dataset conditions, as can be verified in [43], which proposes the use of KFCV to split datasets to feed decision tree, random forest, gradient boosting, and SVM models, aiming at tomato crop yield prediction, based on certain inputs (soil properties, applied fertilizers, and weather conditions). Optuna [44] employed a feature selection technique and, in the end, better performances were found for gradient boosting and SVM. The same tendency of using traditional dataset splitting techniques can be verified in the construction field [45].
From the works addressed above, one can infer that data-based features for setting up ML/DL models are of key importance. In this context, two main steps can be identified: (a) feature extraction, which can be done using specific layers of consolidated CNN architectures, such as VGG16—widely known for its capabilities in artificial deep vision tasks [46,47,48]—benefiting from ImageNet [49] weights; and (b) dimensionality reduction, achievable through techniques such as, for example, principle component analysis (PCA), which is also capable of retaining the relevant variance of the data to preserve its intrinsic characteristics [50,51,52].
To sum up, most of the data splitting-related works rely on techniques that can be computationally burdensome and time-consuming, such as KFCV. In contrast, single passages of HO techniques are likely to lead to uncalibrated datasets in terms of features—it is hypothesized that the presence of elements in training images that, if missing in the validation subset, cannot be confirmed and consolidated—potentially constraining the exploration of the full potential of the models. Therefore, this study proposes methods to work around the identified issues. The goal is to balance features during the training, validation, and test stages. Further details will be explained in the following section.
3. Materials and Methods
This section presents the research approach, detailing the methodical preparation of materials and outlining the methodologies employed in this study. It covers the contextualization of the raw data used for experimentation purposes, as well as specific methods applied for optimizing the dataset splitting techniques.
3.1. Imagery Used for the Empirical Assessment of the Proposed Dataset Splitting Methodology
A couple of distinct groups of imagery involving differentiated contexts are considered to perform empirical experiments on the proposed feature-aware dataset splitting methodology. The first image group, described in [2], within the context of viticulture, is composed of 6 different varieties (Figure 1), summing up a total of 480 images. The varieties involved in this image group are the following: Touriga Nacional, Tinto Cão, Códega, Moscatel, Tinta Roriz, and Rabigato. In terms of acquisition procedure, weekly between 4 May and 31 July 2017, one leaf was picked from the same two previously selected plants of each grapevine variety, put on top of a white sheet of paper (background), and photographed (in the field) without any artificial lighting, using a Canon EOS 600D, equipped with a 50 mm f/1.4 objective lens (Canon, Ota, Tokyo, Japan). For the sake of variability, data collected on cloudy days and in sunny late afternoons was also included. It is worth noting that leaf acquisition and labeling were supported by domain experts.

Figure 1.
Raw data of grapevine leaves composed of 6 classes (phenotypes), acquired over a white background—also documented in previous work [2]. From left to right: Touriga Nacional, Tinto Cão, Códega, Moscatel, Tinta Roriz, and Rabigato.
Table 1 presents the distribution of examples per class, more specifically 80 images evenly assigned.

Table 1.
Distribution of classes and their respective sizes within the grapevine leaves imagery.
The second image group regards the context of bridge defects. This collection was created by capturing photographs of various bridges using a handheld camera and a mobile phone, resulting in a set of images with a diverse range of sizes and resolutions. Afterward, each image was manually labeled using a tool called LabelImg [53] and attributed to one of the six groups representing defect types: paint deterioration, plant, absence of joint cover plate, cracks, pavement crack, and peeling on concrete (Figure 2). In total, 2400 images were labeled. However, a pruning operation to remove unusable data had to be carried out, resulting in a final set of 1872 images. Civil engineers possessing technical expertise in the relevant domain both participated actively in the direct image acquisition process and provided support for the labeling procedures.

Figure 2.
Different types of defects commonly found in bridges, which are also documented in previous work [1].
The distribution of classes in this dataset is illustrated in Table 2. The “pavement crack” class is largest, with 461 images, while the “peeling on concrete” class is the smallest one, containing 101 images. This dataset showcases an uneven distribution of data among the classes.

Table 2.
Distribution of classes and their respective sizes within the bridge defects imagery.
Having both balanced and unbalanced datasets allows a more realistic evaluation of the splitting techniques under comparison.
3.2. Complementary Imagery for Extended Assessments—Models Inference Consistency and Attention Map Analysis
Two other grapevine and bridge defects external datasets were included in this study (Figure 3), envisaging an extended assessment that focuses on the following aspects: (a) the model prediction consistency over data that are characteristically different from the ones used for training; (b) CNNs attention maps-based metrics for a richer interpretation of the trained models.

Figure 3.
External image sets DL models extended assessments: (a) features a set of images for grapevine variety identification through leaf analysis; (b) showcases examples related to the detection of bridge defects. A careful alignment of the classes/labels that compose contextually corresponding sets (grapevine and bridge defects group) was ensured.
Within the vineyard context, another dataset of 12 grapevine varieties was considered, based on imagery captured in a natural background—Códega, Malvasia Fina, Malvasia Preta, Malvasia Rei, Moscatel (Galego), Mourisco Tinto, Rabigato, Tinta Amarela, Tinta Barroca, Tinta Roriz, Tinto Cão, and Touriga Nacional. It resulted from a campaign that took place from 17 July to 20 September 2019, in intervals of 2 weeks, to collect 888 images of leaves, slightly unbalanced in terms of classes distribution. As with the previous grapevine group, lighting conditions were mostly influenced by direct solar incidence, occurring between 1 PM and 3 PM. However, both cloudy and sunny late afternoon illumination conditions were also considered to complement imagery variability. The acquisition equipment was the same as the one previously described for the 6-class grapevine dataset, i.e., a Canon EOS 600D camera. In the scope of this study, a pruning operation was carried out to ensure that the labels/classes of both grapevine datasets involved matched with each other, and a total of 10 samples per class were randomly considered.
The creation of the external assessment set for the bridge defects followed a similar methodology, outlined in the first collected set of this domain. Utilizing the same equipment and conditions, images were captured with a handheld camera and a mobile phone to cover the six defect classes from the bridge: paint deterioration, plant, absence of joint cover plate, cracks, pavement crack, and peeling on concrete. Just like in the latter external grapevine dataset, 10 images per class were randomly selected, setting up the final bridge defects imagery used for extended assessments in this study.
In this work, formal notation is defined to represent the specific datasets as , where
- D represents the dataset;
- i represents a specific dataset chosen from a set of datasets I = {bridge defects imagery (BDI), grapevine leaves imagery (GLI)};
- n represents the specific sets N = {training-validation (Tr-Val), train (Tr), validation (Val), test (Tst), and external test (Ext_Tst)}.
3.3. General Workflow
The process of model development begins with a critical step, which is the division of the original dataset into distinct subsets for training-validation and testing. This process serves as the foundation upon which the subsequent stages of model refinement and evaluation rest. The workflow of this work (Figure 4) begins by partitioning the original raw data into the training-validation and testing subsets, at a rate of 80% and 20%, respectively. Then, the training-validation subset is subdivided once again into train and validation subsets. During the evaluation step, a set of commonly used metrics is employed to assess resulting models, namely, involving accuracy and intersection over union (IOU). These metrics characterization can be found below:
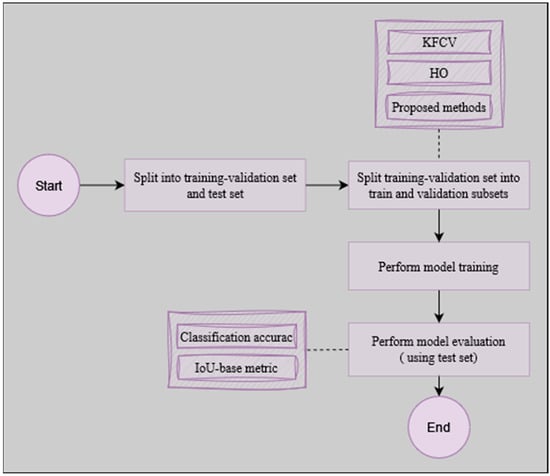
Figure 4.
Data splitting general workflow.
- Accuracy is a fundamental metric in the field of machine learning, measures the proportion of correctly predicted instances out of the total number of instances. It is usually used to evaluate how well the model classified and predicted classes over a testing subset. More specifically, it provides an overall assessment of a model’s correctness (Equation (1)).where true positives (TP) and true negatives (TN) represent, respectively, the number of instances that were correctly classified as positive and negative by the model; in turn, false positives (FP) and false negatives (FN) correspond to the number of instances incorrectly classified as positive and negative, respectively.
- IOU is a spatial overlap metric commonly used in tasks involving object detection and segmentation. It quantifies the degree of overlap between the predicted regions and the ground truth regions. Specifically, IOU calculates the ratio of the intersection area between the predicted and actual regions to the union area of those regions. IOU allows the capture of the spatial alignment and precision of the model’s output in relation to the true object regions. To compute it, the most prominent attention area of CNN’s gradient-weighted class activation mapping (Grad-CAM) is used as a bounding box predictor (Equation (2)).where OverlapArea and UnionArea represent, respectively, the intersection and the union between ground-truth and the predicted bounding boxes of a given object of interest.
Regarding the training process, the Xception architecture is employed using Adam with Nesterov momentum (Nadam), and stochastic gradient descendent (SGD) optimizers with an initial learning rate of 1 × 10−3. To assure the consistency of the training conditions across all dataset splitting approaches, a set of hyperparameters is maintained across the experiments. This includes a batch size of 32, ensuring efficient training iterations; 100 training epochs; and an early stopping callback with a patience of 20 epochs. This former event monitor tracks validation accuracy and triggers in the absence of fluctuations greater than 1 × 10−4 for more than 20 consecutive epochs, indicating model stagnation. Also, a dropout regularization with a weight of 0.2 was included to make the models less prone to overfitting.
It is important to note that the hyperparameters used in the experiments were chosen based on previous work [1] and remained consistent across all training sessions. This seeks to ensure a fairer comparison and consistency in model training, by duly isolating and accommodating the main study object, i.e., the impact of varying splitting techniques.
3.4. Hardware and Software Tools
All the operations related to the deep learning models training and evaluation took place in a computer composed of the following components:
- Processor: an Intel(R) Core (TM) i7-8700 CPU 3.20 GHz 3.19 GHz (Intel Co., Santa Clara, CA, USA);
- Random access memory (RAM): 16.0 GB (Corsair, Fremont, CA, USA);
- Graphic card: NVIDIA GeForce GTX 1080, 16.0 GB (NVIDIA Co., Santa Clara, CA, USA);
- Storage: 500 SSD (Samsung Electronics, Suwon, Republic of Korea);
- Operative system: Windows 10 Pro (Microsoft Co., Redmond, WA, USA).
In terms of software, the implementation of this module was conducted utilizing Python version 3.8. The deep learning library employed in this project was TensorFlow version 2.8, strategically configured to leverage the computational power of the GPU.
3.5. Setting Up the Standards: Traditional Splitting Methodology
Two fundamental strategies commonly employed for dataset split are (i) the HO method; and (ii) the KFCV technique.
HO splitting involves partitioning the dataset into two subsets: the training set and the validation set. The training set, which usually holds most of the dataset, is used for training the models. The validation set, comprising the remaining portion, is kept separate and is used for evaluation. On the other hand, KFCV involves partitioning data into K-folds. The model is trained K times, each time using K-1 folds for training, leaving one for validation (Figure 5).
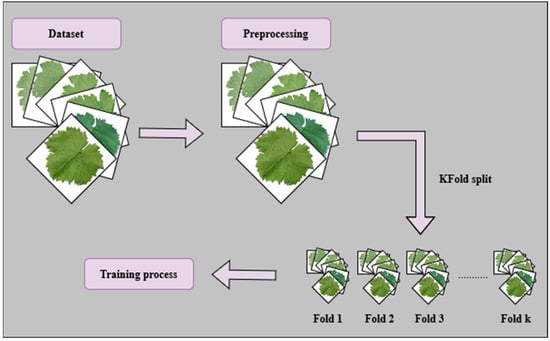
Figure 5.
KFCV process.
The splitting rates adopted in this work are 80% and 20% for training and validation subsets, respectively.
3.6. Proposed Diversity-Oriented Data Split Approaches
The data split approach involves the integration of two key steps: feature engineering and dataset splitting. The general workflow encompassing these steps is depicted in Figure 6.
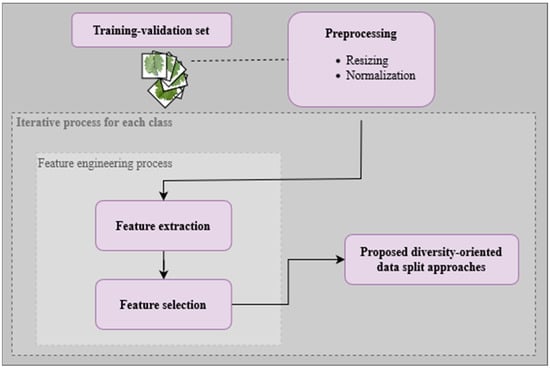
Figure 6.
General workflow of the split process.
3.6.1. Preliminary Feature Engineering
The feature engineering stage stands as the foundational step in the data preprocessing pipeline. Its primary objective is to transform input data into a more representative and informative feature space. This is achieved by extracting relevant characteristics, patterns, and representations from the data. This empowers the subsequent stages of the model to work with more meaningful inputs, leading to enhanced performance and faster convergence.
VGG16 was chosen as a robust CNN architecture for feature extraction due to its ability to effectively capture complex patterns based on deep image features. Moreover, considering the volume of classes and images that compose the two sets of raw data described previously, the extraction process occurs with due immediacy, at least, taking less than 3 s per class, depending on the hardware in use, also detailed earlier.
In addition, PCA was included to systematically perform dimensionality reduction upon the VGG16-based feature maps. A fundamental principle of the PCA implementation was the criterion of maintaining components that collectively explain at least 99% of the variance within the data. By keeping only those components that encapsulate the most significant information, we ensure the preservation of the essence of the dataset while simultaneously eliminating noise and redundancy. To ensure the effectiveness of PCA, a prerequisite step involved the standardization of the data, which involves transforming the variables to have a mean of zero and a standard deviation of one, preventing features with larger scales from disproportionately influencing the PCA process. To reach a functional dimensionality reduction, the selection of the final number of components is vital. To this end, the elbow value is computed by analyzing the explained variance ratio derived from PCA. The elbow value can be interpreted as the inflection point at which the marginal gain in the explained variance diminishes significantly. Once the elbow value was established, it was employed to guide the final reduction of features. Only the relevant components, as determined by the elbow value, were retained for the transformation of the data. This step resulted in the generation of a new feature space, compactly encapsulating the most valuable aspects of the original data. The implemented PCA process is depicted in Figure 7.
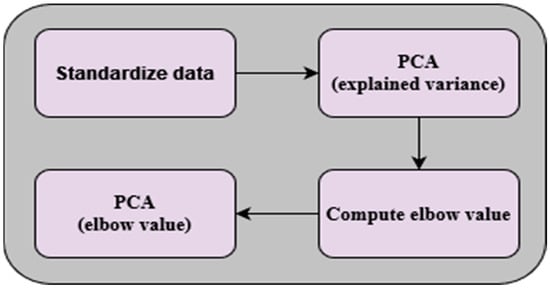
Figure 7.
Key steps of PCA.
By combining VGG16 for robust deep features extraction and PCA for effective dimensionality reduction, a synergetic approach to grouping data by representative characteristics with reduced computational costs was achieved, standing as a key component in the proposed methodology.
For the proposed dataset split, the centroid points of the features are computed, which will be used as a key parameter for the further processes. In Figure 8, an illustrative example of this process is provided, showcasing the centroid denoted by a distinctive red cross.
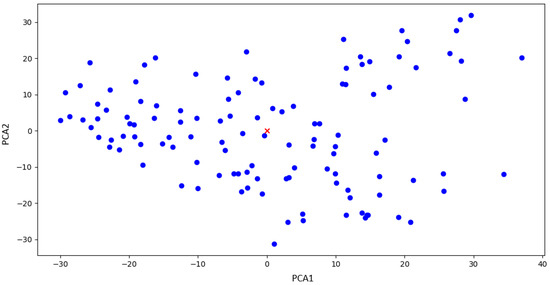
Figure 8.
Visualization of centroid point of features for the class of “absence of joint cover plate” for , for exemplification purposes. The blue dots represent the distribution of features, while the red cross is the global centroid.
Two methods are proposed for systematic feature-aware data splitting, aiming towards diversity-oriented dataset structures: (a) feature clustering distance-based image selection (FCDIS) and (b) feature space center-based image selection (FSCIS). Both methods start by considering 80% of the in the and save the remaining 20% for the .
3.6.2. Feature Clustering Distance-Based Image Selection (FCDIS)
The primary step in the FCDIS method is centered on the clustering technique, where features extracted from each data class are structured using the K-means clustering algorithm. Figure 9 illustrates the process that serves as a foundation for the FCDIS splitting method, accompanied by a plot designed to provide an informative schematic representation of the divisions resulting from the application of this process.
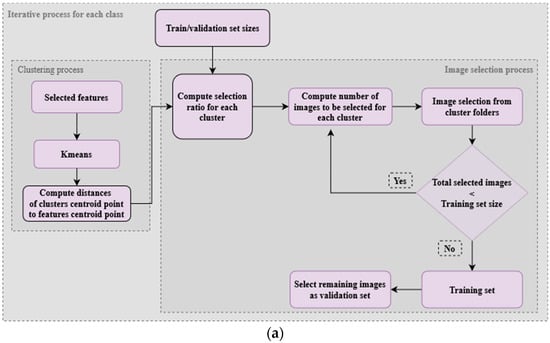
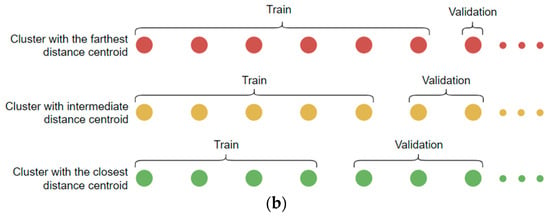
Figure 9.
FCDIS process for setting up training and validation subsets: (a) presents the main pipeline of the process; (b) depicts the pipeline’s general result-oriented concept using 3 abstract clusters as examples, where in red, yellow, green represents the farthest, intermediate, and closer distance to centroid, respectively. Considering the distance of each cluster centroid to a global centroid, the and are assembled, grounded in the following diversity rule: the farthest the cluster centroid is, the more images are used to compose the .
K-means partitions the feature space into K clusters based on the similarity of the deep features, aiming at the creation of distinct groups of related data points. To optimize the clustering process, a crucial step involves fine-tuning the parameter K, using a precomputed elbow value determination step (Figure 10a), aiding in the identification of the optimal number of clusters necessary to effectively segment the data within a specific class [54,55]. Then, an iterative process is employed for each class to select images for training. The essence of this selection lies in the distance ratio, wherein images positioned in farther clusters from the global centroid are accorded higher consideration. More specifically, a computation step of the distance between each cluster’s center and the center of the entire features space is carried out (Figure 10b). The latter center corresponds to the global one, denoted as , which is the mean of the top-2 principal components in the reduced feature space. This distance is computed using the Euclidean distance formula:
where are the coordinates of the -th cluster center and correspond to the coordinates of the global center. Then, a metric-based distance is used to determine the images’ selection size allocation for each cluster, according to the following formula:
where represents the total number of clusters in the class. This ratio is used to determine the relative importance of each cluster in contributing images used for setting up training/validation sets. It is based on the distance of their respective center from the global center, with direct impact.
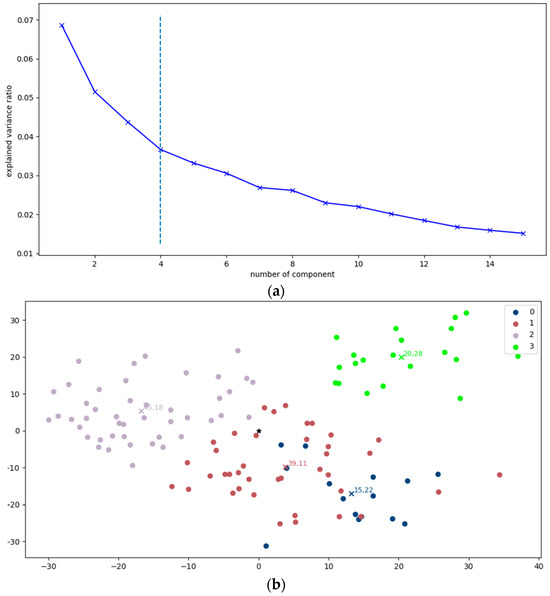
Figure 10.
Example of K-means-based clustering process plot perspective, using a computational method for the determination of K value. In (a), there is a chart depicting the value determined from the elbow technique regarding the “absence of joint cover plate” class belonging to , for exemplification purposes. The resulting clustering operation, based on a predetermined K, is illustrated in (b).
More intuitive results of the FCDIS approach can be seen in Figure 11, considering the bridge defects “absence of joint cover plate” class as an example. Upon closer examination, a noticeable visual similarity becomes apparent among images clustered together. This visual consistency proves that the clustering algorithm successfully identified and grouped images that share common features related to the “absence of joint cover plate” class. In addition, in Figure 11b, a summary of the images collected for constituting , dependent on the distances and sizes of the clusters, is provided.
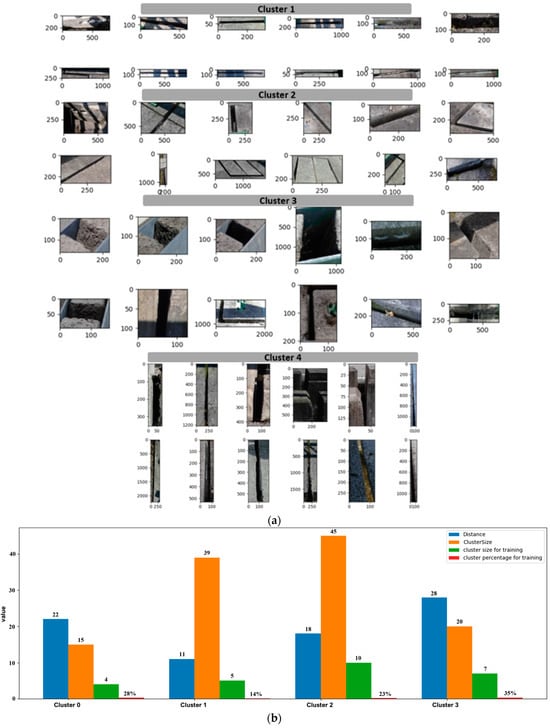
Figure 11.
Visualization of a few samples of each cluster for the “absence of joint cover plate” class concerning : (a) depicts the images grouped by K-means clustering; (b) presents a summary of the images collected for , considering each cluster’s distance and size.
3.6.3. Feature Space Center-Based Image Selection (FSCIS)
The main objective of this approach is to partition a given distance list into multiple sub-lists, subsequently enabling the selection of an image located at the median position within each sub-list. To accomplish this, the following pivotal variables must be considered: the designated size of the –80% of the , as proposed in this work, a sorted list of distances between each image’s features, and the global center of the entire feature space (Figure 12).
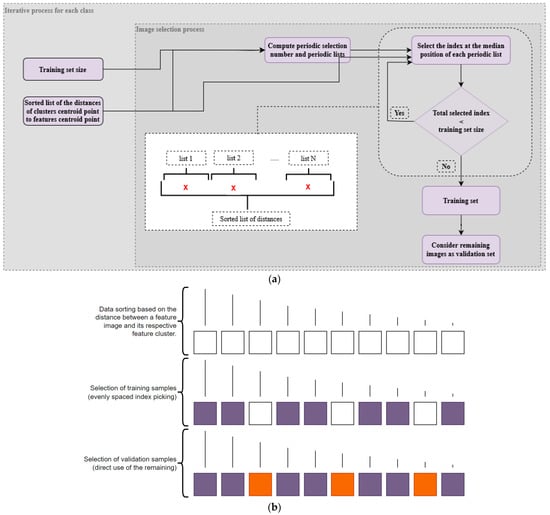
Figure 12.
FSCIS process for setting up training and validation subsets: (a) presents the main pipeline of the process; (b) depicts the result of the pipeline behavior, in which (i) images are firstly sorted by their distance to the feature space centroid, (ii) subgroups are then created, (iii) examples for training are iteratively selected, based on the median element of each created subgroup, until a percentage of 80% of the to is reached, and, finally, (iv) the remaining images are assigned to . Black vertical lines illustrate the referred distance to the feature space centroid, white squares represent the images that have not yet been assigned; orange squares depict the images for ; and, finally, purple squares represent the images that have been assigned for .
These variables are integrated into an image selection process, which performs a series of computations. The first step involves calculating a factor number to divide the main list into evenly weighted subgroups, i.e., as much as possible, with the same number of elements, as shown in Equation (5), and, afterward, determine proper positions/indexes for image extraction. Then, within these formed subgroups, the focal point is the identification of the median-positioned images. Thus, for each subgroup, images at the median index are picked and used to set up the . This median-picking operation is executed until the total number of images within the is reached. Lastly, the remaining images are allocated to the . This approach aims to guarantee that the selected training images are distributed evenly across the spectrum of distances between the features of each image and the centroid point of all features.
4. Experimental Results
To evaluate the proposed feature-aware dataset splitting methods against traditional dataset division approaches, a series of experiments encompassing both bridge defects and grapevine varieties’ raw data was carried out. The architecture considered for the models’ training was Xception, combined with the Nadam and SGD optimizers. The various DL models that resulted from these experiments are analyzed and compared in this section, in terms of consistency through training plot inspection, actual accuracies, and activations indicating the models’ attention.
4.1. Consistency of the Training Metrics: Analyzing the Learning Curves
After training the model, the learning curves were analyzed. By observation, their respective training and validation lines seem smoother and more stable for the models trained with datasets split by the FCDIS and FSCIS approaches, compared to the ones built from datasets derived from traditional techniques. Such an aspect can be found in Figure 13, which shows a set of training/validation accuracy-loss plots, regarding a training session of 100 epochs over datasets built from both of the previously presented image collections (bridge defects and grapevine varieties). As observed, some models finished earlier, due to the use of an early stopping control callback—described in the previous section. This implies that the potential of learning was reached before the last epoch for the training sessions. In Figure 13a, the KFCV10-fold0 finished at epoch 71, while in Figure 13b, for the KFCV10-fold7, the final epoch was 48. Such control over training progress is of high relevance—as demonstrated in previous works [1]—to reach models with optimized performance in a timelier manner while simultaneously preventing overfitting.
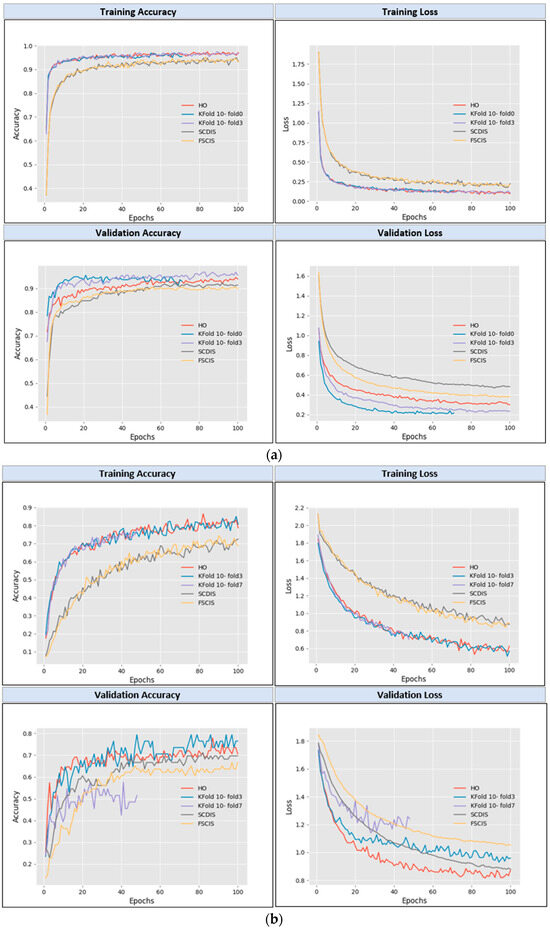
Figure 13.
Learning curves, generated to compare the learning behavior of models over datasets produced based on both traditional techniques and FCDIS/FSCIS methods: (a) Xception/Nadam for bridge defects datasets; (b) Xception/Nadam for .
4.2. Assessment with the Data Reserved for Testing
Based on the previously documented grapevine and bridge defects imagery, datasets compliant with a standard DL training process were built, resorting to both the traditional and proposed approaches. These models were then assessed and compared in terms of accuracy using a reserved for this purpose (i.e., image subsets isolated from the models’ training, as specified in Figure 4). The respective results for and can be consulted in Table 3 and Table 4, respectively.

Table 3.
Accuracy results for models trained with .

Table 4.
Accuracy results for models trained with datasets .
As illustrated in Table 3 and Table 4, the models employing the proposed techniques completed the training up to epoch 100, while some models using traditional techniques failed to reach that limit, due to the transversal use of an early stopping monitor in the supervision of the training process.
In Table 3, the accuracy results demonstrate that the models trained with SCDIS and FSCIS outperform the HO, as well as 90% of the KFCV10 group. Additionally, Table 4 highlights that the proposed methods performed better than the ones with conventional techniques. These findings underscore their continual outperformance relative to the mean performance achieved by KFCV10. Regarding the optimizers, it is worth noting that the models trained with Nadam outperformed the ones supported by SGD.
4.3. Assessment with External Imagery Sources
An extension to the assessment of the previous models was carried out, using and with a set of classes that seamlessly match the one that characterizes the former datasets applied for training, as previously explained in the materials and methods section. To that end and for the sake of contention while still ensuring some representativeness, 10 random images per class were considered.
The trained models were evaluated against the above-mentioned external data and the results are presented in Table 5 for , and in Table 6 for .

Table 5.
Accuracy of models using the .

Table 6.
Accuracy of models using the .
Considering the outcomes presented in Table 5, one can infer that SCDIS- and FSCIS-based Xception/Nadam models clearly outperform HO, and, compared to KFCV10-based models, most of the accuracies are matched or surpassed (8/10). A less noticeable tendency can be observed for the FSCIS-based Xception/SGD model, which was still capable of outperforming both HO and half of the KFCV10-based models. In Table 6, the SCDIS-based model stands out, largely surpassing HO and most of the KFCV10-based models for both Xception/Nadam and Xception/SGD combinations. Less successful was the FSCIS model, which could only prevail over HO and a few KFCV10 models.
4.4. Attention Mechanisms Assessment with External Imagery Sources
Gradient-weighted class activation mapping (Grad-CAM)-based IoU allows a more comprehensive understanding of the model’s performance, more specifically, by exploring the spatial accuracy and localization precision of the predictions. A more detailed examination of the salient features and attention areas associated with the models can be attained, aligning with eXplainable artificial intelligence (XAI) strategies, which promote enhanced interpretability and may provide directions for improving accuracies.
In this section, the models that reached the highest performances in the previous assessment addressing classification tasks were considered. Before applying them in the proposed analysis, a couple of preliminary steps were carried out: (i) determining the Grad-CAM-generated area and (ii) annotating the corresponding ground truth regions in the images involved in the assessment, i.e., those related to Grad-CAM and the masks associated with the samples (Figure 14). One should note that the biases involved are highly dependent on the Grad-CAM estimations provided by the previously trained models upon , .
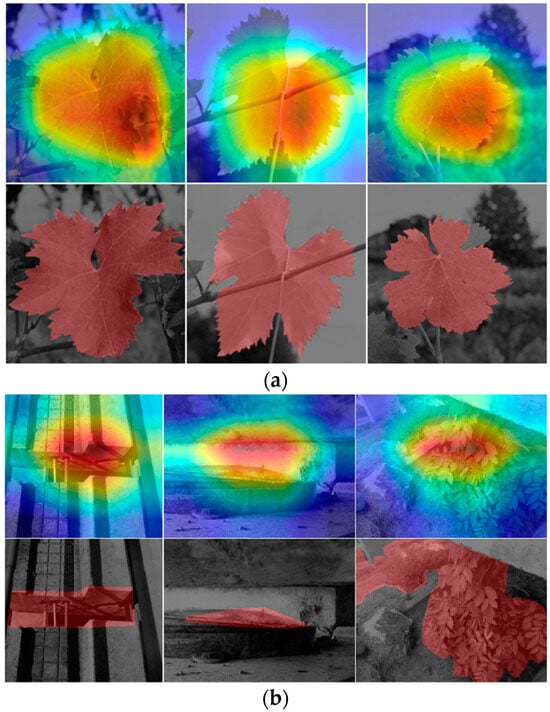
Figure 14.
Visualization of the Grad-CAM evaluation approach: (a,b) show the saliency maps over . and , respectively. In each one, the first row corresponds to the Grad-CAM visualization, while the second row presents the ground-truth.
As for the computation of Grad-CAM for each image, only the most salient attention area is considered, i.e., the zone of the image highlighted in red. Subsequently, for each image, a bounding box is computed around that salient area, and the distance between the resulting delimitation and the corresponding ground-truth region is calculated, based on the respective centroids. Besides the displacement between the computed centroids (Dis), three other Grad-CAM-based elements were considered as key parameters: classification accuracy (Acc), IoU, and Grad-CAM size (GCS).
Regarding the analysis made for the , Figure 15 showcases the Grad-CAM outcomes for the top Xception models trained with the several considered approaches: FSCIS, FCDIS, HO, and the best classifier that resulted from KCVF10. Each image is accompanied by a short text denoting the respective key parameters formerly specified. Following a similar organization and structure, Figure 16 depicts the results in the context of the .
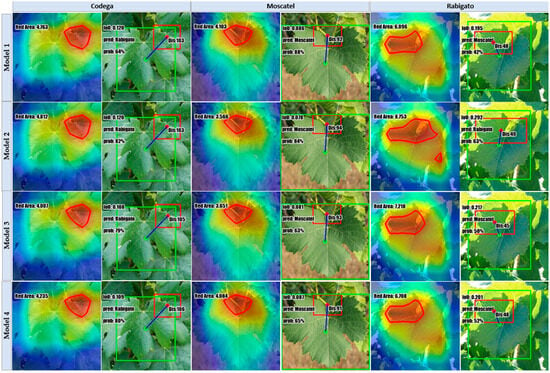
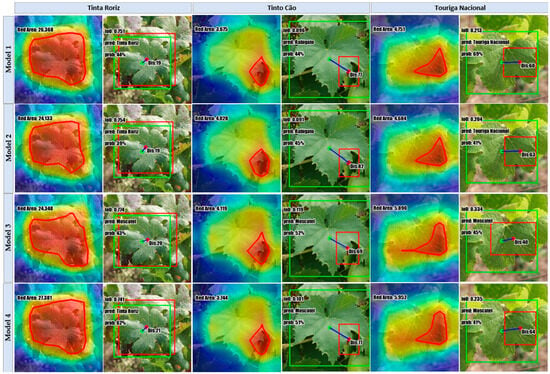
Figure 15.
Attention visualization for is performed using the top Xception/Nadam model trained with the documented splitting techniques. Model1, Model2, Model3, and Model4 correspond, respectively, to the models trained with the variants split using SCDIS, FSCIS, HO, and KFCV10. In the first column, the red rectangle represents the most prominent attention area determined through Grad-CAM, while the green rectangle corresponds to the hand-crafted ground-truth.
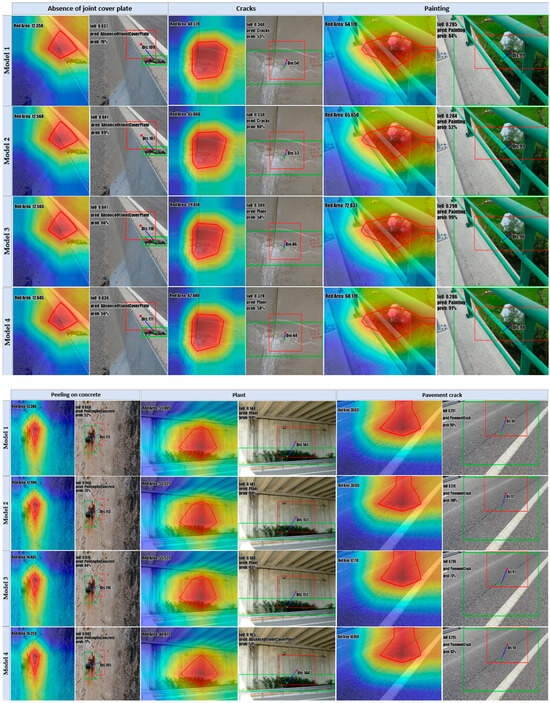
Figure 16.
Attention visualization for is performed using the top Xception/Nadam model trained with the documented splitting techniques. Model1, Model2, Model3, and Model4 correspond, respectively, to the models trained with the variants split using SCDIS, FSCIS, HO, and KFCV10. In the first column, the red rectangle represents the most prominent attention area determined through Grad-CAM, while the green rectangle corresponds to the hand-crafted ground-truth.
Instead of closely examining the parameters for each specific image, the focus was on calculating the mean values of key parameters for each class within both datasets, aiming to provide an overview of the models’ performances at a more generalized level across different classes. Table 7 and Table 8 indicate the numeric results associated with the mean values of key parameters corresponding to Xception/Nadam pairs.

Table 7.
Prediction results upon the for Xception Nadam.

Table 8.
Prediction results for the proposed dataset splits for the Xception model using Nadam optimizer upon . AJCP—absence of joint cover plate; PC—pavement crack; PoC—peeling on concrete.
Table 7 presents the outcomes obtained regarding the , wherein both SCDIS and FSCIS outperform the opponents. In particular, the SCDIS split method was the best in this series, yielding an accuracy of 38%, an µIoU = 0.19, a µGCS = 7220, and a µDis = 68.
Additionally, Table 8 presents the results for the , relying on the same metrics. Once again, the most effective models originated from both of the proposed dataset splitting methods. Notably, these models attained similar performances: µIoU = 0.18, µAcc = 75%, µGCS = 37,604, and µDis = 135 for FSCIS; and µIoU = 0.18, µAcc = 75%, µGCS = 37,538, and µDis = 134 for SCDIS.
On the other hand, the results show a spotlight pattern—greater IoU scores align with higher classification accuracies, particularly when the region of attention is closer to the ground-truth center. This pattern underscores the relationship between precise localization and the model’s effectiveness in correctly classifying objects. These observations across the tables emphasize the significance of spatial awareness in improving the overall accuracy of the classification process.
5. Discussion, Summary, and Conclusions
In this section, the main findings and contributions of this work are summarized. This research work hypothesizes feature-aware data splitting as a strategy to enhance the performance of classification models in a timelier manner, at the expense of traditional techniques, such as KFCV and HO. Therefore, datasets of two distinct contexts were considered for the sake of condition variability: one related to bridge defects and the other associated with grapevine leaves, for phenotyping distinction.
Regarding the proposed splitting approaches, the first one employs a feature-oriented clustering-based splitting technique, with a selection method based on the centroid distance of each cluster to the global centroid—FCDIS. The second approach revolves around sorting and picking images at the feature space level, based on their distance to the global centroid—FSCIS. The main goal is to compare both of these methods with conventional techniques, namely, HO and KFCV with 10 folds.
For training the classification models, the Xception architecture was utilized with a learning rate of 10−3, and optimizers including Nadam and SGD, and the maximum number of training epochs was set to 100. In most of the experiments, the proposed FCDIS and FSCIS methods outperformed the traditional approaches. Furthermore, the accuracy-loss plots illustrated a more stable training process with the proposed methods, characterized by an apparent reduction in abrupt fluctuations associated with these metrics across training sessions.
To assess the trained classifiers, external datasets were considered for a Grad-CAM-based evaluation, while IoU was used as another metric for performance comparison. The results pointed out that the models trained with the proposed methods had a consistently higher capacity in identifying the relevant areas of the images, highlighting them as more effective compared to the ones trained with traditional splitting techniques.
In comparison to the existing approaches, particularly those employing traditional dataset splitting techniques, such as HO, resampling, normal, repeated, nested, and leave-one-out KFCV, the proposed methods of this work—FCDIS and FSCIS—confirm and consolidate the importance of using strategic division for the attainment of more accurate models, with decreased computational burdens, while mitigating the need of multi-step procedures (e.g., KFCV), at least when relatively short volumes of classes and examples are involved.
It is noteworthy that a clustering-based method has been addressed in, at least, one of the aforementioned works found in the literature. However, a K-fold-based strategy was still applied to select data within clusters [37]. In contrast, the proposed FCDIS and FSCIS methods provide strong evidence that one-shot data organization is a possible avenue to attain models of top accuracy, as the experimental results demonstrate. Therefore, this study also intends to inspire and challenge the scientific community and DL practitioners to include strategic dataset splitting methods, either based on the proposed ones or supported in brand-new approaches, to save time and computational resources, while aiming to develop inference models that can operate near their full potential.
Notwithstanding, as the used datasets are relatively short, and the hardware and software setup are more oriented to DL prototyping, further tests are encouraged, involving wider data classes and examples, and resorting to high-performance computing. Moreover, the generalizability of the proposed splitting techniques beyond the addressed datasets and inference tasks requires deeper investigation through, namely, the inclusion of complementary key-factors—for example, considering uncertainty and context-sensitive false/true positives risk assessment—that contribute to explaining the models’ behavior and, therefore, broadly optimize the training processes.
Author Contributions
Conceptualization, T.A., S.S., E.P., R.M. and V.A.; methodology, T.A., L.G.M. and S.S.; software, S.S.; validation, T.A. and V.A.; formal analysis, T.A. and V.A.; investigation, S.S., T.A. and V.A.; resources, T.A. and L.G.M.; data curation, S.S. and T.A.; writing—original draft preparation, S.S.; writing—review and editing, T.A., E.P., R.M., L.G.M. and V.A.; visualization, S.S. and T.A.; supervision, T.A., L.G.M. and V.A.; project administration, R.M.; funding acquisition, E.P. and R.M. All authors have read and agreed to the published version of the manuscript.
Funding
Authors would like to acknowledge the Vine and Wine Portugal Project, co-financed by the RRP—Recovery and Resilience Plan and the European Next Generation EU Funds, within the scope of the Mobilizing Agendas for Reindustrialization, under the reference C644866286-00000011. Finally, this research activity was co-supported by national funds from the FCT-Portuguese Foundation for Science and Technology under the projects UIDB/04033/2020 and LA/P/0126/2020.
Data Availability Statement
The data supporting this work are not publicly available due to intellectual property concerns and legal restrictions associated with the nature of the projects from which the data originated.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shahrabadi, S.; Gonzalez, D.; Sousa, N.; Adao, T.; Peres, E.; Magalhaes, L. Benchmarking Deep Learning Models and Hyperparameters for Bridge Defects Classification. Procedia Comput. Sci. 2023, 219, 345–353. [Google Scholar] [CrossRef]
- Adão, T.; Pinho, T.M.; Ferreira, A.; Sousa, A.; Pádua, L.; Sousa, J.; Sousa, J.J.; Peres, E.; Morais, R. Digital Ampelographer: A CNN Based Preliminary Approach. In Proceedings of the EPIA Conference on Artificial Intelligence, Vila Real, Portugal, 3–6 September 2019; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics). Springer: Berlin/Heidelberg, Germany, 2019; Volume 11804 LNAI, pp. 258–271. [Google Scholar]
- Shahrabadi, S.; Carias, J.; Peres, E.; Magalhães, L.G.; Lopez, M.A.G.; Silva, L.B.; Adão, T. Image-Based Lung Analysis in the Context of Digital Pathology: A Brief Review. In Proceedings of the Hcist—International Conference on Health and Social Care Information Systems and Technologies (HCist), Porto, Portugal, 8–10 November 2023. [Google Scholar]
- Tran, T.-O.; Vo, T.H.; Le, N.Q.K. Omics-Based Deep Learning Approaches for Lung Cancer Decision-Making and Therapeutics Development. Brief. Funct. Genomics 2023, elad031. [Google Scholar] [CrossRef]
- Yuan, Q.; Chen, K.; Yu, Y.; Le, N.Q.K.; Chua, M.C.H. Prediction of Anticancer Peptides Based on an Ensemble Model of Deep Learning and Machine Learning Using Ordinal Positional Encoding. Brief. Bioinform. 2023, 24, bbac630. [Google Scholar] [CrossRef] [PubMed]
- Shahrabadi, S.; Rodrigues, J.; Margolis, I.; Evangelista, L.; Sousa, N.; Sousa, E.; Guevara Lopéz, M.A.; Magalhães, L.G.; Peres, E.; Adão, T. Digital Tools for Aircraft Maintenance: Prototyping Location-Aware AOI for Engine Assessment and Cable Routing Solutions. In Proceedings of the International Conference on Graphics and Interaction (ICGI), Tomar, Portugal, 2–3 November 2023. [Google Scholar]
- Oliveira, J.; Gomes, R.; Gonzalez, D.; Sousa, N.; Shahrabadi, S.; Guevara, M.; Ferreira, M.J.; Alves, P.; Peres, E.; Magalhães, L.; et al. Footwear Segmentation and Recommendation Supported by Deep Learning: An Exploratory Proposal. Procedia Comput. Sci. 2023, 219, 724–735. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Tredennick, A.T.; Hooker, G.; Ellner, S.P.; Adler, P.B. A Practical Guide to Selecting Models for Exploration, Inference, and Prediction in Ecology. Ecology 2021, 102, e03336. [Google Scholar] [CrossRef]
- Xu, C.; Coen-Pirani, P.; Jiang, X. Empirical Study of Overfitting in Deep Learning for Predicting Breast Cancer Metastasis. Cancers 2023, 15, 1969. [Google Scholar] [CrossRef]
- Mathur, J.; Baruah, B.; Tiwari, P. Prediction of Bio-Oil Yield during Pyrolysis of Lignocellulosic Biomass Using Machine Learning Algorithms. Can. J. Chem. Eng. 2023, 101, 2457–2471. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer International Publishing: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Nematzadeh, Z.; Ibrahim, R.; Selamat, A. Comparative Studies on Breast Cancer Classifications with K-Fold Cross Validations Using Machine Learning Techniques. In Proceedings of the 2015 10th Asian Control Conference (ASCC), Kota Kinabalu, Malaysia, 31 May–3 June 2015; pp. 1–6. [Google Scholar]
- Nakatsu, R.T. Validation of Machine Learning Ridge Regression Models Using Monte Carlo, Bootstrap, and Variations in Cross-Validation. J. Intell. Syst. 2023, 32, 20220224. [Google Scholar] [CrossRef]
- Pal, K.; Patel, B.V. Data Classification with K-Fold Cross Validation and Holdout Accuracy Estimation Methods with 5 Different Machine Learning Techniques. In Proceedings of the Proceedings of the 4th International Conference on Computing Methodologies and Communication, ICCMC 2020, Erode, India, 11–13 March 2020; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020; pp. 83–87. [Google Scholar]
- Haq, A.U.; Li, J.P.; Khan, J.; Memon, M.H.; Nazir, S.; Khan, G.A.; Ali, A. Intelligent Machine Learning Approach for Effective Recognition of Diabetes in E-Healthcare Using Clinical Data. Sensors 2020, 20, 2649. [Google Scholar] [CrossRef] [PubMed]
- Lakshmanan, V.; Robinson, S.; Munn, M. Machine Learning Design Patterns; O’Reilly Media, Inc.: Newton. MA, USA, 2020. [Google Scholar]
- Reitermanová, Z. Data Splitting. WDS’10 Proceedings of Contributed Papers(Part I); MatfyzPress: Prague, Czech Republic, 2010; pp. 31–36. [Google Scholar]
- Fox, M.; Schoeffmann, K. The Impact of Dataset Splits on Classification Performance in Medical Videos. In Proceedings of the ICMR 2022—2022 International Conference on Multimedia Retrieval, Newark, NJ, USA, 27–30 June 2022; Association for Computing Machinery, Inc.: Times Square, NYC, USA, 2022; pp. 6–10. [Google Scholar]
- Leibetseder, A.; Petscharnig, S.; Primus, M.; Kietz, S.; Münzer, B.; Schoeffmann, K.; Keckstein, J. Lapgyn4: A Dataset for 4 Automatic Content Analysis Problems in the Domain of Laparoscopic Gynecology. In Proceedings of the 9th ACM Multimedia Systems Conference, Amsterdam, The Netherlands, 12–15 June 2018; pp. 357–362. [Google Scholar]
- Shin, H.; Oh, S. Feature-Weighted Sampling for Proper Evaluation of Classification Models. Appl. Sci. 2021, 11, 2039. [Google Scholar] [CrossRef]
- Kang, D.; Oh, S. Balanced Training/Test Set Sampling for Proper Evaluation of Classification Models. Intell. Data Anal. 2020, 24, 5–18. [Google Scholar] [CrossRef]
- Eliane Birba, D. A Comparative Study of Data Splitting Algorithms for Machine Learning Model Selection. Master’s Thesis, KTH Royal Institute of Technology, Stocksund, Sweden, 2020. [Google Scholar]
- Farias, F.; Ludermir, T.; Bastos-Filho, C. Similarity Based Stratified Splitting: An Approach to Train Better Classifiers. arXiv 2020, arXiv:2010.06099. [Google Scholar]
- Nurhopipah, A.; Hasanah, U. Dataset Splitting Techniques Comparison For Face Classification on CCTV Images. Indonesian J. Comput. Cybern. Syst. 2020, 14, 341. [Google Scholar] [CrossRef]
- Lakshmi, M.J.; Nagaraja Rao, S. Effect Of K Fold Cross Validation on Mri Brain Images Using Support Vector Machine Algorithm. Int. J. Recent Technol. Eng. 2019, 7, 2277–3878. [Google Scholar]
- Sharma, R.C.; Hara, K.; Hirayama, H. A Machine Learning and Cross-Validation Approach for the Discrimination of Vegetation Physiognomic Types Using Satellite Based Multispectral and Multitemporal Data. Scientifica 2017, 2017, 9806479. [Google Scholar] [CrossRef] [PubMed]
- Varma, S.; Simon, R. Bias in Error Estimation When Using Cross-Validation for Model Selection. BMC Bioinform. 2006, 7, 91. [Google Scholar] [CrossRef] [PubMed]
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine Learning Algorithm Validation with a Limited Sample Size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef]
- Kahloot, K.M.; Ekler, P. Algorithmic Splitting: A Method for Dataset Preparation. IEEE Access 2021, 9, 125229–125237. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Astels, S. Hdbscan: Hierarchical Density Based Clustering. J. Open Source Softw. 2017, 2, 205. [Google Scholar] [CrossRef]
- He, X.; Cai, D.; Shao, Y.; Bao, H.; Han, J. Laplacian Regularized Gaussian Mixture Model for Data Clustering. IEEE Trans. Knowl. Data Eng. 2011, 23, 1406–1418. [Google Scholar] [CrossRef]
- Amidan, B.G.; Ferryman, T.A.; Cooley, S.K. Data Outlier Detection Using the Chebyshev Theorem. In Proceedings of the 2005 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2005; pp. 3814–3819. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Doan, Q.H.; Mai, S.H.; Do, Q.T.; Thai, D.K. A Cluster-Based Data Splitting Method for Small Sample and Class Imbalance Problems in Impact Damage Classification [Formula Presented]. Appl. Soft Comput. 2022, 120, 108628. [Google Scholar] [CrossRef]
- Christias, P.; Mocanu, M. A Machine Learning Framework for Olive Farms Profit Prediction. Water 2021, 13, 3461. [Google Scholar] [CrossRef]
- Huang, S.; Liu, W.; Qi, F.; Yang, K. Development and Validation of a Deep Learning Algorithm for the Recognition of Plant Disease. In Proceedings of the 21st IEEE International Conference on High Performance Computing and Communications, 17th IEEE International Conference on Smart City and 5th IEEE International Conference on Data Science and Systems, HPCC/SmartCity/DSS 2019, Zhangjiajie, China, 10–12 August 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 1951–1957. [Google Scholar]
- Durai, S.K.S.; Shamili, M.D. Smart Farming Using Machine Learning and Deep Learning Techniques. Decis. Anal. J. 2022, 3, 100041. [Google Scholar] [CrossRef]
- Alibabaei, K.; Gaspar, P.D.; Lima, T.M.; Campos, R.M.; Girão, I.; Monteiro, J.; Lopes, C.M. A Review of the Challenges of Using Deep Learning Algorithms to Support Decision-Making in Agricultural Activities. Remote Sens. 2022, 14, 638. [Google Scholar] [CrossRef]
- Rao, M.S.; Singh, A.; Reddy, N.V.S.; Acharya, D.U. Crop Prediction Using Machine Learning. In Proceedings of the 2020 Third International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 20–22 August 2020; IOP Publishing Ltd.: Bristol, UK, 2022; Volume 2161. [Google Scholar]
- Suescún, M.F.R. Machine Learning Approaches for Tomato Crop Yield Prediction in Precision Agriculture. Master’s Thesis, Universidade Nova de Lisboa, Lisbon, Portugal, August 2020. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Nguyen, Q.H.; Ly, H.B.; Ho, L.S.; Al-Ansari, N.; Van Le, H.; Tran, V.Q.; Prakash, I.; Pham, B.T. Influence of Data Splitting on Performance of Machine Learning Models in Prediction of Shear Strength of Soil. Math. Probl. Eng. 2021, 2021, 4832864. [Google Scholar] [CrossRef]
- Zhang, Y.; Bakasa, W.; Viriri, S. VGG16 Feature Extractor with Extreme Gradient Boost Classifier for Pancreas Cancer Prediction. J. Imaging 2023, 9, 138. [Google Scholar] [CrossRef]
- Lachmann, M.; Rippen, E.; Rueckert, D.; Schuster, T.; Xhepa, E.; von Scheidt, M.; Pellegrini, C.; Trenkwalder, T.; Rheude, T.; Stundl, A.; et al. Harnessing Feature Extraction Capacities from a Pre-Trained Convolutional Neural Network (VGG-16) for the Unsupervised Distinction of Aortic Outflow Velocity Profiles in Patients with Severe Aortic Stenosis. Eur. Heart J. Dig. Health 2022, 3, 153–168. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.; Guleria, K.; Tiwari, S.; Kumar, S. A Deep Learning Based Convolutional Neural Network Model with VGG16 Feature Extractor for the Detection of Alzheimer Disease Using MRI Scans. Meas. Sensors 2022, 24, 100506. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2010; pp. 248–255. [Google Scholar]
- Lan, T.; Erdogmus, D.; Black, L.; Van Santen, J. A Comparison of Different Dimensionality Reduction and Feature Selection Methods for Single Trial ERP Detection. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010. [Google Scholar] [CrossRef]
- Velliangiri, S.; Alagumuthukrishnan, S.; Thankumar Joseph, S.I. A Review of Dimensionality Reduction Techniques for Efficient Computation. In Proceedings of the Procedia Computer Science, Surabaya, Indonesia, 23–24 July 2019; Elsevier B.V.: Amsterdam, The Netherlands, 2019; Volume 165, pp. 104–111. [Google Scholar]
- Salem, N.; Hussein, S. Data Dimensional Reduction and Principal Components Analysis. In Proceedings of the Procedia Computer Science, Surabaya, Indonesia, 23–24 July 2019; Elsevier B.V.: Amsterdam, The Netherlands, 2019; Volume 163, pp. 292–299. [Google Scholar]
- Tzutalin LabelImg: Image Annotation Tool. Available online: https://github.com/tzutalin/labelImg (accessed on 20 November 2023).
- Syakur, M.A.; Khotimah, B.K.; Rochman, E.M.S.; Satoto, B.D. Integration K-Means Clustering Method and Elbow Method for Identification of the Best Customer Profile Cluster. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Surabaya, Indonesia, 9 November 2017; Institute of Physics Publishing, Ltd.: Bristol, UK, 2018; Volume 336. [Google Scholar]
- Marutho, D.; Handaka, S.H.; Wijaya, E. The Determination of Cluster Number at K-Mean Using Elbow Method and Purity Evaluation on Headline News. In Proceedings of the 2018 International Seminar on Application for Technology of Information and Communication, Semarang, Indonesia, 21–22 September 2018; pp. 533–538. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).