Learning State-Specific Action Masks for Reinforcement Learning

Abstract

Efficient yet sufficient exploration remains a critical challenge in reinforcement learning (RL), especially for Markov Decision Processes (MDPs) with vast action spaces. Previous approaches have commonly involved projecting the original action space into a latent space or employing environmental action masks to reduce the action possibilities. Nevertheless, these methods often lack interpretability or rely on expert knowledge. In this study, we introduce a novel method for automatically reducing the action space in environments with discrete action spaces while preserving interpretability. The proposed approach learns state-specific masks with a dual purpose: (1) eliminating actions with minimal influence on the MDP and (2) aggregating actions with identical behavioral consequences within the MDP. Specifically, we introduce a novel concept called Bisimulation Metrics on Actions by States (BMAS) to quantify the behavioral consequences of actions within the MDP and design a dedicated mask model to ensure their binary nature. Crucially, we present a practical learning procedure for training the mask model, leveraging transition data collected by any RL policy. Our method is designed to be plug-and-play and adaptable to all RL policies, and to validate its effectiveness, an integration into two prominent RL algorithms, DQN and PPO, is performed. Experimental results obtained from Maze, Atari, and $\mu$RTS2 reveal a substantial acceleration in the RL learning process and noteworthy performance improvements facilitated by the introduced approach.

1. Introduction

Reinforcement Learning (RL) is a powerful method for solving long-term decision-making tasks, often performing well in virtual environments such as video games [1,2]. However, applying RL training for strategies in the real world has proven challenging. On tasks such as scheduling [3], power system decision and control problems [4], and recommendation [5], training an RL policy is inefficient and can take days, if not weeks. One of the main reasons is that most real-world problems involve many possible actions, and RL’s performance is highly dependent on how efficiently it explores these possibilities. For instance, in the crude oil chain scheduling problem, there are over 2500 actions daily, making RL policy implementation difficult [6]. Hence, action space reduction is crucial for RL on tasks with extensive choices.

Traditionally, space representation has been a commonly employed technique to reduce dimensionality. While numerous approaches have been developed to handle high-dimensional state spaces through state representation [7,8,9,10], a distinct line of research has concentrated on action space reduction. Typically, these methodologies involve training a policy within a lower-dimensional latent action space and subsequently projecting the actions back into the original action space [11,12,13,14]. However, utilizing a latent action space in RL presents two notable challenges. First, the latent space often lacks interpretability. Many traditional control methodologies, such as PID control [15] and Model Predictive Control based on Linear Programming [16], rely on explicit action values, rendering the use of a latent action space ineffective in directly providing meaningful instructions. Furthermore, maintaining transparency in the output of a policy is important for ensuring safety and accuracy. Second, action representations become closely entwined with the policy itself, resulting in an inseparable connection between the action representation and the policy learning process, hindering the independent use of the action representation network.

On the contrary, we observe that action masking, also known as removing actions, has demonstrated its efficacy in RL training, as indicated by previous studies [17,18]. To illustrate, in games such as Minecraft [19], actions such as "sneak" are often deemed non-critical for gameplay and are, thus, excluded. By intuitively constraining the action space, action masks enhance exploration efficiency and expedite the RL learning process by reducing the time the agent wastes exploring those unnecessary actions. They not only provide a robust means of interpretability but also offer potential standalone utility, such as assistance in crafting rule-based strategies and integration with state representation algorithms. Nevertheless, prior works have predominantly relied on expert knowledge and environmental engineering to design these masks. Consequently, there is a pressing need for automatic learning algorithms that can generate action masks.

Inspired by this, we aim to develop a method to learn state-specific action masks automatically. The masks are expected to endow two properties: (1) they filter out useless actions that do not affect the MDP and (2) actions with identical behavioral consequences in the MDP are filtered to one action by them. To ensure low computational complexity in generating action masks while maintaining their robustness, we propose an action mask model tailored for RL tasks. Prior work on mask learning has been predominantly within the realm of computer vision [20,21], often employing Multi-Layer Perceptron (MLP) layers with clipping to the [0, 1] range or Sigmoid activations. However, in the context of RL, the action mask must be strictly binary along each dimension; otherwise, the agent still should explore all actions with positive probabilities in the distribution. To address this, we introduce a categorical mask model and employ supervised learning to update the probabilities of 0 and 1.

In addition, we propose a novel metric known as Bisimulation Metrics on Actions by States (BMAS), which leverages the concept of bisimulation [22] to gauge the behavioral dissimilarity between actions. Our principal contribution lies in the practical learning procedure for updating the mask model, comprising two alternative stages. In the initial stage, we acquire transition and reward models to forecast the consequences of all actions. Subsequently, we refine the mask model with supervised learning while the mask labels are generated through aggregating states and rewards. We also introduce an auxiliary feature vector for simultaneous aggregation, ensuring that the labels inherit both properties. When training the mask model, transition data can be collected by any policy, indicating that the mask model is separated from the learning procedure of an RL policy. Therefore, our framework can be seamlessly integrated into various RL algorithms. For illustration, we apply it to two representative algorithms, namely Deep Q-Network (DQN) and Proximal Policy Optimization (PPO). We conduct extensive experiments in environments with discrete action spaces, including Maze, Atari, and $\mu$RTS2.

To the best of our knowledge, this work represents the pioneering effort in the automatic learning of action masks for RL, and the key contributions are summarized as:

• Bisimulation Metrics on Actions by States (BMAS): The paper introduces a novel metric, BMAS, based on the concept of bisimulation, which quantifies the behavioral differences between actions by states.
• Automatic Action Masking: The paper introduces a method for automated acquisition of state-specific action masks in RL for environments with discrete action spaces, alleviating the need for expert knowledge or manual design. This contributes to making RL more applicable in real-world scenarios by accelerating exploration efficiency while preserving strong interpretability.
• Experimental Validation: The paper demonstrates the effectiveness of the proposed approach through comprehensive experiments conducted in environments with discrete spaces, including Maze, Atari, and $\mu$RTS2. The results showcase compelling performance, complemented by visualizations that underscore the interpretability of the proposed method.

2. Related Work

In this section, we provide an overview of relevant research that forms the foundation for our work. Specifically, we discuss three key areas in the literature related to action space manipulation in RL.

2.1. Action Space Factorization

A common strategy to enhance the efficiency of RL involves managing the action space by decomposing it into subspaces and solving the problem using multi-agents. Inspired by Factored Action space Representations (FAR), proposed by Sahil et al. [23], existing action space decomposition methods can be theoretically analyzed in two forms. One approach is to select subactions simultaneously and independently, while the other involves selecting them in order [24,25]. In either case, automatically decomposing the origin action space into smaller components is important and challenging. Wang et al. [26] investigated the decomposition of action spaces by clustering them based on their effects on the environment and other agents. Another approach, proposed by Wang et al. [27], automatically identifies roles in an RL problem. It encodes roles through stochastic variables and then associates them with responsibilities using regularizers. Zeng et al. [28] proposed to discover roles by clustering the embedded action space, using three phases called structuralization, sparsification, and optimization. Furthermore, Mahajan et al. [29,30] introduced a tensorized formulation for accurate representations of the action-value function, addressing the challenge of exponential growth in the action space in multi-agent RL scenarios. While each RL policy in the multi-agent system trains more rapidly with a diminished action space, it is important to note that there is no actual reduction in the size of the problem’s action space.

2.2. Action Space Reduction

Diverse strategies have emerged in the quest to streamline action spaces, involving shifts between discrete and continuous representations. Dulac-Arnold et al. [31] seamlessly integrated extensive discrete choices into a continuous space by leveraging prior information. They discern approximate discrete decisions from prototype actions within the continuous action space, employing the k-Nearest Neighbors algorithm (k-NN). Tang et al. [32] affirmed the effectiveness of discretization in enhancing the performance of on-policy RL algorithms for continuous control. They showed that organizing discretized actions into a distribution improves overall performance. In contrast to these approaches, our work distinctively focuses on directly reducing the dimensions of discrete action spaces. An alternative avenue explores representation learning to construct a more compact latent action space. Chandak et al. [11] proposed decomposing the action space into a low-dimensional latent space, transforming representations into actionable outcomes. This involves training the action encoder model, action decoder model, and policy model alternately, estimating actions $a_t$ given states $s_t$ and $s_{t+1}$. Zhou et al. [13] and Allshire et al. [12] employed variational encoder–decoder models to project original actions into a disentangled latent action space in manipulation environments, enhancing exploration efficiency. While these methods, as the mainstream in action space reduction, exhibit good performance, they sacrifice interpretability by projecting actions into a latent space. Some works employ hierarchical learning to select a role at the upper level and decide subspace actions belonging to the role at the lower level. OpenAI Five [24], for instance, sequentially chooses primary actions and parameter actions, where the parameters include unit selection from 189 visible units in the observation. Although these methods to some extent reduce the action space by dimensional selection, they rely on predefined roles based on expert knowledge, whereas our approach learns these roles automatically. An approach akin to our objectives is presented by Wang et al. [33], who eliminated redundant actions directly and automatically by selecting key particles in the action space using a Quadratic Programming Optimization. However, their method is task-specific, tailored solely for deformable object manipulation tasks in 1D and 2D spaces. Our work stands out in its emphasis on dimensionality reduction within discrete action spaces in all tasks while preserving interpretability.

2.3. Action Mask

The utilization of action masks has emerged as a potent strategy for refining action spaces and expediting RL processes. A comprehensive investigation by Kanervisto et al. [18] explored diverse modifications to the action space in RL within video game environments. These modifications included actions such as removal, discretization of continuous actions, and conversion of multi-discrete actions to discrete representations. Their experiments, particularly in the context of the CollectMineralsAndGas mini-game in $\mu$RTS2, demonstrated the significant performance enhancement achieved through action masking. In a related vein, Huang et al. [17] systematically analyzed the impact of action masks in a real-time strategy (RTS) game. Their study illuminated the crucial role of action masks, especially as the number of invalid actions increased. The authors not only examined the working principle of action masking through a state-dependent differentiable function, but also highlighted its scalability with the expansion of the action space compared to adding a reward penalty of exploring invalid actions, substantiated by experiments. It is noteworthy that, in all action mask implementations, the masks are typically crafted based on expert knowledge, often provided by the environment.

3. Background

3.1. MDP Problem

We consider a Markov Decision Process (MDP) with finite discrete action space, represented by the tuple $\mathcal{M}=(\mathcal{S},\mathcal{A},p,r,p_0,\gamma ,T)$. Here, $\mathcal{S}$ is the state space, $\mathcal{A}$ is the action space, p: $\mathcal{S}\times \mathcal{A}\times \mathcal{S}\mapsto \mathbb{R}$ denotes the transition probability, r: $\mathcal{S}\times \mathcal{A}\mapsto \mathbb{R}$ denotes the reward function, $p_0$: $\mathcal{S}\mapsto \mathbb{R}$ denotes the probability distribution of the initial state $s_0$, $\gamma \in [0,1)$ is the discounted factor, and T is the episode horizon. In our work, the action space is restricted to be finite and discrete, so we define the action space size as $\left|\mathcal{A}\right|$. At each timestep t, the agent chooses an action $a_t$ according to its policy $\pi (·|s_t)$, which updates the environment state $s_{t+1}\sim p(·|s_t,a_t)$ and yields a reward $r_t\sim r(·|s_t,a_t)$. The objective of the agent is to maximize its expected accumulated discounted reward, as expressed by the following Equation (1):

$$J\left(\theta \right)=\mathbb{E}\left[\sum _{t=1}^T{\gamma }^{t}r(s_t,a_t)\right]$$

(1)

3.2. Bisimulation

Bisimulation describes the behavioral equivalency of the state space. If $s_i$ and $s_j$ cause the same probability of the accumulated reward for any actions, then $s_i$ and $s_j$ are bisimilar states. A recursive version of this concept is that bisimilar states get the same reward at this timestep and the same transition distribution to the next bisimilar states.

Definition 1

(Bisimulation Relations [34]). The equivalence relation B on the state space of task $\mathcal{M}$ is a bisimulation relation if, for $s_i\in \mathcal{S}$ and $s_j\in \mathcal{S}$ and $s_i=s_j$ under B, the following conditions hold:

$$\begin{array}{cc}\hfill r(s_i,a)& =r(s_j,a)a\in \mathcal{A}\hfill \\ \hfill p\left(S_B\right|s_i,a)& =p\left(S_B\right|s_j,a)a\in \mathcal{A},S_B\in {\mathcal{S}}_B\hfill \end{array}$$

(2)

where $S_B$ is a group of bisimilar states, ${\mathcal{S}}_B$ is the partition of states under B, and $p\left(S_B\right|s,a)={\sum }_{s^{\prime }\in S_B}p\left(s^{\prime }\right|s,a)$.

4. Approach

In this paper, our objective is to autonomously acquire a comprehensive and practical action mask for an RL task characterized by a discrete action space. We define an action mask, represented by $I\in \mathcal{I}$, as a binary vector of the same size as $\mathcal{A}$. The quantity of ones in the mask I is specified as $\left|I\right|$, and $mas{k}_{\varphi }\left(I_t\right|s_t)$ denotes a mask model parameterized by $\varphi$, where $I_t\sim mas{k}_{\varphi }\left(I_t\right|s_t)$. Given that the action space $\mathcal{A}$ is discrete, each dimension’s meaning in the action space is fixed, and we designate the action with index i in the action space as $a^i$. Similarly, the individual mask with index i in mask I is denoted as $I^i$. We employ ${\pi }_{\theta }\left(a_t\right|s_t)$ to represent the original policy and ${\tilde{\pi }}_{\theta ,\varphi }\left({\tilde{a}}_t\right|s_t)$ to represent the composite policy with masks. Here, ${\tilde{a}}_t\in {\tilde{A}}_t$, where ${\tilde{A}}_t$ signifies the masked action space at timestep t. Typically, the action mask model operates on a per-state basis. If a mask is identified as global based on expert knowledge, a straightforward modification to the mask model as $I_{\varphi }$ is adequate (as illustrated in an experimental example in Section 5.2.1).

The objective of the action mask is to reduce the action space, thereby preventing the agent from exploring unnecessary actions. We aim to learn action masks with two key properties: (1) filtering out invalid actions that do not influence the task and (2) filtering out actions that are redundant to the task, meaning other actions can replace them. This problem poses several challenges, including how to define a proper metric to measure the ’validity’ of actions, how to construct the mask model to output a binary vector, and how to design a practical algorithm to learn the mask model. We introduce our work by answering these three fundamental questions.

4.1. Bisimulation Metric on Actions

Bisimulation, as defined by Givan [34], is a widely used concept applied to the state space, signifying behavioral equivalence among states. To establish a reasonable metric for the action mask, we introduce a concept akin to bisimulation, aiming to indicate behavioral equivalence among actions.

Definition 2

(Bisimulation Relations on Actions (BRA)). In task $\mathcal{M}$ with discrete action space $\mathcal{A}$, for $a^i\in \mathcal{A}$ and $a^j\in \mathcal{A}$, define $a^i$ and $a^j$ is equivalent under Bisimulation Relation B if:

$$r(s,a^i)=r(s,a^j)\forall s\in \mathcal{S}$$

(3)

$$p\left(s^{\prime }\right|s,a^i)=p\left(s^{\prime }\right|s,a^j)\forall s\in \mathcal{S}$$

(4)

and we define ${\mathcal{A}}_B$ as a partition of action space $\mathcal{A}$ that $a^i=a^j$ under bisimulation relation B are separated in the same set, and $A_B\in {\mathcal{A}}_B$ is an action group.

In task $\mathcal{M}$, it is obvious that if $a_i$ and $a_j$ belong to the same bisimilar action set $A_B$, then $a_i$ and $a_j$ have the same behavioral consequences. In other words, removing $a_j$ does not affect the MDP.

While a global definition of behavioral equivalence on actions is reasonable, in most tasks, each action group $A_B$ typically contains only one element, implying that not all actions can be removed. For example, in a Maze task with four actions stands for four directions, no two actions yield the same behavioral consequences across all states. However, when the agent moves to a corner, there may be more than one action that leads to staying in the same place and receiving no reward, which causes identical behavioral consequences. Therefore, we adopt a variant of BRA that defines the equivalence relation of actions based on states.

Definition 3

(Bisimulation Relations on Actions by States (BRAS)). In task $\mathcal{M}$ with discrete action space $\mathcal{A}$, given state s, for $a^i\in \mathcal{A}$ and $a^j\in \mathcal{A}$, define $a^i$ and $a^j$ is equivalent under Bisimulation Relation B if:

$$\begin{array}{cc}\hfill r(s,a^i)& =r(s,a^j)\hfill \\ \hfill p\left(s^{\prime }\right|s,a^i)& =p\left(s^{\prime }\right|s,a^j)\hfill \end{array}$$

(5)

and we define ${\mathcal{A}}_{B_s}$ as the partition of action space $\mathcal{A}$ that $a^i=a^j$ under bisimulation relation $B_s$ are separated in the same set, and $A_{B_s}\in {\mathcal{A}}_{B_s}$ is an action group.

We now present our proposition, asserting that equivalent actions under BRAS yield the same behavioral consequence in the MDP, signifying that actions within the set are interchangeable.

Proposition 1.

In task $\mathcal{M}$ with discrete action space $\mathcal{A}$, given state s, if $a^i,a^j\in A_{B_s}$, then the optimal policy of task $\mathcal{M}=(\mathcal{S},\mathcal{A},p,r,p_0,\gamma ,T)$ and task ${\mathcal{M}}^{\prime }=(\mathcal{S},{\mathcal{A}}^{\prime },p,r,p_0,\gamma ,T)$ are same, where:

$${\mathcal{A}}^{\prime }=\mathcal{A}\setminus \left(a^j\right|s)$$

(6)

The proof of Proposition 1 can be found in Appendix A.

Filtering actions strictly according to BRAS is impractical, since BRAS is sensitive to the next state and the reward. Therefore, we propose to measure the distance among actions to soften the BRAS constraints based on the smooth transition assumption that in task $\mathcal{M}$, if $s_i\approx s_j$, then $\forall a\in \mathcal{A}$, $p(·|s_i,a)\approx p(·|s_j,a)$.

Definition 4 (Bisimulation Distance on Actions by States).

Given discrete action $a^i$ and $a^j$ and task $\mathcal{M}$, define bisimulation distance $d(a^i,a^j)$ as the "behavioral distance" between $a^i$ and $a^j$ in task $\mathcal{M}$:

$$d(a^i,a^j|s)=|r(s,a^i)-r(s,a^j)|+|p(·|s,a^i)-p(·|s,a^j)|$$

(7)

When $d(a^i,a^j|s)=0$, it is evident that $a^i$ and $a^j$ belong to the same bisimulation group $A_{B_s}$. Additionally, when $d(a^i,a^j|s)$ is close to 0, it indicates that $a^i$ and $a^j$ result in approximately the same behavioral consequence on state s. Therefore, we define ${\widehat{A}}_{B_s}$ as the approximate action group, and $a^i,a_j\in {\widehat{A}}_{B_s}$ if $d(a^i,a^j)<ϵ$, where $ϵ$ is a small value and ${\widehat{\mathcal{A}}}_{B_s}$ represents the action partition under d.

4.2. A Perfect Mask Model

The main contribution of this work is to learn a mask model $mas{k}_{\varphi }\left(I_t\right|s_t)$ with two objectives.

Firstly, the action masks $I_t\sim mas{k}_{\varphi }\left(I_t\right|s_t)$ should filter out all invalid actions that do not influence state s, e.g., the “up” action when an agent in Maze goes to the top-right corner. Formally, given state s, an invalid action $a^i$ is the action that leads to $p\left(s\right|s,a^i)=1$. Therefore, the perfect mask $I_t\sim mas{k}_{\varphi }\left(I_t\right|s_t)$ should satisfy:

$$I_t^i=0ifp\left(s_t\right|s_t,a^i)=1$$

(8)

where $ϵ$ is a small value.

Secondly, the action masks should aggregate actions with the same behavioral consequences and only reserve actions distinct from each other. We use soft BRAS to illustrate this relation. Formally, given state s, the mask model $mas{k}_{\varphi }\left(I_t\right|s_t)$ should satisfy:

$$\begin{array}{cc}\hfill & \sum _{i\in \mathcal{I}}mas{k}_{\varphi }\left(I_t^i\right|s_t)=1\wedge \prod _{i\in \mathcal{I}}mas{k}_{\varphi }\left(I_t^i\right|s_t)=0,\hfill \\ \hfill & \mathcal{I}=index\left(A_{B_s}\right),\forall A_{B_s}\in {\widehat{\mathcal{A}}}_{B_s}\hfill \end{array}$$

(9)

where $index(·)$ is the index of all actions in the action space.

Different from the mask model commonly used in many computer vision (CV) works [20,21], the mask I on action space for RL serves a more intricate role than a simple attention layer. In prior research, Huang et al. [17] delved into the impact of action masks on the learning process through extensive experiments on $\mu$RTS2. Their findings revealed that even if an RL agent samples actions within a masked action space but updates the policy using the original gradients, it still experiences accelerated exploration. This suggests that the primary role of an action mask is to prevent the agent from sampling invalid actions, necessitating a binary mask.

Therefore, to ensure the mask model outputs a binary vector, we design the mask model as a categorical model, as illustrated in Figure 1.

The mask model outputs real numbers of $2\left|\mathcal{A}\right|$ dimensions indicating logits of the masks and $I_t$ is sampled from them. This design allows the model to achieve an exact binary mask and a differentiable output simultaneously.

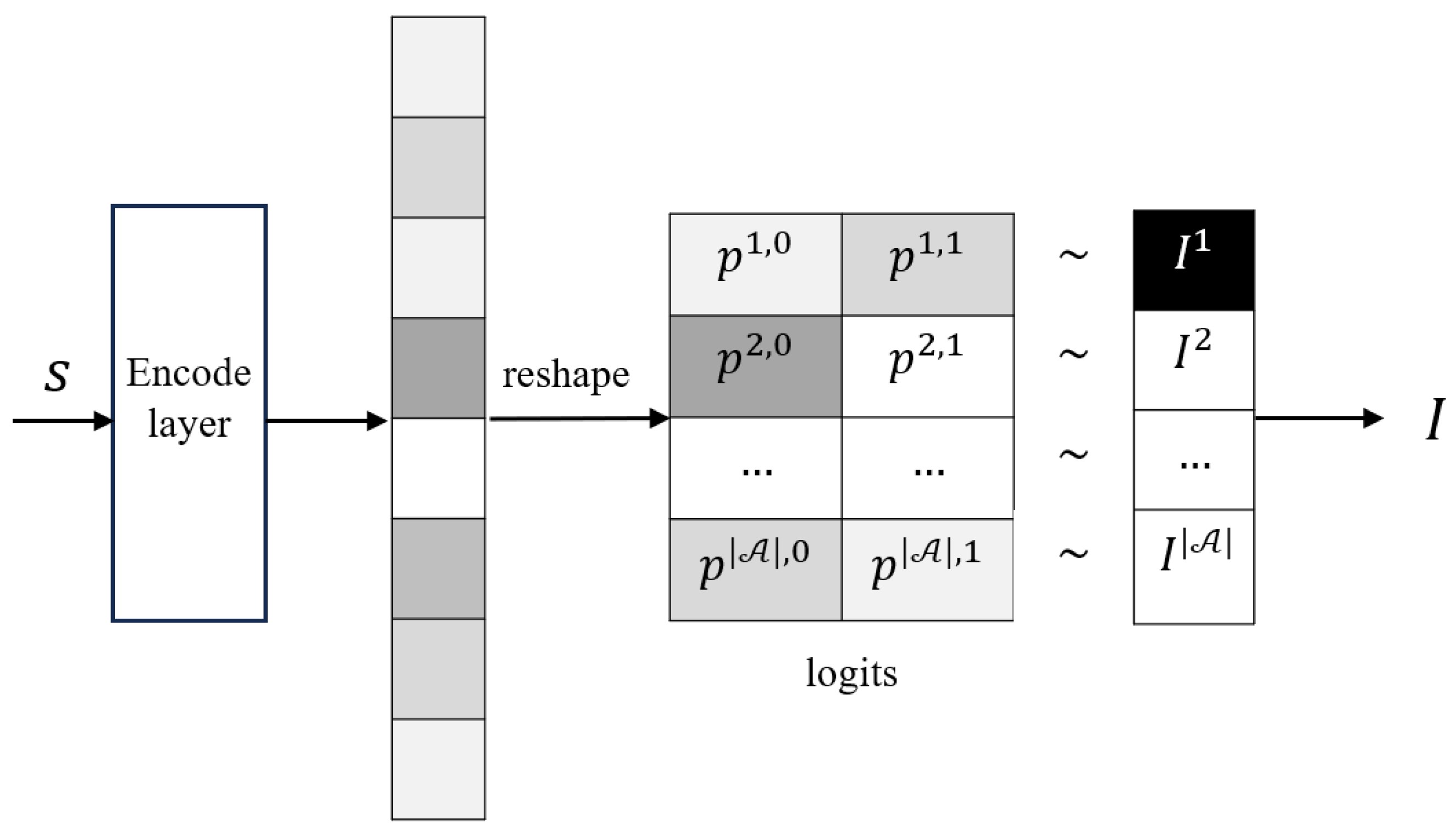
4.3. Learning the Action Mask Supervised

We train the action mask with supervised learning, and the labels are generated through the DBSCAN clustering algorithm [35], as outlined in Algorithm 1. The objective of the mask model is to minimize the Hamming Distance between $I_t$ and label $L_t$, and the loss function of the mask model is:

$${\mathcal{L}}_{(}\varphi )=logmas{k}_{\varphi }\left(I_t\right|s_t)d_{Hamming}(mas{k}_{\varphi }\left(I_t\right|s_t),L_t)$$

(10)

To achieve (9), a natural method is to aggregate all vectors $[s_{t+1},r_t]$, grouping actions with small $d(a^i,a^j)$ as defined in (7) into ${\widehat{A}}_{B_s}$. Additionally, we construct $[s_t,0]$ as an extra vector lead by the invalid action $a^{\left|\mathcal{A}\right|+1}$ and aggregate it with other $[s_{t+1},r_t]$ vectors. Then, those actions that lead to $[s_{t+1},r_t]$ in the same group with $[s_t,0]$ are also invalid actions whose masks should be set to 0.

Algorithm 1 Training an action mask model

Input: batch data B, clustering parameter $ϵ$ and $minPts=1$    for  $s_t\in B$  do       for $a^i\in \mathcal{A}$ do          Get the next states: $s_{t+1}^i\sim \widehat{p}(s_t,a^i)$          Get the reward: $r_t^i\sim \widehat{r}(s_t,a^i)$       end for       Build the behavioral vectors: $V_t=\left[{[s_{t+1}^i,r_{t+1}^i]}_{i=0,\dots ,\left|\mathcal{A}\right|}\right]$       Add the extra feature: $V_t=V_t\bigcup [s_t,0]$       Aggregate $V_t$ using DBSCAN with parameter $ϵ$ and $minPts$: $C_t=[c_t^0,\dots ,c_t^{\left|\mathcal{A}\right|+1}]$       Build mask label $L_t$ to achieve (8) and (9)       Update the mask model with Hamming Distance error: ${\mathcal{L}}_{(}\varphi )$ Equation (10)    end for

At each step, we update the mask model on a sampled batch of states. For each state $s_t$ in the batch, we estimate $s_{t+1}^i$ and $r_t^i$ for each action $a^i\in \mathcal{A}$ and concatenate them as the behavioral vectors $v^0,\dots ,v^{\left|\mathcal{A}\right|}$ of action $a^i$. Then, we construct $v^{\left|\mathcal{A}\right|+1}=[s_t,0]$ as an extra vector indicating the unchanged situation, and aggregate $[v^0,\dots ,v^{\left|\mathcal{A}\right|},v^{\left|\mathcal{A}\right|+1}]$ as clusters C, where $c^i$ is the cluster index number for feature $v^i$. In each cluster, we appoint the action with the lowest index as a kernel whose mask label is 1 and others as alternatives whose mask labels are 0. In particular, all actions cause $[s_{t+1}^i,r_t^i]$ clustered with the extra vector $[s_t,0]$ are seen as invalid actions, and thus, the action masks of them are all 0.

The mask model training is plugged into the vanilla RL training procedure to get a training loop, shown in Algorithm 2. The RL policy ${\pi }_{\theta }\left(a_t\right|s_t)$, the transition model $\widehat{p}\left(s_{t+1}\right|s_t,a_t)$, the reward model $\widehat{r}\left(r_{t+1}\right|s_t,a_t)$ and the mask model $mas{k}_{\varphi }\left(I_t\right|s_t)$ are trained in turn. The blue lines are individualized for the RL algorithms and we combine our method with two popular RL algorithms, DQN and PPO, as examples (see implementation details in Appendix B). When employing the untrained mask model, we eliminate lines 6 and 7 from the Algorithm 2.

Algorithm 2 RL with action mask

1: for $t=0$ to T do 2:    Get masked action ${\tilde{a}}_t\sim {\tilde{\pi }}_{\theta ,\varphi }\left({\tilde{a}}_t\right|s_t)$ 3:    Record data: $\mathcal{D}\leftarrow \mathcal{D}\bigcup (s_t,a_t,s_{t+1},r_{t+1},I_t)$ 4:    Sample data: $B\sim \mathcal{D}$ 5:    Update policy: ${\mathbb{E}}_B\left[J\left(\theta \right)\right]$ 6:    Update transition model and reward model:    ${\mathbb{E}}_B[\widehat{p}(s_t,a_t)-s_{t+1}]$    ${\mathbb{E}}_B[\widehat{r}(s_t,a_t)-r_{t+1}]$ 7:    Update mask model: ${\mathbb{E}}_B\left[J\left(\varphi \right)\right]$ Algorithm 1 8: end for

5. Experiments

Our main objective is to present an algorithm capable of acquiring action masks to filter out unnecessary actions, thereby expediting the RL process. To validate its effectiveness, we integrated our proposed action mask model learning approach into two vanilla RL algorithms, DQN and PPO. We conducted experiments in three environments with discrete action spaces where unnecessary actions may exist.

5.1. Implementation Details

We implemented our algorithms using PyTorch 2.1 and executed them on CUDA 12. The baseline algorithms, classical RL algorithms generated within each environment codebase, were refined into our algorithms by incorporating a three-layer mask model, a three-layer transition model, and a three-layer reward model. We set the clustering parameter $ϵ$ for the DBSCAN algorithm as $0.1$, a well-established hyper-parameter for the standard neural networks. In cases where the environment possesses prior-known dense or sparse invalid actions in states, we recommend experimenting with adjusting $ϵ$ within the range of $0.02$ to $0.2$ to find the optimal solution. The code for our experiments will be made publicly available at https://github.com/Elvirawzy/auto_mask/tree/master accessed on 14 January 2024.

5.2. Domains

5.2.1. Maze

A continuous maze environment is situated within a square space with a width of 1 unit, as depicted in Figure 2a. Both the dot agent and the small square target are consistently spawned at fixed positions, while the blocks are randomly generated within the environment. The state space is defined across eight dimensions, encompassing the coordinates of the dot agent and contextual information represented by a maximum of six radar readings. The agent is equipped with n equally spaced directional actuators emanating from its position, allowing the toggling of each actuator on or off. All actuators share an identical vector length and the agent’s heading is determined by the direction of the vector sum of all open actuators, resulting in a discrete action space of $2^n$, despite redundancies within this space. The agent receives a reward of +1 when it reaches the target square, incurs a penalty of −0.1 for collisions with blocks, and experiences a cost of −0.05 for each movement step. We tested our method in Maze environments with $n=10$ and $n=12$, respectively.

5.2.2. MinAtar

MinAtar implements scaled-down renditions of various Atari 2600 games, employing feature maps with 4 to 10 channels to represent states. The full action space across all MinAtar games encompasses 18 dimensions, including movement and shooting components. However, individual games typically feature minimal action spaces with fewer dimensions. In our study, we focused on two games: Breakout (minimal action space of 3) and Asterix (minimal action space of 5). For further details, please refer to Figure 2b,c.

5.2.3. $\mu$RTS2

$\mu$RTS2 constitutes a minimalistic real-time strategy (RTS) game, as illustrated in Figure 2d. Given a map of dimensions $h\times w$, the observation is represented as a tensor with dimensions $(h,w,n_f)$, where $n_f=27$ denotes a set of features with binary values. The action space is an eight-dimensional vector of discrete values, forming a flattened action space of $2hw+29$ dimensions. The first dimension designates the unit selected to perform an action, and the last dimension designates the unit selected for an attack. The second dimension encompasses action types, including move, harvest, return, produce, and attack, with their respective parameters constituting the remaining dimensions of the action space. In our configuration, following [17], only the base unit and the workers are considered worth selecting, leading to large invalid action spaces in the first and last dimensions.

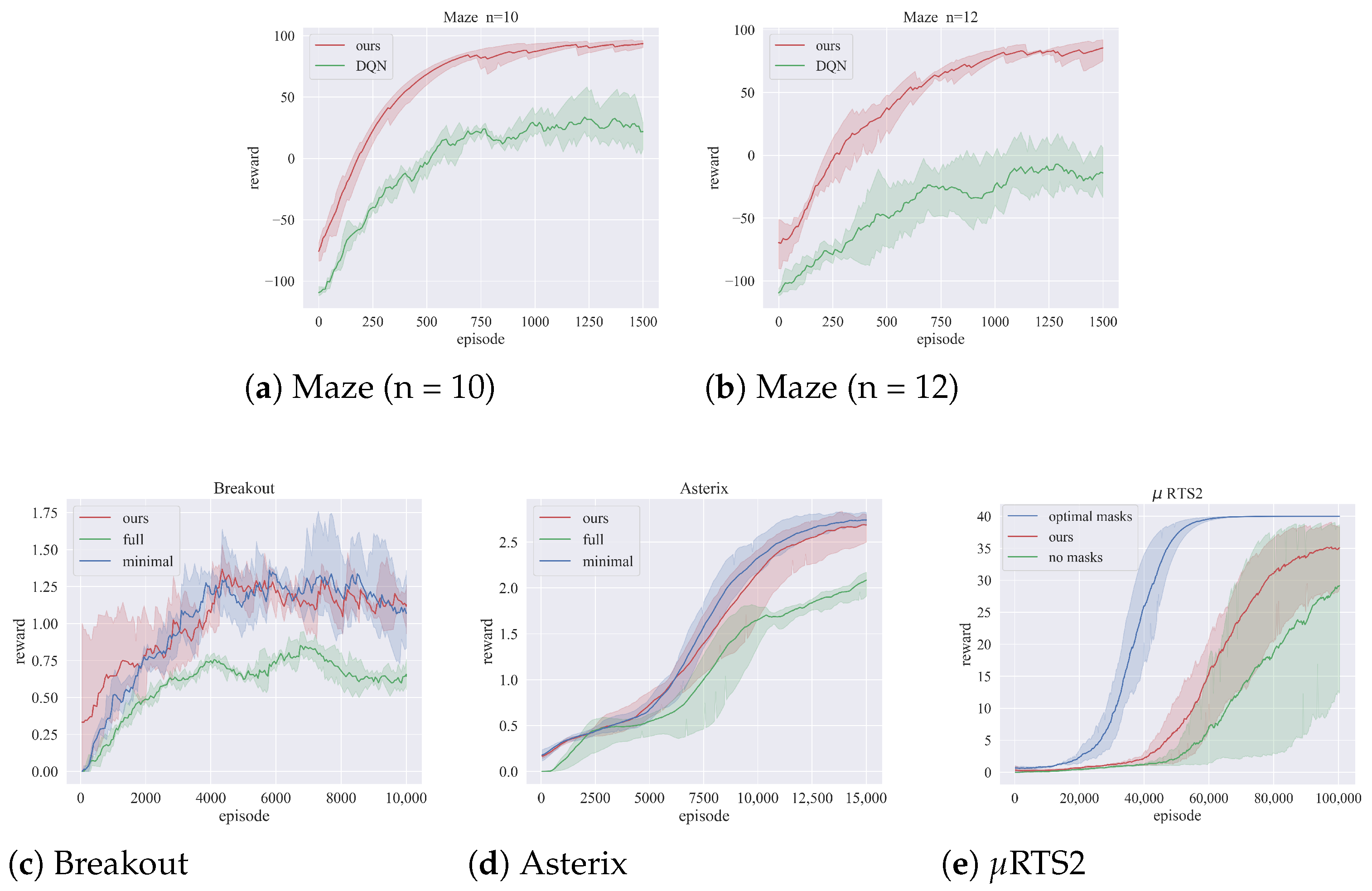
5.3. Results

5.3.1. Main Results

Within each environment, we initially trained an action mask model using the proposed Algorithm 2 and preserved the acquired mask model. Subsequently, we re-trained the RL policy using the loaded action mask model without further updates. Performance comparisons between the RL policy with and without the integrated mask model are presented, showcasing improvements in Figure 3. To ensure robustness, defined as the stability and consistency of the obtained results, different random seeds were employed for initialization across all training sessions. In each setting, we conducted a total of five trials.

In the Maze environment, we integrated the mask model into the vanilla DQN algorithm. As depicted in Figure 3a,b, the vanilla DQN algorithm exhibits suboptimal performance as the action space expands from $2^{10}$ to $2^{12},$ despite identical map size, observation, and goal configurations. However, the learned action mask model discerns that the necessary actions in these environments do not grow exponentially, effectively filtering out actions with identical behavioral consequences as their counterparts. Consequently, while the vanilla DQN algorithm experiences a nearly 40 reduction in total rewards, DQN with the trained mask model achieves significantly higher rewards in less time with lower deviations, experiencing only a loss of two units of final rewards. This outcome substantiates the effectiveness of our learned action mask model.

In MinAtar games, specifically Breakout and Asterix in our experimental setup, minimal action spaces within the full 18-dimensional action space can be identified as superior baselines. Notably, these minimal action spaces remain consistent across states in MinAtar games. In this unique scenario, we made a simple modification to our mask model by directly learning the probabilities of 0 for 1 in each action dimension (output of the last layer of the original mask model). Additionally, we utilized the vanilla DQN algorithm as a baseline in MinAtar settings. Analysis of Figure 3c,d reveals that DQN with our learned mask model achieves performance comparable to the superior baselines, signifying the effectiveness of our algorithm in obtaining near-optimal action masks. Our method eventually obtains an additional 0.55 rewards in Breakout (85% better) and 0.7 rewards in Asterix (35% better) than the vanilla DQN algorithm.

Within the $\mu$RTS2 environment, we employ the vanilla PPO algorithm as a baseline and incorporate our mask model into it. Optimal action masks in $\mu$RTS2, provided by environmental engineering, serve as the superior baseline. As depicted in Figure 3e, the vanilla PPO algorithm encounters challenges in achieving satisfactory performance within this intricate environment characterized by extensive state and action spaces. Conversely, our learned mask model effectively accelerates the RL training process, enhancing both reward and deviation performance. Numerically, while the superior baseline can obtain the utmost returns at 40 and the vanilla PPO algorithm achieves 30 with $\pm 8$ deviations, our method achieves 35 returns with $\pm 3$ deviations. Nevertheless, a performance gap persists when compared to the optimal action masks, indicating opportunities for further refinement in the mask model quality.

We also assess the Time to Threshold metric and present the results in

Table 1. The Time to Threshold performance comparison between vanilla RL algorithms and our proposed method. Refer to the main text for detailed descriptions.

Env	Baseline Training Time	Time to Threshold
Maze (n = 10)	10.3 m ± 183 s	7.8 m ± 192 s
Maze (n = 12)	24.4 m ± 237 s	17.8 m ± 239 s
Breakout	27 m ± 130 s	22.5 m ± 121 s
Asterix	45.3 m ± 162 s	14.3 m ± 153 s
$\mu$RTS2	10.8 m ± 80 s	3.1 m ± 82 s

. The Time to Threshold metric denotes the duration it takes for the baseline to complete training minus the time our method requires to achieve the same performance as the baseline’s final performance. This metric is commonly used to evaluate the improvement in training efficiency. In the Maze and Breakout environments, our method only utilizes around 1/5th to 1/3rd of the time to achieve equivalent performance to the baseline algorithm. In the Asterix and $\mu$RTS2 environments, it takes approximately 2/3rd to 3/4th of the time to reach the same performance. This outcome indicates that, with the same tools and device, our method attains comparable performance with reduced computational time, effectively accelerating the learning procedure.

5.3.2. Visualization

To visually illustrate the effectiveness of our approach in reducing the action space size while maintaining interpretability, we generated visualizations of the masked action spaces. In the Maze environment with n = 10, resulting in a total of 1024 actions at state $s_0$, as shown in Figure 4a,b, the learned mask model adeptly filters out numerous invalid actions while retaining almost all useful actions. A statistical count reveals that the mask model excludes approximately 2/3rd of invalid actions at $s_0$.

In Figure 4c,d, where actual invalid actions are known through expert knowledge in MinAtar and $\mu$RTS2, we evaluate the percentage of encountered invalid action numbers by the agent with and without the learned mask model while training. This analysis provides insights into the learning process of our mask model. In Breakout, our method achieves the optimal global action mask, ensuring that the agent avoids exploring any invalid action space by the end of the process. In Asterix, our method attains a near-optimal global action mask. In $\mu$RTS2, our model learns to mask out approximately $45\%$ of invalid actions by the end of the training process. Across both MinAtar and $\mu$RTS2 environments, the proposed algorithm, when learning with the mask model, significantly enhances the efficiency and smoothness of reducing exploration in the invalid action space.

6. Conclusions

This study introduces an innovative approach to tackle the exploration challenge in RL, particularly in environments characterized by extensive discrete action spaces. The incorporation of Bisimulation Metrics on Actions by States (BMAS) enables the quantification of behavioral differences among actions, forming the basis for our Automatical Action Masking method. We devised a refined action mask model and an effective learning procedure that seamlessly integrates with diverse RL policies. The experiments conducted across Maze, Atari, and $\mu$RTS2 environments illustrate the significant reduction in action space achieved by the learned mask model, thereby accelerating the RL learning process and enhancing overall performance.

Our contributions lay the groundwork for more efficient and interpretable RL algorithms, offering promising prospects for applications in complex real-world scenarios. Nevertheless, there remain gaps between the learned masks and the optimal masks, presenting an opportunity for the design of improved mask models. Additionally, our method is currently limited in its application to environments with discrete action spaces, as it reduces discrete spaces by cutting dimensions rather than managing distributions. Future research endeavors could focus on bridging these gaps and further refining our understanding of automatic action masking for continued advancements in reinforcement learning.