Structural Reliability Analysis Using Stochastic Finite Element Method Based on Krylov Subspace

Abstract

The stochastic finite element method is an important tool for structural reliability analysis. In order to improve the calculation efficiency, a stochastic finite element method based on the Krylov subspace is proposed for the static reliability analysis of structures. The first step of the proposed method is to preprocess the static response equation considering randomness to reduce the condition number of the coefficient matrix. The second step of the proposed method is to construct a Krylov subspace based on the preprocessed static response equation. Then, the static displacement of random sampling is expressed as a linear combination of subspace basis vectors to achieve the purpose of a fast solution. Finally, statistics and failure probability are calculated according to the static response obtained from thousands of random samples. Three numerical examples are given to compare the proposed method with the stochastic finite element method based on the Neumann series. The results show that the stochastic finite element method based on the Krylov subspace is more accurate and efficient than the stochastic finite element method based on the Neumann series.

1. Introduction

In engineering structures, the physical properties of materials are usually random, such as the elastic modulus of concrete and residual stress of steel, which can be regarded as random variables. On the other hand, there will also be random dimensional deviations in the process of making and installing components. The random changes of these physical quantities will affect the bearing capacity and deformation of the whole structure. Therefore, in structural design, reliability analysis is usually necessary [1,2]. The Monte Carlo simulation is one of the most commonly used reliability analysis algorithms [3,4]. Its basic idea is to assume that the physical quantity is a random variable that obeys a certain random distribution and then randomly selects samples from the original structure thousands of times. By calculating the response of each sampling and comparing it with the predetermined threshold, the failure times in these samples that exceed the response threshold can be obtained so as to calculate the failure probability of the structure. In the above operations, the response data of different samples need to be calculated repeatedly. For large-scale structures with a huge number of degrees of freedom, such static or dynamic response analysis requires a huge amount of calculation, which will make it difficult to carry out reliability analysis.

The stochastic finite element (SFE) method is a tool to quickly calculate the random response of structures. With the aid of the stochastic finite element method, the calculation of the Monte Carlo simulation in reliability analysis can be greatly reduced. Lenhardt and Rottner [5] proposed the iterative Krylov subspace method, coupled with diverse preconditioning strategies, to solve nonlinear computational problems. For a parallel implementation, domain decomposition methods are employed, with each processor working on a local grid to compute a partial stiffness matrix, thereby accelerating the computational speed. Shi et al. [6] reviewed the current state of reliability analysis methods based on the SFE method. Emphasis was placed on four prevalent SFE techniques: direct Monte Carlo, Taylor expansion, perturbation, and Neumann expansion. Pang et al. [7] combined a non-invasive SFE method with a direct probability integration technique to generate precise probability density functions for each individual seismic response moment. Do and Tran [8] refined the SFE method to conduct an in-depth investigation into the random vibrations exhibited by functionally graded material plates when subjected to moving loads. Ghannoum et al. [9] employed the SFE method to explore the capacity for accounting for spatial variability in concrete tensile strength. Kamiński et al. [10] employed the SFE method to investigate the natural vibration of thin plates on viscoelastic supports with time-fractional orders. Xiang et al. [11] used the SFE method to analyze the mean and standard deviation of the dynamic response of the train bridge system. Christos [12] introduced a deep learning algorithm grounded on convolutional neural networks and trained it with a probabilistic failure analysis dataset derived from an SFE model. Zheng et al. [13,14] proposed a new method for structural reliability analysis using the SFE approach, as well as solving partial differential equations defined on random domains. Santos et al. [15] used the SFE method to ascertain the spectral response and statistical parameters of the structural natural frequencies. Liu et al. [16] proposed a novel SFE method that leverages the Karhunen–Loéve expansion for discretizing the stochastic field, coupled with the point estimate method for accurately calculating the random response of a structure. Han et al. [17] presented a triangular extended SFE model for simulating random void problems. Kormi T et al. [18] used the SFE method to study the random response of offshore strip foundations on spatially variable soils considering a combination of horizontal and rotational loads. Ahmadi Moghaddam and Mertiny [19] introduced the SFE approach for predicting the properties of filler-modified polymers, with a focus on electrical properties. Lacour et al. [20] proposed an invasive formula for the dynamic SFE method, which propagates cognitive uncertainty in material properties over time into the finite element system. Bouhjiti et al. [21] proposed a global SFM method to simulate the impact of concrete aging uncertainties on the serviceability and durability of large reinforced concrete and prestressed structures. Pengge et al. [22] proposed an interval finite element method based on the Neumann series. By representing the inverse of the stiffness matrix as a Neumann series expansion, they obtained explicit expressions for structural responses with interval variables, enabling the efficient computation of the upper and lower bounds of structural responses. Shinozuka and Yamazaki [23] incorporated Neumann expansion into the Monte Carlo method for deriving the finite element solution under random variations in material properties. They compared the results from the Neumann expansion method with those from the first-order and second-order perturbation approximation methods, as well as the direct Monte Carlo simulation method, in terms of accuracy, convergence, and computational efficiency. Aggarwal et al. [24] proposed an SFE method grounded in the Gaussian Process, enabling the direct utilization of experimental data and the quantification of uncertainties inherent in simulation-based prediction outcomes. Vievering and Le [25] studied how to map the continuous random field of material properties onto the finite element mesh in the stochastic finite element method. Zeng et al. [26] employed the stochastic spectral finite element method to investigate the effects of material randomness and heterogeneity on the seismic response of gravity dam-foundation systems. The results indicate that material randomness and heterogeneity may reduce the seismic response of gravity dams, while deterministic models may overestimate dynamic responses.

Although remarkable progress has been made in SFE methods, the existing calculation algorithms still have the problem of low calculation efficiency when applied to large-scale structures. To enhance the computational efficiency, an SFE approach leveraging Krylov subspace techniques is introduced for assessing the static reliability of structures. This methodology initiates by preprocessing the static response equation, incorporating randomness, to diminish the condition number of the coefficient matrix, thereby facilitating the computation. Subsequently, a Krylov subspace is constructed based on this refined static response equation. By expressing the static displacement under random sampling as a linear superposition of subspace basis vectors, rapid solutions are achieved. Ultimately, statistics and failure probabilities are derived from the static responses acquired through extensive random sampling. Three numerical case studies are presented, contrasting this new method with a stochastic finite element approach grounded in the Neumann series. The outcomes demonstrate that the Krylov subspace-based stochastic finite element method surpasses its Neumann series counterpart in both accuracy and efficiency.

2. Theoretical Development

For a structure with $n$ degrees of freedom (DOFs), its displacement under static load is usually obtained by solving the following linear equations:

$$K\cdot x=l$$

(1)

where $K$ denotes the original stiffness matrix of the structure, $x$ denotes the original displacement vector, and $l$ denotes the static load vector. From Equation (1), the original displacement vector can be calculated using

$$x=K^{-1}l$$

(2)

As mentioned earlier, many physical quantities in the structural finite element model, such as the elastic modulus of materials, are random variables. This leads to the stiffness matrix of the structure also being a random matrix. The structural stiffness matrix considering randomness can be expressed as the sum of the stiffness matrix of each element multiplied by a random coefficient, that is

$$K_d={\displaystyle \sum _{i=1}^N{c}_i{K}_i}$$

(3)

where $K_d$ denotes the random stiffness matrix, and $c_i$ represents a random coefficient that obeys a certain distribution, such as a normal distribution and a uniform distribution. For a random FEM, its displacement under a static load is also obtained by solving the following linear equations as

$$K_d\cdot x_d=l$$

(4)

where $x_d$ represents the displacement of a random FEM sample under the static load. Equation (4) can still be solved using the conventional algorithm as:

$$x_d=K_d^{-1}l$$

(5)

The approach of calculating the structural displacement under each random sampling through the direct inversion of Equation (5) is called the complete analysis method, which is also known as the classical Monte Carlo finite element method. The result obtained using this method is the exact solution, which is usually used to validate the computational accuracy of other stochastic analysis methods. However, for large-scale engineering structures, if the displacement of each random FEM sample is calculated using Equation (5), the calculation cost will be very expensive. In order to save on computation, some fast stochastic finite element methods have been developed in the past decades, such as the Neumann stochastic finite element algorithm (NSFE). The basic idea of the NSFE method is to use Neumann series expansion to quickly obtain the approximate solution of $K_d^{-1}$. To this end, $K_d$ is rewritten as

$$K_d=K+\Delta K$$

(6)

where $\Delta K$ denotes the change in the stiffness matrix. Substituting Equation (6) into (5) yields

$$x_d={(K+\Delta K)}^{-1}l$$

(7)

Equation (7) can be expanded by using the Neumann series [27,28] as

$$x_d=[K^{-1}-(K^{-1}\Delta K)K^{-1}+{(K^{-1}\Delta K)}^2{K}^{-1}-\cdots ]\cdot l$$

(8)

Using Equation (8), the NSFE solutions with different accuracies can be obtained by retaining the first few terms. For example, the NSFE solution with $m$ items can be expressed as:

$$x_d\approx [K^{-1}-(K^{-1}\Delta K)K^{-1}+\cdots +{(K^{-1}\Delta K)}^{m-1}{K}^{-1}]\cdot l$$

(9)

One can conclude from Equation (9) that the NSFE method avoids directly inverting the random stiffness matrix $K_d$ through the Neumann series, thus saving the calculation amount. As noted in the literature [22,29,30,31,32], the computational efficiency and accuracy of the NSFE method are primarily contingent upon the spectral radius of the perturbation matrix $\Delta K$. Specifically, when the spectral radius of $\Delta K$ is small, a relatively modest number of terms $m$ in the NSFE calculations suffices to yield highly precise results. Conversely, if the spectral radius of $\Delta K$ is substantial, a significantly larger number of terms $m$ is required in the NSFE computations to achieve comparable levels of precision. Consequently, the NSFE method is frequently regarded as unsuitable for tackling problems characterized by significant variance in random variables, referred to as “large random fluctuations”. This is due to the potential for large random fluctuations to amplify the spectral radius, thereby destabilizing the numerical solution process and adversely affecting its convergence and accuracy. As such, alternative numerical methods may necessitate exploration for problems exhibiting pronounced randomness in order to safeguard the stability and reliability of the results. In view of this, a stochastic finite element method based on a Krylov subspace (termed as SFE-KS) is developed next for static random analysis. For this purpose, both sides of Equation (4) are multiplied by $K^{-1}$ to obtain

$$K^{-1}{K}_d\cdot x_d=K^{-1}l$$

(10)

The purpose of the above operation is to reduce the condition number of the coefficient matrix because matrix $K^{-1}{K}_d$ is closer to the identity matrix than $K_d$. From Equations (2) and (10), one has

$$G\cdot x_d=x$$

(11)

$$G=K^{-1}{K}_d$$

(12)

From Equation (11), the $m$-dimensional Krylov subspace can be constructed based on $G$ and $x$ as $\{x,Gx,\cdots ,G^{m-1}x\}$. The approximate solution of $x_d$ lies in this $m$-dimensional Krylov subspace; that is, $x_d$ can be approximated using the linear combination of these basis vectors as

$$x_d\approx {\displaystyle \sum _{i=1}^m{y}_i\cdot (G^{i-1}x)}=\Pi \cdot y$$

(13)

$$\Pi =[x,Gx,\cdots ,G^{m-1}x]$$

(14)

$$y={(y_1,y_2,\cdots ,y_m)}^T$$

(15)

Substituting Equation (13) into (4) yields

$$K_d\Pi \cdot y=l$$

(16)

Multiplying both sides of Equation (16) by ${\Pi }^T$ results in

$$D\cdot y=z$$

(17)

$$D={\Pi }^T{K}_d\Pi$$

(18)

$$z={\Pi }^{T}l$$

(19)

Note that the dimension of the matrix $D$ is $m\times m$. Usually, the dimension of a Krylov subspace takes a small value, such as $m$ = 2 or 3. Therefore, Equation (17) can be easily solved by matrix inversion as:

$$\widehat{y}=D^{-1}z$$

(20)

where $\widehat{y}$ denotes the solution of Equation (17). Finally, the approximate solution of $x_d$ based on the $m$-dimensional Krylov subspace can be obtained as

$$x_d\approx \Pi \cdot \widehat{y}$$

(21)

Overall, the proposed method avoids directly inverting the random stiffness matrix $K_d$ through the preprocessed Krylov subspace, thus saving the calculation amount. Upon comparison, it can be observed that the main difference between the complete analysis, the NSFE method, and the proposed SFE-KS method lies in the algorithms used to solve for the displacement under random sampling. Specifically, the complete analysis employs Equation (5), the NSFE approach utilizes Equation (9), and the proposed method adopts Equation (21). As mentioned earlier, the complete analysis refers to the classical Monte Carlo finite element method, and its calculation results in the case studies presented will serve as the exact solution to validate the computational efficiencies and accuracies of the NSFE and SFE-KS methods. The steps of the SFE-KS method are summarized as follows: (1) Establish the FEM without considering randomness to obtain the original stiffness matrix $K$. (2) For a static load $l$, solve Equation (1) to obtain the vector $x$ and the matrix $K^{-1}$. (3) Perform random sampling according to Equation (3) to obtain a random stiffness matrix $K_d$. (4) Calculate the matrix $\Pi$ using Equations (12) and (14). (5) Compute the matrix $D$ and the vector $z$ using Equations (18) and (19). (6) Calculate the vector $\widehat{y}$ using Equation (20). (7) Calculate the displacement vector $x_d$ using Equation (21). (8) Thousands of random samples (Steps 3–7) are obtained to obtain the statistical characteristics of the structural response and the failure probability of the structure. The formula for calculating the probability of structural failure is given as

$$p_f={\displaystyle \frac{q_f}{q_t}}$$

(22)

where $q_f$ represents the number of times the vertex displacement exceeds the threshold, and $q_t$ represents the total number of samples.

Based on the principles of matrix computations [33], an approximate assessment of the computational expense associated with the complete analysis, the NSFE method, and the proposed SFE-KS method is conducted by quantifying the number of floating-point operations (flops) in their computation process. As mentioned previously, the primary distinction among these three methods lies in the differing algorithms employed to calculate displacements under random sampling. Consequently, the subsequent focus will be on estimating the number of floating-point operations corresponding to the distinct operations in each of these three methods. For the complete analysis, the number of flops required for each sampling to compute the displacement using Equation (5) is the sum of the flops needed for inverting matrix $K_d$ and for multiplying matrices $K_d^{-1}$ and $l$. For a system with $n$-DOFs, the number of flops for Equation (5) is about $n^3+n^2$. For the NSFE model, the number of flops required for each sampling to calculate the displacement mainly consists of the following parts: (1) calculating $\Delta K$ using Equation (6) requires $n^2$ times; (2) calculating the second-order and higher-order terms in Equation (9) requires $2(m-1)n^2$ times; and (3) calculating $x_d$ using Equation (9) requires $(m-1)n^2$ times. Therefore, the total number of flops for the NSFE model is about $3m{n}^2-2n^2$ times. For the SFE-KS method, the number of flops required for each sampling to calculate the displacement mainly consists of the following parts: (1) calculating $\Pi$ using Equations (12) and (14) requires $2(m-1)n^2$ times; (2) calculating $D$ using Equation (18) requires $2m{n}^2$ times; (3) calculating $z$ using Equation (19) requires $mn$ times; (4) calculating $\widehat{y}$ using Equation (20) requires $m^3+m^2$ times; and (5) calculating $x_d$ using Equation (21) requires $mn$ times. Therefore, the total number of flops for the SFE-KS model is about $4m{n}^2-2n^2+2mn+m^3+m^2$ times. In the subsequent numerical examples, the number of flops for each method will be estimated according to these formulas, and the computation time for each method will also be provided. These results, taken together, will validate that the proposed method exhibits a high level of computational efficiency. In terms of the computational accuracy, under the condition that the number of terms $m$ is the same, the proposed method is expected to achieve a higher accuracy compared to the NSFE method due to the additional least-squares fitting performed using the basis vectors of the Krylov subspace, as shown in Equations (17)–(20). The key advantage lies in the utilization of the Krylov subspace, which captures important information about the solution space through a sequence of matrix–vector multiplications. By projecting the solution onto this subspace and performing a least-squares fit, the proposed method can better approximate the true solution. It is worth noting that the actual improvement in the accuracy will depend on various factors, including the specific problem being analyzed, the choice of basic functions, the number of samples used, and the computational resources available. However, in general, the proposed method’s use of the Krylov subspace and least-squares fitting provides a solid theoretical foundation for achieving higher accuracy in the computation of failure probabilities and other stochastic quantities of interest. In the subsequent case studies, the computational accuracy will primarily be judged by comparing the errors between the statistical metrics (mean and standard deviation) obtained using various methods and the exact solution derived from a complete analysis.

3. Numerical Verification

3.1. A Beam Structure

The first example used to verify the proposed SFE-KS method is the I-beam structure shown in Figure 1. The structure has a span of 6.2 m and is divided into 62 beam elements. The cross-sectional area of the I-beam used is 53.54 cm², the moment of inertia is 5280 cm⁴, and the density is 7800 kg/m³. Assuming that the elastic modulus of the material follows a normal distribution with a mean value of 200 GPa, three scenarios are considered for the standard deviation: 0.1, 0.15, and 0.2 times the mean value. The determination of the number of random samples can be estimated by dividing 100 by the failure probability. For example, if the failure probability is 0.01, then the number of samples can be taken as 100/0.01 = 10,000. In the calculation process, all samples need to be computed to obtain the failure probability, and there is no specific convergence criterion used to terminate the computation. Theoretically, the more samples are used in the calculation, the more accurate the resulting failure probability will be. However, due to the limitations of computer hardware, only a subset of samples can be practically utilized in this work. Without loss of generality, 10⁴ random samples are taken from the structure to analyze the random response and failure probability of the beam structure under the illustrated load (each concentrated force is 2.5 kN). The vertical displacement at the mid-span point is taken as the observation object. The displacement threshold is set at 1.06 times the mid-span displacement without considering randomness, and samples exceeding this displacement threshold are considered failures. The diagram in Figure 2 intuitively illustrates the detailed operations of each step in the proposed method.

As stated before, the larger the value of $m$ is, the higher the calculation accuracy will be, but the calculation time will also increase. Therefore, the appropriate choice of $m$ should strike a balance between calculation accuracy and efficiency. For random analysis scenarios with relatively small variances, setting $m$ = 4 for the NSFE method and $m$ = 2 for the proposed method can meet the computational requirements. For random analyses with relatively large variances, if necessary, $m$ can be increased to enhance the computational accuracy at the cost of sacrificing the computational efficiency. This beam structure possesses 122 degrees of freedom. Applying the flops estimation formula discussed in the previous section, it was found that the flops counts for a complete analysis, the NSFE algorithm, and the proposed method are 1,830,732, 148,840, and 89,804, respectively. It is clear that the proposed method demands the lowest number of flops, highlighting its efficiency. For the case where the standard deviation is 0.1 times the mean value, the computation times required for the full analysis method, the NSFE algorithm (with $m=4$ items), and the proposed SFE-KS algorithm (with the dimension of the Krylov subspace being $m=2$) are listed in

Table 1. Comparison of calculation times required for 10⁴ random sampling when the standard deviation is 0.1 times the mean value.

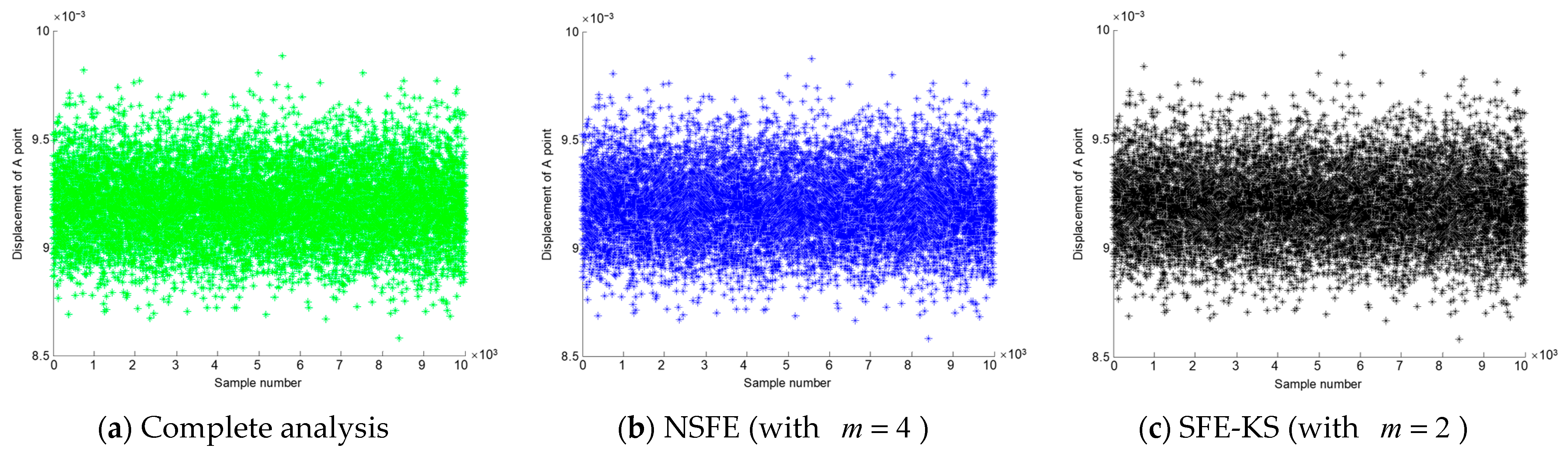
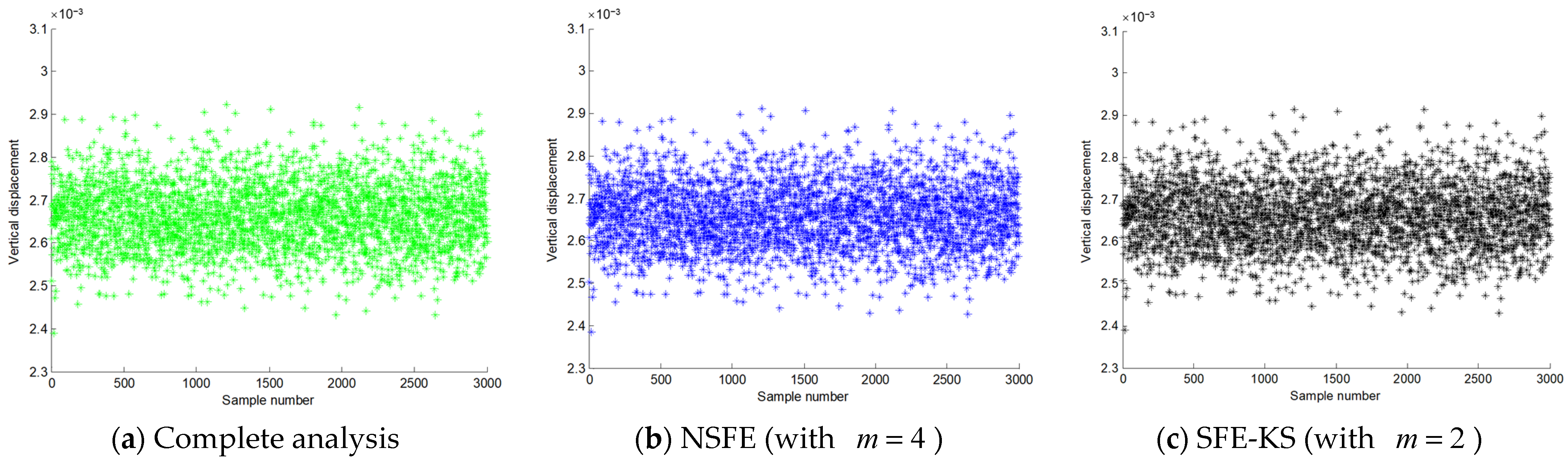
Method	Complete Analysis	$\mathbf{NSFE} (\mathbf{with} \mathit{m}=4$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=2$)
Time, s	2.6630	0.5280	0.4600

. The calculated vertical displacement at the mid-span point is shown in Figure 3. The range, mean, standard deviation, and failure probability of the displacement at the mid-span point are listed in

Table 2. Statistical characteristics of vertical displacement at the mid-span point when the standard deviation is 0.1 times the mean value.

Method	Complete Analysis	$\mathbf{NSFE} (\mathbf{with} \mathit{m}=4$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=2$)
Vertical displacement range, mm	[8.5827, 9.8853]	[8.5796, 9.8743]	[8.5792, 9.8817]
Mean, mm	9.1999	9.1973 (0.028%) *	9.1980 (0.021%)
Standard deviation	0.1689	0.1685 (0.237%)	0.1689 (0.000%)
Failure probability	0.0049	0.0043 (12.245%)	0.0048 (2.041%)

* The data in brackets indicate the relative error between the calculated value and the exact solution.

. As seen in Table 1, the computation times of both the NSFE and SFE-KS algorithms are less than that of the full analysis. Specifically, the time required for the NSFE approach is approximately 20% of the full analysis, while the SFE-KS method requires approximately 17% of the full analysis time and 87% of the NSFE algorithm time. Clearly, the proposed SFE-KS method exhibits the highest computational efficiency. In Table 2, for the vertical displacement at the mid-span point, the calculation results of the SFE-KS method are closer to the results of complete analysis than those of the NSFE method.

For the case where the standard deviation is 0.15 times the mean value, the computation times required for the three algorithms are listed in

Table 3. Comparison of calculation times required for 10⁴ random sampling when the standard deviation is 0.15 times the mean value.

Method	Complete Analysis	$\mathbf{NSFE} (\mathbf{with} \mathit{m}=4$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=2$)
Time, s	2.7440	0.5350	0.4400

. The calculated vertical displacement at the mid-span point is shown in Figure 4. The range, mean, standard deviation, and failure probability of the displacement at the mid-span point are listed in

Table 4. Statistical characteristics of vertical displacement at the mid-span point when the standard deviation is 0.15 times the mean value.

Method	Complete Analysis	$\mathbf{NSFE} (\mathbf{with} \mathit{m}=4$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=2$)
Vertical displacement range, mm	[8.4935, 10.5694]	[8.4616, 10.4601]	[8.4815, 10.5367]
Mean, mm	9.3172	9.3030 (0.152%) *	9.3080 (0.096%)
Standard deviation	0.2622	0.2587 (1.335%)	0.2610 (0.458%)
Failure probability	0.0998	0.0881 (11.723%)	0.0936 (6.212%)

* The data in brackets indicate the relative error between the calculated value and the exact solution.

. From Table 3, one can see that the proposed SFE-KS method has the highest computational efficiency. As shown in Table 4, for the vertical displacement at the mid-span point, the calculation results of the SFE-KS method are closer to the results of complete analysis than those of the NSFE approach.

For the case where the standard deviation is 0.2 times the mean value, the computation times required for the full analysis method, the NSFE algorithm, and the proposed SFE-KS algorithm are listed in

Table 5. Comparison of calculation times required for 10⁴ random sampling when the standard deviation is 0.2 times the mean value.

Method	Complete Analysis	$\mathbf{NSFE} (\mathbf{with} \mathit{m}=4$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=2$)
Time, s	2.6830	0.5600	0.4680

. The calculated vertical displacement at the mid-span point is shown in Figure 5. The range, mean, standard deviation, and failure probability of the displacement at the mid-span point are listed in

Table 6. Statistical characteristics of vertical displacement at the mid-span point when the standard deviation is 0.2 times the mean value.

Method	Complete Analysis	$\mathbf{NSFE} (\mathbf{with} \mathit{m}=4$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=2$)
Vertical displacement range, mm	[8.3197, 18.2692]	[8.2519, 11.2314]	[8.3259, 11.4614]
Mean, mm	9.5103	9.4589 (0.540%) *	9.4768 (0.352%)
Standard deviation	0.3955	0.3670 (7.206%)	0.3748 (5.234%)
Failure probability	0.3277	0.2824 (13.824%)	0.2981 (9.033%)

* The data in brackets indicate the relative error between the calculated value and the exact solution.

. From Table 5, one can see that the proposed SFE-KS method has the highest computational efficiency. In Table 6, for the vertical displacement at the mid-span point, the calculation results of the SFE-KS approach are closer to the results of complete analysis than those of the NSFE method. However, it can also be found in Table 2, Table 4 and Table 6 that with the increase in the standard deviation of the elastic modulus, the error of the calculation results of the proposed method increases accordingly. By comparing Figure 3, Figure 4 and Figure 5 together, it can be observed that the results obtained using the three methods in Figure 3 and Figure 4 show little difference. However, the results from the full analysis in Figure 5 differ significantly from those obtained using the two other rapid algorithms. This is attributed to the increasing standard deviation of the elastic modulus, which leads to increasingly larger computational errors in the two rapid algorithms. Consequently, the graphs representing the results from the two rapid algorithms in Figure 5 differ markedly from the precise solution graph obtained from the complete analysis. If necessary, the calculation accuracy of the proposed method can be improved by increasing the value of $m$.

Table 7. Comparison of calculation times required for 10⁴ random sampling using SFE-KS method with $m=3$ and $m=4$.

Method	Complete Analysis	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=3$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=4$)
Time, s	2.6830	0.5320	0.6800

presents the computational time of the proposed method when $m$ = 3 and $m$ = 4, while

Table 8. Statistical characteristics of vertical displacement at mid-span point using SFE-KS method with $m=3$ and $m=4$.

Method	Complete Analysis	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=3$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=4$)
Vertical displacement range, mm	[8.3197, 18.2692]	[8.3232, 14.9297]	[8.3197, 17.4046]
Mean, mm	9.5103	9.5066 (0.039%) *	9.5099 (0.004%)
Standard deviation	0.3955	0.3874 (2.048%)	0.3935 (0.506%)
Failure probability	0.3277	0.3258 (0.580%)	0.3273 (0.122%)

* The data in brackets indicate the relative error between the calculated value and the exact solution.

and Figure 6 provide the corresponding calculation results for these two cases. It can be seen in Table 7 that the calculation time of the proposed method increases with the increase in $m$. From Table 8, it can be concluded that the calculation result of the proposed method is closer to the exact solution obtained using the complete analysis with the increase in $m$. By comparing Figure 6b with Figure 5a, it can be observed that the calculation results of the proposed method when $m$ = 4 are almost identical to the exact solution of the complete analysis.

3.2. A 1220-Bar Steel Structure

The second example used to verify the proposed SFE-KS method is the 1220-bar structure shown in Figure 7. The structure has 15 spans horizontally (each span being 0.2 m) and 20 layers vertically (each layer being 0.2 m). To conserve space on the graphic, the dashed lines in Figure 6 represent the omitted members of the structure, while the solid lines represent some of the members. The elastic modulus of the material used in this structure is 206 GPa, and the density is 7850 kg/m³. The cross-sectional area of each member is assumed to be a random variable that obeys normal distribution with a mean of 59.66 mm² and a standard deviation of 5.966 mm². Without loss of generality, 1000 samples were gathered to obtain the statistical characteristics of the static response of the structure and the failure probability. Structural failure is defined as the horizontal displacement at the loading point exceeding a certain threshold. This threshold is taken as 1.02 times the displacement of the structural vertex without considering randomness. The truss structure under consideration has 640 degrees of freedom. Utilizing the flops estimation formula detailed in the previous section, it was found that the flops counts for a complete analysis, the NSFE method, and the proposed method are 262,553,600, 4,096,000, and 2,460,172, respectively. The proposed method emerges as the most efficient option, requiring the lowest number of flops. Furthermore,

Table 9. Comparison of calculation times for example 2.

Method	Complete Analysis	$\mathbf{NSFE} (\mathbf{with} \mathit{m}=4$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=2$)
Time, s	8.1250	1.0160	0.6870

provides the calculation time of the complete analysis, NSFE method, and the proposed method to compare the calculation efficiencies of various methods. Figure 8 gives the calculated horizontal displacements at the loading point using the three methods.

Table 10. Statistical characteristics of horizontal displacement for example 2.

Method	Complete Analysis	$\mathbf{NSFE} (\mathbf{with} \mathit{m}=4$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=2$)
Vertical displacement range, mm	[8.1852, 8.6521]	[8.1840, 8.6502]	[8.1847, 8.6513]
Mean, mm	8.3907	8.3900 (0.008%) *	8.3903 (0.005%)
Standard deviation	0.0726	0.0725 (0.138%)	0.0725 (0.138%)
Failure probability	0.052	0.049 (5.769%)	0.051 (1.923%)

* The data in brackets indicate the relative error between the calculated value and the exact solution.

presents the range, mean, standard deviation, and failure probability of the horizontal displacement at the loading point. As shown in Table 9, the time required for the NSFE method is approximately 13% of the full analysis, while the SFE-KS approach requires approximately 8% of the full analysis time and 68% of the NSFE algorithm time. Clearly, the proposed SFE-KS method exhibits the highest computational efficiency. From Table 10, one can find that the calculation results of the proposed method are closer to the exact solution obtained using the complete analysis than those of the NSFE method.

3.3. A Plate Structure

As shown in Figure 9, a plate structure with a geometric size of 120 mm × 40 mm × 20 mm serves as a demonstration for applying the introduced methodology. This structure is digitally replicated utilizing solid elements, each with dimensions of 10 mm × 10 mm × 10 mm. One extremity of the plate is securely anchored, while the opposing end experiences multiple concentrated forces, each individually exerting a force of 5 kN. Assuming that the elastic modulus of the material follows a normal distribution with a mean value of 206 GPa, two scenarios are considered for the standard deviation: 0.05 and 0.2 times the mean value. Without loss of generality, 3000 random samples are taken from the structure to analyze the random response and failure probability of the plate structure. Structural failure is defined as the vertical displacement at the free end of the structure exceeding a certain threshold. This threshold is taken as 1.05 times the vertical displacement of the free end of the structure without considering randomness. The plate structure possesses 540 degrees of freedom. Applying the flops estimation formula, it was found that the total flops required for a comprehensive analysis, the NSFE method, and the proposed method are 157,755,600, 2,916,000, and 1,751,772, respectively. Notably, the proposed method significantly reduces the flops count, demonstrating its efficiency and superiority in terms of computational requirements.

The standard deviation of the elastic modulus being 0.05 times the mean value is used to simulate situations with a very low probability of failure.

Table 11. Comparison of the calculation time for example 3 when the standard deviation is 0.05 times the mean.

Method	Complete Analysis	$\mathbf{NSFE} (\mathbf{with} \mathit{m}=4$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=2$)
Time, s	5.3820	2.3080	1.1830

presents the computation time for the three methods under this scenario. Figure 10 shows the vertical displacements at the free end of the plate obtained using the three methods.

Table 12. Statistical characteristics of horizontal displacement for example 3 when the standard deviation is 0.05 times the mean.

Method	Complete Analysis	$\mathbf{NSFE} (\mathbf{with} \mathit{m}=4$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=2$)
Vertical displacement range, mm	[2.5461, 2.6669]	[2.5461, 2.6668]	[2.5461, 2.6670]
Mean, mm	2.6109	2.6109 (0.00%) *	2.6109 (0.00%)
Standard deviation	0.0175	0.0175 (0.00%)	0.0175 (0.00%)
Failure probability	0	0 (0.00%)	0 (0.00%)

* The data in brackets indicate the relative error between the calculated value and the exact solution.

provides the statistical measures of the vertical displacement at the free end. As shown in Table 11, the time required for the NSFE method is approximately 43% of the complete analysis, while the SFE-KS method requires approximately 22% of the complete analysis time and 51% of the NSFE algorithm time. Clearly, the proposed SFE-KS method exhibits the highest computational efficiency. From Table 12, one can find that the failure probabilities calculated using the three methods are all zero. This shows that when the standard deviation of the elastic modulus is small, the failure probability of the structure is also very small and close to 0. In addition, the ranges, means, and standard deviations of the displacements at the free end of the plate structure obtained using the three methods are almost equal, indicating that both the NSFE and SFE-KS rapid methods can achieve highly accurate calculation results when the standard deviation of the elastic modulus is very small. Taking into account both the computation time and accuracy, it has been demonstrated that the proposed method performs the best.

Table 13. Comparison of calculation time for example 3 when the standard deviation is 0.2 times the mean.

Method	Complete Analysis	$\mathbf{NSFE} (\mathbf{with} \mathit{m}=4$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=2$)
Time, s	5.7450	2.8350	1.4110

presents the computation times for the three methods under the scenario of the standard deviation of the elastic modulus being 0.2 times the mean value. Figure 11 shows the vertical displacements at the free end of the plate obtained using the three methods.

Table 14. Statistical characteristics of horizontal displacement for example 3 when the standard deviation is 0.2 times the mean.

Method	Complete Analysis	$\mathbf{NSFE} (\mathbf{with} \mathit{m}=4$)	$\mathbf{SFE}\text{-}\mathbf{KS} (\mathbf{with} \mathit{m}=2$)
Vertical displacement range, mm	[2.3902, 2.9229]	[2.3861, 2.9114]	[2.3893, 2.9148]
Mean, mm	2.6627	2.6591 (0.135%) *	2.6604 (0.086%)
Standard deviation	0.0752	0.0744 (1.064%)	0.0747 (0.665%)
Failure probability	0.159	0.145 (8.805%)	0.152 (4.403%)

* The data in brackets indicate the relative error between the calculated value and the exact solution.

provides the statistical measures of the vertical displacement at the free end. As shown in Table 13, the time required for the NSFE method is approximately 49% of the full analysis, while the SFE-KS method requires approximately 25% of the full analysis time and 50% of the NSFE algorithm time. Clearly, the proposed SFE-KS method exhibits the highest computational efficiency. From Table 14, one can find that the calculation results of the proposed method are closer to the exact solution obtained using the complete analysis than those of the NSFE method. This indicates that when the standard deviation of the elastic modulus is relatively large, the calculation accuracy of the NSFE method begins to significantly lag behind that of the SFE-KS method. In conjunction with the aforementioned fact that the computation time of the SFE-KS method is roughly half of the NSFE method, it is reiterated that the proposed SFE-KS method outperforms the NSFE and complete analysis approaches.

4. Conclusions

An SFE-KS method has been proposed in this work specifically for the static reliability analysis of structures with the aim of enhancing the calculation efficiency. The initial step involves preprocessing the static response equation, taking into account randomness, to diminish the condition number of the coefficient matrix. Following this, a Krylov subspace is constructed utilizing the preprocessed static response equation. Subsequently, the static displacement resulting from random sampling is formulated as a linear combination of subspace basis vectors, facilitating swift solutions. Ultimately, statistical metrics and failure probabilities are determined based on the static responses garnered from numerous random samples. Three numerical examples are presented to evaluate the performance of the proposed SFE-KS method. The classical finite element method, which is referred to as complete analysis, and the existing NSFE method are used as references to validate the computational accuracy and efficiency of the proposed method. The main conclusions drawn from the comparative study are as follows: (1) In terms of the computational efficiency, both the number of flops and the computation time demonstrate that the proposed method achieves the highest computational efficiency. For example 1, the calculation time of the SFE-KS method is about 17% of that of the complete analysis and 87% of that of the NSFE algorithm. For example 2, the calculation time of the SFE-KS approach is about 8% of that of the complete analysis and 68% of that of the NSFE algorithm. For example 3, the calculation time of the SFE-KS approach is about 25% of that of the complete analysis and 50% of that of the NSFE algorithm. (2) In terms of the calculation accuracy, the calculation results of the SFE-KS method are closer to the exact solution obtained using the complete analysis than those of the NSFE method. Especially for cases where the standard deviation of the random variable is relatively large, the proposed method exhibits significantly better computational accuracy than the NSFE method. For instance, when the standard deviation of the elastic modulus is 0.2 times the mean value, the computational errors of the failure probability using the NSFE and SFE-KS methods in example 1 are approximately 13.8% and 9.0%, while in example 3, the computational errors of the NSFE and SFE-KS methods are approximately 8.8% and 4.4%, respectively. For example 2, when the standard deviation of the cross-sectional area is 0.1 times the mean value, the computational errors of the failure probability using the NSFE and SFE-KS methods are approximately 5.8% and 1.9%, respectively. (3) Considering both the calculation time and accuracy, this new stochastic finite element method is more suitable for the reliability analysis of large-scale engineering structures, particularly in situations where discreteness is prominent.