Sorting by Multi-Cut Rearrangements †
Abstract
1. Introduction
1.1. Notations and Definitions
- Sorting by Multi-Cut Rearrangements (SMCR)
- Instance: Two balanced strings S and T, two integers k and ℓ.
- Question: Is there a sequence of at most ℓ many k-cut rearrangements that transforms S into T?
1.2. Parameterized Algorithmics
1.3. Basic Observations
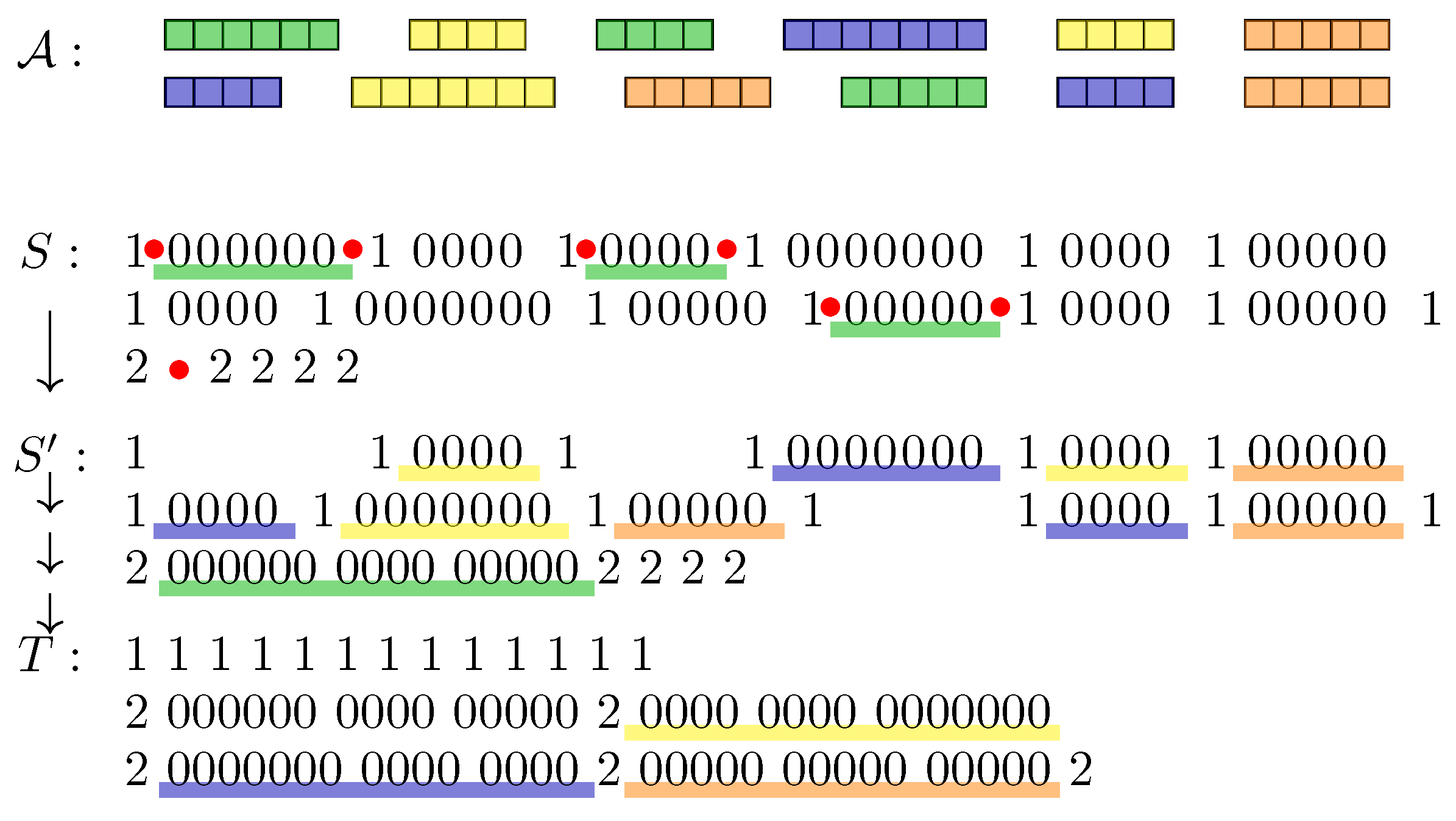
2. Sorting by Multi-Cut Rearrangements in Strings
- Group 1 contains the duos , , and , which each occur times in S and which do not occur in T.
- Group 2 contains the duos , which occur times in S and times in T, and the duos which do not occur in S, and occur times each in T.
- Group 3 contains the duos and , which each occur m times in S and in T.
3. Sorting by Multi-Cut Rearrangements in Permutations
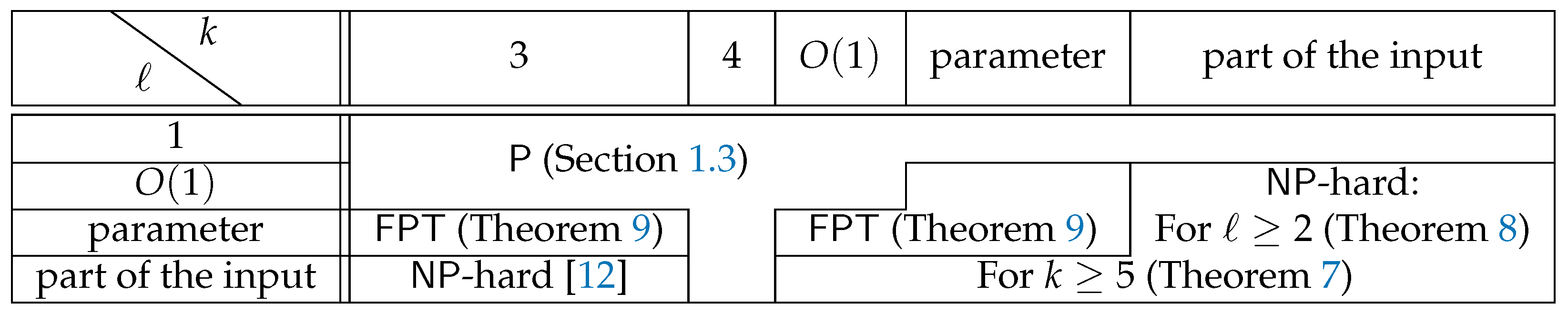
3.1. Hardness for Constant Number of Cuts
3.1.1. Breakpoints and Cycle Graph
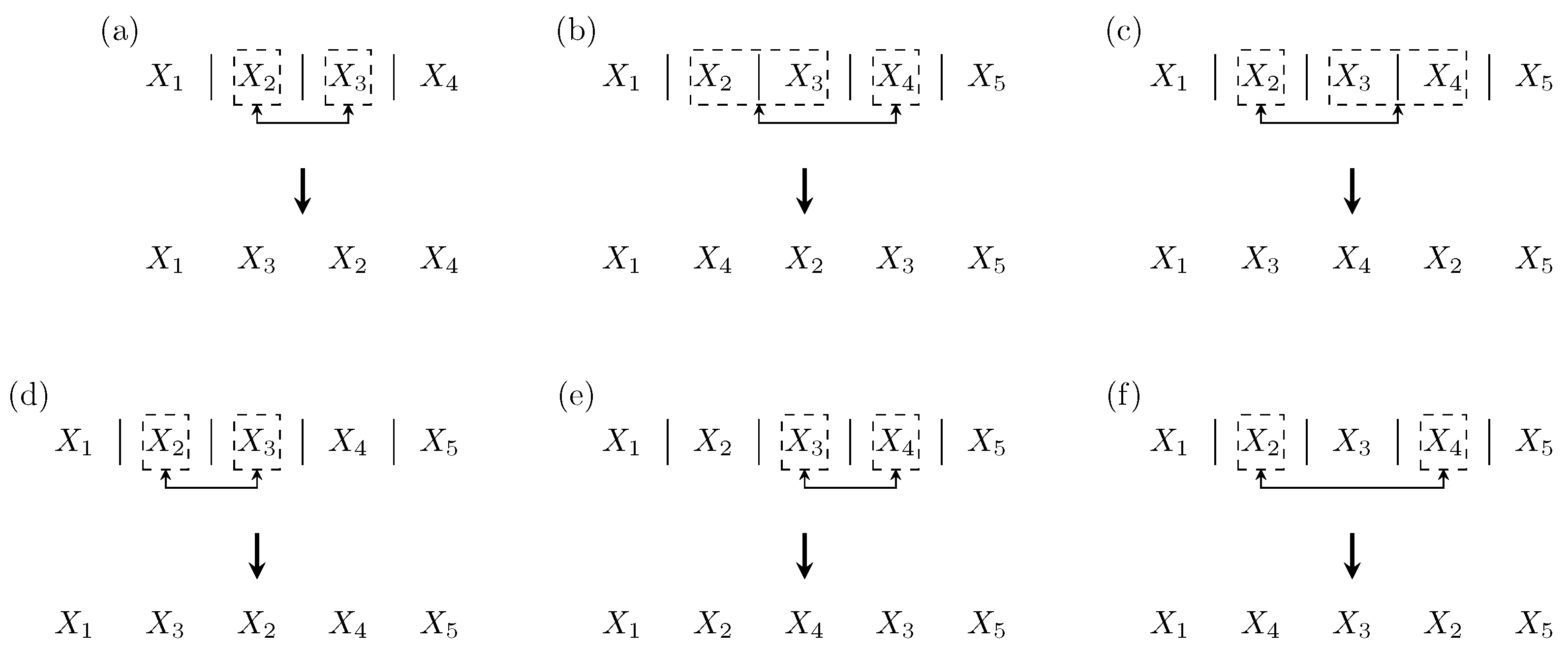
3.1.2. One-Cycle Extensions
- For :
- For :
- if x is an adjacency, it adds p trivial cycles;
- if x is a breakpoint and , it adds and to the cycle containing x;
- if x is a breakpoint and , it adds to the cycle containing x and a 2-cycle tied to the one containing x.
- if r does not cut x, then , cuts the same elements as r, and rearranges the blocks in the same order;
- if r cuts x, then , cuts the same elements as r, as well as , and (when ), and rearranges the blocks in the same way as r, with elements (when ) and inserted after x.
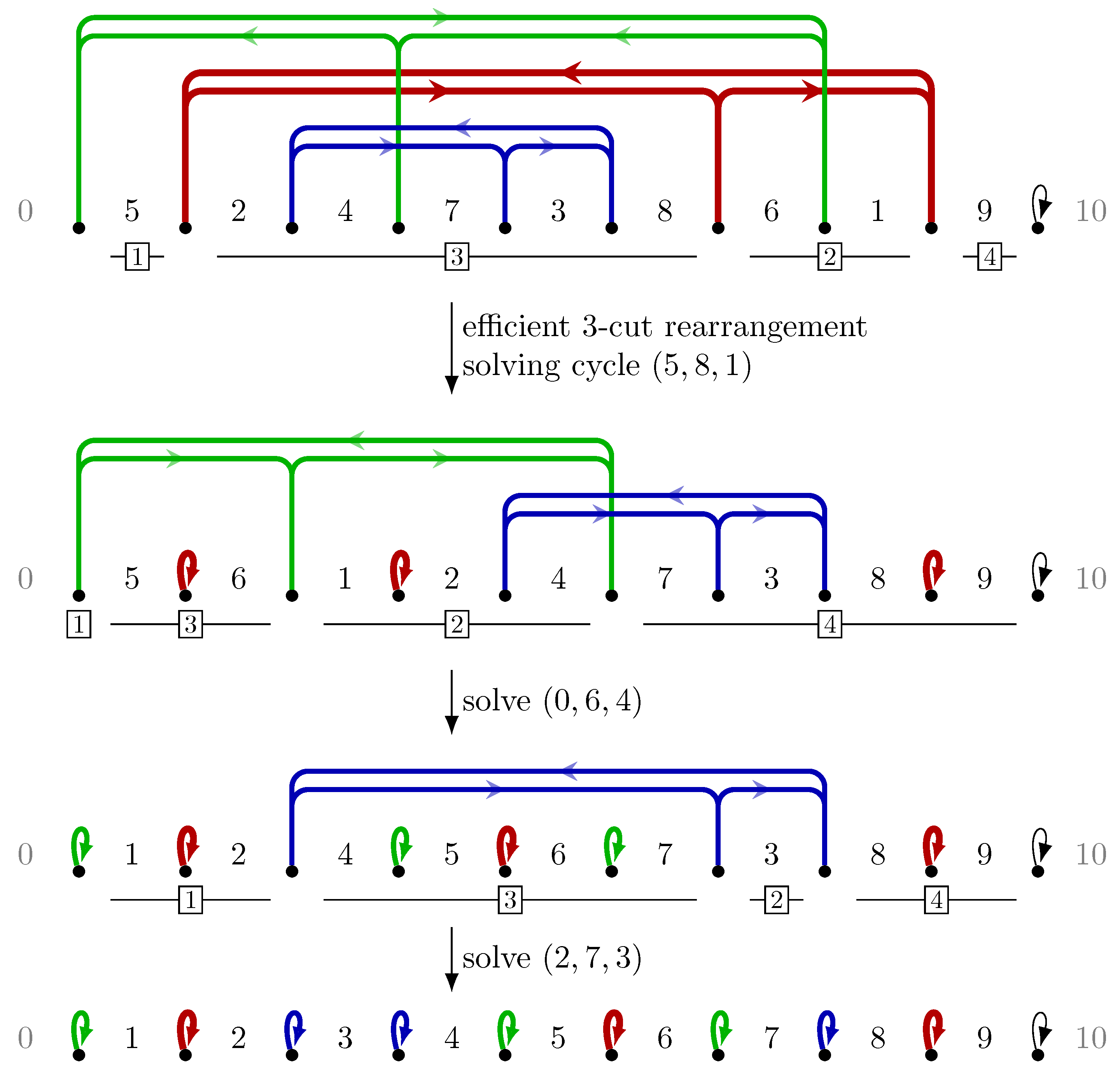
3.1.3. Extending All Cycles
3.2. Hardness for Constant Number of Rearrangements
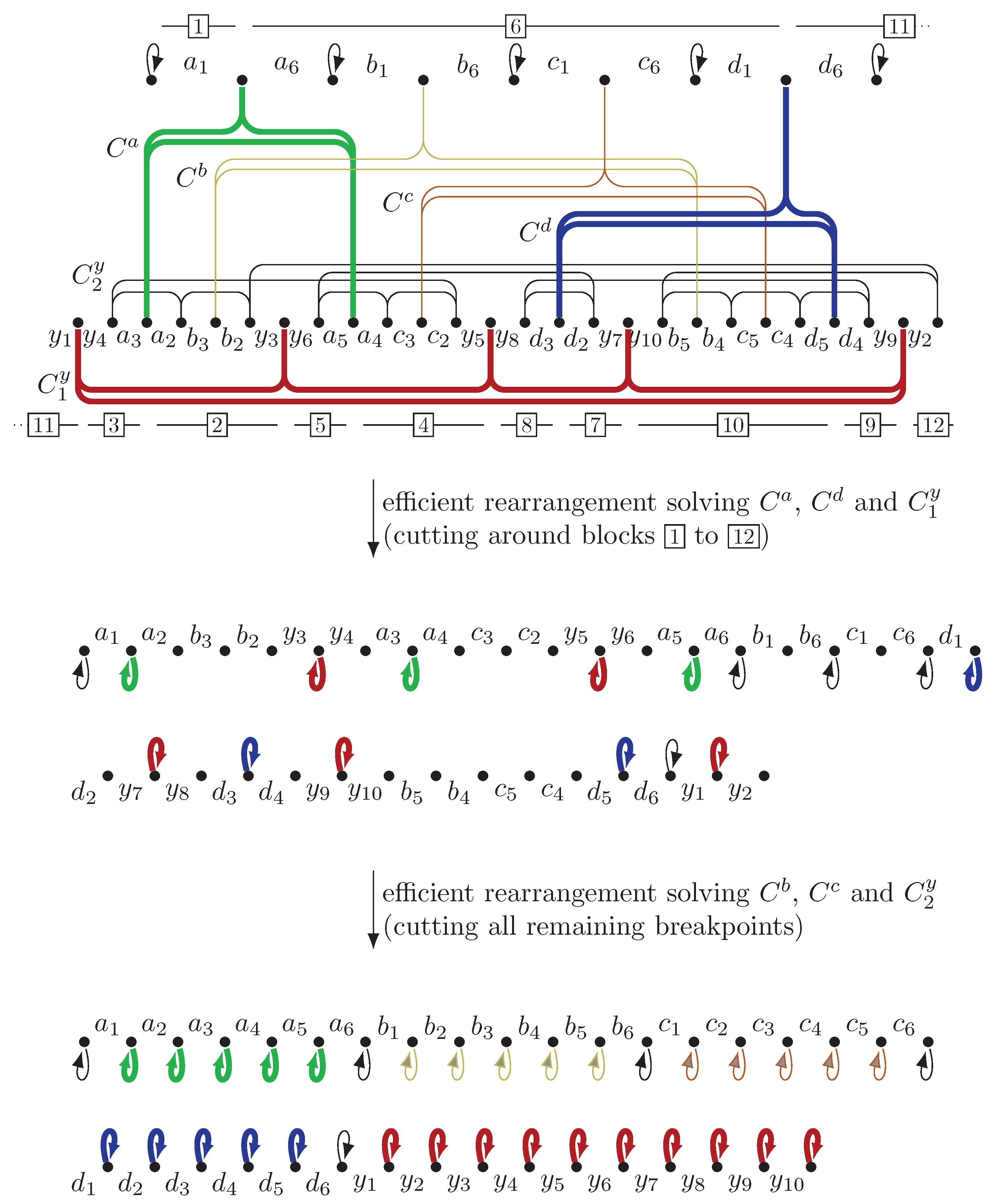
3.3. Fixed-Parameter Tractability and Approximability
- (a)
- rewrite , by contracting adjacencies so as to obtain a permutation containing no adjacencies,
- (b)
- cut around (i.e., right before and right after) the first elements of that permutation, and
- (c)
- rearrange it so as to obtain followed by the rest of the permutation.
- (b’)
- do as (b) and additionally cut to the left of
- (c’)
- do as (c) but rearrange in such a way that and are consecutive.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SMCR | Sorting by Multi-Cut Rearrangements |
| MCSP | Minimum Common String Partition |
| FPT | Fixed-Parameter Tractable |
References
- Bafna, V.; Pevzner, P.A. Genome Rearrangements and Sorting by Reversals. SIAM J. Comput. 1996, 25, 272–289. [Google Scholar] [CrossRef]
- Bafna, V.; Pevzner, P.A. Sorting by Transpositions. SIAM J. Discret. Math. 1998, 11, 224–240. [Google Scholar] [CrossRef]
- Christie, D.A. Sorting Permutations by Block-Interchanges. Inf. Process. Lett. 1996, 60, 165–169. [Google Scholar] [CrossRef]
- Fertin, G.; Labarre, A.; Rusu, I.; Tannier, E.; Vialette, S. Combinatorics of Genome Rearrangements; Computational Molecular Biology; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Stephens, P.J.; Greenman, C.D.; Fu, B.; Yang, F.; Bignell, G.R.; Mudie, L.J.; Pleasance, E.D.; Lau, K.W.; Beare, D.; Stebbings, L.A.; et al. Massive Genomic Rearrangement Acquired in a Single Catastrophic Event during Cancer Development. Cell 2011, 144, 27–40. [Google Scholar] [CrossRef] [PubMed]
- Pellestor, F.; Gatinois, V. Chromoanagenesis: A piece of the macroevolution scenario. Mol. Cytogenet. 2020, 13, 3. [Google Scholar] [CrossRef] [PubMed]
- Hannenhalli, S.; Pevzner, P.A. Transforming Cabbage into Turnip: Polynomial Algorithm for Sorting Signed Permutations by Reversals. J. ACM 1999, 46, 1–27. [Google Scholar] [CrossRef]
- Bulteau, L.; Fertin, G.; Jean, G.; Komusiewicz, C. Sorting by Multi-cut Rearrangements. In Proceedings of the SOFSEM 2021: Theory and Practice of Computer Science—47th International Conference on Current Trends in Theory and Practice of Computer Science, Bolzano-Bozen, Italy, 25–29 January 2021; pp. 593–607. [Google Scholar]
- Downey, R.; Fellows, M.R. Fundamentals of Parameterized Complexity; Springer: London, UK, 2013. [Google Scholar]
- Cygan, M.; Fomin, F.V.; Kowalik, L.; Lokshtanov, D.; Marx, D.; Pilipczuk, M.; Pilipczuk, M.; Saurabh, S. Parameterized Algorithms; Springer: London, UK, 2015. [Google Scholar]
- Bulteau, L.; Hüffner, F.; Komusiewicz, C.; Niedermeier, R. Multivariate algorithmics for NP-hard string problems. Bull. Eur. Assoc. Theor. Comput. Sci. 2014, 114. Available online: https://hal.archives-ouvertes.fr/hal-01260610/document (accessed on 27 May 2021).
- Bulteau, L.; Fertin, G.; Rusu, I. Sorting by Transpositions Is Difficult. SIAM J. Discret. Math. 2012, 26, 1148–1180. [Google Scholar] [CrossRef]
- Radcliffe, A.J.; Scott, A.D.; Wilmer, E.L. Reversals and transpositions over finite alphabets. SIAM J. Discret. Math. 2005, 19, 224–244. [Google Scholar] [CrossRef]
- Christie, D.A. Genome Rearrangement Problems. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 1998. [Google Scholar]
- Lin, Y.C.; Lu, C.L.; Chang, H.Y.; Tang, C.Y. An efficient algorithm for sorting by block-interchanges and its application to the evolution of vibrio species. J. Comput. Biol. 2005, 12, 102–112. [Google Scholar] [CrossRef] [PubMed]
- Kolman, P.; Goldstein, A.; Zheng, J. Minimum Common String Partition Problem: Hardness and Approximations. Electron. J. Comb. 2005, 12. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W. H. Freeman & Co.: New York, NY, USA, 1979. [Google Scholar]
- Bulteau, L.; Komusiewicz, C. Minimum Common String Partition Parameterized by Partition Size Is Fixed-Parameter Tractable. In Proceedings of the Twenty-Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2014, Portland, OR, USA, 5–7 January 2014; pp. 102–121. [Google Scholar]
- Sankoff, D.; Blanchette, M. The Median Problem for Breakpoints in Comparative Genomics. In Proceedings of the Computing and Combinatorics, Third Annual International Conference, COCOON ’97, Shanghai, China, 20–22 August 1997; Springer: London, UK, 1997; Volume 1276, pp. 251–264. [Google Scholar]

 and
and  are swapped). (b) The 2-extension of S for breakpoint , giving cycle . This extended cycle can be solved with a 5-cut rearrangement having an equivalent effect on the sequence (substrings and are swapped). The resulting is the 2-extension of for adjacency . (c) The 3-extension of S for breakpoint , giving cycles and (the latter being tied to the former: there is no way of solving breakpoint without cutting ). These two cycles can be solved with a 6-cut rearrangement having an equivalent effect on the sequence (again, substrings and are swapped). The resulting is the 3-extension of for adjacency .
are swapped). (b) The 2-extension of S for breakpoint , giving cycle . This extended cycle can be solved with a 5-cut rearrangement having an equivalent effect on the sequence (substrings and are swapped). The resulting is the 2-extension of for adjacency . (c) The 3-extension of S for breakpoint , giving cycles and (the latter being tied to the former: there is no way of solving breakpoint without cutting ). These two cycles can be solved with a 6-cut rearrangement having an equivalent effect on the sequence (again, substrings and are swapped). The resulting is the 3-extension of for adjacency .
 and
and  are swapped). (b) The 2-extension of S for breakpoint , giving cycle . This extended cycle can be solved with a 5-cut rearrangement having an equivalent effect on the sequence (substrings and are swapped). The resulting is the 2-extension of for adjacency . (c) The 3-extension of S for breakpoint , giving cycles and (the latter being tied to the former: there is no way of solving breakpoint without cutting ). These two cycles can be solved with a 6-cut rearrangement having an equivalent effect on the sequence (again, substrings and are swapped). The resulting is the 3-extension of for adjacency .
are swapped). (b) The 2-extension of S for breakpoint , giving cycle . This extended cycle can be solved with a 5-cut rearrangement having an equivalent effect on the sequence (substrings and are swapped). The resulting is the 2-extension of for adjacency . (c) The 3-extension of S for breakpoint , giving cycles and (the latter being tied to the former: there is no way of solving breakpoint without cutting ). These two cycles can be solved with a 6-cut rearrangement having an equivalent effect on the sequence (again, substrings and are swapped). The resulting is the 3-extension of for adjacency .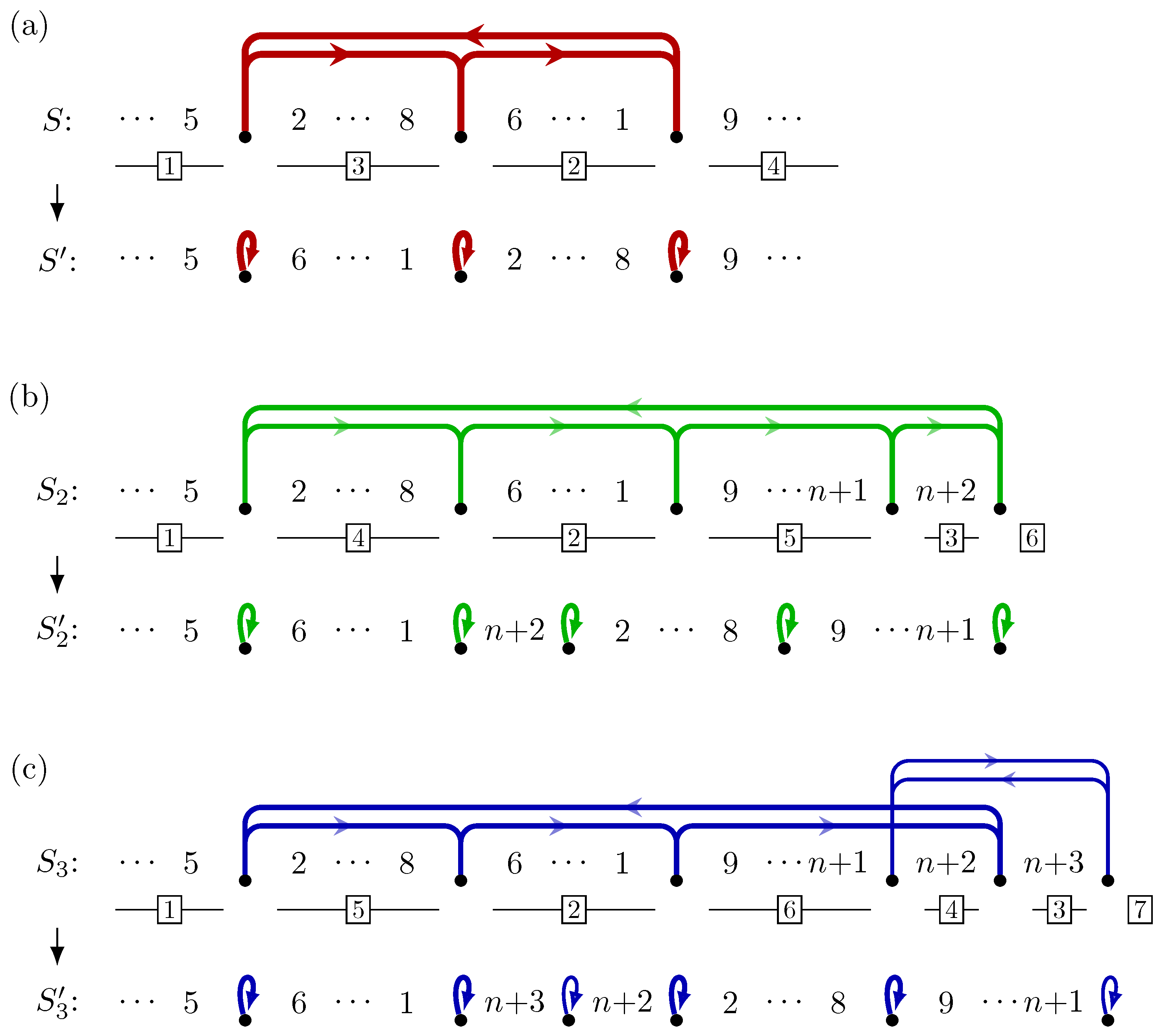

| Duo | Occurrences in S | Occurrences in T |
|---|---|---|
| 0 | ||
| 0 | m | |
| 0 | ||
| 0 | ||
| 1 | 1 | |
| 0 | m | |
| 0 | 0 | |
| m | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulteau, L.; Fertin, G.; Jean, G.; Komusiewicz, C. Sorting by Multi-Cut Rearrangements. Algorithms 2021, 14, 169. https://doi.org/10.3390/a14060169
Bulteau L, Fertin G, Jean G, Komusiewicz C. Sorting by Multi-Cut Rearrangements. Algorithms. 2021; 14(6):169. https://doi.org/10.3390/a14060169
Chicago/Turabian StyleBulteau, Laurent, Guillaume Fertin, Géraldine Jean, and Christian Komusiewicz. 2021. "Sorting by Multi-Cut Rearrangements" Algorithms 14, no. 6: 169. https://doi.org/10.3390/a14060169
APA StyleBulteau, L., Fertin, G., Jean, G., & Komusiewicz, C. (2021). Sorting by Multi-Cut Rearrangements. Algorithms, 14(6), 169. https://doi.org/10.3390/a14060169







