On a Robust and Efficient Numerical Scheme for the Simulation of Stationary 3-Component Systems with Non-Negative Species-Concentration with an Application to the Cu Deposition from a Cu-(β-alanine)-Electrolyte

Abstract

Three-component systems of diffusion–reaction equations play a central role in the modelling and simulation of chemical processes in engineering, electro-chemistry, physical chemistry, biology, population dynamics, etc. A major question in the simulation of three-component systems is how to guarantee non-negative species distributions in the model and how to calculate them effectively. Current numerical methods to enforce non-negative species distributions tend to be cost-intensive in terms of computation time and they are not robust for big rate constants of the considered reaction. In this article, a method, as a combination of homotopy methods, modern augmented Lagrangian methods, and adaptive FEMs is outlined to obtain a robust and efficient method to simulate diffusion–reaction models with non-negative concentrations. Although in this paper the convergence analysis is not described rigorously, multiple numerical examples as well as an application to elctro-deposition from an aqueous ${\mathrm{Cu}}^{2+}$-($\beta$-alanine) electrolyte are presented.

1. Introduction

Diffusion-reaction equations play a central role in the modelling and simulation of chemical processes, as the corresponding system describes the transport of multiple species w.r.t. diffusion and a single reaction. The modelling of processes in the interior of lithium-ion batteries, complexation of metals during electro-plating, the electrical potentials in neurons, diffusion in sensors, etc., are major examples for the usage of three-component systems.

While the classical models in the literature of the speciation and modelling of metal-ions, cf. [1,2,3,4,5,6], are not considering non-negative species-concentrations, this paper aims at a model respecting non-negative species distributions in a simple case and their numerical treatment in a more general setting. This is motivated by the fact that negative species concentrations are unphysical and may and will most likely lead to false conclusions from simulated data.

While the analytical, cf. [7], and numerical, cf. [5,8,9,10], treatment of diffusion–reaction systems, are well known, even under convection, the enforcement of non-negative species distributions, especially in the numerics, are rarely discussed.

The numerical strategy, which is discussed in this article, is based on the reformulation, as discussed in Section 2, of the model equations into a constrained minimization problem in which the positive concentrations are part of the model formulation. The respective mathematical model that is used in this article is an optimization problem of the obstacle type, which is well known in physics and numerics c.f. [11,12,13].

A common strategy, cf. [13,14,15,16], to treat such problems of obstacle type is first to discretize the obstacle-problem and then treat the restrictions. This strategy leads to a restrained minimization problem in finite dimension. The resulting minimization problem can be treated with many methods such as quasi-Newton methods, cf. [17], SQP methods, cf. [18], penalty methods, cf. [19], augmented Lagrangian methods cf. [20,21,22], or Primal-Dual Active-Set Strategies, cf. [23].

This type of strategy (first discretization, then solution) has the advantage to be, in comparison, easy, but have some problems in terms of efficiency, since those methods are iterative methods, due to a fixed triangulation $\mathcal{T}$. Consequence is that for the convergence of the complete scheme, one has to assume that the iterated problems are solvable and stable with respect to $\mathcal{T}$. Hence, one has to invest in a reasonable set of cases more in computation time and data storage than possibly necessary, when using meshes for each iterated problem separately.

Hence, a new methodology will be derived un this article, where the restriction of the constrained minimization problem will first be treated with an augmented Lagrangian method and then a discretization will be made, to use an adaptive FEM, cf. [24], in every iteration of the augmented Lagrangian scheme. As a basis of the algorithm, augmented Lagrangian algorithms, c.f. [25,26], on Banach spaces will be used. As discretization of the considered Banach spaces conforming subspaces will be used, cf. [27,28,29,30].

Because the discretized problems discussed in this paper will be, as quasi-Newtonian schemes, unstable cf. [17], Homotopy methods, cf. [31,32], will be used to gain stability.

For the theoretical background, some fundamental studies on the resulting algorithm, considering some existence theory based on PDE and ODE theory [33,34,35] and the usage of $\mathsf{\Gamma }$-convergence, cf. [36,37,38,39], will be used. The theoretical results are underlined by an extensive numerical verification of the algorithm, as given in Section 4, indicates convergence of the numerical scheme and efficiency for nonlinear problem formulations and formulations on non-convex domains. Nevertheless, a full proof of convergence, stability, and existence theory will not be given in this paper.

As additional part of this article, a model for the static metal-deposition basing the complexation in a laminar boundary layer will be discussed, see Section 5.1, and numerically evaluated via the simulation methodology that is described in this article.

2. A Generalized Mathematical Model

2.1. The Classical Approach

In this article let $\mathsf{\Omega }\subset {\mathbb{R}}^d$, for $d\in \{1,2\}$, be an open, bounded, connected domain with Lipschitz boundary. Furthermore, let the boundary $\partial \mathsf{\Omega }$, be split into a Dirichlet boundary $\varnothing \ne {\mathsf{\Gamma }}_D\subseteq \partial \mathsf{\Omega }$ and a Neumann boundary ${\mathsf{\Gamma }}_N\subset \partial \mathsf{\Omega }$, such that ${\mathsf{\Gamma }}_D$ and ${\mathsf{\Gamma }}_N$ are relative open w.r.t. the restriction topology, ${\mathsf{\Gamma }}_D\cap {\mathsf{\Gamma }}_N=\varnothing$ and for the topological completion of ${\mathsf{\Gamma }}_N\cup {\mathsf{\Gamma }}_D$ one assumes the identity $\overline{{\mathsf{\Gamma }}_N\cup {\mathsf{\Gamma }}_D}=\partial \mathsf{\Omega }$.

During this article, reactions in the following form will be considered:

$$A+B\stackrel{k_1}{\underset{k_2}{\rightleftharpoons }}C.$$

(1)

As is known, cf. [1,2,3,4,7], the concentrations of the species A, B, C are formulated, in the stationary case, as a system of ODEs, for $d=1$, and a system of partial differential equations in multiple space dimensions, i.e., for $d>1$, which is for $f_A,f_B,f_C\in L^2(\mathsf{\Omega })$, for $g_{A,D},g_{B,D},g_{C,D}\in L^{\infty }({\mathsf{\Gamma }}_D)$, and for $g_{A,N},g_{B,N},g_{C,N}\in L^{\infty }({\mathsf{\Gamma }}_N)$, given through the following system of equations

$$\begin{array}{ccc}\hfill 0=& D_A\Delta c_A+k_2{c}_C-k_1{c}_A{c}_B+f_A,\hfill & \hfill \mathrm{in}\mathsf{\Omega },\end{array}$$

(2a)

$$\begin{array}{ccc}\hfill 0=& D_B\Delta c_B+k_2{c}_C-k_1{c}_A{c}_B+f_B,\hfill & \hfill \mathrm{in}\mathsf{\Omega },\end{array}$$

(2b)

$$\begin{array}{ccc}\hfill 0=& D_C\Delta c_C-k_2{c}_C+k_1{c}_A{c}_B+f_C,\hfill & \hfill \mathrm{in}\mathsf{\Omega },\end{array}$$

(2c)

$$\begin{array}{cc}\hfill g_{A,D}=& c_A{|}_{{\mathsf{\Gamma }}_D},g_{B,D}=c_B{{|}_{{\mathsf{\Gamma }}_D},g_{C,D}=c_C|}_{{\mathsf{\Gamma }}_D},\hfill \end{array}$$

(2d)

$$\begin{array}{cc}\hfill g_{A,N}=& \nabla c_A{|}_{{\mathsf{\Gamma }}_N}·{\nu }_{{\mathsf{\Gamma }}_N},g_{B,N}=\nabla c_B{{|}_{{\mathsf{\Gamma }}_N}·{\nu }_{{\mathsf{\Gamma }}_N},g_{C,N}=\nabla c_C|}_{{\mathsf{\Gamma }}_N}·{\nu }_{{\mathsf{\Gamma }}_N}.\hfill \end{array}$$

(2e)

Note that, by $L^2(\mathsf{\Omega })$, in this article, the Hilbert space of square integrable functions is denoted, with scalar product ${(•,•)}_{L^2(\mathsf{\Omega })}:L^2(\mathsf{\Omega })\times L^2(\mathsf{\Omega })\to \mathbb{R}$ and induced norm ${\parallel •\parallel }_{L^2(\mathsf{\Omega })}:L^2(\mathsf{\Omega })\to \mathbb{R}$, c.f. [36,40]. Furthermore, the Banach spaces $L^p(\mathsf{\Omega })$ with associated norms ${\parallel •\parallel }_{L^p(\mathsf{\Omega })}$, will be considered.

As can be seen, the straight-forward formulation given by the Equation (2a)–(2e) does not contain a condition of the non-negativity of the concentrations $c_S$, with $S\in \{A,B,C\}$. This missing formulation of non-negative species distributions will actually lead to unphysical behavior in the computation results. Hence in the following section, the usual approach to reinforce non-negative species distributions will be discussed.

2.2. Reinforcing Non-Negative Species Distributions

Assuming the system above has a unique solution, one obtains that the solution of the system (2a)–(2e) can be identified, for $p_S=\nabla c_S$, with the solution of the following minimization problem: Find ${(c_{S,LS},p_{S,LS})}_{S\in \{A,B,C\}}\in X$, such that

$$\begin{array}{cc}\hfill {(c_{S,LS},p_{S,LS})}_{S\in \{A,B,C\}}=& \underset{{(v_S,q_S)}_{S\in \{A,B,C\}}\in X}{\mathrm{argmin}}LS\left({(v_S,q_S)}_{S\in \{A,B,C\}}\right),\hfill \end{array}$$

(3)

where X is a Banach space, which will be defined later, and the non-linear least-squares functional $LS\left({(v_S,q_S)}_{S\in \{A,B,C\}}\right)$ is given through the following identity:

$$\begin{array}{cc}\hfill & LS\left({(v_S,q_S)}_{S\in \{A,B,C\}}\right):=\hfill \\ \hfill & \parallel D_A\mathrm{div}{q}_A+k_2{v}_C-k_1{v}_A{v}_B+f_A{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel q_A-\nabla v_A{\parallel }_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\parallel D_B\mathrm{div}{q}_B+k_2{v}_C-k_1{v}_A{v}_B+f_B{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel q_B-\nabla v_B{\parallel }_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\parallel D_C\mathrm{div}{q}_C-k_2{v}_C+k_1{v}_A{v}_B+f_C{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel q_C-\nabla v_C{\parallel }_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\sum _{S\in \{A,B,C\}}\left[\parallel v_S-g_{S,D}{\parallel }_{L^2({\mathsf{\Gamma }}_D)}^2+\parallel \nabla v_S·{\nu }_{{\mathsf{\Gamma }}_N}-g_{S,N}{\parallel }_{L^2({\mathsf{\Gamma }}_D)}^2\right]\hfill \end{array}$$

For the last terms of the least squares functional above, one has to note that the space $L^{\infty }(\mathsf{\Omega })$ is continuously embedded into the space $L^2(\mathsf{\Omega })$ and, hence, the evaluation of the terms $\parallel c_S-g_{S,D}{\parallel }_{L^2({\mathsf{\Gamma }}_D)}^2$ and $\parallel \nabla c_S·{\nu }_{{\mathsf{\Gamma }}_N}-g_{S,N}{\parallel }_{L^2({\mathsf{\Gamma }}_D)}^2$ are formally correct and simplify the calculations needed to implement a corresponding solver.

In the following, the space X has to be fixed. The space X is defined s.t. the non-linear functional $LS\left({(v_S,q_S)}_{S\in \{A,B,C\}}\right)$ is well defined, for each element ${(v_S,q_S)}_{S\in \{A,B,C\}}\in X$.

First, note that, for each $S\in \{A,B,C\}$, the conditions $\mathrm{div}{q}_S\in L^2(\mathsf{\Omega })$ and $q\in L^2(\mathsf{\Omega };{\mathbb{R}}^d)$ have to be fulfilled, since for $d=1$, the divergence reduces to a simple derivative, i.e., $\mathrm{div}{q}_S=\frac{\partial }{\partial x}{q}_S$, one obtains, for $d=1$, the inclusion $q_S\in H^1(\mathsf{\Omega })$ and for $d=2,3$ the inclusion $q_S\in H(\mathrm{div};\mathsf{\Omega })$, for the definition of $H(\mathrm{div};\mathsf{\Omega })$ see [36,40].

Furthermore, one observes that the inclusion $v_A{v}_B,v_C\in L^2(\mathsf{\Omega })$ has to be fulfilled, a sufficient condition to fulfil the inclusion above is $v_A,v_B\in L^4(\mathsf{\Omega })$ and $\nabla v_A,\nabla v_B,\nabla v_C\in L^2(\mathsf{\Omega };{\mathbb{R}}^d)$, whence $v_A,v_B\in W^{1,4}(\mathsf{\Omega })$ and $v_C\in H^1(\mathsf{\Omega })$. The spaces $W^{k,p}(\mathsf{\Omega })$ and $H^k(\mathsf{\Omega })$ denote the usual and well known Sobolev spaces, cf. [36,40]. This gives, for $d=1$, the identity ${\left(W^{1,4}(\mathsf{\Omega })\times H^1(\mathsf{\Omega })\right)}^{\times 2}\times \left(H^1(\mathsf{\Omega })\times H^1(\mathsf{\Omega })\right)$ and for $d=2$ the identity ${\left(W^{1,4}(\mathsf{\Omega })\times H(\mathrm{div},\mathsf{\Omega })\right)}^{\times 2}\times \left(H^1(\mathsf{\Omega })\times H(\mathrm{div},\mathsf{\Omega })\right)$.

The reformulation discussed in this article is to introduce the positivity of $c_A$, $c_B$, $c_C$ as side condition, cf. [11,41].

Find ${\left(c_{S,LS},p_{S,LS}\right)}_{S\in \{A,B,C\}}\in X$, such that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\left(c_{S,LS},p_{S,LS}\right)}_{S\in \{A,B,C\}}=\underset{{(v_S,q_S)}_{S\in \{A,B,C\}}\in X}{\mathrm{argmin}}& LS\left({(v_S,q_S)}_{S\in \{A,B,C\}}\right)\hfill \\ \hfill \mathbf{s}.\mathbf{t}.:& 0\le v_S,\forall S\in \{A,B,C\}\hfill \end{array}\end{array}$$

(4)

where the non-linear least-squares functional $LS\left({(v_S,q_S)}_{S\in \{A,B,C\}}\right)$ is the same as in (3).

3. Numerical Scheme

This section is devoted to the construction of a robust numerical scheme to approximate a solution to (4). This section provides an outline of the numerical scheme and ommites the proof of convergence. In contrast to [5,42] no finite-difference scheme will be discussed, but a finite-element discretization, which allows for us to employ augmented Lagrangian methods, cf. [25,26], on the continuous level of the model.

In this section, a numerical scheme for a generalized problem in the form (3) will be discussed, by adding additional reaction terms ${\gamma }_S{c}_S$. The respective generalized least-squares functional is given through

$$\begin{array}{cc}\hfill & LS\left({(v_S,q_S)}_{S\in \{A,B,C\}}\right):=\hfill \\ \hfill & \parallel D_A\mathrm{div}{q}_A+{\gamma }_A{v}_A+k_2{v}_C-k_1{v}_A{v}_B+f_A{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel q_A-\nabla v_A{\parallel }_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\parallel D_B\mathrm{div}{q}_B+{\gamma }_B{v}_B+k_2{v}_C-k_1{v}_A{v}_B+f_B{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel q_B-\nabla v_B{\parallel }_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\parallel D_C\mathrm{div}{q}_C+{\gamma }_C{v}_C-k_2{v}_C+k_1{v}_A{v}_B+f_C{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel q_C-\nabla v_C{\parallel }_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\sum _{S\in \{A,B,C\}}\left[\parallel v_S-g_{S,D}{\parallel }_{L^2({\mathsf{\Gamma }}_D)}^2+\parallel \nabla v_S·{\nu }_{{\mathsf{\Gamma }}_N}-g_{S,N}{\parallel }_{L^2({\mathsf{\Gamma }}_D)}^2\right]\hfill \end{array}$$

In contrast to the usual numerical schemes, as described above, the current augmented Lagrangian methods work on the continuous level of the problem. Applying the algorithms given in [26] and in [25] to (4) yields the following Algorithm 1:

Algorithm 1: augmented Lagrangian algorithm

Input: $j=0$, $\left(x^{(0)},{\mu }^{(0)}\in X\times L^2{(\mathsf{\Omega })}^{\times 3}\right)$, $0<{\lambda }^{max}$, $0<{\alpha }_0$, $\tau \in ]0,1[$, $1<\gamma$, $\epsilon >0$.  Output: Approximate solution $\left({(c_{S,LS}^{(j+1)},p_{S,LS}^{(j+1)})}_{S\in \{A,B,C\}}\right)\in X$ to (4) and approximation ${\lambda }^{(j)}$ of the Lagrangian multiplier.  Follow the steps  S1.:   Define ${\lambda }^{(j)}:=min\left({\mu }^{(j)},{\lambda }^{max}\right)$ and approximate a solution to $$\left({(c_{S,LS}^{(j+1)},p_{S,LS}^{(j+1)})}_{S\in \{A,B,C\}}\right)=\underset{{(v_S,q_S)}_{S\in \{A,B,C\}}\in X}{\mathrm{argmin}}L{S}_{{\alpha }_j}\left({(v_S,q_S)}_{S\in \{A,B,C\}},\frac{{\lambda }^{(j)}}{{\alpha }_j}\right)$$ (5)  S2.:   Define $${\mu }^{(j+1)}:={\left({\lambda }^{(j)}-{\alpha }_j[c_A^{(j+1)},c_B^{(j+1)},c_C^{(j+1)}]\right)}_{+}.$$  If $j=0$ or if $${∥min\left[[c_A^{(j+1)},c_B^{(j+1)},c_C^{(j+1)}],\frac{{\lambda }^{(j)}}{{\alpha }_j}\right]∥}_{L^2(\mathsf{\Omega })}\le \tau {∥min\left[[c_A^{(j)},c_B^{(j)},c_C^{(j)}],\frac{{\lambda }^{(j-1)}}{{\alpha }_{j-1}}\right]∥}_{L^2(\mathsf{\Omega })}$$ (6)  then set ${\alpha }_{j+1}:={\alpha }_j$, otherwise set ${\alpha }_{j+1}=\gamma {\alpha }_j$.  S3.:   If $$\left|\left[c_A^{(j+1)},c_B^{(j+1)},c_C^{(j+1)}\right]·{\mu }^{(j+1)}\right|\le \epsilon$$  and $${∥\left[c_A^{(j+1)},c_B^{(j+1)},c_C^{(j+1)}\right]-{\left(\left[c_A^{(j+1)},c_B^{(j+1)},c_C^{(j+1)}\right]\right)}_{+}∥}_{L^2(\mathsf{\Omega })}\le \epsilon$$  then break the algorithm.  S4.:   Set $j=j+1$ and go to S1.

For $f\in L^2(\mathsf{\Omega })$, the map ${(•)}_{+}:L^2(\mathsf{\Omega })\to L^2(\mathsf{\Omega })$ is defined as ${(f)}_{+}:=max(0,f)$, almost everywhere. Furthermore, let $L{S}_{{\alpha }_k}\left({(v_S,q_S)}_{S\in \{A,B,C\}},\lambda \right)$ be given for all ${(v_S,q_S)}_{S\in \{A,B,C\}}\in X$ and for all $\lambda \in L^2{(\mathsf{\Omega })}^{\times 3}$ through the following non-linear functional:

$$\begin{array}{cc}\hfill & L{S}_{\alpha }\left({(v_S,q_S)}_{S\in \{A,B,C\}},\lambda \right):=\hfill \\ \hfill & \parallel D_A\mathrm{div}{q}_A+{\gamma }_A{c}_A+k_2{v}_C-k_1{v}_A{v}_B+f_A{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel q_A-\nabla v_A{\parallel }_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\parallel D_B\mathrm{div}{q}_B+{\gamma }_B{c}_B+k_2{v}_C-k_1{v}_A{v}_B+f_B{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel q_B-\nabla v_B{\parallel }_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\parallel D_C\mathrm{div}{q}_C+{\gamma }_C{c}_C-k_2{v}_C+k_1{v}_A{v}_B+f_C{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel q_C-\nabla v_C{\parallel }_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\sum _{S\in \{A,B,C\}}\frac{\alpha }{2}{∥{\left({\lambda }_S-v_S\right)}_{+}∥}_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\sum _{S\in \{A,B,C\}}\left[\parallel v_S-g_{S,D}{\parallel }_{L^2({\mathsf{\Gamma }}_D)}^2+\parallel \nabla v_S·{\nu }_{{\mathsf{\Gamma }}_N}-g_{S,N}{\parallel }_{L^2({\mathsf{\Gamma }}_N)}^2\right]\hfill \end{array}$$

Remark 1.

Note that the iterated minimization problem (5) generalizes the unrestrained minimization problem (3) through the choice of $\alpha =0$ and $\lambda =0$, as well as ${\gamma }_S=0$, for all $S\in \{A,B,C\}$. Hence, the choice of a numerical scheme for (5) directly implies a numerical scheme for (3).

The augmented Lagrangian algorithm leaves the unrestrained minimization problems (5) to approximate. As a first step, (5) will be discretized. The essential key to discretize (5) is the discretization of the space X. In this paper a conforming discretization of X was chosen, by choosing a finite-dimensional subspace $X_h\subset X$. The choice of $X_h$ will be discussed in the following.

Let $\mathcal{T}$, in the respective dimension, be at first, an arbitrary fixed triangulation of $\mathsf{\Omega }$. The index h of the finite dimensional space $X_h$ refers to the diameter of $\mathcal{T}$, which is in one space dimension the maximal length of an interval $T\in \mathcal{T}$ and in two, the length of the longest edge in the set of edges $\mathcal{E}$.

For $d=1$, the discrete (finite dimensional) space $X_h\subset X$ is constructed by the lowest order conforming discretization $S^1(\mathcal{T})\subset W^{k,p}(\mathsf{\Omega })$, where $S^1(\mathcal{T})$ is the space of affine splines that is defined by

$$S^1(\mathcal{T}):=P_1(\mathcal{T})\cap C_0(\mathsf{\Omega }),$$

where

$$\begin{array}{c}\hfill P_1(\mathcal{T}):=\left\{v\in L^2{(\mathcal{T})|\forall T\in \mathcal{T}\exists a,b\in \mathbb{R}:v|}_T=a+bx\right\},\end{array}$$

cf. [43]. Hence, in this paper, the discrete space $S^1{(\mathcal{T})}^{\times 6}=:X_h\subset X$ is used as discretization.

For $d=2$, the vector space affine splines $S^1(\mathcal{T})$, defined analogous as before as

$$\begin{array}{c}\hfill S^1(\mathcal{T}):=P_1(\mathcal{T})\cap C_0(\mathsf{\Omega }),\end{array}$$

are used as a conforming discretization of $W^{k,p}(\mathsf{\Omega })$, cf. [27,28,30], and the Raviart–Thomas elements given by

$$R{T}_0(\mathcal{T}):=P_1(\mathcal{T},{\mathbb{R}}^d)\cap H(\mathrm{div},\mathsf{\Omega }),$$

with

$$P_1(\mathcal{T},{\mathbb{R}}^d):=\left\{v\in L^2(\mathsf{\Omega };{\mathbb{R}}^d)|\forall T\in \mathcal{T}\exists a\in {\mathbb{R}}^d{,b\in \mathbb{R}:v|}_T=a+bx\right\},$$

as discretization of $H(\mathrm{div},\mathsf{\Omega })$. Hence, in this paper, the lowest order discretization $X_h\subset X$, will be discussed, which is given by

$$\begin{array}{c}\hfill X_h:=\left\{\begin{array}{cc}{\left(S^1(\mathcal{T})\times S^1(\mathcal{T})\right)}^{\times 3},\hfill & \mathrm{for}d=1,\hfill \\ {\left(S^1(\mathcal{T})\times R{T}_0(\mathcal{T})\right)}^{\times 3},\hfill & \mathrm{for}d=2.\hfill \end{array}\right.\end{array}$$

(7)

This leaves the following discrete problem to solve or to approximate:

Find $x_h\in X_h$ such that

$$\begin{array}{c}\hfill \left({(c_{S,LS,h},p_{S,LS,h})}_{S\in \{A,B,C\}}\right)=\underset{{(v_S,q_S)}_{S\in \{A,B,C\}}\in X_h}{\mathrm{argmin}}L{S}_{{\alpha }_j}\left({(v_S,q_S)}_{S\in \{A,B,C\}},\frac{{\lambda }^{(j)}}{{\alpha }_j}\right)\end{array}$$

(8)

As a fundamental step of the numerical scheme, a linearization of (8) is introduced. For this, a few calculations are necessary. First, remark that, in contrast to the non-linear functional $LS\left((v_{S,C},q_{S,RT})\right)$, the functional $L{S}_{\alpha }\left((v_{S,C},q_{S,RT}),\mu \right)$ is, for $\alpha >0$, not differentiable. The non-differentiability lies in the evaluation of the function ${\left(\mu -v_{S,C}\right)}_{+}$. Hence, for the linearization of ${\left(\mu -v_{S,C}\right)}_{+}$, one has to use a different notion of differentiability than the common Fréchet-differential. Therefore for the linearization of ${\left(\mu -v_{S,C}\right)}_{+}$ in this article, the convex subdifferential ${\partial }_{cvx}$ as defined, c.f. [44], was used. For a convex function $f:Y\to \mathbb{R}$, for a Banach space Y, its topological dual $Y^{\ast }$, and the dual pairing ${⟨•,•⟩}_{Y^{\ast },Y}$, cf. [40], in a point $y_0\in Y$ is given through

$$\begin{array}{c}\hfill {\partial }_{cvx}f(y_0):=\left\{g\in X^{\ast }|⟨g,x-x_0⟩+f(y_0)\le f(y),\forall y\in X\right\}.\end{array}$$

As it is commonly known, the subdifferential ${\partial }_{cvx}{\left(\left[{\mu }_S-c_S\right](•)\right)}_{+}$ is for almost all $x_0\in \mathsf{\Omega }$ and all $S\in \{A,B,C\}$, given through

$$\begin{array}{cc}\hfill {\partial }_{cvx}{\left(\left[{\mu }_S-c_S\right](•)\right)}_{+}(x_0)=& \left\{\begin{array}{cc}\left\{0\right\},\hfill & \mathrm{for}\left[{\mu }_S-c_S\right](x_0)<0,\hfill \\ \{-1\},\hfill & \mathrm{for}\left[{\mu }_S-c_S\right](x_0)>0,\hfill \\ [-1,0],\hfill & \mathrm{for}\left[{\mu }_S-c_S\right](x_0)=0.\hfill \end{array}\right.\hfill \end{array}$$

(9)

Furthermore, for $c_{A,h},c_{B,h}\in S^1(\mathcal{T})$ and arbitrary fixed $v_{A,h},v_{B,h}$, the following Taylor approximation is considered

$$\begin{array}{cc}\hfill v_{A,h}{v}_{B,h}\approx & c_{A,h}{c}_{B,h}+c_{A,h}\left[v_{B,h}-c_{B,h}\right]+c_{B,h}\left[v_{A,h}-c_{A,h}\right]\hfill \\ \hfill =& c_{A,h}{v}_{B,h}+v_{A,h}{c}_{B,h}-c_{A,h}{c}_{B,h}.\hfill \end{array}$$

(10)

An additional approximation of $c_{S,h}$, for $S\in \{A,B\}$, is made through

$$c_{S,h}\approx {\prod }_0{c}_{S,h}$$

In the notation above, the map, ${\prod }_0:L^2(\mathsf{\Omega })\to P_0(\mathcal{T})$ denotes the orthogonal $L^2$-projection onto the space of piecewise constant functions, which is given through:

$$P_0(\mathcal{T}):=\left\{v\in L^2{(\mathsf{\Omega })|\forall T\in \mathcal{T}\exists c\in \mathbb{R}:v|}_T\equiv c\right\}.$$

i.e., for all $f\in L^2(\mathsf{\Omega })$, the image of ${\prod }_{0}f$ is given as the solution of the following minimization problem, cf. [30]:

$$\begin{array}{c}\hfill {\prod }_{0}f=\underset{w_0\in P_0(\mathcal{T})}{\mathrm{argmin}}\parallel f-w_0{\parallel }_{L^2(\mathsf{\Omega })}^2.\end{array}$$

(11)

Furthermore, for $f\in H^1(\mathsf{\Omega })$, due to the Poincaré inequality, cf. [40] or [30], there exists a constant $0<c$, such that

$$\begin{array}{c}\hfill {\parallel f\parallel }_{L^2(\mathsf{\Omega })}^2=\parallel {\prod }_{0}f{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel (1-{\prod }_0)f{\parallel }_{L^2(\mathsf{\Omega })}^2\le \parallel {\prod }_{0}f{\parallel }_{L^2(\mathsf{\Omega })}^2+c{h}^2,\end{array}$$

(12)

where the equality results from the pythagorean theorem, [40].

The identities (9), (10), and (12) inspire the following quasi-Newton scheme given, for a starting value $x_0\in X_h$, through the iterative solution of the following minimization problem:

Find ${\left(c_{S,LS,h}^{(n)},p_{S,LS,h}^{(n)}\right)}_{S\in \{A,B,C\}}\in X_h$, such that the following identity holds true

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\left(v_{S,h}^{(n)},q_{S,h}^{(n)}\right)}_{S\in \{A,B,C\}}=\underset{{\left(v_{S,h},q_{S,h}\right)}_{S\in \{A,B,C\}}}{\mathrm{argmin}}L{S}_{\alpha }\left({(v_{S,h},q_{S,h})}_{S\in \{A,B,C\}},\mu ;\mathcal{T},n\right)\end{array}\end{array}$$

(13)

where $L{S}_{\alpha }\left({(v_{S,h},q_{S,h})}_{S\in \{A,B,C\}},\mu ;\mathcal{T}\right)$ is, for all ${(v_{S,h},q_{S,h})}_{S\in \{A,B,C\}}\in X_h$, defined as

$$\begin{array}{cc}\hfill & L{S}_{\alpha }\left({(v_{S,h},q_{S,h})}_{S\in \{A,B,C\}},\mu ;\mathcal{T}\right):=\hfill \\ \hfill & \parallel D_A\mathrm{div}{q}_A+{\gamma }_A{v}_{A,h}+k_2{v}_{C,h}-k_1\left[{\prod }_0(c_{A,h}^{(n-1)})v_{B,h}+{\prod }_0(c_{B,h}^{(n-1)})v_{A,h}-{\prod }_0(c_{A,h}^{(n-1)}{c}_{B,h}^{(n-1)})\right]+{\prod }_0{f}_A{\parallel }_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\parallel D_B\mathrm{div}{q}_B+{\gamma }_B{v}_{B,h}+k_2{v}_{C,h}-k_1\left[{\prod }_0(c_{A,h}^{(n-1)})v_{B,h}+{\prod }_0(c_{B,h}^{(n-1)})v_{A,h}-{\prod }_0(c_{A,h}^{(n-1)}{c}_{B,h}^{(n-1)})\right]+{\prod }_0{f}_B{\parallel }_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\parallel D_C\mathrm{div}{q}_C+{\gamma }_C{v}_{C,h}-k_2{v}_{A,h}+k_1\left[{\prod }_0(c_{A,h}^{(n-1)})v_{B,h}+{\prod }_0(c_{B,h}^{(n-1)})v_{A,h}-{\prod }_0(c_{A,h}^{(n-1)}{c}_{B,h}^{(n-1)})\right]+{\prod }_0{f}_C{\parallel }_{L^2(\mathsf{\Omega })}^2\hfill \\ \hfill & +\sum _{S\in \{A,B,C\}}\left[\parallel {\prod }_0{q}_{S,h}-\nabla v_{S,h}{\parallel }_{L^2(\mathsf{\Omega })}^2+\frac{\alpha }{2}{∥{\chi }_{A^{(n-1)}}(\frac{{\mu }_S}{\alpha }-v_S)∥}_{L^2(\mathsf{\Omega })}^2\right]\hfill \\ \hfill & +\sum _{S\in \{A,B,C\}}\left[\parallel v_S-g_{S,D}{\parallel }_{L^2({\mathsf{\Gamma }}_D)}^2+\parallel \nabla v_S·{\nu }_{{\mathsf{\Gamma }}_N}-g_{S,N}{\parallel }_{L^2({\mathsf{\Gamma }}_N)}^2\right]\hfill \end{array}$$

where the set $A_S^{(n-1)}\subset \mathsf{\Omega }$ is the support of ${\left({\mu }_S-c_S^{(n-1)}\right)}_{+}$, where the support of a function $f\in L^2(\mathsf{\Omega })$ is defined as $\mathrm{supp}(f):=\overline{\{x\in \mathsf{\Omega }|f(x)\ne 0\}}$. Hence, $A_S^{(n-1)}$ is defined as:    

$$A_S^{(n-1)}=\mathrm{supp}\left[{\left({\mu }_S-c_S^{(n-1)}\right)}_{+}\right]$$

furthermore for a subset $B\subset \mathsf{\Omega }$, the map ${\chi }_B:\mathsf{\Omega }\to [0,1]$ is given by

$${\chi }_B(x):=\left\{\begin{array}{cc}1,\hfill & \mathrm{for}x\in B,\hfill \\ 0,\hfill & \mathrm{else}.\hfill \end{array}\right.$$

As it can directly be seen, the inclusion ${\chi }_{A^{(n-1)}}(x)\subseteq {\partial }_{cvx}{\left(\left[{\mu }_S-c_S\right](•)\right)}_{+}(x)$ holds true.

As it is commonly known, cf. [17,45,46] Newton and quasi-Newton schemes tend to be unstable. One strategy, as described in [46], is to use stabilized quasi-Newton methods based on a coupling of a quasi-Newton method with a subgradient scheme, on a not linearised problem. Another option, which is used and implemented for the numerical examples, as discussed in the Section 4 and Section 5, are homotopy methods, cf. [31,32], which is a scheme for the solution (13), based on the iterative transformation of a system with known solution into the non-linear system associated to (13). The homotopy methodology is probably the easiest way to stabilize the numerical strategy and increase the robustness.

Remark 2.

The strategy refereed to as quasi-Newtonian scheme is in fact a disturbed variant of a ‘normal’ quasi-Newtonian scheme. The difference between the ‘normal’ quasi-Newtonian scheme and the quasi-Newtonian scheme discussed in this paper is the application of the projections ${\prod }_0$. The sequence that is generated by the corresponding quasi-Newtonian scheme is denoted by $y^{(k)}$.

Some notations are needed to describe the used transformation. First, let, for $M\in \mathbb{N}$, the following discretisation of the interval $[0,1]$ be given through $0=t_1\le \dots \le t_j\le \dots \le t_M=1$. Subsequently, a homotopy method is given by the solution, for $1\le j\le N$, by computing the following Algorithm 2:

Algorithm 2: Homotopie-Loop

Input: Inital discretization $0=t_1\le \dots \le t_j\le \dots \le t_M$ of the interval $[0,1]$, system parameters $D_A$, $D_B$, $D_C$, $k_1$, $k_2$ and set $j=0$, set initial value $x^{(0)}\in X^h$, $0<\epsilon$.  Output: Approximate solution to (8) and set ${(c_{LS,S,h}^{(n)},p_{LS,S,h}^{(n)})}_{S\in \{A,B,C\}}={(c_{LS,S,h}^{(n,1)},p_{LS,S,h}^{(n,1)})}_{S\in \{A,B,C\}}$.  The homotopy algorithm is given through the following steps.  S1:   For $n=1,2,\dots$ solve the following problem.  Find ${\left((c_{LS,S,h}^{(n,j)},p_{LS,S,h})\right)}_{S\in \{A,B,C\}}\in X_h$ s.t. $$\begin{array}{c}\hfill \begin{array}{cc}\hfill {(c_{LS,S,h}^{(n,j)},p_{LS,S,h}^{(n,j)})}_{S\in \{A,B,C\}}=\underset{{(v_{S,h},q_{S,h})}_{S\in \{A,B,C\}}\in X_h}{\mathrm{argmin}}& L{S}_{\alpha }\left({(v_{S,h},q_{S,h})}_{S\in \{A,B,C\}};\mathcal{T},n,j\right)\hfill \end{array}\end{array}$$ (14)  and break if $$\sum _{S\in \{A,B,C\}}\left[\parallel c_{S,h}^{j,n}-c_{S,h}^{j,n-1}{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel q_{S,h}^{j,n}-q_{S,h}^{j,n-1}{\parallel }_{L^2(\mathsf{\Omega })}^2\right]<\epsilon$$  and for all ${(v_{S,h},q_{S,h})}_{S\in \{A,B,C\}}\in X_h$, the linear functional $L{S}_{\alpha }\left({(v_{S,h},q_{S,h})}_{S\in \{A,B,C\}};\mathcal{T},n,j\right)$ is given by $$\begin{array}{cc}\hfill & L{S}_{\alpha }\left({(v_{S,h},q_{S,h})}_{S\in \{A,B,C\}};\mathcal{T},n,j\right)\hfill \\ \hfill & :=(1-t_j)\sum _{S\in \{A,B,C\}}\left[\parallel v_{S,h}{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel q_{S,h}{\parallel }_{L^2(\mathsf{\Omega })}^2\right]\hfill \\ \hfill & +t_{j}L{S}_{\alpha }\left({(v_{S,h},q_{S,h})}_{S\in \{A,B,C\}};\mathcal{T},n\right).\hfill \end{array}$$  S2:   If (14) converges for $n\to \infty$, go to S3 else refine the decomposition $0\le t_0\le \dots \le t_M=1$, set $j=0$ and go to S1.  S3:   If $t_j=1$ break the loop, else set $j=j+1$ and go to S1.

The usage of the homotopy-algorithm, as described above, yields a cost-intensive numerical scheme. Hence, the usage of adaptive schemes for (5) is the best choice at hand to treat the iterate problems. Adaptive schemes in the homotopy steps are possible, but not implemented for this paper.

Adaptive FEM is used as the last step of the numerical scheme. As described in [24,47,48] the adaptive scheme is given through the following Algorithm 3:

Algorithm 3: AFEM-loop

Input: Initial regular triangulation ${\mathcal{T}}_0$, system parameters, set $j=0$.  Output: Fine mesh ${\mathcal{T}}_{\ell }$, approximate limit of the solutions to (13), estimation of the error.  The adaptive FEM algorithm is given by the following steps:  S1:   Solve: Take the limit of the solutions iterated problems (13), approximated through Algorithm 2.  S2:   Estimate: Estimate the error of the current discrete problem on each element $T\in {\mathcal{T}}_j$ with an estimator $\eta$.  S2:   Break: If the triangulation is fine enough or the estimated error is lower than a given Tolerance, then break the condition.  S4:   Mark: Mark the elements of the triangulation $T\in {\mathcal{T}}_j$ with the highest estimated local errors.  S5:   Refine: Refine all marked elements and additonal elements, such that the result ${\mathcal{T}}_{j+1}$ is again a regular triangulation.  S6:   Set $j=j+1$ and go to S1:

At the end of the section, a few remarks have to be made:

Remark and Definition 1

(Used setup of the AFEM-Algorithm for this paper). Note that:

(i) 

In S2 of Algorithm 3, an estimator is evaluated on each element $T\in {\mathcal{T}}_j$, which has to be defined. Assuming that for the exact solution ${(u_{LS,S},p_{LS,S})}_{S\in \{A,B,C\}}\in X$ of (3), the equality

$$\begin{array}{c}\hfill LS\left({(u_{LS,S},p_{LS,S})}_{S\in \{A,B,C\}}\right)=0\end{array}$$

(15)

holds true. In this paper, the estimator $\sigma :\mathcal{T}\to {\mathbb{R}}_{\ge 0}$ and the discrete solution of the discrete solution from S1: of Algorithm 3, for $\alpha =0$ and $\mu \equiv 0$, is defined as

$$\begin{array}{cc}\hfill {\eta }^2(T)& :=\parallel D_A\mathrm{div}{q}_A+{\gamma }_A{c}_A+k_2{v}_C-k_1{v}_A{v}_B+f_A{\parallel }_{L^2(T)}^2+\parallel q_A-\nabla v_A{\parallel }_{L^2(T)}^2\hfill \\ \hfill & +\parallel D_B\mathrm{div}{q}_B+{\gamma }_B{c}_B+k_2{v}_C-k_1{v}_A{v}_B+f_B{\parallel }_{L^2(T)}^2+\parallel q_B-\nabla v_B{\parallel }_{L^2(T)}^2\hfill \\ \hfill & +\parallel D_C\mathrm{div}{q}_C+{\gamma }_C{c}_C-k_2{v}_C+k_1{v}_A{v}_B+f_C{\parallel }_{L^2(T)}^2+\parallel q_C-\nabla v_C{\parallel }_{L^2(T)}^2\hfill \\ \hfill & +\sum _{S\in \{A,B,C\}}\frac{\alpha }{2}{∥{\left({\lambda }_S-v_S\right)}_{+}∥}_{L^2(T)}^2\hfill \\ \hfill & +\sum _{S\in \{A,B,C\}}\left[\parallel v_S-g_{S,D}{\parallel }_{L^2({\mathsf{\Gamma }}_D\cap \partial T)}^2+\parallel \nabla v_S·{\nu }_{{\mathsf{\Gamma }}_N}-g_{S,N}{\parallel }_{L^2({\mathsf{\Gamma }}_N\cap \partial T)}^2\right].\hfill \end{array}$$

(ii) 

Because, for the solution $(u_{LS,S}^{(j)},p_{LS,S}^{(j)})\in X$ of (5), in the iteration $j\in \mathbb{N}$, for given ${\alpha }_j$ and ${\mu }^{(j)}$, one cannot expect the identity

$$\begin{array}{c}\hfill L{S}_{{\alpha }_j}\left((u_{LS,S}^{(j)},p_{LS,S}^{(j)}),{\mu }^{(j)}\right)=0\end{array}$$

(16)

to hold true, since a solution of (5) is in general not a solution to a system of non-linear equations. Hence, the usage of

$$\begin{array}{c}\hfill \rho (T):=L{S}_{{\alpha }_j}\left((u_{LS,S,h}^{(j)}{|}_T,p_{LS,S,h}^{(j)}{|}_T{{)}_{S\in \{A,B,C\}},{\mu }^{(j)}|}_T\right)=0,\end{array}$$

for the solution ${(u_{LS,S,h}^{(j)},p_{LS,S,h}^{(j)})}_{S\in \{A,B,C\}}$ of the discrete problem of S 1 of Algorithm 3, is not practical. In the spirit of the usage of adaptive schems an estimator τ, basing on ρ, is used, which gives an estimation on the local changes w.r.t. the elements $T\in \mathcal{T}$ of the evaluation of ρ. For the definition of a practical estimator let for an arbitrary fixed $T\in \mathcal{T}$ the element patch $\mathcal{T}(T)$ be given through

$$\mathcal{T}(T):=\left\{\widehat{T}\in \mathcal{T}|\partial \widehat{T}\cap \partial T\ne \varnothing \right\}.$$

Afterwards, the new estimator σ is given through:

$$\begin{array}{c}\hfill {\sigma }^2(T)=\underset{\widehat{T}\in \mathcal{T}(T)}{max}|{\rho }^2(\widehat{T})-\rho {(T)}^2|.\end{array}$$

(17)

(iii) 

A common strategy, used for the marking is the so-called Dörfler marking, cf. [49]. In this strategy, a set $\mathcal{M}$ is chosen for which, ${\tau }^2\in \{{\eta }^2,{\sigma }^2,{\rho }^2\}$, for a given bulk parameter $\theta \in [0,1]$ the inequality

$$\begin{array}{c}\hfill \theta \sum _{T\in \mathcal{T}}{\tau }^2(T)\le \sum _{T\in \mathcal{M}}{\tau }^2(T)\end{array}$$

(18)

holds true.

(iv) 

Note that the Dörfler marking implies for $\theta =1$ a simple uniform marking scheme.

(v) 

As discussed in [50,51], one can usually prove convergence of the adaptive scheme by using, as in this article, the least-squares functional as error estimator, but cannot expect optimal convergence rates as discussed in [24] or [47]. Hence, another error estimator has to be derived for which optimal convergence rates are provable.

With the remark and definition above, the numerical scheme is completed. The numerical validation will be made in Section 4, the numerical scheme will be validated.

3.1. Remarks on Existence and Convergence Theory to the Numerical Scheme

This subsection is devoted to a first discussion of some fundamental convergence and existence properties of the algorithm and the underlying optimization methods. The discussion in this section is incomplete, but it gives an important first glance at the theoretical background of the algorithm.

3.1.1. Notes on the Existence Theory

In this section, some theoretical notes on the existence theory will be given. While the existence theory in one space dimension, thanks to the ODE theory and, in particular, thanks to the theorem of Picard–Lindelölf, cf. [35], and for linear PDEs is well known, cf. [33], the existence theory for nonlinear PDEs is, in most of the cases, not known, cf. [34]. The following discussion only tangents the cases known in literature.

Remark 3

(The 1d-case). In this remark, a the 1d case will be discussed.

(i) 

The system of second order ODEs, as given by (2a)–(2e), can equivalently reformulated into a System of first order ODEs, which are uniquely solvable due to the theorem of Picard-Lindelölf, cf. [35].

(ii) 

The assertion in (i) gives directly the solvability of (3)–(5), due to the fact that in the derivation of the least squares functional exactly the needed first order reformulation was used, which was needed for the assertion.

After the remark above on ODE theory, a further remark on the linear PDE theory will by given:

Remark 4

(The linear 2d-case). In this remark, the discussion of linear variants of (2a)–(2e) will be treated. i.e., during this remark $k_1=0$ is assumed. In this case the continuous space X can be extended to $X={\left(H^1(\mathsf{\Omega })\times H(\mathrm{div},\mathsf{\Omega })\right)}^3$, which makes the theory reasonable easier since in this case X is an Hilbert space.

(i) 

First, similar as in [52], the case of minimal assumptions to the problem formulation will be discussed. Essentially one assumes $0<D_A,D_B,D_C$ and the injectivity of the linear operator $\mathcal{L}:H_D^1{(\mathsf{\Omega })}^3\to {\left(H_D^1{(\mathsf{\Omega })}^3\right)}^{\ast }=H_D^{-1}{(\mathsf{\Omega })}^3$, used in the operator Equation (2a)–(2e). For this, one assumes that $k_2,{\gamma }_A,{\gamma }_B$ and ${\gamma }_C$ are assumed to be chosen in a way that 0 is no eigenvalue of $\mathcal{L}$.

Indeed, the injectivity, i.e., there is no 0-Eigenvalue of the corresponding operator, assumption together with the assumption of the existence of solutions for given $f_A,f_B,f_C\in L^2(\mathsf{\Omega })$, gives the unique solvability due to Fredholm’s alternative, cf. [53].

The results above directly apply to the PDE equation that is given by

$$\begin{array}{ccc}\hfill 0=& D_A\mathrm{div}{p}_A+k_2{c}_C+f_A,\hfill & \hfill in\mathsf{\Omega },\end{array}$$

(19a)

$$\begin{array}{ccc}\hfill 0=& p_A-\nabla c_A,\hfill & \hfill in\mathsf{\Omega },\end{array}$$

(19b)

$$\begin{array}{ccc}\hfill 0=& D_B\mathrm{div}{p}_B+k_2{c}_C+f_B,\hfill & \hfill in\mathsf{\Omega },\end{array}$$

(19c)

$$\begin{array}{ccc}\hfill 0=& p_B-\nabla c_B,\hfill & \hfill in\mathsf{\Omega },\end{array}$$

(19d)

$$\begin{array}{ccc}\hfill 0=& D_C\mathrm{div}{p}_C-k_2{c}_C+f_C,\hfill & \hfill in\mathsf{\Omega },\end{array}$$

(19e)

$$\begin{array}{ccc}\hfill 0=& p_C-\nabla c_C,\hfill & \hfill in\mathsf{\Omega },\end{array}$$

(19f)

$$\begin{array}{cc}\hfill g_{A,D}=& c_A{|}_{{\mathsf{\Gamma }}_D},g_{B,D}=c_B{{|}_{{\mathsf{\Gamma }}_D},g_{C,D}=c_C|}_{{\mathsf{\Gamma }}_D},\hfill \end{array}$$

(19g)

$$\begin{array}{cc}\hfill g_{A,N}=& \nabla c_A{|}_{{\mathsf{\Gamma }}_N}·{\nu }_{{\mathsf{\Gamma }}_N},g_{B,N}=\nabla c_B{{|}_{{\mathsf{\Gamma }}_N}·{\nu }_{{\mathsf{\Gamma }}_N},g_{C,N}=\nabla c_C|}_{{\mathsf{\Gamma }}_N}·{\nu }_{{\mathsf{\Gamma }}_N}.\hfill \end{array}$$

(19h)

and one obtains unique solvability of (19a)–(19h). The corresponding Operator is denoted by $\mathcal{O}:{\left(H^1(\mathsf{\Omega })\times H(\mathrm{div};\mathsf{\Omega })\right)}^3\to {\left[{\left(H^1(\mathsf{\Omega })\times H(\mathrm{div};\mathsf{\Omega })\right)}^3\right]}^{\ast }$, the RHS is given by a functional $g\in {\left[{\left(H^1(\mathsf{\Omega })\times H(\mathrm{div};\mathsf{\Omega })\right)}^3\right]}^{\ast }$.

This solvabllity of (19a)–(19h) directly implies the unique solvability of (3).

(ii) 

Note that in (i) only necessary conditions for the unique solvability are discussed. Some sufficient conditions can be obtained by the decoupling of the PDE. Where in fact the sufficient conditions for the unique solvability can be obtained by sufficient conditions to scalar Diffusion reaction equations, cf. [33,54].

(iii) 

By some standard calculations, as given in e.g., [19,28], one obtains that $x^{\ast }\in X$ solves (3) if the first order optimality in form of the Euler–Lagrange equations is fulfilled, which is given by the following equation:

Find $x^{\ast }\in X$ such that for all $y\in X$ the following equation holds true:

$$\begin{array}{c}\hfill a(x^{\ast },y):={\left(\mathcal{O}{x}^{\ast }-g,\mathcal{O}y\right)}_X={\left(g,\mathcal{O}y\right)}_X.\end{array}$$

(20)

Note that, due to the unique solvability of (3) and the problem equivalence described above, one obtains the unique solvability of (20).

(iv) 

From the unique solvability of (3), c.f. (i) and (iii), it directly follows, cf. theorem 3.6 on page 120 in [30], that the bilinear form $a(•,•):X\times X\to \mathbb{R}$ is elliptic.

(v) 

From the ellipticity of the bilinear form a, cf. (iv), one directly obtains the unique solvability of (4).

3.1.2. Notes on the Convergence Theory

In this section, a few notes on the convergence theory will be made. Although a proof of convergence of the solutions to the discretisation of (5), will be given in this section, the convergence analysis will be incomplete. For the rest of the necessary convergence theorems, some notes on what to be shown will be given.

First, some remarks on the quasi-Newtonian scheme, as given by the iterative solution of (13) and the Homotopy loop will be made. The remark below gives a sketch of the proof of convergence of the discussed quasi-Newtonian scheme. A mathematical rigorous proof has to be given in a future paper.

Remark 5. 

(i)  First note that the least squares functional $LS\left({(v_S,q_S)}_{S\in \{A,B,C\}}\right)$ is Fréchet differentiable and explicitly $A\left({(v_S,q_S)}_{S\in \{A,B,C\}}\right)=v_A{v}_B$ is Fréchet differentiable. Recall that the Notion of Fréchet derivatives yields that for given $x\in X$ and for all $0<\epsilon$, there exists a $0<\delta$, such that

$$\begin{array}{c}\hfill \parallel A(x+h)-A(x)-A^{\prime }(x)d{\parallel }_Y\le {\epsilon \parallel d\parallel }_X,\forall {\parallel d\parallel }_X<\delta .\end{array}$$

• This yields that there exists a constant $0<c$, such that for a solution $x_h^{(n)}\in X$ of (13) the following estimate holds true, if the initial value $x_0\in X_h$ is sufficiently close to the exact solution to (8):

  $$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \left|L{S}_{{\alpha }^{(k)}}\left(x_h^{(n)},\frac{{\lambda }^{(k)}}{{\alpha }^k}\right)-L{S}_{{\alpha }^{(k)}}\left(x_h^{(n)},\frac{{\lambda }^{(k)}}{{\alpha }^k};\mathcal{T},n\right)\right|\hfill \\ \hfill & \le \epsilon \parallel x_h^{(n)}-x_h^{(n-1)}{\parallel }_X\hfill \\ \hfill & +c{\displaystyle \sum _{S\in \{A,B,C\}}}\left[\parallel (1-{\prod }_0)p_{S,h}^{(n)}{\parallel }_{L^2(\mathsf{\Omega };{\mathbb{R}}^d)}+\parallel (1-{\prod }_0)c_{S,h}^{(n)}{\parallel }_{L^2(\mathsf{\Omega })}\right]\hfill \end{array}\end{array}$$

  (21)
• As discussed in Remark 2, a direct application of a classical quasi-Newtonian scheme to (8) yields a convergent sequence $(y^n)\subset X_h$, if the initial value $y_0$ is sufficiently close to the solution $x_h^{\ast }\in X_h$ to (8) and it follows with inequality (21), the convergence of $x_h^{(n)}$.
• A similar interpretation, as in Remark 2 of the sequences $y_h^k,x_h^{(k)}\subset X_h$ and the inequality (21), indicate that there exists a constant $c_1>0$, such that for initial values $y^{(0)}$ sufficiently close to the solution $x_h^{\ast }$ of (8) and the initial value $x_h^{(0)}$ are sufficiently close to the limit of the quasi-Newtonian scheme, the following inequality holds true:

  $$\begin{array}{cc}\hfill & \parallel x_h^{(n)}-y_h^{(n)}{\parallel }_X\hfill \\ \hfill & \le c_1\sum _{S\in \{A,B,C\}}\left[\parallel (1-{\prod }_0)p_{S,h}^{(n)}{\parallel }_{L^2(\mathsf{\Omega };{\mathbb{R}}^d)}+\parallel (1-{\prod }_0)c_{S,h}^{(n)}{\parallel }_{L^2(\mathsf{\Omega })}\right].\hfill \end{array}$$
• It directly follows

  $$\begin{array}{c}\hfill \underset{h\downarrow 0}{lim}{\parallel x_h^{(n)}-y_h^{(n)}\parallel }_{X_h}=0.\end{array}$$

  (22)

(ii) 

The discussion (i) indicates that the quasi-Newtonian scheme described by the iterative solution by (13) has the same issue with stability as classical quasi-Newtonian schemes, cf. [17]. To stabilize the quasi-Newtonian scheme, it was coupled to a homotopy method, cf. [32]. As already discussed, the idea of the method is to solve for a continuous function $H:X_h\times [0,1]\to X_h$, with $H(x_h,0)=i{d}_{X_h}$ and $H(x_h,1)=L{S}_{{\alpha }_k}\left(x_h,\frac{{\mu }^{(k)}}{{\alpha }_k};\mathcal{T},n\right)$ and a decomposition $0=t_0<\dots <t_j<\dots <t_M$ to solve the minimization problem that is given by:

Find $x_h^{(j)}\in X_h$ susch that

$$\begin{array}{c}\hfill x_h^{(j)}=\underset{x_h\in X_h}{\mathrm{argmin}}H(x_h,t_j).\end{array}$$

(23)

As a solution step, the quasi-Newtonian scheme (13) can be used. For $j=0$, an initial value $x_0$ for the algorithm is given through $x_0$ and for $j>0$ the $x_h^{(j-1)}$ is given as an initial value for the quasi-Newtonian scheme.

In the following lemma, a theoretical statement will be proven, which will be essential for the proof of a simple convergence result for solutions of (8).

For the proof of the following Lemma, recall the $\mathsf{\Gamma }$-convergence. As defined in [36,37,38,39], a sequence of nonlinear functionals $F_n:X\to \mathbb{R}$ is said to $\mathsf{\Gamma }$-converge to a functional $F:X\to \mathbb{R}$ if the following two conditions are fulfilled:

(i)

For every sequence $(x_n)\subset X$, with $x=\underset{n\to \infty }{lim}{x}_n$, the following inequality holds true:

$$\begin{array}{c}\hfill F(x)\le \underset{n\to \infty }{lim\; inf}{F}_n(x_n)\end{array}$$

(24)

(ii)

For every $x\in X$, there exists a sequence $(x_n)\subset X$ with $x=\underset{n\to \infty }{lim}{x}_n$, such that the following inequality holds true:

$$\begin{array}{c}\hfill F(x)\ge \underset{n\to \infty }{lim\; sup}{F}_n(x_n).\end{array}$$

(25)

Lemma 1.

Let ${\mathcal{T}}_n$ be a sequence of tirangulations with $h_n\downarrow 0$, where $h_n$ denotes the diameter of ${\mathcal{T}}_n$, which fulfills $0=\underset{n\to \infty }{lim}{h}_n$, as well as that ${\mathcal{T}}_{n+1}$ is a refinement of ${\mathcal{T}}_n$, i.e., the set of nodes ${\mathcal{N}}_n$ of ${\mathcal{T}}_n$ is included in the set of nodes ${\mathcal{N}}_{n+1}$ of ${\mathcal{T}}_{n+1}$, i.e., ${\mathcal{N}}_n\subset {\mathcal{N}}_{n+1}$, then the sequence $F_n:X\to \mathbb{R}$ given through,

$$F_n:=F+{\delta }_{{\mathcal{T}}_n},$$

Γ-converges to $F:=L{S}_{{\alpha }_j}(x,{\lambda }^{´(j)})$. In the notation above, ${\delta }_n$ is given through the following definition:

$$\begin{array}{c}\hfill {\delta }_n(x)=\left\{\begin{array}{cc}0,\hfill & \mathit{for}x\in X_{h_n},\hfill \\ \infty ,\hfill & \mathit{else}.\hfill \end{array}\right.\end{array}$$

Proof. 

To prove the $\mathsf{\Gamma }$-convergence of the sequence $(F_n)$, the assertions (24) and (25) have to be proven.

(i)

ad (24): for the proof of this claim one needs to distinguish two cases. However, first, let $x\in X$ and $x^{(k)}\subset X$ with $x={lim}_{k\to \infty }{x}^{(k)}$ be arbitrary fixed.

(a)

First, assume that up to finitely many $n\in \mathbb{N}$ one has $\neg (x_n\in X_{h_n})$. From the definition of $F_n$ it follows then that, up to finitely many $n\in \mathbb{N}$, the lowest accumulation point of the sequence $F_n(x_n)=+\infty$. Hence, one obtains the following inequality:

$$\begin{array}{c}\hfill F(x)\le \underset{n\to \infty }{lim\; inf}{F}_n(x_n)=\infty .\end{array}$$

The inequality above shows the assertion for this case.

(b)

For the second case, assume that there are infinitely many $n\in \mathbb{N}$, such that $x_n\in X_{h_n}$. Subsequently, there exists a subsequence $(x_{n_l})\subset (x_n)$ with

$$F_{n_l}(x_{n_l})=F(x_{n_l}).$$

Because of the continuity of F and the definition of $F_n$, it follows:

$$F(x)=\underset{l\to \infty }{lim}F(x_{n_l})=\underset{l\to \infty }{lim}{F}_{n_l}(x_{n_l})=\underset{n\to \infty }{lim\; inf}{F}_n(x_n).$$

The equalities above yield that the claim for the second case holds true.

The discussion of the two cases above proves the claim.

(ii)

ad (25): first, note that, for all $n\in \mathbb{N}$, one has a continuous embedding $S^1(\mathcal{T})\times \hookrightarrow W^{k,2}(\mathcal{T})$ and ${\displaystyle \bigcup _{n\to \infty }}{S}^1({\mathcal{T}}_n)$ is a dense subset of $W^{k,2}(\mathsf{\Omega })$, c.f. [19,27,28,29]. Similarly, one has a continuous embedding $R{T}_0(\mathcal{T})\hookrightarrow H(\mathrm{div},\mathsf{\Omega })$ furthermore ${\displaystyle \bigcup _{n\to \infty }}R{T}_0(\mathcal{T})$ is a dense subset of $H(\mathrm{div},\mathsf{\Omega })$, c.f. [19,27,28,29]. From the definitions of $X_h$ and X, it follows with the both densities, where ${\displaystyle \bigcup _{n\to \infty }}{X}_{h_n}$ is a dense subset of X. From the assumptions on the sequence ${\mathcal{T}}_n$ and the density of ${\displaystyle \bigcup _{n\to \infty }}$ it follows that there exist, for all $x\in X$, a sequence with $x_n\in X_{h_n}$ s.t. $x=\underset{n\to \infty }{lim}{x}_n$. Furthermore, it follows from the continuity of F and the definitions above:

$$\begin{array}{c}\hfill F(x)=\underset{n\to \infty }{lim}F(x_n)=\underset{n\to \infty }{lim}{F}_n(x_n)=\underset{n\to \infty }{lim\; sup}{F}_n(x_n).\end{array}$$

(26)

The equalities above prove the statement.

From (i) and (ii), the claim of the Lemma follows by definition.    □

Corollary 1.

Let ${\mathcal{T}}_n$ be a sequence of triangulations fulfilling ${\mathcal{N}}_n\subset {\mathcal{N}}_{n+1}$ and $h_n\downarrow 0$ as $n\to \infty$, then the following two statements hold true:

(i) 

Let ${(y^{(n)})}_{h_n}\subset X$, be the sequence of minimizers of (8) generated by the usage of $X_{h_n}$ as discrete subspace $X_{h_n}\subset X$ in the problem formulation of (4), then every accumulation point of $(y_{h_n}^{(n)})$ is a minimizer of (4).

(ii) 

Let $x_{h_n}^{(n)}\subset X$ be the sequence of limits of the sequences that are generated by the solution of (13) on the triangulations ${\mathcal{T}}_n$, then every accumulation point of the sequence $x_{h_n}^{(n)}$ is a minimizer of (4).

Proof. 

Let the sequences ${\mathcal{T}}_n$, ${(y^{(n)})}_{h_n}\subset X$, $x_{h_n}^{(n)}\subset X$ be given, as stated in the corollary.

(i)

A common result in the context of $\mathsf{\Gamma }$-convergence, c.f. in [36,37,38,39], is that if $G_n:X\to \mathbb{R}$ $\mathsf{\Gamma }$-converges to $G:X\to \mathbb{R}$ then every accumulation point of the sequence of minimizers ${(x_n)}_{n\in \mathbb{N}}$, i.e., $x_n$ minimizes $G_n$, is a minimizer of G.

Applying this theoretical result to the setup of Lemma 1, one obtains the statement in the corollary.

(ii)

The statement of the lemma directly follows by (i) and by (22).

   □

Remark 6. 

(i)  The convergence proof above is a first result underlining the plausibillity of the described discretization of (5). But first note that from the proof of convergence above no rates of convergence can be obtained. From the classical theory, cf. [19,27,28,29], convergence to a certain rate seems to be a valid hypothesis, at least for the linear cases of the PDE (2a)–(2e), cf. [14,15,19].

(ii) 

Note that convergence of the sequence of limits $x_{h_k}=\underset{n\to \infty }{lim}{x}_{h_k}^{(n)}$, where $x_{h_k}^{(n)}$ is a solution to (13), will only be obtained if one accumulation point of $x_{h_k}$ exists, this is fulfilled if (5) is uniquely solvable.

With this result, this section will be concluded. For future discussions, the following discussions have to be made:

• The stability and the convergence of the augmented Lagrangian Algorithm 1 is proven in [25,26], to prove stability and the convergence of Algorithm 1 for the case that is considered in this article the assumptions of the corresponding theorem in [25] have to be verified.
• The convergence of the quasi-Newtonian scheme (13) has to be discussed in a much more rigorous way than done in Remark 5.
• Convergence to a certain rate has to be verified for the discretization of (5).
• As known to the authors, the existence theory, as described in Section 3.1.1, is for the problem (2a)–(2e) incomplete. A careful study of sufficient and necessary condition has to be made.

4. Numerical Examples and Validation of the Software

In this section, multiple numerical experiments are treated to validate the robustness and the functionality of the numerical scheme. In all three subsections, the numerical examples that are given through the parameters in the Table 1, Table 2 and Table 3 are discussed. Furthermore, for all numerical examples, the starting values for the augmented Lagrangian algorithm were chosen as ${\alpha }^{(0)}=\frac{5}{6}$, ${\mu }^{(0)}(x)=0$ for all $x\in \mathsf{\Omega }$, $\tau =0.9$, and ${\lambda }^{max}(x)=0.02$ for all $x\in \mathsf{\Omega }$.

Table 1. The first example of physical parameters of the diffusion–reaction model for the complexation of K.

Species	D in $\frac{{\mathbf{m}}^2}{\mathbf{s}}$	${\mathit{k}}_1$ in $\frac{1}{\mathit{s}}$	${\mathit{k}}_2$ in $\frac{{\mathbf{m}}^3}{\mathbf{mol}\mathbf{s}}$	${\mathit{\gamma }}_{\mathit{S}}$
A	$1/2$	-	-	0
B	$1/3$	-	-	0
C	$1/4$	0	0	0

Table 2. Second example of physical parameters of the diffusion–reaction model for the complexation of K.

Species	D in $\frac{{\mathbf{m}}^2}{\mathbf{s}}$	${\mathit{k}}_1$ in $\frac{1}{\mathit{s}}$	${\mathit{k}}_2$ in $\frac{{\mathbf{m}}^3}{\mathbf{mol}\mathbf{s}}$	${\mathit{\gamma }}_{\mathit{S}}$
A	$1/2$	-	-	0
B	$1/3$	-	-	0
C	$1/4$	0	1	0

Table 3. Third example of physical parameters of the diffusion–reaction model for the complexation of K.

Species	D in $\frac{{\mathbf{m}}^2}{\mathbf{s}}$	${\mathit{k}}_1$ in $\frac{1}{\mathit{s}}$	${\mathit{k}}_2$ in $\frac{{\mathbf{m}}^3}{\mathbf{mol}\mathbf{s}}$	${\mathit{\gamma }}_{\mathit{A}}$
A	$1/2$	-	-	0
B	$1/3$	-	-	0
C	$1/4$	1	1	0

4.1. Numerical Examples in 1d

For the numerical examples presented in this section, let $\mathsf{\Omega }:=]0,2[$. For the examples that are discussed in this section, let an exact solutions $c_A,c_B,c_C$ of the unrestrained problem (3) be given through

$$\begin{array}{c}\hfill c_A:=c_B:=c_C:=x(x-2)+\frac{1}{2}\end{array}$$

(27)

and let ${\mathsf{\Gamma }}_D=\partial \mathsf{\Omega }$ and $g_{A,D}=g_{B,D}=g_{C,D}\equiv 1$. Afterwards, the functions $f_A,f_B,f_C\in L^2(\mathsf{\Omega })$ are given through

$$\begin{array}{cc}\hfill f_A=& -2D_A-k_2\left(x(x-2)+\frac{1}{2}\right)+k_1{\left(x(x-2)+\frac{1}{2}\right)}^2,\hfill \end{array}$$

(28a)

$$\begin{array}{cc}\hfill f_B=& -2D_B-k_2\left(x(x-2)+\frac{1}{2}\right)+k_1{\left(x(x-2)+\frac{1}{2}\right)}^2,\hfill \end{array}$$

(28b)

$$\begin{array}{cc}\hfill f_C=& -2D_C+k_2\left(x(x-2)+\frac{1}{2}\right)-k_1{\left(x(x-2)+\frac{1}{2}\right)}^2.\hfill \end{array}$$

(28c)

As breaking conditions for the simulations, in this subsection, the fulfillment of the following conditions were set:

• The breaking condition from S3 in Algorithm 1 is fulfilled with a tolerance $\epsilon :={10}^{-4}$.
• The number of nodes in the current mesh increases $\mathrm{10,000}$ nodes.
• More than 100,000 iterations of the augmented Lagrangian algorithm were performed.

Before the numerical examples are discussed, note that the exact error is given through:

$$\begin{array}{c}\hfill \parallel x-x_h{\parallel }_X^2=\sum _{S\in \{A,B,C\}}\left[\parallel \nabla c_S-\nabla u_S{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel p_{S,h}-\nabla u_S{\parallel }_{L^2(\mathsf{\Omega })}^2+{∥\frac{\partial }{\partial x}{p}_{S,h}-\frac{{\partial }^2}{\partial x^2}{u}_S∥}_{L^2(\mathsf{\Omega })}^2\right].\end{array}$$

(29)

Simulating the unrestrained problem (3), for the the given RHS, as defined above, for the parameters that are defined in the Table 1, Table 2 and Table 3, with the reduced numerical scheme, see Remark 1, one obtains approximations of the defined exact solution (27). For a number of $\mathrm{10,000}$ DoFs, one obtains the results that are shown in Figure 1, which were simulated for the parameters defined in Table 1. Because no visible difference to the other experiments can be seen, Figure 1 will be the only given pictures of approximate solutions to (3) in this section.

Figure 1. Concentration profiles with negative concentrations $c_A$ (a), $c_B$ (b) and $c_C$ (c), obtained by approximation of (3), for the parameters that are given in Table 1.

Furthermore, note that, for the simulations, the following setup was chosen:

For all simulations of the ‘classical’ concentration-profiles, with no restrictions on the positivity of the concentrations, the reduced method, as described in Remark 1, was used. Furthermore, in all cases of simulations of (3), the estimtor $\eta$ was used. For the adaptive refinement of (5), the practical error estimator $\sigma$ was used for all approximations of solutions of (5). Furthermore, for all adaptive refinement Dörfler marking, cf. Remark 1, was used as marking strategy with common bulk parameter $\theta =0.5$.

The first example that will be discussed in the following in more detail is given by the parameters in Table 1. As mentioned before, Figure 1 provides the simulations with a minimum number of ${10}^4$ nodes in the AFEM loop as breaking-condition.

By the evaluation of the error estimators for this example, cf. Figure 2, one can observe convergence of the estimators, except for the practical estimator $\sigma$ for the uniform refinement. As expected, the rest of the estimators are parallel, from which the equivalence of estimators can be formulated as a conjecture.

Figure 2. Developement of the error estimators for the uniform and adaptive mesh refinement, for the approximation of (3) with the parameters given in Table 1.

In Figure 3, some iterations of the augmented Lagrangian scheme with uniform refinement are shown. The augmented Lagrangian scheme needed 85 steps to obtain non-negative species distributions. The augmented Lagrangian scheme converges to set a non-negative species distributions for this example, as shown in the subfigures (a), (d), (g).

Figure 3. Concentrationprofiles (a,d,g), evaluation of the Lagrangian multipliers (b,e,h) and estimators (c,f,i) during the augmented Lagrangian scheme in the 1-st, 43-rd, and 85-th itartion w.r.t. parameters that are given in Table 1 and uniform mesh refinement.

Furthermore, as predicted in Remark 1, the localized evaluation of the least-squares functional, which is given by the estimator $\eta$, does not converge to zero in all examples. In this case, for the uniform refinement, the practical error estimator converges $\underset{h\downarrow 0}{lim}\sigma =0$.

Additionally, this example also shows the convergence of the multipliers ${\mu }_A$, ${\mu }_B$, and ${\mu }_C$ as well, which also seems to converge.

The parameter $\alpha$ grows exponentially over the iterations of the augmented Lagrangian algorithm, as shown in the Figure 4.

Figure 4. Development of $\alpha$ during the augmented Lagrangian algorithm.

In Figure 5, the development of the augmented Lagrangian algorithm is shown, applying the adaptive algorithm in each iteration of (5). The augmented Lagrangian algorithm takes, like for uniform mesh refinement, 85 iterations to guarantee non-negative species distributions, as can be seen in this case. Just observing the discrete solutions $c_{A,h}$, cf. Figure 5a, $c_{B,h}$ (d), and $c_{C,h}$ (g), and the Lagrangian multipliers ${\mu }_A$ (b), ${\mu }_B$ (e), and ${\mu }_C$ (h), one obtains the same result as for the uniform refinement. The limit of the solutions seems to be identical, but the interesting aspect is the estimators, which are given in the subfigures (c), (f), and (i). The practical errors $\sigma$ seem to converge to a value $b\ne 0$, as well as the estimators $\eta$ do, as expected to a value $a\ne 0$.

Figure 5. Concentration profiles (a,d,g), evaluation of the Lagrangian multipliers (b,e,h) and estimators (c,f,i) during the augmented Lagrangian scheme in the 1-st, 43-rd and 85-th itartion w.r.t. parameters that are given in Table 1 and adaptive mesh refinement.

The development of the parameter $\alpha$ for the augmented Lagrangian algorithm with adaptive mesh refinement is similar to the development of the augmented Lagrangian algorithm with uniform mesh refinement. No further pictures are given due to the fact that no differences are visible between the developments of $\alpha$ with uniform or adaptive mesh refinement.

The second example that is discussed in this section is given by the parameters shown in Table 2. In Figure 6, the convergence graphs for the approximation of the solution (3), for the given parameters, are shown. In this setting, the evaluation of the least squares functional $\eta$ for uniform and adaptive refinement are shown, as well as the exact error for uniform and adaptive refinement and the practical error $\sigma$ again for uniform and adaptive refinement are given. The corresponding graphs are, at most, parallel and show the same behavior and indicate convergence of the numerical scheme for the simulation, as can be seen in Figure 6. The graph indicates that the estimators could be equivalent for the simulation.

Figure 6. Developement of the error estimators for the uniform and adaptive mesh refinement, for the approximation of (3) with the parameters given in Table 2.

Applying the augmented Lagrangian Algorithm 1 onto (4) with the parameters that are given in Table 2 and applying uniform refinement on the mesh, $\mathcal{T}$ one obtains, after 89 iterations of the augmented Lagrangian scheme, non-negative species distributions, as seen in Figure 7.

Figure 7. Concentration profiles (a,d,g), evaluation of the Lagrangian multipliers (b,e,h) and estimators (c,f,i) during the augmented Lagrangian scheme in the 1-st, 44-th, and 89-th itartion w.r.t. parameters that are given in Table 2 and uniform mesh refinement.

The estimator $\eta$ converges not to 0 in each iteration of the augmented Lagrangian method, as expected, but the practical estimator does converge to 0 in each iteration, as can be seen in Figure 7.

In Figure 8, the application of the augmented Lagrangian algorithm is shown for multiple iterations with the application of adaptive mesh refinement, as described above. The algorithm needed, as for treating the iterate problems with uniform refinement, 89 iterations. As it can be seen, the algorithm outputs non-negative species distributions. In principle, equivalent results in the output can be seen in Figure 7. However, the principal behavior of the practical error estimator differs while using adaptive schemes from the same methodology but using uniform mesh refinement. The estimator $\eta$, cf. remark and Definition 1, converges, but not to 0, as expected, while the convergence of the practical error $\sigma$ seem to also be given, as can be seen in Figure 8c,f,i.

Figure 8. Concentration profiles (a,d,g), evaluation of the Lagrangian multipliers (b,e,h) and estimators (c,f,i) during the augmented Lagrangian scheme in the 1-st, 44-th and 89-th itartion w.r.t. parameters that are given in Table 2 and adaptive mesh refinement.

The developments of the parameter $\alpha$ during the augmented Lagrangian algorithm are for the adaptive and uniform refinement identical for linear reaction terms and they are very similar to the development for the pure diffusive case given in Figure 4.

The third example that is discussed in this section is given by the parameters in Table 3. The discrete solutions to (3) w.r.t. the parameters above are close to identical to the discrete solution given in Figure 1, as discussed previously. In fact no differences are visible. Hence, the corresponding figure will not be displayed in this paper.

The evaluation of the error estimators, which are defined in remark and Definition 1, cf. Figure 9, are yielding that the numerical scheme converges for both the uniform and adaptive refinement scheme. Furthermore, it is shown in Figure 9 that the localized evaluation of the non-linear least-squares functional, as beforehand $\eta$, seems to be equivalent to the exact error for uniform and adaptive refinement. Furthermore, up to a value of approximately ${10}^4$ DoF, the corresponding practical estimators $\sigma$ are decreasing for uniform and adaptive refinement. At this stage, the convergence of the numerical schemes is given from a practical viewpoint.

Figure 9. Development of the error estimators for the uniform and adaptive mesh refinement, for the approximation of (3) with parameters given in Table 3.

Applying the augmented Lagrangian algorithm, cf. Algorithm 1, to (4) with the parameters that are given in the Table 3 and applying uniform refinement, one obtains non-negative species distributions after 89 iterations of the augmented Lagrangian scheme, c.f. Figure 3. Furthermore, it is observable that the practical error estimator $\eta$, cf. definition and Remark 1, converges, but not to 0 in each setting. Furthermore, it is observable that the practical $\sigma$, cf. definition and Remark 1, converges to zero for each iteration.

Applying the augmented Lagrangian algorithm to (4) with the parameters that are given in Table 3 and applying adaptive mesh refinement to the iterative defined problem (5), one obtains the results given in Figure 10. The iterates converge to a species distributions with non-negative species concentrations, as seen in the corresponding figure. After 89 iterations, non-negative species distributions are obtained. Furthermore, it is visible that the estimator $\eta$, cf. remark and Definition 1, that is based on the piecewise evaluation of the corresponding least-squares functional converges, but not to 0. In contrast to the setting shown in Figure 11, the practical error $\sigma$, cf. remark and Definition 1, one obtains convergence, but not to 0, as beforehand.

Figure 10. Concentration profiles (a,d,g), evaluation of the Lagrangian multipliers (b,e,h) and estimators (c,f,i) during the augmented Lagrangian scheme in the 1-st, 44-th and 89-th iteration w.r.t. the parameters given in Table 3 and uniform mesh refinement.

Figure 11. Concentration profiles (a,d,g), evaluation of the Lagrangian multipliers (b,e,h) and estimators (c,f,i) during the augmented Lagrangian scheme in the 1-st, 44-th and 89-th iteration w.r.t. parameters given in Table 3 and adaptive mesh refinement.

The developments of the parameter $\alpha$ during the augmented Lagrangian algorithm for the adaptive and uniform refinement are identical for the full reaction terms and they are very similar to the development for the pure diffusive case, as given in Figure 4, also in this case, a figure is not given in this paper.

As a remaining part of the discussions to the 1d examples, a comparison of the CPU running times of the different examples will be discussed. One observes that, for the given examples, the number of iterations of the augmented Lagrangian algorithm do not differ between uniform and adaptive mesh refinement, as seen in Table 4. However, one sees, in Table 4, that the usage of the adaptive algorithm is far more efficient than the usage of the uniform refinement. Especially for the nonlinear system of ODEs, as described by the parameter set given in Table 3, a massive reduction of computation time was obtained.

Table 4. Overview of number of iterations of the augmented Lagrangian Algorithm 1 and CPU times for the different parameter sets and uniform resp. adaptive mesh refinement.

Parameter Set	Type of Refinement	Number of Iterations	CPU-Time
Table 1	Uniform	85	$4.3157e+04$ s
Table 1	Adaptive	85	$1.0347e+04$ s
Table 2	Uniform	89	$5.0281e+04$ s
Table 2	Adaptive	89	$9.9426e+03$ s
Table 3	Uniform	89	$2.0356e+05$ s
Table 3	Adaptive	89	$4.7214e+04$ s

All together, one can conclude that the numerical scheme works for the given scheme and examples. Because of the fact that no rigorous proofs are done in this paper, the convergence remains as conjecture, based on the numerical results in this section.

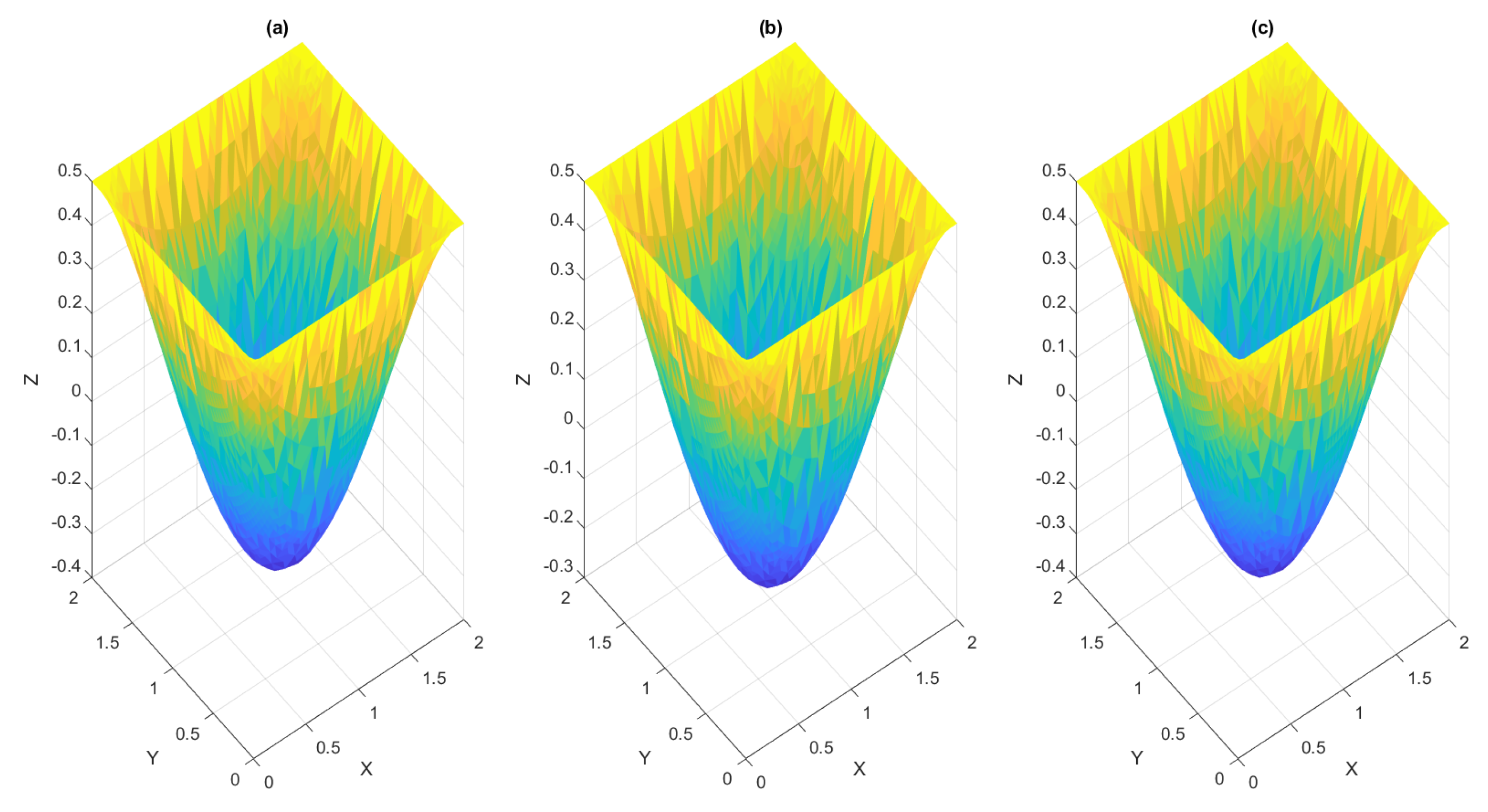
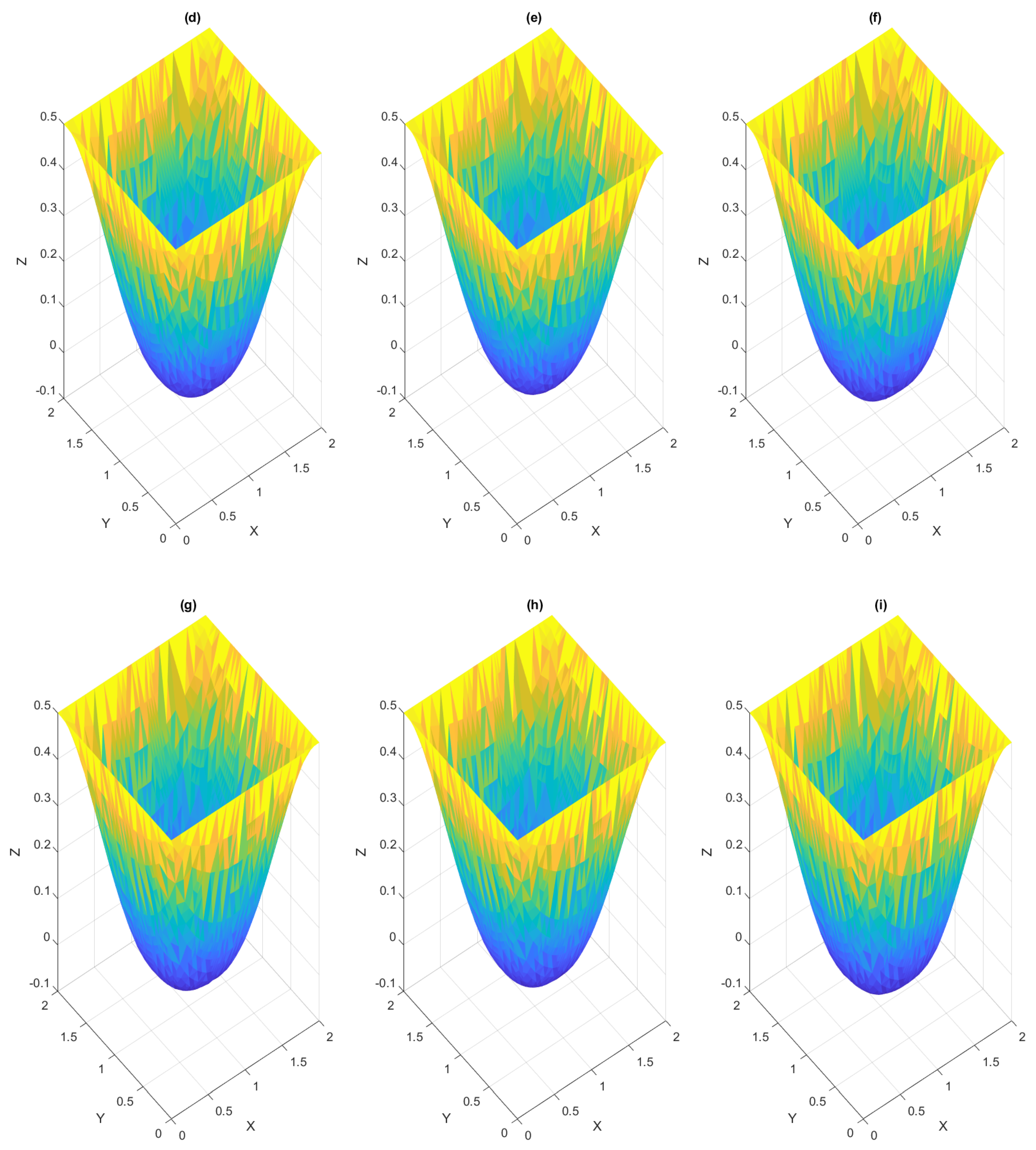
4.2. Examples in 2d

In this section, two examples will be discussed for the parameter sets that are given in the Table 1 and Table 2. For the treatment of the augmented Lagrangian algorithms, the same parameters were used as before. Furthermore, in every numerical example in this section, the estimators $\eta$ and $\sigma$ from remark and Definition 1 were used. Furthermore, note that the refinement algorithms that were implemented in [55] were used to treat the examples of the adaptive scheme.

For the numerical examples in 2d, similar breaking conditions on the algorithms were set:

• The breaking condition from S3 in Algorithm 1 is fulfilled with a tolerance $\epsilon :={10}^{-4}$.
• The number of nodes in the current mesh increases 1000 nodes.
• More than 100,000 iterations of the augmented Lagrangian algorithm were performed.

In contrast to the examples in 1d, a lower number of nodes was used as breaking condition for the refinement algorithm.

4.2.1. Examples on a Convex Domain

Similar to Section 4.1, non-trivial examples will be discussed in this section. First, let $\mathsf{\Omega }={]0,2[}^2$ be given, as well as ${\mathsf{\Gamma }}_D=\partial \mathsf{\Omega }$. In this section, an exact solution of (3) will be fixed. As done before, the concentrations $c_A,c_B,c_C$ will be given as:

$$c_A:=c_B:=c_C:=x(x-2)y(y-2)+\frac{1}{2}.$$

This yields the RHS for the Dirichlet condition as $g_{S,A}\equiv \frac{1}{2}$, for $S\in \{A,B,C\}$, and the RHS $f_A,f_B,f_C\in L^2(\mathsf{\Omega })$ are given through:

$$\begin{array}{cc}\hfill f_A=& -2D_A\left(y(y-2)+x(x-2)\right)-k_2\left(x(x-2)y(y-2)+\frac{1}{2}\right)+k_1{\left(x(x-2)y(y-2)+\frac{1}{2}\right)}^2,\hfill \end{array}$$

(30a)

$$\begin{array}{cc}\hfill f_B=& -2D_B\left(y(y-2)+x(x-2)\right)-k_2\left(x(x-2)y(y-2)+\frac{1}{2}\right)+k_1{\left(x(x-2)y(y-2)+\frac{1}{2}\right)}^2,\hfill \end{array}$$

(30b)

$$\begin{array}{cc}\hfill f_C=& -2D_C\left(y(y-2)+x(x-2)\right)+k_2\left(x(x-2)y(y-2)+\frac{1}{2}\right)-k_1{\left(x(x-2)y(y-2)+\frac{1}{2}\right)}^2.\hfill \end{array}$$

(30c)

Before the discussion of the examples is done, note that the exact error for the problems above is given by

$$\begin{array}{c}\hfill \sum _{S\in \{A,B,C\}}\left[\parallel \nabla c_S-\nabla c_{S,h}{\parallel }_{L^2(\mathsf{\Omega })}^2+\parallel p_{S,h}-\nabla c_S{\parallel }_{L^2(\mathsf{\Omega })}^2+{\parallel \mathrm{div}{p}_{S,h}-\Delta c_S\parallel }_{L^2(\mathsf{\Omega })}^2\right].\end{array}$$

(31)

The first example that is discussed in this section is given by the parameters that are defined in Table 1. When simulating the problem (3) with uniform refinement, one obtains the species concentration that is displayed in Figure 12. Furthermore, note that, for the adaptive scheme, one obtains close to identical figures, hence it will be omitted in this article.

Figure 12. Concentration profiles $c_A$, $c_B$ and $c_C$ with negative concentrations for (3) with parameters given in Table 1 and adaptive mesh refinement in 2d.

When evaluating the error estimators as well as the exact error, c.f. Figure 13, one obtains that the exact error, the estimator $\eta$ given by the localized evaluation of the corresponding least-squares functional as well as the practical error estimator $\sigma$ can be considered to be parallel for both refinement schemes. As can be seen, the adaptive scheme gives no prior advantage besides a better estimator $\eta$, which was used in the adaptive scheme.

Figure 13. Developement of the error estimators for the uniform and adaptive mesh refinement, for the approximation of (3) with the parameters given in Table 1, in 2d.

When evaluating the augmented Lagrangian scheme, cf. Algorithm 1, one sees that the scheme converges after 166 iterations, cf. Figure 14, to species distributions with non-negative concentrations. One already obtains a state with small negativities after 316 iterations, as seen in Figure 14. Furthermore, one can see that the estimator $\eta$ in each iteration does not converge to 0. However, in contrast to the examples in Section 4.1, the practical error seems to converge to 0.

Figure 14. Species distributions $c_A$ (a,d,g), $c_B$ (b,e,h) and $c_C$ (c,f,i) as well as error estimators (j,k,l) in the 1st, 83rd and 166th iteation of the augmented Lagrangian algorithm with adaptive mesh refinement, w.r.t. the parameters that are given in Table 1.

The second example that is discussed in this section is given by the parameters that were defined in Table 2. When simulating the corresponding example (3) one obtains an analogous Figure 12, which are not displayed in this article, since no major difference to Figure 12 is visible.

When evaluating the augmented Lagrangian scheme for the example that is given by the set of parameters defined in Table 2 with adaptive mesh refinement, one obtains non-negative species distributions after 188 iterations, cf. Figure 15, although the history given in the figure indicates states close to the approximated solution after 1161 iterations of the augmented Lagrangian schemes.

Figure 15. Species distributions $c_A$ (a,d,g), $c_B$ (b,e,h) and $c_C$ (c,f,i) in the 1st, 80th and 181st iteation of the augmented Lagrangian algorithm with adaptive mesh refinement, w.r.t. the parameters that are given in Table 2.

4.2.2. Examples on a Non-Convex Domain

In this section, two examples on non-convex domains will be discussed. In this section, let the domain be given $\mathsf{\Omega }={]0,1[}^2\backslash \left([0,1]\times [-1,0]\right)$. For the numerical experiments, the boundary conditions are defined analogously as in Section 4.2.1. The Dirichlet boundary is assumed to be given as ${\mathsf{\Gamma }}_D=\partial \mathsf{\Omega }$, the Neumann-boundary given as ${\mathsf{\Gamma }}_N:=\varnothing$ and

$$c_A{|}_{{\mathsf{\Gamma }}_D}=c_A{{|}_{{\mathsf{\Gamma }}_D}=c_A|}_{{\mathsf{\Gamma }}_D}=\frac{1}{2}.$$

Furthermore, let the RHSs $f_A,f_B,f_C\in {Ł}^2(\mathsf{\Omega })$ be given, as follows:

$$\begin{array}{cc}\hfill f_A(x):=& f_B(x):=f_C(x):=-2.\hfill \end{array}$$

(32)

The first example that is discussed in this subsection is given for the parameters defined in Table 1.

When calculating an approximate solution to the minimization problem (3), one obtains discrete solutions in the form, as shown in Figure 16, for uniform mesh refinement. Because of the fact that the approximate solution w.r.t. adaptive mesh refinement only gives small differences to the displayed figure, it is not shown in this paper.

Figure 16. Concentration profiles $c_A$, (a), $c_B$, (b), $c_C$ (c) as approximate result to (3), with parameters, as given in Table 1.

When evaluating the estimators $\eta$ and $\sigma$, as defined in definition and Remark 1, for the approximation of (3) for adaptive and uniform mesh refinement, one obtains that the estimators $\eta$ and $\sigma$ are restricted parallel to the refinement type, cf. Figure 17. Furthermore, one sees, as expected, that the estimators for adaptive refinement are steeper in the $loglog$ plot given in Figure 17, which indicates the expected increase of efficiency obtained by adaptive schemes.

Figure 17. Developement of the error estimators for the uniform and adaptive mesh refinement, for the approximation of (3) with parameters that are given in Table 1 on the L-shaped domain.

When comparing the triangulation generated by uniform refinement, cf. left image in Figure 18, and the triangulation, cf. right image in Figure 18, one observes that, while the uniform triangluation has a homogeneous distribution of triangles, in the adaptively generated mesh, the triangles accumulate in the non-convex vertex. This behavior is commonly known in the literature, cf. [27,30].

Figure 18. Triangulations generated by uniform (left) and adaptive (right) refinement for the approximate solution of (3) with the parameters that are given in the Table 1.

The evaluation of the augmented Lagrangian algorithm, cf. Figure 19, with the use of adaptive refinement with estimator $\eta$ yields that 188 iterations of the augmented Lagrangian algorithm are needed to guarantee non-negative species distributions.

Figure 19. Species distributions $c_A$ (a,d,g), $c_B$ (b,e,h) and $c_C$ (c,f,i) in the 1st, 94th and 188th iteation of the augmented Lagrangian algorithm with adaptive mesh refinement, w.r.t. the parameters that are given in Table 1.

The second example that is given in this section is, as before, given by the parameters that are defined in Table 2. When simulating the minimization problem (3), approximately one obtains an approximation of the form, as shown in Figure 20, which was obtained by simulation under uniform refinement. Because there are no visible differences between the picture generated under uniform refinement and generated under adaptive refinement, only the approximate solution under the usage of adaptive mesh-refinement will be given in this paper.

Figure 20. Concentration profiles $c_A$, (a), $c_B$, (b), $c_C$ (c) as approximative result to (3) with parameters in Table 2.

After the evaluation of the error estimators $\eta$ and $\sigma$, as defined in remark and Definition 1, one obtains that the practical error $\sigma$ and the classical error estimator $\eta$ are parallel in both cases, uniform and adaptive refinement. Furthermore, one obtains that all error-terms converge to zero. Furthermore, it can be seen that the given error estimators that were induced by adaptive refinement seem to converge with a higher rate, since the corresponding graphs in the $loglog$ plot shown in Figure 21 are steeper than the graphs associated to uniform refinement.

Figure 21. Developement of the error estimators for the uniform and adaptive mesh refinement, for the approximation of (3) with parameters that are given in Table 2 on the L-shaped domain.

Similar to the previous example, one sees, in Figure 22, a uniform triangulation of the L-shaped domain in Figure 22 on the left side and right side one generated by the adaptive algorithm. The triangulation that is generated by the AFEM-loop is dominantly refined in the neighbourhood of the non-convex vertex. This clearly coincides with the theory about singular solutions to elliptic PDEs, cf. [33] and their treatment, cf. [27,30].

Figure 22. Triangulations generated by uniform (left) and adaptive (right) refinement for the approximate solution of (3) with the parameters that are given in the Table 2.

When applying the augmented Lagrangian algorithm to problem (4) and applying the adaptive scheme to treat the iterate problem (5), one needs 35,057 iterations to guarantee non-negative species distributions, but it is also clear that a close fit to non-negative species distributions are already obtained after 17,528 iterations, cf. Figure 23.

Figure 23. Species distributions $c_A$ (a,d,g), $c_B$ (b,e,h) and $c_C$ (c,f,i) in the 1st, 141st, and 283th iteration of the augmented Lagrangian algorithm with adaptive mesh refinement, w.r.t. the parameters given in Table 2.

As last point of the discussion of the numerical experiments in 2d, the evaluation of the CPU running time has to be discussed. Table 5 presents the results discussed in the following.

Table 5. An overview of number of iterations of the augmented Lagrangian Algorithm 1 and CPU running times for the different parameter sets and uniform resp. adaptive mesh refinement.

Parameter Set	Type of Refinement	Geomety	Number of Iterations	CPU-Time
Table 1	Square	Uniform	280	$730.5068$ s
Table 1	Square	Adaptive	166	$615.8496$ s
Table 1	L-Shaped	Uniform	$\mathrm{53,639}$	3.1204$e+05$ s
Table 1	L-Shaped	Adaptive	188	$662.2452$ s
Table 2	Square	Uniform	287	$881.2332$ s
Table 2	Square	Adaptive	181	$645.7126$ s
Table 2	L-Shaped	Uniform	$\mathrm{53,553}$	3.1554$e+05$ s
Table 2	L-Shaped	Adaptive	283	$742.0187$ s

First, note that the number of iterations as well as the computation time reduce by using adaptive schemes. The reduction of computation time is for the the convex square domain is somehow remarkable, since the gain of efficiency, when using adaptive schemes, for convex domains is, in comparison to uniform refinement, rather low. The observed reduction of CPU time can be explained by the reduction of iterations in the augmented Lagrangian scheme, cf. Algorithm 1. However, the gain of efficiency, when using adaptive schemes to non-convex domains is remarkable, since a reduction of over 50,000 iterations of the augmented Lagrangian algorithm to under 300 is an extreme gain of efficiency.

Remark 7.

Note that the high number of needed iterations of the augmented Lagrangian algorithm for the L-shaped domain results of the singularity at the non-convex vertex of the geometry, which is a common result for non-convex domains. The adaptive scheme refines dominantly at the non-convex vertex of the geometry, which enhances the approximation in a way such that the augmented Lagrangian algorithm becomes enhanced, as can be seen in Figure 18.

When summarizing the results from this Section 4.2, it can been seen that the augmented Lagrangian scheme is more cost intensive than its correspondence in 1d. Furthermore, it can be seen in Section 4.2.1 that the practical estimator $\sigma$, as defined in the remark and Definition 1, behaves differently than in 1d under adaptive refinement, where it converges to zero, which justifies the use of the practical error. Additionally, one can observe, cf. Table 5, that a massive gain of efficiency can be made by using adaptive schemes in the discretization of (5).

4.3. Comparison to Other Methods

This section is devoted to the comparison of the augmented Lagrangian method, as described in this paper, with the classical augmented Lagrangian regime as described in [20,22] and the Primal-Dual Active-Set Strategy, as described in [23].

4.3.1. Theoretical Setup for the Classical Augmented Lagrangian Scheme and the Primal-Dual Active-Set Strategy

This section is devoted to description of the theoretical setup for the application of the classical augmented Lagrangian scheme [20,22] and the classical Primal-Dual Active-Set Strategy, c.f. [23].

The classical approaches to treat (4) is to discretize the optimization problem (4) and then use an optimization algorithm for the solution, as discussed in [14,15,16,19]. For an arbitrary fixed triangulation $\mathcal{T}$ with diameter $0<h$ and for the usage of the discretization $X_h$ of X, as defined in Section 3, one obtains the following discrete optimization problem:

Find $x_h={\left(c_{S,h},p_{S,h}\right)}_{S\in \{A,B,C\}}\in X_h$ such that the following equality holds true

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill x_h=\underset{{(v_{S,h},q_{S,h})}_{S\in \{A,B,C\}}}{\mathrm{argmin}}& LS\left(\left(v_{S,h},q_{S,h}\right)\right)\hfill \\ \hfill \mathbf{s}.\mathbf{t}.& 0<v_{S,h},\forall S\in A,B,C\hfill \end{array}\end{array}$$

(33)

The classical approaches use the fact that $X_h$ is a finite dimensional subspace of X and, thus, (33) is an finite dimensional optimization problem, for which a lot of theory is known, i.e., for the approximation of solutions (33), the augmented Lagrangian schemes can directly be applied, as described in [20,22].

In contrast to augmented Lagrangian methods, the Primal-Dual Active-Set Strategy, as in the form described in [23], cannot be indirectly applied to (33). For the application of Primal-Dual Active-Set Strategies, in this paper it is assumed that the operator in the ODE, resp. PDE, is linear, (2a)–(2e), is linear, i.e., the equality $k_1=0$ is assumed. In this case, one obtains, by using a basis of $X_h$, and using the Euler Lagrange Equation (20), one obtains a minimization problem of the following form:

Find $x_h^v\in {\mathbb{R}}^d$, such that the following equation holds true

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill x_h^v=\underset{y\in {\mathbb{R}}^d}{\mathrm{argmin}}& \frac{1}{2}{y}^{T}A{x}_h^v-y^{T}f\hfill \\ \hfill \mathbf{s}.\mathbf{t}.:& 0\le v_{S,h}^v\hfill \end{array}\end{array}$$

(34)

In the problem above, $d_h\in \mathbb{N}$ is the dimension of $X_h$, i.e., $d_h=dim{X}_h$, $x_h^v\in {\mathbb{R}}^{d_h}$ is the coefficient vector of the solution $x_h\in X_h$ of (33) and $v_{S,h}^v$ is the coefficient vector of $v_h\in S^1(\mathcal{T})$. Furthermore, for all $y\in {\mathbb{R}}^{d_h}$, the equality

$$y^{T}Ay+2y^{T}f+f^{T}f=LS\left(y_h\right)$$

holds true, where $y\in {\mathbb{R}}^d$ is the coefficient vector of $y_h\in X_h$.

4.3.2. Description Classical Augmented Lagrangian Regime

This section is devoted to the description of the use of the classical augmented Lagrangian algorithm to the problem (33).

The classical augmented Lagrangian scheme is given through the following Algorithm 4, cf. [20,22].

Algorithm 4: Classical augmented Lagrangian method

Input: Define a starting values $x_h^{(0),s}$, ${\lambda }^{(0)}$, ${\alpha }_0$ and define $j:=0$.  Output: Approximate solution $x_h$ to (33) and approximate Lagrangian function ${\lambda }_h$.  The classical augmented Lagrangian algorithm is given through the following steps.  S1:   Approximate a solution to the following optimization problem.  Find $x_h^{(j+1)}:={\left(c_{S,h}^{(j)},p_{S,h}^j\right)}_{S\in \{A,B,C\}}\in X_h$ such that the following equation holds true: $$\begin{array}{c}\hfill \begin{array}{cc}\hfill x_h^{(j+1)}=\underset{{(v_{S,h},q_{S,h})}_{S\in \{A,B,C\}}}{\mathrm{argmin}}& L{S}_{{\alpha }_j}\left({\left(v_{S,h},q_{S,h}\right)}_{S\in \{A,B,C\}},{\lambda }^{(j)}\right)\hfill \end{array}\end{array}$$ (35)  and use $x_h^{(0),s}$ as initial  S2:   If ${\left({\lambda }^j,x_h^{(j)}\right)}_{L^2(\mathsf{\Omega })}<\epsilon$ break the algorithm.  S3:   Update ${\lambda }^{(j)}$ via the update rule: $${\lambda }^{(j+1)}:={\left({\lambda }^{(j)}-{\alpha }_j[c_A^{(j+1)},c_B^{(j+1)},c_C^{(j+1)}]\right)}_{+}.$$  Furthermore update $x_h^{(j+1),s}:=x_h^{(j+1)}$ ${\alpha }_{j+1}$ such that ${\alpha }_j\le {\alpha }_{j+1}$.  S2:   Set $j:=j+1$ and go to S1.

The experimental setup needs to be described before the numerical experiments will be discussed in detail.

First, note that, for all simulations discussed with Algorithm 4, the parameter ${\alpha }_j$ was for all $j\in \mathbb{N}$ given as ${\alpha }_j=1$. For the comparison of the algorithm on different meshes, the algorithm was coupled with a loop of uniform refinements. The global Algorithm 5 is given through the following:

Algorithm 5: Refinement strategy with the classical augmented Lagrangian algorithm

Input: Initial Triangulation ${\mathcal{T}}_0$. Define a starting values $x_h^{(0),s}$, ${\lambda }^{(0)}$, ${\alpha }_0$ and define $j:=0$.  Output: Approximate solution $x_h$ to (33) and approximate Lagrangian function ${\lambda }_h$ and final triangulation $\mathcal{T}$.  Perform the following steps:  S1:   Compute an Approximation $x_{h_{\ell }}$ of a solution and a Lagrangian multiplier ${\lambda }_{\ell }$ to (33) on the current triangulation ${\mathcal{T}}_{\ell }$ using the initial values $x_{h_{\ell }}^{(0),s}$ and ${\lambda }_{\ell }^{(0)}$ using the Algorithm 4.  S2:   If ${\mathcal{T}}_{\ell }$ has more than N nodes then break the loop.  S3:   Define the mesh ${\mathcal{T}}_{\ell +1}$ as uniform red refinement of the triangulation ${\mathcal{T}}_{\ell }$. For a definition of the uniform red refinement see [27].  S4:   Define $x_{h_{\ell }}^{(0),s}:=x_{h_{\ell }}$ and ${\lambda }_{\ell }^{(0)}:={\lambda }_{\ell }$.  S5:   Set $\ell :=\ell +1$ and go to S1.

The statement of the algorithm above finishes the description of the used classical augmented Lagrangian scheme.

4.3.3. Description of the Primal-Dual Active-Set Strategy

This subsection is devoted to the explicit description of the Primal-Dual Active-Set Strategy that is considered in this article.

As discussed before for a basis $\{b_1,\dots ,b_{n_h}\}$, a basis of $X_h$ the problem (33) can be equivalently reformulated to (34).

The corresponding representation of $X_h$, see (7), indicates that a basis ${\mathcal{B}}_h=\{b_1,\dots ,b_{n_h}\}\}$ of $X_h$ can be chosen, such that, for all coefficient vectors $y_h^v$ of element $y_h\in X_h$ for all $S\in \{A,B,C\}$, there exists an index set $J_S\subset \{1,\dots ,n_h\}$, such that the restriction of the coefficient vector $(y_h^v)$ on the subindexset $J_S$ ${(y_h^v)}_{J_S}$ is the coefficient vector of $c_S$. In this notation, define the index-set J as

$$J:=\bigcup _{S\in \{A,B,C\}}{J}_S.$$

Applying the Primal-Dual Active-Set Strategy, cf. [23] as a method to approximate solutions to (34), together with the notation above, one obtains the following Algorithm 6.

Algorithm 6: Primal-Dual Active-Set Strategy

Input: Define a starting values $x_h^{(0),s}$, ${\lambda }^{(0)}$, ${\alpha }_0$ and define $k:=0$.  Output: Approximate solution $x_h$ to (33) and approximate Lagrangian function ${\lambda }_h$.  With the notation above the Primal-Dual Active-Set Strategy for this problem type  S1:   Define the inactive set ${\mathcal{I}}_k$ and active set ${\mathcal{A}}_k$ as follows: $${\mathcal{I}}_k:=\left\{i\in \{1,\dots ,n\}|{\lambda }_i^{(k)}+\frac{1}{2}{y}_i^k>0\right\}\cap J,$$  and $${\mathcal{A}}_k:=\left\{i\in \{1,\dots ,n\}|{\lambda }_i^{(k)}+\frac{1}{2}{y}_i^k\le 0\right\}\cap J.$$  S2:   Solve the following system of linear equations $$\begin{array}{cc}\hfill A{y}^{(k+1)}+{\lambda }^{(k+1)}& =f,\hfill \end{array}$$ (36a) $$\begin{array}{cc}\hfill y^{(k+1)}& =0,\mathrm{on}{\mathcal{A}}_k\hfill \end{array}$$ (36b) $$\begin{array}{cc}\hfill {\lambda }^{(k+1)}& =0,\mathrm{on}{\mathcal{I}}_k.\hfill \end{array}$$ (36c)  S3:   Stop the algorithm, or set $k:=k+1$ and return to S1.

Remark 8.

Note that, by the problem formulation (36a)–(36c) directly implies, by the split of the indices into an active set $\mathcal{A}$ and an inactive set $\mathcal{I}$, the orthogonality $c_S\perp {\mu }_S$ for all $S\in \{A,B,C\}$ is fulfilled. Thus, the usage of the relative error

$$\mathit{err}=\left|\sum _{S\in \{A,B,C\}}{\mu }_A·c_A\right|$$

for a breaking condition of the corresponding algorithm is not applicable.

Before the actual comparison between the Primal-Dual Active-Set Strategy and the augmented Lagrangian method will be made, some additional remarks on the coupling between refinement and Algorithm 6 have to be made:

For the comparison of the algorithm on different meshes, the algorithm was coupled with a loop of uniform refinements. The global Algorithm 7 is given through the following:

Algorithm 7: Primal-Dual Active-Set strategy with refinement strategy

Input: Define a starting values $x_h^{(0),s}$, ${\lambda }^{(0)}$, ${\alpha }_0$ and define $k:=0$. Furthermore define an initial triangulation ${\mathcal{T}}_0$.  Output: Approximate solution $x_h$ to (33) and approximate Lagrangian function ${\lambda }_h$. Additionally the algorithm outputs the final triangulation ${\mathcal{T}}_{\ell }$  Perform the following steps:  S1:   Compute an Approximation $x_{h_{\ell }}$ of a solution and a Lagrangian multiplier ${\lambda }_{\ell }$ to (33) on the current triangulation ${\mathcal{T}}_{\ell }$ using the initial values $x_{h_{\ell }}^{(0),s}$ and ${\lambda }_{\ell }^{(0)}$ using the Algorithm 4.  S2:   If ${\mathcal{T}}_{\ell }$ has more than N nodes then break the loop.  S3:   Define the mesh ${\mathcal{T}}_{\ell +1}$ as uniform red refinement of the triangulation ${\mathcal{T}}_{\ell }$. For a definition of the uniform red refinement see [27].  S4:   Define $x_{h_{\ell }}^{(0),s}:=x_{h_{\ell }}$ and ${\lambda }_{\ell }^{(0)}:={\lambda }_{\ell }$.  S5:   Set $\ell :=\ell +1$ and go to S1.

The statement of the algorithm above finishes the description of the Primal-Dual Active-Set Strategy.

4.3.4. Comparrison of the Different Mehtods

This section is devoted to the explicit comparison of the different numerical schemes. However, before the actual comparison is undertaken the general setup of the experiments have to be stated.

First, note that the parameters of the mathematical problems to approximate in this section are given in the Table 2 and Table 3. The corresponding RHS are the same as in the respective examples above. Furthermore, in the 2d experiments, the geometry considered is the L-Shaped domain.

Furthermore, for every method, the initial mesh ${\mathcal{T}}_0$ for the refinement scheme was always the same in the respective dimension. Furthermore, note that refinement loops are broken if the mesh has 10,000 nodes in one space dimension and 1000 nodes in two space dimensions.

The loops of the respective augmented Lagrangian algorithms are broken if the relative error

$$\mathrm{err}=\left|\sum _{S\in \{A,B,C\}}{\left({\mu }_S,c_{S,h}\right)}_{L^2(\mathsf{\Omega })}\right|$$

is bounded by the tolerance $\epsilon$ = 1$e-4$.

First, note that there is no visual remarkable difference between the outputs of the algorithms. Hence, in this algorithm only the CPU times of the algorithms will be compared. Table 6 assembles the actual data for the comparrison.

Table 6. Comparison of the augmented Lagrangian scheme discussed in this paper with adaptive mesh refinement (AALA), the classical augmented Lagrangian algorithm (CALA), and the Primal-Dual Active-Set Strategy (PDAS), for different space dimensions and parameter sets.

Parameter Set	Dimension	CPU Time AALA	CPU Time CALA	CPU Time PDAS
cf. Table 2	1d	$9.9426e+03$ s	8.8871$e+03$ s	$4.1808e+03$ s
cf. Table 2	2d	$742.0187$ s	4.4895$e+04$ s	$1.1331e+04$ s
cf. Table 3	1d	$4.7214e+04$ s	2.0356$e+05$ s	-

In the context of the described algorithms, one would expect that the Primal-Dual Active-Set Strategy is the most inefficient in terms of needed RAM space during the computation due to the fact that the system of Equation (36a)–(36c) contain more variables than the other optimization-problems, since the augmented Lagrangian methods treat the multiplier $\lambda$ as constant and not as a variable.

In one space dimension and for the parameters given in Table 2, the Primal-Dual Active-Set Strategy is the most efficient, while the two augmented Lagrangian schemes need approximately the same CPU time, as seen in Table 6. In contrast to that the augmented Lagrangian algorithm that is introduced in this paper is more efficient for non-convex domains and nonlinear problems than the other algorithms.

5. Modelling the Stationary Species Transport in the Diffusion-Boundary Layer during the Metal Deposition from a ${\mathrm{Cu}}^{2+}$ Electrolyte

This section is devoted to the derivation a model, see Section 5.1, for the metal deposition from a Cu-electrolyte, taking the complexation with $\beta$-alanine ($\beta$-ala) in the diffusion-boundary layer into account. In Section 5.2, the numerical strategy, which is discussed in this article, will be applied to the model.

5.1. Theoretical Model

In this section, an abstract model for the static metal deposition in galvanic cells will be discussed. As a model that is falling into the discussed model types, the static metal deposition with speciation in a single diffusion boundary layer will be studied, c.f. [1,2,3].

A few remarks on the physical setting will be made before the model will be discussed in detail. In an electrolyte, a metal M, in this case Cu, and a ligand L, in this case $\beta$-ala, is assumed, with the reaction

$$\begin{array}{c}\hfill \mathrm{Cu}+(\beta -\mathrm{ala})\rightleftharpoons \mathrm{Cu}(\beta -\mathrm{ala}).\end{array}$$

(37)

Furthermore, in the bath, there is an anode and a cathode, where, at the cathode, the metal is deposited. In the global setting, there is a transport of Cu-ions from the anode, with anodic current density $j_A$, to the cathode, with cathodic current density $j_C$. In this model, one assumes that $j_C=j_A$.

For the model, assume that there exists a laminar boundary layer at the cathode, which includes the diffusion boundary layer with thickness of ${\delta }_x={10}^{-4}$ m. Furthermore, assume that, outside the diffusion boundary layer, the concentration $c_{C{u}^{2+}}$ of $C{u}^{2+}$, the concentration $c_{{\mathrm{Cu}}^{2+}}$ of $c_{\beta -\mathrm{ala}}$ and $c_{\mathrm{Cu}-\beta -\mathrm{ala}}$ are constant. Furthermore, the concentration the bath is set by $c_S^b=0.5\frac{\mathrm{mol}}{\ell }$, for each $S\in \{{\mathrm{Cu}}^{2+},\beta -\mathrm{ala},\mathrm{Cu}(\beta -\mathrm{ala})\}$.

Furthermore, let the only deposited species at the cathode, at position $x=0$, be the Cu-ions and the species distribution in the diffusion boundary layer geometrically only be dependant on the distance to the cathode and the concentrations in the diffusion-boundary layer can be described by the diffusion–reaction problem (4), with diffusion coefficients and reaction rate constants, as given in Table 7, and let no further reactive force be given.

Table 7. Physical parameters of the diffusion–reaction model for the complexation of $\mathrm{Cu}L$, with $\beta$-alanine as ligand L, in a diffusion boundary-layer.

Species	D in $\frac{{\mathbf{m}}^2}{\mathbf{s}}$	${\mathit{k}}_1$ in $\frac{1}{\mathit{s}}$	${\mathit{k}}_2$ in $\frac{{\mathbf{m}}^3}{\mathbf{mol}\mathbf{s}}$	${\mathit{\gamma }}_{\mathit{S}}$
Cu	$7.14\times {10}^{-10}$	-	-	0
L	$9.29\times {10}^{-10}$	-	-	0
$\mathrm{Cu}L$	$9.29\times {10}^{-10}$	$2\times {10}^5$	11	0

When translating the assumptions above into boundary-data one obtains for all $S\in \{\mathrm{Cu},\beta -\mathrm{ala},\mathrm{Cu}-(\beta -\mathrm{ala})\}$ the identity $c_S({\delta }_x)=c_S^b$. At the cathode for the species $S\in \{S\in \{\beta -\mathrm{ala},\mathrm{Cu}-(\beta -\mathrm{ala})\}$, the identities $\frac{\mathrm{d}}{\mathrm{d}x}{c}_S=0$ will be used and $\frac{\mathrm{d}}{\mathrm{d}x}{c}_{\mathrm{Cu}}=\frac{j}{D_{\mathrm{Cu}}zF}$, where F is Faraday’s constant and $z=2$ is the valency of the copper-ions ${\mathrm{Cu}}^{2+}$. The absence of reactive forces is modeled by defining the functions $f_A,f_B,f_C\in L^2(\mathsf{\Omega })$ through $f_A=f_B=f_C=0$.

For the diffusion coefficients cf. to supplementary matrerial of [4] and for the kinetic parameters, cf. [3].

5.2. Simulation

In this section, the simulations according to the model above will be discussed. Assuming concentrations of $c_S^b=0.5\frac{\mathrm{mol}}{{\mathrm{m}}^3}$, for $S\in \{\mathrm{Cu},\beta -\mathrm{ala},Cu-\beta -\mathrm{ala}\}$ in the bath and a current density of $j=0.6\frac{A}{m^2}$ on the cathode, one obtains the concentration profile shown in Figure 24 by evaluating the classical model 3, with the numerical scheme described for the treatment of (5) under the reduction described in Remark 1. As seen in the figure, one obtains a concentration of $-0.4\frac{\mathrm{mol}}{\ell }$, which can be considered to be unphysical.

Figure 24. Concentration profiles $c_{{\mathrm{Cu}}^{2+}}$, $c_{\beta -\mathrm{ala}}$ $c_{\mathrm{Cu}(\beta -\mathrm{ala})}$ with negative concentrations w.r.t. the model parameters discussed in Table 7.

When applying the augmented Lagrangian method with adaptive meshrefinement on (4), cf. Figure 25, one obtains that 75 iterations of the augmented Lagrangian algorithm were needed to evaluate non-negative concentrations. As seen in the corresponding figures, not only the behavior of $c_{{\mathrm{Cu}}^{2+}}$, but, as directly seen, the behavior of $c_{\beta -\mathrm{ala}}$, in the close area of the cathode the concentration of $c_{\beta -\mathrm{ala}}$ increases. Furthermore, it can be seen that the augmented Lagrangian algorithm needs 75 steps for the simulation of non-negative species concentrations.

Figure 25. Concentration profiles $c_{{\mathrm{Cu}}^{2+}}$, $c_{\beta -\mathrm{ala}}$ $c_{\mathrm{Cu}(\beta -\mathrm{ala})}$ (a,c,e) with corresponding Lagrangian multipliers (b,d,f) in the 1st, 38th, and 75th iteration of the augmented Lagrangian algorithm.

Remark 9.

During the application of the numerical scheme that is described in Section 3, one observes that the adaptive scheme converges relative fast for the respective model 4 given through the parameters that are defined in Table 7 and the given boundary conditions, while the quasi-Newtonian part of the numerical scheme based on the uniform refinement does not converge, unless a high number of homotopy steps $>{10}^6$ is used.

In summary, the numerical methodology that is derived in this article is applicable to practical relevant settings, and the adaptive scheme has a major part on the efficiency of the described.

6. Discussion and Conclusions

Although, in this article, the rigorous mathematical proofs are not done, in Section 4 various numerical examples are discussed, which show convergence. Hence, the convergence of all included algorithms can be stated as a founded conjecture. Although some mathematical considerations are made in this paper, some rigorous mathematical work still has to be done. In detail, the following formal proofs have to be made in some future work:

(i)

There exist, at least locally, a unique solution to (3) and (4).

(ii)

The iterated minimization problems (5) are, at least locally, uniquely solvable and the sequence of solutions $\left({(u_S^{(n)},p_S^{(n)})}_{S\in \{A,B,C\}}\right)\in X$, generated by the augmented Lagrangian method, converges to the solution ${(u_S,p_S)}_{S\in \{A,B,C\}}\in X$ of (4).

(iii)

For a triangulation $\mathcal{T}$, with low enough diameter $0<h$ and a stable starting point of the quasi-Newton scheme described by solutions of (13), every iterate problem of (13) is uniquely solvable.

(iv)

The quasi-Newton method given by the iterative solution $x_h^{(n)}$ of (13) converges in $X_h$. i.e., there exists a $x_h\in X_h$, such that $x_h=\underset{n\to \infty }{lim}{x}_h^{(n)}$.

(v)

For $h\downarrow 0$ the limits described in (iv) converge against the solution of (5).

(vi)

The adaptive scheme that is described in Algorithm 3 converges.

Furthermore, the numerical experiments show that the application of the practical error $\sigma$, as defined in Definition and Remark 1, can be used in two space dimensions. In addition, the behavior seems to indicate the needed norm equivalences in two space dimensions. Furthermore, in one space dimension, it can be seen that the practical error estimator is not sufficient for the required norm equivalence, but the numerical examples nevertheless show good results, which allow the use as above.

Although the numerical schemes are still cost intensive, they converge and, hence, give physical behavior for three compound systems. In addition, as to be seen in Section 5, in this article, a numerical scheme was introduced that is able to treat the high rate constants given in real-world problems, cf. supplement to [4]. Hence, the numerical scheme can be used in most relevant settings when considering three-component systems.

Furthermore, note that the algorithm that is described in this section seems, due to the discussions for the numerical examples, to be especially efficient for nonlinear and non-convex geometries. Especially, the efficiency for those two cases makes the algorithm interesting for further applications.

The model that is presented in the Section 5 gives a first glance at the process of metal deposition, but one has to expect that the model is improvable. Firstly, the assumption of the existence of a uniform laminar boundary layer on any complex geometry is questionable since fluid dynamics tend to be strongly geometry dependant, cf. [56]. Furthermore in galvanic processes ${\mathrm{H}}_2$ development at the cathode can be expected, which questions the existence of a laminar boundary layer in many cases. Although the concentration gradients in a galvanic bath can be assumed to be low in some cases, the species-transport in the bath, as described in [1,2,3], cannot necessarily be neglected. Furthermore, the processes in the bath can be described by a multi physics coupling of fluid dynamics, diffusion, reactions, and electro-magnetics. Furthermore, as seen in [3], the reaction kinetics that were discussed in this article are not complete. Hence, a further discussion of this type of model needs to be done.

As is well known, most of the real world processes do not reduce to static problems, but, nevertheless, important limiting factors can be obtained from static laws. Furthermore, from a technical numerical perspective, time-dependent laws can be approximately treated as systems of static laws, c.f. [57] or [58]. Hence, this article gives a good first foundation for further discussions and investigations.