Study of Motion Control and a Virtual Reality System for Autonomous Underwater Vehicles
Abstract
1. Introduction
- (1)
- We proposed a kind of neuro-fuzzy controller design for path tracking, which can be adapted to any AUV without establishing a dynamic model of the AUV. An improved learning algorithm proposed can reduce the amount of calculation in the process of finding the error function gradient and improve the learning efficiency of the network. The effectiveness of the algorithm and the accuracy of its theoretical analysis are verified by numerical experiments.
- (2)
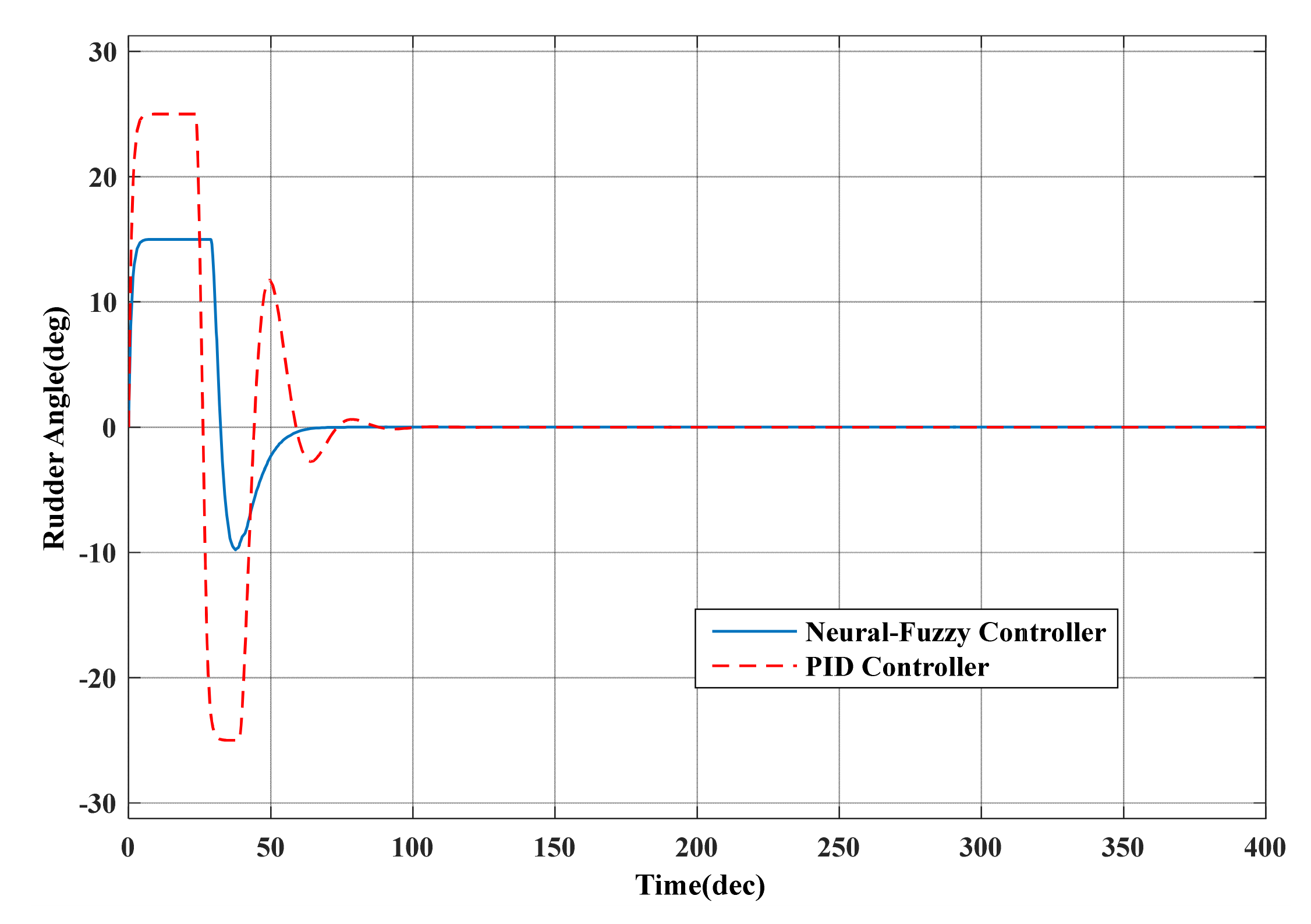
- The proposed algorithm is simulated and experimented taking several aspects into consideration. Tracking control effects of the algorithm proposed in the paper are preliminarily tested in the MATLAB simulation environment. A visual simulation platform has been developed to test the proposed algorithm, which can not only observe the movement of the AUV but also observe the output value of control quantity in real-time. The data visualization of process control can thus be realized.
2. Dynamic System of AUV
3. Design of AUV Motion Control Algorithm
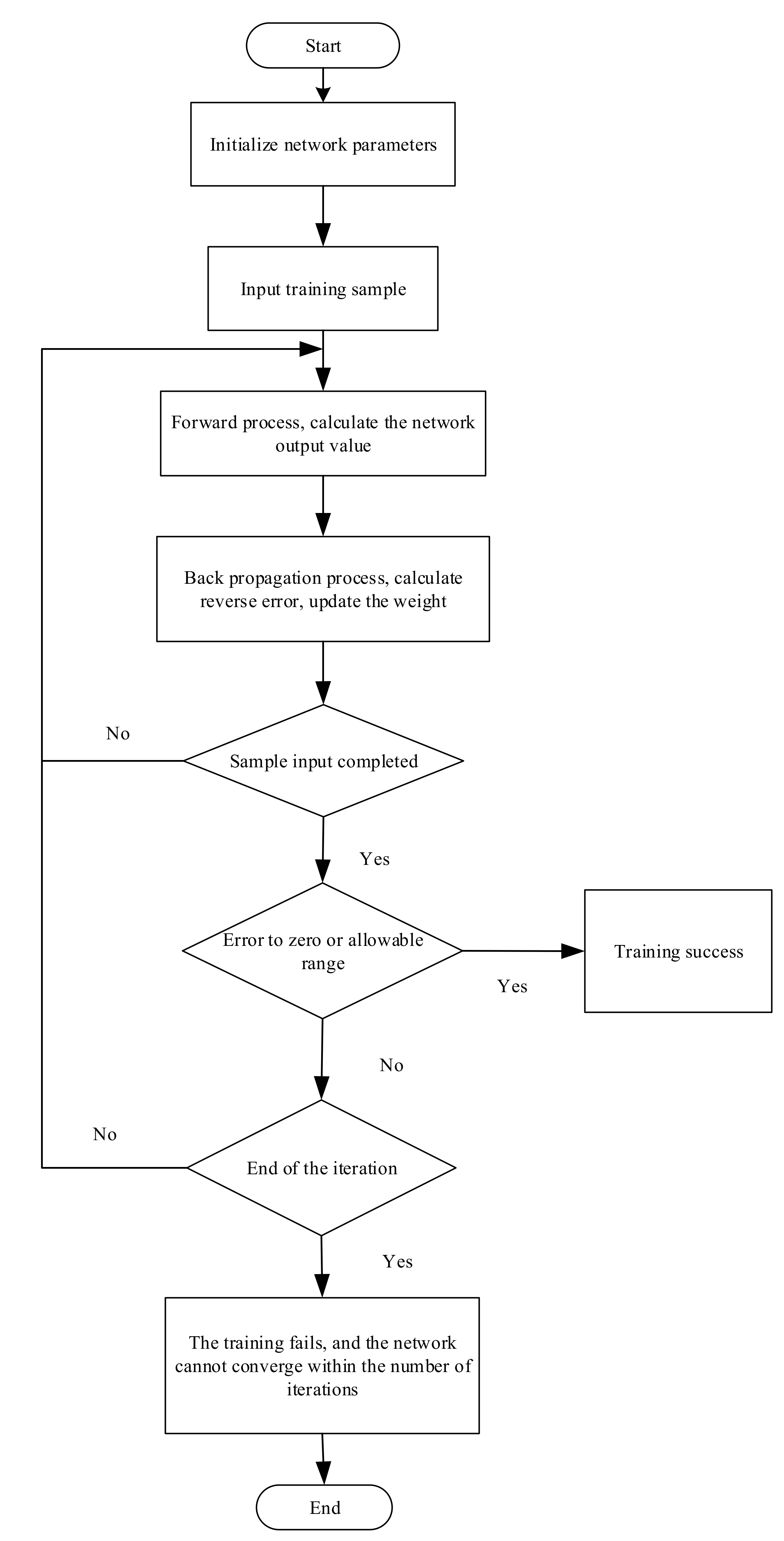
3.1. Design of Neuro-Fuzzy Controller for AUV Path Tracking
3.2. Optimization and Analysis of Controller Parameters
- (1)
- The number of layers in the network
- (2)
- Number of hidden layer neurons
- (a)
- When the number of neurons is too small, the network cannot learn efficiently, the number of training iterations is relatively large, and the training accuracy is low.
- (b)
- When the number of neurons is too large, the more powerful the network function, the higher is the network accuracy, and the number of training iterations is also large, which may result in overfitting. Therefore, depending on the accuracy of the AUV heading error, we divide them into seven levels, so the number of neurons in the hidden layer is seven.
- (3)
- Selection of the initial weights
- (4)
- Learning rate
3.3. Convergence Analysis
- (i)
- There is a constant such that for any, there is:
- (ii)
- There is a setfor, and a set, that contains only a finite number of points.
- (i)
- Let the error function E(W) be defined by Equation (31). Starting from the initial point, {wk}, is the weight sequence of the network is obtained by Equation (40). If hypothesis (i) is satisfied, then.
- (ii)
- If hypothesis (ii) is also true, then there is a pointthat makes
- (iii)
- .
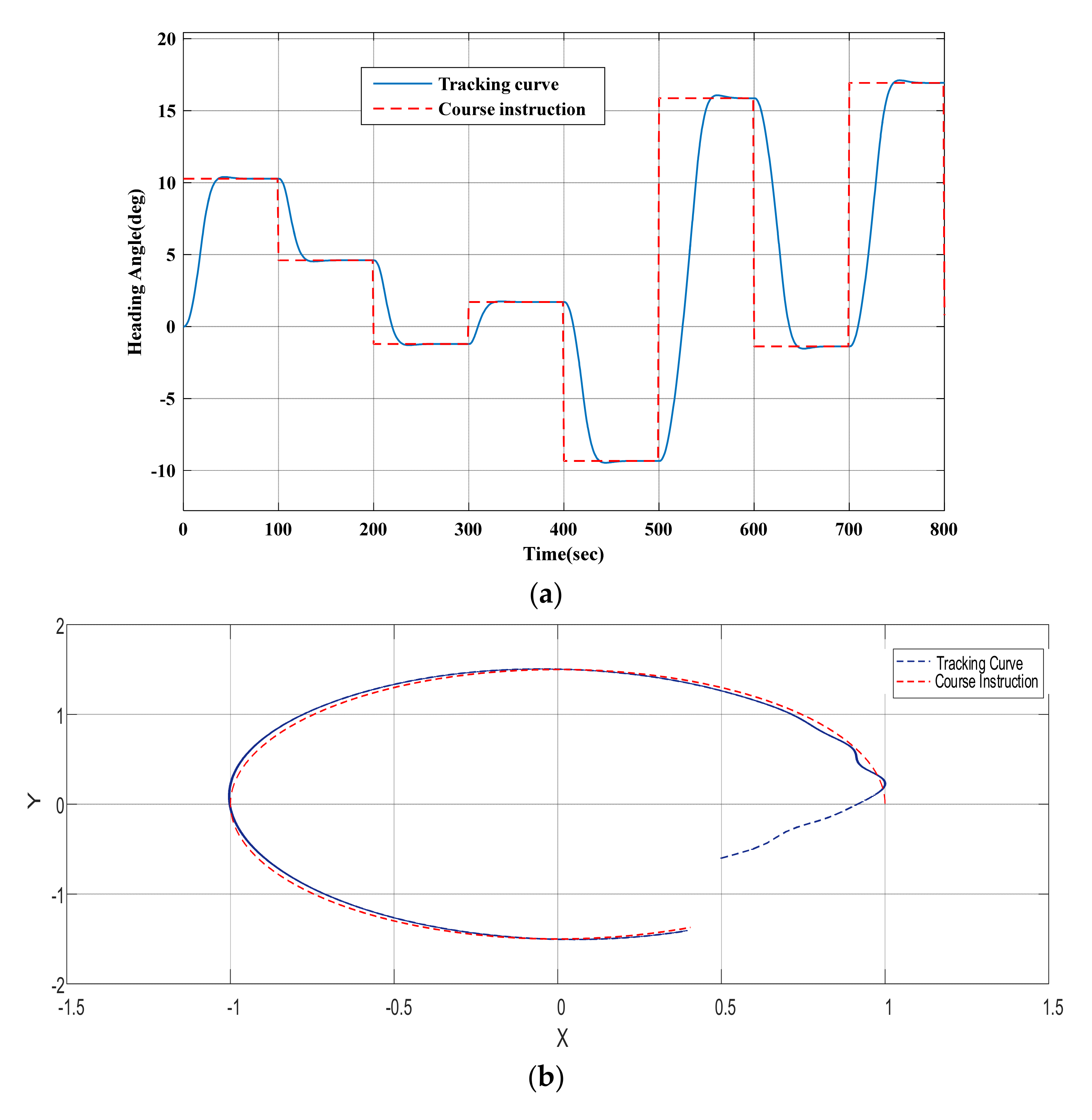
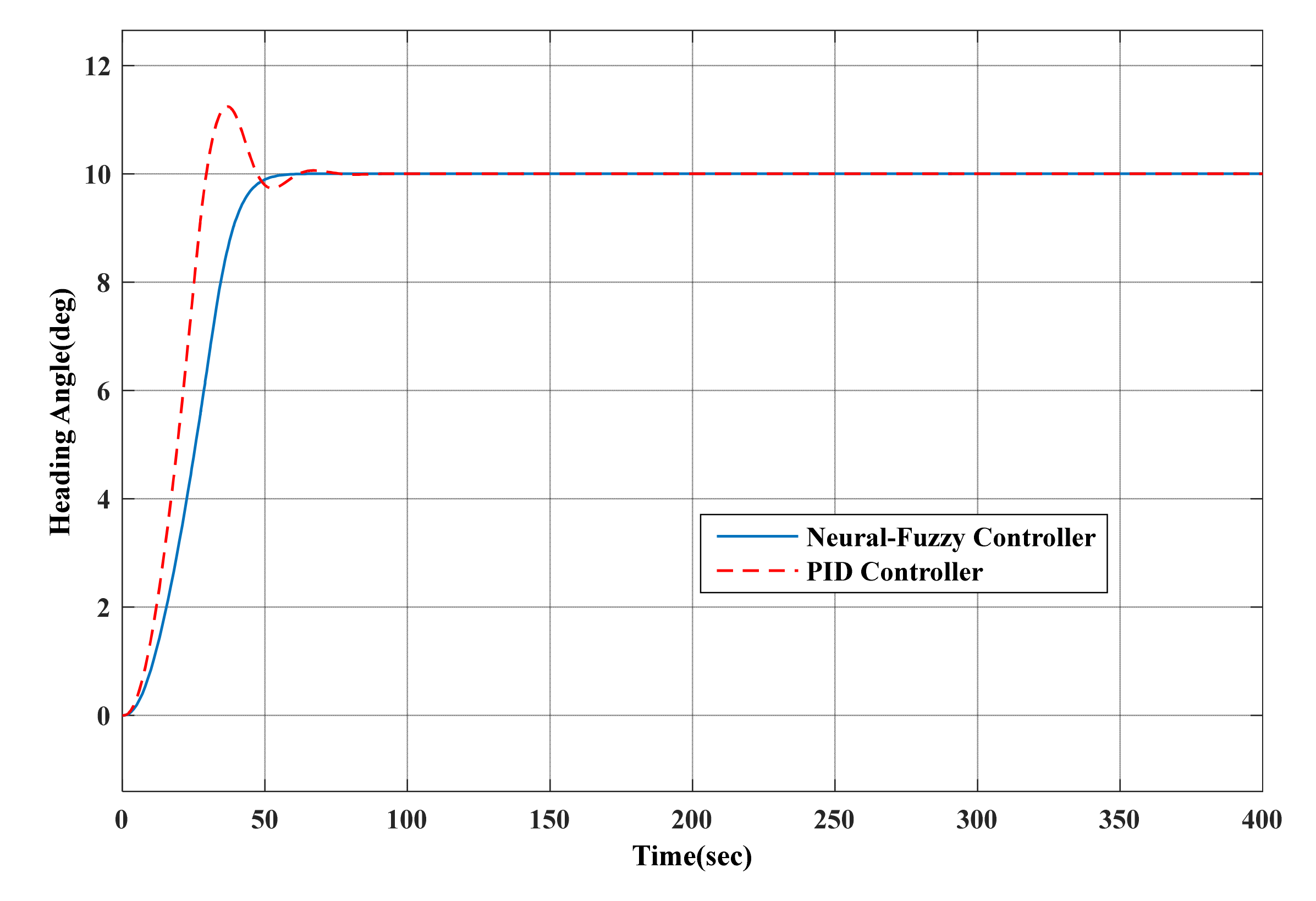
3.4. MATLAB Simulation
4. Development of the AUV Motion Control Virtual Reality System
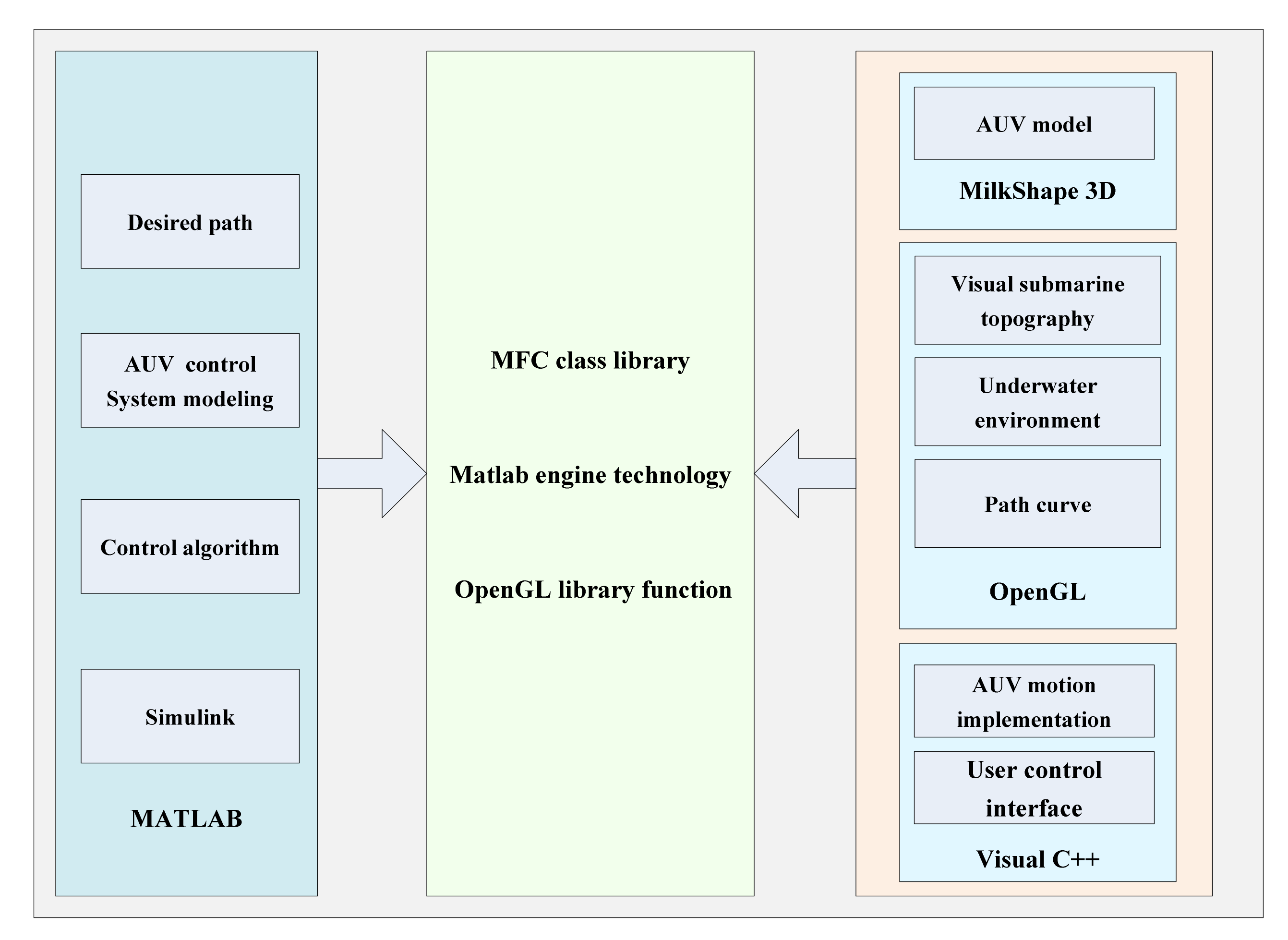
4.1. Overall Design
- Construction and display of 3D AUV and virtual environment scene: A 3D modeling software is used to generate the AUV 3D model and other environmental element models. Each element is appropriately deployed to generate a 3D virtual scene of underwater robotic motion.
- AUV motion control realization and output display: This paper provides two methods for the realization and output of the AUV motion control. The first method directly uses Visual C++ programming in the virtual reality system to realize the AUV motion control algorithm and displays the results on the AUV motion visual simulation interface. In the second method, the system first uses MATLAB to design the AUV motion control algorithm, and then uses the MATLAB engine to execute the commands and perform the data transmission between MATLAB and the virtual simulation system under the Visual C++ environment. The output of the AUV motion control system designed using MATLAB can be shown in the virtual reality system.
- Design of AUV motion control virtual reality system: The key functionalities of a virtual reality system are a) how to “control” the virtual scenes, b) how to integrate and synchronize the AUV motion control and virtual scene under the same software platform, and c) how to realize the poses of the AUV 3D model motion and the “communication” of the control algorithm.
4.2. The Framework of AUV Motion Control VR System
4.3. Construction of AUV Model
4.4. Construction of the Underwater Virtual Scene
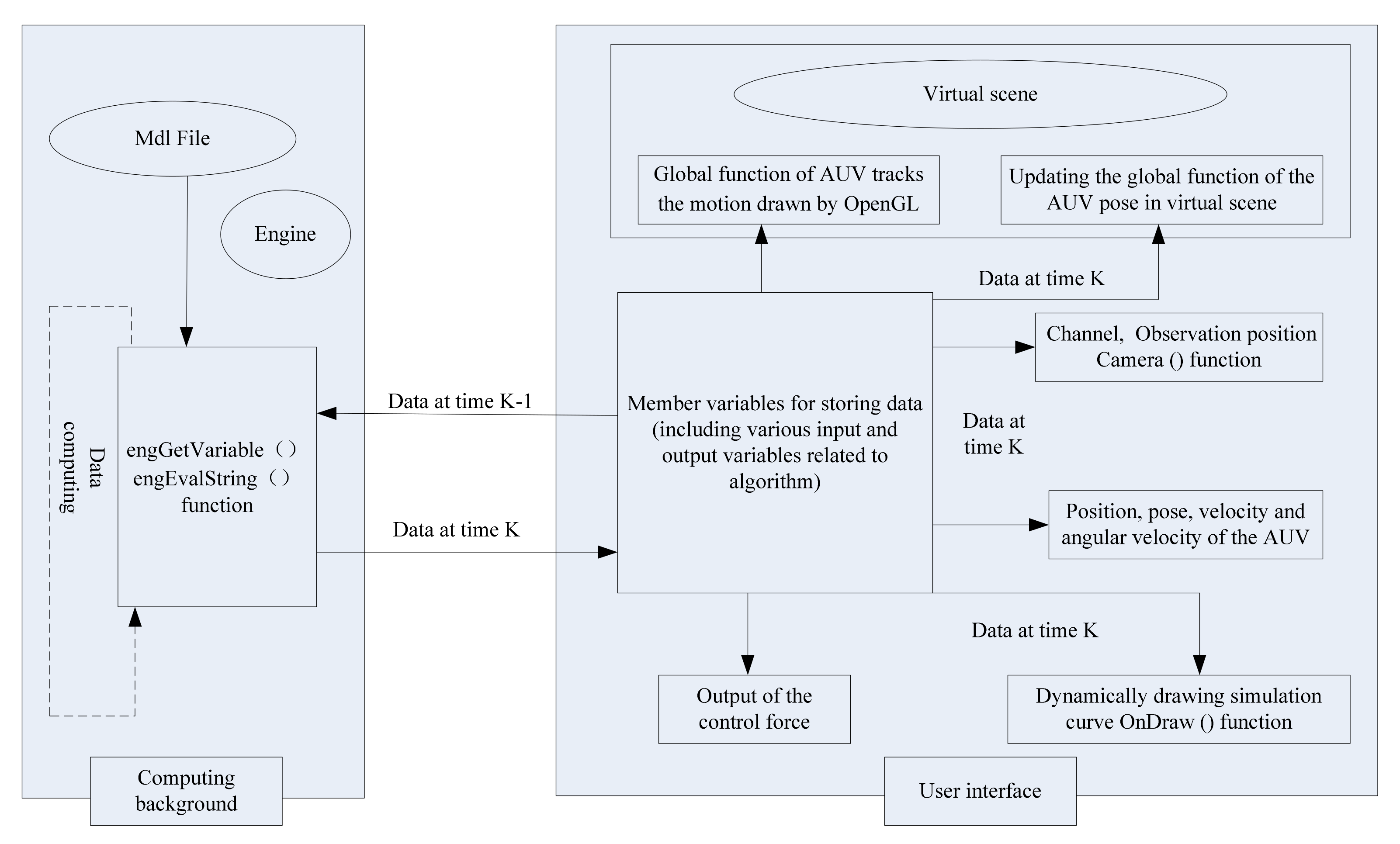
5. Data Communication between the Virtual Reality System and MATLAB
6. Visual Simulation of the Virtual Reality System
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, C.; Xiang, X.; Lapierre, L.; Zhang, Q. Robust Magnetic Tracking of Subsea Cable by AUV in the Presence of Sensor Noise and Ocean Currents. IEEE J. Ocean. Eng. 2018, 43, 311–322. [Google Scholar] [CrossRef]
- Xu, H.; Soares, C.G. Vector field path following for surface marine vessel and parameter identification based on LS-SVM. Ocean Eng. 2016, 113, 151–162. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X. Three-dimensional trajectory tracking control of an underactuated autonomous underwater vehicle based on ocean current observer. Int. J. Adv. Robot. Syst. 2018, 15, 1–9. [Google Scholar] [CrossRef]
- Caharija, W.; Pettersen, K.Y. Integral line-of-sight guidance and control of underactuated marine vehicles: Theory, simulations, and experiments. IEEE Trans. Control Syst. Technol. 2016, 24, 1623–1628. [Google Scholar] [CrossRef]
- Fossen, T.I.; Pettersen, K.Y. Line-of-sight path following for Dubins paths with adaptive sideslip compensation of drift forces. IEEE Trans. Control Syst. Technol. 2015, 23, 820–829. [Google Scholar] [CrossRef]
- Fossen, T.I.; Lekkas, A.M. Direct and indirect adaptive integral line-of-sight path-following controllers for marine craft exposed to ocean currents. Int. J. Adapt. Control Signal Process. 2017, 31, 445–451. [Google Scholar] [CrossRef]
- Li, Y.; Wei, G. Study of 3 dimension trajectory tracking of underactuated autonomous underwater vehicle. Ocean Eng. 2015, 105, 270–274. [Google Scholar] [CrossRef]
- Yao, S.; Zhang, J.; Hu, Z.; Wang, Y.; Zhou, X. Autonomous-driving vehicle test technology based on virtual reality. J. Eng. 2018, 16, 1768–1771. [Google Scholar] [CrossRef]
- Uchida, N.; Tagawa, T.; Sato, K. Development of an Augmented Reality Vehicle for Driver Performance Evaluation. IEEE Intell. Transp. Syst. Mag. 2017, 9, 35–41. [Google Scholar] [CrossRef]
- Turner, C.J.; Hutabarat, W.; Oyekan, J.; Tiwari, A. Discrete Event Simulation and Virtual Reality Use in Industry: New Opportunities and Future Trends. IEEE Trans. Hum. Mach. Syst. 2016, 46, 882–894. [Google Scholar] [CrossRef]
- Duan, H.; Zhang, Q. Visual Measurement in Simulation Environment for Vision-Based UAV Autonomous Aerial Refueling. IEEE Trans. Instrum. Meas. 2015, 64, 2468–2480. [Google Scholar] [CrossRef]
- Chen, C.-W.; Kouh, J.-S.; Tsai, J.-F. Modeling and Simulation of an AUV Simulator with Guidance System. IEEE J. Ocean. Eng. 2013, 38, 211–225. [Google Scholar] [CrossRef]
- Hu, F.; Hao, Q.; Sun, Q.; Cao, X.; Ma, R.; Zhang, T.; Patil, Y.; Lu, J. Cyberphysical System with Virtual Reality for Intelligent Motion Recognition and Training. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 347–363. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Adaptive Second-Order Fast Nonsingular Terminal Sliding Mode Tracking Control for Fully Actuated Autonomous Underwater Vehicles. IEEE J. Ocean. Eng. 2019, 44, 363–385. [Google Scholar] [CrossRef]
- Makavita, C.D.; Jayasinghe, S.G.; Nguyen, H.D.; Ranmuthugala, D. Experimental Study of Command Governor Adaptive Control for Unmanned Underwater Vehicles. IEEE Trans. Control Syst. Technol. 2019, 27, 332–345. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.; Wei, Y.; Zhang, C. Three-Dimensional Path Following of an Underactuated AUV Based on Neuro-Adaptive Command Filtered Backstepping Control. IEEE Access 2018, 6, 74355–74365. [Google Scholar] [CrossRef]
- Wang, N.; Su, S.-F.; Yin, J.; Zheng, Z.; Er, M.J. Global Asymptotic Model-Free Trajectory-Independent Tracking Control of an Uncertain Marine Vehicle: An Adaptive Universe-Based Fuzzy Control Approach. IEEE Trans. Fuzzy Syst. 2018, 26, 1613–1625. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, J.; Qiu, J.; Yang, W.; Sun, H.; Chen, Q. A Novel Fuzzy Observer-Based Steering Control Approach for Path Tracking in Autonomous Vehicles 2019. IEEE Trans. Fuzzy Syst. 2018, 27, 278–290. [Google Scholar]
- Wang, N.; Er, M.J.; Sun, J.; Liu, Y. Adaptive Robust Online Constructive Fuzzy Control of a Complex Surface Vehicle System. IEEE Trans. Cybern. 2016, 46, 1511–1523. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Sun, J.; Er, M.J. Tracking-Error-Based Universal Adaptive Fuzzy Control for Output Tracking of Nonlinear Systems with Completely Unknown Dynamics. IEEE Trans. Fuzzy Syst. 2018, 26, 869–883. [Google Scholar] [CrossRef]
- Wang, N.; Er, M.J. Direct Adaptive Fuzzy Tracking Control of Marine Vehicles with Fully Unknown Parametric Dynamics and Uncertainties. IEEE Trans. Control Syst. Technol. 2016, 24, 1845–1852. [Google Scholar] [CrossRef]
- Wang, S.; Fu, M.; Wang, Y.; Tuo, Y.; Ren, H. Adaptive Online Constructive Fuzzy Tracking Control for Unmanned Surface Vessel with Unknown Time-Varying Uncertainties. IEEE Access 2018, 6, 70444–70455. [Google Scholar] [CrossRef]
- Wang, M.H.; Yu, Y.Q.; Zeng, B. Hybrid Intelligent Control for Submarine Stabilization. Int. J. Adv. Robot. Syst. 2013, 10, 1–11. [Google Scholar] [CrossRef]
- Park, B.S.; Kwon, J.-W.; Kim, H. Neural network-based output feedback control for reference tracking of underactuated surface vessels. Automatica 2017, 77, 353–359. [Google Scholar] [CrossRef]
- Gao, J.; Proctor, A.A.; Shi, Y.; Bradley, C. Bradley, Hierarchical model predictive image-based visual servoing of underwater vehicles with adaptive neural network dynamic control. IEEE Trans. Cybern. 2016, 46, 2323–2334. [Google Scholar] [CrossRef]
- Zhu, D.; Cao, X.; Sun, B.; Luo, C. Biologically Inspired Self-Organizing Map Applied to Task Assignment and Path Planning of an AUV System. IEEE Trans. Cogn. Dev. Syst. 2018, 10, 304–313. [Google Scholar] [CrossRef]
- Cui, J.; Zhao, L.; Yu, J.; Lin, C.; Ma, Y. Neural Network-Based Adaptive Finite-Time Consensus Tracking Control for Multiple Autonomous Underwater Vehicles. IEEE Access 2019, 7, 33064–33074. [Google Scholar] [CrossRef]
- Sun, B.; Zhu, D.; Tian, C.; Luo, C. Complete Coverage Autonomous Underwater Vehicles Path Planning Based on Glasius Bio-Inspired Neural Network Algorithm for Discrete and Centralized Programming. IEEE Trans. Cogn. Dev. Syst. 2019, 11, 73–84. [Google Scholar] [CrossRef]
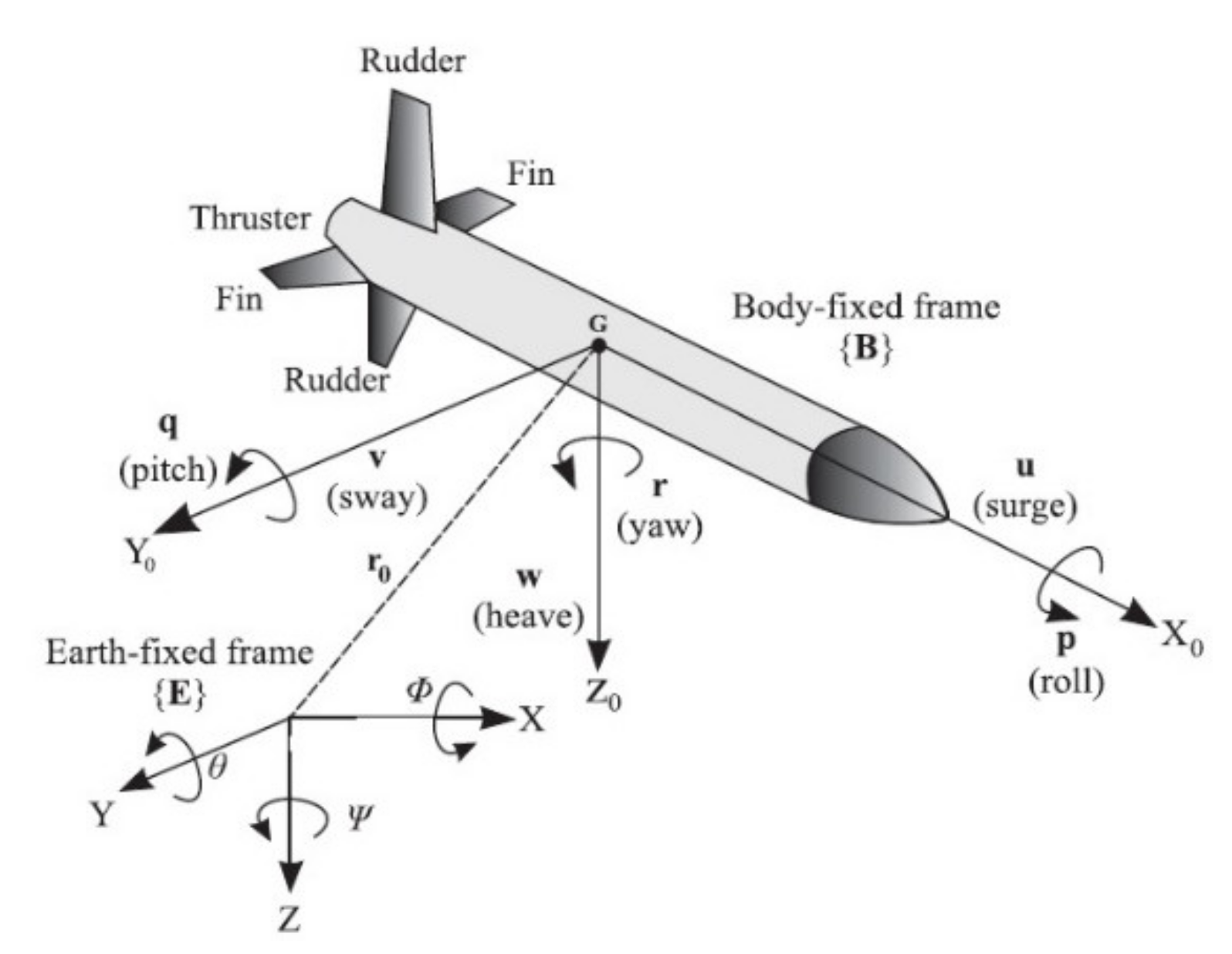





| Degree of Freedom Motion | External Forces and Moments | Rate Notation | Displacement Notation |
|---|---|---|---|
| 6-DOF motion | G | V | η |
| 3-DOF motion | 1, 2, | v1, v2 | η1, η2 |
| Translation in the x-direction surge | Xext | u | x |
| Translation in the y-direction surge | Yext | v | y |
| Translation in the z-direction surge | Zext | w | z |
| Rotation about the x-axis roll | Kext | p | φ |
| Rotation about the y-axis roll | Mext | q | θ |
| Rotation about the z-axis roll | Next | r | ψ |
| Parameter | Definition |
|---|---|
| (x,y,φ)T | Position and orientation vectors |
| (ur, vr, r)T | Relative surge, sway, and yaw velocities |
| M | Mass of the vehicle |
| (xg, yg)T | Locations of the vehicle center of gravity |
| Izz | Diagonal inertia tensor |
| Δ | Rudder Angle |
| Δmax | The upper limit of rudder angle |
| du, dv, dr | Compound uncertainties in dynamic model |
| Vx, Vy | velocity components of the ocean currents |
| m = 56 kg | δmax = 35° Yν = −24.6 kg |
| xg = 0 m | Nuv = −21 kg |
| yg = 0 m | Xu = −0.45 kg |
| Yr|r| = 0.84 kg·m/rad2 | Yuv = −32.4 kg/m |
| Nur = −3.5 kg·m/rad | Xvr = 62.1 kg/rad |
| Yp = 3.42 kg·m/rad | Nν= 2.34 kg/m |
| Nr = −6.35 kg·m2/rad | Izz = 2.78 kg·m2 |
| Xu|u| = −1.56 kg/m | Nuuδr = −7.21 kg/rad |
| Yur = 4.78 kg/rad | Xrr = −1.43 kg·m/rad |
| Nv|v| = −2.56 kg | XT max = 5.78 N |
| Yv|v| = −11.25 kg/m | Nr|r| = −6.9 kg ·m2/rad |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zeng, B.; Wang, Q. Study of Motion Control and a Virtual Reality System for Autonomous Underwater Vehicles. Algorithms 2021, 14, 93. https://doi.org/10.3390/a14030093
Wang M, Zeng B, Wang Q. Study of Motion Control and a Virtual Reality System for Autonomous Underwater Vehicles. Algorithms. 2021; 14(3):93. https://doi.org/10.3390/a14030093
Chicago/Turabian StyleWang, Minghui, Bi Zeng, and Qiujie Wang. 2021. "Study of Motion Control and a Virtual Reality System for Autonomous Underwater Vehicles" Algorithms 14, no. 3: 93. https://doi.org/10.3390/a14030093
APA StyleWang, M., Zeng, B., & Wang, Q. (2021). Study of Motion Control and a Virtual Reality System for Autonomous Underwater Vehicles. Algorithms, 14(3), 93. https://doi.org/10.3390/a14030093





