Abstract
Continuous-time linear systems with uncertain parameters are widely used for modeling real-life processes. The uncertain parameters, contained in the system and input matrices, can be constant or time-varying. In the latter case, they may represent state dependencies of these matrices. Assuming bounded uncertainties, interval methods become applicable for a verified reachability analysis, for feasibility analysis of feedback controllers, or for the design of robust set-valued state estimators. The evaluation of these system models becomes computationally efficient after a transformation into a cooperative state-space representation, where the dynamics satisfy certain monotonicity properties with respect to the initial conditions. To obtain such representations, similarity transformations are required which are not trivial to find for sufficiently wide a-priori bounds of the uncertain parameters. This paper deals with the derivation and algorithmic comparison of two different transformation techniques for which their applicability to processes with constant and time-varying parameters has to be distinguished. An interval-based reachability analysis of the states of a simple electric step-down converter concludes this paper.
1. Introduction
In previous work, Raïssi et al. [1,2] and Mazenc et al. [3] derived various techniques for a transformation of uncertain linear systems into cooperative state-space representations. An autonomous set of ordinary differential equations (ODEs)
is cooperative [4,5,6] if the property
holds for two vectors and of initial conditions which satisfy the inequalities
Cooperativity can be checked by the sufficient sign conditions
for all off-diagonal elements of the Jacobian
of the right-hand side of the state equations evaluated for all reachable states . Matrices satisfying this non-negativity property for the off-diagonal elements are also denoted as Metzler matrices in the literature [1,5,7,8].
For such systems, general-purpose, interval-based or other set-valued solvers [9] (AWA [10,11], CAPD [12], Cosy-VI [13,14], DynIBEX [15,16], ValEncIA-IVP [17,18,19,20,21], VNODE-LP [22,23], VSPODE [24]) for initial value problems (IVPs) can be replaced by point-valued simulations of a finite number of extremal realizations that can be extracted from the interval box
of initial conditions. These point-valued extremal system realizations are denoted as bounding systems throughout this paper.
A special case of these cooperative systems are so-called positive systems [25]. For initial conditions starting in the positive orthant
their trajectories will remain in the positive orthant for all due to
Then, worst-case enclosures in the form are obtained from the decoupled IVPs [26,27]
and
with the initial conditions
Transformations of linear state equations which enforce cooperativity can be classified into either point-valued approaches or into techniques that employ an interval-valued change of coordinates [28]. In general, point-valued transformations are applicable for parameter-dependent linear systems with purely real eigenvalues. However, finding such transformations becomes more complex for an increasing degree of uncertainty in the system matrix. A failure of the similarity transformation approach by Raïssi et al. [1,2] can be recognized by the alternative formulation proposed by the authors in [29]. There, the transformation was cast into an optimization problem constrained by linear matrix inequalities (LMIs). Those LMIs may become infeasible (as a verification that the solution procedure is not successful) or the step size of the iteration in [29] reduces below a certain threshold leading to an excessively slow progress (a non-strict indicator that a point-valued similarity transformation may not exist). Even if interval-valued Metzler matrices can be found for the transformation of a provable asymptotically stable state equation, the transformed dynamics matrix may consist of an unstable upper bound. This commonly results from the wrapping effect in interval computations [30,31,32]. Using the aforementioned approaches, it is impossible to systematically avoid this phenomenon. However, it can be countered by the subdivision procedure introduced in this paper.
In contrast to point-valued transformations, also interval-valued approaches exist in the literature. They were originally developed by Mazenc et al. [3] for systems with complex eigenvalues and can be used as a fallback procedure if the point-valued transformation approach is not successful [28]. As shown in Section 2.4 of this paper, they have to be treated with care if uncertain parameters are time-varying. Time-varying parameters occur typically if nonlinear state equations are cast into sets of quasi-linear models. Then, the dynamics’ matrices themselves become functions of the system states [33]. A drawback of these interval-valued similarity transformations is an inevitable introduction of the wrapping effect [10,30]. As demonstrated in this paper, this is often counterproductive with respect to the tightness of the obtained state enclosures.
In Section 2, fundamentals of cooperative dynamic systems and existing similarity transformation procedures are summarized. Section 3 deals with the novel subdivision-based approach before a simulation-based comparison is given in Section 4. This comparison does not only investigate point- and interval-valued similarity transformations but also performs a comparison with the Taylor model-based verified ODE solver verifyode [34]. The application scenario considered in Section 4 is an electric step-down converter with a predefined duty cycle. Finally, conclusions and an outlook on future work are given in Section 5.
2. Cooperativity-Enforcing Similarity Transformations
2.1. Special Case: Linear and Quasi-Linear Systems with Bounded Parameters
As a special case of the general system model introduced in (1), assume the parameter-dependent linear ODEs
Here, the parameter vector can either be uncertain but constant or time-varying within its interval bounds. For a scenario where the latter case was accounted for during a robust control synthesis, the reader is referred to [33].
For a compact notation of the system model (12), which contains all possible parameter-dependent realizations of , we introduce an interval matrix that is formed of the bounds for each entry . Those bounds are obtained according to the generally not minimal interval extension [30,31]
In this paper, it is foremost desired to find a time-invariant change of coordinates for the case that the inequalities
are not satisfied for at least one , , i.e., that the uncertain linear system model is not proven to be cooperative. The change of coordinates should then lead to a set of state equations
with an interval-valued system matrix with non-negative off-diagonal elements for each . Unfortunately, this change of coordinates may lead to the case that—despite the original system model (12) was asymptotically stable for all possible —the transformed matrix contains unstable realizations due to the wrapping effect.
Especially in the area of control engineering, dynamic system models are often not purely autonomous as stated in (12). They typically contain additive input terms . Due to the fact that these terms can be included additively in Equation (12), they can also be included additively in the transformed model (15) by the term
where uncertainty needs to be taken into account by the same and operators that are included subsequently in Equation (17).
As described in the introduction, cooperativity (together with stability) allows for simplifying the simulation of the transformed system model (15). Guaranteed bounds of all reachable states in the new coordinate frame are obtained by an evaluation of the following coupled set of state equations (which are a direct consequence of [35])
with the resulting state bounds
where couplings between the vectors and can be ignored if the system is positive, i.e., holds for all as discussed in (9)–(11).
Then, the bounding systems given in (17) simplify to
2.2. Illustrating Example
As an illustrating example for the evaluation of uncertain system models according to Equations (17), consider a set of ODEs with the uncertain parameters and initial conditions
An equidistant gridding of all six independently uncertain intervals for the initial conditions and matrix entries into eight points for the initial states and four points for each entry in the matrix (resulting in 16,384 simulations of systems of order ) yields the gray trajectories in Figure 1, while the black enclosures are obtained by a single simulation of the bounding system (17) of order .
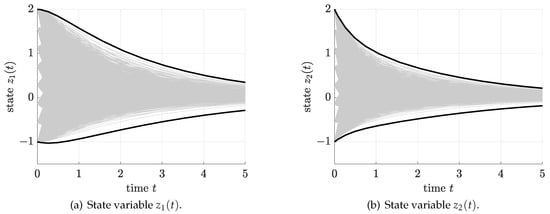
Figure 1.
State enclosures by means of exploiting cooperativity for the simple benchmark system in (20).
The following two subsections make a distinction between changes of coordinates that are applicable if the original system (12) has only purely real eigenvalues or if it may also contain conjugate-complex ones. The respective two methods are only briefly presented in the following because they are a result of the previous publications [2,28,29].
2.3. Purely Real Eigenvalues
In this case, the transformation is based on the work of Raïssi et al. in [2]. There, a general method to transform uncertain systems with purely real eigenvalues into a cooperative form (15) was presented. To extend its applicability towards larger uncertainty bounds, an extension was derived in [29], where the original approach was redesigned into an LMI-constrained optimization task [37] to make it more generally applicable and to simplify its practical use.
We assume that the uncertain system matrix can be enclosed by the element-wise defined inequality
for all defined in (13), where in (21) is a point matrix. Typical choices for are the midpoint of if this matrix is diagonally dominant (with ) or the midpoint of a matrix obtained after a principal axis transformation using the invertible real-valued eigenvector matrix .
Next, a Metzler matrix is searched for, which has the same eigenvalues as . For that, is a constant, is a matrix with all elements equal to 1, and is a diagonal matrix. Following the procedure detailed in [2], there exists an orthogonal matrix such that is Metzler with and , where is the maximum absolute value of . The overall transformation according to (15) becomes , which is point-valued and time-invariant. The LMI-based optimization in [29] automatizes the search for the matrix . It terminates successfully, if all realizations of the interval matrix are Metzler.
Remark 1.
The LMI-based optimization may fail to find a solution because of two reasons. Either the LMI solver (e.g., SeDuMiin combination with Yalmip [38,39]) may produce the output of being infeasible. Then, it is ensured that the problem formulation does not have a suitable solution. However, previous work has shown that this is typically not the case. Mostly, the step size control procedure, which increases the parameter μ defined above up to the point where is satisfied, progresses too slowly to find a solution in acceptable time. This is an indicator that the intervals are too wide to find a common point-valued transformation for the uncertain system model.
Instabilities and the failure of the LMI-based solution are countered by the subdivision in Section 3.
2.4. Mixed and Conjugate-Complex Eigenvalues
If the original system (12) contains conjugate-complex eigenvalues or if a solution with the help of the previous approach cannot be found for the complete uncertainty domain, the following procedure can be applied. The most important differences in comparison with the previous approach are:
- the transformation is usually time-varying [1,3];
- mapping the uncertainty directly into the location of the eigenvalues turns the transformation into an interval-valued expression.
Hence, evaluating the system matrix in (12) for the whole range of parameters leads to a variability of the real and imaginary parts and of the eigenvalues, where
are their respective interval bounds. Typically, it is necessary to determine these bounds with the help of interval techniques. Possible solution procedures (verifyeig) are included in the Matlab toolbox IntLab [40].
Assume that the system under investigation contains mutually disjoint conjugate-complex eigenvalue pairs with as the number of remaining real eigenvalues. To simplify the notation, assume further that all eigenvalues are sorted so that all complex pairs are listed first, cf. [28].
Now, an equivalent system representation in block diagonal structure with
can be obtained, where pairs of conjugate-complex eigenvalues with
lead to the blocks
with , while an uncertain real eigenvalue is reflected by
The respective transformation between the original system matrix and the representation in (23) is given by the column-wise partitioned matrix
with
consisting of interval enclosures for the real and imaginary parts of the eigenvectors of the interval matrix and the eigenvectors
for each of the real eigenvalues with .
In a second stage, a (generally) time-varying transformation is performed according to
where
consists of the orthogonal blocks
and
A symbolic simplification of the transformed state-space representation according to
yields a purely diagonal system matrix
in the new coordinates. For simulation purposes, the system model (34) with (35) is evaluated for the interval matrix
where the change of coordinates (15) is based on the overall interval-valued transformation
As shown before, the advantage of this transformation procedure is that it is equally applicable to systems with real and complex eigenvalues. Moreover, for the purely real case, it breaks again down to a time-invariant transformation because all matrices in (32) then become equal to the identity matrix. However, although the system dynamics according to (36) are fully decoupled in the new frame of coordinates, overestimation occurs due to the fact that an interval-valued transformation needs to be employed even if the initial conditions according to (6) were given by point-valued data.
Remark 2.
Because the approaches in Section 2.3 and Section 2.4 lead to time-invariant coordinate transformations with a single resulting set of bounding systems and because the time derivative in the square brackets of (34) cancels out for purely real eigenvalues, both procedures are equally applicable if the matrix is influenced by either constant or time-varying bounded parameters . For complex eigenvalues, the transformation in Section 2.4 and its simplification according to (34) are only valid if all are constant for known time intervals on which the simulation is carried out. For fast, arbitrary variation rates of , implying fast changes of , this equation needs to be treated with special care.
3. Novel Subdivision-Based State-Space Transformation
As the bridging element between both transformations summarized in the previous Section 2.3 and Section 2.4, a novel subdivision-based procedure is introduced. Its basic components are summarized in the following Algorithms 1–4. In a first stage, the procedure given in Section 2.3 for systems with real eigenvalues is employed (line 1 in Algorithm 1). The novel components of this algorithm are activated in the case that—after a predefined wall-clock time—no suitable transformation of the uncertain system model into an interval-valued Metzler matrix has been found, or if the resulting transformed model contains unstable realizations despite provable asymptotic stability of the original state Equation (12).
To reduce the wrapping effect during the transformation of the state equations, this novel algorithm does not only try to find transformations for the complete parameter domain (which denotes a storage element of the currently investigated interval box for the system parameter) as a whole. In addition, the list elements of yet undecided parameter subintervals (i.e., those intervals for which a solution of the desired transformation has not yet been found) also carry several subintervals, which are all stored in . In such a way, it becomes possible to individually investigate each of the corresponding subboxes, whether at least for some of them the algorithm of Section 2.3 produces stable realizations of the transformed system model.
According to Remark 1, a stopping criterion needs to be implemented which avoids an endless search for point-valued transformations. Currently, this is done by checking whether a timeout occurred (line 1 in Algorithm 1). Suitable alternatives would be progression rates for the parameter which fall below a certain threshold or a maximum number of non-successful trials. If this stopping criterion becomes active, the stable intervals—transformed into interval-valued Metzler matrices—are appended to the list (starting in line 1 of Algorithm 1, as well as Algorithm 2).
| Algorithm 1: Splitting-based transformation |
 |
| Algorithm 2: Stability analysis |
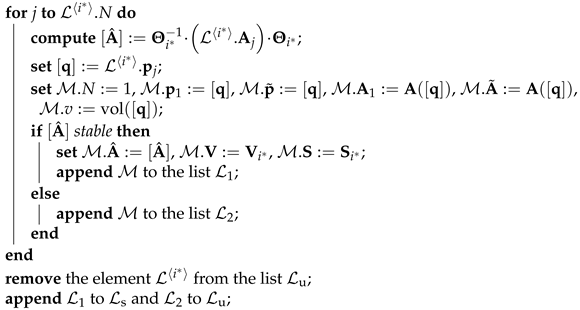 |
For all undecided intervals (either without existing cooperativity-enforcing transformation or lacking the property of asymptotic stability), two different subdivision procedures are used in lines 1, 1, and 1 of Algorithm 1. Details about their distinction are summarized in Algorithms 3 and 4. Basically, they either break up the collection of subintervals into yet undecided individual boxes in Algorithm 3, or split the largest parameter box into smaller subintervals after appending the individual entries to the undecided list in Algorithm 4.
| Algorithm 3: Subdivision procedure A |
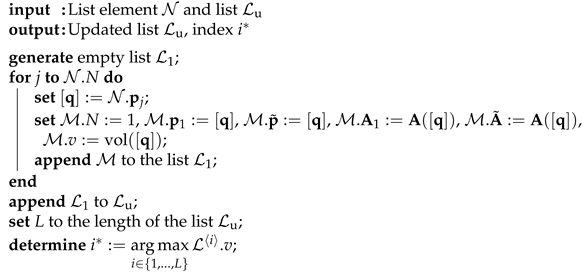 |
| Algorithm 4: Subdivision procedure B |
 |
In such a way, the list , obtained after completion of the while-loop in Algorithm 1, contains individual state-space transformations into asymptotically stable subsystem models. The resulting transformed subsystems are always valid for uncertain but constant parameters. Temporal variations, however, are now no longer admissible within the complete initial parameter box. Instead, due to the subdivision into a collection of mutually independent subsystem models (corresponding to the length of ), temporal variations of parameters are only allowed within each individual box . Finally, in cases in which it is not a-priori known that the original system model has purely real eigenvalues and that the while-loop in line 1 of Algorithm 1—based on the procedure from Section 2.3—will, hence, terminate after a sufficiently large number of subdivisions, a fallback to the interval-based transformation of Section 2.4 should be included.
4. Application Scenario: Step-Down Converter
The algorithms for a transformation of dynamic system models into a cooperative state-space representation are now compared by means of numerical simulations for the state equations of a linear step-down converter circuit. All interval evaluations are performed in IntLab V. 12 [40]. For the numerical simulation of point-valued bounding systems, the floating-point solver ode23 with standard tolerance setting and the maximum step size was used. This solver is sufficiently accurate and more effective than, for example, ode45 for the moderately stiff system model under consideration. For this application, the resulting approximation errors are also several orders of magnitude smaller than the absolute values of the corresponding states. This was checked by a computation of the corresponding solutions with the help of symbolic formula manipulation in Matlab. In addition to the presentation of the transformation approaches introduced in this paper, a comparison with the verified ODE solver verifyode is illustrated. This solver is also included in IntLab.
4.1. Modeling
According to Figure 2, a step-down converter is combined with a fuse for excessive current protection, a variable load , and the variably connectable additional resistor . For simplicity of the following state equations, the diode forward bias is assumed to be zero. In future work, it can be included in a straightforward manner by means of an additional system parameter in the corresponding voltage loop equation.
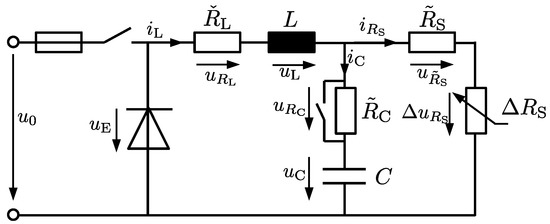
Figure 2.
Step-down converter.
Here, the equations (denoted for brevity without explicitly mentioning time arguments)
with
describe the two voltage loops, while
results from Kirchhoff’s node equation. The component equations of all Ohmic resistances are given by
with . Furthermore, the inductivity and capacity are represented by
Here, the physical energy storage is expressed by the current and the voltage , which results in the ODE
to describe variations of the magnetic field energy and in
for changes of the electric field energy. The corresponding state-space representation with
results in
For the simulations in the following subsection with , the parameters in Equation (46) are set to , (together mimicking a real inductor with non-zero internal resistance; which can be implemented for a test rig with the help of an operational amplifier-based gyrator circuit), , , and .
In addition, the input voltage of the system is defined as a piecewise constant, periodic signal of duration according to
where the constant parameter specifies the length of the duty cycle.
4.2. Simulation-Based Comparison of Two Cooperativity-Enforcing Similarity Transformations
Considering the parameters listed in the previous subsection, it can be shown that there does not exist a common, point-valued transformation matrix according to Section 2.3 that simultaneously leads to a Metzler matrix representation for the transformed system dynamics stated in Equation (15) and at the same time preserves the asymptotic stability of the original system (46).
Hence, a transformation of the system model into an interval-valued diagonal structure according to (34) and (36) has been performed first. After a subdivision of the parameter box
in a regular grid with subintervals, the following eigenvalue bounds were obtained by using IntLab’s verifyeig routine:
Due to the fact that these eigenvalues are purely real, the transformation matrix from (37) becomes time-invariant according to
Here, the entries are displayed after outward rounding to four decimals. The simulation routine makes use of to convert the results back into the original state variables . The inverse
of this matrix is required to express the influence of the control action according to (16). The interval enclosures for the temporal evolution of the state variables are depicted in Figure 3. These bounds are valid both, see Remark 2, for time-invariant uncertain parameters and for parameters that are changing their values arbitrarily within the complete uncertainty intervals.
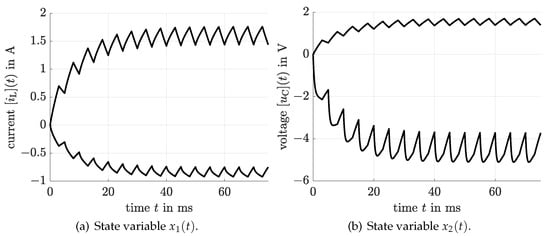
Figure 3.
State enclosures in terms of their lower and upper bounds for the step-down converter after backward transformation into the original state-space using the procedure in Section 2.4.
In contrast, the novel solution procedure, with and in Algorithm 1 yields significantly tighter state enclosures as shown in Figure 4. Here, the solution is represented by the interval hull over all individual state enclosures, restricting the validity of the computed bounds to variations of the parameters within each of the boxes displayed in Figure 5. Please note that increasing the parameter N in the multi-sectioning strategy does not necessarily lead to tighter interval bounds. Hence, its systematic optimization in combination with a sensitivity-based selection of the splitting direction [41,42] will be especially helpful to make the procedure applicable to systems with a larger number of uncertain parameters in future work.
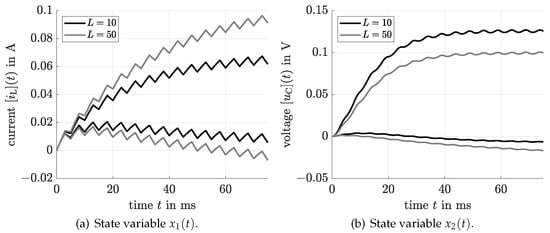
Figure 4.
State enclosures for the step-down converter using the novel procedure according to Section 3 in combination with the real-valued transformation approach of Section 2.3.
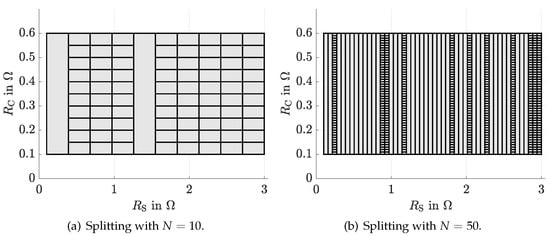
Figure 5.
Partitioning of the parameter domain according to Section 3 for two different parameterizations of the multi-sectioning strategy.
4.3. Comparison with a Taylor Model-Based Solution Approach
In general, there exist two different options to account for the uncertain parameter vector defined in Equation (48) when using a general-purpose verified ODE solver. In this section, the solver verifyode [34,43] is employed to obtain a representative comparison.
When appending the uncertain parameters to the state vector , introduced in (45), and accounting for the time invariance of these parameters by the so-called integrator disturbance model in the state equations, the solver verifyode does not at all succeed in computing guaranteed state bounds. This results from a division by zero when substituting the Taylor model representations of both uncertain parameters into the system model (46). This problem is independent whether identical Taylor model orders are chosen for all four state variables or if the Taylor model order for the interval parameters is reduced to its minimum value 1 as described in [43].
A simulation of this augmented state-space representation becomes possible—even with the default setting of identical Taylor model orders for all state variables—if the uncertainty in both parameters is reduced significantly. This, however, changes the system dynamics and can therefore not be used for a fair comparison with the proposed cooperativity-enforcing simulation approaches.
Successful simulations with this ODE solver become possible if the uncertain parameters are not appended to the state vector but if they are specified instead within the state equations as interval variables (datatype intval). Then, manually specifying the initial step size of the solver as , the minimum step size as , the Taylor model orders as either 10, 12 (the default setting), or 30, performing either a QR preconditioning or a curvilinear preconditioning with or without blunting (a strategy of widening the angles between the column vectors of an ill-conditioned preconditioning matrix to reduce overestimation [44]) and/or shrink wrapping (aiming at an elimination of additive error intervals and incorporating them in the Taylor model coefficients [45]), it is possible to simulate the system model.
For the comparison with the proposed solution approach described in Section 3, the outcome of verifyode is investigated for the following solver settings:
- case 1
- with default settings (order 12) for all options [43] except for the step size parameters and the choice of a QR preconditioningverifyodeset(’h0’, 1e-4, ’h_min’, 1e-6, ’precondition’, 1);
- case 2
- with order 10, manually specified small tolerances, and QR preconditioningverifyodeset(’order’, 10, ’shrinkwrap’, 0, ’precondition’, 1, ’blunting’, 0, ...’h0’, 1e-4, ’h_min’, 1e-6, ’loc_err_tol’, 1e-11, ’sparsity_tol’, 1e-20);
- case 3
- with order 30, manually specified small tolerances, and QR preconditioningverifyodeset(’order’, 30, ’shrinkwrap’, 0, ’precondition’, 1, ’blunting’, 0, ...’h0’, 1e-4, ’h_min’, 1e-6, ’loc_err_tol’, 1e-11, ’sparsity_tol’, 1e-20);
- case 4
- with order 10, manually specified small tolerances, and curvilinear preconditioningverifyodeset(’order’, 10, ’shrinkwrap’, 0, ’precondition’, 3, ’blunting’, 0, ...’h0’, 1e-4, ’h_min’, 1e-6, ’loc_err_tol’, 1e-11, ’sparsity_tol’, 1e-20);
- case 5
- with order 30, manually specified small tolerances, and curvilinear preconditioningverifyodeset(’order’, 30, ’shrinkwrap’, 0, ’precondition’, 3, ’blunting’, 0, ...’h0’, 1e-4, ’h_min’, 1e-6, ’loc_err_tol’, 1e-11, ’sparsity_tol’, 1e-20);
The simulations have shown that the cases 1–3 complete successfully up to the point (the same final time instant as in Figure 3 and Figure 4, comprising 15 full duty cycles), while the state enclosures in the cases 4–5, in which the QR preconditioning was replaced by the curvilinear one blow up and break down shortly after because the integration step size falls below the specified threshold. Setting the step size parameters to the default values as described in [43] does not resolve this issue. Activating the options for blunting and/or shrink wrapping did not influence the solutions for the considered application. Hence, they are not investigated further in this paper. Therefore, the following graphical comparison in Figure 6, Figure 7 and Figure 8 will be restricted to the cases 1–3.
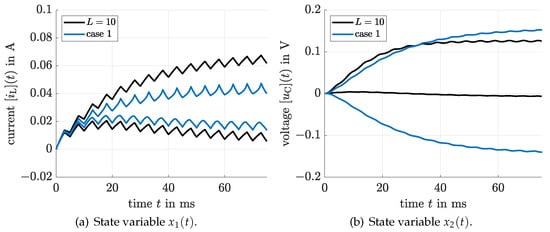
Figure 6.
Comparison of the proposed approach with with the results of verifyode for the case 1.
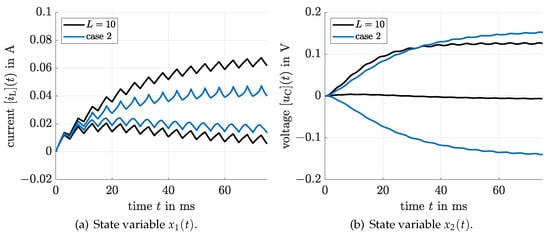
Figure 7.
Comparison of the proposed approach with with the results of verifyode for the case 2.
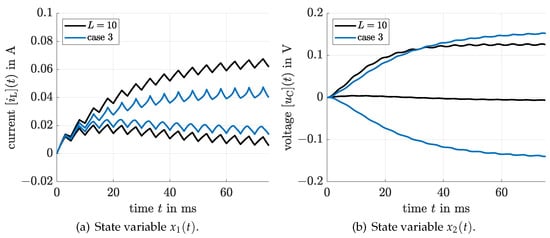
Figure 8.
Comparison of the proposed approach with with the results of verifyode for the case 3.
When comparing Figure 6, Figure 7 and Figure 8, it can be seen clearly that the computed bounds for the electric current obtained with the help of verifyode are tighter than those of the proposed approach but that the interval bounds for the capacitor’s voltage are much wider if the Taylor model solver is employed. Especially the fact that this simulation is practically not able to predict the correct sign of the voltage is counterproductive for practical applications where the simulation results may be employed to forecast the magnitude and direction of power flows towards a consumer (represented by the resistance in the considered scenario). The new solution approach (without counting the offline parameter splitting) is faster by a factor of at least 100 than the alternative solver despite the use of multiple parameter intervals in the simulation if both are executed on the same computer using Matlab 2019b.
Remark 3.
Due to the linearity of the point-valued bounding systems produced by the new Algorithms 1–4, it is even possible (in the case when the dimension n is sufficiently small) to compute the worst-case state enclosures efficiently in closed form by using techniques for symbolic formula manipulation. The existence of such symbolic expressions can be exploited in future work to design fast model-predictive control strategies for uncertain dynamic systems.
Remark 4.
Due to cooperativity of the transformed system models—which are obtained with the approach presented in this paper—they are less affected by overestimation resulting from the wrapping effect, even if simulations were carried out for the corresponding interval boxes of the uncertain parameter and not for the decoupled bounding systems as suggested. Therefore, the obtained changes of coordinates could be employed also by general-purpose verified ODE solvers. This represents a further means to reduce overestimation in addition to the typically employed options such as QR preconditioning [11,34].
5. Conclusions and Future Work
In this paper, a novel subdivision-based transformation approach was presented that allows for computing the domains of reachable states of an uncertain dynamic system in terms of point-valued bounding models. This transformation significantly reduces computing times and overestimation in the computed results and outperforms general-purpose solvers such as verifyeig, as long as the assumption on limited parameter variabilities, detailed in this paper, are satisfied.
Methods, allowing the extension of the procedure further to mixed real and complex eigenvalues, resulting, for example from larger uncertainty in the resistances in the application considered in this paper will be investigated in future work. In addition, further research should be directed towards extensions for arbitrarily fast changes of parameters occurring in a time- or event-triggered framework as well as to interfacing the proposed methodology with techniques for gain scheduling control of uncertain dynamic systems [33]. Moreover, possible generalizations towards the simulation of uncertain fractional-order differential equations will be investigated [46,47,48].
Author Contributions
The algorithm was designed jointly by A.R. and J.K.; implementation and numerical validation by A.R. The paper was jointly written by A.R. and J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Raïssi, T.; Efimov, D.; Zolghadri, A. Interval State Estimation for a Class of Nonlinear Systems. IEEE Trans. Autom. Control 2012, 57, 260–265. [Google Scholar] [CrossRef]
- Efimov, D.; Raïssi, T.; Chebotarev, S.; Zolghadri, A. Interval State Observer for Nonlinear Time Varying Systems. Automatica 2013, 49, 200–205. [Google Scholar] [CrossRef]
- Mazenc, F.; Bernard, O. Asymptotically Stable Interval Observers for Planar Systems With Complex Poles. IEEE Trans. Autom. Control 2010, 55, 523–527. [Google Scholar] [CrossRef]
- Angeli, D.; Sontag, E. Monotone Control Systems. IEEE Trans. Autom. Control 2003, 48, 1684–1698. [Google Scholar] [CrossRef]
- Smith, H.L. Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems; Mathematical Surveys and Monographs, American Mathematical Soc.: Providence, RI, USA, 1995; Volume 41. [Google Scholar]
- Hirsch, M. On the Nonchaotic Nature of Monotone Dynamical Systems. Eur. J. Pure Appl. Math. 2019, 12, 680–688. [Google Scholar] [CrossRef]
- Rauh, A.; Kersten, J.; Aschemann, H. Interval and Linear Matrix Inequality Techniques for Reliable Control of Linear Continuous-Time Cooperative Systems with Applications to Heat Transfer. Int. J. Control 2020, 93, 2771–2788. [Google Scholar] [CrossRef]
- Raïssi, T.; Efimov, D. Some Recent Results on the Design and Implementation of Interval Observers for Uncertain Systems. at-Automatisierungstechnik 2018, 66, 213–224. [Google Scholar] [CrossRef]
- Nedialkov, N.S. Interval Tools for ODEs and DAEs. In Proceedings of the 12th GAMM-IMACS Intl. Symposium on Scientific Computing, Computer Arithmetic, and Validated Numerics SCAN 2006, Duisburg, Germany, 26–29 September 2006; IEEE Computer Society: Duisburg, Germany, 2007. [Google Scholar]
- Lohner, R. On the Ubiquity of the Wrapping Effect in the Computation of the Error Bounds. In Perspectives on Enclosure Methods; Kulisch, U., Lohner, R., Facius, A., Eds.; Springer–Verlag: Wien, NY, USA, 2001; pp. 201–217. [Google Scholar]
- Lohner, R. Enclosing the Solutions of Ordinary Initial and Boundary Value Problems. In Computer Arithmetic: Scientific Computation and Programming Languages; Kaucher, E.W., Kulisch, U.W., Ullrich, C., Eds.; Wiley-Teubner Series in Computer Science: Stuttgart, Germany, 1987; pp. 255–286. [Google Scholar]
- Kapela, T.; Mrozek, M.; Wilczak, D.; Zgliczynski, P. CAPD::DynSys: A Flexible C++ Toolbox for Rigorous Numerical Analysis of Dynamical Systems. Commun. Nonlinear Sci. Numer. Simul. 2020, 105578. [Google Scholar] [CrossRef]
- Berz, M.; Makino, K. COSY INFINITY Version 8.1. User’s Guide and Reference Manual; Technical Report MSU HEP 20704; Michigan State University: East Lansing, MI, USA, 2002. [Google Scholar]
- Hoefkens, J. Rigorous Numerical Analysis with High-Order Taylor Models. Ph.D. Thesis, Michigan State University, East Lansing, MI, USA, 2001. Available online: http://www.bt.pa.msu.edu/cgi-bin/display.pl?name=hoefkensphd (accessed on 14 January 2021).
- Alexandre dit Sandretto, J.; Chapoutot, A. Validated Explicit and Implicit Runge–Kutta Methods. Reliab. Comput. 2016, 22, 79–103. [Google Scholar]
- Mullier, O.; Chapoutot, A.; Alexandre dit Sandretto, J. Validated Computation of the Local Truncation Error of Runge–Kutta Methods with Automatic Differentiation. Optim. Methods Softw. 2018, 33, 718–728. [Google Scholar] [CrossRef]
- Rauh, A.; Auer, E.; Hofer, E.P. ValEncIA-IVP: A Comparison with Other Initial Value Problem Solvers. In Proceedings of the 12th GAMM-IMACS International Symposium on Scientific Computing, Computer Arithmetic, and Validated Numerics SCAN 2006, Duisburg, Germany, 26–29 September 2006; IEEE Computer Society: Duisburg, Germany, 2007. [Google Scholar]
- Auer, E.; Rauh, A.; Hofer, E.P.; Luther, W. Validated Modeling of Mechanical Systems with SmartMOBILE: Improvement of Performance by ValEncIA-IVP. In Proceedings of the Dagstuhl Seminar 06021: Reliable Implementation of Real Number Algorithms: Theory and Practice; Lecture Notes in Computer Science; Springer–Verlag: Berlin, Heidelberg, Germany, 2008; pp. 1–27. [Google Scholar]
- Rauh, A.; Westphal, R.; Aschemann, H.; Auer, E. Exponential Enclosure Techniques for Initial Value Problems with Multiple Conjugate Complex Eigenvalues. In Proceedings of 16th GAMM-IMACS International Symposium on Scientific Computing, Computer Arithmetic, and Validated Numerics SCAN2014; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9553, pp. 87–122. [Google Scholar]
- Rauh, A.; Westphal, R.; Auer, E.; Aschemann, H. Exponential Enclosure Techniques for the Computation of Guaranteed State Enclosures in ValEncIA-IVP. 2013. Available online: http://interval.louisiana.edu/reliable-computing-journal/volume-19/reliable-computing-19-pp-066-090.pdf (accessed on 13 January 2021).
- Rauh, A.; Westphal, R.; Aschemann, H. Verified Simulation of Control Systems with Interval Parameters Using an Exponential State Enclosure Technique. In Proceedings of the IEEE 2013 18th International Conference on Methods and Models in Automation and Robotics MMAR, Miedzyzdroje, Poland, 26–29 August 2013. [Google Scholar]
- Nedialkov, N.S. Computing Rigorous Bounds on the Solution of an Initial Value Problem for an Ordinary Differential Equation. Ph.D. Thesis, Graduate Department of Computer Science, University of Toronto, Toronto, ON, Canada, 1999. [Google Scholar]
- Nedialkov, N.S. Implementing a Rigorous ODE Solver through Literate Programming. In Modeling, Design, and Simulation of Systems with Uncertainties; Rauh, A., Auer, E., Eds.; Mathematical Engineering, Springer: Berlin/Heidenberg, Germany, 2011; pp. 3–19. [Google Scholar]
- Lin, Y.; Stadtherr, M.A. Validated Solutions of Initial Value Problems for Parametric ODEs. Appl. Numer. Math. 2007, 57, 1145–1162. [Google Scholar] [CrossRef]
- Kaczorek, T. Positive 1D and 2D Systems; Springer–Verlag: London, UK, 2002. [Google Scholar]
- Gennat, M.; Tibken, B. Computing Guaranteed Bounds for Uncertain Cooperative and Monotone Nonlinear Systems. IFAC Proc. Vol. 2008, 41, 4846–4851. [Google Scholar] [CrossRef]
- Aschemann, H.; Rauh, A.; Kletting, M.; Hofer, E.; Gennat, M.; Tibken, B. Interval Analysis and Nonlinear Control of Wastewater Plants with Parameter Uncertainty. IFAC Proc. Vol. 2005, 38, 55–60. [Google Scholar] [CrossRef]
- Rauh, A.; Kersten, J.; Aschemann, H. Techniques for Verified Reachability Analysis of Quasi-Linear Continuous-Time Systems. In Proceedings of the 24th International Conference on Methods and Models in Automation and Robotics 2019, Miedzyzdroje, Poland, 26–29 August 2019. [Google Scholar]
- Kersten, J.; Rauh, A.; Aschemann, H. State-Space Transformations of Uncertain Systems With Purely Real and Conjugate-Complex Eigenvalues Into a Cooperative Form. In Proceedings of the 23rd International Conference on Methods and Models in Automation and Robotics 2018, Miedzyzdroje, Poland, 27–30 August 2018. [Google Scholar]
- Jaulin, L.; Kieffer, M.; Didrit, O.; Walter, É. Applied Interval Analysis; Springer–Verlag: London, UK, 2001. [Google Scholar]
- Mayer, G. Interval Analysis and Automatic Result Verification; De Gruyter Studies in Mathematics, De Gruyter: Berlin, Germany; Boston, MA, USA, 2017. [Google Scholar]
- Kühn, W. Rigorous Error Bounds for the Initial Value Problem Based on Defect Estimation; Technical Report. 1999. Available online: http://www.decatur.de/personal/papers/defect.zip (accessed on 13 January 2021).
- Kersten, J.; Rauh, A.; Aschemann, H. Interval Methods for Robust Gain Scheduling Controllers: An LMI-Based Approach. Granul. Comput. 2020, 5, 203–216. [Google Scholar] [CrossRef]
- Bünger, F. A Taylor Model Toolbox for Solving ODEs Implemented in MATLAB/INTLAB. J. Comput. Appl. Math. 2020, 368, 112511. [Google Scholar] [CrossRef]
- Müller, M. Über die Eindeutigkeit der Integrale eines Systems gewöhnlicher Differenzialgleichungen und die Konvergenz einer Gattung von Verfahren zur Approximation dieser Integrale; Sitzungsbericht Heidelberger Akademie der Wissenschaften; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 1927. [Google Scholar]
- Rauh, A.; Kersten, J.; Aschemann, H. Interval Methods and Contractor-Based Branch-and-Bound Procedures for Verified Parameter Identification of Quasi-Linear Cooperative System Models. J. Comput. Appl. Math. 2020, 367, 112484. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Sturm, J. Using SeDuMi 1.02, A MATLAB Toolbox for Optimization over Symmetric Cones. Optim. Methods Softw. 1999, 11–12, 625–653. [Google Scholar] [CrossRef]
- Löfberg, J. YALMIP: A Toolbox for Modeling and Optimization in MATLAB. In Proceedings of the IEEE International Symposium on Computer Aided Control Systems Design, Taipei, Taiwan, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Rump, S. IntLab—INTerval LABoratory. In Developments in Reliable Computing; Csendes, T., Ed.; Kluver Academic Publishers: Dordrecht, The Netherlands, 1999; pp. 77–104. [Google Scholar]
- Freihold, M.; Hofer, E. Derivation of Physically Motivated Constraints for Efficient Interval Simulations Applied to the Analysis of Uncertain Dynamical Systems. Appl. Math. Comput. Sci. 2009, 19, 485–499. [Google Scholar] [CrossRef]
- Freihold, M.; Rauh, A.; Hofer, E.P. Physically Motivated Constraints for Efficient Interval Simulations Applied to the Analysis of Uncertain Models of Blood Cell Dynamics. In Progress in Industrial Mathematics at ECMI 2008; Fitt, A.D., Norbury, J., Ockendon, H., Wilson, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 563–569. [Google Scholar]
- Bünger, F. DEMOTAYLORMODEL Short Demonstration of the Taylor Model Toolbox. Available online: www.ti3.tuhh.de/intlab/demos/html/dtaylormodel.html (accessed on 16 February 2021).
- Bünger, F. Preconditioning of Taylor Models, Implementation and Test Cases. Nonlinear Theory Its Appl. IEICE 2021, 12, 2–40. [Google Scholar] [CrossRef]
- Bünger, F. Shrink Wrapping for Taylor Models Revisited. Numer. Algorithms 2018, 78, 1001–1017. [Google Scholar] [CrossRef]
- Rauh, A.; Kersten, J. Toward the Development of Iteration Procedures for the Interval-Based Simulation of Fractional-Order Systems. Acta Cybern. 2020. [Google Scholar] [CrossRef]
- Rauh, A.; Kersten, J. Verification and Reachability Analysis of Fractional-Order Differential Equations Using Interval Analysis. In Proceedings 6th International Workshop on Symbolic-Numeric Methods for Reasoning about CPS and IoT, Online, 31 August 2020; Electronic Proceedings in Theoretical Computer Science; Dang, T., Ratschan, S., Eds.; Open Publishing Association: Den Haag, The Netherlands, 2021; Volume 331, pp. 18–32. [Google Scholar] [CrossRef]
- Rauh, A.; Jaulin, L. Novel Techniques for a Verified Simulation of Fractional-Order Differential Equations. Fractal Fract. 2021, 5, 17. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).