Abstract
Collision between rigid three-dimensional objects is a very common modelling problem in a wide spectrum of scientific disciplines, including Computer Science and Physics. It spans from realistic animation of polyhedral shapes for computer vision to the description of thermodynamic and dynamic properties in simple and complex fluids. For instance, colloidal particles of especially exotic shapes are commonly modelled as hard-core objects, whose collision test is key to correctly determine their phase and aggregation behaviour. In this work, we propose the Oriented Cuboid Sphere Intersection (OCSI) algorithm to detect collisions between prolate or oblate cuboids and spheres. We investigate OCSI’s performance by bench-marking it against a number of algorithms commonly employed in computer graphics and colloidal science: Quick Rejection First (QRI), Quick Rejection Intertwined (QRF) and a vectorized version of the OBB-sphere collision detection algorithm that explicitly uses SIMD Streaming Extension (SSE) intrinsics, here referred to as SSE-intr. We observed that QRI and QRF significantly depend on the specific cuboid anisotropy and sphere radius, while SSE-intr and OCSI maintain their speed independently of the objects’ geometry. While OCSI and SSE-intr, both based on SIMD parallelization, show excellent and very similar performance, the former provides a more accessible coding and user-friendly implementation as it exploits OpenMP directives for automatic vectorization.
1. Introduction
Employing computer programs and algorithms to generate 2D or 3D images is referred to as rendering. Rendering is a topic of striking relevance in computer graphics with practical impact on many heterogeneous disciplines, spanning engineering, simulators, video games and movie special effects. Collision detection and collision determination are key elements of rendering as they determine the distance between two objects and their possible intersection [1]. Due to their widespread use in video representation of time-evolving systems, with tens of frames displayed per second, algorithms for rendering are expected to be very efficient [2,3]. Generally, to assess whether two complex objects collide, the distance between their respective bounding volumes is evaluated first. Common bounding volumes are cuboidal boxes, whose axes might or might not be aligned, or spheres. Due to their simple geometry, the collision between cuboids and/or spheres is computationally easier [4,5,6,7], thus enhancing the speed and efficiency of the overall rendering process [2]. Collision detection algorithms are of utmost relevance in many heterogeneous applications spanning computer graphics for shape modelling and video games [8,9,10,11,12], robotics to prevent potential collisions in man–robot interactions [13,14,15,16,17], risk assessment associated to vessel collision [18] or machining of sculptured surfaces [19], and simulations of molecular or particle systems to estimate their thermodynamic properties [20,21].
Collision algorithms have also been key to address the thermodynamics of liquid and solid phases and their phase transition by early molecular simulation studies that employed the hard-sphere model [22,23,24]. More recently, and following the seminal theory by Onsager on the isotropic-to-nematic transition of hard rods [25], they were fundamental to confirm the crucial role of excluded volume effects in the formation of colloidal liquid crystal phases of anisotropic particles [20]. Realising the practical impact of the particle shape on the design of nanomaterials triggered the blooming of biosynthetic [26], chemical [27] and physical [28] experimental routes to manufacture precise building blocks with ad hoc properties, including lock-and-key particles [29], fused spheres [30], superballs [31] and cuboids [32,33,34,35]. The appearance of these exotic shapes unveiled a realm of novel opportunities in nanomaterials science by offering an increasingly varied selection of morphologies for state-of-the-art applications spanning medicine (controlled drug delivery), smart materials (self-healing coatings) and photonics (light detection), among others. Often anticipating experimental evidence, computer simulations have significantly contributed to our comprehension of the effect of particle shape and interaction at the nanoscale on the material properties at the macroscale [36,37,38,39]. Understanding the fundamentals of such a complex correlation, which develops over orders of magnitude in length and time scales, dramatically depends on the existence of reliable force fields mimicking the interactions between particles. This is not always the case for most exotic particle shapes, whose force field is assumed to be described by mere excluded volume effects and thus only incorporates a hard-core interaction potential. Consequently, efficient and robust algorithms able to detect collisions and intersections between objects become essential to extract structural, thermodynamic and dynamic properties of such systems from a molecular simulation. In colloid science, cuboids are especially intriguing building blocks that can form a rich variety of liquid crystal phases [40,41,42,43,44]. Incorporating guest spherical particles in these phases is relevant to understand phenomena of diffusion in crowded environments that display a significant degree of ordering.
In light of these considerations, which highlight the harmonious inter-disciplinary convergence of computer graphics and colloid science, here we report on the specific case of cuboid-sphere collision detection. In particular, we propose our own Oriented Cuboid Sphere Intersection (OCSI) algorithm to detect collisions in monodisperse systems of cuboids and spheres oriented in a 3D space. OCSI is found to be especially efficient when compared to the Quick Rejection First (QRI) and the Quick Rejection Intertwined (QRF) algorithms, and more user-friendly and easier to implement than the vectorized version of the algorithm that employs SIMD Streaming Extension (SSE) intrinsic functions [7]. For simplicity, we refer to the vectorized version of the collision detection algorithm developed by Larsson et al. with the abbreviation “SSE-intr”, since it uses Intel® intrinsic functions specific for SSE instruction set. In particular, QRI and QRF make use of a quick rejection test that discards overlaps if the minimum distance, , between the surface of a cuboid and the centre of a sphere is larger than the sphere radius. As a result that this test depends on the cuboid size and shape, the efficiency of both QRI and QRF is expected to be determined, to some extent, by the specific sphere and cuboid geometry. By contrast, SSE-intr, which runs in parallel and is therefore significantly faster than QRI and QRF, does not need quick rejection tests and makes use of vectorization to estimate . Our algorithm, available in C and Fortran 90, incorporates a few key elements (e.g., the absolute value to estimate the minimum distance and OpenMP directives to parallelize the code with no use of SIMD intrinsics) that make it faster than QRI and QRF and more versatile than SEE-intr. This paper is organised as follows. In Section 2, we detail the theoretical framework of the cuboid-sphere intersection problem and the state-of-the-art in software implementation. In Section 3, we describe the code that we have specifically developed to test each of the above-mentioned algorithms’ efficiency for cuboids of different shape and spheres of different size. The comparison between the algorithms is then discussed in Section 4, while, in Section 5, we draw our conclusions.
2. Algorithms
In geometry, a sphere is identified by its radius, R, and the position of its centre, , with respect to a reference point. Similarly, a cuboid can be defined by the extension of its thickness, , length, and width, , the position of its centre of mass, and the unit vectors , and that indicate the orientation of its three orthogonal axes. As a result, all the points within the volume occupied by the cuboid can be indicated by a vector that reads
where T, L and W indicate, respectively, the cuboid thickness, length and width, whereas is a scalar interval. With these essential definitions, the minimum distance, , between the surface of a randomly oriented cuboid and the centre of a sphere can be calculated as follows:
where and is the Heaviside step function:
The interested reader is referred to Appendix A for a formal derivation of Equation (2). To the best of our knowledge, Arvo was the first to propose an algorithm detecting the intersection between a sphere and an axis-aligned cuboid, that is a cuboid whose orientation matches that of the reference axes [5]. For this specific case, we assume that the cuboid thickness is aligned with the x axis, i.e., , its length with the y axis, i.e., and its width with the z axis, i.e., . Following this assumption, Equation (1) can be rewritten as
where are the reference axes for T, L and W, respectively, and , and . Therefore, for an axis-aligned cuboid, can be calculated as
By using the infimum and supremum of , the terms in the above sum can be easily calculated:
- if , then ,
- if , then ,
- if , then .
Consequently, the algorithm proposed by Arvo only requires the extreme values of along with the sphere radius and position and detects cuboid-sphere collisions if . An illustrative example of a pseudocode describing its main steps is reported in Algorithm 1.
| Algorithm 1- Arvo |
|
The alignment of the cuboid unit vectors with the reference axes is a particular case of a more general scenario with the cuboid randomly oriented. Eventually, Arvo’s algorithm can also be applied to randomly oriented cuboids by performing a transformation of the vectors involved in the calculation of in the reference frame of . Rokne and Ratschek proposed to estimate by employing interval analysis and reported a test to determine whether a point is within a sphere delimited by four peripheral points [6]. The algorithms proposed by Larsson and co-workers employ quick rejection overlap tests to enhance the efficiency of collision detection between a sphere and either an aligned or a randomly oriented cuboid [7]. The pseudocode of these algorithms are reported in Algorithms 2 and 3, respectively. Both QRI and QRF are based on the implementation of a quick rejection test that immediately excludes an overlap if at least one of the summands in Equation (2) or Equation (5) is larger than . For the general case of a randomly oriented cuboid, this condition reads
A geometrical representation of this condition is provided in Figure 1, where a sphere of radius R and centred at is at the distance from the centre of mass of a cuboid that is centred at . For this specific arrangement, the left-hand side of Equation (6) measures the distance of from the face of delimited by T and W and schematically identified by the vertical solid line of Figure 1. QRI applies this rejection criterion within the loop that evaluates the minimum distance, precisely at lines 6 and 9 of Algorithm 2. By contrast, QRF performs the three quick rejection tests, one for each summand of Equation (2), before the computation of the minimum distance, between lines 3 and 6 of Algorithm 3. In this case, the scalar products are stored in line 4 and eventually employed to compute in the following loop.
| Algorithm 2 QRI |
|
| Algorithm 3 QRF |
|
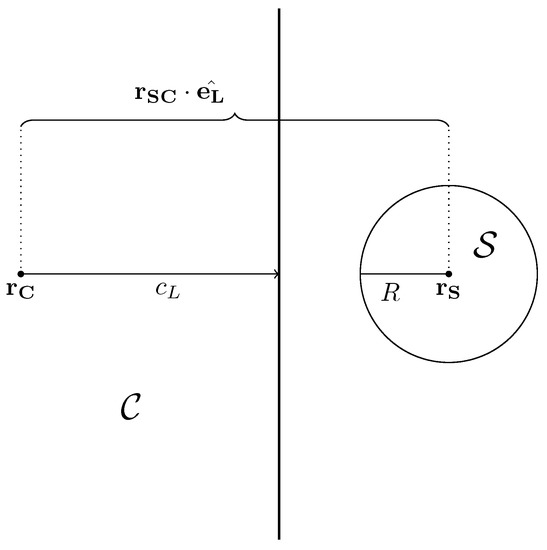
Figure 1.
Schematic representation of a sphere and a cuboid at relative distance . Sphere and cuboid are centred, respectively, at and , and is half of the cuboid length. If , then and do not overlap.
The different location of the quick rejection tests in QRI and QRF is expected to determine a difference in the efficiency of the two algorithms, which is analysed in detail in Section 4. Additionally, QRI and QRF quick rejection tests depend on both and R, so these algorithms’ efficiency are expected to be influenced also by sphere and cuboid geometry. Finally, keeping in mind the potential application in computational colloid science, where crowded systems are usually simulated, the efficiency of QRI and QRF is also influenced by the system packing, which determines the probability for an attempted move to produce an overlap.
Larsson et al. also proposed a parallel version of Algorithm 1, generalised for randomly oriented cuboids and using SSE intrinsic functions (SSE-intr) [7]. SSE is an instruction set available in x86 architectures; it uses 128-bit registers to process simple instructions on multiple data in parallel [45]. By substituting the if statements in lines 8 and 11 of Algorithm 3 to compute the minimum distance, with the max and min functions available in SSE instruction set, the computation of the minimum distance can be vectorized. This algorithm, running in parallel and thus significantly faster than QRI and QRF, does not need quick rejection tests. A pseudocode for this algorithm, here named after the SSE instruction set, is presented in Algorithm 4 for the general case of randomly oriented cuboids.
| Algorithm 4 SSE-intr |
|
Finally, we present our own algorithm, which incorporates a number of elements providing additional efficiency when compared to Algorithms 1, 2 and 3, and versatility when compared to Algorithm 4. A new element that significantly simplifies the algorithm is the use of the absolute value to estimate the minimum distance. In addition, we employed OpenMP directives for an SIMD parallelization of the two loops, one over the computation of the dot products of the distance of the centres of mass of the two particles with the orientation of the cuboid, and the other over the computation of the minimum distance, without using SSE intrinsic instructions. OpenMP is an application programming interface specification composed of compiler directives, library routines and environment variables for parallel programming in Fortran and C/C++. From version 4.0, it provides mechanisms to assist SIMD parallelization of loops [46]. The advantage of avoiding explicit SIMD vectorization is the possibility to vectorize the algorithm using different instruction set architectures, such as the more modern Advanced Vector Extensions (AVX) instruction set [47], by simply changing compiler settings during compilation. Moreover, in this way, vectorization of the algorithm can be assisted for different programming languages, e.g., Fortran, since SIMD intrinsic functions are available only in C and C++. Given the heterogeneous nature of the communities using collision-detection algorithms and their preference for likely different programming languages, an user-friendly code is a crucial advantage. Our algorithm, referred to as Oriented Cuboid Sphere Intersection (OCSI), proved to be efficient and functional for both C and Fortran 90 (F90). Its pseudocode is presented in Algorithm 5.
| Algorithm 5 OCSI |
|
3. Computational Details
To test the relative performance of the above algorithms, we have developed two versions of the same program in C and in F90 that detect collision between one cuboid and one sphere. For compatibility with the benchmark program by Larsson et al., all the floating point variables are expressed in 32-bit single precision. The dimensions of the cuboid and sphere are given in units of the cuboid thickness T, which is our unit length, and do not change within the same detection-collision test. In particular, the colloid length and width are and width , respectively, whereas the sphere radius is . For each of the cuboid shapes analysed, we have pondered the impact on the algorithms’ efficiency of changing the sphere radius between and . To control the value of the acceptance ratio, i.e., the percentage of random configurations that do not produce overlaps, the sphere is generated within a spherocuboid. This spherocuboid, centred and oriented as , results from the Minkowski addition [48] of and a sphere larger than and whose diameter is optimized to obtain the desired acceptance rate. A dedicated program optimises the volume of the spherocuboid according to the target value of the acceptance ratio and the dimensions of both and , which are specified as input parameters. To generate a configuration, is initially aligned with the reference axes and its centre is set as origin, while the centre of is randomly positioned within the volume of the spherocuboid. Then, the reference system is randomly rotated and the cuboid-sphere overlap checked. For consistency, the section of the code that calls the overlap function is the same as that proposed by Larsson et al. [7]. The time spent by each algorithm to detect collisions for a specific case of cuboid and sphere (in term of radius of the sphere and dimensions of the cuboid) is computed for 3 independent sets of configurations and then averaged out. The efficiency of the algorithms has been assessed on a Lenovo ThinkCentre M920s Desktop PC, with 8 Gb of DDR4 RAM and Intel® Core™ i5-8500 CPU @ 3.00GHz (Coffee Lake) CPU with 9 Mb of cache, with Ubuntu 18.04 Desktop version OS. In order to prove the versatility of our algorithm, we performed benchmarks using two different compilers. In particular, we compiled the F90 and C/C++ versions of the program using Intel® Fortran and C Compilers version 19 [49] and GNU Fortran and C++ Compilers version 10 [50]. Both the compilers used OpenMP API 4.5 Specification for vectorization [51]. In addition, for all the cases listed above, we compiled two versions of the same program, enabling the generation of SSE or AVX instructions. In this work, configurations of cuboids with , and spheres with with an average acceptance ratio of 40% have been tested.
4. Results and Discussion
Due to the large number of benchmarks performed, we intended to report here the behaviour of the run-time efficiency of the algorithms with respect to the shape of the cuboid and the sphere only for the programs compiled using Intel® C and Intel® Fortran Compiler, enabling the use of AVX instruction set for SIMD parallelization. The dependence of the algorithms run-time with respect to the shape of the cuboid and the sphere is generally similar for all the compilers and the instruction sets specified during compilation. All the results obtained for the other cases are reported in the Supplementary Information. The relative performance of each algorithm is assessed in Figure 2 and Figure 3 for codes written in C and F90, respectively.
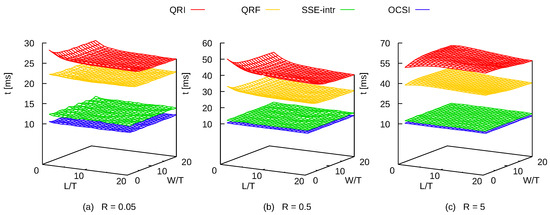
Figure 2.
Run-times of algorithms written in C/C++ that detect collision between one cuboid of length and width and one sphere of radius (a), 0.5 (b) and 5 (c). The program was compiled using Intel® C Compiler and enabled the generation of Advanced Vector Extensions (AVX) instructions. Each test generates random configurations at constant acceptance ratio of 40%.
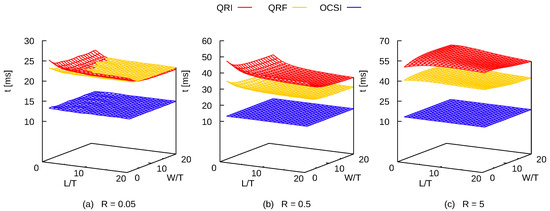
Figure 3.
Run-times of algorithms written in F90 that detect collision between one cuboid of length and width and one sphere of radius (a), 0.5 (b) and 5 (c). The program was compiled using Intel® Fortran Compiler and enabled the generation of AVX instructions. Each test generates random configurations at constant acceptance ratio of 40%.
Figure 2 offers a benchmark between QRI, QRF, SSE-intr and OCSI, while Figure 3 only for QRI, QRF and OCSI, since SSE-intr uses specific Intel® intrinsic functions: these sets of functions enable to use SIMD instructions (like SSE and AVX) without the need of an assembly code for vectorization, but they are available only for C programming language. Both figures report the run-times for detecting collisions between one cuboid of and and one sphere of radius (frames a), 0.5 (frames b) and 5 (frames c). The random configurations tested per run have been produced at the constant acceptance ratio of 40%, which is within the usual range of values employed in Metropolis Monte Carlo simulations of hard-core particles [52]. It is evident that SSE-intr and OCSI perform significantly better than QRI and QRF under the conditions specified here, although we have also tested cuboids of larger length and width (up to ) with the same acceptance ratio and observed very similar tendencies. The difference in performance is especially evident at as SSE-intr and OCSI run-times are up to 5 and 6 times faster than QRF and QRI, respectively. In general, C codes show a better performance than F90 codes, although this difference is not substantial. Interestingly enough, SSE-intr and OCSI do not present any relevant dependence on the cuboid and sphere geometry, being the run-times basically constant across the whole range of dimensions. This is probably due to the SIMD parallelism implemented, different from QRI and QRF, which have to run in serial for their use of quick rejection tests (see lines 6 and 9 in QRI and line 5 in QRF). Basically, if the quick rejection test is true for the first dot product, the algorithms exit the loop with negative result ( and do not overlap) with no need to compute the remaining two.
The geometry of both cuboid and sphere exhibits a very intriguing effect on the performance of QRI and QRF as the shape of the run-time surfaces in the plane suggests. More specifically, for spheres with (frames b in Figure 2 and Figure 3) the time required for the collision detection decreases upon increasing the cuboid dimensions, with the shortest time detected at (disk-like cuboid). Larger spheres, with (frames c in Figure 2 and Figure 3), induce a different performance resulting in an opposite concavity of the run-time surface as compared to that observed for smaller spheres. In this case, for the results obtained using Intel® Compilers and specifying AVX instruction set during compilation, the slowest detection is measured at and for QRI and QRF in C/C++ program, respectively, and and for QRI and QRF in F90 program, respectively. For the parameters set in these benchmarks, in terms of acceptance ratio and shapes of cuboids and spheres, QRF is generally faster than QRI. The only exceptions to this tendency are observed for the C/C++ program compiled either with Intel® C Compilers with AVX instructions (panel (a) of Figure 2) or with GNU C++ Compiler with SSE instructions (see Supplementary Information), in both cases when the spheres are especially small (). The difference in performance between QRI and QRF might also be due to how data are stored and read by C/C++ and F90 compilers. As a matter of fact, Larsson and coworkers had already noticed that the run-times of QRI and QRF were very similar for acceptance ratios of approximately 50%, although their collision-detection method tests run-times for sets of configurations with cuboids and sphere of random dimensions [7]. Despite the main differences between C /C++ and Fortran programming languages, the average run-time performance of QRI and QRF with respect to the radius of the sphere available in C is similar to the ones we translated and provide also in Fortran in our benchmark source code.
To more easily compare the efficiency of the algorithms tested, the run-times computed for each possible combination of cuboid and sphere size studied here have been averaged out for each value of . The resulting averaged run-times for all these cases, which are 400 considering all the possible combinations of and of the cuboids, are reported in Table 1 and Table 2. For every averaged run-time reported in both tables, we evaluated also its standard deviation, which resulted to be less than 0.5 ms for all the cases. For comparison with benchmarks performed by Larsson et al., the run-times are reported with a precision of 1 ms [7]. We stress that these average run-times should be taken as indicative values for QRI and QRF as their speed strongly depends on the cuboid geometry. We observe that QRI and QRF average run-times tend to be longer for larger spheres, with no significant difference between C/C++ and F90. In contrast, both SSE-intr and OCSI are completely insensible to the sphere radius as no relevant change in their average run-time is detected between and 0.5.

Table 1.
Average run-times of the C/C++ version of algorithms for collision detection between one cuboid of and and one sphere of radius over configurations with 40% of acceptance ratio. Results, reported in ms, are obtained compiling the benchmark program using Intel® C Compiler and GNU C++ Compiler, enabling the generation of SSE and AVX instructions. The standard deviations of all the run-times are <0.5 ms.

Table 2.
Average run-times of the F90 version of algorithms for collision detection between one cuboid of and and one sphere of radius over configurations with 40% of acceptance ratio. Results, reported in ms, are obtained compiling the benchmark program using Intel Fortran® Compiler and GNU Fortran Compiler, enabling the generation of SSE and AVX instructions. The standard deviations of all the run-times are <0.5 ms.
Regarding the performance of OCSI, we notice that its C version is faster than the F90 version for both the compilers. Moreover, checking the optimization report of the two compilers, we observed that GNU compilers were not capable of vectorizing the first loop of OCSI over the dot products. This seems to be the reason why Intel® Compilers performed better in terms of run-time efficiency. Anyway, except the F90 version compiled with GNU Fortran Compiler, for all the other cases the average OCSI run-time to analyse cuboid–sphere configurations oscillates between 10 and 12 ms. Even for the worst-case scenario, OCSI is still faster than QRI and QRF.
We also notice that the performance of OCSI compiled using SSE and AVX instruction sets is very similar to that of SSE-intr, with our algorithm approximately 1 ms faster or slower than SSE-intr, depending on the compiler and the instruction sets called during compilation. This difference, per se, would not be especially significant if the overlap checks were limited to configurations. However, the typical number of configurations generated in Monte Carlo simulations of colloids is usually a few millions per particle, which are rarely less than a few thousands. Moreover, because colloids can be especially dense systems, one random configuration might generate more than a single collision. Consequently, it is reasonable to assume that, within a single Monte Carlo simulation, a collision-detection algorithm might be called between and times the configurations explored here. This would produce a difference of seconds between OCSI and SSE-intr, which is still not especially relevant.
The main advantage of using OCSI is that it is based on automatic vectorization and employs OpenMP libraries to be parallelized, making it a very user-friendly algorithm. Since SSE-intr uses intrinsic functions that are specific for SSE, this version of the algorithm for cuboid-sphere collision detection is limited only to that instruction set. Moreover, Intel® intrinsic functions are available only in C and cannot be used in Fortran, unless we compile a mixed C/Fortran program. In contrast, OCSI is based on automatic vectorization by the compiler, guided using OpenMP pragmas and directives. In this way, the algorithm can be extended to different instruction sets without changing the source code, simply specifying the instruction set during compilation. It can also implement vectorization in Fortran and extend its use to 64-bit floating point arithmetic, which is commonly used in molecular modelling. OCSI proved to be efficient for the most two common compilers, for two different programming languages and for two different instruction sets, SSE and AVX, highlighting its versatility with respect to SSE-intr.
5. Conclusions
In summary, we have benchmarked four different collision-detection algorithms that check the occurrence of overlaps between one cuboid and one sphere. Our analysis focused on a specific acceptance ratio, which is within the usual range applied to efficiently sample the configuration space of hard-core systems in Monte Carlo simulations [52]. We notice that SSE-intr has been previously tested for different acceptance ratios and did not show relevant changes in performance [7]. A similar tendency is also expected for OCSI, but should be confirmed by further tests. While QRI and QRF are observed to be geometry-dependent, SSE-intr and OCSI are basically insensible to the cuboid anisotropy and sphere radius and, thanks to automatic vectorization, they are also significantly faster. According to these results, we expect OCSI and SSE-intr run-times to be constant also for bigger spheres, while QRI and QRF run-times can show a different behaviour than the ones observed so far. To ascertain these tendencies, further tests should be performed. In particular, the OCSI algorithm proved to be especially valuable in terms of performance and simplicity of implementation in both C and F90. Intel ®compilers and GNU Compilers were not able to automatically vectorize QRI and QRF. Anyway, there are ways to perform conditional statements like the ones used in the quick rejection test implementing SIMD parallelism [53]. Whether or not vectorized versions of QRF and QRI are possible and, if so, how efficient they would be as compared to the current versions requires further study.
It should be stressed that the method applied to generate the sphere around the cuboid is crucial to provide a robust comparison between different algorithms. The choice of the spherocuboid as a sampling volume allows to precisely set the desired acceptance ratio and guarantees that the algorithms are tested for all the possible positions of the sphere around or inside the cuboid. This is especially relevant to fairly assess the performance of QRI and QRF, due to their use of quick rejection tests. In Monte Carlo simulations, where the generation of configurations follows a different procedure, the performance of collision-detection algorithms, most likely affected by the degree of system order and packing, should be tested. Finally, it is important to mention that the OCSI algorithm allows for the calculation of the cuboid-sphere minimum distance, hence suggesting a future study to determine a suitable interaction potential beyond mere hard-core interactions. The formal proof reported here can also be useful to test the intersection of cuboids with particles of different shape. As a final note, we stress that our algorithm has been only tested for specific pairs of geometries (cuboids and spheres), while it might be relevant, in computational colloid science as well as in computer graphics, to assess its performance with other geometries. We are currently working on extending our algorithm to detect collisions between cuboids and oblate or prolate spherocylinders. It would also be especially interesting to investigate to what extent our methodology could be applied to more complex geometries, whose collision is generally detected by more sophisticated decomposition techniques, such as e.g., Voronoi diagrams [54] or convex polygon triangulations [55,56]. We hope that our contribution might stimulate further research in this direction.
Supplementary Materials
The source code of the program for the optimisation of the spherocuboid volume, the C/C++ and F90 benchmark programs and the raw data required to reproduce our findings can be downloaded at http://dx.doi.org/10.17632/w7g3ynkc6n.2.
Author Contributions
Conceptualization, A.P.; methodology, L.T.; software, L.T.; validation, L.T. and A.P.; formal analysis, L.T.; investigation, L.T. and A.P.; resources, A.P.; data curation, L.T.; writing—original draft preparation, L.T.; writing—review and editing, A.P.; visualization, L.T.; supervision, A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Leverhulme Trust grant number RPG-2018-415.
Acknowledgments
The authors acknowledge the use of Computational Shared Facility at the University of Manchester and Benedetto Di Paola (University of Palermo) for a critical reading of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. On the Minimum Distance between a Sphere and a Randomly Oriented Cuboid
Let be a n-dimensional vector space in an orthonormal basis , with the Kronecker delta. The set of points of a cuboid in is
where is the position of the centre of the cuboid, is a scalar equal to half of the cuboid length, width or thickness, is also a scalar with values in and is a unit vector that defines the orientation of . Specifically , so also is an orthonormal basis for . The minimum distance between and a random point reads
Since is an orthonormal basis for , the vector can be written as
and substituting Equation (A3) in Equation (A2)
The last term in Equation (A4) has been obtained considering that and that every member of the sum depends on just one value , hence they are all independent. It is sufficient to calculate only one term of this sum as all dimensions are equivalent. In particular, this term equals zero if the following conditions are met:
As a result that , this implies that
If , then or . The former inequality implies that
while, the latter inequality implies
As a result that the solution of Equation (A7) is the same as that of (A8), if , then one can write
The solutions of Equations (A5) and (A9) can be incorporated in a single equation by using a step function defined as
Therefore, the minimum distance of a point from the surface of a cuboid reads
Finally, a cuboid overlaps with a sphere of radius R and centre in , if the following inequality is satisfied:
References
- Ericson, C. Real-Time Collision Detection; Morgan Kaufmann Series in Interactive 3D Technology; Taylor and Francis: Abingdon, UK, 2004. [Google Scholar]
- Akenine-Möller, T.; Haines, E.; Hoffman, N.; Pesce, A. Real-Time Rendering, 4th ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- Chang, J.W.; Wang, W.; Kim, M.S. Efficient collision detection using a dual OBB-sphere bounding volume hierarchy. Comput.-Aided Des. 2010, 42, 50–57. [Google Scholar] [CrossRef]
- Gottschalk, S.; Lin, M.C.; Manocha, D. OBBTree: A Hierarchical Structure for Rapid Interference Detection. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 4–9 August 1996; pp. 171–180. [Google Scholar]
- Arvo, J. A simple method for box-sphere intersection testing. In Graphic Gems; Glassner, A.S., Ed.; Academic Press: Cambridge, MA, USA, 1990; pp. 335–339. [Google Scholar]
- Ratschek, H.; Rokne, J. Box-sphere intersection tests. Comput.-Aided Des. 1994, 26, 579–584. [Google Scholar] [CrossRef]
- Larsson, T.; Akenine-Möller, T.; Lengyel, E. On faster sphere-box overlap testing. J. Graph. Tools 2007, 12, 3–8. [Google Scholar] [CrossRef]
- Moore, M.; Wilhelms, J. Collision Detection and Response for Computer Animation. In Proceedings of the 15th Annual Conference on Computer Graphics and Interactive Techniques, Atlanta, GA, USA, 1–5 August 1988; pp. 289–298. [Google Scholar]
- Pungotra, H.; Knopf, G.K.; Canas, R. Efficient algorithm to detect collision between deformable B-spline surfaces for virtual sculpting. Comput.-Aided Des. 2008, 40, 1055–1066. [Google Scholar] [CrossRef]
- Pan, J.; Manocha, D. GPU-based parallel collision detection for fast motion planning. Int. J. Robot. Res. 2012, 31, 187–200. [Google Scholar] [CrossRef]
- Govender, N.; Wilke, D.N.; Kok, S. Collision detection of convex polyhedra on the NVIDIA GPU architecture for the discrete element method. Appl. Math. Comput. 2015, 267, 810–829. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, X.; Wei, J. Collision detection Based on OBB Simplified modeling. J. Phys. Conf. Ser. 2019, 1213, 042079. [Google Scholar] [CrossRef]
- Yang, C.; Wang, X.; Cheng, L. Neural-learning-based telerobot control with guaranteed performance. IEEE Trans. Cybern. 2017, 47, 3148–3159. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, P.X.; Li, C.; Cheng, Q. Collision detection for virtual environment using particle swarm optimization with adaptive cauchy mutation. Cluster. Comput. 2017, 20, 1765–1774. [Google Scholar] [CrossRef]
- Tomić, T.; Ott, C.; Haddadin, S. External Wrench Estimation, Collision Detection, and Reflex Reaction for Flying Robots. IEEE Trans. Robot. 2017, 33, 1467–1482. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, Q.; Wang, Y.H.; Zeng, F. Collision detection algorithm for collaborative robots considering joint friction. IJARS 2018, 15, 1–13. [Google Scholar] [CrossRef]
- Ren, T.; Dong, Y.; Wu, D.; Chen, K. Collision detection and identification for robot manipulators based on extended state observer. Control Eng. Pract. 2018, 79, 144–153. [Google Scholar] [CrossRef]
- Nguyen, M.; Zhang, S.; Wang, X.A. A Novel Method for Risk Assessment and Simulation of Collision Avoidance for Vessels based on AIS. Algorithms 2018, 11, 204. [Google Scholar] [CrossRef]
- Tang, T.D. Algorithms for collision detection and avoidance for five-axis NC machining: A state of the art review. Comput.-Aided Des. 2014, 51, 1–17. [Google Scholar] [CrossRef]
- Frenkel, D.; Lekkerkerker, H.N.W.; Stroobants, A. Thermodynamic stability of a smectic phase in a system of hard rods. Nature 1988, 332, 822–823. [Google Scholar] [CrossRef]
- Anderson, J.A.; Glaser, J.; Glotzer, S.C. HOOMD-blue: A Python package for high-performance molecular dynamics and hard particle Monte Carlo simulations. Comput. Mater. Sci. 2020, 173, 109363. [Google Scholar] [CrossRef]
- Rosenbluth, M.N.; Rosenbluth, A.W. Further results on Monte Carlo Equations of State. J. Chem. Phys. 1954, 22, 881–884. [Google Scholar] [CrossRef]
- Wood, W.W.; Jacobson, J.D. Preliminary Results from a Recalculation of the Monte Carlo Equation of State of Hard Spheres. J. Chem. Phys. 1957, 27, 1207–1208. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Phase Transition for a Hard Sphere System. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Shankar, S.S.; Rai, A.; Ankamwar, B.; Singh, A.; Ahmad, A.; Sastry, M. Biological synthesis of triangular gold nanoprisms. Nat. Mat. 2004, 3, 482–488. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Xia, Y. Shape-Controlled Synthesis of Gold and Silver Nanoparticles. Science 2002, 298, 2176–2179. [Google Scholar] [CrossRef] [PubMed]
- Manoharan, V.N.; Elsesser, M.T.; Pine, D.J. Dense Packing and Symmetry in Small Clusters of Microspheres. Science 2003, 301, 483–487. [Google Scholar] [CrossRef] [PubMed]
- Sacanna, S.; Irvine, W.T.M.; Chaikin, P.M.; Pine, D.J. Lock and key colloids. Nature 2010, 464, 575–578. [Google Scholar] [CrossRef]
- Sacanna, S.; Korpics, M.; Rodriguez, K.; Colón-Meléndez, L.; Kim, S.H.; Pine, D.J.; Yi, G.R. Shaping colloids for self-assembly. Nat. Comm. 2013, 4, 1688. [Google Scholar] [CrossRef]
- Rossi, L.; Soni, V.; Ashton, D.J.; Pine, D.J.; Philipse, A.P.; Chaikin, P.M.; Dijkstra, M.; Sacanna, S.; Irvine, W.T.M. Shape-sensitive crystallization in colloidal superball fluids. Proc. Natl. Acad. Sci. USA 2015, 112, 5286–5290. [Google Scholar] [CrossRef]
- Xiang, Y.; Wu, X.; Liu, D.; Jiang, X.; Chu, W.; Li, Z.; Ma, Y.; Zhou, W.; Xie, S. Formation of Rectangularly Shaped Pd/Au Bimetallic Nanorods: Evidence for Competing Growth of the Pd Shell between the 110 and 100 Side Facets of Au Nanorods. Nano Lett. 2006, 6, 2290–2294. [Google Scholar] [CrossRef]
- Okuno, Y.; Nishioka, K.; Kiya, A.; Nakashima, N.; Ishibashia, A.; Niidome, Y. Uniform and controllable preparation of Au–Ag core–shell nanorods using anisotropic silver shell formation on gold nanorods. Nanoscale 2010, 2, 1489–1493. [Google Scholar] [CrossRef]
- Cortie, M.B.; Liu, F.; Arnold, M.D.; Niidome, Y. Multimode Resonances in Silver Nanocuboids. Langmuir 2012, 28, 9103–9112. [Google Scholar] [CrossRef]
- Khlebtsov, B.N.; Liuc, Z.; Yec, J.; Khlebtsov, N.G. Au@Ag core/shell cuboids and dumbbells: Optical properties and SERS response. J. Quant. Spectrosc Radiat. Transf. 2015, 167, 64–75. [Google Scholar] [CrossRef]
- Glotzer, S.C.; Solomon, M.J. Anisotropy of building blocks and their assembly into complex structures. Nat. Mat. 2007, 6, 557–562. [Google Scholar] [CrossRef]
- Damasceno, P.F.; Engel, M.; Glotzer, S.C. Crystalline Assemblies and Densest Packings of a Family of Truncated Tetrahedra and the Role of Directional Entropic Forces. ACS Nano 2012, 6, 609–614. [Google Scholar] [CrossRef]
- Van Anders, G.; Ahmed, N.K.; Smith, R.; Engel, M.; Glotzer, S.C. Entropically Patchy Particles: Engineering Valence through Shape Entropy. ACS Nano 2014, 8, 931–940. [Google Scholar] [CrossRef]
- De Nijs, B.; Dussi, S.; Smallenburg, F.; Meeldijk, J.D.; Groenendijk, D.J.; Filion, L.; Imhof, A.; van Blaaderen, A.; Dijkstra, M. Entropy-driven formation of large icosahedral colloidal clusters by spherical confinement. Nat. Mat. 2015, 14, 56–60. [Google Scholar] [CrossRef]
- Cuetos, A.; Dennison, M.; Masters, A.; Patti, A. Phase behaviour of hard board-like particles. Soft Matter 2017, 13, 4720–4732. [Google Scholar] [CrossRef]
- Cuetos, A.; Patti, A. Monte Carlo simulation of binary mixtures of hard colloidal cuboids. Mol. Sim. 2018, 44, 516–522. [Google Scholar]
- Cuetos, A.; Mirzad Rafael, E.; Corbett, D.; Patti, A. Biaxial nematics of hard cuboids in an external field. Soft Matter 2019, 15, 1922–1926. [Google Scholar] [CrossRef] [PubMed]
- Cuetos, A.; Patti, A. Dynamics of hard colloidal cuboids in nematic liquid crystals. Phys. Rev. E 2020, 101, 052702. [Google Scholar] [CrossRef]
- Mirzad Rafael, E.; Corbett, D.; Cuetos, A.; Patti, A. Self-assembly of Freely-rotating Polydisperse Cuboids: Unveiling the Boundaries of the Biaxial Nematic Phase. Soft Matter 2020, 16, 5565–5570. [Google Scholar] [CrossRef] [PubMed]
- Thakkar, S.; Huff, T. Internet Streaming SIMD Extensions. Computer 1999, 32, 26–34. [Google Scholar] [CrossRef]
- Van der Pas, R.; Stotzer, E.; Terboven, C. Using OpenMP-The Next Step: Affinity, Accelerators, Tasking, and SIMD; MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Intel Advanced Vector Extensions Programming Reference, Ref # 319433-011. Available online: www.intel.com (accessed on 25 February 2021).
- Schneider, R. Minkowski addition. In Convex Bodies: The Brunn-Minkowski Theory; Cambridge University Press: Cambridge, UK, 1993; Chapter 3; pp. 139–207. [Google Scholar]
- Intel® Corporation. Intel® C++ Compiler Classic Developer Guide and Reference. Available online: https://software.intel.com/content/www/us/en/develop/documentation/cpp-compiler-developer-guide-and-reference/top.html2020 (accessed on 25 February 2021).
- Stallman, R.M.; the GCC Developer Community. Using the GNU Compiler Collection, for gcc version 10.2.0. 2020. Available online: https://gcc.gnu.org/onlinedocs/gcc-10.2.0/gcc/ (accessed on 25 February 2021).
- OpenMP Architecture Review Board. OpenMP Application Programming Interface Version 4.5. 2015. Available online: https://www.openmp.org/wp-content/uploads/openmp-4.5.pdf (accessed on 25 February 2021).
- Frenkel, D.; Smit, B. Monte Carlo Simulations. In Understanding Molecular Simulation-From Algorithms to Applications; Academic Press: Cambridge, MA, USA, 1996; Chapter 3; pp. 45–46. [Google Scholar]
- Sun, H.; Gorlatch, S.; Zhao, R. Vectorizing programs with IF-statements for processors with SIMD extensions. J. Supercomput. 2020, 76, 4731–4746. [Google Scholar] [CrossRef]
- Aurenhammer, F. Voronoi Diagrams—A Survey of a Fundamental Geometric Data Structure. ACM Comput. Surv. 1991, 23, 345–405. [Google Scholar] [CrossRef]
- Saračević, M.; Selimi, A. Convex polygon triangulation based on planted trivalent binary tree and ballot problem. Turk. J. Elec. Eng. Comp. Sci. 2019, 27, 346–361. [Google Scholar] [CrossRef]
- Stanimirović, P.S.; Krtolica, P.V.; Saračević, M.H.; Mašović, S.H. Decomposition of Catalan numbers and convex polygon triangulations. Int. J. Comput. Math. 2014, 91, 1315–1328. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).