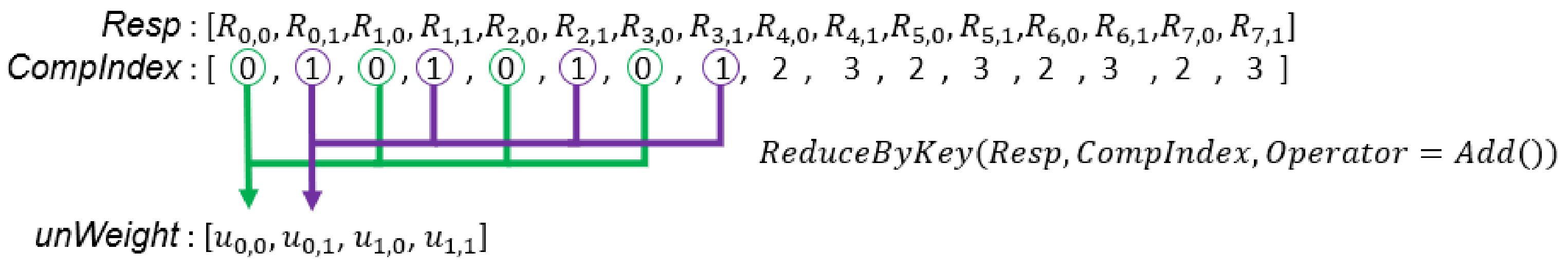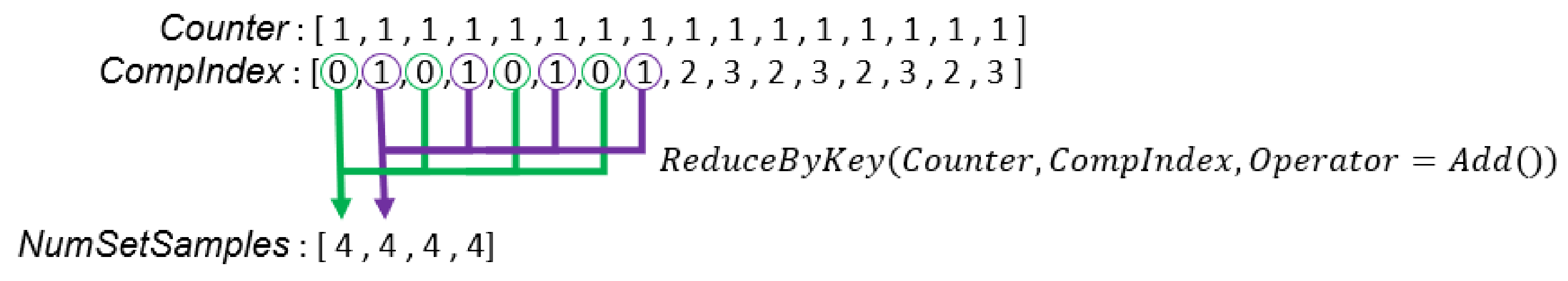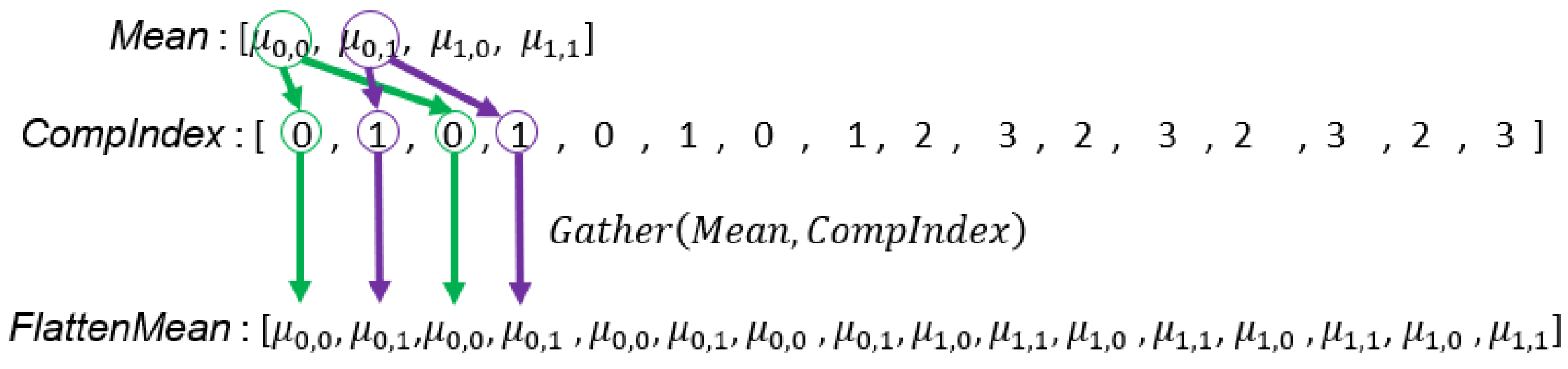Figure 1.
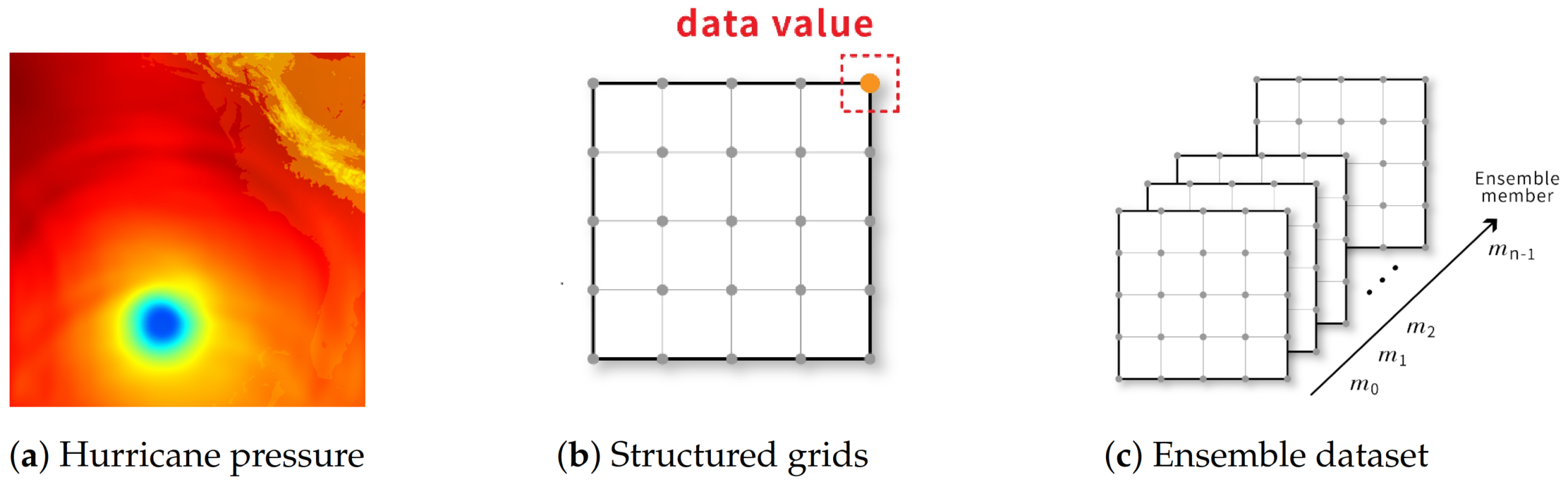
(a) is the visualization of a 2D slice of a 3D hurricane pressure dataset; (b) is the illustration of the corresponding grid structure of (a) and the pressure values are stored at grid points; (c) is an illustration of an ensemble dataset. In this example, we have n ensemble members and each ensemble member is a volume data or vector data from the same simulation.
Figure 1.
(a) is the visualization of a 2D slice of a 3D hurricane pressure dataset; (b) is the illustration of the corresponding grid structure of (a) and the pressure values are stored at grid points; (c) is an illustration of an ensemble dataset. In this example, we have n ensemble members and each ensemble member is a volume data or vector data from the same simulation.
Figure 2.
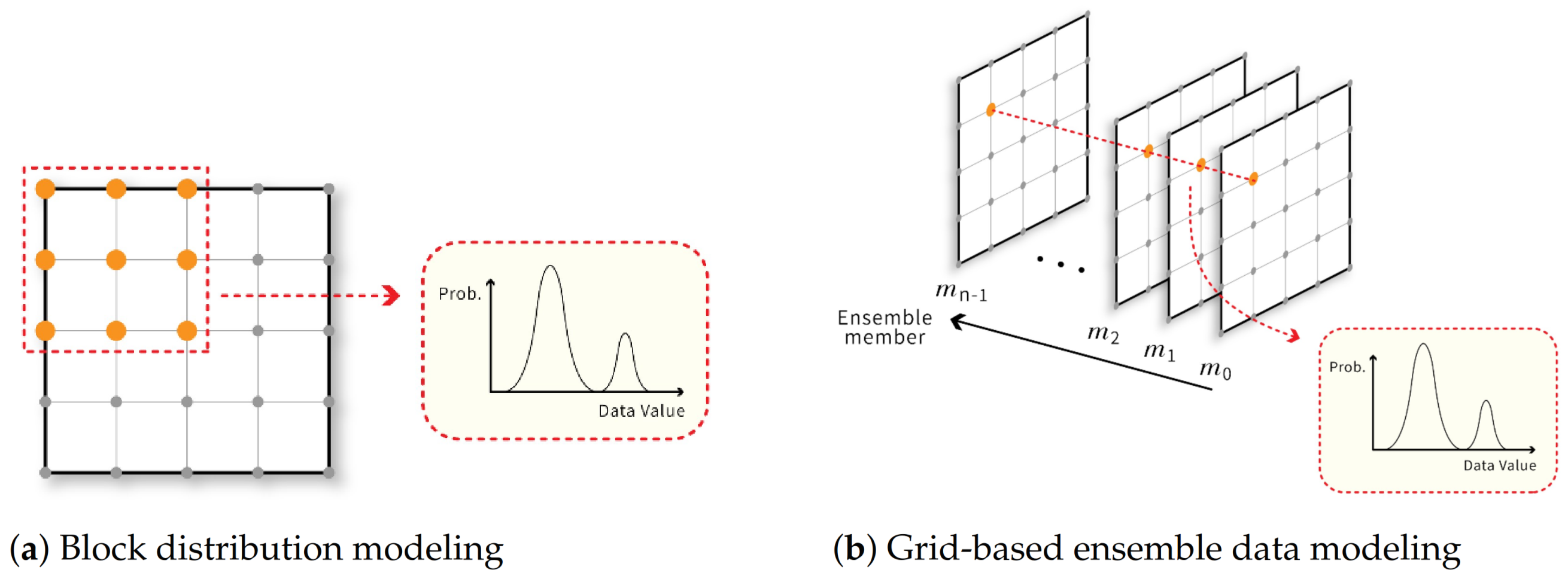
(a) illustrates the approach that uses a distribution to model data values in each sub-block to compactly represent a volume or vector dataset. If the data is a vector dataset, the distributions should be multivariant distributions; (b) shows the use of a distribution to model data values of all ensemble members at the same grid point to compactly store an ensemble dataset.
Figure 2.
(a) illustrates the approach that uses a distribution to model data values in each sub-block to compactly represent a volume or vector dataset. If the data is a vector dataset, the distributions should be multivariant distributions; (b) shows the use of a distribution to model data values of all ensemble members at the same grid point to compactly store an ensemble dataset.
Figure 3.
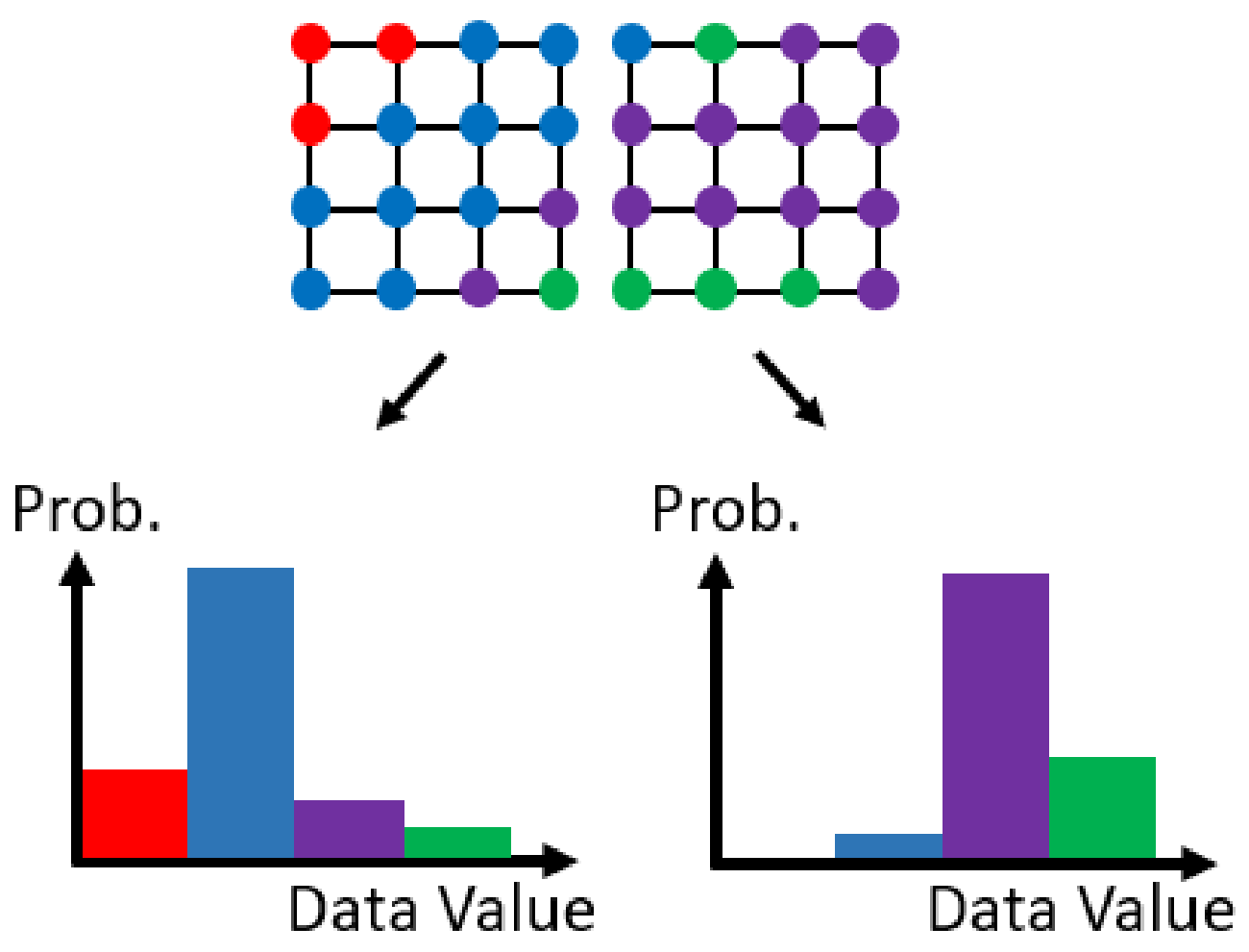
An example of dividing a scientific dataset into two sets and transforming the data values in each set into a histogram.
Figure 3.
An example of dividing a scientific dataset into two sets and transforming the data values in each set into a histogram.
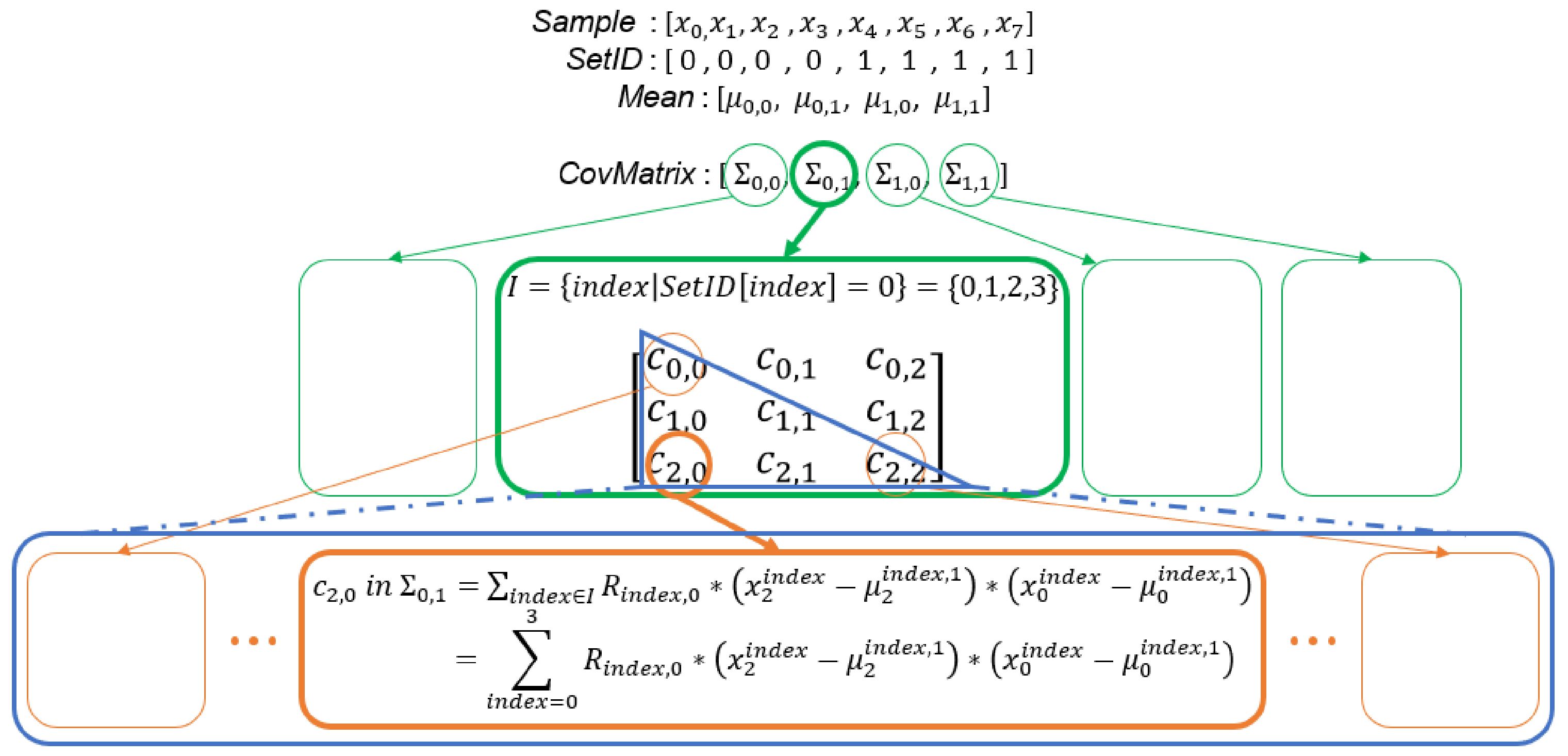
Figure 4.
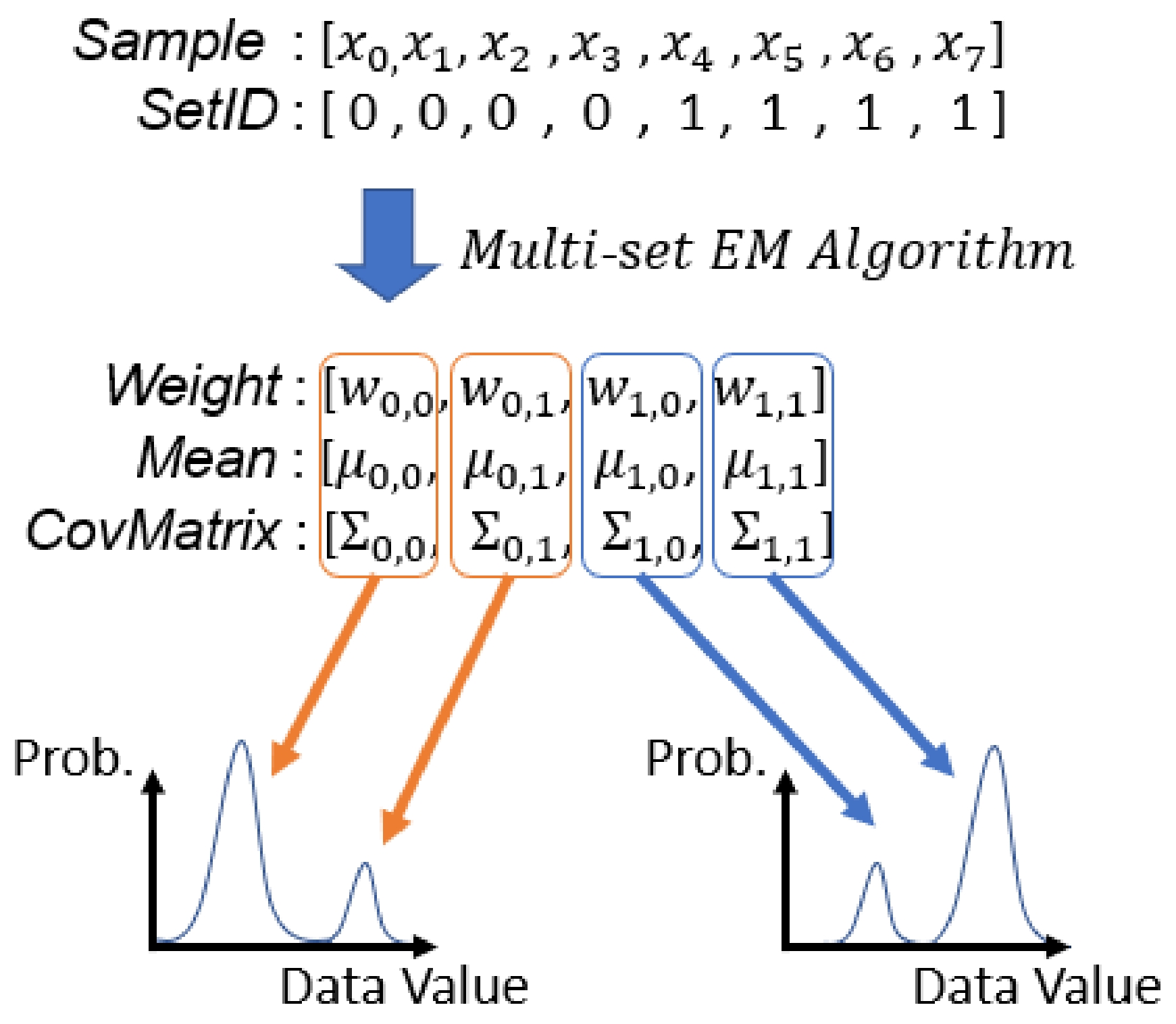
Examples of input and output arrays of running EM algorithm with two sets of samples when the number of Gaussian components (K) of each GMM is 2. In this example, to are all in the first set and to are in the second set. , and are the parameters of the Gaussian component in the set.
Figure 4.
Examples of input and output arrays of running EM algorithm with two sets of samples when the number of Gaussian components (K) of each GMM is 2. In this example, to are all in the first set and to are in the second set. , and are the parameters of the Gaussian component in the set.
Figure 5.
In this example, there are two sets of samples, and each GMM has two Gaussian components. is the probability that the is generated by the Gaussian component. is the non-normalized weight of the Gaussian component in the set.
Figure 5.
In this example, there are two sets of samples, and each GMM has two Gaussian components. is the probability that the is generated by the Gaussian component. is the non-normalized weight of the Gaussian component in the set.
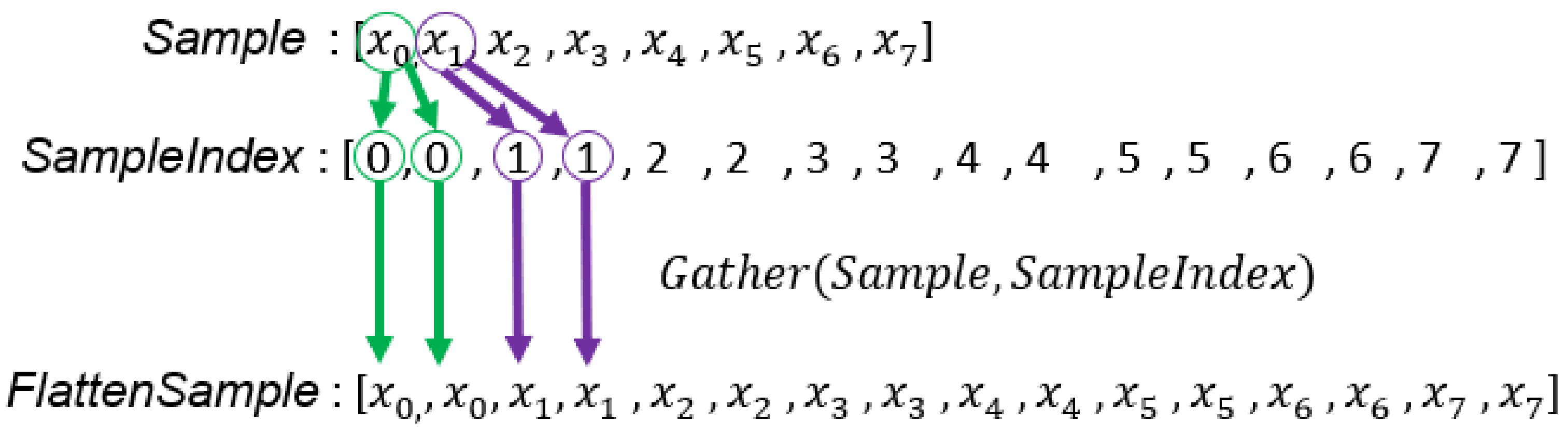
Figure 6.
The generation process of .
Figure 6.
The generation process of .
Figure 7.
The generation process of . For example, is copied twice because each GMM has two Gaussian components and each sample will be accessed to compute .
Figure 7.
The generation process of . For example, is copied twice because each GMM has two Gaussian components and each sample will be accessed to compute .
Figure 8.
The computation process of . is a responsibility computed from the sample and Gaussian component. is the mean vector of the Gaussian component in the set.
Figure 8.
The computation process of . is a responsibility computed from the sample and Gaussian component. is the mean vector of the Gaussian component in the set.
Figure 9.
Illustration of the creation of duplicated mean vectors (Line 23 in Algorithm 4). In this example, the GMM of each set has two Gaussian components, and each mean vector will match with four samples because every set has four input samples. Therefore, the length of the duplicated mean vector array is 16 (the total number of mean vectors multiplied by the sample count in each set).
Figure 9.
Illustration of the creation of duplicated mean vectors (Line 23 in Algorithm 4). In this example, the GMM of each set has two Gaussian components, and each mean vector will match with four samples because every set has four input samples. Therefore, the length of the duplicated mean vector array is 16 (the total number of mean vectors multiplied by the sample count in each set).
Figure 10.
Illustration of computation of mean deviations and the transpose of mean deviations. is the mean deviation computed from the mean vector of the Gaussian component in the set and the sample.
Figure 10.
Illustration of computation of mean deviations and the transpose of mean deviations. is the mean deviation computed from the mean vector of the Gaussian component in the set and the sample.
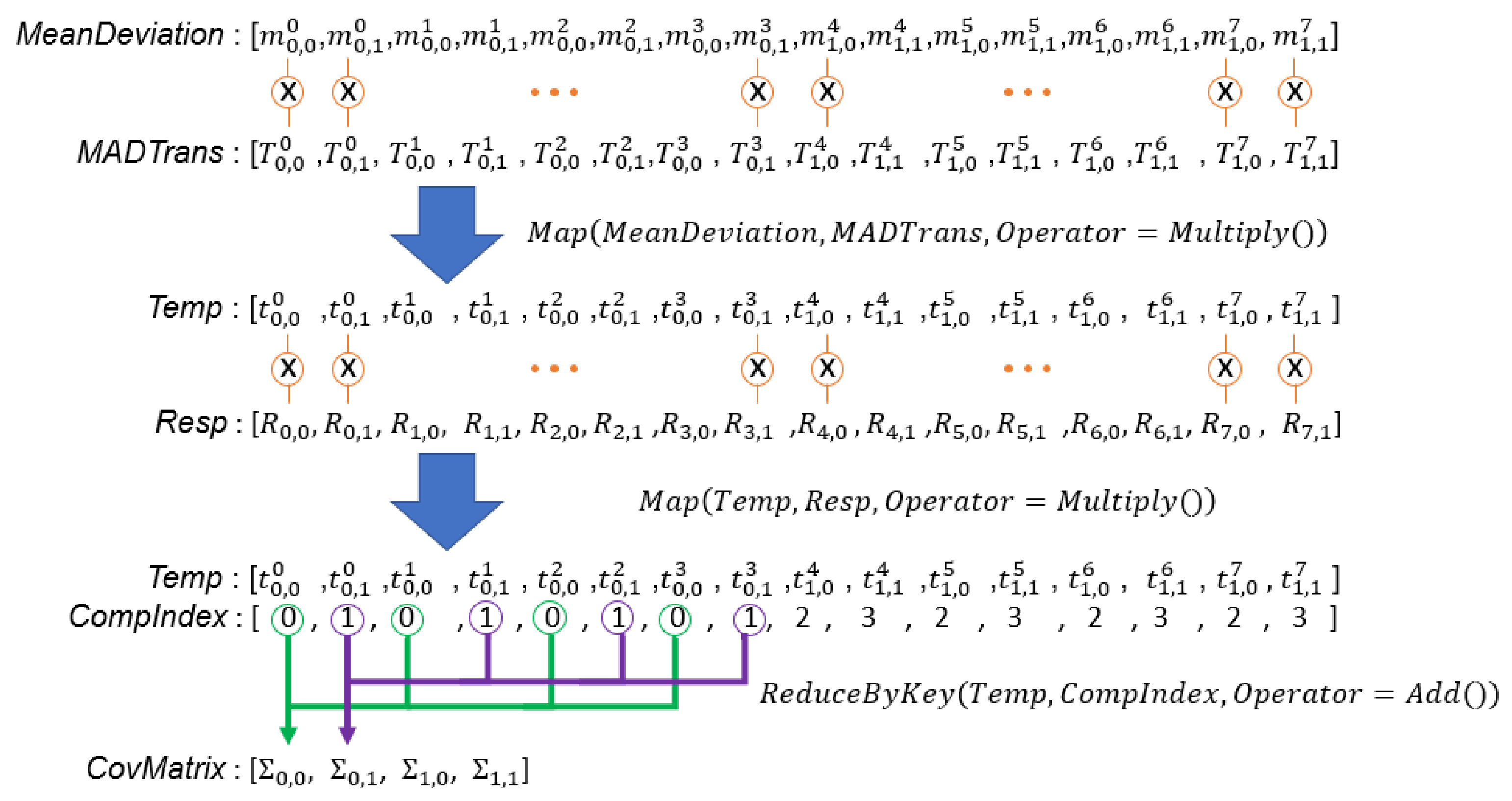
Figure 11.
Illustration of computation of covariance matrices of all sets. is an n by 1 vector, is a 1 by n vector, is an n by n matrix, and is a scalar value.
Figure 11.
Illustration of computation of covariance matrices of all sets. is an n by 1 vector, is a 1 by n vector, is an n by n matrix, and is a scalar value.
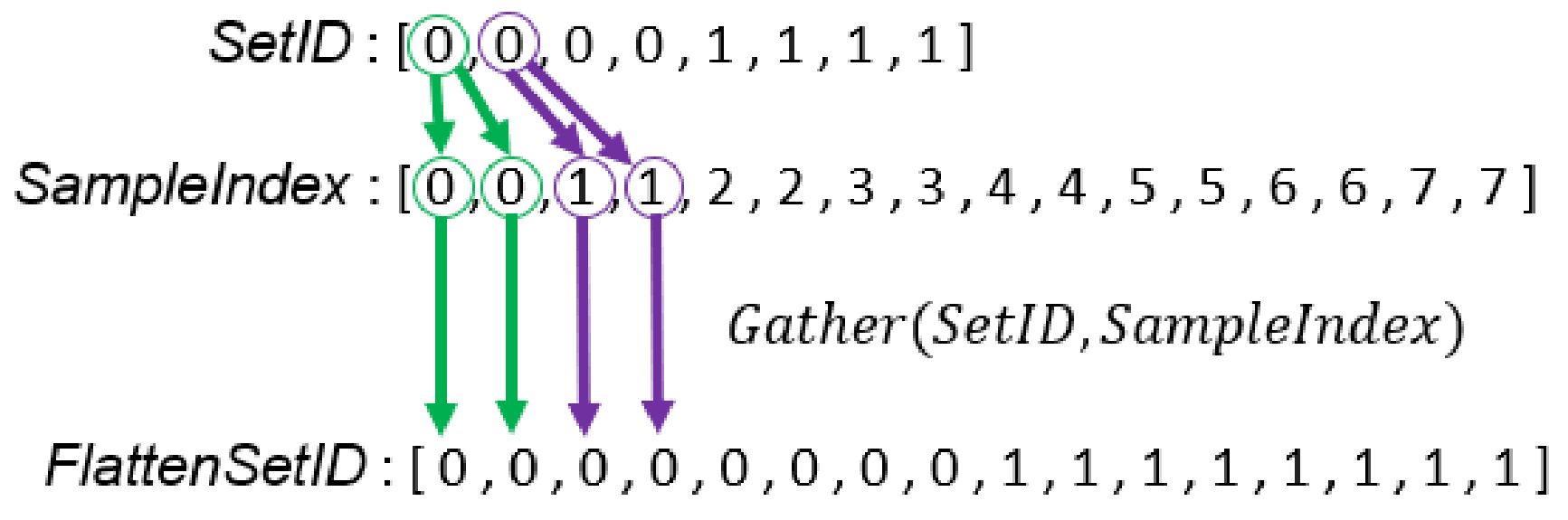
Figure 12.
Illustration of creating the array which stores the corresponding set ID of array.
Figure 12.
Illustration of creating the array which stores the corresponding set ID of array.
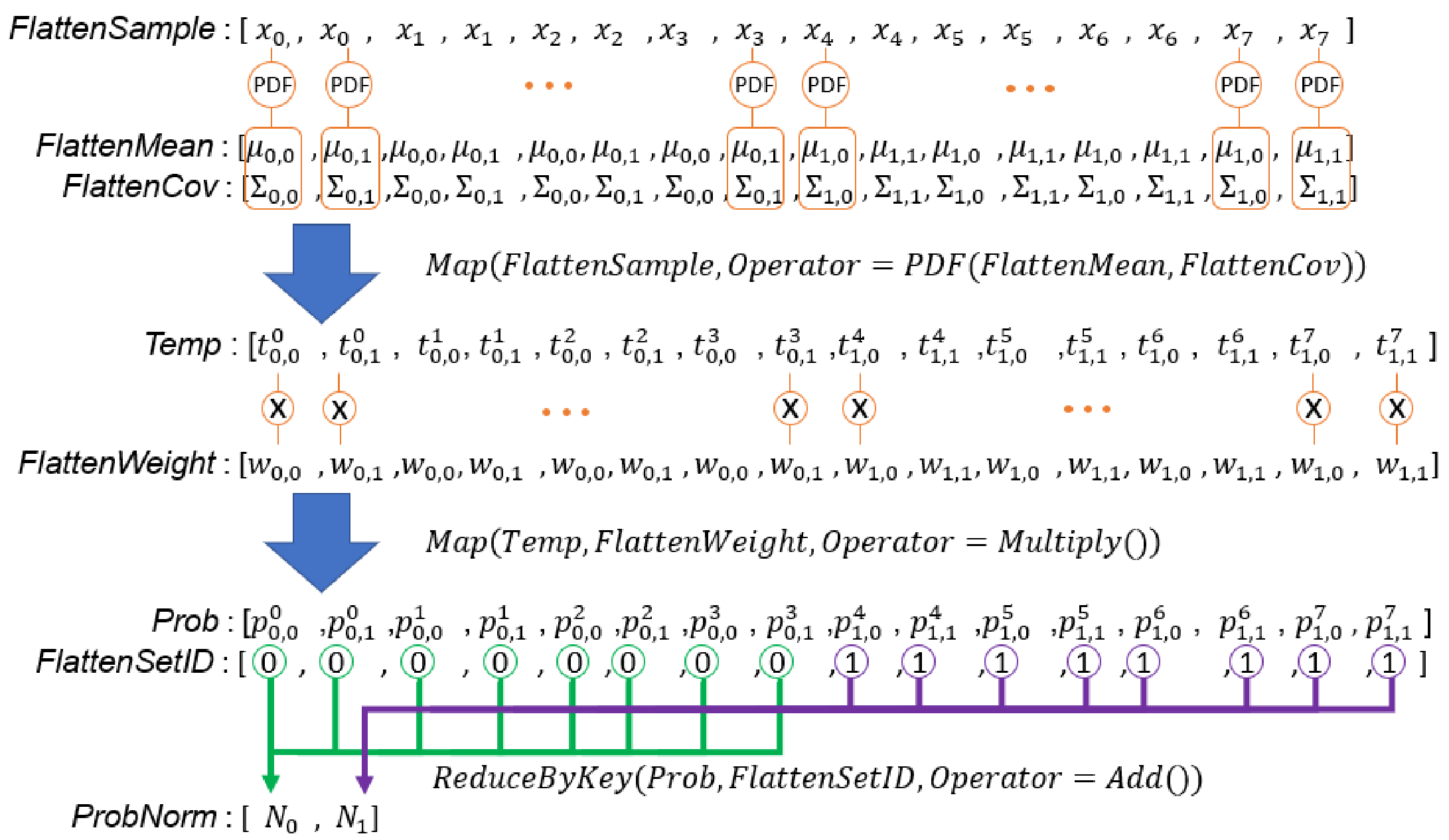
Figure 13.
Illustration of E-step computation by data-parallel primitives. , , and are the weight, mean vector, and covariance matrix of the Gaussian component in the set. is a probability density computed from the sample and the Gaussian component in the set. is of the GMM of set.
Figure 13.
Illustration of E-step computation by data-parallel primitives. , , and are the weight, mean vector, and covariance matrix of the Gaussian component in the set. is a probability density computed from the sample and the Gaussian component in the set. is of the GMM of set.
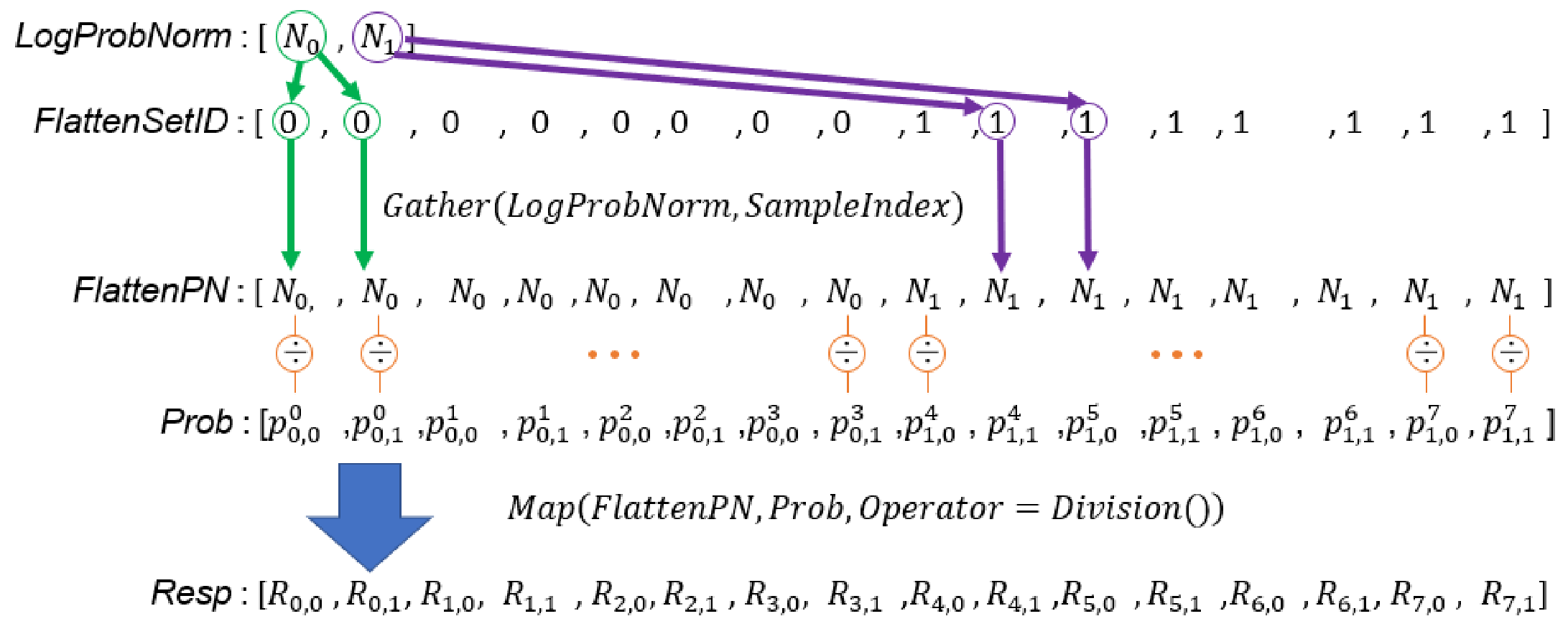
Figure 14.
Illustration of the process of updating responsibilities by data-parallel primitives.
Figure 14.
Illustration of the process of updating responsibilities by data-parallel primitives.
Figure 15.
In this example, two 3-variate GMMs are modeled at the same time, and each GMM has two Gaussian components. The level of parallelism is when the optimization introduced in this section is applied.
Figure 15.
In this example, two 3-variate GMMs are modeled at the same time, and each GMM has two Gaussian components. The level of parallelism is when the optimization introduced in this section is applied.
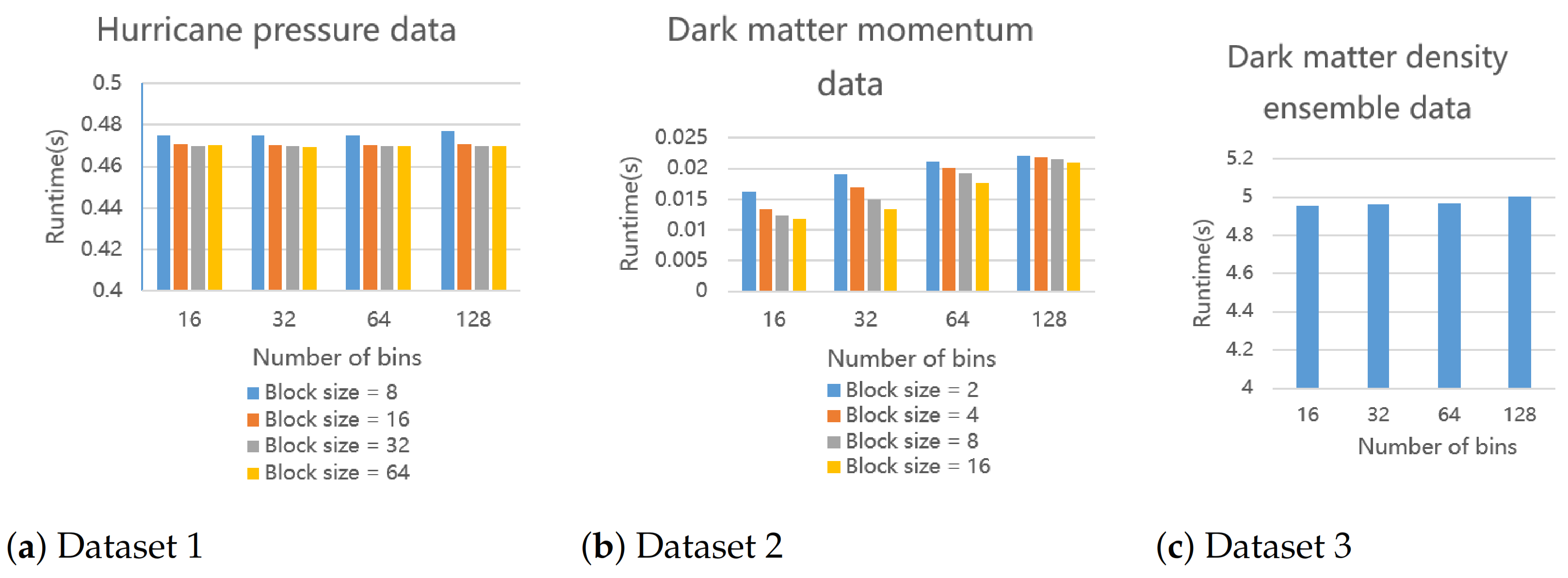
Figure 16.
The execution time of our proposed parallel histogram modeling algorithm. We run it for three datasets on a 16-core CPU under given parameter settings. Dataset 3 is an ensemble data so there is no block size to change.
Figure 16.
The execution time of our proposed parallel histogram modeling algorithm. We run it for three datasets on a 16-core CPU under given parameter settings. Dataset 3 is an ensemble data so there is no block size to change.
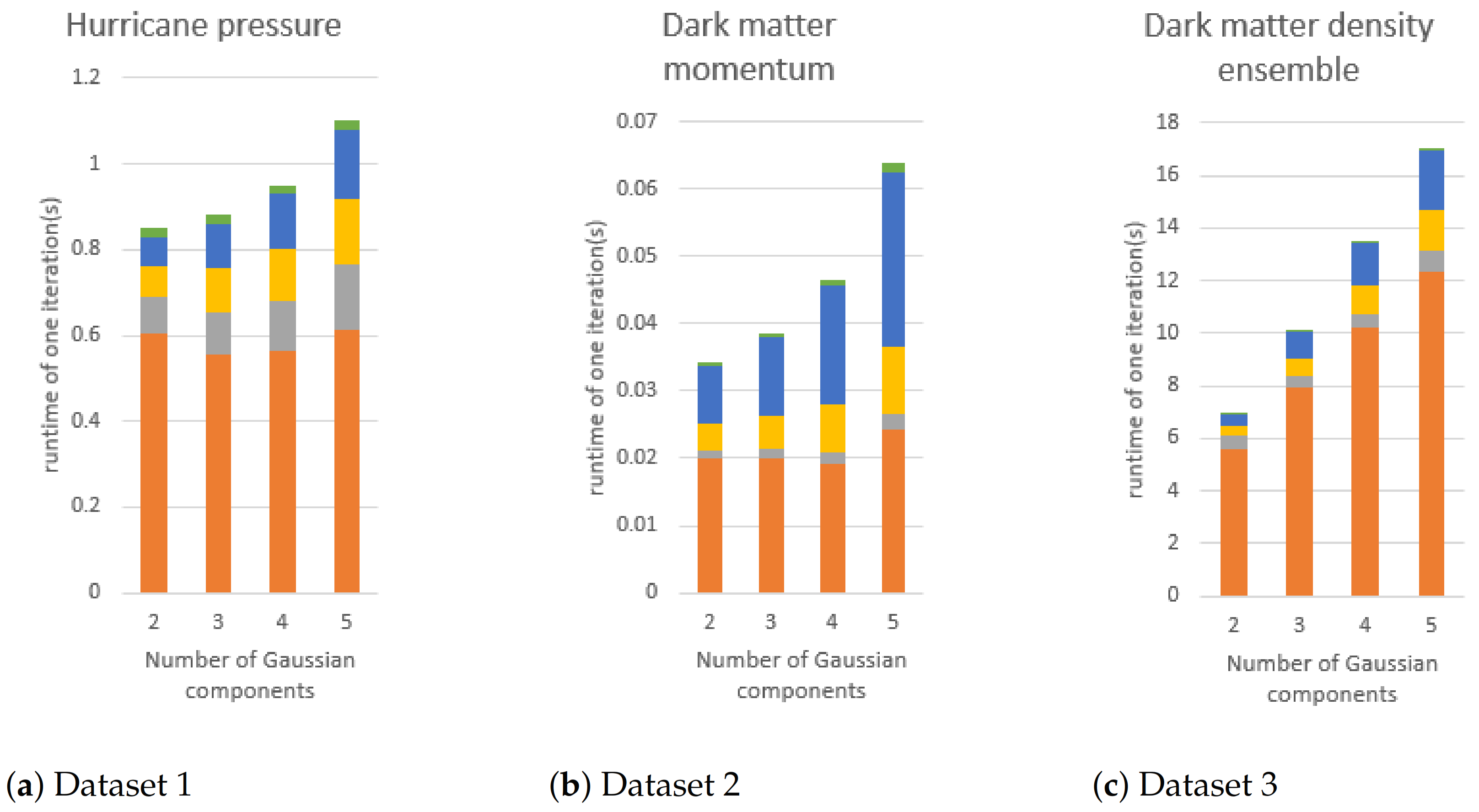
Figure 17.
The execution time of GMM modeling if the number of Gaussian components is changed. The block size of (a,b) is fixed to 16. In the figures, orange, gray, yellow, blue, and green bars are the execution times of E-step, mean vector updating, covariance matrix flattening, and covariance matrix updating, respectively.
Figure 17.
The execution time of GMM modeling if the number of Gaussian components is changed. The block size of (a,b) is fixed to 16. In the figures, orange, gray, yellow, blue, and green bars are the execution times of E-step, mean vector updating, covariance matrix flattening, and covariance matrix updating, respectively.
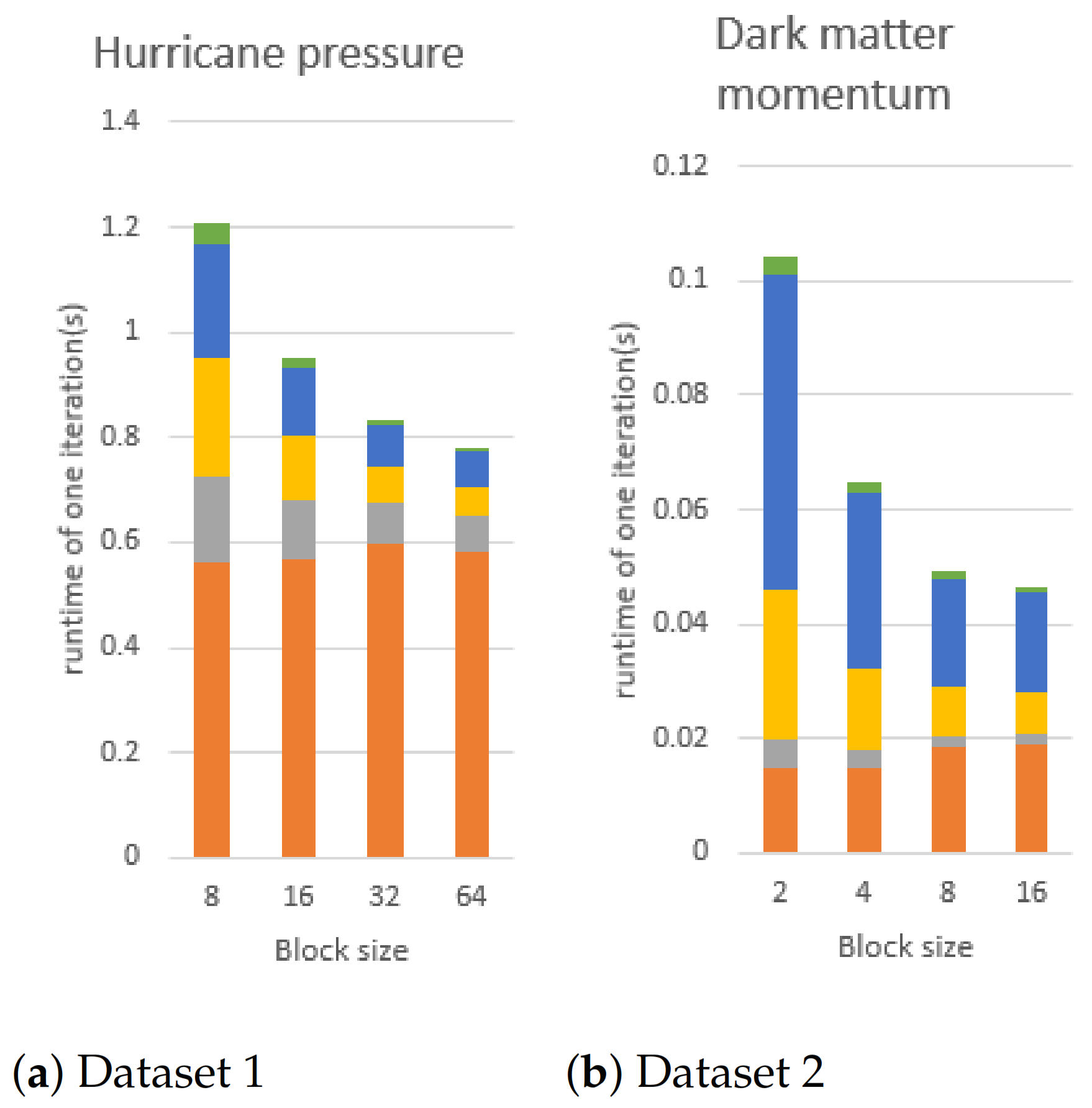
Figure 18.
We fix the number of Gaussian components to 4 and change the block size to conduct this experiment, using dataset1 and dataset2 on the CPU using 16 core. In the figures, orange, gray, yellow, blue, and green bars are the execution time of E-step, mean vector updating, covariance matrix flattening, and covariance matrix updating, respectively. Dataset 3 is an ensemble data so there is no block size to change.
Figure 18.
We fix the number of Gaussian components to 4 and change the block size to conduct this experiment, using dataset1 and dataset2 on the CPU using 16 core. In the figures, orange, gray, yellow, blue, and green bars are the execution time of E-step, mean vector updating, covariance matrix flattening, and covariance matrix updating, respectively. Dataset 3 is an ensemble data so there is no block size to change.
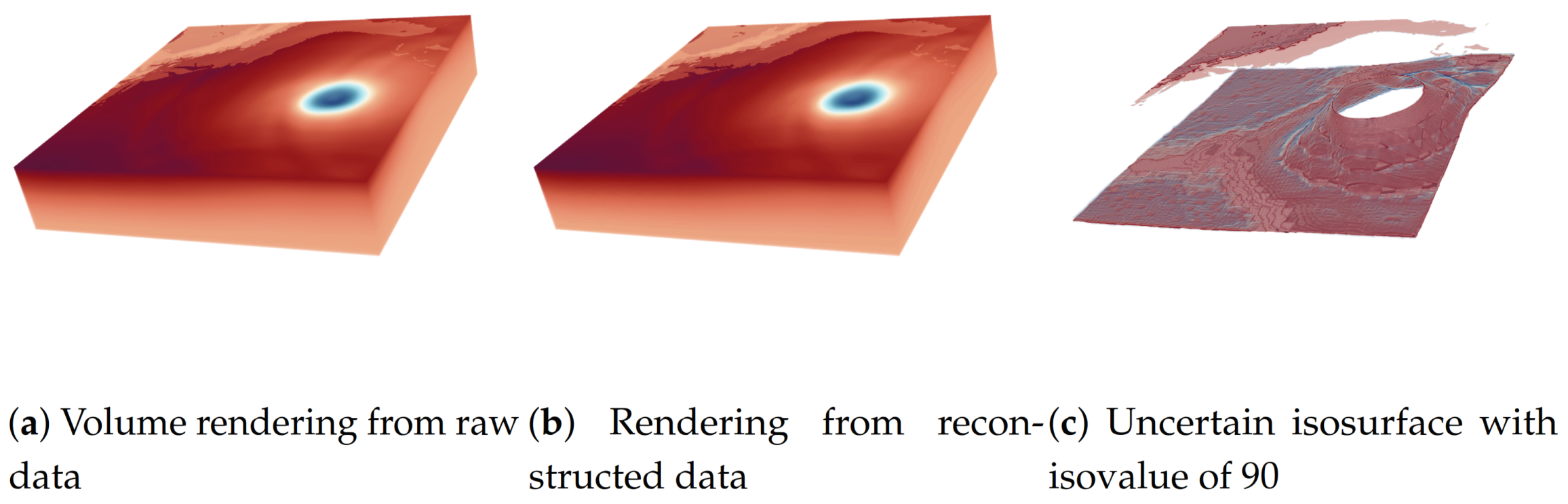
Figure 19.
The result of using the two proposed parallel multi-set distribution modeling algorithms in a real application.
Figure 19.
The result of using the two proposed parallel multi-set distribution modeling algorithms in a real application.
Table 1.
Speedup of our proposed parallel multi-set histogram modeling algorithm.
Table 1.
Speedup of our proposed parallel multi-set histogram modeling algorithm.
| Computing Node | Dataset 1 | Dataset 2 | Dataset 3 |
|---|
| 1-core CPU | 1 | 1 | 1 |
| 2-core CPU | 1.985425841 | 1.988104127 | 2.001024069 |
| 4-core CPU | 3.8213887 | 3.84097158 | 3.888216077 |
| 8-core CPU | 7.162903579 | 7.223857685 | 7.471058016 |
| 16-core CPU | 12.47168401 | 12.56068722 | 13.72269326 |
| 18-core CPU | 13.30148627 | 13.55864188 | 14.22243753 |
| GPU | 98.5314432 | 37.02952644 | 48.27058739 |
Table 2.
Speedup of our proposed parallel multi-set GMM modeling algorithm.
Table 2.
Speedup of our proposed parallel multi-set GMM modeling algorithm.
| Computing Node | Dataset 1 | Dataset 2 | Dataset 3 |
|---|
| 1-core CPU | 1 | 1 | 1 |
| 2-core CPU | 1.988480932 | 1.993276194 | 1.985682702 |
| 4-core CPU | 3.918983877 | 3.991065867 | 3.871235734 |
| 8-core CPU | 7.615474127 | 7.840609266 | 7.441185576 |
| 16-core CPU | 14.35827021 | 15.54666768 | 13.37958625 |
| 18-core CPU | 15.91859022 | 17.77076412 | 14.74770303 |
| GPU | 141.2707969 | 460.7890873 | 71.19877168 |
Table 3.
The computation time of our proposed parallel multi-set histogram algorithm and the parallel single-set histogram modeling algorithm. The computation time is in seconds.
Table 3.
The computation time of our proposed parallel multi-set histogram algorithm and the parallel single-set histogram modeling algorithm. The computation time is in seconds.
| Number of Cores | Serial | Single-Set | Ours | Single-Set | Ours |
|---|
| 8 × 8 × 8 | 2 × 2 × 2 | 2 × 2 × 2 | 8 × 8 × 8 | 8 × 8 × 8 |
|---|
| 1-core CPU | 1.28263 | 4.61334 | 11.7526 | 1.49209 | 10.3738 |
| 2-core CPU | - | 8.29002 | 5.96604 | 1.11556 | 5.55225 |
| 4-core CPU | - | 9.03034 | 3.05083 | 0.842128 | 2.66296 |
| 8-core CPU | - | 14.3831 | 1.59801 | 0.810271 | 1.4501 |
| 16-core CPU | - | 22.0338 | 0.911604 | 0.900354 | 0.77688 |
| 32-core CPU | - | 64.3039 | 0.544077 | 1.57874 | 0.482417 |
Table 4.
The computation time of our proposed parallel multi-set EM algorithm and the parallel single-set histogram modeling algorithm.
Table 4.
The computation time of our proposed parallel multi-set EM algorithm and the parallel single-set histogram modeling algorithm.
| Number of Cores | Serial | Single-Set | Ours | Single-Set | Ours |
|---|
| 8 × 8 × 8 | 2 × 2 × 2 | 2 × 2 × 2 | 8 × 8 × 8 | 8 × 8 × 8 |
|---|
| 1-core CPU | 4.71137 | 67.3893 | 58.118. | 6.01607 | 30.7055 |
| 2-core CPU | - | 106.751 | 29.4688. | 7.48694 | 15.606 |
| 4-core CPU | - | 114.94 | 14.8209. | 8.21759 | 7.79179 |
| 8-core CPU | - | 182.37 | 7.57408. | 8.27328 | 3.93791 |
| 16-core CPU | - | 434.22 | 4.01025. | 12.071 | 2.10316 |
| 32-core CPU | - | 645.74 | 2.19219. | 22.6585 | 1.08166 |