Abstract
Genetic Algorithms are stochastic optimization methods where solution candidates, complying to a specific problem representation, are evaluated according to a predefined fitness function. These approaches can provide solutions in various tasks even, where analytic solutions can not be or are too complex to be computed. In this paper we will show, how certain set of problems are partially solvable allowing us to grade segments of a solution individually, which results local and individual tuning of mutation parameters for genes. We will demonstrate the efficiency of our method on the N-Queens and travelling salesman problems where we can demonstrate that our approach always results faster convergence and in most cases a lower error than the traditional approach.
1. Introduction
Genetic algorithm (GA) is a probabilistic and heuristic search approach to investigate encoded solutions in an iterative manner, which was successfully applied in various practical applications, ranging from image processing [1], general optimization problems [2], biological sciences and bioinformatics [3,4], finance, economics and social sciences [5,6], speech processing [7] to path planning [8].
In case of evolutionary algorithms, a fitness function, determining the quality of each solution is used instead of a detailed formal description and analytical solution of the problem. The algorithm starts the search for the optimal solution with an initial generation encoding a set of randomly created solution candidates. Genetic algorithm in most common cases consists of three operations (selection, crossover and mutation) which are used repeatedly to create a new generation until reaching the solution with the designated threshold or stopping after a fixed number of generations. We produce a new generation by using the aforementioned fitness function to select a percentage of the best solutions from the current generation and then recombine them to yield new offspring (solution candidates). Before evaluating the new generation, we apply mutation inducing small changes in the solution candidates to maintain population diversity. Although some papers [9] have used only mutation algorithm to create newer generations, combination of crossover and elitism usually increases convergence speed towards the optimal solution [10].
Genetic algorithm as any other optimization algorithm could get stuck in a local optimum; a problem which can be solved by increasing the exploration rate. The Exploration-Exploitation dilemma is the most common trade-off problem between obtaining new knowledge and the necessity to use that knowledge to improve performance; a problem which can be found everywhere in nature [11]. This problem manifests in genetic algorithm as well where applying solely mutation and randomly creating chromosomes increases the exploration rate to the utmost resembling random search which is time consuming and impractical in high-dimensional problems. On the other hand, selecting only the best solution and spreading it in the next population would increase the exploitation rate making the algorithm unrobust which will only lead to the first local optimum in the initial population. One would like to exploit moving toward the best solution, but also explore maintaining a diverse population; and delve in the best current solutions finding the optimal or sub-optimal solutions, but still avoid local optimum.
The most important factors affecting the accuracy of the final solution and the convergence of the algorithm are the format of the problem representation and the fitness function, which we need to assess the validity of each solution. These two factors will determine the space of all solution candidates. These elements are usually determined by heuristic approaches and are always problem dependent. Other factors, like different mutation and crossover methods, can be investigated more generally.
One of the most important and ubiquitous operation is mutation which has a large effect on the convergence of GAs [12]. Throughout the literature, researchers have been using static or adaptive mutation [13]. In the early implementations, static mutation probability was applied, where the mutation rate was optimized by heuristic approaches with trial and error. In these approaches, a single parameter was identified determining the rate of mutation and was applied in the same manner for each gene in each chromosome. Later, adaptive versions have appeared where mutation rate can be changed according to other state variables of the algorithm, like iteration number, quality of the selected solution candidates or average fitness of all the solutions.
One of the major hinder of most algorithms is parameter tuning where an appropriate parameter setting has to be chosen, but it can be a hard task due to parameters’ reliance on the representation of the optimization problem. Parameter tuning relies on experimenting many fixed parameters reaching the supposedly optimal parameter setting without taking into account the possible changes throughout the optimization process. Beside the problem of tedious time-consumption, another problem of parameter tuning is that the chosen parameters may only work well starting from a specific state of the search space. Another parameter scheme is dynamic parameter control which changes parameters adaptively, during execution. When first introduced, it relies on the state of the optimization process or on time [14]. Parameter control later adopted self-correcting, self-adaptive, approach adjusting parameters while in progress relying on the feedback from the algorithm’s recent performance. Self-adaptation can be used as a strong, effective tool steering parameters with the help of some performance assistance e.g the fitness of a chromosome and the fitness of a population.
There is a huge focus recently in the machine learning community on gradient descent which can give you the optimal direction inside your local search space toward the local minimum or maximum. Using gradient descent with back propagation, which can tell you the optimal location for a change, solves the optimization problem faster by exploiting the neighbors of the current parameters. Although gradient descent seems like the perfect approach for any optimization problem, it is not applicable and ill-defined for non-differentiable objective functions and it is vulnerable against non-convex problems [15]. Evolutionary Algorithms are good alternatives which can overcome the limitation of gradient descent and sometimes can be even faster than hill-climbing optimization [16]. Evolutionary Algorithms can provide a solution; sometimes sub-optimal but still applicable in practice, without any deep knowledge of the system due to the random generation of a new population. Gradient based methods like stochastic gradient descent [17] or ADAM optimizer [18] have been the key for the recent advancements of deep learning which surpass any other optimization approach. Researchers started to integrate the two approaches striving for the optimal solution where evolutionary algorithms have been used for hyperparameter search [19] and reinforcement learning [20], which demonstrates the importance of GAs in machine learning as well.
Our method, called Locus mutation, extends the traditional approach of mutation where the probability of the alteration of a gene is uniformly distributed over each position of the genome in one sample. Locus mutation applies an additional probabilistic weight for each gene (i.e., location or dimension), thus, dimensions with higher probability will be selected more frequently, where an alteration could lead to a better solution with higher accuracy. Locus mutation resembles the traditional optimization approaches, back-propagation or gradient descent; where in case of a solution which is represented as a vector, our approach would point out the location which is recommended to be changed and keep satisfying segments intact.
In Section 2 we will introduce Genetic Algorithms, in Section 3 we will describe our alterations, describe our method and demonstrate results on the N-Queen problem, in Section 4 we will show how our approach can be used on other problems as well, like the travelling salesman problem and in the last Section we will conclude our results.
2. Genetic Algorithm
Genetic algorithm is a heuristic approach, exploring the search space and exploiting local optima. A gene is a singular element, encoding one dimension of the problem and representing a fragment of a solution. Problem representation is an essential prerequisite which can heavily determine the result of the algorithm. Another essential prerequisite condition to any optimization approach is its fitness function F which depends on the problem itself. Most sophisticated optimization approaches only deal with differentiable loss functions, fitness functions, which do not always exist. In case of general problems, the loss function is not differentiable, but we still have estimation about the quality of a solution which can be used in evolutionary algorithm.
Since algorithm convergence is determined heavily by the selected heuristics, we will distinguish between two different problems. In case of many practical problems, the fitness function measures a deviation from the optimal solution where the value of the best possible solution is known (and usually is zero, like in case of the N-queen problem [21]), meanwhile in other set of problems (like traveling salesman [22] or knapsack problem [23]) the fitness value of the optimal solution is unknown. Unlike the second set of problems, the first set of problems have a stopping criteria yielding a conceptual optimum. First we will demonstrate our solution using the first set of problems, but later we will present that it can be applied in case of the latter problems types as well.
The population will evolve exploiting the best solutions by selection then applying crossover operations amongst them. Ordering the chromosomes using the contrived fitness function then selecting a fixed percentage of the most fitted ones would help converging the population towards a better solution. Copying a small unchanged proportion of the fittest chromosomes into the next generation is called elitism which can steer the algorithm towards local optima. The new population consists of the selected elite chromosomes, combined chromosomes from the selected ones and new random chromosomes. Crossover exploits the best candidate solutions by combining them taking into account problem representation, creating only valid solution candidates. In addition to the randomly generated solutions, mutation has been used to increase the exploration rate searching for the optima. Intuitively, an adaptive mutation rate has been adopted where the mutation will be mitigated over time while converging to the optimal solution.
The traditional approach of genetic algorithm is presented in Algorithm 1 as a pseudo-code in forms of simple functions. Searching for the optimal solution , we initialize the population with random values. There is a trade-off problem between the size of the population and the number of populations which can be investigated with parameter tuning. Starting with an enormous and small could increase the exploration rate but yield a small exploitation rate. On the other hand, having small and large would limit the exploration of the search space. Our work focused on the mutation rate which drives the mutation operation . A fitness function is used to select the elite which is a small percentage of the fittest chromosomes. Crossover is used after the selection process exploiting the elite. Lastly, we mutate the current with probability. With a repetitive manner as many as the and in chronological order, we apply the previously mentioned steps.
| Algorithm 1: Genetic algorithm main steps |
 |
Adaptive mutation can be divided into three categories: population level, individual level, and component level adaptation [24]. Population level adaptation changes the mutation probability globally using feedback information from the previous population which means all the chromosomes have the same probabilistic chance for modification. At the individual level, each chromosome has its own adaptive operator which have been induced from the statistics of the previous generations. While the component level adaptation tries to combine the two previous methods by grouping the chromosomes and setting a different adaptive operator for each group.
However, it is important to note that none of the previously mentioned approaches utilize the statistic information inside the chromosome, which can be induced from the genes. To overcome this deficiency, we come up with the novel idea of locus mutation, where every gene has its own different adaptive operator and problematic genes have higher chance for change. Identifying the problematic genes is an important factor of our algorithm, and in our approach problematic means those genes which are mostly responsible for the high values in the error function (e.g., number of queens hitting each others in Case of the N-Queen problems).
3. Locus Adaptive Genetic Algorithm
All possible solutions in the initial population () are sampled randomly from the search space. The algorithm is iterated times where at each step, the population is continuously changing and better samples are selected and recombined; this helps increasing the average fitness value of the population over time. Thus, the time dependency of the population can be noted by which denotes the population at iteration t. At each iteration within the population, each sample is usually referenced to as a chromosome. A chromosome is one possible solution; a solution candidate; and this can be referenced to as where chromosomes. A chromosome is a vector representing a solution, which can be further divided into individual elements (Like a position of a single queen on a chessboard) this is noted by a third index where genes. In the traditional approach, selection of a position for mutation is a random process and its major goal is the exploration of the high-dimensional search space without taking the current state of the chromosome into account. Optimal selection of the gene which will be modified requires a comprehensive knowledge of three different variables; the statistics of the inter and intra populations, the chromosomes as a function of time and the statistic of the genes’ competences. Scrutinizing the relation between this three variables and the fitness function will lead us to the optimal modification of every gene. Although seemingly the optimal solution can be attained from Equation (1), it is not practical and both memory and time consuming because you need to keep track of all generations, chromosomes and genes throughout the algorithm.
calculates the probability of mutation for a given gene j and F is a function calculating the mutation rate of gene j taking into account all previous generations (q), chromosomes (k) and genes (l). A lot of attempts have been made to calculate an adaptive mutation operator using one of the aforementioned variables, but the authors are not aware of any method that has used the genes statistic to form a gene level mutation. Any mutation method can be rewritten as in Equation (1) using constant parameters as we will see in the following paragraphs. Traditional Genetic algorithm uses static operators as defined in Equation (2) which means that all chromosomes and genes throughout all generations would have the same mutation probability although some candidate solutions are closer to the optimal solution than others.
C is a constant value for every iteration, chromosome and gene. Static mutation is good until it gets stuck in a local minimum. After we reach a local minimum, we can walk back down the hill and try another angle craving for the optimal solution or try to jump from the local minima by increasing/decreasing the mutation rate or applying crossover. Parameter tuning is a manual, time consuming and unpleasant road which can be superseded with parameter control [13]. Parameter control means to start from an initial value then tune it adaptively during execution as in the following approaches. With the presupposition of converging to the optimal solution over time, an adaptive mutation subjected to time as in Equation (3) has been proposed.
F is a function of time which depends on t but does not depend on the chromosome i or the gene j. Once the population is determined the probability of mutation is the same for every chromosome and gene () in that iteration. Dynamic mutation takes the number of the current iteration as an input and gives us the mutation rate as an output. The function used to calculate the mutation rate can be a linear function which relies on the fact that it is beneficial to have a high mutation rate at the beginning and lower mutation rate during convergence [25], a gaussian function [26] where the mutation rate is going to increase smoothly until reaching an apex then decrease steadily converging to zero, Lévy distribution [27] or any arbitrary function. It is not the best approach having the same probability for each chromosome which could be very close to the optimal solution or far away from it.
Another approach with the same problem is population adaptive operator [28,29] as in Equation (4) where each generation has a different mutation operator which is deduced from the generation statistics. In [30], more than one mutation operators are used with an equal initial probability (1/the number of operators), but after each iteration the probabilities will increase/decrease according to the fitness values of each operator designated offspring. In general these approaches can be defined as:
F will determine how the mutation depends on all the fitness values in the current population for every i and j (chromosome and gene). Again once the population is determined, the probability of mutation is the same for every chromosome and gene (). To solve this problem an individual adaptive mutation [31,32] was proposed as in Equation (5) where each chromosome has its own different mutation operator that can be concluded from the statistic about the search space of each chromosome through the populations which is, the statistic, implicitly maintained by the algorithm. Mutation rate can change not only in different iterations, but also at the same generation where better candidates will have lower mutation rate, meanwhile worse candidates will have higher mutation rates. Each chromosome will have a different mutation rate which is proportional with comparison to the other chromosomes in the current population.
F is a function depending on the fitness function of the selected chromosome i, and the fitness of all the chromosomes k in the population. Even though chromosomes which are closer to the optimal solution has a smaller probability for mutation, their mutation most probably is going to diverge them from the optima. Thus, most of the genes are in a good position and any random modification is going to be mostly harmful. Hence uniformly distributed mutation over the genes is not the best option; assume we have an almost perfect solution (nine genes are perfect and one is bad), we have a 9/10 chance with uniform mutation to make this instance worse.
To tackle this problem, we have designated a different probability operator for each gene in a chromosome which can only be possible in partially solvable problems. To think about it, the mutation happens in gene level where we choose one or two genes randomly and then we change their values. Thus, a gene which is in a good position should be less prone to mutation. The simplest model for gene level mutation is locus mutation as in Equation (6) where all generations and chromosomes have the same mutation rate but each gene has a different mutation rate which corresponds with the other genes.
F is a function depending on the fitness function of the selected gene l. Once the mutation rate is set, the probability of mutation is the same for every chromosome at all time (). To grasp the concept before diving into details, we can simply state that measuring the fitness of each gene in a partially solvable problem will deduce a unique customized distribution for each chromosome yielding a gene level mutation. As an advantage of our approach, we can combine locus mutation with any of the other proposed methods. Returning to the first and most generalized Equation (1), we can use locus mutation with an adaptive individual level where each chromosome and each gene has an individual mutation rate which may give us a better result but certainly will make the whole process slower and resource consuming. We have only focused on the simplest version of our novel idea which is locus mutation.
Algorithm 2 depicts GA with locus mutation. All parameters remain the same as in the original Algorithm 1 setting parameter to one, but we do have a newly introduced gene level mutation () which depends on partial fitness (). Although in our experiments we will always set to one only focusing on the effect of locus mutation without taking into account parameter, a detailed investigation Section 5.4 will be conducted illustrating the advantage which can be garnered using parameter.
| Algorithm 2: Genetic algorithm main steps |
 |
In a partially solvable problem, partial fitness can be calculated leading to mutation with probabilistic gene selection. In a problem representation, one could identify parts which are good, and parts which are bad. A good gene should be changed less frequently, a worse element should be changed more often exploring further regions away from local optima. To illustrate the importance of in calculating the probabilistic mutation factor of each gene, we will discuss the partial solution of 8 queens problem as it has been depicted in Figure 1. In 8 queens problem, the chromosome has eight genes which refer to the number of the row, while the index of each gene refers to the column. A chromosome with zero queens hitting each other is optimal. Intuitively, the fitness function calculates the number of hits. In the example depicted in Figure 1, the loss is four (Calculating hitting pairs only once.) where queens 1, 2, 3, 4, 7, 8 are hitting 8, 3 and 4, 2 and 7, 2, 3, 1 respectively. On the other hand, partial fitness will give a different loss for each gene representing the number of queens hitting the current queen. In our example, partial values are [1 2 2 1 0 0 1 1] where for example queen number three is hitting two other queens (2 and 7) which means it is a bad queen and a high mutation rate should be assigned to it and likewise for queen number two. Whereas, queens five and six are not hitting any other queens, meaning that low mutation rates should be assigned to them.

Figure 1.
Potential chromosome for 8-Queens Problem where queen 1 is hitting queen 8, and two queens (2, 3) are hitting each other and also hitting two other queens (4, 7) yielding a loss of 4 where the four hitting pairs are ([1, 8], [2, 3], [2, 4], [3, 7]).
Instead of using uniform distribution as in the traditional algorithm, we are using a probabilistic function conveying the information about the fitness of each gene. The mutating rate of each gene does not only depend on its partial value, but it is also proportional with other genes’ partial value, also every gene has a minimal mutation rate, this ensures that even a gene with zero hitting queens, will have a non-zero mutation probability.
4. Heuristically Partially Solvable Problems with Unknown Optimum
As we saw earlier, locus mutation works well with a partially solvable problem outperforming the traditional approach using gene level information. Although Locus mutation is only applicable for partially solvable problems e.g., N-Queens problem [33], heuristic partial solution can be sufficient which can only be inferred with a comprehensive understanding of the problem. One of the most elusive problem is traveling salesmen problem (finding the shortest route to visit a set of cities), where the optimal solution is undefined making the optimization process interminable, and a heuristic threshold has to be used. In the N-Queens problem, calculating the partial solution was a straight forward process which is the number of queens hitting the current gene taking all the other genes into consideration. Having us doing so in the traveling salesman problem (TSP) [34] requires a modification signifying the distance between the current gene (city) and the next gene with contrast to its distance with the other genes. Since traditionally the fitness of the entire chromosome relies solely on the distance between each gene and its next neighbor without taking into account any other genes, we came up with a new idea which we will call normalized comparative loss to calculate the partial fitness of each gene taking into consideration all other genes.
An example has been depicted in Figure 2 showing a simple example of TSP problem with 10 cities. Each city has two indices, the first index indicates the order of the city in the candidate chromosome [6 3 4 9 5 1 10 7 8 2] and the second one refers to the actual label of the city e.g., the first gene in our chromosome has the label . To explain the partial fitness value of a gene, we have used the same candidate chromosome but focused on the penultimate gene, gene , as in Figure 3. This gene refers to the city number 8 which is located at the gene before the last gene in the candidate solution. The red line depicts the relevant connection between our gene and gene number two; the last gene in the current chromosome and the next neighboring gene. The gene which is the farthest away from our gene of interest has been linked to our gene with green line, while the blue line portrays the closest gene. Using the three previously mentioned distances;the pertinent distance between the current gene and next gene, the distance between the current gene and the gene which is farthest away from the current gene and the distance between the current gene and the gene which is closest to the current gene; we can calculate a heuristic partial fitness as in Equation (7) where i is the concerned gene while and give us respectively the minimum and the maximum distance between gene i and the other genes.
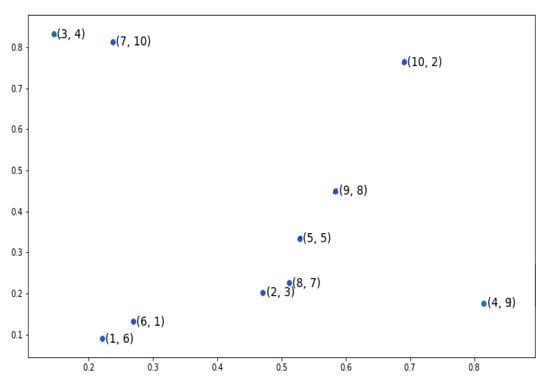
Figure 2.
Traveling salesman Problem with 10 cities, chromosomes. The vertices depict the cities where the first index refers to the position of the city inside the chromosome while the other index refers to the city label. An edge can be formed between each two sequential cities to show the path which the traveling salesman should take.
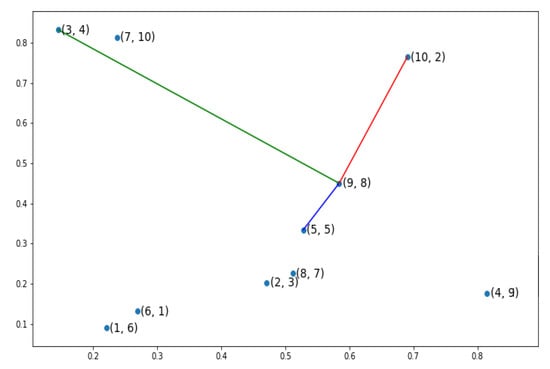
Figure 3.
This figure depicts the pertinent distances of a specific gene (gene (9,8)) for a Traveling salesman Problem with 10 cities chromosome. The red vertex depicts the pertinent path between our gene and next gene. The green and blue vertices link the gene of interest with the farthest and closest gene in respect.
Before moving to the results section demonstrating the effectiveness of locus mutation, we will substantiate the advantage of using locus mutation by applying Wilcoxon test which is a non-parametric statistical test used to determine if two sets of distributions are different from each other in a statistically significant manner. We investigated a TSP instance with 48 cities, 1000 chromosomes, 20 generations. We used the same initial population for baseline and locus mutation then stored the evolved two populations after the 20th generation. Figure 4 demonstrates the distribution of the fitness of the chromosomes for the initial population, the 20th baseline population and the 20th locus population. Figure 4 illustrates visually the benefit of locus mutation where we can see that the distribution of the fitness of the 20th generation using locus mutation is closer to zero with smaller mean value. We applied Wilcoxon matched pairs test to the fitness of the evolved baseline and locus population obtaining a very small p value, . We can conclude from the minute p value that the two distributions have different medians and reject the idea that the difference is due to chance.
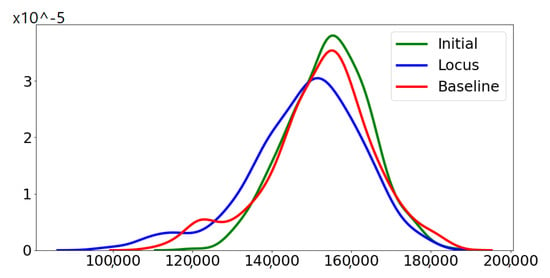
Figure 4.
The figure shows the distribution of the fitness of the chromosomes in a generation in three different cases, initial generation, 20th generation using baseline mutation and the 20th generation using locus mutation. Locus mutation is not just attaining better chromosomes, smaller fitness, but also moving the entire distribution closer to zero.
5. Results
5.1. N-Queens Problem
To validate our hypotheses, detailed comparison with the traditional mutation have been investigated proving a superior performance with a different set of parameters as in Figure 5. The results have been averaged out for 50 different experiments. The best solution has been selected out of 5 unique mutation rate values [0.01, 0.1, 0.6, 0.3, 0.9] which are distributed over the entire parameter space search. All experiments have been conducted using the traditionally applied crossover method as well. For the sake of reproducibility, you can find our codes online (https://github.com/Al-Afandi/Adaptive-Gene-Level-Mutation) alongside the chosen investigated parameters.
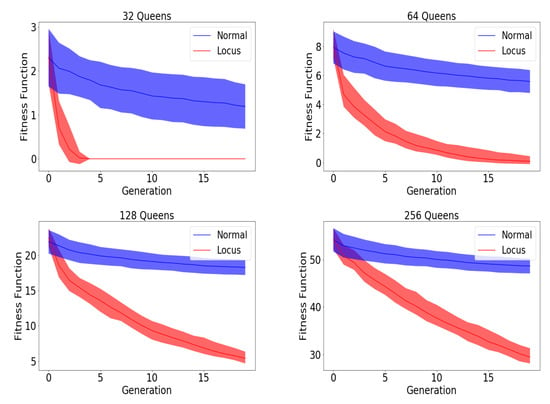
Figure 5.
It depicts a comparison between Locus mutation and traditional mutation with different sets of parameters. The figures depict N-queens problem with 32, 64, 128 and 256 queens where the results have been averaged out with two different generation size [200, 400], [400, 600], [600, 800] and [800, 1000] respectively. We only selected the best solution out of these five different values of mutation rate [0.01, 0.1, 0.6, 0.3, 0.9]. The center of the curve is the expected value while the range visualize the standard deviation. All the experiments have been repeated 50 times and then averaged out. We can notice that the number of hitting queens is escalating when we increase the number of queens.
Figure 5 and Table 1 demonstrate a quantitative and qualitative superiority of our approach always leading to a better solution with a reasonable margin. Our approach could almost always solve the N-Queens problem with a population of 32 while the traditional approach could never reach the optimal solution. With a population of 128, our approach is two to three times better than the traditional approach in terms of the final loss. Even with a huge population of 256 queens, our approach is 1.6 times better in terms of the fitness function.

Table 1.
N-Queens optimal solution, minimum number of hitting queens, after 20 generations. Two different population size , 200 and 400, have been investigated with 50 different repetitions. All the runs have been averaged out.
To demonstrate the effectiveness of our new approach with comparison to other recent attempts working on improving mutation operator, we have compared our mutation method with traditional and individual level adaptive mutation [35] using the same set of parameters which is 64 Queens, , and as depicted in Figure 6. For individual adaptive level mutation, we have investigated 30 different ranges of while using a static mutation rate, 0.5 the middle of all ranges, for the other two methods. The ranges have been centered around 0.5 and varied from a very small range [0.485, 0.515] to a very large one [0.05, 0.95]. Although the results of the two other methods, traditional and adaptive approaches, have been obtained from selecting the best solution averaging out ten different experiments while only calculating the average results of our method, our approach have a superior performance and a faster convergence.

Figure 6.
The fitness value of 64-Queens problem as a function of the number of generations comparing locus mutation with traditional and adaptive mutation. For adaptive mutation, We have averaged out 30 different ranges and used the center of each range for traditional and locus mutation. All the experiments have been repeated 10 times with the same set of parameters. Although we have used the mean solution for locus mutation, we have selected the best solution for adaptive and traditional mutation.
We have shown one comparison between locus mutation and another mutation method; Figure 6, but the advantage of our method is that it is compatible with any other generally applied mutation e.g., population level mutation and individual level mutation; to the extent where you can obtain statistic information from generations, populations, chromosomes and even genes (Locus mutation) as in Equation (1).
5.2. Traveling Salesman Problems
Apart from the results on the N-Queen problem, we have also investigated another commonly examined problem, the TSP problem. Detailed comparison with the traditional mutation have been investigated manifesting a superior performance with a big set of different parameters as in Figure 7 and Table 2. The best solution have been selected out of 5 unique mutation rate values [0.01, 0.1, 0.6, 0.3 and 0.9] expanding through the parameter space. All the experiments have been repeated 100 times and then averaged out. With every repeat, TSP problem (cities location, weights and initial population) will be created automatically by randomly placing N cities on a small grid.

Figure 7.
Comparison between Locus mutation and traditional mutation with different sets of parameters. The figures depict TSP problem with 32, 64, 124 and 254 cites. We averaged out the runs with two different generation size [400,600], [400,600], [600,1000] and only 1000 for 254 cities constellation. We only selected the best solution out of these five different values of mutation rate [0.01, 0.1, 0.6, 0.3 and 0.9]. The center of each curve is the expected value while the range visualizes the standard deviation. All the experiments have been repeated 100 times and then averaged out

Table 2.
TSP optimal solution after 100 generation. Two different population size, 200 and 400, have been investigated with a 100 different repetition. All the runs have been averaged out. is the number of cities (population number), while is the mutation factor.
Figure 7 and Table 2 demonstrate a quantitative and qualitative superiority of our approach always leading to a smaller distance. Having bigger and bigger population increases the gap between the two approaches e.g., the gap was maximum 1 at the beginning with 32 cities to reach 5 at the end with 254 cities.
5.3. Using Locus Mutation with Other Heuristic Algorithms
Mutation can be a substantial operation for other heuristic algorithms as well e.g., simulated annealing [36], variable neighborhood search [37], tabu search [38] and Hill climbing [39]. Locus mutation works well with genetic algorithm solving TSP problem giving better results than the baseline, as we illustrated in earlier paragraphs. In the previous results, TSP instances were created by randomly sampling the interval where these samples composed the cities coordinates. To further instantiate our results, we did investigate TSP problem with genuine data provided from TSPLIB dataset. We only investigated the instances which have less than 101 cities, 16 instances. We investigated the efficiency of locus mutation in two other heuristic algorithms (simulated annealing (SA) and variable neighborhood search (VNS)). Table 3 demonstrates the conspicuous advantage of using locus mutation. The experiments for the three algorithms were repeated 10 times and with two different setups (one run with simple parameters and another one with complex parameters). In most cases, using locus mutation gives a better results, and the best solutions were obtained from VNS algorithm with locus mutation. Although, in most instances, we didn’t reach the optimal solution, We were only focusing on the benefit of using locus mutation with other algorithms, apart from GA, without thoroughly investigating other enhanced versions of the same algorithms.

Table 3.
Comparison between baseline (Base) and locus (Loc) mutation for three different algorithm, genetic algorithm (GA), simulated annealing (SA) and Variable neighborhood search (VNS). We applied these algorithms on 16 different instances from TSPLIB dataset. In most cases, locus mutation is enhancing the performance of the algorithms.
5.4. Exploiting the Tuning of the Power Parameter
The importance of each loss (partial fitness) can be changed by using a power function which can raise the partial fitness vector to a power (). Using a power function with , you get the uniform mutation back making our approach an extension of the original method.
For further illustration, we will go back to the previous example as in Figure 1. Partial fitness, which is the main bulk calculating the mutation rate of each gene, equals [1 2 2 1 0 0 1 1]. Using the parameter, we would have the following updated partial fitness values:
We can notice that when we will get back to the uniform distribution where all genes have the same probability for a mutation. When , queens 2 and 3 have a bigger chance for a mutation. Increasing the value of drastically decreases the comparatively good genes’ probability for a mutation. When , All probabilities are going to be zero except the genes with the worst partial fitness. As we mentioned earlier, partial fitness will always have a non-zero mutation operator; thus in practice, we will add a low mutation operator for every gene e.g., 0.001.
The effectiveness of parameter is illustrated in Figure 8 depicting the fitness value(The number of hits) of the best optimal candidate solution () with regards to Parameter (). The figure start with uniform distribution;the traditional approach; then depicts the optimal solution using the default value and end up with norm which will deterministically select the worst genes for mutation. The best result with the same set of parameters, which have been chosen arbitrary, can be obtained with .
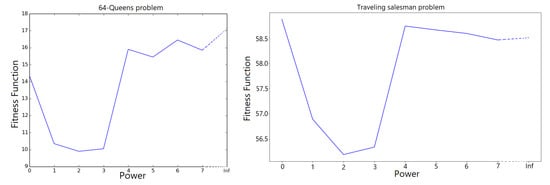
Figure 8.
The fitness value of the best optimal solution for 64-Queens problem and TSP problem respectively as a function of Powers where we averaged out ten runs. It starts with uniform distribution then uses a logarithmic scale of , and end up with L-infinite norm. We have achieved similar results with two separate problems.
Regarding N-Qeens problem, the experiments have been done with 64 Queens, , , , , and a logarithmic scale of values where is the lower bound of gene mutation operator. We have also obtained a similar results investigating parameter on the TSP problem using normalized comparative loss, as in Figure 8, where we have arbitrarily chosen a set of parameters; 128 cities, 400 population size and 30 generations. All experiments have been repeated ten times, and the fitness functions at the last generation have been aggregated. can give us the best result for the two problems. Locus mutation works very well relying on the selfishness of each gene where each gene wants to mutate craving for perfection i.e., in the TSP problem, each gene is eager to be connected with the closest city. The idea of Selfish gene is manifested in nature [40] leading to prosperity. Although this seemingly would lead to local optimum, sometimes the interest of individuals meets the interest of the population, and the interest of genes meets the interest of individuals where all genes are striving for excellence. We can even escalate the selfishness of the genes by increasing the power parameter .
5.5. Running Time Comparison
Using this heuristic method, calculating the partial fitness and fulfilling the only prerequisite for locus mutation, requires some additional computations. , , and even the denominator in Equation (7) are only vectors or matrices which can be pre-calculated once, but applying locus mutation will require operations (the number of genes multiplied by the size of the population). This big number of operations is needed because locus mutation gives each gene a distinct mutation rate, which correspond with the normalized, comparative and partial loss, taking other partial fitnesses into account. We have only investigated TSP extra time consumption due to the fact that for the N-Queens problem, beside the operations, no extra calculations are needed. According to our extensive experiments with a vast set of parameters, As in Table 4, Our approach can be in maximum two times slower than the traditional approach, but it will saturate with a better solution as we can see in Figure 9 where our solution converged to the optimal solution but the traditional approach did saturate before approaching the optimum which we calculate using brute force method searching through each and every possible combination. To demonstrate the performance advantage of our approach having a same wall time, as in Figure 10, we ran the traditional approach for two times more generations, 600 generations for the traditional approach and 300 generations for locus mutation, proving that on the long run our approach will saturate to a better solution consuming the same time.

Table 4.
Time comparison between locus and baseline mutation where PN is the number of cites, PS is population size, GN is the number of generations and MR is mutation rate. TSP timing gives us the time consumption for each algorithm using the specified parameters. Ratio gives us the speed rate, speed advantage, of the original approach.

Figure 9.
This Figure depicts TSP Problem with 10 cities manifesting the speed and the ability of our approach to nearly reach the optimal solution in comparison with the traditional approach. All the experiments have been conducted with 200 population size, 200 generations and 0.5 mutation rate. The optimal solution has been obtained using brute force algorithm. The experiments were repeated 100 times.
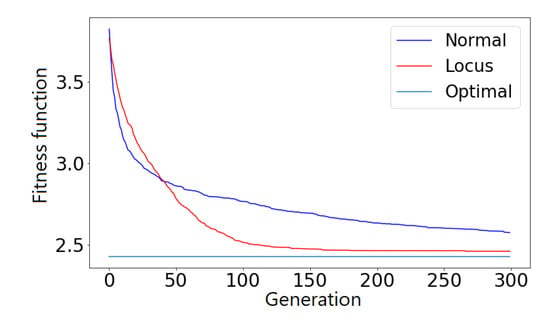
Figure 10.
This Figure depicts TSP Problem with 10 cities manifesting the ability of our approach to surpass the traditional approach consuming the same time. We did run the the traditional approach for two times more generations e.g., when axis x equals 25 generations for locus mutation (as in the figure), it equals 25 * 2 generations for traditional mutation. All the experiments have been conducted with 200 population size and 0.5 mutation rate. We run the traditional approach for 600 generations, while we run locus mutation only for 300 generations. The optimal solution has been obtained using brute force algorithm and the experiments were repeated 100 times.
6. Conclusions
We have illustrated that using a gene-dependent local mutation operator where every gene has a different mutation rate induced from a heuristic and partial fitness function will speed up the convergence of the algorithm and yield more accurate final solution. We have investigated two common problems, traveling salesman problem (TSP) and N-Queens problem. In case of the N-Queens problem, Locus mutation has resulted better solutions in all cases, regardless of the investigated parameters. Even with a big population number of 254, locus mutation yields a 1.5 times lower error than its traditional counterpart. Similar results were obtained using locus mutation for the TSP problem where our approach has always surpassed the baseline solution.
Author Contributions
Conceptualization, J.A.-A. and A.H.; methodology, J.A.-A. and A.H.; software, J.A.-A. and A.H.; validation, J.A.-A. and A.H.; formal analysis, J.A.-A. and A.H.; investigation, J.A.-A. and A.H.; resources, J.A.-A. and A.H.; data curation, J.A.-A.; writing—original draft preparation, J.A.-A.; writing—review and editing, J.A.-A. and A.H.; visualization, J.A.-A.; supervision, A.H.; project administration, A.H.; funding acquisition, A.H. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Acknowledgments
This research has been partially supported by the Hungarian Government by the following grant: 2018-1.2.1-NKP-00008: Exploring the Mathematical Foundations of Artificial Intelligence and the support of the grant EFOP-3.6.2-16-2017-00013 is also gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Talbi, H.; Batouche, M.; Draa, A. A quantum-inspired evolutionary algorithm for multiobjective image segmentation. Int. J. Math. Phys. Eng. Sci. 2007, 1, 109–114. [Google Scholar]
- Jin, Y.; Branke, J. Evolutionary optimization in uncertain environments-a survey. IEEE Trans. Evol. Comput. 2005, 9, 303–317. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Du, W.; Sun, F.; Wang, X.; Zhou, C.; Liang, Y. A multi-approaches-guided genetic algorithm with application to operon prediction. Artif. Intell. Med. 2007, 41, 151–159. [Google Scholar] [CrossRef] [PubMed]
- Krawiec, K.; Pawlak, M. Genetic programming with alternative search drivers for detection of retinal blood vessels. In Proceedings of the European Conference on the Applications of Evolutionary Computation, Copenhagen, Denmark, 8–10 April 2015; Springer: Cham, Switzerland, 2015; pp. 554–566. [Google Scholar]
- Buurman, J.; Zhang, S.; Babovic, V. Reducing risk through real options in systems design: The case of architecting a maritime domain protection system. Risk Anal. Int. J. 2009, 29, 366–379. [Google Scholar] [CrossRef]
- Zhang, S.X.; Babovic, V. An evolutionary real options framework for the design and management of projects and systems with complex real options and exercising conditions. Decis. Support Syst. 2011, 51, 119–129. [Google Scholar] [CrossRef]
- Milone, D.H.; Merelo, J.J.; Rufiner, H. Evolutionary algorithm for speech segmentation. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1115–1120. [Google Scholar]
- Vadakkepat, P.; Tan, K.C.; Ming-Liang, W. Evolutionary artificial potential fields and their application in real time robot path planning. In Proceedings of the 2000 congress on evolutionary computation, CEC00 (Cat. No. 00TH8512), La Jolla, CA, USA, 16–19 July 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 1, pp. 256–263. [Google Scholar]
- Pan, X.; Zhang, J.; Szeto, K.Y. Application of Mutation Only Genetic Algorithm for the Extraction of Investment Strategy in Financial Time Series. In Proceedings of the 2005 International Conference on Neural Networks and Brain, Beijing, China, 13–15 October 2005; Volume 3, pp. 1682–1686. [Google Scholar]
- Corus, D.; Oliveto, P.S. Standard Steady State Genetic Algorithms Can Hillclimb Faster than Mutation-only Evolutionary Algorithms. arXiv 2017, arXiv:1708.01571. [Google Scholar] [CrossRef]
- Berger-Tal, O.; Nathan, J.; Meron, E.; Saltz, D. The exploration-exploitation dilemma: A multidisciplinary framework. PLoS ONE 2014, 9, e95693. [Google Scholar]
- Abdoun, O.; Abouchabaka, J.; Tajani, C. Analyzing the Performance of Mutation Operators to Solve the Travelling Salesman Problem. arXiv 2012, arXiv:1203.3099. [Google Scholar]
- Eiben, A.; Michalewicz, Z.; Schoenauer, M.; Smith, J. Parameter Control in Evolutionary Algorithms. In Parameter Setting in Evolutionary Algorithms; Lobo, F.G., Lima, C.F., Michalewicz, Z., Eds.; Studies in Computational Intelligence Book Series; Springer: Berlin/Heidelberg, Germany, 2007; Volume 54, pp. 19–46. Available online: http://www.springerlink.com/content/978-3-540-69431-1/ (accessed on 9 January 2021). [CrossRef]
- Case, B.; Lehre, P.K. Self-adaptation in non-Elitist Evolutionary Algorithms on Discrete Problems with Unknown Structure. arXiv 2020, arXiv:2004.00327. [Google Scholar]
- Baldi, P. Gradient descent learning algorithm overview: A general dynamical systems perspective. IEEE Trans. Neural Netw. 1995, 6, 182–195. [Google Scholar] [CrossRef]
- Ma, Y.A.; Chen, Y.; Jin, C.; Flammarion, N.; Jordan, M.I. Sampling Can Be Faster Than Optimization. arXiv 2018, arXiv:1811.08413. [Google Scholar] [CrossRef] [PubMed]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the COMPSTAT’2010, Paris, France, 22–27 August 2010; Springer: Cham, Switzerland, 2010; pp. 177–186. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Young, S.R.; Rose, D.C.; Karnowski, T.P.; Lim, S.H.; Patton, R.M. Optimizing deep learning hyper-parameters through an evolutionary algorithm. In Proceedings of the Workshop on Machine Learning in High-Performance Computing Environments, Austin, TX, USA, 15–20 November 2015; ACM: New York, NY, USA, 2015; p. 4. [Google Scholar]
- Such, F.P.; Madhavan, V.; Conti, E.; Lehman, J.; Stanley, K.O.; Clune, J. Deep neuroevolution: Genetic algorithms are a competitive alternative for training deep neural networks for reinforcement learning. arXiv 2017, arXiv:1712.06567. [Google Scholar]
- Bezzel, M. Proposal of 8-queens problem. Berl. Schachzeitung 1848, 3, 1848. [Google Scholar]
- Gupta, S.; Panwar, P. Solving Travelling Salesman Problem Using Genetic Algorithm. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2013, 3, 376–380. [Google Scholar]
- Chu, P.C.; Beasley, J.E. A genetic algorithm for the multidimensional knapsack problem. J. Heuristics 1998, 4, 63–86. [Google Scholar] [CrossRef]
- Korejo, I.; Yang, S. A Comparative Study of Adaptive Mutation Operators for Genetic Algorithms. In Proceedings of the 8th Metaheuristic International Conference, Hamburg, Germany, 13–16 July 2009. [Google Scholar]
- Jeong, I.K.; Lee, J.J. Adaptive Simulated Annealing Genetic Algorithm for System Identification. Eng. Appl. Artif. Intell. 1996, 9. [Google Scholar] [CrossRef]
- Hinterding, R. Gaussian Mutation and Self-Adaptation for Numeric Genetic Algorithms. In Proceedings of the 1995 IEEE International Conference on Evolutionary Computation, Perth, WA, Australia, 29 November–1 December 1995; Volume 1, p. 384. [Google Scholar] [CrossRef]
- Lee, C.Y.; Yao, X. Evolutionary Programming Using Mutations Based on the LÉvy Probability Distribution. Evol. Comput. IEEE Trans. 2004, 8, 1–13. [Google Scholar] [CrossRef]
- Hong, T.P.; Wang, H.S.; Chen, W.C. Simultaneously Applying Multiple Mutation Operators in Genetic Algorithms. J. Heuristics 2000, 6, 439–455. [Google Scholar] [CrossRef]
- Fan, Q.; Yan, X. Self-adaptive differential evolution algorithm with zoning evolution of control parameters and adaptive mutation strategies. IEEE Trans. Cybern. 2015, 46, 219–232. [Google Scholar] [CrossRef]
- Li, C.; Yang, S.; Korejo, I. An Adaptive Mutation Operator for Particle Swarm Optimization. Available online: https://bura.brunel.ac.uk/handle/2438/5884 (accessed on 9 January 2021).
- Yang, S. Adaptive Mutation Using Statistics Mechanism for Genetic Algorithms. In Proceedings of the International Conference on Innovative Techniques and Applications of Artificial Intelligence, Cambridge, UK, 13–15 December 2004; pp. 19–32. [Google Scholar] [CrossRef]
- Yang, S.; Etaner-Uyar, A. Adaptive mutation with fitness and allele distribution correlation for genetic algorithms. In Proceedings of the 2006 ACM Symposium on Applied Computing, Dijon, France, 23–27 April 2006; Volume 2, pp. 940–944. [Google Scholar] [CrossRef]
- Sarkar, U.; Nag, S. An Adaptive Genetic Algorithm for Solving N-Queens Problem. arXiv 2018, arXiv:1802.02006. [Google Scholar]
- Hussain, A.; Muhammad, Y.S.; Nauman Sajid, M.; Hussain, I.; Shoukry, A.; Gani, S. Genetic Algorithm for Traveling Salesman Problem with Modified Cycle Crossover Operator. Comput. Intell. Neurosci. 2017, 2017, 7430125. [Google Scholar] [CrossRef] [PubMed]
- Patil, S.; Bhende, M. Comparison and analysis of different mutation strategies to improve the performance of genetic algorithm. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 4669–4673. [Google Scholar]
- Zhan, S.H.; Lin, J.; Zhang, Z.J.; Zhong, Y.W. List-based simulated annealing algorithm for traveling salesman problem. Comput. Intell. Neurosci. 2016, 2016, 1712630. [Google Scholar] [CrossRef]
- Hore, S.; Chatterjee, A.; Dewanji, A. Improving variable neighborhood search to solve the traveling salesman problem. Appl. Soft Comput. 2018, 68, 83–91. [Google Scholar] [CrossRef]
- Xu, D.; Weise, T.; Wu, Y.; Lässig, J.; Chiong, R. An investigation of hybrid tabu search for the traveling salesman problem. In Proceedings of the Bio-Inspired Computing-Theories and Applications, Hefei, China, 25–28 September 2015; Springer: Cham, Switzerland, 2015; pp. 523–537. [Google Scholar]
- O’Neil, M.A.; Burtscher, M. Rethinking the parallelization of random-restart hill climbing: A case study in optimizing a 2-opt TSP solver for GPU execution. In Proceedings of the 8th Workshop on General Purpose Processing Using GPUs, San Francisco, CA, USA, 7–8 February 2015; pp. 99–108. [Google Scholar]
- Dawkins, R. The Selfish Gene; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).