Two NEH Heuristic Improvements for Flowshop Scheduling Problem with Makespan Criterion
Abstract
1. Introduction
2. Problem Description
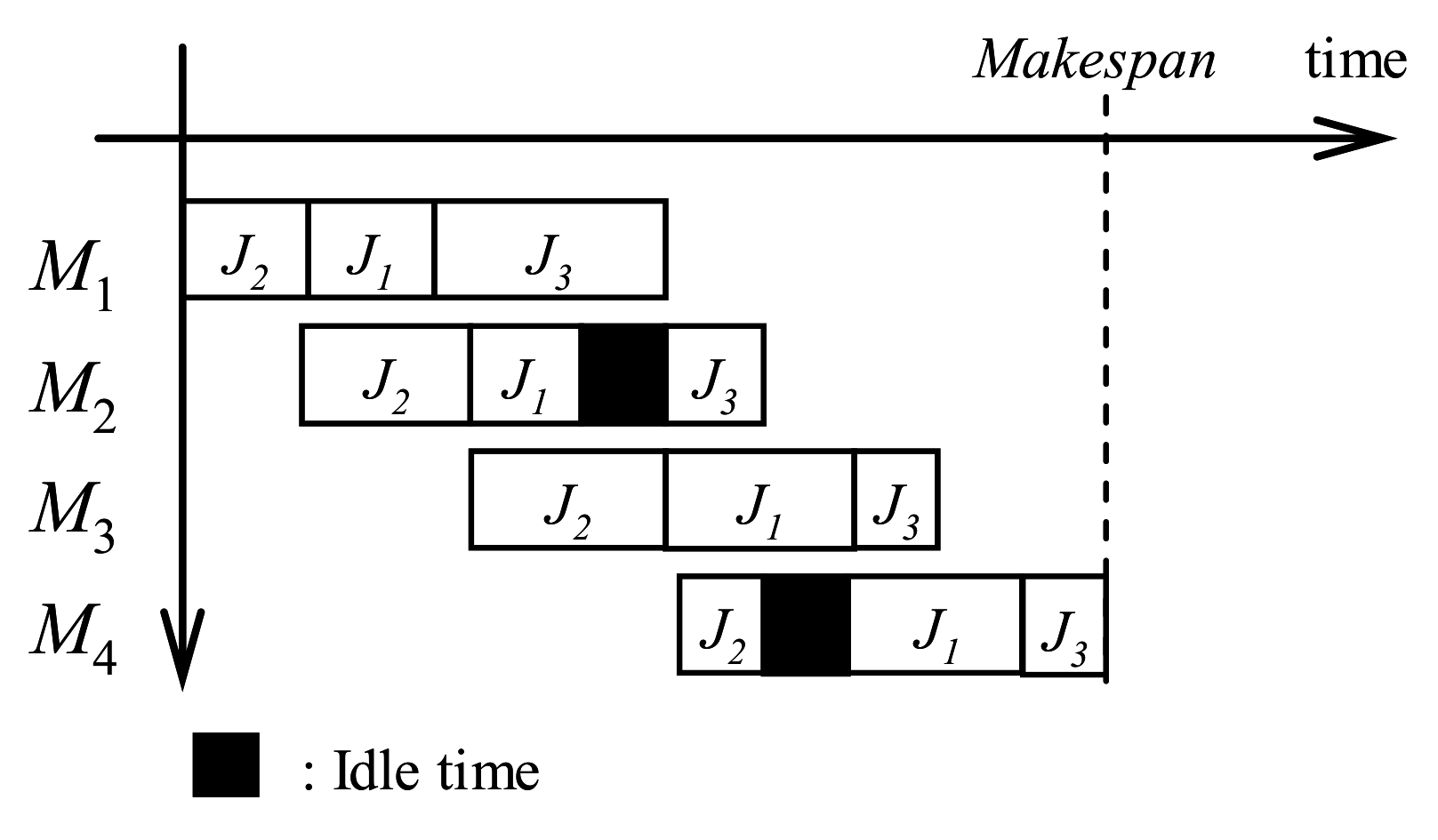
2.1. Flowshop Scheduling Problem
2.2. NEH Heuristic Analysis
| Algorithm 1: (NEH heuristic) |
| Rank jobs in decreasing order of total processing time // (First point sort) Remove first job of ranked list and insert it as first element of current partial sequence k = 1 Do { Take the first job of ranked list Insert it in all of k+1 possible places of current partial sequence Evaluate all of k+1 resulting partial sequences Keep the best sequence as new current partial sequence // (Second point choice) k = k+1 } While (k ≤ number of jobs to schedule) |
3. First Improvement Method, NEH-SS1
3.1. Factorial Basis Decomposition
75 = 2!.( 2!.( 2!.( 2!.(3! 0 + 4) + 1) + 0) + 1) + 1
3.2. Method Description
3.3. Results and Discussion
4. Second Improvement Method NEH-SS2
4.1. Method Description
| Algorithm 2: (NEH-SS2 improvement heuristic) |
| Rank jobs in decreasing order of total processing time // (First point sort) Remove first job of ranked list and insert it as the first element of partial sequence k = 1 Give Size_LPS1 and Size_LPS2 Do { Take the first job of ranked list For (each partial sequence of LPS1) Evaluate all of k+1 possible partial schedule Keep the best partial sequence(s) in LPS2. // (Second point choice) // If there is only one best partial sequence, we save only one partial sequence. End For k = k+1 If (number of best partial sequences in LPS2 ≤ Size_LPS1) Copy LPS2 in LPS1 Else Choose Size_LPS1 sequences in LPS2 Copy them in LPS1 End If Empty LPS2 } While (k ≤ number of jobs to schedule) |
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Johnson, S.M. Optimal two- and three-stage production schedules with setup times included. Nav. Res. Logist. Q. 1954, 1, 61–68. [Google Scholar] [CrossRef]
- Nawaz, M.; Enscore, E.E.J.; Ham, I. A heuristic algorithm for the m-machine, n-job flowshop sequencing problem. OmegaInt. J. Manag. Sci. 1983, 11, 91–95. [Google Scholar] [CrossRef]
- Ruiz, R.; Marotto, C. A comprehensive review and evaluation of permutation flowshop heuristics. Eur. J. Oper. Res. 2005, 165, 479–494. [Google Scholar] [CrossRef]
- Palmer, D. Sequencing jobs through a multi-stage process in the minimum total time - a quick method of obtaining a near optimum. Oper. Res. Q. 1965, 16, 101–107. [Google Scholar] [CrossRef]
- Hundal, T.S.; Rajgopal, J. An extension of Palmer’s heuristic for the flow shop scheduling problem. Int. J. Prod. Res. 1988, 26, 1119–1124. [Google Scholar] [CrossRef]
- Campbell, H.G.; Dudek, R.A.; Smith, M.L. A heuristic algorithm for the n job, m machine sequencing problem. Manag. Sci. 1970, 16, B630–B637. [Google Scholar] [CrossRef]
- Dannenbring, D.G. An evaluation of flow shop sequencing heuristics. Manag. Sci. 1977, 23, 1174–1182. [Google Scholar] [CrossRef]
- Ho, J.C.; Chang, Y.-L. A new heuristic for the n-job, m-machine flow-shop problem. Eur. J. Oper. Res. 1991, 52, 194–202. [Google Scholar] [CrossRef]
- Koulamas, C. A new constructive heuristic for the flowshop scheduling problem. Eur. J. Oper. Res. 1998, 105, 66–71. [Google Scholar] [CrossRef]
- Suliman, S. A two-phase heuristic approach to the permutation flow-shop scheduling problem. Int. J. Prod. Econ. 2000, 64, 143–152. [Google Scholar] [CrossRef]
- Pour, H.D. A new heuristic for the n-job, m-machine flow-shop problem. Prod. Plan. Control 2001, 12, 648–653. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Ma, Z. A hybrid local search algorithm for the sequence dependent setup times flowshop scheduling problem with makespan criterion. Sustainability 2017, 9, 2318. [Google Scholar] [CrossRef]
- Yang, D.L.; Kuo, W.H. Minimizing Makespan in A Two-Machine Flowshop Problem with Processing Time Linearly Dependent on Job Waiting Time. Sustainability 2019, 11, 6885. [Google Scholar] [CrossRef]
- Fuchigami, H.Y.; Sarker, R.; Rangel, S. Near-optimal heuristics for just-in-time jobs maximization in flowshop scheduling. Algorithms 2018, 11, 43. [Google Scholar] [CrossRef]
- Huang, K.W.; Girsang, A.S.; Wu, Z.X.; Chuang, Y.W. A Hybrid Crow Search Algorithm for Solving Permutation Flow Shop Scheduling Problems. Appl. Sci. 2019, 9, 1353. [Google Scholar] [CrossRef]
- Bewoor, L.A.; Chandra Prakash, V.; Sapkal, S.U. Evolutionary hybrid particle swarm optimization algorithm for solving NP-hard no-wait flow shop scheduling problems. Algorithms 2017, 10, 121. [Google Scholar] [CrossRef]
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Stützle, T. Applying Iterated Local Search to the Permutation Flow Shop Problem; Technical Report 1998; AIDA-98-04; FG Intellektik, TU Darmstadt: Darmstadt, Germany, 1998. [Google Scholar]
- Zobolas, G.I.; Tarantilis, C.D.; Ioannou, G. Minimizing makespan in permutation flow shop scheduling problems using a hybrid metaheuristic algorithm. Comput. Oper. Res. 2009, 36, 1249–1267. [Google Scholar] [CrossRef]
- Dong, X.; Huang, H.; Chen, P. An improved NEH-based heuristic for the permutation flowshop problem. Comput. Oper. Res. 2008, 35, 3962–3968. [Google Scholar] [CrossRef]
- Ruiz, R.; Stützle, T. A simple and effective iterated greedy algorithm for the permutation flowshop scheduling problem. Eur. J. Oper. Res. 2007, 177, 2033–2049. [Google Scholar] [CrossRef]
- Bansal, J.C.; Deep, K. A modified binary particle swarm optimization for knapsack problems. Appl. Math. Comput. 2012, 218, 11042–11061. [Google Scholar] [CrossRef]
- Li, Y.; He, Y.; Li, H.; Guo, X.; Li, Z. A Binary Particle Swarm Optimization for Solving the Bounded Knapsack Problem. In International Symposium on Intelligence Computation and Applications; Springer: Singapore, October 2018; pp. 50–60. [Google Scholar] [CrossRef]
- Sauvey, C.; Trabelsi, W.; Sauer, N. Mathematical Model and Evaluation Function for Conflict-Free Warranted Makespan Minimization of Mixed Blocking Constraint Job-Shop Problems. Mathematics 2020, 8, 121. [Google Scholar] [CrossRef]
- Maassen, K.; Hipp, A.; Perez-Gonzalez, P. Constructive heuristics for the minimization of core waiting time in permutation flow shop problems. In Proceedings of the International Conference on Industrial Engineering and Systems Management (IESM), Shanghai, China, 25–27 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Fernandez-Viagas, V.; Framinan, J.M. NEH-based heuristics for the permutation flowshop scheduling problem to minimise total tardiness. Comput. Oper. Res. 2015, 60, 27–36. [Google Scholar] [CrossRef]
- Pan, Q.K.; Gao, L.; Wang, L.; Liang, J.; Li, X.Y. Effective heuristics and metaheuristics to minimize total flowtime for the distributed permutation flowshop problem. Expert Syst. Appl. 2019, 124, 309–324. [Google Scholar] [CrossRef]
- Gao, J.; Chen, R. An NEH-based heuristic algorithm for distributed permutation flowshop scheduling problems. Sci. Res. Essays 2011, 6, 3094–3100. [Google Scholar] [CrossRef]
- Liu, W.; Jin, Y.; Price, M. A new improved NEH heuristic for permutation flowshop scheduling problems. Int. J. Prod. Econ. 2017, 193, 21–30. [Google Scholar] [CrossRef]
- Kalczynski, P.J.; Kamburowski, J. An improved NEH heuristic to minimize makespan in permutation flow shops. Comput. Oper. Res. 2008, 35, 3001–3008. [Google Scholar] [CrossRef]
- Kalczynski, P.J.; Kamburowski, J. An empirical analysis of the optimality rate of flow shop heuristics. Eur. J. Oper. Res. 2009, 198, 93–101. [Google Scholar] [CrossRef]
- Fernandez-Viagas, V.; Framinan, J.M. On insertion tie-breaking rules in heuristics for the permutation flowshop scheduling problem. Comput. Oper. Res. 2014, 45, 60–67. [Google Scholar] [CrossRef]
- Fernandez-Viagas, V.; Ruiz, R.; Framinan, J.M. A new vision of approximate methods for the permutation flowshop to minimise makespan: State-of-the-art and computational evaluation. Eur. J. Oper. Res. 2017, 257, 707–721. [Google Scholar] [CrossRef]
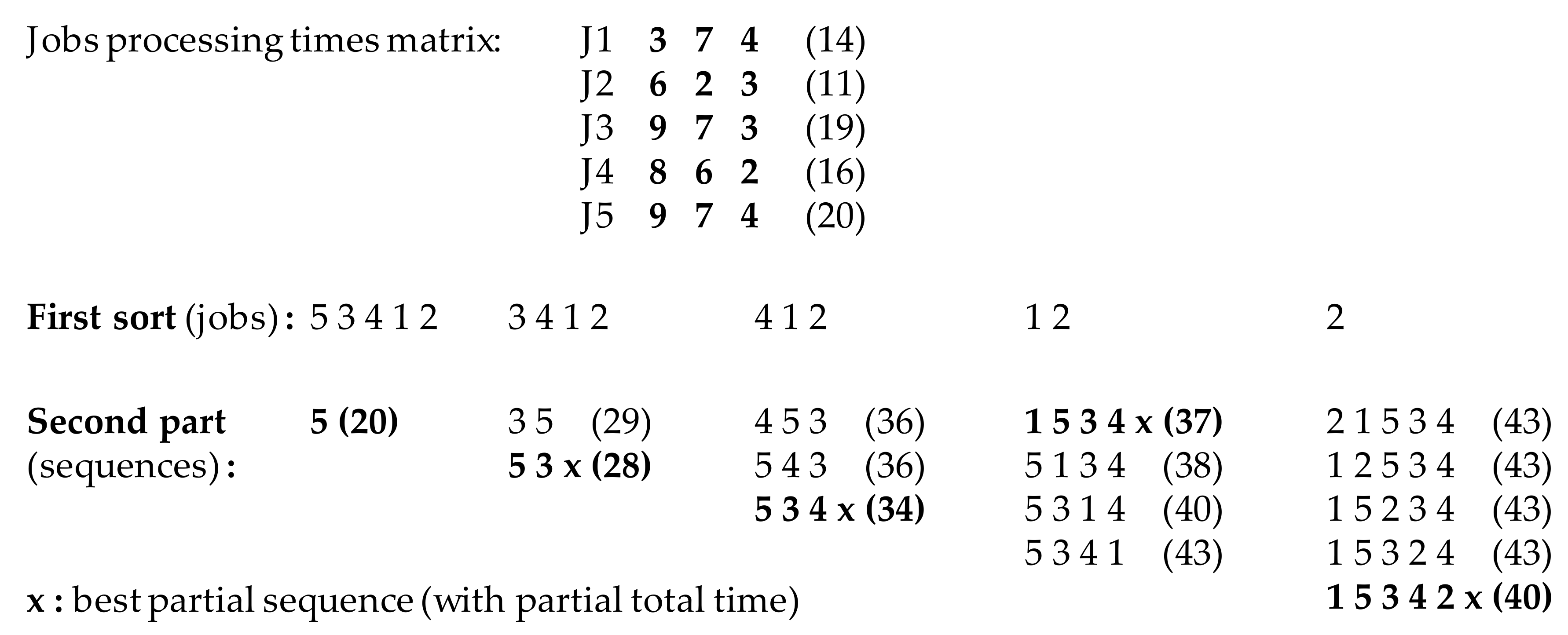
| Number | 3! | 2! | 1! | Permutation | Number | 3! | 2! | 1! | Permutation |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | abcd | 12 | 2 | 0 | 0 | cabd |
| 1 | 0 | 0 | 1 | abdc | 13 | 2 | 0 | 1 | cadb |
| 2 | 0 | 1 | 0 | acbd | 14 | 2 | 1 | 0 | cbad |
| 3 | 0 | 1 | 1 | acdb | 15 | 2 | 1 | 1 | cbda |
| 4 | 0 | 2 | 0 | adbc | 16 | 2 | 2 | 0 | cdab |
| 5 | 0 | 2 | 1 | adcb | 17 | 2 | 2 | 1 | cdba |
| 6 | 1 | 0 | 0 | bacd | 18 | 3 | 0 | 0 | dabc |
| 7 | 1 | 0 | 1 | badc | 19 | 3 | 0 | 1 | dacb |
| 8 | 1 | 1 | 0 | bcad | 20 | 3 | 1 | 0 | dbac |
| 9 | 1 | 1 | 1 | bcda | 21 | 3 | 1 | 1 | dbca |
| 10 | 1 | 2 | 0 | bdac | 22 | 3 | 2 | 0 | dcab |
| 11 | 1 | 2 | 1 | bdca | 23 | 3 | 2 | 1 | dcba |
| J/M | Ta_ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 20/5 | 00x | 1 | 8 | 2 | 2 | 1 | 1 | 2 | 4 | 1 | 1 |
| 20/10 | 01x | 1 | 4 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 6 |
| 20/20 | 02x | 1 | 1 | 2 | 1 | 1 | 1 | 2 | 1 | 4 | 2 |
| 50/5 | 03x | 16 | 16 | 16 | 384 | 16 | 96 | 2304 | 64 | 64 | 64 |
| 50/10 | 04x | 16 | 4 | 32 | 4 | 16 | 4 | 48 | 4 | 16 | 8 |
| 50/20 | 05x | 8 | 1 | 8 | 16 | 4 | 4 | 2 | 64 | 1 | 2 |
| 100/5 | 06x | 1.2 × 1010 | 8.8 × 105 | 2.8 × 107 | 147,456 | 524,288 | 4.7 × 106 | 3.4 × 108 | 512 | 73,728 | 73,728 |
| 100/10 | 07x | 16,384 | 55,296 | 384 | 9216 | 24,576 | 55,296 | 9216 | 4096 | 18,432 | 7.1 × 106 |
| 100/20 | 08x | 2048 | 16 | 512 | 12,288 | 1024 | 512 | 48 | 3072 | 192 | 32 |
| 200/10 | 09x | 4.3 × 1016 | 6.5 × 1016 | 8.9 × 1013 | 1.8 × 1016 | 2.0 × 1014 | 2.2 × 1016 | 2.2 × 1013 | 2.3 × 1018 | 9.6 × 1016 | 7.2 × 1015 |
| 200/20 | 10x | 4.0 × 1015 | 3.5 × 1011 | 2.4 × 1015 | 5.2 × 1011 | 2.2 × 1016 | 5.2 × 1011 | 2.5 × 1013 | 5.8 × 1010 | 3.6 × 109 | 5.7 × 1012 |
| 500/20 | 11x | 1.0 × 1072 | 6.0 × 1068 | 4.3 × 1076 | 6.1 × 1072 | 2.9 × 1065 | 1.2.1073 | 1.7 × 1069 | 2.8 × 1069 | 1.9 × 1070 | 1.2 × 1070 |
| J/M | Benchmark | NEH | NEH-SS1 | Improvement | ||
|---|---|---|---|---|---|---|
| (%) | (s) | (%) | (s) | (%) | ||
| 20/5 | Ta001-Ta010 | 3.11 | 0.0 | 3.02 | 0.0 | 2.9 |
| 20/10 | Ta011-Ta020 | 4.50 | 0.0 | 4.50 | 0.0 | 0.0 |
| 20/20 | Ta021-Ta030 | 3.76 | 0.0 | 3.76 | 0.0 | 0.0 |
| 50/5 | Ta031-Ta040 | 0.52 | 0.0 | 0.27 | 28.6 (*) | 48.1 (*) |
| 50/10 | Ta041-Ta050 | 3.66 | 0.0 | 2.91 | 1.3 | 20.5 |
| 50/20 | Ta051-Ta060 | 6.39 | 0.0 | 5.94 | 1.5 | 7.0 |
| 100/5 | Ta061-Ta070 | 0.44 | 0.0 | 0.32 | 2.0 | 27.3 |
| 100/10 | Ta071-Ta080 | 2.00 | 0.0 | 1.81 | 2.6 | 9.5 |
| 100/20 | Ta081-Ta090 | 5.27 | 1.0 | 4.95 | 4.3 | 6.1 |
| 200/10 | Ta091-Ta100 | 1.14 | 7.0 | 0.99 | 25.9 | 13.2 |
| 200/20 | Ta101-Ta110 | 3.46 | 10.1 | 3.26 | 39.1 | 5.8 |
| 500/20 | Ta111-Ta120 | 1.65 | 157.4 | 1.48 | 429.0 | 10.3 |
| Average | 2.99 | 2.77 | 7.4 | |||
| NEH | NEH-SS1 | NEH-SS2 (2) | NEH-SS2 (3) | NEH-SS2 (5) | Improvement | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| J/M | (%) | (s) | (%) | (s) | (%) | (s) | (%) | (s) | (%) | (s) | (%) |
| 20/5 | 3.11 | 0.0 | 3.02 | 0.0 | 2.58 | 0 | 2.58 | 0 | 2.40 | 0 | 22.8 |
| 20/10 | 4.50 | 0.0 | 4.50 | 0.0 | 3.61 | 0 | 3.61 | 0 | 3.61 | 0 | 19.8 |
| 20/20 | 3.76 | 0.0 | 3.76 | 0.0 | 3.14 | 0 | 3.14 | 0 | 3.14 | 0 | 16.5 |
| 50/5 | 0.52 | 0.0 | 0.27 | 28.6 (*) | 0.27 | 124 | 0.27 | 128 | 0.26 | 196 | 50.0 |
| 50/10 | 3.66 | 0.0 | 2.91 | 1.3 | 2.53 | 6.5 | 2.53 | 6.7 | 2.60 | 9.1 | 30.9 |
| 50/20 | 6.39 | 0.0 | 5.94 | 1.5 | 5.78 | 5.6 | 5.78 | 5.9 | 5.73 | 6.3 | 10.3 |
| 100/5 | 0.44 | 0.0 | 0.32 | 2.0 | 0.27 | 12.6 | 0.27 | 12.9 | 0.29 | 22.1 | 38.6 |
| 100/10 | 2.00 | 0.0 | 1.81 | 2.6 | 1.42 | 13.1 | 1.43 | 14.1 | 1.49 | 21.1 | 29.0 |
| 100/20 | 5.27 | 1.0 | 4.95 | 4.3 | 4.61 | 15.9 | 4.47 | 17.4 | 4.63 | 19.3 | 15.2 |
| 200/10 | 1.14 | 7.0 | 0.99 | 25.9 | 0.90 | 186 | 0.87 | 191 | 0.96 | 215 | 23.7 |
| 200/20 | 3.46 | 10.1 | 3.26 | 39.1 | 2.80 | 203 | 2.83 | 201 | 2.94 | 223 | 19.1 |
| 500/20 | 1.65 | 157 | 1.48 | 429 | 1.31 | 2140 | 1.33 | 2440 | 1.40 | 3053 | 20.6 |
| Avg. | 2.99 | 2.77 | 2.43 | 2.42 | 2.46 | 24.7 | |||||
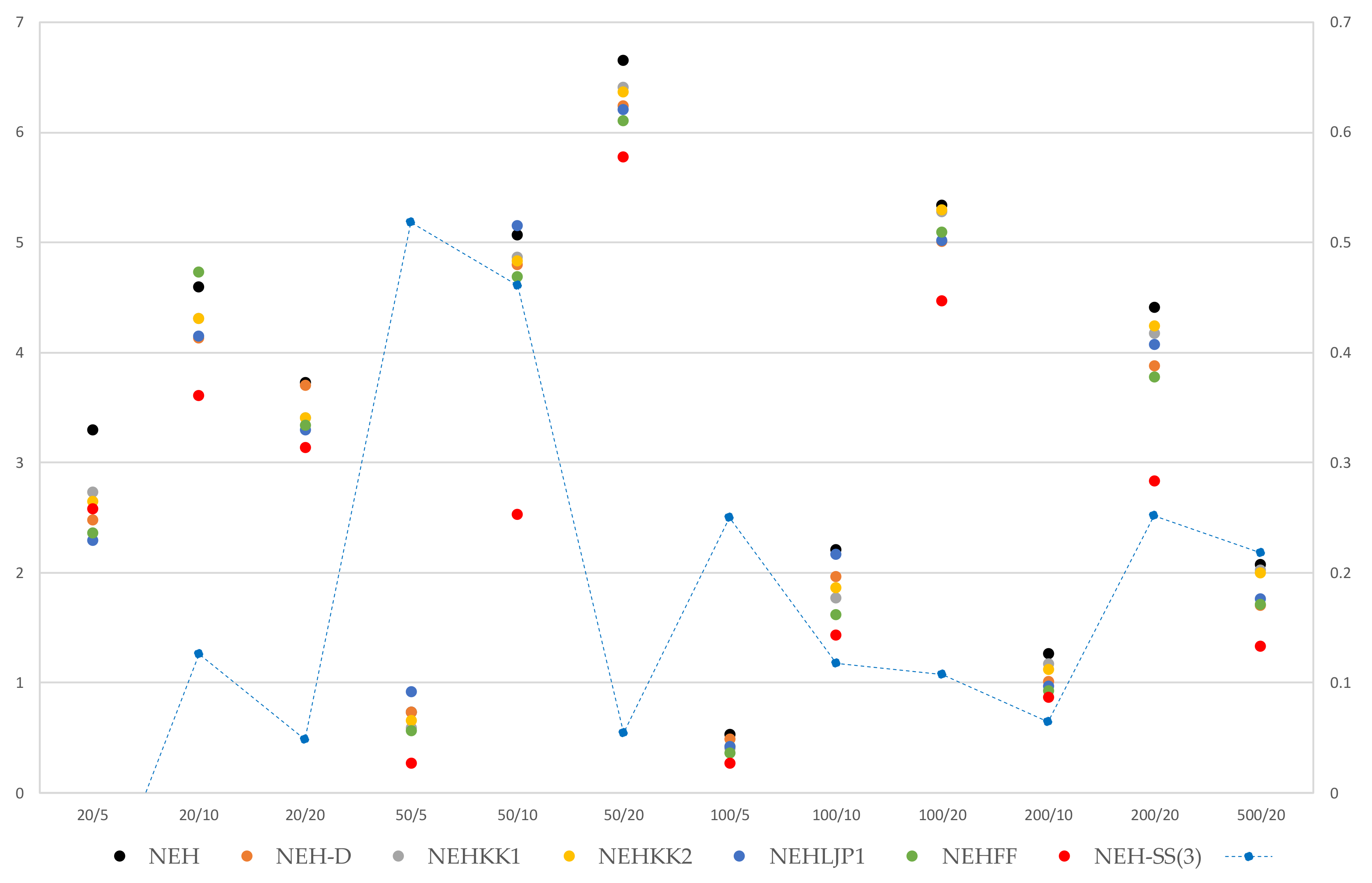
| J/M | NEH | NEH-D | NEHKK1 | NEHKK2 | NEHLJP1 | NEHFF | NEH-SS2 (3) |
|---|---|---|---|---|---|---|---|
| 20/5 | 3.30 | 2.48 | 2.73 | 2.65 | 2.29 | 2.36 | 2.58 |
| 20/10 | 4.60 | 4.13 | 4.31 | 4.31 | 4.15 | 4.73 | 3.61 |
| 20/20 | 3.73 | 3.70 | 3.41 | 3.41 | 3.30 | 3.34 | 3.14 |
| 50/5 | 0.73 | 0.73 | 0.59 | 0.66 | 0.92 | 0.56 | 0.27 |
| 50/10 | 5.07 | 4.80 | 4.87 | 4.83 | 5.15 | 4.69 | 2.53 |
| 50/20 | 6.65 | 6.24 | 6.41 | 6.37 | 6.21 | 6.11 | 5.78 |
| 100/5 | 0.53 | 0.49 | 0.40 | 0.42 | 0.42 | 0.36 | 0.27 |
| 100/10 | 2.21 | 1.96 | 1.77 | 1.86 | 2.17 | 1.62 | 1.43 |
| 100/20 | 5.34 | 5.01 | 5.28 | 5.30 | 5.02 | 5.09 | 4.47 |
| 200/10 | 1.26 | 1.01 | 1.17 | 1.12 | 0.97 | 0.93 | 0.87 |
| 200/20 | 4.41 | 3.88 | 4.17 | 4.24 | 4.07 | 3.78 | 2.83 |
| 500/20 | 2.07 | 1.70 | 2.02 | 2.00 | 1.76 | 1.71 | 1.33 |
| Avg. | 3.32 | 3.01 | 3.09 | 3.10 | 3.04 | 2.94 | 2.42 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sauvey, C.; Sauer, N. Two NEH Heuristic Improvements for Flowshop Scheduling Problem with Makespan Criterion. Algorithms 2020, 13, 112. https://doi.org/10.3390/a13050112
Sauvey C, Sauer N. Two NEH Heuristic Improvements for Flowshop Scheduling Problem with Makespan Criterion. Algorithms. 2020; 13(5):112. https://doi.org/10.3390/a13050112
Chicago/Turabian StyleSauvey, Christophe, and Nathalie Sauer. 2020. "Two NEH Heuristic Improvements for Flowshop Scheduling Problem with Makespan Criterion" Algorithms 13, no. 5: 112. https://doi.org/10.3390/a13050112
APA StyleSauvey, C., & Sauer, N. (2020). Two NEH Heuristic Improvements for Flowshop Scheduling Problem with Makespan Criterion. Algorithms, 13(5), 112. https://doi.org/10.3390/a13050112




