Abstract
Since its creation by Nawaz, Enscore, and Ham in 1983, NEH remains the best heuristic method to solve flowshop scheduling problems. In the large body of literature dealing with the application of this heuristic, it can be clearly noted that results differ from one paper to another. In this paper, two methods are proposed to improve the original NEH, based on the two points in the method where choices must be made, in case of equivalence between two job orders or partial sequences. When an equality occurs in a sorting method, two results are equivalent, but can lead to different final results. In order to propose the first improvement to NEH, the factorial basis decomposition method is introduced, which makes a number computationally correspond to a permutation. This method is very helpful for the first improvement, and allows testing of all the sequencing possibilities for problems counting up to 50 jobs. The second improvement is located where NEH keeps the best partial sequence. Similarly, a list of equivalent partial sequences is kept, rather than only one, to provide the global method a chance of better performance. The results obtained with the successive use of the two methods of improvement present an average improvement of 19% over the already effective results of the original NEH method.
1. Introduction
“Classical flowshop problems have been so widely treated in scheduling literature that nothing new can appear. Everything has been done on the subject”. If you think so, do not waste your time reading this paper. Indeed, this provocative statement is mostly true. The permutation flowshop sequencing problem (PFSP) is part of one of the best-known production scheduling problems, and has been tackled for decades by researchers. Since Johnson’s work and famous rule [1], a large number of problems have interested academic researchers globally. This class of problems, in which jobs are processed by a series of machines in exactly the same order, is one of the most widely studied scheduling problems. A large number of heuristics, methods, and meta-heuristics have been proposed and validated for this kind of problem. Currently, this well-known scheduling problem is used as a basis on which a large number of constraints are imposed to best correspond with industrial requirements. Nawaz, Enscore, and Ham (NEH) proposed their famous method in 1983 [2]. In the intervening 40 years, a better method has yet to be proposed. An interesting review paper compares 25 of the most famous methods to solve this problem [3].
Among these methods, some of the most famous heuristic methods that have been proposed to solve the flowshop scheduling problem can be cited. Palmer proposed the assignation of a slope index to each job and scheduling by sorting jobs according to the assigned slope indexes [4]. Hundal and Rajgopal analyzed and extended this method in 1988, calculating two supplementary slope indexes [5]. In 1970, Campbell, Dudek, and Smith developed a heuristic algorithm hat is basically an extension of Johnson’s algorithm. This heuristic, known as CDS, builds m-1 schedules by clustering the m original machines into two virtual machines and solves the m-1 generated two-machine problem by repeatedly using Johnson’s rule [6]. Dannenbring’s rapid access heuristic is a mix of Johnson’s algorithm and Palmer’s slope index: a virtual two-machine problem is defined as it is in the CDS heuristic, but Johnson’s algorithm is applied only after a weighting scheme is applied to each machine [7]. In 1983, Nawaz, Enscore, and Ham developed the NEH heuristic, which is still considered the best for the permutation flowshop scheduling problem [2]. It is based on the idea that jobs with high processing times on all machines should be scheduled as early in the sequence as possible. This heuristic is the subject of this paper. In 1991, Ho and Chang proposed a method based on the minimization of elapsed time between the end of the execution time of a job on a machine and the beginning of this job on the following machine in routing [8]. In 1998, Koulamas proposed a two-phase heuristic called HFC [9]. In the first phase, the HFC heuristic makes extensive use of Johnson’s algorithm. The second phase improves the resulting schedule from the first phase by allowing jobs to pass between machines, thus allowing non-permutation schedules. In 2000, Suliman developed a two-phase improvement heuristic. The first phase generates a schedule with the CDS heuristic. In the second phase, this schedule is improved with a pair exchanging mechanism [10]. In 2001, Pour proposed an insertion method similar to that used in the NEH method, which was revealed to be effective for problems with a high number of machines [11].
However, even if the literature seems to confirm it is true, this provocative statement is also false, and this is the subject of this paper. This paper addresses this problem precisely because it is so famous. Many researchers have worked on the problem and continue to do so currently [12,13,14,15]. This problem provides a good laboratory to test new methods in discrete optimization. This method was chosen because it is known to be the best for solving this problem. Continuing research about the permutation flowshop problem is worthy, because new heuristics can always be imagined, as well as new improvement methods for heuristics or meta-heuristics. Moreover, ongoing improvement of heuristic methods for basic problems may have better results than for more complicated ones. This is never a waste of time.
“Nothing new to learn from a 40-year-old method.” This second provocative statement is also mostly true. Indeed, this method is sufficiently famous and, moreover, easy to program, that a large number of researchers have taken this method as a base of comparison to their own approaches [14,16]. This is the first point of reflection: Why do all papers presenting the results of the same heuristic, based on the same benchmarks [17], not give the same results? General performances are similar, but precise results are different; for illustration, see refs. [18,19,20,21]. Sorting jobs in decreasing order of their total completion time is not particularly complicated, but this paper shows how it can lead to very different results. In addition, maintaining the best partial sequence is easy. However, what do we do in case of equality? We choose. In such a case, what is the reason for choosing one partial sequence instead of another? These remain open questions, even for the NEH heuristic.
It is worth trying to improve NEH, because: (i) it is the best heuristic method for permutation flowshop scheduling developed since 1983, thus, improving this method is the first step to obtaining better results; (ii) all problems derived from flowshop-type modelling would yield improved heuristic performances; and (iii) heuristics are necessary to tackle such problems because they are usually quicker than meta-heuristics. However, meta-heuristics correctly perform at continuous and binary problem resolutions. For scheduling problems, particle swarm optimization (PSO) algorithms [22,23], as well as genetic algorithms [24], continue to show good results. NEH is also useful for solving flowshop scheduling problems with objective functions different from the makespan, such as minimizing the core waiting time [25], total tardiness [26], total flowtime [27], or makespan [28] for the distributed permutation flowshop problem.
A large amount of research continues to be undertaken on the improvement of the NEH method. Dong et al. investigated the field of the NEH heuristic improvement and proposed a method based on the first two statistical moments of the vector of job processing times (the average and the standard deviation), and their results showed significant improvement [12]. Based on this work, Liu et al. investigated the third and fourth statistical moments, respectively the skewness and the kurtosis, and showed both the effectiveness of the priority rule based on skewness and the inefficiency of that based on the kurtosis [29]. Kalczynski and Kamburowski also proposed improvements to the NEH method [30,31], in addition to Fernandez-Viagas and Framinan [32]. They also proposed new unified notation for NEH modifications and improvements formed by three fields. This notation is NEH (a|b|c), where a represents the initial order used by the NEH, b represents the tie-breaking rules used in the second point choice, and c is associated with the reversibility property of the problem [33]. Using this unified notation, this paper proposes the first NEH (All|n|d) method.
In this paper, the NEH algorithm is analyzed to propose an improvement, but our proposal is oriented on the two points where the original method leads to a possible choice in the case of an equality. The first point deals with the total operating times of the process and yields the order in which jobs will be considered in the algorithm. The second point concerns partial sequences of each algorithm iteration. This paper proposes a new way of significantly improving the algorithm performance.
This paper is organized as follows. In Section 2, the flowshop scheduling problem is described, and the NEH heuristic analyzed. In Section 3, the factorial basis decomposition is defined and explained. Its use is proposed to develop the first improvement method, based on the first point related to NEH, and the corresponding results are given. In Section 4, the second improvement method, based on the second point related to the NEH method is described and its results are given, in conjunction with those obtained when both improvement methods are applied together. Section 5 concludes this paper, and perspectives are given for this research work.
2. Problem Description
2.1. Flowshop Scheduling Problem
A flowshop scheduling problem is considered where n jobs, each composed of m operations, must be processed non-preemptively on m machines. All jobs need to be processed in the same order on all machines (i.e., routing does not differ from one job to another). Intermediate buffer space is of infinite capacity, and a machine can only execute one job at a time. The objective function consists of minimizing total completion time, also called makespan. The challenge is to find a schedule (a throughput order of jobs in the constant suite of machines). Figure 1 presents an example of a flowshop problem with three jobs and four machines. This schedule should be accurate (as close as possible to the optimal makespan) and quickly obtainable. The two basic formulae allowing the scheduling of the jobs are the following:
where Si,j: is the starting time of the ith operation of the jth job in the sequence; Ci,j: is the completion time of the ith operation of the jth job in the sequence; Pi,j: is the processing time of the ith operation of the jth job in the sequence.
Ci,j = Si,j + Pi,j , for all i and j
Si,j = max( Ci-1,j ; Ci,j-1 ) , for all i and j
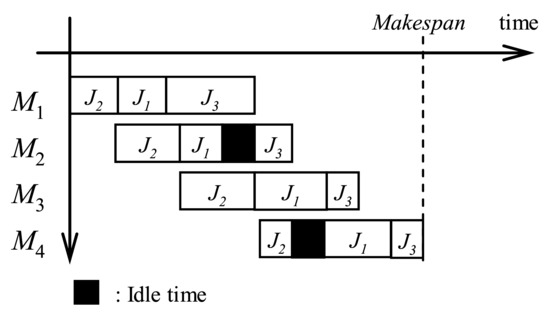
Figure 1.
Flowshop problem with three jobs and four machines.
This problem has been widely studied over the past 70 years. Benchmarks exist and Taillard’s benchmark is widely used to test heuristics and meta heuristics [17].
For large problems, good heuristics offer significant advantages as they generally yield good solutions in an acceptable time. Moreover, in some cases, sufficiently good heuristics are more accurate than meta heuristics. This is true of NEH compared to some genetic algorithms [3].
The NEH heuristic is one of the most famous heuristics known for flowshop scheduling [2]. This heuristic is not only efficient, it is also simple to compute, and thus widely used. A large number of studies have used this heuristic as a reference against which to compare their results [19,21]. A pedagogical comparative study of some heuristics is performed in ref. [2], where interested readers can also find a metaheuristic comparison that provides a good overview of the current status of international research into flowshop scheduling problem solving. In this paper, the graphics presented by the authors also prove that the NEH heuristic is more accurate than some meta heuristic algorithms.
2.2. NEH Heuristic Analysis
The pseudo-code of the NEH method is recalled in Algorithm 1, highlighting the first sort and the second point where a choice is required to be made. Consequently, the improvement ideas proposed in this paper will be better illustrated. Figure 2 gives an example of the application of the original NEH heuristic using a five jobs/three machines example. It presents, step by step, how the first sort is used in the heuristic and how the second part of the heuristic inserts jobs in successive partial sequences.
| Algorithm 1: (NEH heuristic) |
| Rank jobs in decreasing order of total processing time // (First point sort) Remove first job of ranked list and insert it as first element of current partial sequence k = 1 Do { Take the first job of ranked list Insert it in all of k+1 possible places of current partial sequence Evaluate all of k+1 resulting partial sequences Keep the best sequence as new current partial sequence // (Second point choice) k = k+1 } While (k ≤ number of jobs to schedule) |
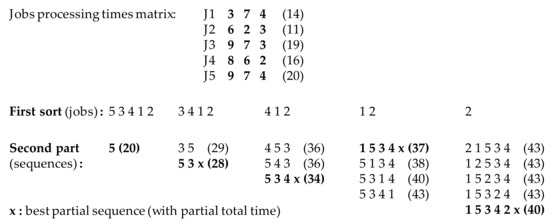
Figure 2.
Illustration of the two points of choice in the Nawaz, Enscore, and Ham (NEH) heuristic in a five jobs, three machines problem.
The two points of choice in the NEH heuristic have been clearly highlighted within Algorithm 1 and Figure 2. At the first point, jobs are ranked in decreasing order of processing time, and at the second point, only the best sequences are kept depending on their partial makespan. For the first point, a sorting routine is necessary. Then, depending on which sorting routine is used, the results of the NEH heuristic can differ. For the second point, a choice may have to be made between two equivalent partial schedules; again, the choices can lead to different results. Indeed, they do differ. This difference explains why a large number of studies, in which NEH heuristic results are presented with the well-known Taillard flowshop benchmarks, are different [18,19,20,21]. This is also why observing the different possible orders of Taillard’s benchmarks is of interest. The two improvement methods proposed in this paper are direct consequences of this observation. The first improvement consists of testing the equivalent possibilities in the first sort, and the second consists of testing some equivalent possibilities for the second choice.
3. First Improvement Method, NEH-SS1
In this section, first, the factorial basis decomposition method to match a number to a particular combination of permutations is presented. Then, this is used to make the improvement proposed in this section, based on the first sort of the NEH method. A discussion of the results obtained with this improvement method concludes this section.
3.1. Factorial Basis Decomposition
Computationally, to accurately perform the method once, and only once, on all possible equivalent job orders, it is necessary to initially count how many orders have to be tried, and, subsequently, to identify a means of testing each equivalent sequence one by one. Counting equivalent job orders after the first sort consists of multiplying together the number of equal successive total operating times.
To find a way to computationally describe all the possible different orders of the first job sort to perform the second loop of the NEH routine, the method, named factorial basis decomposition, described below is proposed. To clearly and pedagogically explain this method with an example, the problem Ta036 is chosen.
In the Ta036 problem, two jobs (J13 and J17) present a total operating time of 377 time units (tu), three others (J6, J10, and J14) a total operating time of 308 tu, two others (J39 and J42) 272 tu, two others (J12 and J29) 205 tu, and the final two (J40 and J41) 193 tu. Each of the 39 other jobs of this problem present different total operating times. Considering this, it is easy to find the value given in Table 2 regarding Problem Ta036: 2! × 3! × 2! × 2! × 2! = 96. In the second loop of the NEH heuristic, the 96 equivalent orders resulting from the first jobs sort need to be tested. Then, in order to describe each of these 96 possible orders, it is possible to count from 0 to 95, and to match each of these numbers with a particular permutation. Factorial basis decomposition is the means to match a number and with its permutation. For this example, let us take the raw job orders as given after the first sort, only taking into account the five sets giving way to equalities in terms of total operating times. Firstly, the groups of jobs are memorized in order to remember the original sort result. In this example, in the interests of clarity the jobs have been ranked, in each set, by the increasing value of job number: (J7 – J13) – (J6 – J10 – J14) – (J39 – J42) – (J12 – J29) – (J40 – J41).
Then, to make a correspondence between a number n (i.e., between 0 and 95) correspond to a permutation, the following steps are followed. First, the number of jobs equalities are ranked in increasing order. Indeed, the triple of jobs (J6–J10–J14) is situated in second position in the sort, but will be considered in the last position in the factorial basis decomposition, and (2 3 2 2 2) becomes (2 2 2 2 3).
Then, for each number n between 0 and 95, its factorial basis decomposition is calculated, in the same way as to convert a number to base-2, for example, but here the base is given by the factorials of the numbers between parenthesis, in increasing order, such as (2 2 2 2 3). For n = 75 for instance, the calculus is as follows:
75 = 2! (37) +1 = 2!.(2! 18 + 1) + 1 = 2!.( 2!.( 2! 9 + 0) + 1) + 1 = 2!.( 2!.( 2!.( 2! 4 + 1) + 0) + 1) + 1
75 = 2!.( 2!.( 2!.( 2!.(3! 0 + 4) + 1) + 0) + 1) + 1
75 = 2!.( 2!.( 2!.( 2!.(3! 0 + 4) + 1) + 0) + 1) + 1
As can be seen in this example, the successive rests of the successive Euclidian divisions of the initial number by the successive factorials in increasing order are calculated. Consequentially, five rests are obtained, which correspond to a unique permutation directly linked to the given number. Here, the rests corresponding to the factorials (2 2 2 2 3) are (1 1 0 1 4). This decomposition insures that all convenient permutations will be tested.
For several jobs, when the encountered rest is 1, a permutation in the job concerned is performed and, when it is 0, the first order remains unchanged. For a triple of jobs, the rest of the Euclidian division by 3! is an integer between 0 and 5. When it is 0, the first order remains unchanged. For example, an original triple abc remains in the order abc. When the rest is 1, it becomes acb. When the rest is 2, it becomes bac. When the rest is 3, it becomes bca. When the rest is 4, it becomes cab, and when the rest is 5, it becomes cba. When the number of jobs j concerned with permutations is greater than or equal to 3, it proceeds in the same way because the rest of the division is between 0 and (j! − 1) and yields exactly j! possibilities to arrange j jobs. In order to perfectly understand how it is possible to describe all the possible permutations for a number of jobs greater than or equal to 4, the complete matching table between the numbers and the 24 permutations of a set of 4 elements are presented in the Table 1. To build the permutation corresponding to a given number, it is decomposed on the basis of all precedent factorials. For example, the equality 14 = 2 × 3! + 1 × 2! + 0 × 1! links the value 14 to the permutation cbad. Indeed, to recompose the corresponding permutation, the four values from the order (abcd) are taken, and are counted from 0 to 3 for the first set (of four values), from 0 to 2 for the second set (of three values), and from 0 to 1 for the third set (of two values). Then, the element corresponding to the value 2 is extracted first (i.e., c). Then, the element corresponding to the value 1 in the remaining sequence set (b), is extracted. Then, the element corresponding to the value 0 in the remaining sequence (a), is extracted. At the end of extraction process, the last element (d) remains, which is put at the end of the permutation. It can be noticed that there is a complete bijection between a number j and its permutation, and it can also thus be easily understand how the remaining Euclidian division by j! is directly linked to a unique permutation inside a group of j jobs.

Table 1.
Illustration of the factorial basis decomposition of the 24 possible permutations of the group of four elements {a,b,c,d}.
To conclude this example, to finally see which permutation corresponds to the number n = 75, the values of the remaining Euclidian divisions are re-attributed to the correct groups of jobs. In this way, (1 1 0 1 4) becomes (1 4 1 0 1). It only remains to perform permutations for all groups of jobs as a function of their corresponding numbers. Then, the following permutation comes:
75 = 1 4 1 0 1
Permutation: (J13 – J7) – (J14 – J6 – J10) – (J42 – J39) – (J12 – J29) – (J41 – J40)
This way of describing all available equivalent possible jobs orders is not only useful for describing all possible orders (for numbers of jobs up to 50), but also for choosing a few orders from a large number (i.e., numbers of jobs higher than 100). It is sufficient to apply a random number to obtain a new jobs order to test.
3.2. Method Description
In the NEH heuristic method, the first ranking is performed with total job processing times. It is easy to detect when two consecutive ranked jobs have identical total processing times. Then, when total processing times are equal for at least two consecutive ranked jobs, no reason exists to treat the jobs in a particular order, because both are equivalent from the original NEH heuristic’s point of view. Nevertheless, when the classical NEH procedure is programmed, one order is preferred, which is the order resulting from the sorting method. This is the first source of difference between the results presented in different papers: different authors program their job sorting routines differently to perform their first loop in the NEH heuristic. In order not to be trapped by the chosen sorting method, each of the different job rankings were tested in comparison with the classically computed NEH heuristic (with first jobs ranking). Then, when the second loop in the algorithm starts with a different job order, it may find different solutions (Table 2).

Table 2.
Possible orders of Taillard’s benchmark after jobs ranking in the NEH heuristic.
3.3. Results and Discussion
The results obtained with this new improvement method (NEH-SS1) are presented in Table 3. For SS1, all possible configurations numbered in Table 2 for the problems of 20 and 50 jobs were tested. For a higher number of jobs, it would be impossible to test all possibilities for each problem instance. This is why only some, randomly chosen thanks to factorial basis decomposition, are tested. In order to limit the execution time of this method, it was limited to three times the execution time of the classic NEH heuristic for problems with 100 and 200 jobs, and to two times this execution time for problems with 500 jobs. Computational experiments were performed using Dev-C++ 4.9.9.2 software with a laptop Acer TravelMate 6292 with a 2 GHz Core 2 Duo T7300 processor and 2 Gb DDR2 RAM. Results presented in Table 3 give the average relative percentage deviation (ARPD) over optimum, of classic NEH and NEH-SS1 heuristics. The average CPU times of heuristics, presented in seconds, are those measured on the computer noted above. The final column of Table 3 presents the improvement percentage obtained with the NEH-SS1 method with regard to NEH initial results, thanks to the following equation:
Improvement = (NEH − NEH-SS1)/(NEH)

Table 3.
NEH-SS1 improvement heuristic results (average relative percentage deviation (ARPD) in % and average CPU times in s).
Percentages calculated above the line in Table 3 were calculated with regard to optimal values, and those calculated below the line were calculated with regard to a lower bound. The sorting methods employed in the classic NEH and the new (NEH-SS1) methods are identical. This has little influence on the first sorting because in SS1 all possibilities are tested. However, it is important to note that the computation is equivalent in the second part of both of the NEH heuristic runs.
The number of different possible job orders after job ranking (first sort), for each of Taillard’s benchmark problems, are presented in Table 2. It can be noted that, from the Ta001 to Ta060 problems, it is conceivable to test all of the possible initial orders with a computer, because the maximal number of permutation cases to be treated is 2304 (for the Ta_037 problem) and remains less than 100 in the wide majority of cases. However, for the problems with 100 or more jobs, it is far more complicated to test all of the possible permutation cases. Such instances will thus remain an ongoing source of difference between authors. In the following paragraphs, all the possible equivalent orders for problems with 20 and 50 jobs have been treated, thanks to the factorial basis decomposition.
Improvement may or may not be significant in the function of how the first jobs ranking can be different. Impressive improvement is visible for problems with 50 jobs/5 machines due to the relatively higher number of job rankings tested (see Table 2). This comes at the cost of higher computing time. A total of 219 s were necessary to solve instance Ta037, and 36 s to solve Ta034, instead of between 1 and 9 s to solve the others.
It is difficult to conclude whether a high number of possibilities improves accuracy. Even if a good improvement for problems of 50 jobs/10 machines (20.5%) can be observed, relatively weak improvements for other problems with a number of jobs fewer than 50 can also be noted. If the causality link between Table 2 and the results obtained with the SS1 heuristic presented in Table 3 is difficult to establish, an outstanding improvement for large problem instances can be noted.
Testing all the possibilities indicates that they were reasonably effective. Thus, examination of this first improvement reaffirms that the NEH method is good and globally robust in terms of the first sort, at least in cases of up to 50 jobs.
Nevertheless, even when the improvement is slight, it is useful to be able to propose an improvement to an already efficient method. Indeed, Ruiz and Marotto presented NEH as the best existing heuristic for flowshop problems [3]. Thus, further improving the best existing heuristic is a desirable result. Average improvement of 7.4% is obtained with the NEH-SS1 heuristic. In the next section, another improvement is proposed, which further improves these good results.
4. Second Improvement Method NEH-SS2
In this section, the second proposed improvement is presented, based on the second choice performed in the original NEH method. First, the method is described and its pseudo-code is given. Then, the results obtained with this method are presented in conjunction with the first improvements already obtained with NEH-SS1.
4.1. Method Description
As presented in Algorithm 1, a second choice is performed at each loop of the NEH heuristic. Indeed, there is no ambiguity in terms of retaining the best sequence if there is only one best sequence. However, if more than one sequence can be “the” best sequence, it could be worth looking at each of them. The second choice improvement proposed in this paper is based on this idea. It consists of making a list of the best intermediary solutions, and treating equally all of the equivalent partial sequences of the second choice, when possible.
The algorithm is described below (Algorithm 2). For the purposes of illustration, only two lists of partial schedules, LPS1 and LPS2, are included. The list LPS2 is filled with the best partial schedules of the current iteration. If the number of equivalent partial schedules is greater than Size_LPS1, then a set of partial schedules is randomly extracted and copied to LPS1, in order to limit the number of tested combinations at each step of the algorithm process. Each of the selected partial lists is then treated in the next step of the algorithm. These two lists make it possible to cope with different ranges of problems, in terms of the number of jobs, number of machines, difficulty, and computation time. In order to adapt the heuristic to a problem with a high number of jobs, it is necessary to avoid increasing too widely the computing time. This is the reason why suitable values of Size_LPS1 have been investigated.
| Algorithm 2: (NEH-SS2 improvement heuristic) |
| Rank jobs in decreasing order of total processing time // (First point sort) Remove first job of ranked list and insert it as the first element of partial sequence k = 1 Give Size_LPS1 and Size_LPS2 Do { Take the first job of ranked list For (each partial sequence of LPS1) Evaluate all of k+1 possible partial schedule Keep the best partial sequence(s) in LPS2. // (Second point choice) // If there is only one best partial sequence, we save only one partial sequence. End For k = k+1 If (number of best partial sequences in LPS2 ≤ Size_LPS1) Copy LPS2 in LPS1 Else Choose Size_LPS1 sequences in LPS2 Copy them in LPS1 End If Empty LPS2 } While (k ≤ number of jobs to schedule) |
4.2. Results and Discussion
The algorithm NEH-SS2 was tested after the application of the first heuristic NEH-SS1. The NEH-SS2 heuristic was not tested in isolation because its results would have been exposed to the first bias treated with the NEH-SS1 heuristic. The results obtained with the values of Size_LPS1 equal to 2, 3, and 5 are presented in Table 4, under their respective NEH-SS2 (Size_LPS1) column, in terms of accuracy (in %) and computing time (in s). These results give both average relative percentage deviation (ARPD) over optimum and average CPU times, over the 10 problems per instance size of Taillard’s benchmarks [17]. The last column presents the improvement measured with the three proposed sizes of Size_LPS1, and is calculated with the following equation:
Improvement = [NEH – min(NEH-SS2(2); NEH-SS2(3); NEH-SS2(5))]/(NEH)

Table 4.
NEH-SS2 improvement heuristic results (ARPD in % and average CPU times in s).
The experiments confirmed that the heuristic time is globally dependent and increases quickly with Size_LPS1. On average, with Size_LPS1 = 10, two hours are necessary to solve one problem with 500 jobs and 20 machines. However, the computing time does not vary significantly for the values of Size_LPS1 reported. For higher values of Size_LPS1, combinatory explosion occurs and computing time becomes unreasonable. For heuristic methods designed to treat operational level problems, it would be harmful to improve already efficient methods in terms of accuracy by too widely increasing the computing time. If the computing time is relatively acceptable up to 200 jobs, it becomes unreasonable for instances of 500 jobs.
In terms of precision, NEH-SS2 further improved the results already obtained with NEH-SS1 with all the tested couples, for all the problem instances. This is already the case from Size_LPS1 = 2. For the problem instances with a high number of jobs, precision decreases when Size_LPS1 increases. On the contrary, for problem instances with a fewer number of jobs, variability of results as a function of Size_LPS1 is negligible. Indeed, for instances with a low numbers of jobs, values taken by Size_LPS1 are not limiting, and allow coverage of a significant portion of the total tree. This consideration becomes less true as the number of jobs increases. The order in which the jobs are considered in the NEH method seems to have greater influence on results as the number of jobs increases.
For the use of this method, it can be recommended to set the value Size_LPS1 = 3, with the tests realized, in order not to be too time consuming. This choice seems to be the best compromise between gain in precision and computing time. With this combination, on average the two methods improve the existing method by 19%, with a best average relative percentage deviation of 2.42%.
One weakness of this method is that it only partially takes into account the ranking bias; nonetheless, it is better than only taking one out of all possible sequences. Zobolas et al. proposed a greedy randomized heuristic based on the NEH heuristic, called GRNEH [19], which is similar to the work presented here, except that they randomly chose one partial sequence from a set of five in the second loop.
The results obtained with the proposed improvement methods, with NEH-SS2 (3), are compared in Table 5 with some recently developed state-of-the-art methods, such as NEH-D [20], NEHKK1 [30], NEHKK2 [31], NEHLJP1 [29], and NEHFF [32]. As can be seen in Table 5, all these methods improve NEH performance compared to Taillard’s benchmark. The new proposed NEH improvement method outperforms all existing methods with an ARPD value of 2.42, achieving the best performances for 11 of the 12 sizes of problems.

Table 5.
ARPD values of different improvement methods compared to Taillard’s benchmark.
Figure 3 graphically presents these results by benchmark problem size. It can be noted that this method significantly stands out from the already existing results for large problems, and particularly when the number of machines increases. The outstanding performance of this heuristic for the 50/10 problem size is due to the particularity of Ta_034 and Ta_037, dealt with in Table 2 and remarkably solved with the NEH-SS1 method. In addition, it can also be seen with the dotted line, for which the ordinate secondary scale is available on the right of the figure, that the performance of NEH-SS2(3) averages between 10% and 25% for large problem instances, thus confirming the interest in, and the efficiency of, the methods presented in this paper.
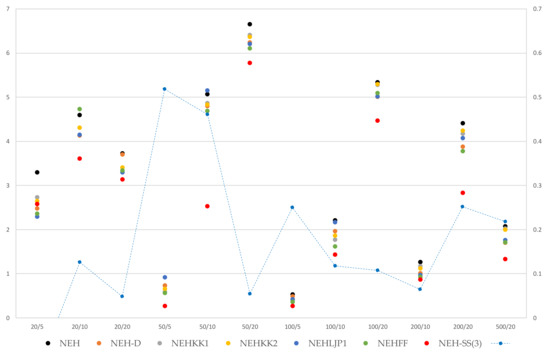
Figure 3.
ARPD (in %) of different improvement methods compared to Taillard’s benchmark problem sizes, and improvement percentage over the best of the other heuristics (in dotted line, secondary scale).
5. Conclusions
In this paper, an examination was made of the flowshop scheduling problem and its resolution with the NEH method, which is the best heuristic method, to date, for solving this kind of problem. Two improvements are proposed for this method, based on its two independent phases where a choice between two equivalent possibilities has to be made. The first phase occurs when the jobs are sorted in decreasing order of total operating time. The second occurs recurrently in the method process when, at each step, insertions of a new job in the current partial sequence leading to the best partial makespan are kept.
Equalities can occur during both procedures, and the improvement methods have been designed to be the least sensitive to the cases of equality. Factorial basis decomposition was introduced and developed in order to insure that all possible orders are tested for instances of small problems. For large problem instances, this factorial basis decomposition allows the random choice of particular orders from all of the possible options. NEH results were significantly improved with the research methods presented in this paper, which are easily implementable in already existing code. This improvement is one of the most significant enhancements to heuristic methods applied to flowshop scheduling since the work of Nawaz, Enscore, and Ham in 1983. Each of the two proposed methods significantly improves the quality of the solutions given by the original NEH algorithm. Moreover, the combination of the two improvement methods (NEH-SS) shows good efficiency and a global improvement of 19% compared to the classic NEH, as well as an average relative improvement compared to the best existing improvement methods of between 10% and 25% for large problem instances. Indeed, the improvement of NEH-SS1 method is further improved with the subsequent application of the NEH-SS2 method.
In future work, the efficiency of this method could be further improved, especially in terms of computation time for the second choice improvement method. In particular, it would be of interest to detect, among all possibilities of jobs orders, the job orders that were most likely to result in an improvement, in order to reduce the number of tests and time taken to identify the best solutions, especially for big problems. More generally, due to the effectiveness of heuristic methods, hybrids with more generic meta-heuristics are promising, and this research would be an interesting approach to further improve the performance of global algorithms.
Author Contributions
C.S. proposed the idea, designed and developed the programs as well as the computing tests. He prepared and wrote the original draft manuscript. N.S. acknowledged the ideas, supervised this work and the methodology, reviewed and edited the original draft manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Johnson, S.M. Optimal two- and three-stage production schedules with setup times included. Nav. Res. Logist. Q. 1954, 1, 61–68. [Google Scholar] [CrossRef]
- Nawaz, M.; Enscore, E.E.J.; Ham, I. A heuristic algorithm for the m-machine, n-job flowshop sequencing problem. OmegaInt. J. Manag. Sci. 1983, 11, 91–95. [Google Scholar] [CrossRef]
- Ruiz, R.; Marotto, C. A comprehensive review and evaluation of permutation flowshop heuristics. Eur. J. Oper. Res. 2005, 165, 479–494. [Google Scholar] [CrossRef]
- Palmer, D. Sequencing jobs through a multi-stage process in the minimum total time - a quick method of obtaining a near optimum. Oper. Res. Q. 1965, 16, 101–107. [Google Scholar] [CrossRef]
- Hundal, T.S.; Rajgopal, J. An extension of Palmer’s heuristic for the flow shop scheduling problem. Int. J. Prod. Res. 1988, 26, 1119–1124. [Google Scholar] [CrossRef]
- Campbell, H.G.; Dudek, R.A.; Smith, M.L. A heuristic algorithm for the n job, m machine sequencing problem. Manag. Sci. 1970, 16, B630–B637. [Google Scholar] [CrossRef]
- Dannenbring, D.G. An evaluation of flow shop sequencing heuristics. Manag. Sci. 1977, 23, 1174–1182. [Google Scholar] [CrossRef]
- Ho, J.C.; Chang, Y.-L. A new heuristic for the n-job, m-machine flow-shop problem. Eur. J. Oper. Res. 1991, 52, 194–202. [Google Scholar] [CrossRef]
- Koulamas, C. A new constructive heuristic for the flowshop scheduling problem. Eur. J. Oper. Res. 1998, 105, 66–71. [Google Scholar] [CrossRef]
- Suliman, S. A two-phase heuristic approach to the permutation flow-shop scheduling problem. Int. J. Prod. Econ. 2000, 64, 143–152. [Google Scholar] [CrossRef]
- Pour, H.D. A new heuristic for the n-job, m-machine flow-shop problem. Prod. Plan. Control 2001, 12, 648–653. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Ma, Z. A hybrid local search algorithm for the sequence dependent setup times flowshop scheduling problem with makespan criterion. Sustainability 2017, 9, 2318. [Google Scholar] [CrossRef]
- Yang, D.L.; Kuo, W.H. Minimizing Makespan in A Two-Machine Flowshop Problem with Processing Time Linearly Dependent on Job Waiting Time. Sustainability 2019, 11, 6885. [Google Scholar] [CrossRef]
- Fuchigami, H.Y.; Sarker, R.; Rangel, S. Near-optimal heuristics for just-in-time jobs maximization in flowshop scheduling. Algorithms 2018, 11, 43. [Google Scholar] [CrossRef]
- Huang, K.W.; Girsang, A.S.; Wu, Z.X.; Chuang, Y.W. A Hybrid Crow Search Algorithm for Solving Permutation Flow Shop Scheduling Problems. Appl. Sci. 2019, 9, 1353. [Google Scholar] [CrossRef]
- Bewoor, L.A.; Chandra Prakash, V.; Sapkal, S.U. Evolutionary hybrid particle swarm optimization algorithm for solving NP-hard no-wait flow shop scheduling problems. Algorithms 2017, 10, 121. [Google Scholar] [CrossRef]
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Stützle, T. Applying Iterated Local Search to the Permutation Flow Shop Problem; Technical Report 1998; AIDA-98-04; FG Intellektik, TU Darmstadt: Darmstadt, Germany, 1998. [Google Scholar]
- Zobolas, G.I.; Tarantilis, C.D.; Ioannou, G. Minimizing makespan in permutation flow shop scheduling problems using a hybrid metaheuristic algorithm. Comput. Oper. Res. 2009, 36, 1249–1267. [Google Scholar] [CrossRef]
- Dong, X.; Huang, H.; Chen, P. An improved NEH-based heuristic for the permutation flowshop problem. Comput. Oper. Res. 2008, 35, 3962–3968. [Google Scholar] [CrossRef]
- Ruiz, R.; Stützle, T. A simple and effective iterated greedy algorithm for the permutation flowshop scheduling problem. Eur. J. Oper. Res. 2007, 177, 2033–2049. [Google Scholar] [CrossRef]
- Bansal, J.C.; Deep, K. A modified binary particle swarm optimization for knapsack problems. Appl. Math. Comput. 2012, 218, 11042–11061. [Google Scholar] [CrossRef]
- Li, Y.; He, Y.; Li, H.; Guo, X.; Li, Z. A Binary Particle Swarm Optimization for Solving the Bounded Knapsack Problem. In International Symposium on Intelligence Computation and Applications; Springer: Singapore, October 2018; pp. 50–60. [Google Scholar] [CrossRef]
- Sauvey, C.; Trabelsi, W.; Sauer, N. Mathematical Model and Evaluation Function for Conflict-Free Warranted Makespan Minimization of Mixed Blocking Constraint Job-Shop Problems. Mathematics 2020, 8, 121. [Google Scholar] [CrossRef]
- Maassen, K.; Hipp, A.; Perez-Gonzalez, P. Constructive heuristics for the minimization of core waiting time in permutation flow shop problems. In Proceedings of the International Conference on Industrial Engineering and Systems Management (IESM), Shanghai, China, 25–27 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Fernandez-Viagas, V.; Framinan, J.M. NEH-based heuristics for the permutation flowshop scheduling problem to minimise total tardiness. Comput. Oper. Res. 2015, 60, 27–36. [Google Scholar] [CrossRef]
- Pan, Q.K.; Gao, L.; Wang, L.; Liang, J.; Li, X.Y. Effective heuristics and metaheuristics to minimize total flowtime for the distributed permutation flowshop problem. Expert Syst. Appl. 2019, 124, 309–324. [Google Scholar] [CrossRef]
- Gao, J.; Chen, R. An NEH-based heuristic algorithm for distributed permutation flowshop scheduling problems. Sci. Res. Essays 2011, 6, 3094–3100. [Google Scholar] [CrossRef]
- Liu, W.; Jin, Y.; Price, M. A new improved NEH heuristic for permutation flowshop scheduling problems. Int. J. Prod. Econ. 2017, 193, 21–30. [Google Scholar] [CrossRef]
- Kalczynski, P.J.; Kamburowski, J. An improved NEH heuristic to minimize makespan in permutation flow shops. Comput. Oper. Res. 2008, 35, 3001–3008. [Google Scholar] [CrossRef]
- Kalczynski, P.J.; Kamburowski, J. An empirical analysis of the optimality rate of flow shop heuristics. Eur. J. Oper. Res. 2009, 198, 93–101. [Google Scholar] [CrossRef]
- Fernandez-Viagas, V.; Framinan, J.M. On insertion tie-breaking rules in heuristics for the permutation flowshop scheduling problem. Comput. Oper. Res. 2014, 45, 60–67. [Google Scholar] [CrossRef]
- Fernandez-Viagas, V.; Ruiz, R.; Framinan, J.M. A new vision of approximate methods for the permutation flowshop to minimise makespan: State-of-the-art and computational evaluation. Eur. J. Oper. Res. 2017, 257, 707–721. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).