A New Lossless DNA Compression Algorithm Based on A Single-Block Encoding Scheme
Abstract
1. Introduction
2. Proposed Methodology
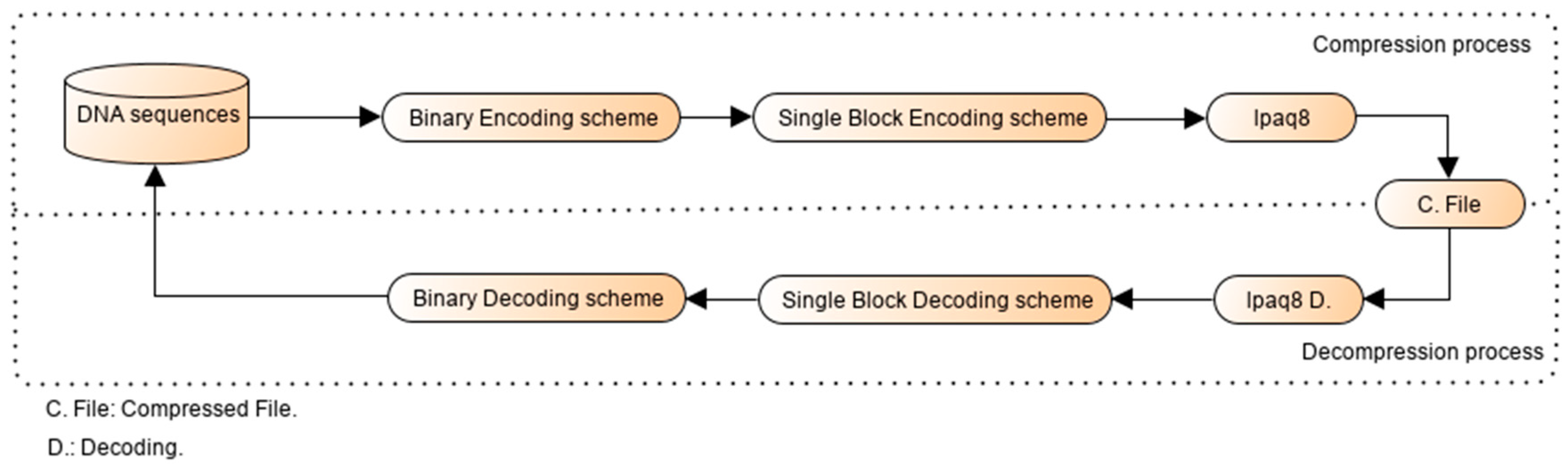
2.1. Overview
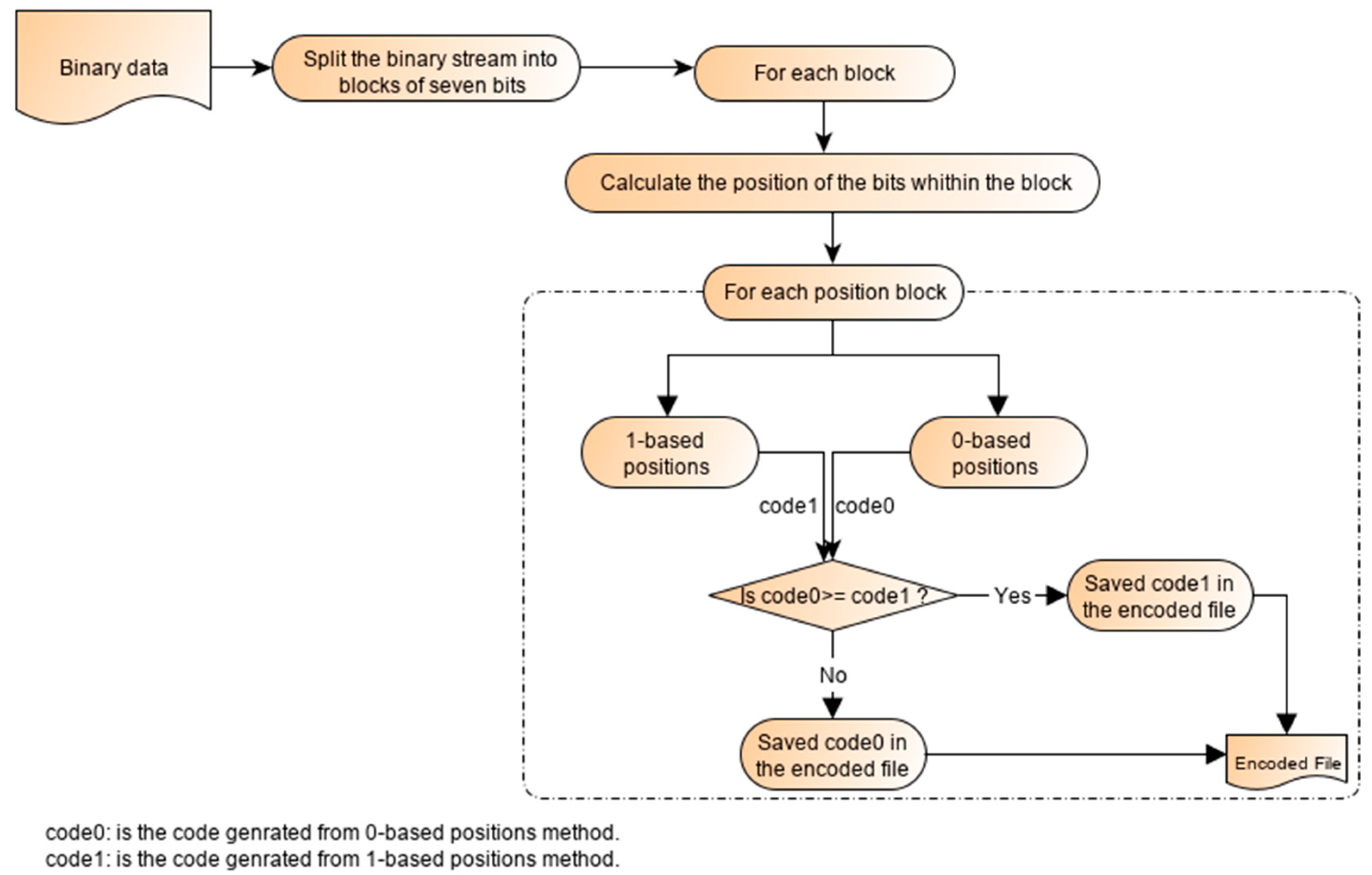
2.2. Binary Encoding Scheme
| Algorithm 1. Binary Encoding Scheme |
| Begin First phase (Binary Encoding Scheme) Input: A DNA sequence {b1 b2 b3 ……. bn} Output files: File1, File2 … Filen−1. Initialization: Filei (Bi)= {} Algorithm: Let B1, B2, B3 and B4 is the descending frequencies order. For each element of the sequence (j from 1 to n) if (Bi = bj) Add 1 to Filei else if (Bi != bj && Fr (Bi) > Fr(bj)) Add 0 to Filei else Ignore it and pass to the next base endif endif End. |
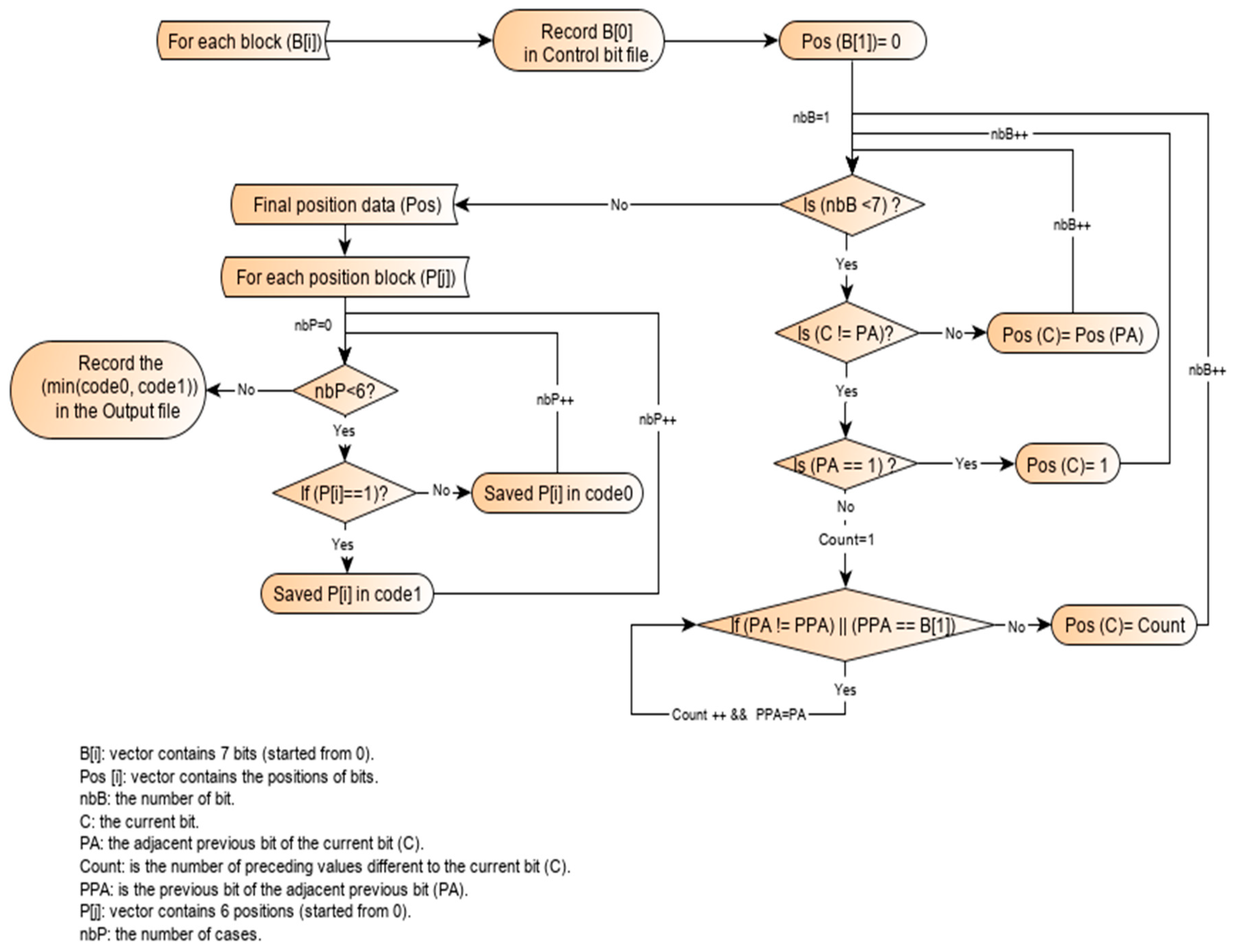
2.3. Working Principle of the Single-Block Encoding Algorithm
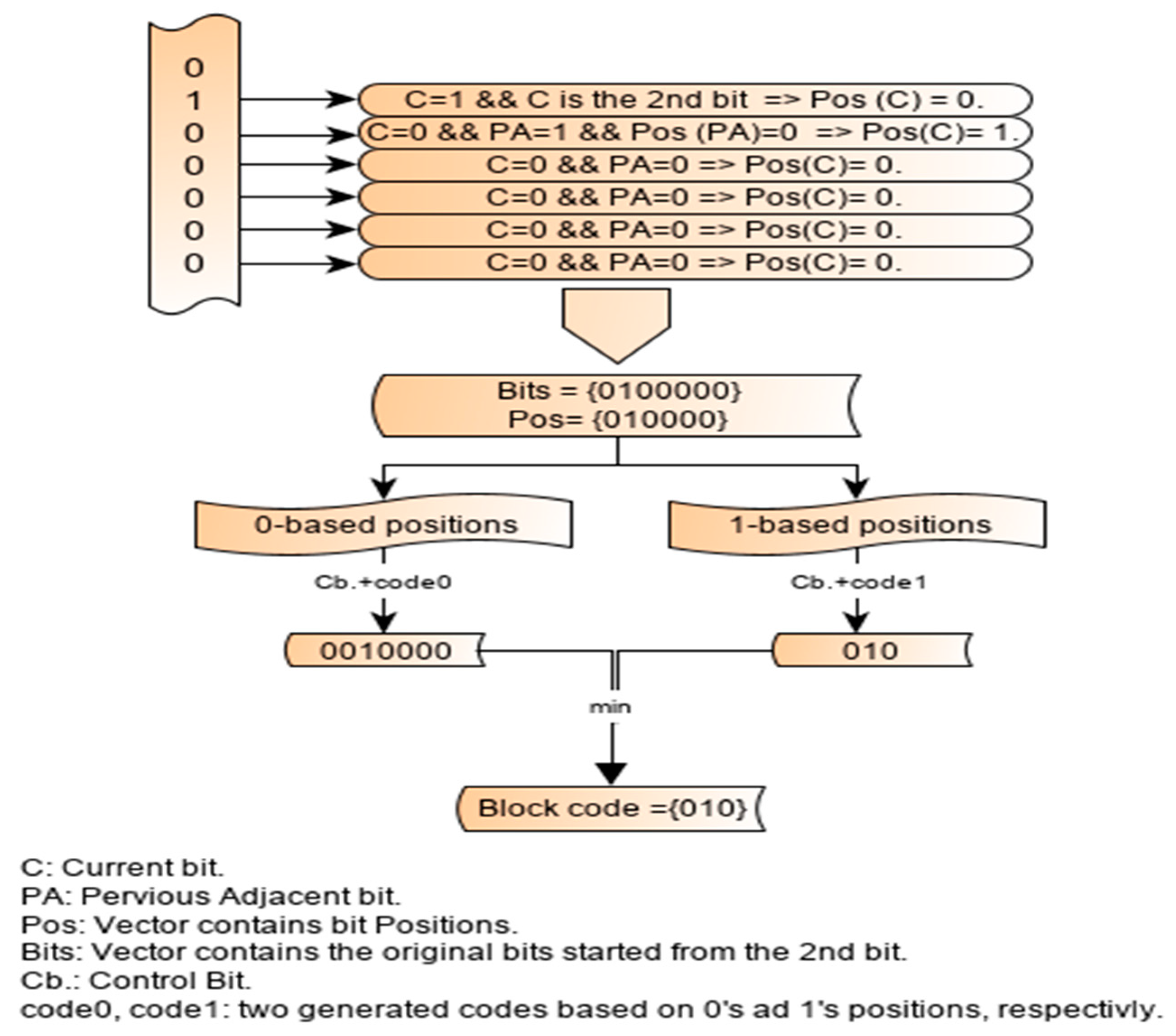
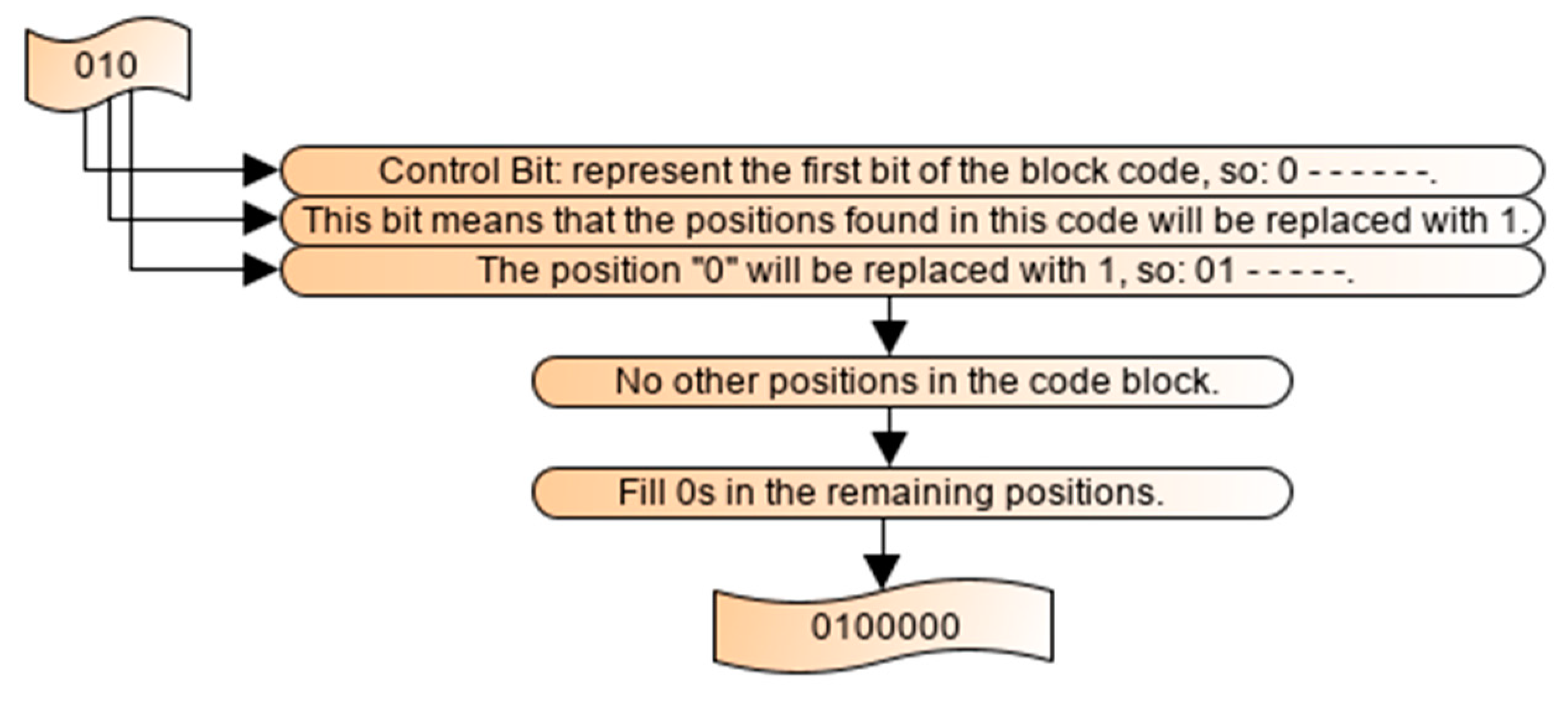
2.4. Illustration
2.5. Decoding Process
3. Performance Evaluation
3.1. Dataset Used
3.2. Compression Performance
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Availability of Data and Materials
References
- Lander, E.S.; Linton, L.M.; Birren, B.; Nusbaum, C.; Zody, M.C.; Baldwin, J.; Devon, K.; Dewar, K.; Doyle, M.; FitzHugh, W.; et al. Initial sequencing and analysis of the human genome. Nature 2001, 409, 860–921. [Google Scholar] [PubMed]
- Saada, B.; Zhang, J. Vertical DNA sequences compression algorithm based on hexadecimal representation. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 21–23 October 2015; pp. 21–25. [Google Scholar]
- Jahaan, A.; Ravi, T.; Arokiaraj, S. A comparative study and survey on existing DNA compression techniques. Int. J. Adv. Res. Comput. Sci. 2017, 8, 732–735. [Google Scholar]
- Rajarajeswari, P.; Apparao, A. DNABIT Compress–Genome compression algorithm. Bioinformation 2011, 5, 350. [Google Scholar] [CrossRef] [PubMed]
- Grumbach, S.; Tahi, F. A new challenge for compression algorithms: Genetic sequences. Information Process. Manag. 1994, 30, 875–886. [Google Scholar] [CrossRef]
- Majumder, A.B.; Gupta, S. CBSTD: A Cloud Based Symbol Table Driven DNA Compressions Algorithm. In Industry Interactive Innovations in Science, Engineering and Technology; Springer: Singapore, 2018; pp. 467–476. [Google Scholar]
- Mohammed, M.H.; Dutta, A.; Bose, T.; Chadaram, S.; Mande, S.S. DELIMINATE—a fast and efficient method for loss-less compression of genomic sequences: Sequence analysis. Bioinformatics 2012, 28, 2527–2529. [Google Scholar] [CrossRef]
- Pinho, A.J.; Pratas, D. MFCompress: A compression tool for FASTA and multi-FASTA data. Bioinformatics 2014, 30, 117–118. [Google Scholar] [CrossRef]
- Sardaraz, M.; Tahir, M.; Ikram, A.A.; Bajwa, H. SeqCompress: An algorithm for biological sequence compression. Genomics 2014, 104, 225–228. [Google Scholar] [CrossRef]
- Deorowicz, S.; Grabowski, S. Compression of DNA sequence reads in FASTQ format. Bioinformatics 2011, 27, 860–862. [Google Scholar] [CrossRef]
- Bonfield, J.K.; Mahoney, M.V. Compression of FASTQ and SAM format sequencing data. PloS ONE 2013, 8, e59190. [Google Scholar] [CrossRef]
- Aly, W.; Yousuf, B.; Zohdy, B. A Deoxyribonucleic acid compression algorithm using auto-regression and swarm intelligence. J. Comput. Sci. 2013, 9, 690–698. [Google Scholar] [CrossRef][Green Version]
- Hosseini, M.; Pratas, D.; Pinho, A.J. A survey on data compression methods for biological sequences. Information 2016, 7, 56. [Google Scholar] [CrossRef]
- Numanagić, I.; Bonfield, J.K.; Hach, F.; Voges, J.; Ostermann, J.; Alberti, C.; Mattavelli, M.; Sahinalp, S.C. Comparison of high-throughput sequencing data compression tools. Nat. Methods 2016, 13, 1005. [Google Scholar] [CrossRef]
- Xing, Y.; Li, G.; Wang, Z.; Feng, B.; Song, Z.; Wu, C. GTZ: A fast compression and cloud transmission tool optimized for FASTQ files. BMC bioinformatics 2017, 18, 549. [Google Scholar] [CrossRef] [PubMed]
- Behzadi, B.; Le Fessant, F. DNA compression challenge revisited: A dynamic programming approach. In Proceedings of the Annual Symposium on Combinatorial Pattern Matching, Heidelberg, Jeju Island, Korea, 19–22 June 2005; pp. 190–200. [Google Scholar]
- Kuruppu, S.; Puglisi, S.J.; Zobel, J. Reference sequence construction for relative compression of genomes. In Proceedings of the International Symposium on String Processing and Information Retrieval, Pisa, Italy; 2011; pp. 420–425. [Google Scholar]
- GenBank and WGS Statistics (NCBI). Available online: https://www.ncbi.nlm.nih.gov/genbank/statistics/ (accessed on 29 June 2019).
- 1000 Genomes Project Consortium “a map of human genome variation from population-scale sequencing”, Nature 467 (2010) 1061–1073. Available online: www.1000genomes.org/ (accessed on 19 April 2020).
- Consortium, E.P. The ENCODE (ENCyclopedia of DNA elements) project. Science 2004, 306, 636–640. [Google Scholar] [CrossRef] [PubMed]
- Keerthy, A.; Appadurai, A. An empirical study of DNA compression using dictionary methods and pattern matching in compressed sequences. IJAER 2015, 10, 35064–35067. [Google Scholar]
- Arya, G.P.; Bharti, R.; Prasad, D.; Rana, S.S. An Improvement over direct coding technique to compress repeated & non-repeated nucleotide data. In Proceedings of the 2016 International Conference on Computing, Communication and Automation (ICCCA), Noida, India, 29–30 April 2016; pp. 193–196. [Google Scholar]
- Rastogi, K.; Segar, K. Analysis and performance comparison of lossless compression techniques for text data. Int. J. Eng. Comput. Res. 2014, 3, 123–127. [Google Scholar]
- Singh, A.V.; Singh, G. A survey on different text data compression techniques. Int. J. Sci. Res. 2012, 3, 1999–2002. [Google Scholar]
- Al-Okaily, A.; Almarri, B.; Al Yami, S.; Huang, C.-H. Toward a Better Compression for DNA Sequences Using Huffman Encoding. J. Comput. Biol. 2017, 24, 280–288. [Google Scholar] [CrossRef]
- Sharma, K.; Gupta, K. Lossless data compression techniques and their performance. In Proceedings of the 2017 International Conference on Computing, Communication and Automation (ICCCA), Greater Noida, India, 5–6 May 2017; pp. 256–261. [Google Scholar]
- Gzip. Available online: http://www.gzip.org/ (accessed on 29 June 2019).
- Bzip. Available online: http://www.bzip.org/ (accessed on 29 June 2019).
- Bakr, N.S.; Sharawi, A.A. DNA lossless compression algorithms. Am. J. Bioinformatics Res. 2013, 3, 72–81. [Google Scholar]
- Grumbach, S.; Tahi, F. Compression of DNA sequences. In Proceedings of the Data Compression Confonference (DCC-93), Snowbird, UT, USA, 30 March–2 April 1993; pp. 340–350. [Google Scholar]
- Chen, X.; Kwong, S.; Li, M. A compression algorithm for DNA sequences and its applications in genome comparison. Genome Inf. 1999, 10, 51–61. [Google Scholar]
- Chen, X.; Li, M.; Ma, B.; Tromp, J. DNACompress: Fast and effective DNA sequence compression. Bioinformatics 2002, 18, 1696–1698. [Google Scholar] [CrossRef] [PubMed]
- Korodi, G.; Tabus, I. An Efficient Normalized Maximum Likelihood Algorithm for DNA Sequence Compression. ACM Trans. Inf. Syst. 2005, 23, 3–34. [Google Scholar] [CrossRef]
- Tan, L.; Sun, J.; Xiong, W. A Compression Algorithm for DNA Sequence Using Extended Operations. J. Comput. Inf. Syst. 2012, 8, 7685–7691. [Google Scholar]
- Ma, B.; Tromp, J.; Li, M. PatternHunter—Faster and more sensitive homology search. Bioinformatics 2002, 18, 440–445. [Google Scholar] [CrossRef]
- Tabus, I.; Korodi, G.; Rissanen, J. DNA sequence compression using the normalized maximum likelihood model for discrete regression. In Proceedings of the Data Compression Conference (DCC ’03), Snowbird, UT, USA, 25–27 March 2003; pp. 253–262. [Google Scholar]
- Cao, M.D.; Dix, T.I.; Allison, L.; Mears, C. A simple statistical algorithm for biological sequence compression. In Proceedings of the 2007 Data Compression Conference (DCC’07), Snowbird, UT, USA, 27–29 March 2007; pp. 43–52. [Google Scholar]
- Mishra, K.N.; Aaggarwal, A.; Abdelhadi, E.; Srivastava, D. An efficient horizontal and vertical method for online DNA sequence compression. Int. J. Comput. Appl. 2010, 3, 39–46. [Google Scholar] [CrossRef]
- Rajeswari, P.R.; Apparo, A.; Kumar, V. GENBIT COMPRESS TOOL (GBC): A java-based tool to compress DNA sequences and compute compression ratio (bits/base) of genomes. Int. J. Comput. Sci. Inform. Tech. 2010, 2, 181–191. [Google Scholar]
- Rajeswari, P.R.; Apparao, A.; Kumar, R.K. Huffbit compress—Algorithm to compress DNA sequences using extended binary trees. J. Theor. Appl. Inform. Tech. 2010, 13, 101–106. [Google Scholar]
- Ouyang, J.; Feng, P.; Kang, J. Fast compression of huge DNA sequence data. In Proceedings of the 2012 5th International Conference on BioMedical Engineering and Informatics, Chongqing, China, 16–18 October 2012; pp. 885–888. [Google Scholar]
- Li, P.; Wang, S.; Kim, J.; Xiong, H.; Ohno-Machado, L.; Jiang, X. DNA-COMPACT: DNA compression based on a pattern-aware contextual modeling technique. PLoS ONE 2013, 8, e80377. [Google Scholar] [CrossRef]
- Roy, S.; Bhagot, A.; Sharma, K.A.; Khatua, S. SBVRLDNAComp: An Effective DNA Sequence Compression Algorithm. Int. J. Comput. Sci. Appl. 2015, 5, 73–85. [Google Scholar]
- Roy, S.; Mondal, S.; Khatua, S.; Biswas, M. An Efficient Compression Algorithm for Forthcoming New Species. Int. J. Hybrid Inf. Tech. 2015, 8, 323–332. [Google Scholar] [CrossRef]
- Eric, P.V.; Gopalakrishnan, G.; Karunakaran, M. An optimal seed-based compression algorithm for DNA sequences. Adv. Bioinform. 2016. [Google Scholar] [CrossRef] [PubMed]
- Rexline, S.J.; Aju, R.G.; Trujilla, L.F. Higher compression from burrows-wheeler transform for DNA sequence. Int. J. Comput. Appl. 2017, 173, 11–15. [Google Scholar]
- Keerthy, A.; Priya, S.M. Lempel-Ziv-Welch Compression of DNA Sequence Data with Indexed Multiple Dictionaries. Int. J. Appl. Eng. Res. 2017, 12, 5610–5615. [Google Scholar]
- Habib, N.; Ahmed, K.; Jabin, I.; Rahman, M.M. Modified HuffBit Compress Algorithm–An Application of R. J. Integr. Bioinform. 2018. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Li, R.; Yang, L. Optimized Context Weighting for the Compression of the Un-repetitive Genome Sequence Fragment. Wirel. Personal Commun. 2018, 103, 921–939. [Google Scholar] [CrossRef]
- Mansouri, D.; Yuan, X. One-Bit DNA Compression Algorithm. In Proceedings of the International Conference on Neural Information Processing, Siam reap, Cambodia, 13–16 December 2018; Springer: Siam reap, Cambodia; pp. 378–386. [Google Scholar]
- Priyanka, M.; Goel, S. A compression algorithm for DNA that uses ASCII values. In Proceedings of the 2014 IEEE International Advance Computing Conference, Gurgaon, India, 21–22 February 2014; pp. 739–743. [Google Scholar]
- Bose, T.; Mohammed, M.H.; Dutta, A.; Mande, S.S. BIND–An algorithm for loss-less compression of nucleotide sequence data. J. Biosci. 2012, 37, 785–789. [Google Scholar] [CrossRef]
- Jones, D.; Ruzzo, W.; Peng, X.; Katze, M. Compression of next-generation sequencing reads aided by highly efficient de novo assembly. Nucleic Acids Res. 2012, 40. [Google Scholar] [CrossRef]
- Uthayakumar, J.; Vengattaraman, T.; Dhavachelvan, P. A new lossless neighborhood indexing sequence (NIS) algorithm for data compression in wireless sensor networks. Ad Hoc Netw. 2019, 83, 149–157. [Google Scholar]
- Bakr, N.S.; Sharawi, A.A. Improve the compression of bacterial DNA sequence. In Proceedings of the 2017 13th International Computer Engineering Conference (ICENCO), Cairo, Egypt, 27–28 December 2017; pp. 286–290. [Google Scholar]
- National Center for Biotechnology Information. Available online: https://www.ncbi.nlm.nih.gov/ (accessed on 30 March 2019).
- Roy, S.; Khatua, S. DNA data compression algorithms based on redundancy. Int. J. Found. Comput. Sci. Technol. 2014, 4, 49–58. [Google Scholar] [CrossRef]
- Willems, F.M.J.; Shtarkov, Y.M.; Tjalkens, T.J. The context tree weighting method: Basic properties. IEEE Trans. Inf. Theory 1995, 41, 653–664. [Google Scholar] [CrossRef]

| Sequence | Description | Source | Uncompressed Size (bytes) |
|---|---|---|---|
| CHMPXX | Marchantia polymorpha chloroplast genome DNA | Chloroplasts | 121,024 |
| CHNTXX | Nicotiana tabacum chloroplast genome DNA | 155,844 | |
| HUMHBB | Human beta globin region on chromosome 11. | Human | 73,308 |
| HUMGHCSA | Human growth hormone (GH1 and GH2) and chorionic somatomammotropin (CS-1, CS-2 and CS-5) genes, complete cds. | 66,495 | |
| HUMHPRTB | Human hypoxanthine phosphoribosyl transferase gene, complete cds. | 56,737 | |
| HUMDYSTROP | Homo sapiens dystrophin (DHD) gene, intron 44 | 38,770 | |
| MTPACGA | Marchantia, complete genome. | Viruses | 100,314 |
| MPOMTCG | Marchantia polymorpha mitochondrion, complete genome. | 186,609 | |
| HEHCMVCG | Human cytomegalovirus strain AD169 complete genome. | Mitochondria | 229,354 |
| VACCG | Vaccinia virus, complete genome. | 191,737 |
| Genome | Species | Size (bytes) |
|---|---|---|
| KOREF 2009024 | Homo sapiens | 3,131,781,939 |
| NC 017652 | E. coli | 5,106,565.12 |
| NC_017526 | L. pneumophila | 2,715,811.84 |
| Ce10 | C. elegans | 102,288,589 |
| sacCer3 | S. cerevisiae | 12,394,168.3 |
| Eukaryotic | Haploid set of human chromosomes | 2,509,353,796 |
| Chimpanzee | Pan troglodytes | 3,333,423,104 |
| Data | Species/Type | DNA Sequence Size (bytes) |
|---|---|---|
| ERR005143_1 | P. syringae | 127,840,788 |
| ERR005143_2 | 127,840,788 | |
| SRR554369_1 | Pseudomonas aeruginosa | 165,787,101 |
| SRR554369_2 | 165,787,101 |
| Sequence | CH-MPXX | HUMD-YTROP | HUM-HBB | HEHC-MVCG | MPO-MTCG | VAC-CG | MTP-ACGA | HUMH-PRTB |
|---|---|---|---|---|---|---|---|---|
| Length | 121024 | 38770 | 73308 | 229354 | 186609 | 191737 | 100314 | 56737 |
| Biocompress2 | 1.684 | 1.926 | 1.880 | 1.848 | 1.937 | 1.761 | 1.875 | 1.907 |
| CTW+LZ | 1.669 | 1.916 | 1.808 | 1.841 | 1.900 | 1.761 | 1.856 | 1.843 |
| GenCompress | 1.671 | 1.923 | 1.820 | 1.847 | 1.901 | 1.761 | 1.862 | 1.847 |
| DNACompress | 1.672 | 1.911 | 1.789 | 1.849 | 1.892 | 1.758 | 1.856 | 1.817 |
| DNA Pack | 1.660 | 1.909 | 1.777 | 1.835 | 1.893 | 1.758 | - | 1.789 |
| GeNML | 1.662 | 1.909 | 1.752 | 1.842 | 1.882 | 1.764 | 1.844 | 1.764 |
| XM | 1.656 | 1.910 | 1.751 | 1.843 | 1.878 | 1.765 | 1.845 | 1.736 |
| Genbit | 2.225 | 2.234 | 2.226 | - | 2.24 | 2.237 | 2.243 | 2.240 |
| Improved RLE | - | 1.948 | 1.911 | 1.885 | 1.961 | 1.862 | - | - |
| DNA-COMP | 1.653 | 1.930 | 1.836 | 1.808 | 1.907 | - | 1.849 | - |
| FS4CP | 1.996 | 2.068 | - | 2.00 | 1.98 | 1.967 | 1.978 | 1.981 |
| OBComp | 1.652 | 1.910 | 1.911 | 1.862 | 1.971 | 1.850 | 1.831 | 1.910 |
| OPGC | 1.643 | 1.904 | 1.748 | 1.838 | 1.868 | 1.762 | 1.878 | 1.726 |
| Modified Huffbit | 1.931 | 2.040 | 2.09 | 2.14 | 1.94 | 2.003 | 1.944 | 2.231 |
| DNAC-SBE | 1.604 | 1.724 | 1.717 | 1.741 | 1.721 | 1.671 | 1.650 | 1.720 |
| Sequence | HEHCMVCG | HUMHBB | VACCG |
|---|---|---|---|
| gzip | 1.85 | 2.23 | 2.19 |
| Bzip2 | 2.17 | 2.15 | 2.10 |
| Arithm. | 2.05 | 2.12 | 1.86 |
| CTW | 1.84 | 1.92 | 1.86 |
| BWT+MTF+RLE +arithm. | 2.24 | 2.21 | 2.18 |
| BWT+MTF+ arithm. | 2.03 | 2.02 | 2.07 |
| BWT+MTF | 2.02 | 2.00 | 1.95 |
| DNAC-SBE | 1.74 | 1.72 | 1.67 |
| Dataset | Original Size | 7z | Bind | Deliminate | MF-Compress | Seq-Compress | DNAC-SEB |
|---|---|---|---|---|---|---|---|
| NC_017526 | 2.59 | 0.72 | 11.11% | 12.5% | 9.72% | 16.67% | 23.61% |
| NC_017652 | 4.87 | 1.36 | 11.76% | 12.5% | 10.29% | 16.91% | 22.06% |
| Ce10 | 97.55 | 27.81 | 5.11% | 14.42% | 17.12% | 18.62% | 28.98% |
| sacCer3 | 11.82 | 3.33 | 16.68% | 19.6% | 22.08% | 23.44% | 25.53% |
| Eukaryotic | 2139.98 | 527.27 | 11.31% | 15.44% | 17.35% | 17.11% | 19.71% |
| Dataset | Method | Metrics | ||||
|---|---|---|---|---|---|---|
| C-Size | C-Mem | D-Mem | C-Time | D-Time | ||
| NC_017526 | Bind | 0,64 | 3.67 | 8.6 | 0.64 | 0.26 |
| Deliminate | 0.63 | 3.66 | 6.55 | 0.37 | 0.23 | |
| MFCompress | 0.65 | 514.16 | 513.13 | 0.66 | 0.55 | |
| DNAC-SEB | 0.55 | 36.71 | 64.31 | 1.78 | 1.24 | |
| NC_017652 | Bind | 1.2 | 4.04 | 8.6 | 0.49 | 0.36 |
| Deliminate | 1.19 | 4.02 | 6.55 | 0.44 | 0.25 | |
| MFCompress | 1.22 | 514.34 | 513.13 | 1.26 | 0.95 | |
| DNAC-SEB | 1.06 | 49.03 | 101.45 | 1.67 | 1.27 | |
| sacCer3 | Bind | 3.16 | 5.75 | 8.12 | 2.78 | 2.41 |
| Deliminate | 2.85 | 2.56 | 6.19 | 5.26 | 4.94 | |
| MFCompress | 2.77 | 473.9 | 473.78 | 4.32 | 3.5 | |
| DNAC-SEB | 2.48 | 5.09 | 13.54 | 26.57 | 9.71 | |
| Ce10 | Bind | 23.17 | 37.92 | 7.54 | 11 | 7.27 |
| Deliminate | 22.36 | 70.29 | 7.11 | 8.55 | 8.54 | |
| MFCompress | 21.67 | 433.92 | 431.49 | 20.16 | 19.04 | |
| DNAC-SEB | 19.75 | 68.75 | 212.75 | 73.13 | 45.04 | |
| Chimpanzee | Bind | 619.35 | 274.48 | 28.52 | 350.84 | 180.28 |
| Deliminate | 590.48 | 284.02 | 29.44 | 257.02 | 172.83 | |
| MFCompress | 581.12 | 482.8 | 465.12 | 575.22 | 426.53 | |
| DNAC-SEB | 570.73 | 522.23 | 792.9 | 1445.15 | 1155.97 | |
| Korea2009024 | Bind | 693.14 | 295.05 | 30.06 | 380.38 | 207.44 |
| Deliminate | 604.16 | 305.41 | 31.07 | 303.15 | 194.99 | |
| MFCompress | 604.12 | 665.44 | 577.45 | 503.18 | 500.31 | |
| DNAC-SEB | 577.23 | 649.56 | 703.69 | 1479.57 | 1003.27 | |
| Eukaryotic | Bind | 466.98 | 387.81 | 39.12 | 285.24 | 154.01 |
| Deliminate | 445.89 | 389.1 | 40.3 | 206.43 | 136.83 | |
| MFCompress | 435.79 | 478.86 | 477.89 | 468.18 | 419.15 | |
| DNAC-SEB | 423.32 | 1859 | 1349.05 | 1117.44 | 903.1 | |
| Dataset | Original Size (MB) | gzip | DSRC | Quip | Fqzcomp | GTZ | DNAC-SEB |
|---|---|---|---|---|---|---|---|
| ERR005143_1 | 121.92 | 1.020 | 0.238 | 0.250 | 0.227 | 0.230 | 0.219 |
| ERR005143_2 | 121.92 | 1.086 | 0.249 | 0.239 | 0.229 | 0.230 | 0.219 |
| SRR554369_1 | 158.11 | 0.209 | 0.250 | 0.223 | 0.222 | 0.233 | 0.220 |
| SRR554369_2 | 158.11 | 0.209 | 0.249 | 0.227 | 0.222 | 0.234 | 0.220 |
| Dataset | Method | Metrics | ||||
|---|---|---|---|---|---|---|
| C-Size | C-Mem | D-Mem | C-Time | D-Time | ||
| ERR005143_1 | DSRC | 30.46 | 166.45 | 100.56 | 5.54 | 3.4 |
| Quip | 28.96 | 393.7 | 389.02 | 10.63 | 22.09 | |
| Fqzcomp | 27.73 | 79.46 | 67.33 | 7.88 | 10.08 | |
| Gzip | 124.36 | 0.86 | 1.39 | 28.94 | 2.7 | |
| DNAC-SEB | 26.81 | 580.38 | 563,91 | 38.08 | 18.64 | |
| ERR005143_2 | DSRC | 30.41 | 168.56 | 106.5 | 5.83 | 4.09 |
| Quip | 29.25 | 395.25 | 389.54 | 11.07 | 23.95 | |
| Fqzcomp | 27.9 | 79.46 | 59.3 | 8.45 | 10.35 | |
| Gzip | 132.42 | 0.86 | 1.39 | 29.45 | 2.79 | |
| DNAC-SEB | 26.28 | 580.57 | 524.57 | 72.06 | 20.54 | |
| SRR554369_1 | DSRC | 39.52 | 183.42 | 152.65 | 4.11 | 4.46 |
| Quip | 35.26 | 383.95 | 382.59 | 10.86 | 22.93 | |
| Fqzcomp | 35.13 | 79.47 | 67.34 | 7.21 | 10.4 | |
| Gzip | 45.97 | 0.87 | 1.39 | 28.51 | 1.05 | |
| DNAC-SEB | 34.9 | 702.18 | 615.97 | 43.71 | 31.34 | |
| SRR554369_2 | DSRC | 39.38 | 173.57 | 132.1 | 4.23 | 4.6 |
| Quip | 35.93 | 383.84 | 382.1 | 11.63 | 23.62 | |
| Fqzcomp | 35.12 | 66.41 | 57.179 | 7.86 | 10.52 | |
| Gzip | 45.89 | 0.87 | 1.39 | 27.98 | 1.05 | |
| DNAC-SEB | 34.84 | 781.98 | 644.66 | 43.18 | 30.8 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mansouri, D.; Yuan, X.; Saidani, A. A New Lossless DNA Compression Algorithm Based on A Single-Block Encoding Scheme. Algorithms 2020, 13, 99. https://doi.org/10.3390/a13040099
Mansouri D, Yuan X, Saidani A. A New Lossless DNA Compression Algorithm Based on A Single-Block Encoding Scheme. Algorithms. 2020; 13(4):99. https://doi.org/10.3390/a13040099
Chicago/Turabian StyleMansouri, Deloula, Xiaohui Yuan, and Abdeldjalil Saidani. 2020. "A New Lossless DNA Compression Algorithm Based on A Single-Block Encoding Scheme" Algorithms 13, no. 4: 99. https://doi.org/10.3390/a13040099
APA StyleMansouri, D., Yuan, X., & Saidani, A. (2020). A New Lossless DNA Compression Algorithm Based on A Single-Block Encoding Scheme. Algorithms, 13(4), 99. https://doi.org/10.3390/a13040099





