Investigating Feature Selection and Random Forests for Inter-Patient Heartbeat Classification
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Feature Extraction
- Heart rate related features (3 features): the current R–R interval () defined by the heartbeat being classified, the previous R–R interval (), and the next R–R interval (). R–R intervals are calculated from the location of R spikes provided with the database.
- HBF coefficients (15 features): each beat segment, here defined by the samples located 250 ms before and after each R spike, is decomposed using 3, 4, and 5 Hermite functions as described in [21]. The coefficients obtained from fitting Hermite polynomials of degrees 3, 4, and 5 are calculated using the function hermfit provided by the Scikit-Learn package for Python [30].
- HOS (10 features): the third-, and fourth-order cumulant functions (kurtosis and skewness, respectively) for each beat segment are computed. The parameters as defined in [25] are used: the lag parameters range from ms to 250 ms centered on the R spike and five equally spaced sample points.
- DWT coefficients (23 features): the DWT of each beat segment is computed using the same parameters defined in [25]: the Daubechies wavelet function (db1) is used with three levels of decomposition.
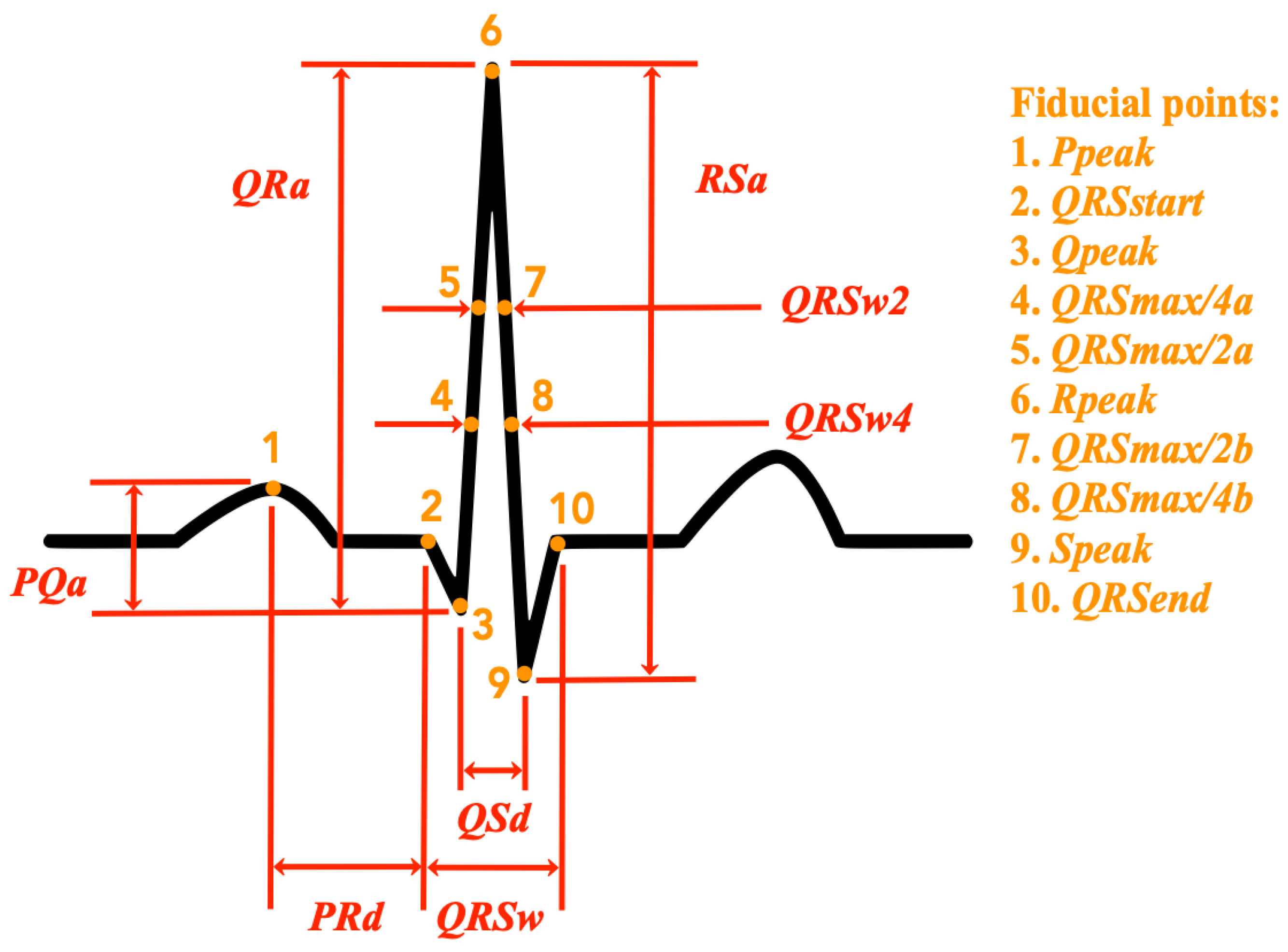
- QRS temporal characteristics (4 features): the following temporal characteristics of the QRS complex are calculated: the total duration of the QRS complex (), the width of the QRS complex at half of the peak value (), the width of the QRS complex at a quarter of the peak value (), the distance between the peak of the Q wave, and the peak of the S wave (). Figure 1 shows an illustration of these features in relation to the ECG signal of a normal heartbeat. A detailed description of the extraction procedure is provided in Appendix A.
- Amplitude differences (8 features): the following amplitude difference features as defined in [16] are extracted: the amplitude difference between the P and the Q waves (), the amplitude difference between the Q and the R waves (), the amplitude difference between the R and the S waves (), the distance between the peak of the P wave and the beginning of the QRS complex (), and the peak value of each of the considered waves (, , , and ). Figure 1 shows an illustration of these features in relation to the ECG signal of a normal heartbeat. A detailed description of the extraction procedure is provided in Appendix A.
- Euclidean distances (4 features): the Euclidean distance (sample, amplitude) between the R spike peak and four points of the beat segment are obtained as described in [25]. These points correspond to the maximum amplitude value between 250 ms and 139 ms before the R spike, the minimum value between 42 ms and 14 ms before the R spike, the minimum value between 14 ms and 42 ms after the R spike, and maximum value between 139 ms and 250 ms after the R spike.
- Normalized heart rate features (6 features): divided by the average of the last 32 beats (/), divided by the average of the last 32 R–R intervals (/), divided by the average of the last 32 R–R intervals (/), divided by (/), divided by (/), and the t-statistic of () defined by the difference between and divided by the standard deviation of the last 32 R–R intervals.
- Normalized QRS temporal characteristics and amplitude differences (12 features): the same QRS temporal characteristics and amplitude differences previously specified, except that they are divided by their average value in the last 32 heartbeats.
2.3. Feature Selection
2.4. Classification Performance Measures
2.5. Heartbeat Classification
- Select a random sample from the training dataset.
- Grow a tree for each random sample with the following modification: at each node, select the best split among a randomly selected subset of input variables, which is the tuning parameter of the random forest algorithm. The tree is fully grown until no further splits are possible and not pruned.
- Repeat steps 1 and 2 until C such trees are grown.
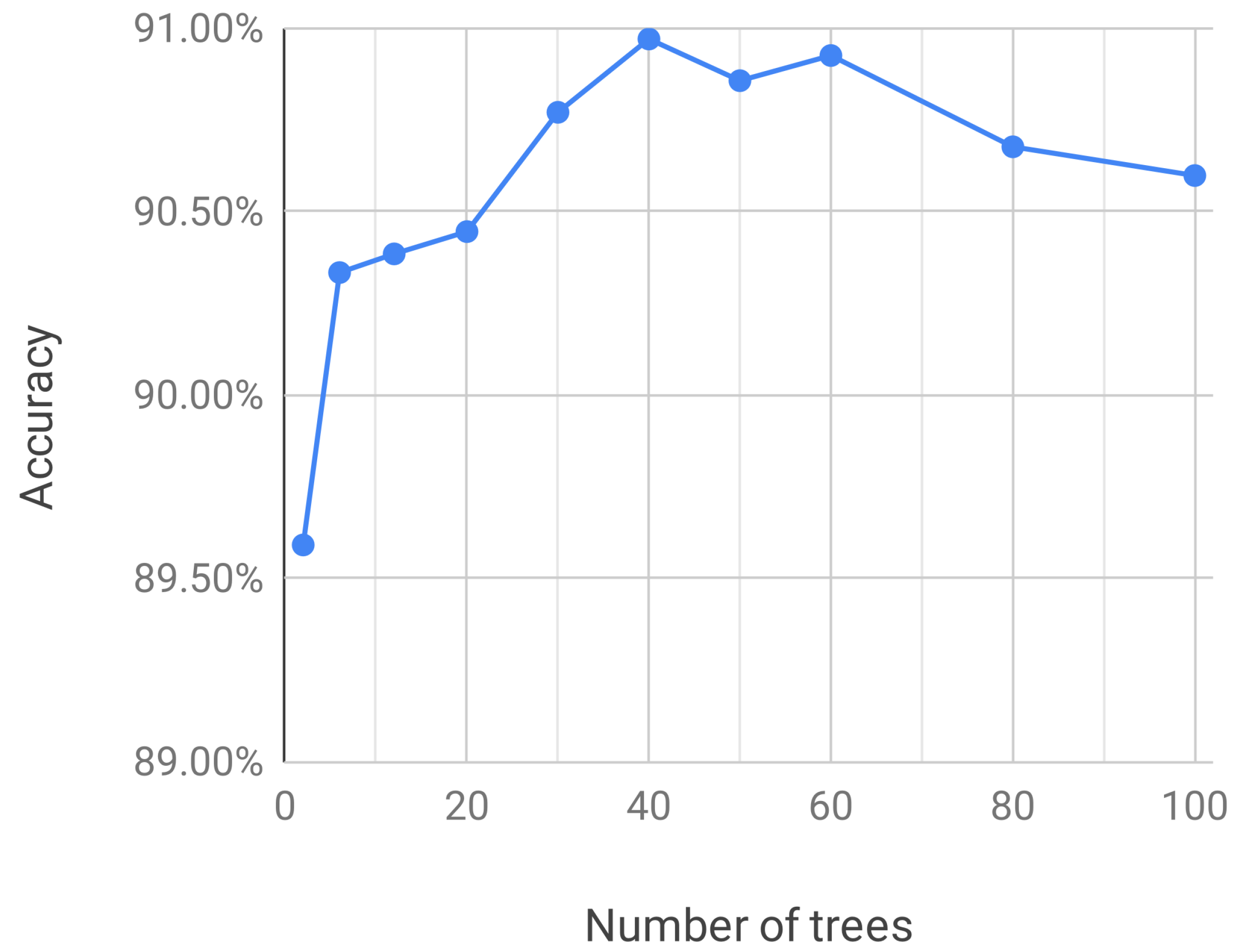
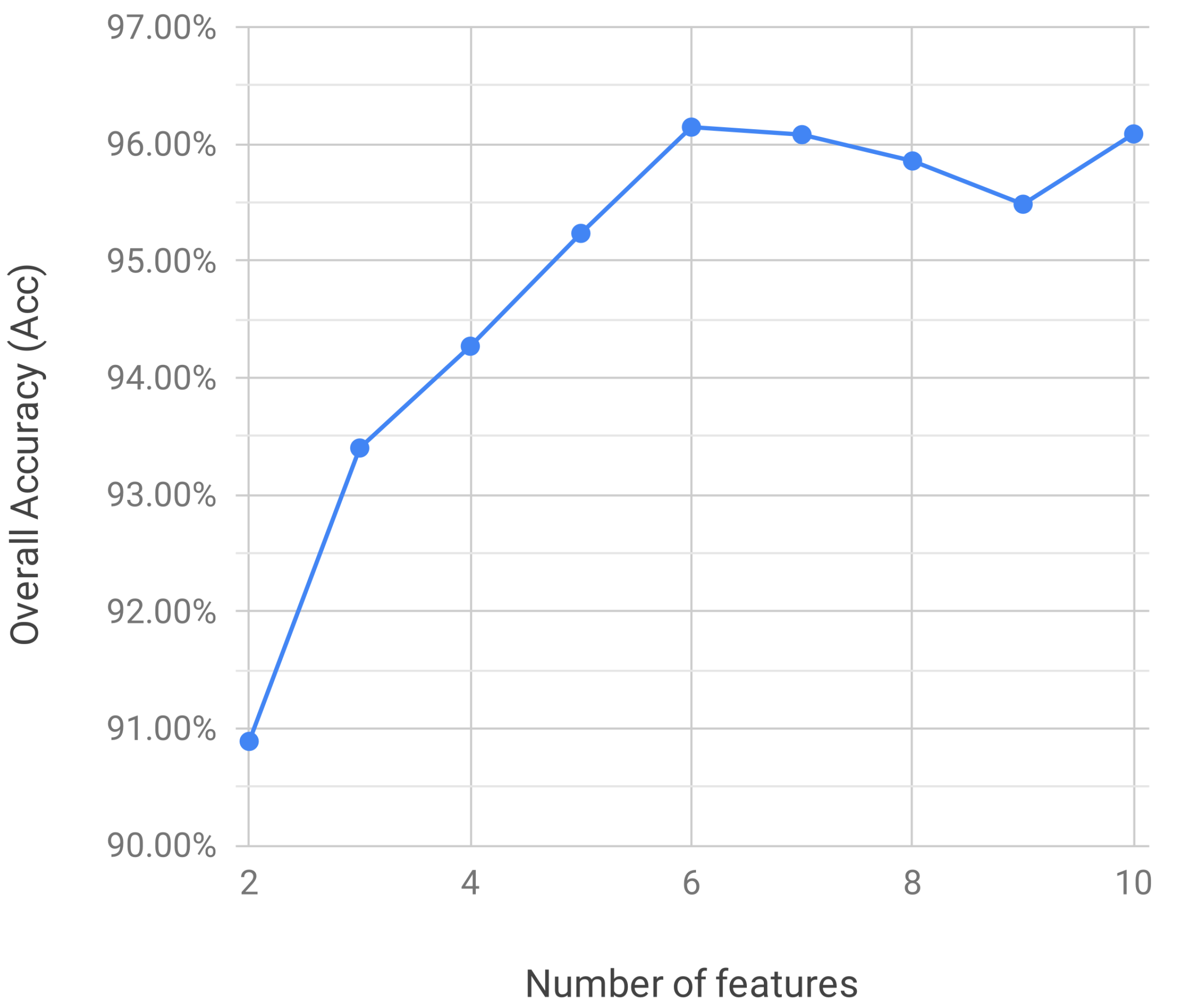
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Extraction of QRS Temporal Characteristics and Amplitude Differences
- Assume that , , , and equal zero and that the corresponding waves are not present.
- If is positive, then make equal to .
- Look backward from and evaluate the signal and its inflection points in this way:
- (a)
- Make equal to the first location where the signal goes below half of .
- (b)
- Make equal to the first location where the signal goes below a quarter of .
- (c)
- If the first inflection point is negative and is not zero, then equals the value at such point.
- (d)
- If the first inflection point is positive or zero and is not zero, then it is marked as , and is considered zero.
- (e)
- If the first inflection point is positive and is zero, then make equal to the value at such point and make equal to QRS max.
- (f)
- If the second inflection point is negative, is zero, and is positive, then make equal to the value at such point.
- (g)
- If is not zero and the signal crosses zero, then the first non-negative point is marked as .
- (h)
- If the second inflection point is positive or zero and has not been found yet, then it is marked as .
- Look forward from and evaluate the signal and its inflection points in this way:
- (a)
- Make equal to the first location where the signal goes below half of .
- (b)
- Make equal to the first location where the signal goes below a quarter of .
- (c)
- If the first inflection point is negative and is not zero, then make equal to the value at such point.
- (d)
- If is not zero and the signal cross zero, then the first non-negative point is marked as .
- (e)
- If the second inflection point is positive or zero and has not been found yet, then it is marked as .
- Find the maximum value of the signal in the segment that goes between 233 ms (35 samples) and 67 ms (10 samples) before . If such value is greater than three times, the standard deviation of the signal during the 67 ms preceding the segment in consideration, and its position corresponds to an inflection point in the signal, then make equal to such a value.
References
- Scirè, A.; Tropeano, F.; Anagnostopoulos, A.; Chatzigiannakis, I. Fog-Computing-Based Heartbeat Detection and Arrhythmia Classification Using Machine Learning. Algorithms 2019, 12, 32. [Google Scholar] [CrossRef]
- Dukes, J.W.; Dewland, T.A.; Vittinghoff, E.; Mandyam, M.C.; Heckbert, S.R.; Siscovick, D.S.; Stein, P.K.; Psaty, B.M.; Sotoodehnia, N.; Gottdiener, J.S.; et al. Ventricular Ectopy as a Predictor of Heart Failure and Death. J. Am. Coll. Cardiol. 2015, 66, 101–109. [Google Scholar] [CrossRef]
- Acharya, T.; Tringali, S.; Bhullar, M.; Nalbandyan, M.; Ilineni, V.K.; Carbajal, E.; Deedwania, P. Frequent Atrial Premature Complexes and Their Association With Risk of Atrial Fibrillation. Am. J. Cardiol. 2015, 116, 1852–1857. [Google Scholar] [CrossRef]
- Luz, E.J.d.S.; Schwartz, W.R.; Cámara-Chávez, G.; Menotti, D. ECG-based heartbeat classification for arrhythmia detection: A survey. Comput. Methods Programs Biomed. 2016, 127, 144–164. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Saffari, A.; Leistner, C.; Santner, J.; Godec, M.; Bischof, H. On-line Random Forest. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009. [Google Scholar]
- Saki, F.; Kehtarnavaz, N. Background noise classification using random forest tree classifier for cochlear implant applications. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 3591–3595. [Google Scholar]
- Donos, C.; Dümpelmann, M.; Schulze-Bonhage, A. Early Seizure Detection Algorithm Based on Intracranial EEG and Random Forest Classification. Int. J. Neural Syst. 2015, 25, 1550023. [Google Scholar] [CrossRef]
- Ani, R.; Krishna, S.; Anju, N.; Aslam, M.S.; Deepa, O. Iot based patient monitoring and diagnostic prediction tool using ensemble classifier. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; pp. 1588–1593. [Google Scholar]
- Hermawan, I.; Alvissalim, M.S.; Tawakal, M.I.; Jatmiko, W. An integrated sleep stage classification device based on electrocardiograph signal. In Proceedings of the 2012 International Conference on Advanced Computer Science and Information Systems (ICACSIS), Depok, Indonesia, 1–2 December 2012; pp. 37–41. [Google Scholar]
- Emanet, N. ECG beat classification by using discrete wavelet transform and Random Forest algorithm. In Proceedings of the 2009 Fifth International Conference on Soft Computing, Computing with Words and Perceptions in System Analysis, Decision and Control, Famagusta, Cyprus, 2–4 September 2009; pp. 1–4. [Google Scholar]
- Alickovic, E.; Subasi, A. Medical decision support system for diagnosis of heart arrhythmia using DWT and random forests classifier. J. Med. Syst. 2016, 40, 108. [Google Scholar] [CrossRef]
- Pan, G.; Xin, Z.; Shi, S.; Jin, D. Arrhythmia classification based on wavelet transformation and random forests. Multimed. Tools Appl. 2018, 77, 21905–21922. [Google Scholar] [CrossRef]
- Kumar, R.G.; Kumaraswamy, Y. Investigating cardiac arrhythmia in ECG using random forest classification. Int. J. Comput. Appl. 2012, 37, 31–34. [Google Scholar]
- Mahesh, V.; Kandaswamy, A.; Vimal, C.; Sathish, B. Random Forest Classifier Based ECG Arrhythmia Classification. In Int. J. Healthc. Inf. Syst. Inform. 2012, 5, 189–198. [Google Scholar]
- Park, J.; Lee, S.; Kang, K. Arrhythmia detection using amplitude difference features based on random forest. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 5191–5194. [Google Scholar]
- Park, J.; Kang, M.; Gao, J.; Kim, Y.; Kang, K. Cascade Classification with Adaptive Feature Extraction for Arrhythmia Detection. J. Med. Syst. 2017, 41, 11. [Google Scholar] [CrossRef] [PubMed]
- Luz, E.; Menotti, D. How the choice of samples for building arrhythmia classifiers impact their performances. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 4988–4991. [Google Scholar]
- Mar, T.; Zaunseder, S.; Martínez, J.P.; Llamedo, M.; Poll, R. Optimization of ECG classification by means of feature selection. IEEE Trans. Biomed. Eng. 2011, 58, 2168–2177. [Google Scholar] [CrossRef] [PubMed]
- al Fahoum, A.S.; Howitt, I. Combined wavelet transformation and radial basis neural networks for classifying life-threatening cardiac arrhythmias. Med. Biol. Eng. Comput. 1999, 37, 566–573. [Google Scholar] [CrossRef] [PubMed]
- Lagerholm, M.; Peterson, C.; Braccini, G.; Edenbrandt, L.; Sornmo, L. Clustering ECG complexes using Hermite functions and self-organizing maps. IEEE Trans. Biomed. Eng. 2000, 47, 838–848. [Google Scholar] [CrossRef] [PubMed]
- Park, K.; Cho, B.; Lee, D.; Song, S.; Lee, J.; Chee, Y.; Kim, I.Y.; Kim, S. Hierarchical support vector machine based heartbeat classification using higher order statistics and hermite basis function. In Proceedings of the 2008 Computers in Cardiology, Bologna, Italy, 14–17 September 2008. [Google Scholar]
- Osowski, S.; Hoai, L.T.; Markiewicz, T. Support vector machine-based expert system for reliable heartbeat recognition. IEEE Trans. Biomed. Eng. 2004, 51, 582–589. [Google Scholar] [CrossRef]
- de Lannoy, G.; Francois, D.; Delbeke, J.; Verleysen, M. Weighted conditional random fields for supervised interpatient heartbeat classification. IEEE Trans. Biomed. Eng. 2012, 59, 241–247. [Google Scholar] [CrossRef]
- Mondéjar-Guerra, V.; Novo, J.; Rouco, J.; Penedo, M.G.; Ortega, M. Heartbeat classification fusing temporal and morphological information of ECGs via ensemble of classifiers. Biomed. Signal Process. Control 2019, 47, 41–48. [Google Scholar] [CrossRef]
- Osowski, S.; Linh, T.H. ECG beat recognition using fuzzy hybrid neural network. IEEE Trans. Biomed. Eng. 2001, 48, 1265–1271. [Google Scholar] [CrossRef]
- De Lannoy, G.; François, D.; Delbeke, J.; Verleysen, M. Weighted SVMs and feature relevance assessment in supervised heart beat classification. In International Joint Conference on Biomedical Engineering Systems and Technologies; Springer: Berlin, Germany, 2010; pp. 212–223. [Google Scholar]
- Doquire, G.; de Lannoy, G.; François, D.; Verleysen, M. Feature Selection for Interpatient Supervised Heart Beat Classification. Comput. Intell. Neurosci. 2011, 2011, 1–9. [Google Scholar] [CrossRef]
- de Chazal, P.; O’Dwyer, M.; Reilly, R.B. Automatic classification of heartbeats using ECG morphology and heartbeat interval features. IEEE Trans. Biomed. Eng. 2004, 51, 1196–1206. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Huang, H.; Liu, J.; Zhu, Q.; Wang, R.; Hu, G. A new hierarchical method for inter-patient heartbeat classification using random projections and RR intervals. Biomed. Eng. Online 2014, 13, 90. [Google Scholar] [CrossRef] [PubMed]
- Llamedo, M.; Martinez, J.P. Heartbeat classification using feature selection driven by database generalization criteria. IEEE Trans. Biomed. Eng. 2011, 58, 616–625. [Google Scholar] [CrossRef] [PubMed]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Tsipouras, M.G.; Fotiadis, D.I.; Sideris, D. An arrhythmia classification system based on the RR-interval signal. Artif. Intell. Med. 2005, 33, 237–250. [Google Scholar] [CrossRef] [PubMed]
- Afkhami, R.G.; Azarnia, G.; Tinati, M.A. Cardiac arrhythmia classification using statistical and mixture modeling features of ECG signals. Pattern Recognit. Lett. 2016, 70, 45–51. [Google Scholar] [CrossRef]
- Banfield, R.E.; Hall, L.O.; Bowyer, K.W.; Kegelmeyer, W.P. A comparison of decision tree ensemble creation techniques. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 173–180. [Google Scholar] [CrossRef]
- Chen, S.; Hua, W.; Li, Z.; Li, J.; Gao, X. Heartbeat classification using projected and dynamic features of ECG signal. Biomed. Signal Process. Control 2017, 31, 165–173. [Google Scholar] [CrossRef]
- Marinho, L.B.; de Nascimento, M.M.N.; Souza, J.W.M.; Gurgel, M.V.; Filho, P.P.R.; de Albuquerque, V.H. A novel electrocardiogram feature extraction approach for cardiac arrhythmia classification. Future Gener. Comput. Syst. 2019, 97, 564–577. [Google Scholar] [CrossRef]
- Tafreshi, R.; Jaleel, A.; Lim, J.; Tafreshi, L. Automated analysis of ECG waveforms with atypical QRS complex morphologies. Biomed. Signal Process. Control 2014, 10, 41–49. [Google Scholar] [CrossRef]
| Dataset | NB | SVEB | VEB | FB | UB | Total |
|---|---|---|---|---|---|---|
| Train (DS1) | 45,866 | 944 | 3788 | 415 | 8 | 51,021 |
| Test (DS2) | 44,259 | 1837 | 3221 | 388 | 7 | 49,712 |
| Rank | Feature |
|---|---|
| 1 | (normalized) |
| 2 | (normalized) |
| 3 | / |
| 4 | / |
| 5 | |
| 6 | Fitting coefficient 1 of HBF with degree 4 () |
| 7 | |
| 8 | |
| 9 | |
| 10 | / |
| Prediction | ||||
|---|---|---|---|---|
| NB | SVEB | VEB | ||
| Label | NB | 43,494 | 655 | 67 |
| SVEB | 369 | 1443 | 25 | |
| VEB | 383 | 13 | 2814 | |
| FB | 277 | 0 | 65 | |
| QB | 4 | 2 | 3 | |
| NB | 97.68% | 98.27% | 97.97% | 96.14% |
| SVEB | 68.29% | 78.55% | 73.06% | |
| VEB | 94.62% | 87.36% | 90.85% |
| Work | Classifier | Type of Features | Number of Features Used | of Class NB | of Class SVEB | of Class VEB | |
|---|---|---|---|---|---|---|---|
| Llamedo and Martinez [32] | LD | R–R-intervals, WT, and time domain morphology | 8 | 96.48% | 17.16% | 83.89% | 93% |
| Huang et al. [31] | Ensemble of SVM + Threshold | R–R-intervals, Random projections | 101 | 97.59% | 57.68% | 92.37% | 93.8% |
| Afkhami et al. [35] | Ensemble of BDT | R–R-intervals, HOS, GMM | 33 | 97.89% | 88.64% | 85.82% | 96.15% |
| Chen et al. [37] | SVM | R–R-intervals, DCT Random projections | 33 | 96.88% | 33.37% | 77.29% | 93.1% |
| Marinho et al. [38] | Naive Bayes | HOS | 4 | (65.6%) * | (0.4%) * | (84.7%) * | 94.0% |
| Mondéjar- Guerra et al. [25] | Ensemble of SVM | R–R-intervals, HOS, WT, and time domain morphology | 45 | 97.04% | 60.74% | 94.29% | 94.5% |
| This work | RF | R–R-intervals, HBF and time domain morphology | 6 | 97.97% | 73.06% | 90.85% | 96.14% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saenz-Cogollo, J.F.; Agelli, M. Investigating Feature Selection and Random Forests for Inter-Patient Heartbeat Classification. Algorithms 2020, 13, 75. https://doi.org/10.3390/a13040075
Saenz-Cogollo JF, Agelli M. Investigating Feature Selection and Random Forests for Inter-Patient Heartbeat Classification. Algorithms. 2020; 13(4):75. https://doi.org/10.3390/a13040075
Chicago/Turabian StyleSaenz-Cogollo, Jose Francisco, and Maurizio Agelli. 2020. "Investigating Feature Selection and Random Forests for Inter-Patient Heartbeat Classification" Algorithms 13, no. 4: 75. https://doi.org/10.3390/a13040075
APA StyleSaenz-Cogollo, J. F., & Agelli, M. (2020). Investigating Feature Selection and Random Forests for Inter-Patient Heartbeat Classification. Algorithms, 13(4), 75. https://doi.org/10.3390/a13040075





