Non Data-Aided SNR Estimation for UAV OFDM Systems
Abstract
1. Introduction
2. Signals Model of UAV OFDM
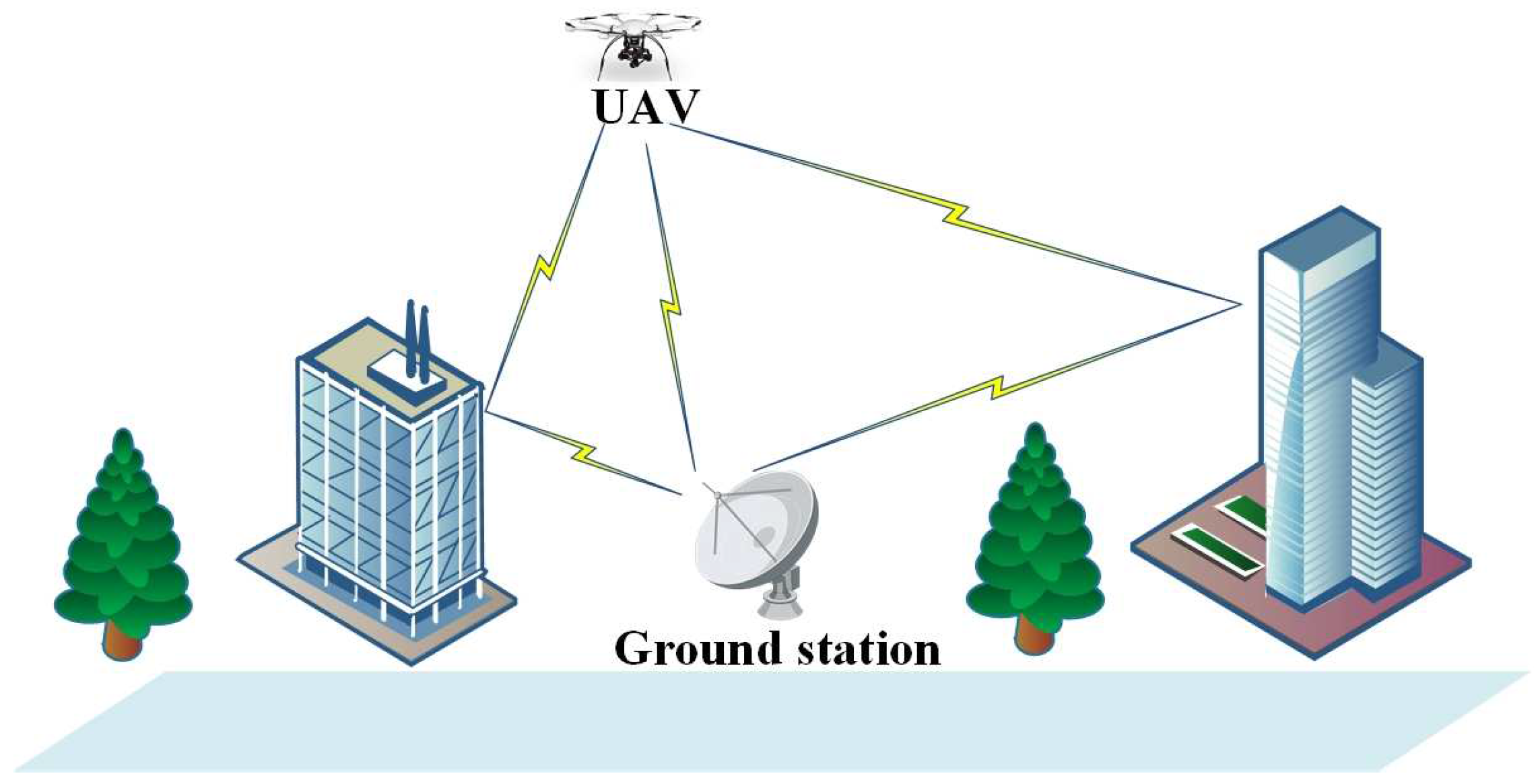
2.1. UAV Channel Model
2.2. The OFDM Model over UAV Channel
3. The Proposed NDA SNR Estimation Method
4. Numeric Simulation and Discussion
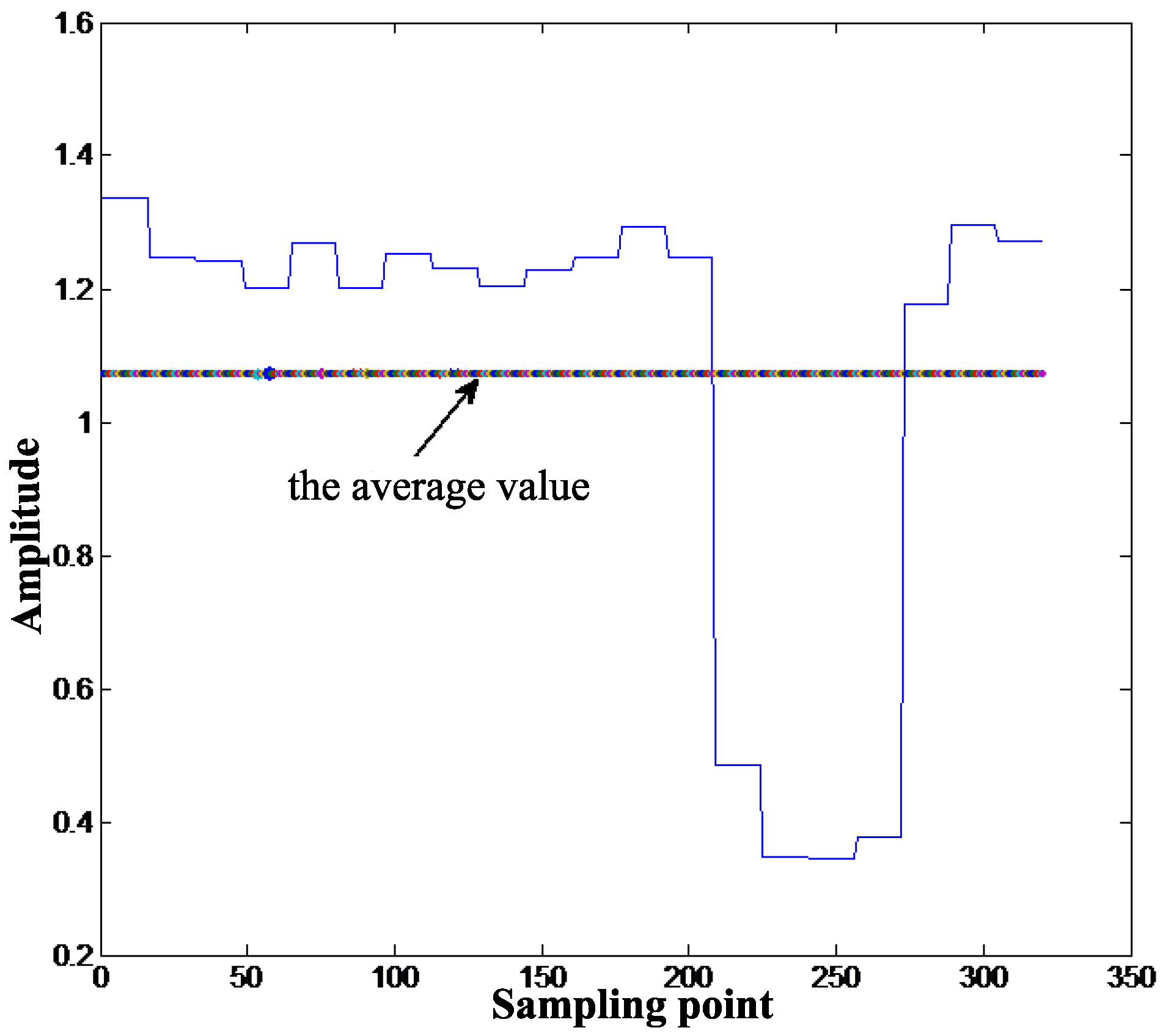
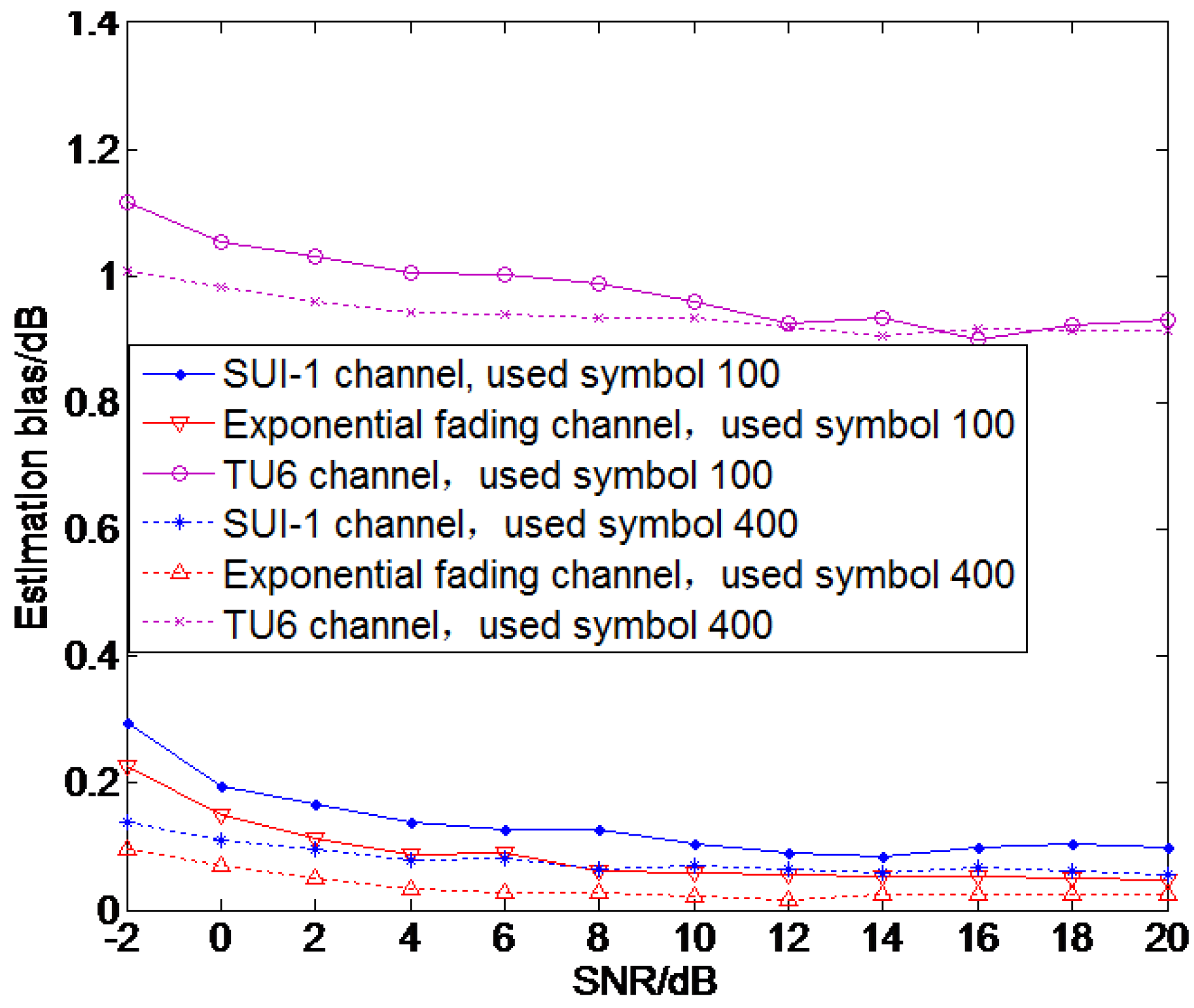
4.1. SNR Estimation Performance with Different Number of Symbols
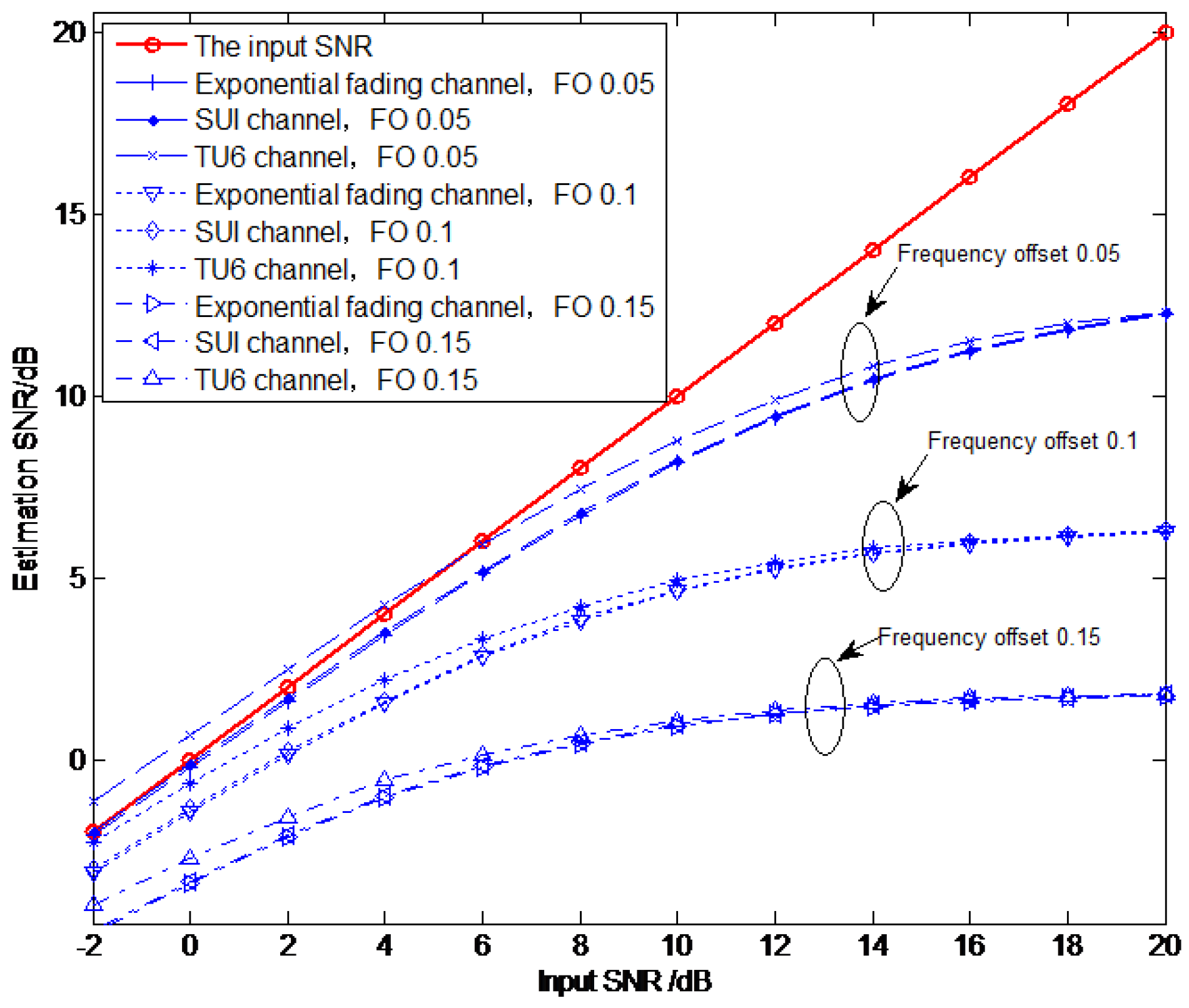
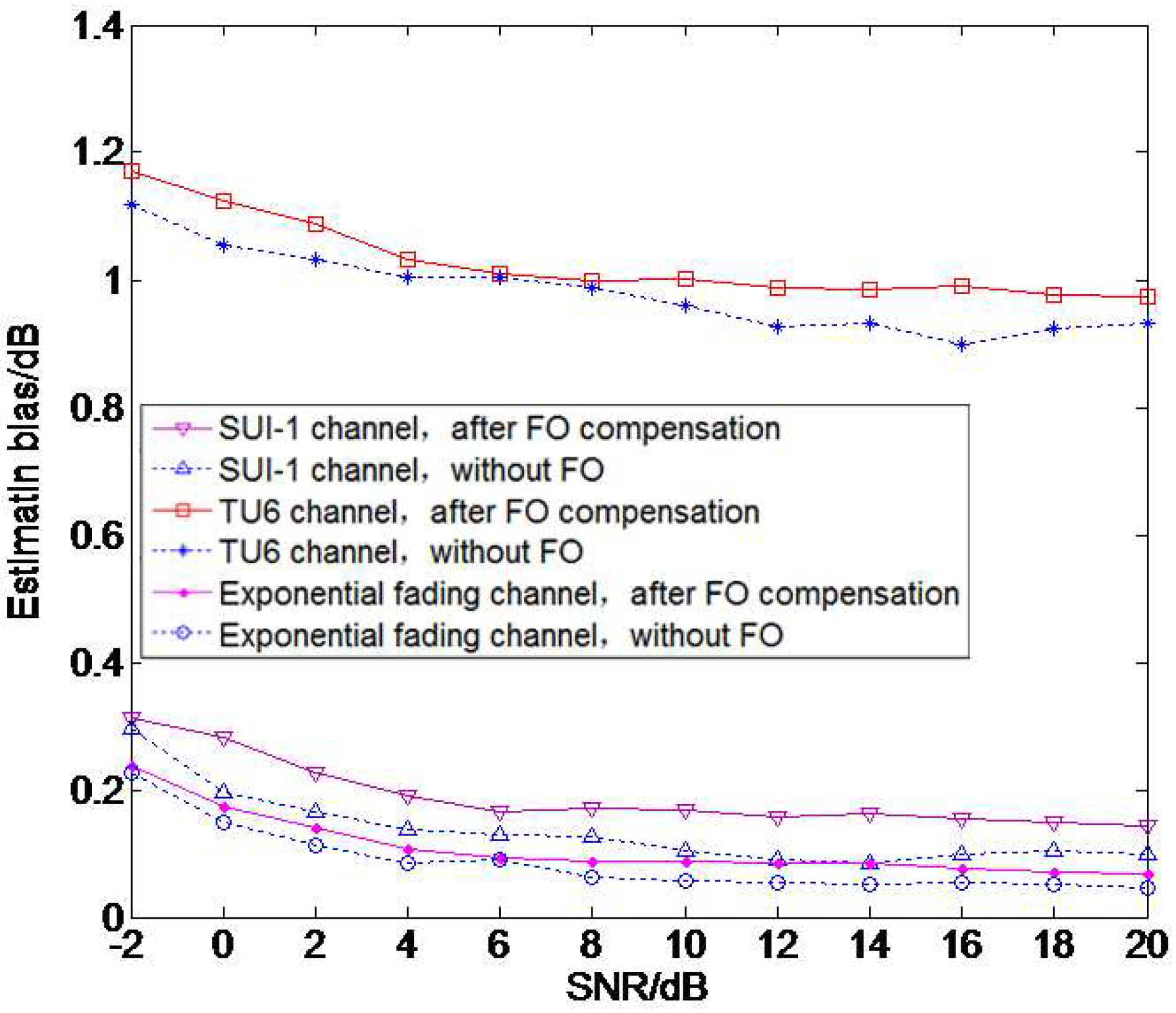
4.2. SNR Estimation Performance with Different Frequency Offsets
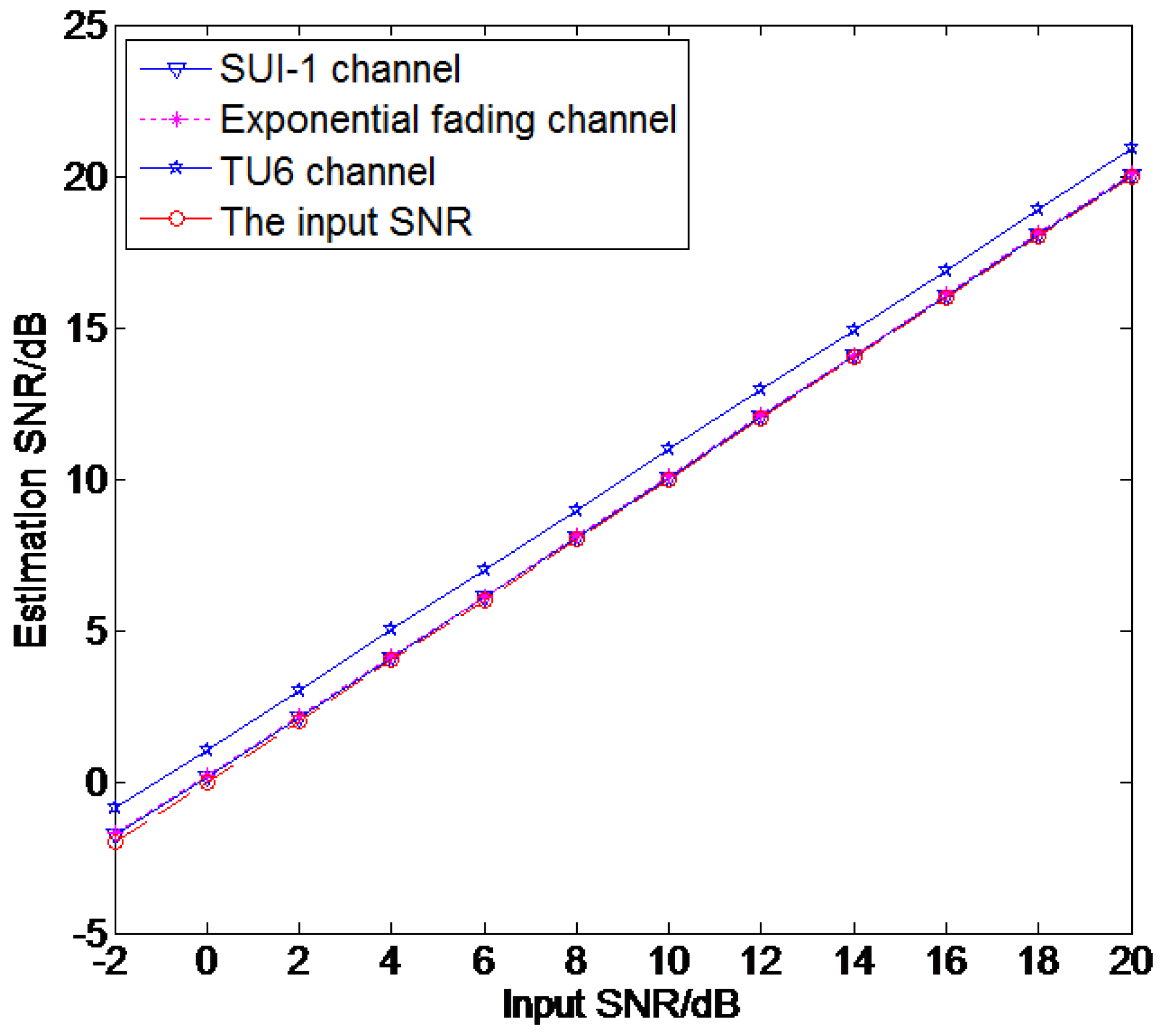
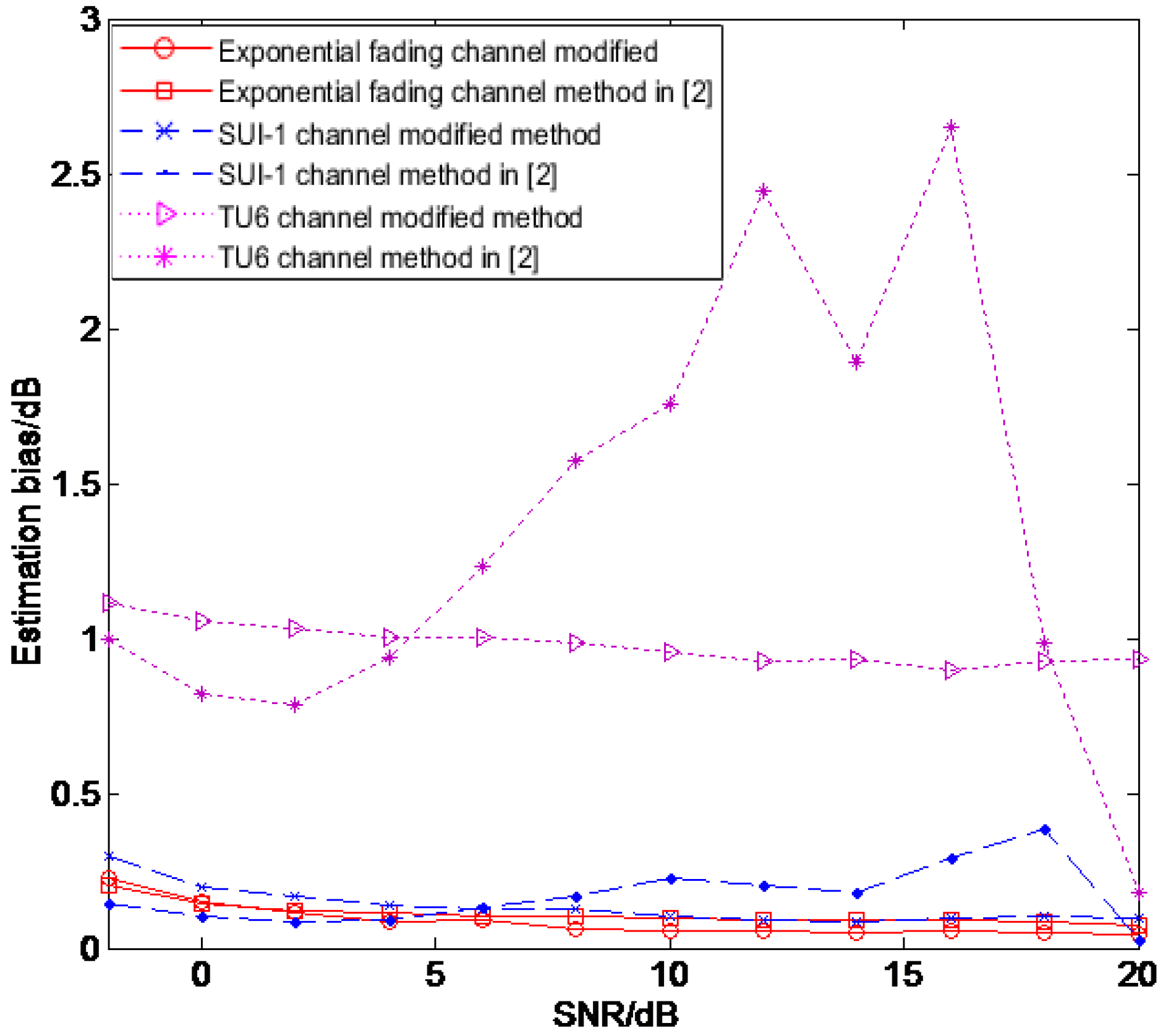
4.3. Estimation Performance Comparison of Different SNR Estimation Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, N.; Cheng, F.; Yu, F.R.; Tang, J.; Chen, Y.F.; Gui, G. Caching UAV assisted secure transmission in hyper-dense networks based on interference alignment. IEEE Trans. Commun. 2018, 66, 2281–2294. [Google Scholar] [CrossRef]
- Cui, T.; Tellambura, C. Power delay profile and noise variance estimation for OFDM. IEEE Commun. Lett. 2006, 10, 25–27. [Google Scholar] [CrossRef]
- Ding, X.; Li, Q. Optimization of Wireless Information and Power Transfer in Multiuser OFDM Systems. AEU Int. J. Electron. Commun.. 2018, 90, 171–174. [Google Scholar]
- Cheng, F.; Gui, G.; Zhao, N.; Chen, Y.; Tang, J.; Sari, H. UAV-relaying-assisted secure transmission with caching. IEEE Trans. Commun. 2019, 67, 3140–3153. [Google Scholar] [CrossRef]
- Zhao, N.; Yu, F.R.; Fan, L.S.; Chen, Y.F.; Tang, J.; Nallanathan, A.; Leung, V.C. Caching unmanned aerial vehicle-enabled small-cell networks: Employing energy-efficient methods that store and retrieve popular content. IEEE Veh. Technol. Mag. 2019, 14, 71–79. [Google Scholar] [CrossRef]
- Zhao, N.; Lu, W.D.; Sheng, M.; Chen, Y.F.; Tang, J.F.; Yu, R.; Wong, K. UAV-asisted emergency networks in disasters. IEEE Wirel. Commun. 2019, 26, 45–51. [Google Scholar] [CrossRef]
- Vahidi, V.; Saberinia, E. OFDM for payload communications of UAS: Channel estimation and ICI mitigation. IET Commun. 2017, 11, 2050–2356. [Google Scholar] [CrossRef]
- Vahidi, V.; Saberinia, E. Orthogonal frequency division multiplexing and channel models for payload communications of unmanned aerial systems. In Proceedings of the IEEE International Conference on Unmanned Aircraft Systems, Arlington, VA, USA, 7–10 June 2016; pp. 1156–1161. [Google Scholar]
- He, J.; Zhang, Y.T. Impact of doppler on high speed UAV OFDM system. In Proceedings of the IEEE International Conference on Communication Software and Networks, Macau, China, 27–28 Feburary 2009; pp. 742–745. [Google Scholar]
- Vappangi, S.; Vakamulla, V.M. Channel estimation in ACO-OFDM employing different transforms for VLC. AEU Int. J. Electron. Commun. 2018, 84, 111–122. [Google Scholar] [CrossRef]
- Singh, H.; Bansal, S. Channel Estimation with ISFLA based Pilot pattern Optimization for MIMO OFDM System. AEU Int. J. Electron. Commun. 2017, 81, 143–149. [Google Scholar] [CrossRef]
- Socheleau, F.X.; Aïssa-El-Bey, A.; Houcke, S. Non data-aided SNR estimation of OFDM signals. IEEE Commun. Lett. 2008, 12, 813–815. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, X.D. Blind noise variance and SNR estimation for OFDM systems based on information theoretic criteria. IEEE Trans. Signal Process. 2010, 90, 2766–2772. [Google Scholar] [CrossRef]
- Kim, S.A.; An, D.G.; Ryu, H.G.; Kim, J.U. Efficient SNR estimation in OFDM system. In Proceedings of the IEEE International Conference on Radio and Wireless Symposium, Phoenix, AZ, USA, 16–19 January 2011; pp. 182–185. [Google Scholar]
- Baumgartner, S.; Hirtz, G. A blind ML-SNR estimation method for OFDM systems in dispersive fading channels. In Proceedings of the Fourth International Conference on Consumer Electronics Berlin, Berlin, Germany, 7–10 September 2014; pp. 475–479. [Google Scholar]
- Tian, J.F.; Zhou, T.; Xu, T.H.; Hu, H.L.; Li, M.Q. Blind estimation of channel order and SNR for OFDM Systems. IEEE Access 2018, 6, 12656–12664. [Google Scholar] [CrossRef]
- Kim, J.W.; Park, H.S.; Bang, Y.J.; Kim, I. Precise estimation of noise power and SNR from OFDM signals. In Proceedings of the Seventh International Conference on Ubiquitous and Future Networks, Sapporo, Japan, 7–10 July 2015; pp. 367–371. [Google Scholar]
- He, P.; Li, Z.X.; Wang, X. A Low-complexity SNR estimation algorithm and channel estimation method for OFDM systems. In Proceedings of the IEEE International Conference On Information Science and Technology, Shenzhen, China, 26–28 April 2014; pp. 698–701. [Google Scholar]
- Baumgartner, S.; Hirtz, G.; Baumgartner, A. A modified maximum likelihood method for SNR estimation in OFDM based systems. In Proceedings of the IEEE International Conference On Consumer Electronics, Las Vegas, NV, USA, 10–13 January 2014; pp. 155–158. [Google Scholar]
- Cong, B.; Liu, Y.; Wang, T.Y.; Gu, F.F.; Shen, X.Q.; Yu, Q.H. Blind estimation of primary signal in cognitive satellite communication systems. In Proceedings of the IEEE International Conference On Optical Communications and Networks, Wuzhen, China, 7–10 August 2017; pp. 1–3. [Google Scholar]
- Morelli, M.; Moretti, M. Joint maximum likelihood estimation of CFO, noise power, and SNR in OFDM systems. IEEE Wirel. Commun. Lett. 2013, 2, 42–45. [Google Scholar] [CrossRef]
- Manzoor, S.; Othman, N.S. Signal to noise ratio estimation in OFDM based cooperative communication system. In Proceedings of the IEEE International Conference On Communications, Johor Bahru, Malaysia, 28–30 November 2017; pp. 84–89. [Google Scholar]
- Liu, M.; Ju, W.; Li, B. Non-data aided Joint Estimation of Symbol Timing Offset and Carrier Frequency Offset for OFDM/OQAM Systems. AEU Int. J. Electron. Commun. 2018, 87, 164–172. [Google Scholar] [CrossRef]
- Lin, S.F.; Wang, N.; Guo, C.P.; Shi, Y.H. Study on application of adoptive CP-OFDM in tactical UAV downlink transmission. In Proceedings of the IEEE International Conference On Smart Grid and Electrical Automation, Changsha, China, 9–10 June 2018; pp. 368–372. [Google Scholar]
- Tang, N.J.; Li, B.B.; Liu, M.Q. A modified blind OFDM systems parameters estimation method. In Proceedings of the IEEE International Conference On Communication Technology, Nanjing, China, 11–14 November 2010; pp. 1279–1282. [Google Scholar]
- Himeur, Y.; Boukabou, A. An adaptive recursive noise compensator for impulsive noise mitigation over OFDM power line communication. AEU Int. J. Electron. Commun. 2016, 70, 105–112. [Google Scholar] [CrossRef]
- Chin, W.L. ML estimation of timing and frequency offsets using distinctive correlation characteristics of OFDM signals over dispersive fading channels. IEEE Trans. Veh. Technol. 2011, 60, 444–456. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, M.; Tang, N.; Shang, B. Non Data-Aided SNR Estimation for UAV OFDM Systems. Algorithms 2020, 13, 22. https://doi.org/10.3390/a13010022
Li J, Liu M, Tang N, Shang B. Non Data-Aided SNR Estimation for UAV OFDM Systems. Algorithms. 2020; 13(1):22. https://doi.org/10.3390/a13010022
Chicago/Turabian StyleLi, Junfang, Mingqian Liu, Ningjie Tang, and Bodong Shang. 2020. "Non Data-Aided SNR Estimation for UAV OFDM Systems" Algorithms 13, no. 1: 22. https://doi.org/10.3390/a13010022
APA StyleLi, J., Liu, M., Tang, N., & Shang, B. (2020). Non Data-Aided SNR Estimation for UAV OFDM Systems. Algorithms, 13(1), 22. https://doi.org/10.3390/a13010022





