4.1. Mathematical Background
In this section, we give a brief introduction to directed flag complexes of directed graphs, and to persistent homology. For more detail, see [
6,
20,
21].
Definition 1. A graph G is a pair , where V is a finite set referred to as the vertices of G, and E is a subset of the set of unordered pairs of distinct points in V, which we call the edges of G. Geometrically the pair indicates that the vertices u and v are adjacent to each other in G. A directed graph, or a digraph, is similarly a pair of vertices V and edges E, except the edges are ordered pairs of distinct vertices, i.e., the pair indicates that there is an edge from v to w in G. In a digraph we allow reciprocal edges, i.e., both and may be edges in G, but we exclude loops, i.e., edges of the form .
Next we define the main topological objects considered in this article.
Definition 2. An abstract simplicial complex on a vertex set V is a collection X of non-empty finite subsets that is closed under taking non-empty subsets. An ordered simplicial complex on a vertex set V is a collection of non-empty finite ordered subsets that is closed under taking non-empty ordered subsets. Notice that the vertex set V does not have to have any underlying order. In both cases the subsets σ are called the simplices of X, and σ is said to be a k-simplex, or a k-dimensional simplex, if it consists of vertices. If is a simplex and , then τ is said to be a face of σ. If τ is a subset of V (ordered if X is an ordered simplicial complex) that contains σ, then τ is called a coface of σ. If is a k-simplex in X, then the i-th face of σ is the subset where by we mean omit the i-th vertex. For denote by the set of all d-dimensional simplices of X.
Notice that if X is any abstract simplicial complex with a vertex set V, then by fixing a linear order on the set V, we may think of each one of the simplices of X as an ordered set, where the order is induced from the ordering on V. Hence any abstract simplicial complex together with an ordering on its vertex set determines a unique ordered simplicial complex. Clearly any two orderings on the vertex set of the same complex yield two distinct but isomorphic ordered simplicial complexes. Hence from now on we may assume that any simplicial complex we consider is ordered.
Definition 3. Let be a directed graph. The directed flag complex is defined to be the ordered simplicial complex whose k-simplices are all ordered -cliques, i.e., -tuples , such that for all i, and for . The vertex is called the initial vertex of σ or the source of σ, while the vertex is called the terminal vertex of σ or the sink of σ.
Let
be a field, and let
X be an ordered simplicial complex. For any
let
be the
-vector space with basis given by the set
of all
k-simplices of
X. If
is a
k-simplex in
X, then the
i-th face of
is the subset
, where
means that the vertex
is removed to obtain the corresponding
-simplex. For
, define the
k-th boundary map
by
The boundary map has the property that
for each
[
21]. Thus
and one can make the following fundamental definition:
Definition 4. Let X be an ordered simplicial complex. The k-th homology group of X (over ) denoted by is defined to be If
X is an ordered simplicial complex, and
is a subcomplex, then the inclusion
induces a chain map
, i.e., a homomorphism
for each
, such that
. Hence one obtains an induced homomorphism for each
,
This is a particular case of a much more general property of homology, namely its functoriality with respect to so called simplicial maps. We will not however require this level of generality in the discussion below.
Definition 5. A filtered simplicial complex is a simplicial complex X together with a filter function , i.e., a function satisfying the property that if σ is a face of a simplex τ in X, then . Given , define the sublevel complex to be the inverse image .
Notice that the condition imposed on the function f in Definition 5 ensures that for each , the sublevel complex is a subcomplex of X, and if then . By default we identify X with . Thus a filter function f as above defines an increasing family of subcomplexes of X that is parametrised by the real numbers.
If the values of the filter function
f are a finite subset of the real numbers, as will always be the case when working with actual data, then by enumerating those numbers by their natural order we obtain a finite sequence of subspace inclusions
For such a sequence one defines its persistent homology as follows: for each
and each
one has a homomorphism
induced by the inclusion
. The image of this homomorphism is a
k-th persistent homology group of
X with respect to the given filtration, as it represents all homology classes that are present in
and carry over to
. To use the common language in the subject,
consists of the classes that were “born” at or before filtration level
i and are still “alive” at filtration level
j. The rank of
is a persistent Betti number for
X and is denoted by
.
Persistent homology can be represented as a collection of persistence pairs, i.e., pairs
, where
. The multiplicity of a persistence pair
in dimension
k is, roughly speaking, the number of linearly independent
k-dimensional homology classes that are born in filtration
i and die in filtration
j. More formally,
Persistence pairs can be encoded in persistence diagrams or persistence barcodes. See [
22] for more detail.
Flagser computes the persistent homology of filtered directed flag complexes. The filtration of the flag complexes is based on filtrations of the 0-simplices and/or the 1-simplices, from which the filtration values of the higher dimensional simplices can then be computed by various formulas. When using the trivial filtration algorithm of assigning the value 0 to each simplex, for example, Flagser simply computes the ordinary simplicial Betti numbers. The software uses a variety of tricks to shorten the computation time (see below for more details), and outperforms many other software packages, even for the case of unfiltered complexes (i.e., complexes with the trivial filtration). In the following, we mainly focus on (persistent) homology with coefficients in finite fields, and if we don’t mention it explicitly we consider the field with two elements .
4.2. Representing the Directed Flag Complex in Memory
An important feature of F
lagser is its memory efficiency which allows it to carry out rather large computations on a laptop with a mere 16 GB of RAM (see controlled examples in
Section 2). In order to achieve this, the directed flag complex of a graph is generated on the fly and not stored in memory. An
n-simplex of the directed flag complex
corresponds to a directed
-clique in the graph
. Hence each
n-simplex is identified with its list of vertices ordered by their in-degrees in the corresponding directed clique from 0 to
n. The construction of the directed flag complex is performed by a double iteration:
For an arbitrary fixed vertex , we iterate over all simplices which have as the initial vertex.
Iterate Step 1 over all vertices (but see 3 below).
This procedure enumerates all simplices exactly once.
In more detail, consider a fixed vertex
. The first iteration of Step 1 starts by finding all vertices
w such that there exists a directed edge from
to
w. This produces the set
of all 1-simplices of the form
, i.e., all 1-simplices that have
as their initial vertex. In the second iteration of Step 1, construct for each 1-simplex
obtained in the first iteration, the set
by finding the intersection of the two sets of vertices that can be reached from
and
, respectively. In other words,
This is the set of all 2-simplices in of the form . Proceed by iterating Step 1, thus creating the prefix tree of the set of simplices with initial vertex . The process must terminate, since the graph G is assumed to be finite. In Step 2 the same procedure is iterated over all vertices in the graph (under the constraint described in 3 below.)
This algorithm has three main advantages:
The construction of the directed flag complex is very highly parallelisable. In theory one could use one CPU for each of the vertices of the graph, so that each CPU computes only the simplices with this vertex as initial vertex.
Only the graph is loaded into memory. The directed flag complex, which is usually much bigger, does not have any impact on the memory footprint.
The procedure skips branches of the iteration based on the prefix. The idea is that if a simplex is not contained in the complex in question, then no simplex containing it as a face can be in the complex. Therefore, if we computed that a simplex is not contained in our complex, then we don’t have to iterate Step 1 on its vertices to compute the vertices w that are reachable from each of the . This allows us to skip the full iteration branch of all simplices with prefix . This is particularly useful for iterating over the simplices in a subcomplex.
In the code, the adjacency matrix (and for improved performance its transpose) are both stored as bitsets (Bitsets store a single bit of information (0 or 1) as one physical bit in memory, whereas usually every bit is stored as one byte (8 bit). This representation improves the memory usage by a factor of 8, and additionally allows the compiler to use much more efficient bitwise logical operations, like “AND” or “OR”. Example of the bitwise logical “AND” operation:
0111 and 1101 = 0101). This makes the computation of the directed flag complex more efficient. Given a
k-simplex
in
, the set of vertices
is computed as the intersection of the sets of vertices that the vertices
have a connection to. Each such set is given by the positions of the
1’s in the bitsets of the adjacency matrix in the rows corresponding to the vertices
, and thus the set intersection can be computed as the logical “AND” of those bitsets.
In some situations, we might have enough memory available to load the full complex into memory. For these cases, there exists a modified version of the software that stores the tree described above in memory, allowing to
perform computations on the complex such as counting, or computing co-boundaries etc., without having to recompute the intersections described above, and
associate data to each simplex with fast lookup time.
The second part is useful for assigning unique identifiers to each simplex. Without the complex in memory a hash map with custom hashing function has to be created for this purpose, which slows down the lookup of the global identifier of a simplex dramatically.
4.3. Computing the Coboundaries
In R
ipser, [
10], cohomology is computed instead of homology. The reason for this choice is that for typical examples, the coboundary matrix contains many more columns that can be skipped in the reduction algorithm than the boundary matrix [
23].
If is a simplex in a complex X, then is a canonical basis element in the chain complex for X with coefficients in the field . The hom-dual , i.e., the function that associates with and 0 with any other simplex, is a basis element in the cochain complex computing the cohomology of X with coefficients in . The differential in the cochain complex requires considering the coboundary simplices of any given simplex, i.e., all those simplices that contain the original simplex as a face of codimension 1.
In Ripser, the coboundary simplices are never stored in memory. Instead, the software enumerates the coboundary simplices of any given simplex by a clever indexing technique, omitting all coboundary simplices that are not contained in the complex defined by the filtration stage being computed. However, this technique only works if the number of theoretically possible coboundary entries is sufficiently small. In the directed situation, and when working with a directed graph with a large number of vertices, this number is typically too large to be enumerated by a 64-bit integer. Therefore, in Flagser we pre-compute the coboundary simplices into a sparse matrix, achieving fast coboundary iteration at the expense of longer initialisation time and more memory load. An advantage of this technique is that the computation of the coboundary matrices can be fully parallelised, again splitting the simplices into groups indexed by their initial vertex.
Given an ordered list of vertex identifiers characterising a directed simplex , the list of its coboundary simplices is computed by enumerating all possible ways of inserting a new vertex into this list to create a simplex in the coboundary of . Given a position , the set of vertices that could be inserted in that position is given by the intersection of the set of vertices that have a connection from each of the vertices and the set of vertices that have a connection to each of the vertices . This intersection can again be efficiently computed by bitwise logical operations of the rows of the adjacency matrix and its transpose (the transpose is necessary to efficiently compute the incoming connections of a given vertex).
With the procedure described above, we can compute the coboundary of every k-simplex. The simplices in this representation of the coboundary are given by their ordered list of vertices, and if we want to turn this into a coboundary matrix we have to assign consecutive numbers to the simplices of the different dimensions. We do this by creating a hash map, giving all simplices of a fixed dimension consecutive numbers starting at 0. This numbering corresponds to choosing the basis of our chain complex by fixing the ordering, and using the hash map we can lookup the number of each simplex in that ordering. This allows us to turn the coboundary information computed above into a matrix representation. If the flag complex is stored in memory, creating a hash map becomes unnecessary since we can use the complex as a hash map directly, adding the dimension-wise consecutive identifiers as additional information to each simplex. This eliminates the lengthy process of hashing all simplices and is therefore useful in situations where memory is not an issue.
4.4. Performance Considerations
Flagser is optimised for large computations. In this section we describe some of the algorithmic methods by which this is carried out.
4.4.1. Sorting the Columns of the Coboundary Matrix
The reduction algorithm iteratively reduces the columns in order of their filtration value (i.e., the filtration value of the simplex that this column represents). Each column is reduced by adding previous (already reduced) columns until the pivot element does not appear as the pivot of any previous column. While reducing all columns the birth and death times for the persistence diagram can be read off: roughly speaking, if a column with a certain filtration value ends up with a pivot that is the same as the pivot of a column with a higher filtration value , then this column represents a class that is born at time and dies at time . Experiments showed that the order of the columns is crucial for the performance of this reduction algorithm, so Flagser sorts the columns that have the same filtration values by an experimentally determined heuristic (see below). This is of course only useful when there are many columns with the same filtration values, for example when taking the trivial filtration where every simplex has the same value. In these cases, however, it can make very costly computations tractable.
The heuristic to sort the columns is applied as follows:
Sort columns in ascending order by their filtration value. This is necessary for the algorithm to produce the correct results.
Sort columns in ascending order by the number of non-zero entries in the column. This tries to keep the number of new non-zero entries that a reduction with such a column produces small.
Sort columns in descending order by the position of the pivot element of the unreduced column. This means that the larger the pivot (i.e., the higher the index of the last non-trivial entry), the lower the index of the column is in the sorted list. The idea behind this is that “long columns”, i.e., columns whose pivot element has a high index, should be as sparse as possible. Using such a column to reduce the columns to its right is thus more economical. Initial coboundary matrices are typically very sparse. Thus ordering the columns in this way gives more sparse columns with large pivots to be used in the reduction process.
Sort columns in descending order by their “pivot gap”, i.e., by the distance between the pivot and the next nontrivial entry with a smaller row index. A large pivot gap is desirable in case the column is used in reduction of columns to its right, because when using such a column to reduce another column, the added non-trivial entry in the column being reduced appears with a lower index. This may yield fewer reduction steps on average.
Remark 1. We tried various heuristics—amongst them different orderings of the above sortings—but the setting above produced by far the best results. Running a genetic algorithm in order to find good combinations and orderings of sorting criteria produced slightly better results on the small examples we trained on, but it did not generalise to bigger examples. It is known that finding the perfect ordering for this type of reduction algorithm is NP-hard [24]. 4.4.2. Approximate Computation
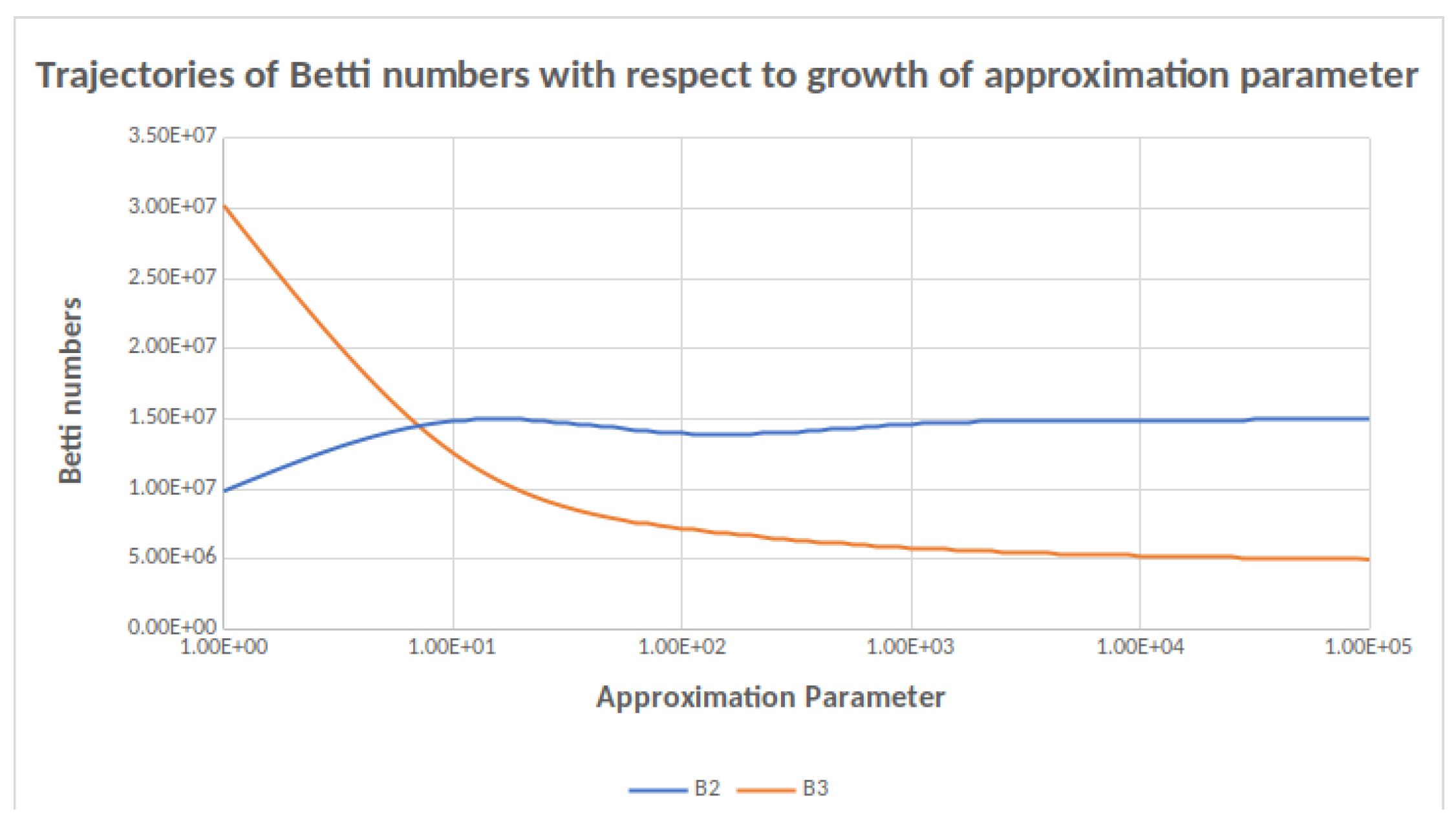
Another method that speeds up computations considerably is the use of Approximate computation. This simply means allowing Flagser to skip columns that need many reduction steps. The reduction of these columns takes the most time, so skipping even only the columns with extremely long reduction chains gives significant performance gains. By skipping a column, the rank of the matrix can be changed by at most one, so the error can be explicitly bounded. This is especially useful for computations with trivial (i.e., constant) filtrations, as the error in the resulting Betti numbers is easier to interpret than the error in the set of persistence pairs.
Experiments on smaller examples show that the theoretical error that can be computed from the number of skipped columns is usually much bigger than the actual error. Therefore, it is usually possible to quickly get rather reliable results that afterwards can be refined with more computation time. See
Table 9 for an example of the speed-up gained by Approximate computation. The user of F
lagser can specify an approximation level, which is given by a number (defaulting to infinity). This number determines after how many reduction steps the current column is skipped. The lower the number, the more the performance gain (and the more uncertainty about the result). At the current time it is not possible to specify the actual error margin for the computation, as it is very complicated to predict the number of reductions that will be needed for the different columns.
4.4.3. Dynamic Priority Queue
When reducing the matrix, Ripser stores the column that is currently reduced as a priority queue, ordering the entries in descending order by filtration value and in ascending order by an arbitrarily assigned index for entries with the same filtration value. Each index can appear multiple times in this queue, but due to the sorting all repetitions are next to each other in a contiguous block. To determine the final entries of the column after the reduction process, one has to loop over the whole queue and sum the coefficients of all repeated entries.
This design makes the reduction of columns with few reduction steps very fast but gets very slow (and memory-intensive) for columns with a lot of reduction steps: each time we add an entry to the queue it has to “bubble” through the queue and find its right place. Therefore, Flagser enhances this queue by dynamically switching to a hash-based approach if the queue gets too big: after a certain number of elements were inserted into the queue, the queue object starts to track the ids that were inserted in a hash map, storing each new entry with coefficient 1. If a new entry is then already found in the hash map, it is not again inserted into the queue but rather the coefficient of the hash map is updated, preventing the sorting issue described above. When removing elements from the front, the queue object then takes for each element that is removed from the front of the queue the coefficient stored in the hash map into account when computing the final coefficient of that index.
4.4.4. Apparent Pairs
In R
ipser, so-called apparent pairs are used in order to skip some computations completely. These rules are based on discrete Morse theory [
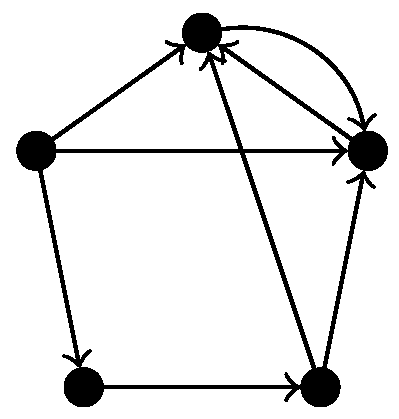
25], but they only apply for non-directed simplicial complexes. Since we consider directed graphs, the associated flag complex is a semi-simplicial rather than simplicial complex, so we cannot use this simplification. Indeed, experiments showed that enabling the skipping of apparent pairs yields wrong results for directed flag complexes of certain directed graphs. For example, when applied to the directed flag complex of the graph in
Figure 5, using apparent pairs gives
and not using apparent pairs gives
, which is visibly the correct answer.
Experiments showed that when applied to directed flag complexes that arise from graphs without reciprocal connections (so that the resulting directed flag complex is a simplicial complex), enabling the skipping of apparent pairs does not give a big performance advantage. In fact, we found a significant reduction in run time for subgraphs of the connectome of the reconstruction of the neocortical column based data averaged across the five rats that were used in [
6], the Google plus network and the Twitter network from KONECT [
11].