Comparative Analysis of Different Model-Based Controllers Using Active Vehicle Suspension System
Abstract
1. Introduction
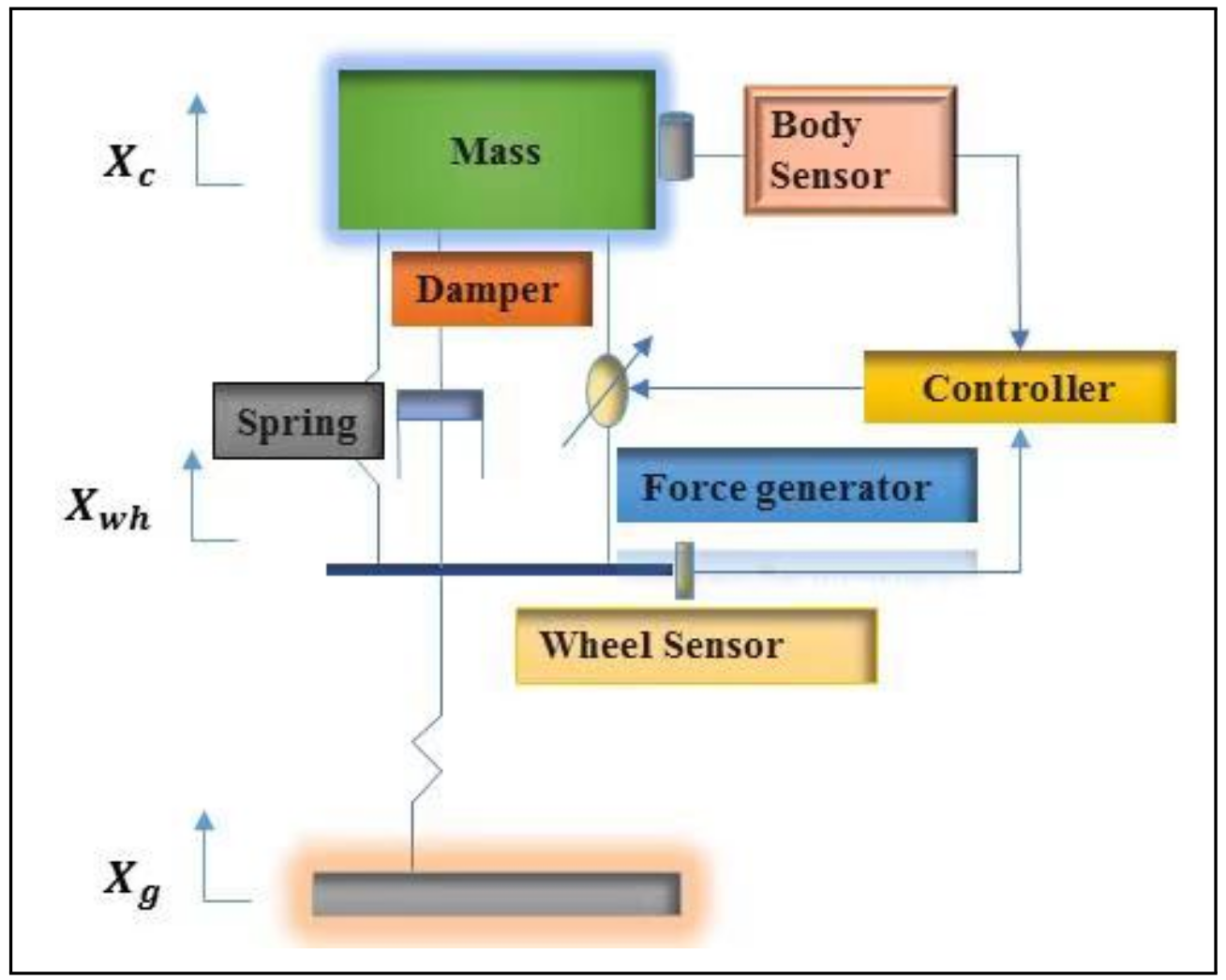
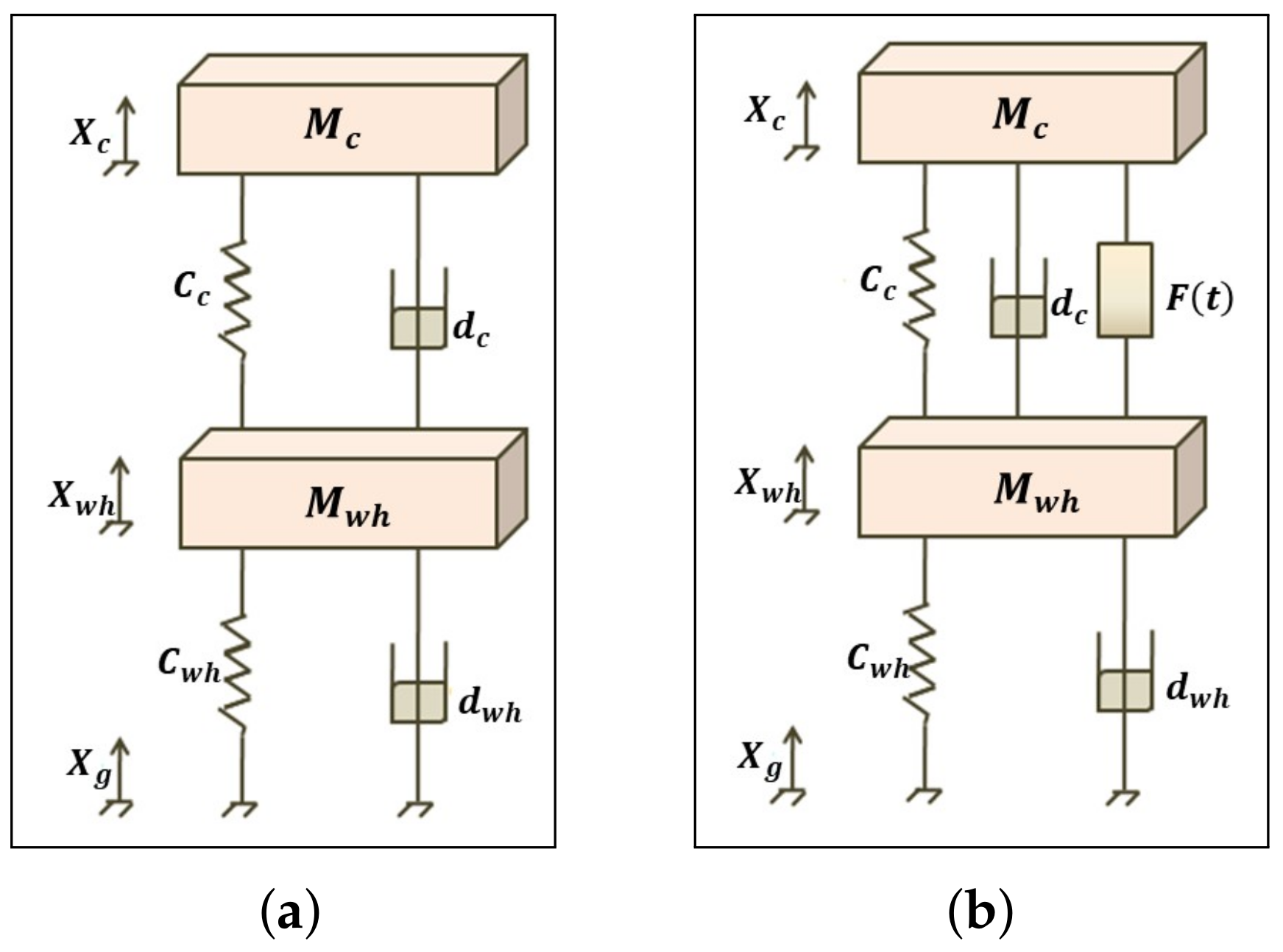
2. Mathematical Model of Quarter-Car Active Suspension System
2.1. Mathematical Model
2.2. Active Suspension System
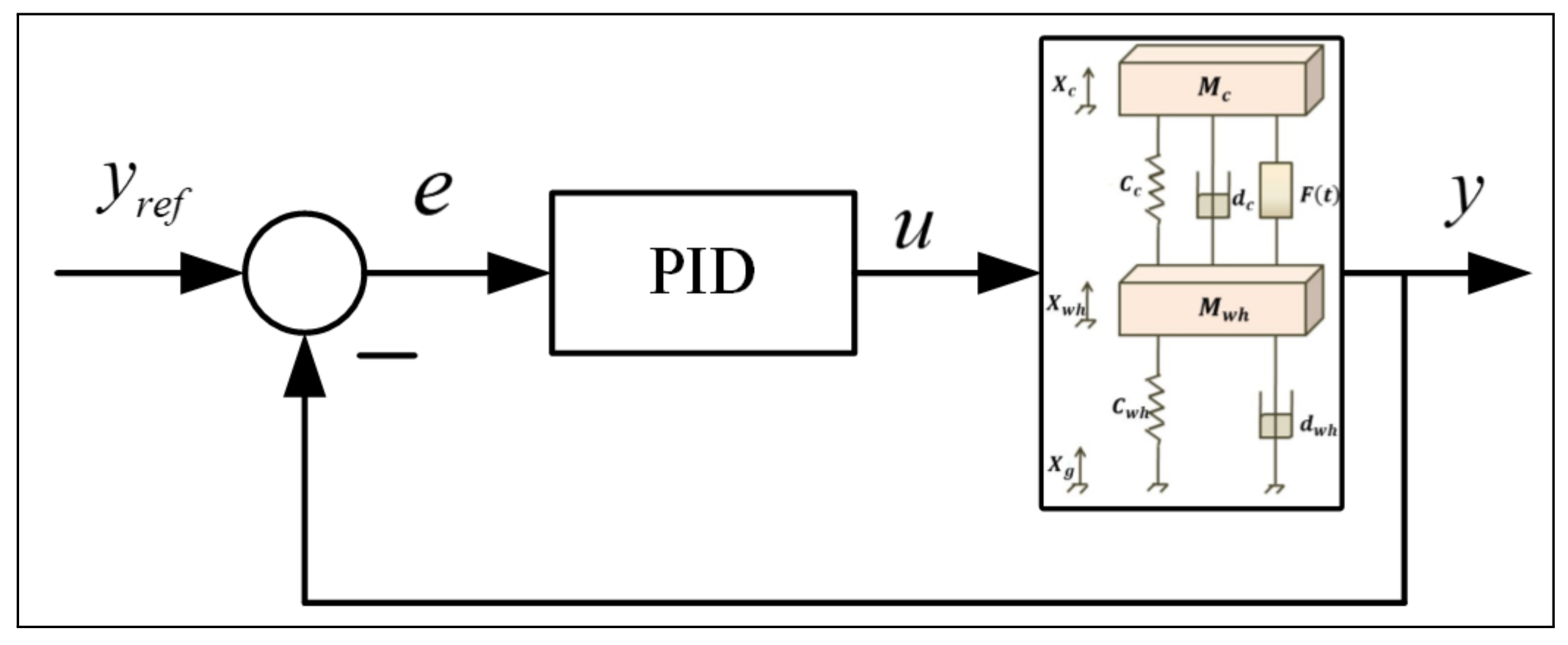
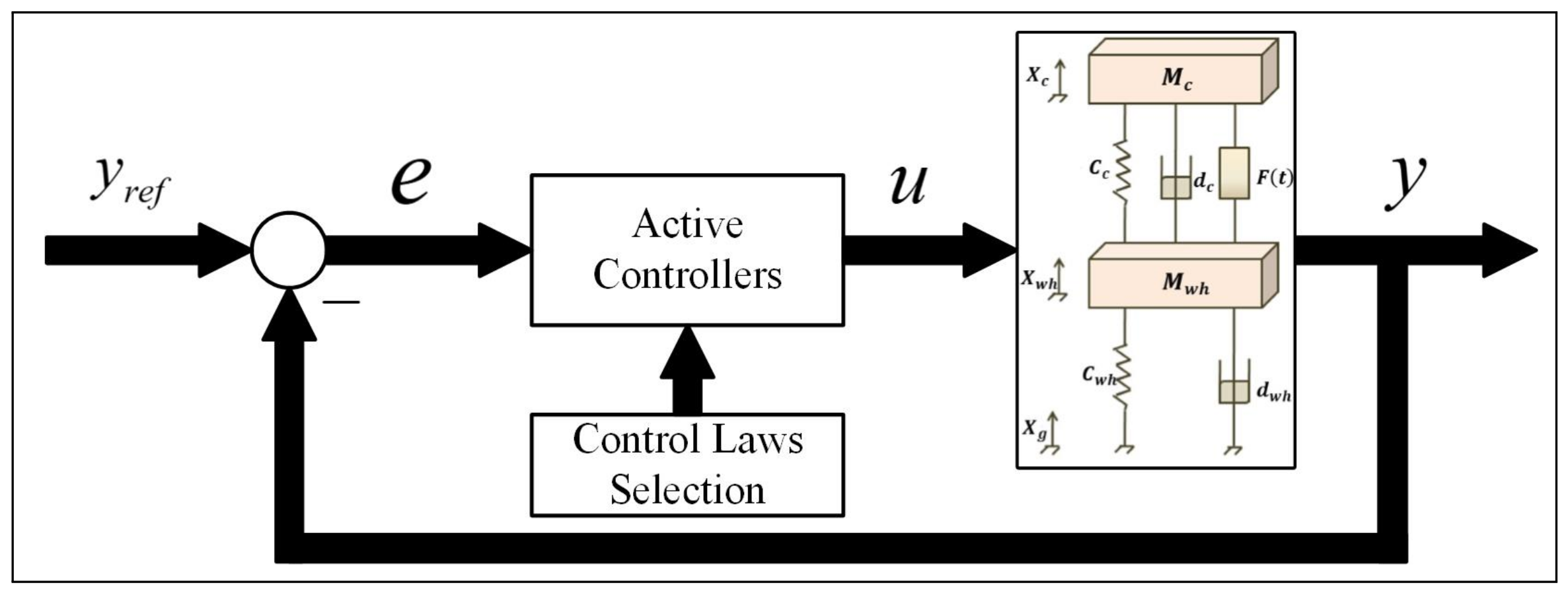
3. Control Methods
3.1. PID Controller
3.2. Linear Quadratic Regulator
3.3. First-Order Sliding Mode Control
3.4. Integral Sliding Mode Control
3.5. High Order Sliding Mode Controller with Super Twisting Algorithm
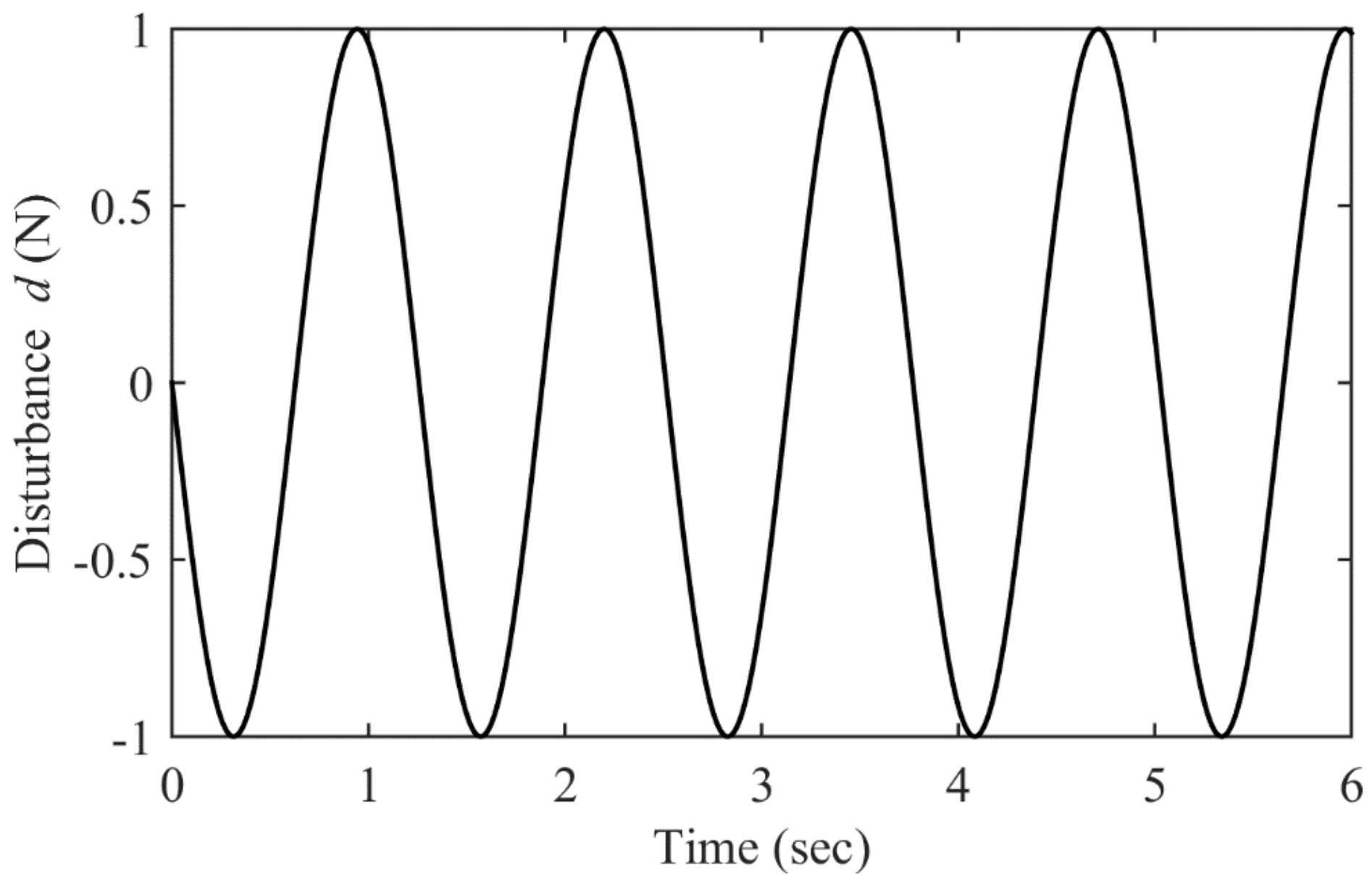
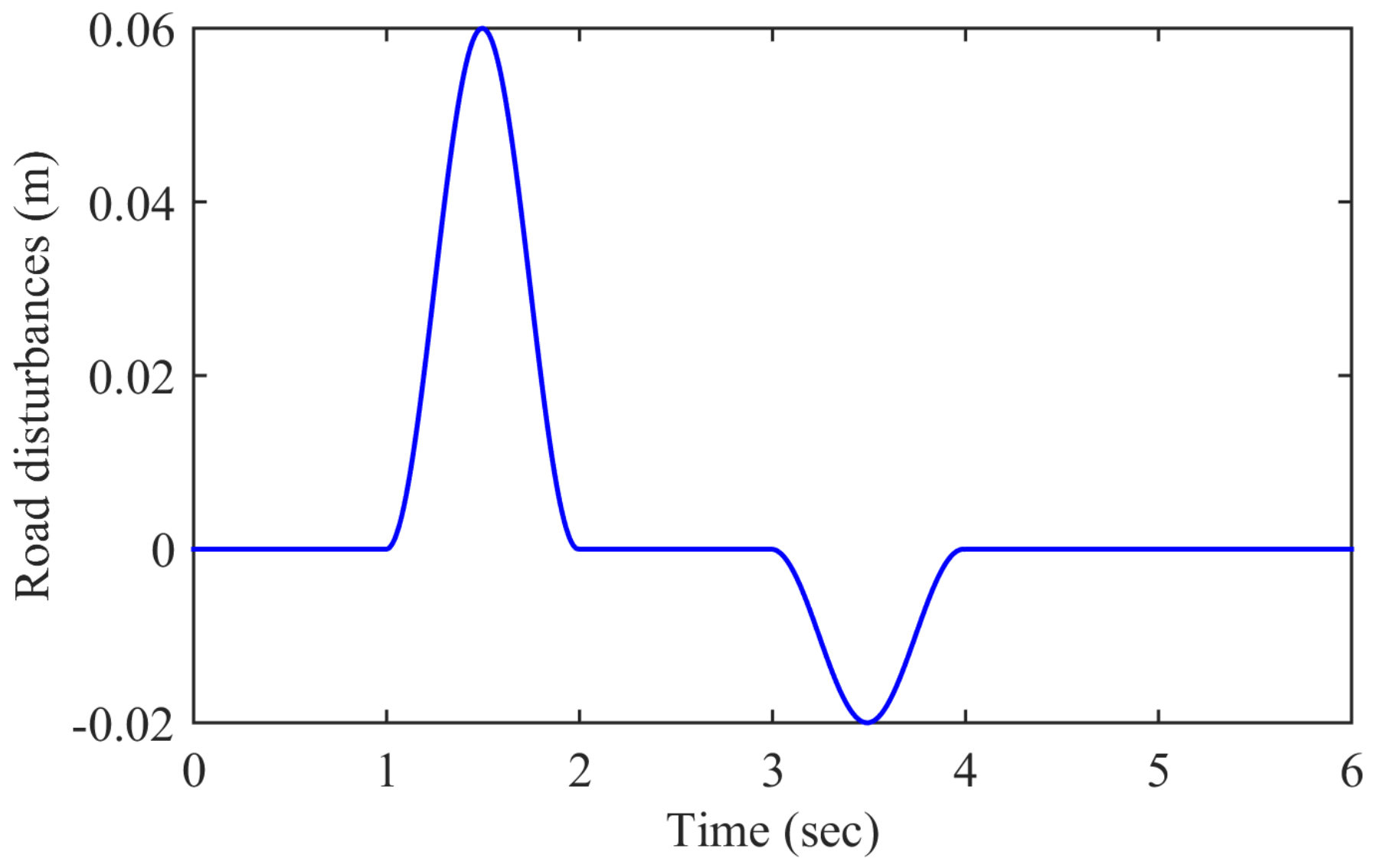
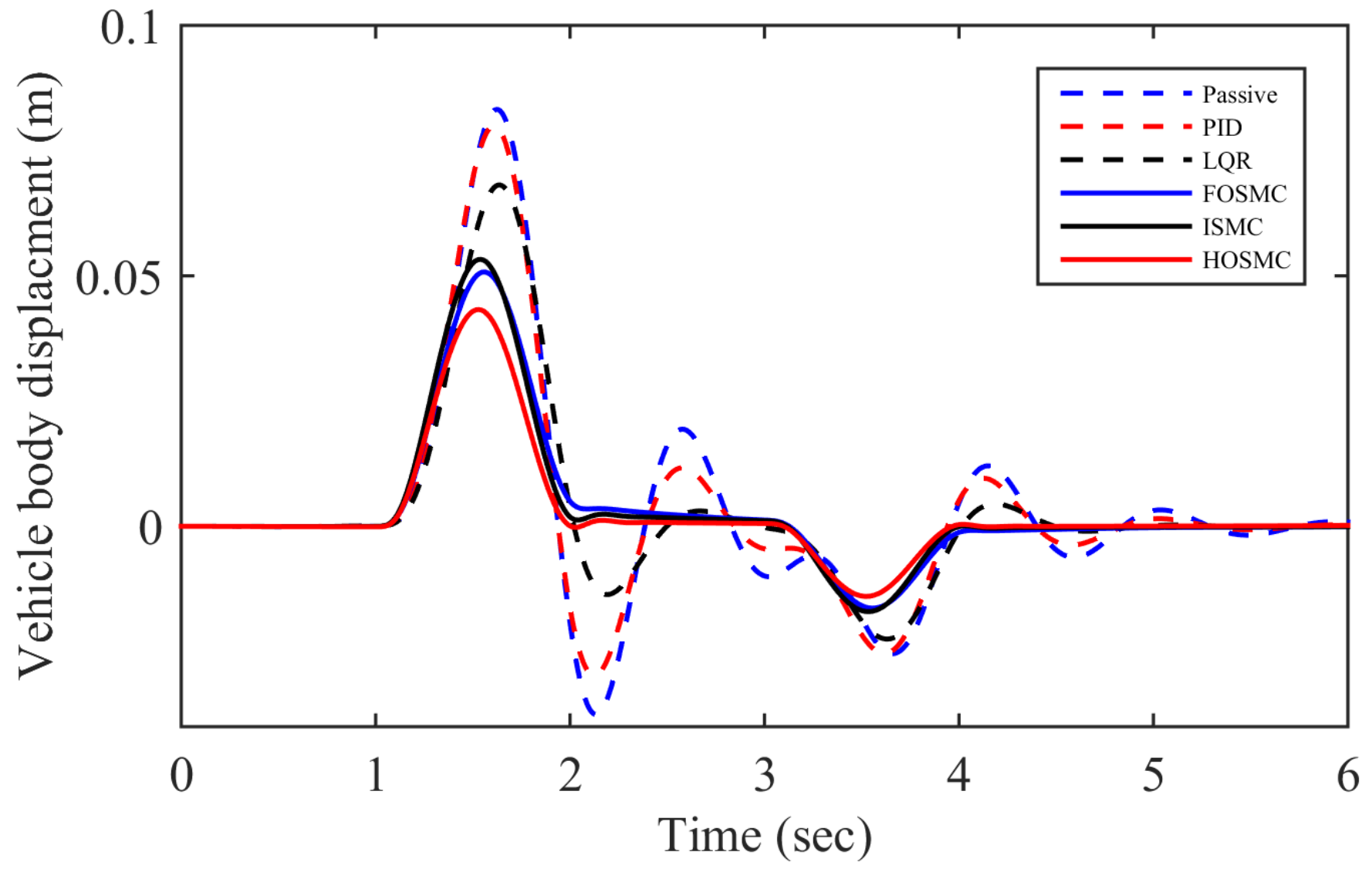
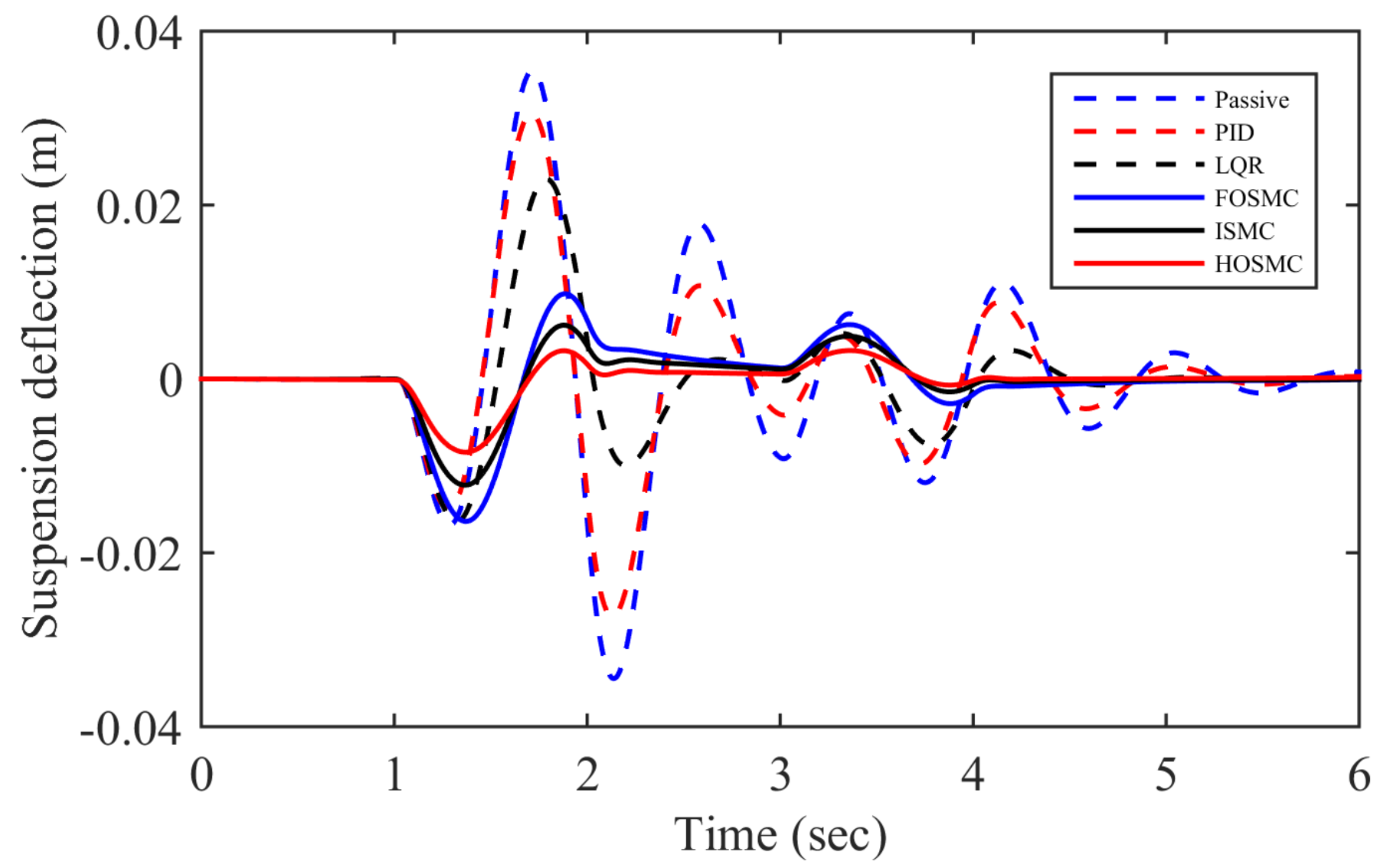
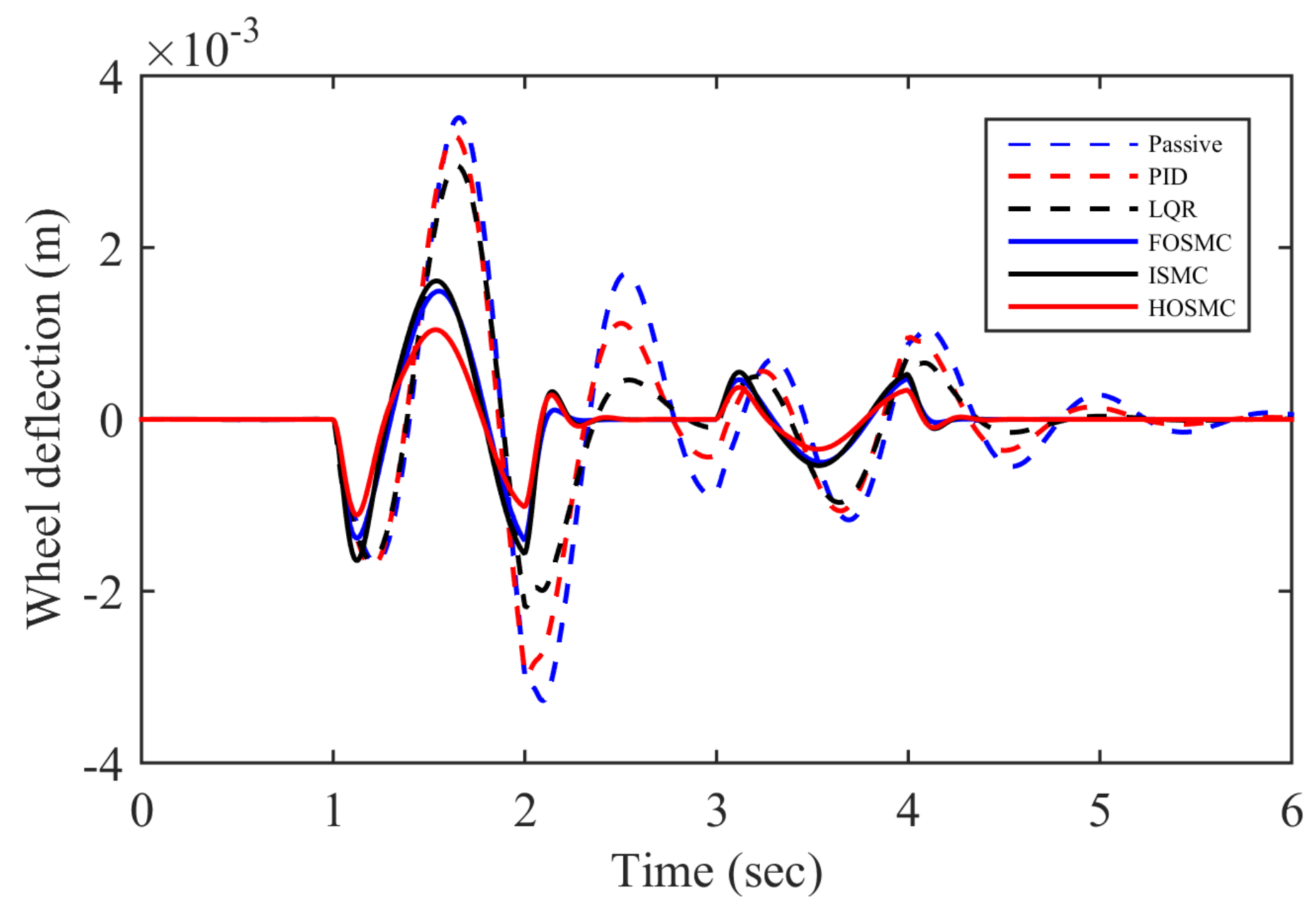
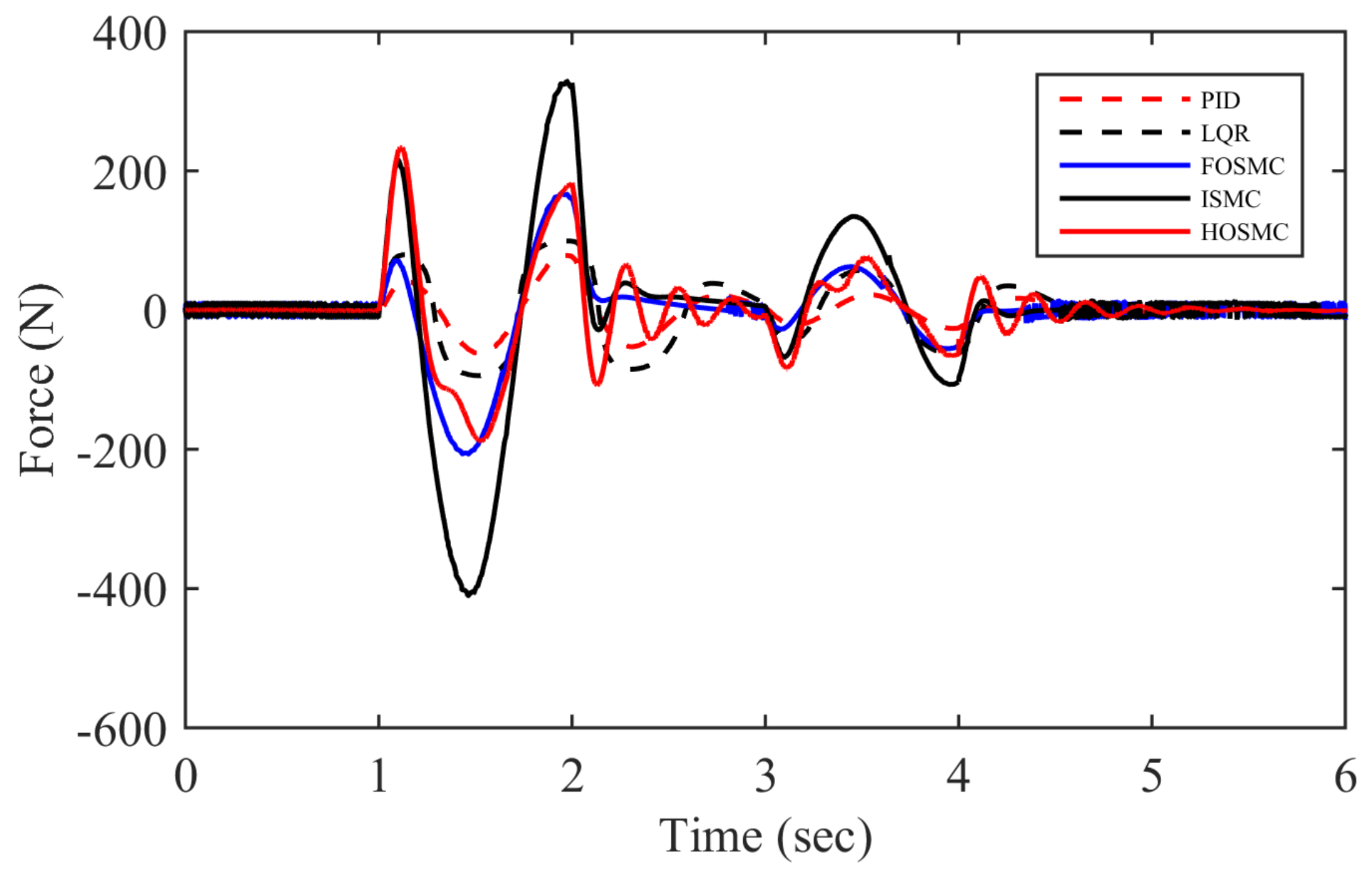
4. Numerical Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Du, M.; Zhao, D.; Yang, B.; Wang, L. Terminal sliding mode control for full vehicle active suspensionsystems. J. Mech. Sci. Technol. 2018, 32, 2851–2866. [Google Scholar] [CrossRef]
- Wang, H.; Mustafa, G.I.; Tian, Y. Model-free fractional-order sliding mode control for an active vehiclesuspension system. Adv. Eng. Softw. 2018, 115, 452–461. [Google Scholar] [CrossRef]
- Daniyan, I.; Mpofu, K.; Daniyan, O.; Adeodu, A. Dynamic modelling and simulation of rail car suspension systems using classic controls. Cogent Eng. 2019, 6, 1602927. [Google Scholar] [CrossRef]
- Gao, H.; Xue, S.; Yin, S.; Qiu, J.; Wang, C. Output feedback control of multirate sampled-data systems with frequency specifications. IEEE Trans. Control Syst. Technol. 2016, 25, 1599–1608. [Google Scholar] [CrossRef]
- Han, S.Y.; Zhong, X.F.; Chen, Y.H.; Tang, G.Y. Discrete approximate optimal vibration control for nonlinear vehicle active suspension. J. Vibro Eng. 2017, 19, 1287–1300. [Google Scholar] [CrossRef][Green Version]
- Harrag, A.; Messalti, S. PSO-based SMC variable step size P & O MPPT controller for PV systems under fast changing atmospheric conditions. Int. J. Numerical Model. Electronic Netw. Devices Fields 2019, e2603. [Google Scholar] [CrossRef]
- M’Sirdi, N.; Rabhi, N.; Fridman, A.; Davila, L.; Delanne, J. Second Order Sliding-Mode Observer for Estimation of Vehicle Dynamic Parameters. Int. J. Veh. Des. 2008, 48, 190–207. [Google Scholar] [CrossRef]
- Kashem, S.B.A.; Ektesabi, M.; Nagarajah, R. Comparison between different sets of suspension parameters and introduction of new modified skyhook control strategy incorporating varying road condition. Veh. Syst. Dyn. 2012, 50, 1173–1190. [Google Scholar] [CrossRef]
- M’Sirdi, N.; Rabhi, N.; Fridman, A.; Davila, L.; Delanne, J. Load-dependent observer design for active suspension systems. Int. J. Veh. Des. 2015, 68, 163–190. [Google Scholar]
- Bai, R.; Guo, D. Sliding-Mode Control of the Active Suspension System with the Dynamics of a Hydraulic Actuator. Complexity 2018, 18, 5907208. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Y.; Geng, Y. Fault-tolerant sliding mode control for uncertain active suspension systems against simultaneous actuator and sensor faults via a novel sliding mode observer. Opt. Control Appl. Methods 2018, 39, 1728–1749. [Google Scholar] [CrossRef]
- Dong, X.; Zhao, D.; Yang, B.; Han, C. Fractional-order control of active suspension actuator based on parallel adaptive clonal selection algorithm. J. Mech. Sci. Technol. 2016, 30, 2769–2781. [Google Scholar] [CrossRef]
- Khan, L.; Qamar, S.; Khan, M.U. Comparative analysis of adaptive NeuroFuzzy control techniques for full car active suspension system. Arabian J. Sci. Eng. 2014, 39, 2045–2069. [Google Scholar] [CrossRef]
- Xia, G.; Hua, Y.; Tang, X.; Zhao, L.; Chen, W. Internal-model control of vehicle chassis based on wavelet-network dynamic inversion method. Int. J. Veh. Auton. Syst. 2018, 14, 170–195. [Google Scholar] [CrossRef]
- Hasbullah, F.; Faris, W.F. Simulation of disturbance rejection control of half-car active suspension system using active disturbance rejection control with decoupling transformation. J. Phys. Conf. Ser. IOP Publ. 2017, 949, 012025. [Google Scholar] [CrossRef]
- Khan, L.; Qamar, S.; Khan, U. 2016. Adaptive PID control scheme for full car suspension control. J. Chin. Ins. Eng. 2016, 39, 169–185. [Google Scholar] [CrossRef]
- Huang, Y.; Na, J.; Wu, X.; Gao, G.B.; Guo, Y. Robust adaptive control for vehicle active suspension systems with uncertain dynamics. Trans. Inst. Meas. Control 2018, 40, 1237–1249. [Google Scholar] [CrossRef]
- Ikenaga, S.; Lewis, F.L.; Campos, J.; Davis, L. Active suspension control of ground vehicle based on a full-vehicle model. In Proceedings of the 2000 American Control Conference, ACC (IEEE Cat. No. 00CH36334), Chicago, IL, USA, 28–30 June 2000; Volume 6, pp. 4019–4024. [Google Scholar]
- Chen, Y.; Wang, Z.L.; Qiu, J.; Huang, H.Z. Hybrid fuzzy skyhook surface control using multi-objective microgenetic algorithm for semi-active vehicle suspension system ride comfort stability analysis. J. Dyn. Syst. Meas. Control 2012, 134, 041003. [Google Scholar] [CrossRef]
- Rizvi, S.M.H.; Abid, M.; Khan, A.Q.; Satti, S.G.; Latif, J. H∞ control of 8 degrees of freedom vehicle active suspension system. J. King Saud Univ.-Eng. Sci. 2018, 30, 161–169. [Google Scholar] [CrossRef]
- Yagiz, N.; Hacioglu, Y. Backstepping control of a vehicle with active suspensions. Control Eng. Pract. 2008, 16, 1457–1467. [Google Scholar] [CrossRef]
- Martins, I.; Esteves, J.; Marques, G.D.; Da Silva, F.P. Permanent-magnets linear actuators applicability in automobile active suspensions. IEEE Trans. Veh. Technol. 2006, 55, 86–94. [Google Scholar] [CrossRef]
- Rosenfield, S. Pros and Cons of Pneumatic, Hydraulic, and Electric Actuation. Motor Control and Switchgear. 2017. Available online: https://electronics360.globalspec.com/article/9480/pros-and-cons-of-pneumatic-hydraulic-and-electric-actuation (accessed on 8 December 2019).
- Pujol, G.; Acho, L. Stabilization of the Furuta Pendulum with backlash using H-LMI technique: Experimental validation. Asian J. Control 2010, 12, 460–467. [Google Scholar]
- Ding, R.; Wang, R.; Meng, X.; Chen, L. A modified energy-saving skyhook for active suspension based on a hybrid electromagnetic actuator. J. Vib. Control 2019, 25, 286–297. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Valderrabano-Gonzalez, A.; Favela-Contreras, A.; Hernandez-Avila, J.L.; Lopez-Garcia, I.; Tapia-Olvera, R. An Active Vehicle Suspension Control Approach with Electromagnetic and Hydraulic Actuators. In Actuators; Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2019; Volume 8, p. 35. [Google Scholar]
- Ozer, H.O.; Hacioglu, Y.; Yagiz, N. High order sliding mode control with estimation for vehicle active suspensions. Trans. Inst. Meas. Control 2018, 40, 1457–1470. [Google Scholar] [CrossRef]
- Wang, G.; Chen, C.; Yu, S. Finite-time sliding mode tracking control for active suspension systems via extended super-twisting observer. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2018, 231, 459–470. [Google Scholar] [CrossRef]
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Levant, A. Principles of 2-sliding mode design. Automatica 2007, 43, 576–586. [Google Scholar] [CrossRef]
- Qamar, S.; Khan, L.; Ali, S. Adaptive B-spline based neuro-fuzzy control for full car active suspension system. Middle-East J. Sci. Res. 2013, 16, 1348–1360. [Google Scholar]
- Irfan, S.; Mehmood, A.; Razzaq, M.T.; Iqbal, J. Advanced sliding mode control techniques for inverted pendulum: Modelling and simulation. Eng. Sci. Technol. Int. J. 2018, 21, 753–759. [Google Scholar] [CrossRef]
- Youness, S.; Lobusov, E. Networked control for active suspension system. Procedia Comput. Sci. 2019, 150, 123–130. [Google Scholar] [CrossRef]
| Model Parameters | Symbol Representation | Values | Standard Units |
|---|---|---|---|
| Damping Unsprung Coefficient | 1000 | Ns/m | |
| Damping Sprung Coefficient | 18,000 | Ns/m | |
| Stiffness Value of Wheel | 16,182 | N/m | |
| Stiffness Value of Suspension Spring | 190,000 | N/m | |
| Sprung Mass or Vehicle Body Mass | 290 | Kg | |
| Unsprung Mass or Suspension Mass | 60 | Kg |
| Active Controllers | k | Q | R | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HOSMC | - | - | 100 | 31.5 | 2.2 | - | - | - | - | - |
| ISMC | 10 | 0.5 | 50 | - | - | - | - | - | - | - |
| FOSMC | - | - | - | - | - | diag(1000, 20, 80) | 1 | - | - | - |
| LQR | 20 | 0.04 | 3 | - | - | - | - | - | - | - |
| PID | - | - | - | - | - | - | - | 100 | 4000 | 50 |
| Sprung Mass | Active Controller | |||
|---|---|---|---|---|
| Passive | 0.00075 | 0.0222 | 0.7583 | |
| PID | 0.00060 | 0.0209 | 0.6556 | |
| LQR | 0.00054 | 0.01989 | 0.5799 | |
| Body displacement | FOSMC | 0.00043 | 0.01792 | 0.4478 |
| ISMC | 0.00021 | 0.01298 | 0.3007 | |
| HOSMC | 0.00019 | 0.01156 | 0.2883 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahid, Y.; Wei, M. Comparative Analysis of Different Model-Based Controllers Using Active Vehicle Suspension System. Algorithms 2020, 13, 10. https://doi.org/10.3390/a13010010
Shahid Y, Wei M. Comparative Analysis of Different Model-Based Controllers Using Active Vehicle Suspension System. Algorithms. 2020; 13(1):10. https://doi.org/10.3390/a13010010
Chicago/Turabian StyleShahid, Yumna, and Minxiang Wei. 2020. "Comparative Analysis of Different Model-Based Controllers Using Active Vehicle Suspension System" Algorithms 13, no. 1: 10. https://doi.org/10.3390/a13010010
APA StyleShahid, Y., & Wei, M. (2020). Comparative Analysis of Different Model-Based Controllers Using Active Vehicle Suspension System. Algorithms, 13(1), 10. https://doi.org/10.3390/a13010010




