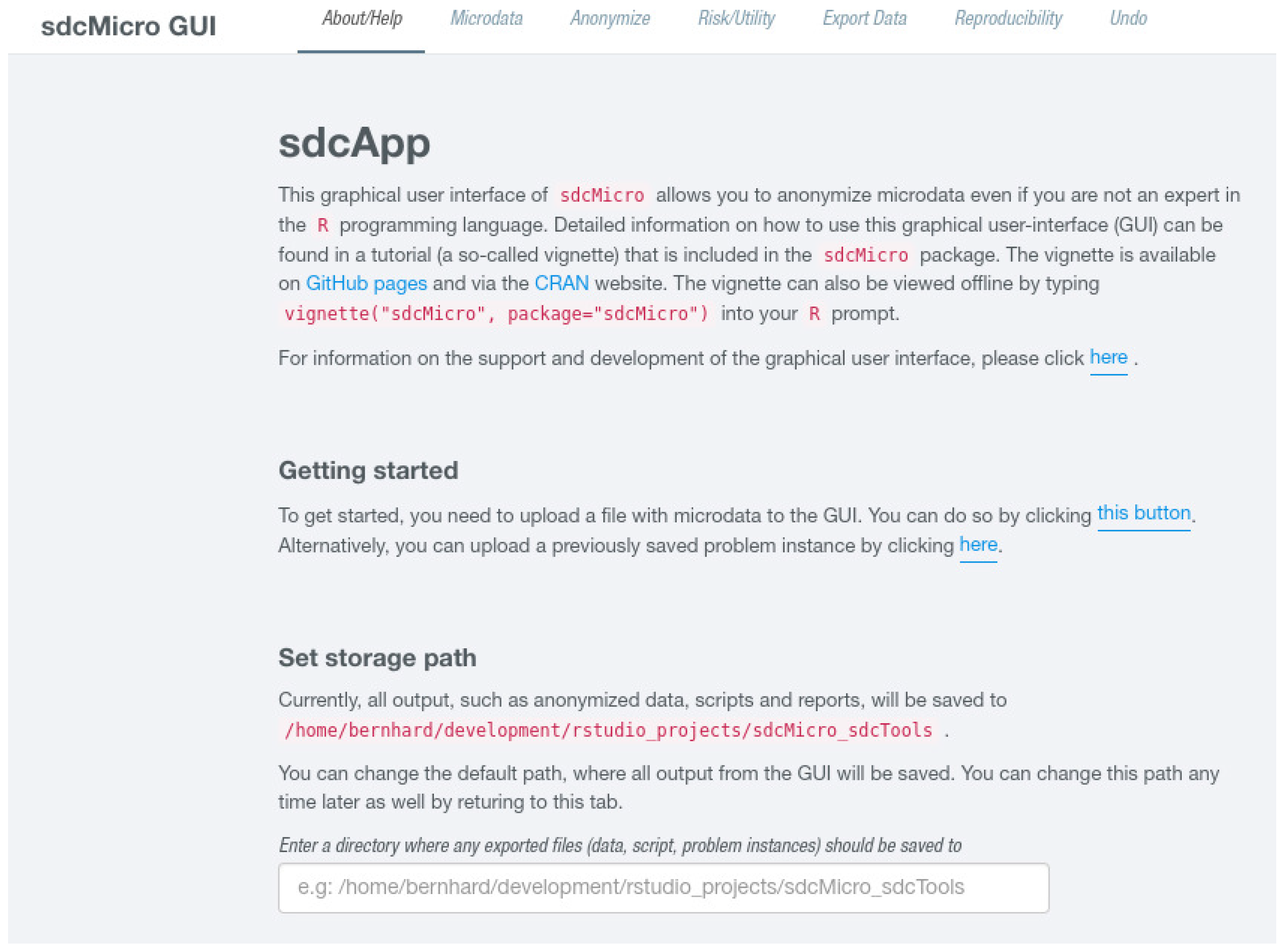
2.3.1. Defining a SDC Problem
The layout of this page is split into two parts and can be accessed by clicking on
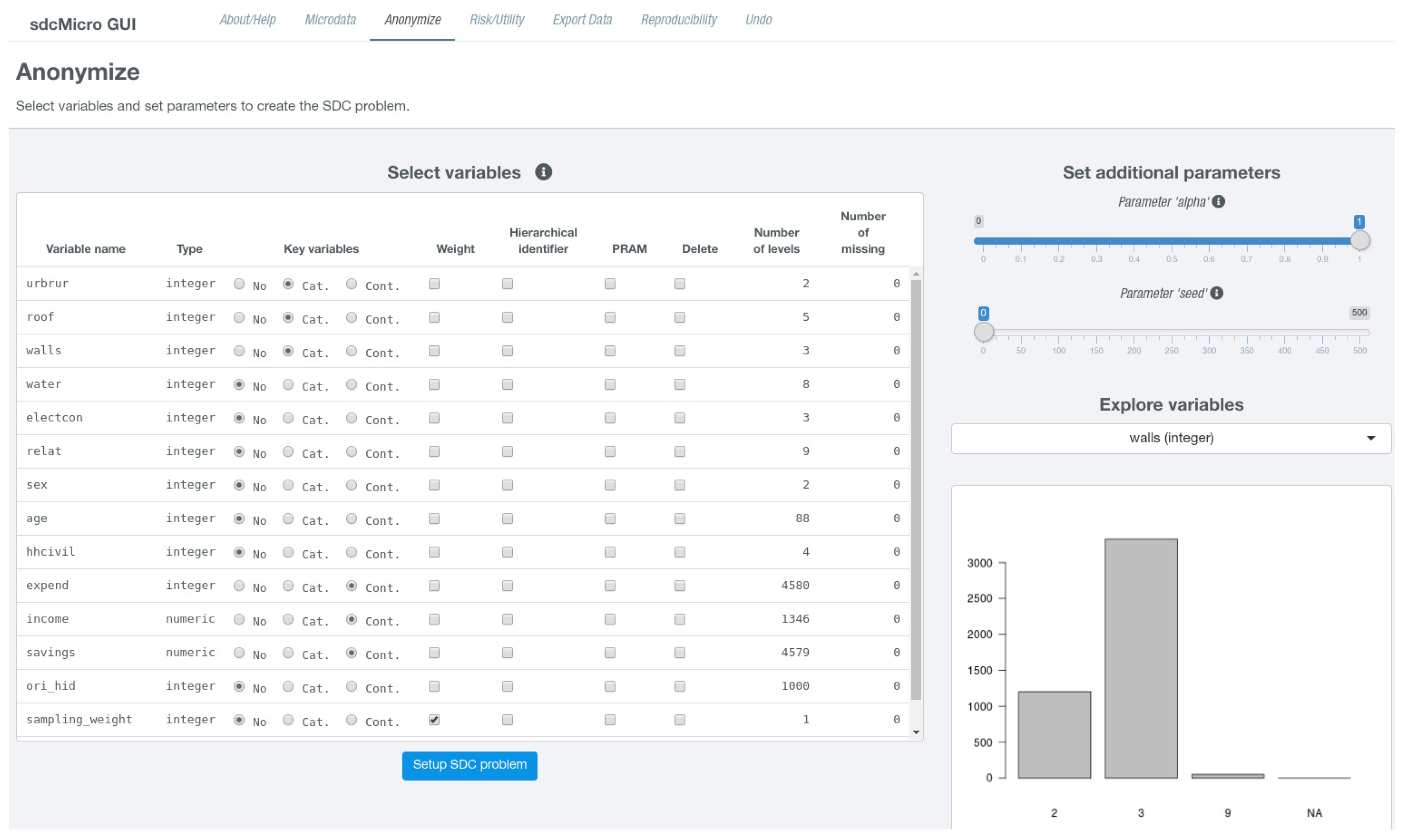
Anonymize in the top navigation bar. On the left hand side, an interactive table is shown that needs to be modified in order to define a new problem instance. On the right hand side, the user is given the possibility to select a single variable from the dataset for further exploration, which is shown in
Figure 2.
The exploration of variables on the same page is useful to decide which variables should be used as key variables. Below, the variable selection dropdown field, a suitable graph depending on the scale of the selected variable is shown. Below the plot (not shown in
Figure 2), summary statistics such as the number of unique values including missing instances of (
NA) or a 6-number summary in case of continuous variable are shown while for non-numeric variables a frequency table is displayed. The columns of the interactive table that consists of a single row for each variable from the micro-dataset are listed in
Table 3. The page also features two slider inputs labeled
Parameter “alpha” and
Parameter “seed”. The latter is relevant for specifying an initial start value for the random number generator which is useful if results should be reproducible. The former parameter specifies how
sdcMicro should deal with missing values in categorical key variables. Details about this parameter can be found in the help-page of the
freqCalc-function.
In column Key variables, radio buttons indicate if a variable should be used as categorical or numerical key variable, which is by default not the case for any variable. However, multiple variables may be uses as categorical and numerical key variables. For columns PRAM, Weight, Hierarchical identifier, and Delete, check boxes are present in the table that are by default not selected and can be enabled by simply clicking on them. Although there can at most be one variable selected as weight variable and variable holding cluster ids, multiple variables may be checked in columns Delete or PRAM. Whenever the table is changed, it is internally checked if all conditions for a successful generation of a new problem instance are fulfilled. In the case that some restrictions are violated, the user is provided visual feedback (either via a popup or red error button) giving information on what needs to be changed. If all checks are passed, a blue button labeled Setup SDC problem appears below the table. Clicking on this button creates the new problem instance. The page then refreshes and the screen layout changes and is divided into two parts. The left sidebar is further subdivided into three sections where different anonymization techniques can be selected. At the bottom of the sidebar there is a button labeled Reset SDC problem that allows deleting the current SDC problem and to create a different instance. The main content either shows results or allows to specify parameters for specific anonymization methods. For all views except for the default view, which summarizes the current problem instance, a right sidebar is displayed in which important measures about the anonymization process as well as risk and data utility measures are shown.
2.3.2. View/Analyze the SDC Instance
The first part of the left navigation sidebar labeled
View/Analyze existing sdcProblem allows to select from four different features which are summarized in
Table 4.
In the
Show Summary-view, the SDC problem is summarized by showing the most important (key) variables of the problem and some statistics, such as the number of suppressed values for each categorical key variable. Furthermore, a table showing the number and percentages of records violating
k-anonymity [
12,
13] for
k of 2, 3, and 5 is displayed both for the current problem as well as for the initial problem to which no anonymization procedures have been applied. The user is also presented with information about risk in numerical key variables if any have been defined. In this case, additional tables show the estimated minimal and maximum risk for numeric key variables for both the original and the (possibly) modified continuous key variables as well as measures of information loss. Specifically, measures
IL1s [
14] and the
Difference of Eigenvalues [
15] are shown for both the original and (possibly) modified variables. If numeric key variables have been modified, a table containing the six-number summary (identically to the one on the right-hand side below the plot in the page when the problem was defined, see “Defining a SDC problem” in
Section 2.3.1) for each the unmodified variable from the micro-dataset and the perturbed variable. Finally, at the bottom all the anonymization procedures that have already been applied are listed.
Clicking on
Explore variables allows to explore all variables in their current state. The functionality is exactly the same as it was already described in Modify and analyze microdata (see
Section 2.2.2) for original microdata. The only difference being that the analyzed variables are now those from the current SDC problem. The other two features in this section are modifying the SDC problem.
Using Add linked variables it is possible to connect a set of variables to a specific categorical key variable. This variable then serves as a "donor variable. This means that after the anonymization process, all suppressions of the donor variable will be transferred to the variables linked to it.
Sometimes it is useful to create a new random identifying variable. Therefore, this task can also be performed within the GUI by clicking on the link “Create new IDs”. After specifying a new variable name and optionally a variables that serves as grouping variable (the new variable will have random, but common values for each value of the grouping variable), the new variable can be created by clicking on a button labeled Add new ID variable which appears at the bottom of the page. After the variable has been created, the page switches to the Show Summary view.
2.3.3. Anonymization of Categorical Data
The second subsection of the left sidebar labeled
Anonymize categorical variables allows applying anonymization methods to categorical key variables. The available methods are listed in
Table 5.
Selecting Recoding allows reducing the level of detail of categorical key variables by combining levels into a new, common category which can optionally be renamed; it is also possible to add missing values to the newly generated category. Once the re-coding is done, the page refreshes and the content in the right sidebar like the number of observations violating k-anonymity was updated.
It is very common feature that a safe micro-dataset features
k-anonymity [
12,
13]. This feature specifies that each combination of the levels of the categorical key variables occurs at least
k times in the data. Choosing
k-Anonymity allows creating a
k-anonym dataset for all or (independently) for given subsets of the categorical key variables. The latter approach is useful if the number of categorical key variables is large. Furthermore it is also possible to set different values of
k for the subsets. The algorithm works by setting specific values in key variables to missing (
NA). Users can also rank variables by importance to be selected as variable in which values should be removed. This allows to specify variables that are deemed so important that no missing values should be introduced by the algorithm. By default the key variables are ordered in a way that the variables with the most number of levels are most likely to be selected as variable in which suppressions are introduced. The implementation of the algorithm also allows to apply the method independently on groups defined by a stratification variable. If the user opts for this approach, a variable defining the grouping needs to be selected from a drop-down menu. For any way, the value of
k is typically set using slider inputs. Once the user has finished setting the parameters, an action button appears at the bottom of the page. Clicking this button starts the process to establish
k-anonymity which might take some time. While the algorithm runs, a progress bar is displayed. Once the calculation has finished, the page refreshes and the right sidebar was updated. Users should especially have a look at the first table in which the number of suppressions for each key variable is shown. Also, the section
k-anonymity in the sidebar is updated.
Post-randomization (PRAM) [
16] is a statistical process that possibly changes values of a variable given a specific transition matrix. In the GUI, PRAM can be applied in two different ways by either choosing
PRAM (simple) or
PRAM (expert). In both cases, at least one variable needs to be selected that should be post-randomized. We note that only those variables can be selected that have been defined as being suitable for post-randomization when defining the SDC problem as discussed in
Section 2.3.1. We note that it is possible to select a single stratification variable. If this is the case, the post-randomization procedure is performed independently for each unique value of the grouping variable. The definition of the transition matrix is different for the “simple” and the “expert” mode. In
PRAM (simple), two parameters must be specified using slider inputs.
pd refers to the minimum diagonal values in the (internally) generated transition matrix. The higher this value is, the more likely it is that a value stays the same and remains unchanged. Parameter
alpha allows to add some perturbation to the calculated transition matrix. The lower this number is, the less perturbed the matrix will get. This information is also displayed when hovering over question mark icons next to the slider inputs. In
PRAM (expert), the user needs to manually create a transition matrix by changing cell values of an interactive table. The diagonal values of the table are by default 100 which results in a transition matrix in which no value would be changed. For any given row, the numbers are defined as percentages that the current value of the selected variable (the row name) changes to the value specified by the respective column name. The user needs to make sure that the sum of values in each row equals 100. If this is not the case, a red button appears below the table, giving instant feedback that the table needs to be modified. Values in specific cells may be changed by clicking into the cell and entering a new values. If the inputs were specified correctly, a button appears at the bottom of the page. Pressing this button applies PRAM using the defined parameters. Once finished, the page refreshes and in the right sidebar a section called
PRAM summary either appears or is extended. In this part of the right sidebar, for each variable that has been post-randomized the number and percentages of value changes are listed.
Clicking on
Suppress values with high risks makes it possible to set values for the most risky records to
NA. It is required to select a categorical key variable and specify using a slider input an appropriate threshold value which will be used to identify the “risky” records. These records are defined as those having an individual re-identification risk [
17] larger than the selected threshold value. The threshold can be changed by updating the slider. Below the inputs, a histogram displaying the distribution of the individual risk values is shown. In this graph, a vertical black line representing the current value of the threshold is plotted. Finally, at the bottom of the page, a button with a dynamic label is shown. The label contains the number of records that would be suppressed as well as the selected variable. Once the button is pressed, records in the selected variable whose individual risks are above the threshold are set to
NA. The view then changes to the
Show summary view.
2.3.4. Anonymization of Continuous Data
The third section in the left-hand sidebar shows the methods that can be applied to numerical (key) variables.
Table 6 summarizes the possible choices.
We note that only the first choice (
Top/Bottom coding) is always listed; the remaining choices only appear if at least one variable has been set as continuous key variable when defining the problem, as discussed in
Section 2.3.1.
Selecting Top-/Bottom-Coding enables the user to replace values that are above (top-coding) or below (bottom-coding) a threshold with a different number, which is typically the threshold itself. In the GUI, the user needs to select a variable from a drop-down field that should be re-coded. This field only allows to select continuous variables in order to prevent the application of the method to categorical variables. Then it must be set if top- or bottom coding should be performed using a radio button input field. Furthermore, two numbers—the threshold value and the replacement value—must be set. To help users find suitable threshold values, a box plot showing the distribution of the currently selected variable is shown below the input controls. After all inputs have been set, additional elements appear between the input fields and the box plot. The first additional element is a text stating how many of the values would be replaced as well as the corresponding percentage. Below this information, a button appears. Once this button is pressed, the values are replaced according to the current settings and the page refreshes. The box plot is updated as well as the right hand sidebar. If the selected and re-coded variable was defined as a numeric key variable, the values referring to risk in numerical key variables and information loss measures change in the sidebar.
Microaggregation [
18] is a method in which records are grouped based on a proximity measure of variables of interest. In a second step, for each group, a summary statistic (aggregate value), which is typically the arithmetic mean, is computed and then released for all records in the group, instead of the original, individual record values. This method reduces the variation of a continuous key variable and additionally protects against (direct) matching. It also can be interpreted as
k-anonymity for continuous variables. In
sdcMicro, non-cluster-based and cluster-based methods are distinguished. Users can choose from a total of eight non-cluster-based and four cluster-based methods. The grouping can also be can be nonrobust (for example, the default algorithm Maximum Distance to Average Vector (MDAV) [
3]) or robust such as the Robust Maximum Distance (RMD) algorithm [
19].
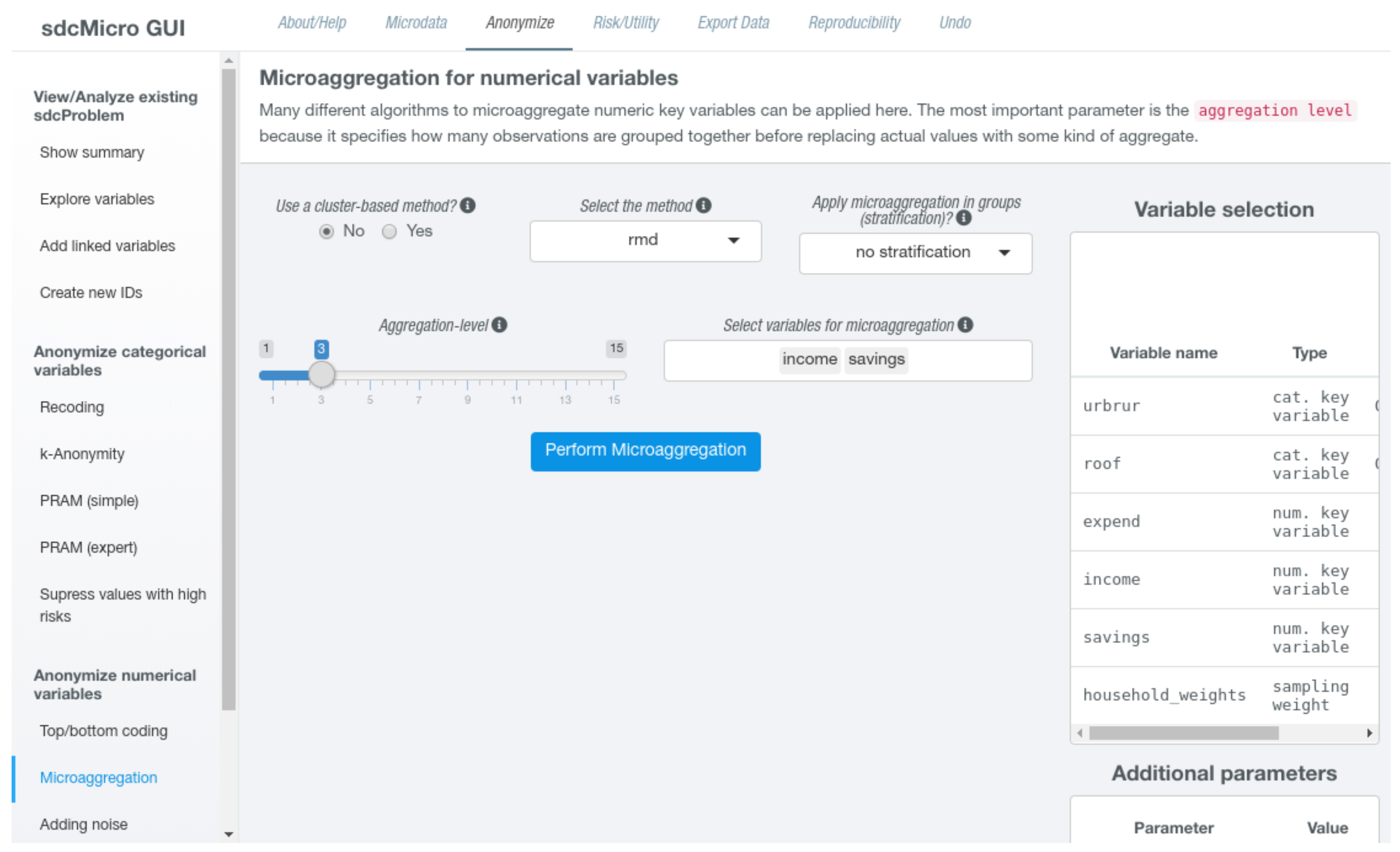
If the users chooses to apply microaggregation to numeric key variables, the first choice is to select one of the available methods from a drop-down menu. The user also needs to specify an aggregation level using a slider input. This value refers to the size of the groups that will be formed by the algorithm. Further options that can be made include the selection of a subset of numerical key variables for which should be microaggregated (by default, all key variables will be used) or if the algorithm should be applied independently given the characteristics of a stratification variable that needs also be chosen in this case.
Figure 3 features a screen shot how the RMD algorithm may be specified for some continuous key variables without stratification for a group size of 3.
Additionally, question mark icons are shown next to most input fields. By hovering over these icons, additional information is shown in a pop-up window, which will facilitate users to find appropriate parameter settings. For some methods, several additional inputs are shown. For example, when using cluster-based methods, it is possible to select the clustering algorithm (such as “kmeans”, “cmeans”, or “bclust”) as well as possible data transformations (“log”, “box-cox”, or “none”) that should be applied before the cluster algorithm is applied. For some non cluster-based methods, it is possible to choose the aggregation statistics (such as the mean or the median). Once all required options have been set, an action button appears below all inputs. Clicking on this button performs the microaggregation of the selected variables according to the options that have been set. As the computation might take some time, on the bottom right screen, a progress bar showing that the process is running appears. Once the algorithm has finished, the page updates and the “Show summary” page is displayed. On this page, all measures depending on numerical key variables have been recomputed and show current values.
Another popular way to mask numerical variable is to overlay original numbers with a stochastic noise distribution that has typically a mean of 0. Selecting
Adding Noise allows to modify numerical key variables with noise. Users can select one or more numerical key variable from a input field which is by default empty. If it is left empty, all numerical key variables will be perturbed. Next to the variable selection field, a single specific algorithms needs to be selected. While some of the algorithms (e.g., “additive”) add noise completely at random to each variable depending on its size and standard deviation, other methods are more sophisticated. Algorithms “correlated” and “correlated2” [
20] try to preserve the covariance structure of the input variables. Method “ROMM” [
21] is an implementation of the Orthogonalized Matrix Masking method) and algorithm “outdect” [
19] adds noise only to outliers. These outliers are identified by univariate and robust multivariate procedures based on a robust Mahalanobis distance which is computed by the MCD estimator [
22].
Below these inputs, the amount of perturbation needs to be specified by changing the value of a slider input. This input is dynamically labeled depending on the previous choice of the method. Since the parameterization for the different methods is different, this slider has different default values and different ranges depending on the choice of the method. If all options have been set, pressing a button that is shown at the bottom of the page finally applies the stochastic noise to the selected variables. Once the algorithm finished, the page view changes to the Show summary page, where again all relevant measures were recalculated.
The last method that can be applied to numerical key variables is rank swapping [
23]. The main idea of this algorithm is to swap values within a given range so that the correlation structure of the original variables is (mostly) preserved and some perturbation is added to the variables. After specifying the numerical key variables to which the algorithm should be applied, the parameters for the procedure needs to be specified using five different slider inputs. Two sliders are used to define percentages of values to be bottom- or top-coded before the algorithm starts, which allows to deal with outlying observations. The sliders named “Subset-mean preservation factor” and “Multivariate preservation factor” allow further fine-tuning of the algorithm. The first one defines how the maximum percentage means before and after the perturbation are allowed to differ, while the second slider specifies a limit on how much correlations between non-swapped and swapped variables are allowed to differ. Using the fifth and last slider allows defining a maximum distance relative to their ranks, which needs to be fulfilled for two records to be eligible for swapping. For details on the impact of these parameters, please see the help page for the rankSwap-function
?rankSwap. After all options were set, clicking on an action button at the bottom of the page starts the swapping procedure. Once finished, the page view changes as already previously described to the summary view where all the relevant statistics are shown and can be analyzed.