A FEAST Algorithm for the Linear Response Eigenvalue Problem
Abstract
:1. Introduction
2. Preliminaries
- (a)
- There exists a nonsingular such that:where , and .
- (b)
- If K is also definite, then all , and H is diagonalizable:
- (c)
- The eigen-decomposition of and is:respectively.
3. The FEAST Algorithm for LREP
3.1. The Main Algorithm
| Algorithm 1 The FEAST algorithm for LREP. |
| Input: Given an initial block . Output: Converged approximated eigenpairs . 1: for , until convergence do 2: Compute by (6), and . 3: Compute , , , and . 4: Compute the spectral decomposition and approximate eigenpairs where by (9) for . 5: If convergence is not reached then go to Step 2, with . 6: end for |
3.2. Convergence Analysis
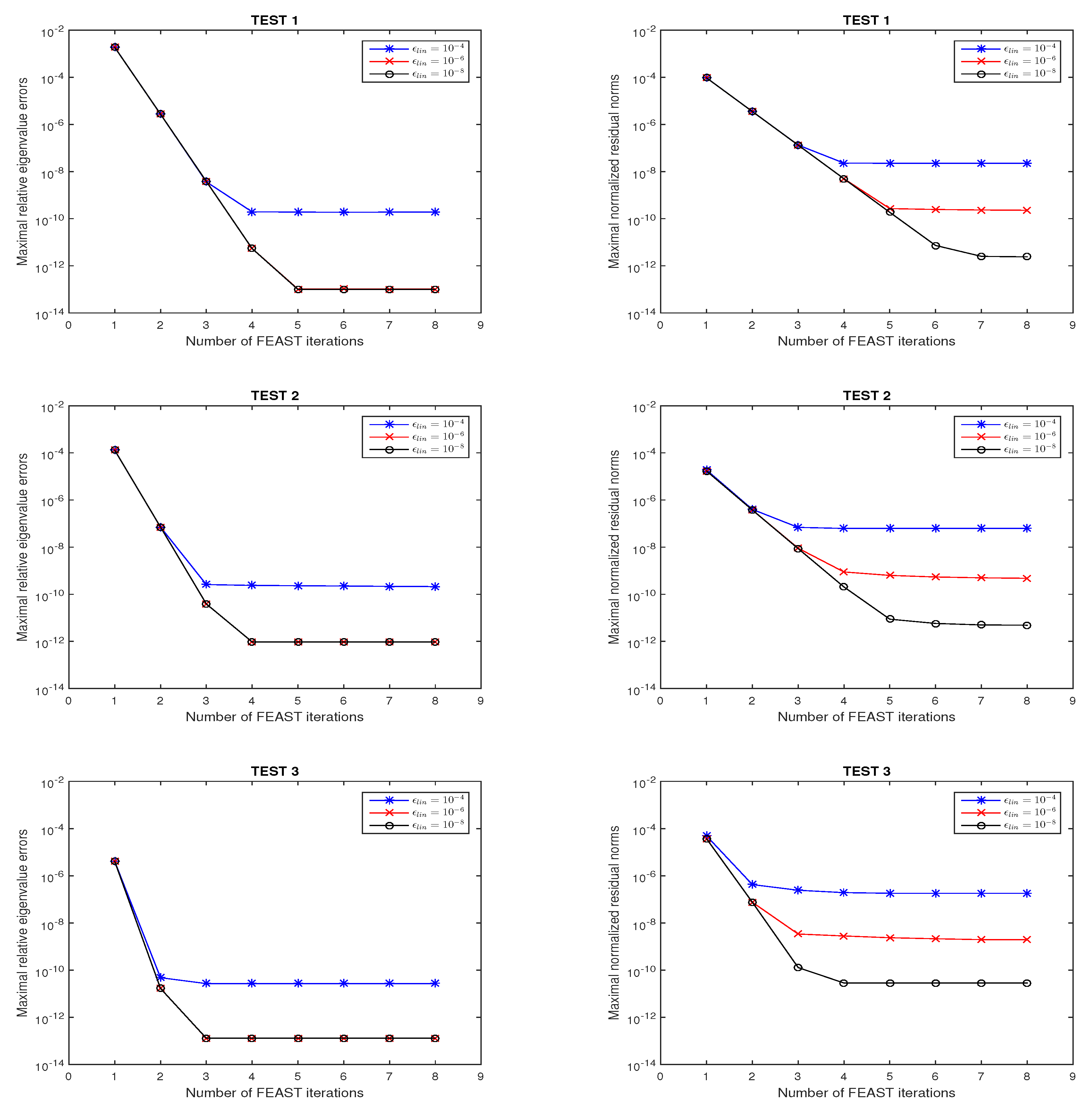
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saad, Y.; Chelikowsky, J.R.; Shontz, S.M. Numerical methods for electronic structure calculations of materials. SIAM Rev. 2010, 52, 3–54. [Google Scholar] [CrossRef]
- Shao, M.; da Jornada, F.H.; Lin, L.; Yang, C.; Deslippe, J.; Louie, S.G. A structure preserving Lanczos algorithm for computing the optical absorption spectrum. SIAM J. Matrix Anal. Appl. 2018, 39, 683–711. [Google Scholar] [CrossRef]
- Bai, Z.; Li, R.C. Minimization principle for linear response eigenvalue problem, I: Theory. SIAM J. Matrix Anal. Appl. 2012, 33, 1075–1100. [Google Scholar] [CrossRef]
- Li, T.; Li, R.C.; Lin, W.W. A symmetric structure-preserving ΓQR algorithm for linear response eigenvalue problems. Linear Algebra Appl. 2017, 520, 191–214. [Google Scholar] [CrossRef]
- Wang, W.G.; Zhang, L.H.; Li, R.C. Error bounds for approximate deflating subspaces for linear response eigenvalue problems. Linear Algebra Appl. 2017, 528, 273–289. [Google Scholar] [CrossRef]
- Bai, Z.; Li, R.C. Minimization principle for linear response eigenvalue problem, II: Computation. SIAM J. Matrix Anal. Appl. 2013, 34, 392–416. [Google Scholar] [CrossRef]
- Papakonstantinou, P. Reduction of the RPA eigenvalue problem and a generalized Cholesky decomposition for real-symmetric matrices. Europhys. Lett. 2007, 78, 12001. [Google Scholar] [CrossRef]
- Teng, Z.; Li, R.C. Convergence analysis of Lanczos-type methods for the linear response eigenvalue problem. J. Comput. Appl. Math. 2013, 247, 17–33. [Google Scholar] [CrossRef]
- Teng, Z.; Zhang, L.H. A block Lanczos method for the linear response eigenvalue problem. Electron. Trans. Numer. Anal. 2017, 46, 505–523. [Google Scholar]
- Teng, Z.; Zhou, Y.; Li, R.C. A block Chebyshev-Davidson method for linear response eigenvalue problems. Adv. Comput. Math. 2016, 42, 1103–1128. [Google Scholar] [CrossRef]
- Rocca, D.; Lu, D.; Galli, G. Ab initio calculations of optical absorpation spectra: solution of the Bethe-Salpeter equation within density matrix perturbation theory. J. Chem. Phys. 2010, 133, 164109. [Google Scholar] [CrossRef] [PubMed]
- Shao, M.; Felipe, H.; Yang, C.; Deslippe, J.; Louie, S.G. Structure preserving parallel algorithms for solving the Bethe-Salpeter eigenvalue problem. Linear Algebra Appl. 2016, 488, 148–167. [Google Scholar] [CrossRef]
- Vecharynski, E.; Brabec, J.; Shao, M.; Govind, N.; Yang, C. Efficient block preconditioned eigensolvers for linear response time-dependent density functional theory. Comput. Phys. Commun. 2017, 221, 42–52. [Google Scholar] [CrossRef] [Green Version]
- Zhong, H.X.; Xu, H. Weighted Golub-Kahan-Lanczos bidiagonalization algorithms. Electron. Trans. Numer. Anal. 2017, 47, 153–178. [Google Scholar] [CrossRef]
- Zhong, H.X.; Teng, Z.; Chen, G. Weighted block Golub-Kahan-Lanczos algorithms for linear response eigenvalue problem. Mathematics 2019, 7. [Google Scholar] [CrossRef]
- Bai, Z.; Li, R.C.; Lin, W.W. Linear response eigenvalue problem solved by extended locally optimal preconditioned conjugate gradient methods. Sci. China Math. 2016, 59, 1–18. [Google Scholar] [CrossRef]
- Polizzi, E. Density-matrix-based algorithm for solving eigenvalue problems. Phys. Rev. B 2009, 79, 115112. [Google Scholar] [CrossRef] [Green Version]
- Tang, P.T.P.; Polizzi, E. FEAST as a subspace iteration eigensolver accelerated by approximate spectral projection. SIAM J. Matrix Anal. Appl. 2014, 35, 354–390. [Google Scholar] [CrossRef]
- Kestyn, J.; Polizzi, E.; Tang, P.T.P. FEAST eigensolver for non-Hermitian problems. SIAM J. Sci. Comput. 2016, 38, S772–S799. [Google Scholar] [CrossRef]
- Gavin, B.; Miedlar, A.; Polizzi, E. FEAST eigensolver for nonlinear eigenvalue problems. J. Comput. Sci. 2018, 27, 107–117. [Google Scholar] [CrossRef] [Green Version]
- Krämer, L.; Di Napoli, E.; Galgon, M.; Lang, B.; Bientinesi, P. Dissecting the FEAST algorithm for generalized eigenproblems. J. Comput. Appl. Math. 2013, 244, 1–9. [Google Scholar] [CrossRef]
- Guttel, S.; Polizzi, E.; Tang, P.T.P.; Viaud, G. Zolotarev quadrature rules and load balancing for the FEAST eigensolver. SIAM J. Matrix Anal. Appl. 2015, 37, A2100–A2122. [Google Scholar] [CrossRef]
- Ye, X.; Xia, J.; Chan, R.H.; Cauley, S.; Balakrishnan, V. A fast contour-integral eigensolver for non-Hermitian matrices. SIAM J. Matrix Anal. Appl. 2017, 38, 1268–1297. [Google Scholar] [CrossRef]
- Yin, G.; Chan, R.H.; Yeung, M.C. A FEAST algorithm with oblique projection for generalized eigenvalue problems. Numer. Linear Algebra Appl. 2017, 24, e2092. [Google Scholar] [CrossRef] [Green Version]
- Li, R.C.; Zhang, L.H. Convergence of the block Lanczos method for eigenvalue clusters. Numer. Math. 2015, 131, 83–113. [Google Scholar] [CrossRef]
- Stein, E.M.; Shakarchi, R. Complex Analysis; Princeton University Press: New Jersey, NJ, USA, 2010. [Google Scholar]
- Futamura, Y.; Tadano, H.; Sakurai, T. Parallel stochastic estimation method of eigenvalue distribution. J. SIAM Lett. 2010, 2, 127–130. [Google Scholar] [CrossRef] [Green Version]
- Napoli, E.D.; Polizzi, E.; Saad, Y. Efficient estimation of eigenvalue counts in an interval. Numer. Linear Algebra Appl. 2016, 23, 674–692. [Google Scholar] [CrossRef] [Green Version]
- Saad, Y. Numerical Methods for Large Eigenvalue Problems: Revised Version; SIAM: Philadelphia, PA, USA, 2011. [Google Scholar]
- Yin, G. A harmonic FEAST algorithm for non-Hermitian generalized eigenvalue problems. Linear Algebra Appl. 2019, 578, 75–94. [Google Scholar] [CrossRef]
- Yin, G. On the non-Hermitian FEAST algorithms with oblique projection for eigenvalue problems. J. Comput. Appl. Math. 2019, 355, 23–35. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Saad, Y.; Schultz, M.H. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
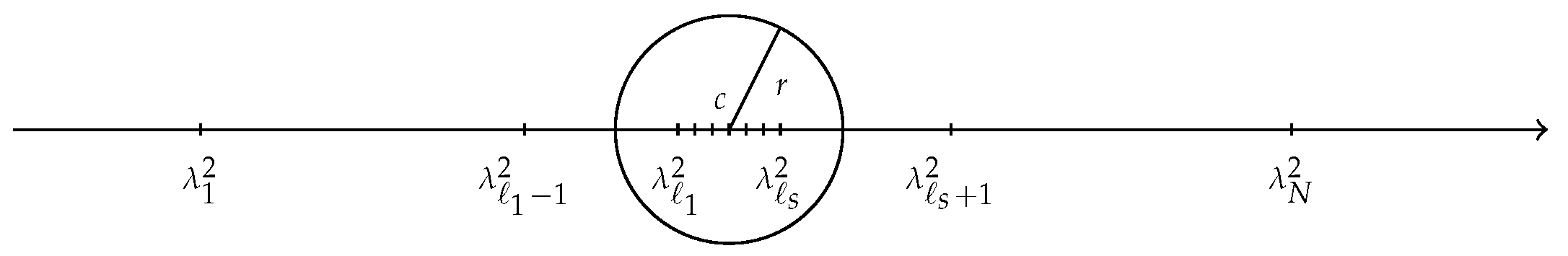
| (for ) | () | () | () | |
|---|---|---|---|---|
| Problem | N | K | M | (, ) | (, ) | (, ) | |||
|---|---|---|---|---|---|---|---|---|---|
| test 1 | 1862 | Na | Na | (0.40,0.50) | 3 | (0.60,0.70) | 3 | (1.50,1.60) | 3 |
| test 2 | 2834 | Na | Na | (0.03,0.04) | 4 | (0.05,0.06) | 4 | (0.32,0.33) | 5 |
| test 3 | 5660 | SiH4 | SiH4 | (0.25,0.30) | 3 | (0.75,0.80) | 6 | (1.75,1.80) | 8 |
| q | TEST 1 | TEST 2 | TEST 3 | |||
|---|---|---|---|---|---|---|
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | ||||||
| 9 | ||||||
| Problem | eig | Algorithm 1 |
|---|---|---|
| test 1 | 45.82 | 15.88 |
| test 2 | 159.77 | 37.08 |
| test 3 | 1200.71 | 233.12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, Z.; Lu, L. A FEAST Algorithm for the Linear Response Eigenvalue Problem. Algorithms 2019, 12, 181. https://doi.org/10.3390/a12090181
Teng Z, Lu L. A FEAST Algorithm for the Linear Response Eigenvalue Problem. Algorithms. 2019; 12(9):181. https://doi.org/10.3390/a12090181
Chicago/Turabian StyleTeng, Zhongming, and Linzhang Lu. 2019. "A FEAST Algorithm for the Linear Response Eigenvalue Problem" Algorithms 12, no. 9: 181. https://doi.org/10.3390/a12090181
APA StyleTeng, Z., & Lu, L. (2019). A FEAST Algorithm for the Linear Response Eigenvalue Problem. Algorithms, 12(9), 181. https://doi.org/10.3390/a12090181






