1. Introduction
Breast cancer is a common malignant tumor with high morbidity and mortality. It has become one of the main threats of women’s health and life. According to data provided by the American Cancer Society (ACS) in 2019, there are 1,762,450 new cancer cases in the United States and 606,880 deaths caused by cancer. The United States will have 271,270 women with breast cancer that year, and 42,260 expected cases of breast cancer deaths [
1]. Moreover, 274,000 new cases of breast cancer with 66,000 deaths are expected to be annually diagnosed in China. It is found that the breast cancer is the fastest growing rate of cancer in China [
2].
The exact cause of breast cancer is unclear and there is no effective way to prevent breast cancer. However, a large number of studies have shown that breast cancer screening is an effective way to improve the early detection and cure rates of breast cancer. Common methods for breast cancer diagnosis include the clinical breast examination, imaging diagnosis, and histopathological biopsy. Moreover, commonly used examination methods for breast include mammography, ultrasound, magnetic resonance imaging, and the computed tomography [
3]. Due to mammography non-invasiveness, reproducibility and comprehensive sampling, it has occupied a privileged position in the diagnosis of breast diseases. It is relatively inexpensive and yields a clear image. Moreover, mammography can show early lesions that are not easily detectable by visual inspection. It is highly sensitive to the intramammary calcification, especially small the calcification. Common X-ray findings of breast cancer include mass, microcalcification, changes in the nipple and areola, structural distortion, and increased vascular deformation [
4]. Among them, the mass and microcalcification are the most important and obvious pathological signs of breast cancer, which are of great significance from cancer detection and diagnosis point of view.
Microcalcification may occur in both benign and malignant breast lesions. Especially for the early “occult” breast cancer, microcalcification is usually the only sign [
5]. Meanwhile, mammography is more sensitive to microcalcification.
With the development of computer-based technologies, the computer-aided diagnosis has been introduced into the medical field and, has enabled doctors to make more accurate clinical diagnoses. Computer diagnostics can save doctors’ diagnostic time and increase the accuracy of diagnostic results. Statistics show that with the advent of computer-aided diagnosis systems, the detection rate of breast cancer increased by 20% [
6]. Between anatomic pathology and imaging diagnosis, R Bonfiglio [
7] offers a significant new way to improve the analysis of microcalcification for breast cancer. R Bonfiglio [
8] aimed of this study was to explore the relationship between the imaging parameters most commonly used for the study of mammary microcalcification and the corresponding histological and chemical properties. M Scimeca [
9] study that breast sample biopsies with microcalcification underwent energy dispersive X-ray microanalysis to better define the elemental composition of the microcalcification. M Scimeca [
10] uses digital pathology to lay the foundation for teamwork between anatomical pathology and nuclear medicine. Zhang L [
11] selected from patients who had been examined using breast mammography. The control group did not have detectable microcalcification and was matched in a ratio of 1:3. The clinic-pathological factors, progression-free survival, and overall survival were evaluated by SPSS.
2. Related Work
Characteristic calcification is an important and most common manifestation in the early stage of breast cancer. The microcalcification point usually presents a small bright spot in the mammogram. It usually shows that several microcalcifications are clustered together, similar to the distribution of clusters. Each microcalcification has a good grayscale consistency, high brightness, few edge burrs, and high contrast with the surrounding background breast tissue, it is difficult to find microcalcification spots by the naked eye. Therefore, it is usually missed by doctors, which may lead to cancer misdiagnosis. Sometimes clinicians use a magnifying glass to check the mammogram. However, this method is not accurate and requires considerable time and energy. In recent years, researchers have used computers to begin diagnosis of breast calcification. There are three general classification methods for the detection of calcifications in mammography: (1) based on the image enhancement method, McLoughlin [
12] proposed a quantum noise model by simply averaging the square root of the gray level to improve the local contrast and achieve microcalcification. Li et al. [
13] employed commonly used enhancement techniques to compare detected results of microcalcification points, such as the contrast stretching, histogram modeling, convolution filters, region-based enhancement methods, and morphological methods.
Based on the method of multi-scale decomposition (2), Wang [
14] proposed a method to extract high-frequency signals and noises using different images. Then, he used the wavelet reduction to suppress noises and employed the neural network classification to extract the distribution of microcalcification. Yoshida et al. [
15] defined a cost function by modifying the weight of wavelet coefficients by a conjugate gradient algorithm. They minimized the cost function and detected microcalcifications in second and third layers of high-frequency subbands, after the wavelet decomposition. (3) Based on the machine learning method, Lee et al. [
16] used the SVM algorithm to automatically detect microcalcifications. They showed that experimental results are superior to the commonly used artificial neural network classification methods. Moreover, Issam et al. [
17] used supervised learning to detect the image segmentation. They used SVM to probe each region of the image to determine if it contains microcalcifications. Gabriele Valvano [
18] proposed a novel approach based on convolutional neural networks for the detection and segmentation of microcalcification clusters. They used 283 mammograms to train and validate our model, obtaining an accuracy of 99.99% on microcalcification detection and a false positive rate of 0.005%. A Duggento [
19] explored a total of 260 model architectures in a train-validation-test split in order to propose a model selection criterion which can pose the emphasis on reducing false negatives while still retaining acceptable accuracy. We achieve an area under the receiver operatic characteristics curve of 0.785 (accuracy 71.19%) on the test set.
3. Method
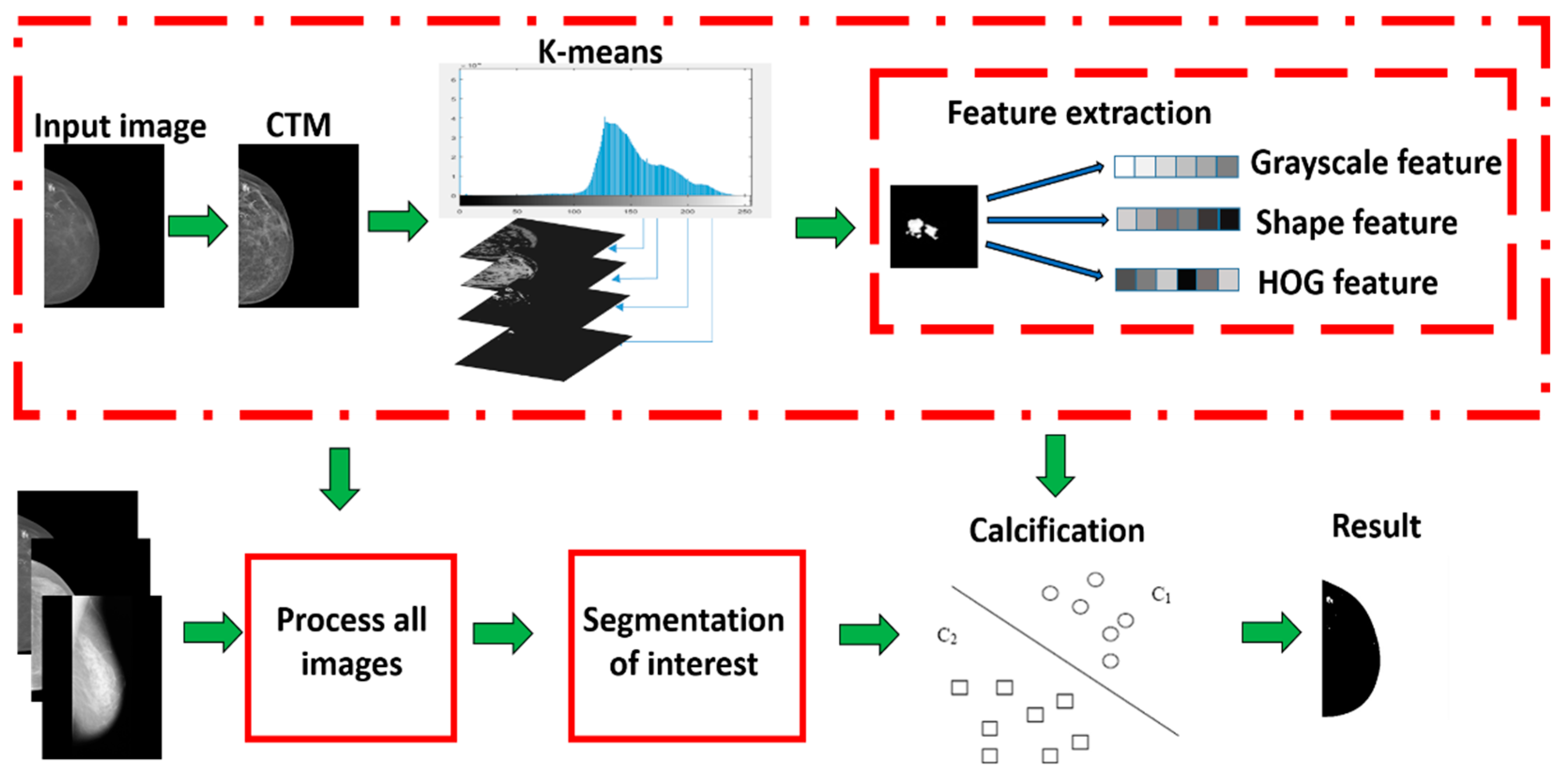
The computer-aided calcification lesion detection method includes several parts, such as mammography preprocessing, region of interest segmentation, feature extraction, and classifier design. Details are comprehensively described in the following sections (See
Figure 1).
3.1. Preprocessing
In the process of shooting, transmission, and digitization, mammograms are inevitably doped with noise, especially they are doped with salt and pepper noise. If the corresponding inhibition is not given in advance, it will often lead to a large number of false positive areas, which has an adverse impact on the test. Image enhancement is widely used in image processing to improve image quality. The purpose of image enhancement is to enhance weak edges or weak features in images. Recently, many methods are based on wavelet transform, because wavelet transform has multi-scale structure and good results can be achieved. However, all existing methods are unable to obtain geometric information in the image for image enhancement.
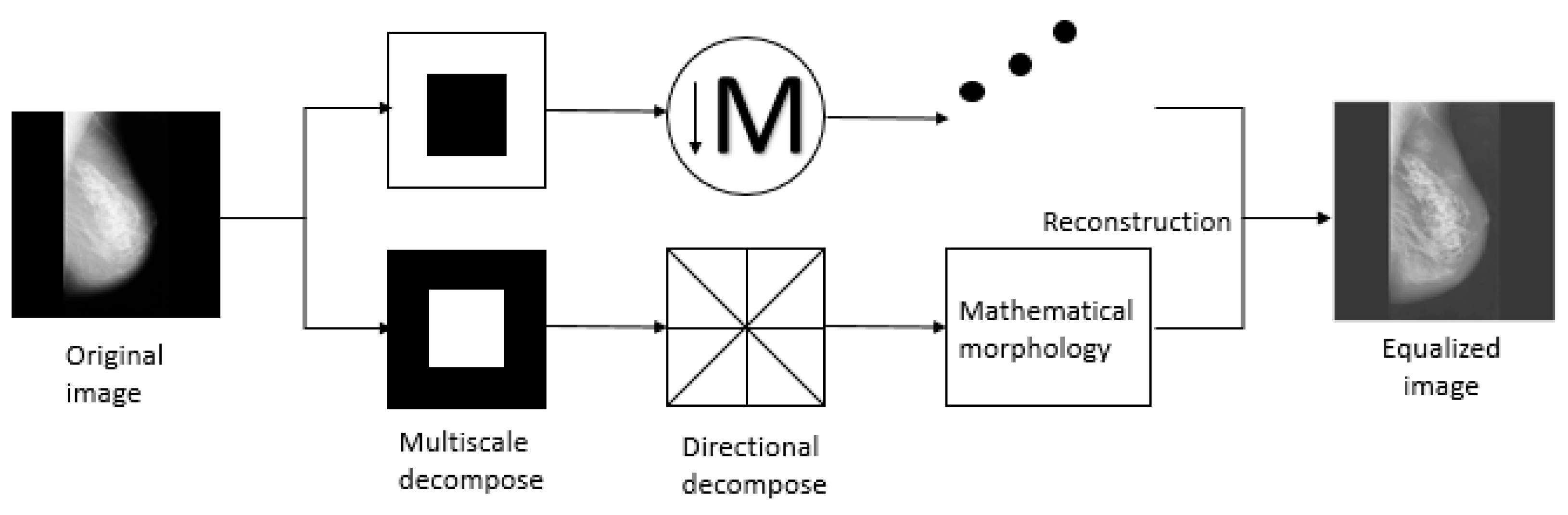
In 2002, MN Do [
20] proposed a tower-shaped directional filter bank, which is an analysis method superior to the wavelet transform and is a new extension of the multi-resolution and multi-directional wavelet transform. Firstly, the image is multiscale scaled by the Laplacian pyramid transform to capture singular points. Directional filters are applied to synthesize singular points into coefficients, where points are distributed in the same direction. It should be indicated that the base support space is a rectangle that varies in length and width with scale. Therefore, not only the multi-resolution and time-frequency local characteristics of the wavelet transform are obtained, basic functions are distributed in multiple scales and multiple directions. However, only a small number of coefficients can be effectively captured. Because the noise is mainly in the high-frequency subband, I mainly deal with the bandpass image (see
Figure 2).
Mathematical morphology is a commonly used nonlinear filtering method, based on the dilatation and erosion. They are often used to solve problems, such as feature extraction, image segmentation and the edge detection of binary images. The theory of mathematical morphology is very complicated, but its basic idea is simple and perfect. It regards the image as a set of points and uses the structure matrix to shift, intersect, and combine operations to form various algorithms of morphology. Since noises are mostly located in the high-frequency subband, the bandpass sub-image is filtered by the median, which is beneficial to remove the high-frequency noise and perform the mathematical morphology calculation. Nonlinear mapping function [
21,
22] removes isolated dots and burrs and preserves the overall shape of the image. Formula (1) express the nonlinear mapping function.
Figure 2 introduces the specific process of the algorithm.
Our image enhancement algorithm is based on Contourlet transform and mathematical morphology, which makes full use of the multi-resolution analysis of Contourlet transform and the characteristics of image edge information processing and mathematical morphology. The algorithm proposed in this paper effectively solves the contradiction between suppressing noise and retaining edges.
3.2. Adaptive Multi-Threshold Segmentation
Threshold segmentation is the simplest method of image segmentation. According to the number of selected thresholds, it is divided into the single threshold segmentation and multi-threshold segmentation. Moreover, the single threshold segmentation divides the image into two categories: target and background. On the other hand, the multi-threshold method is divided into multiple areas, the target and the background areas. The gray values between the target in the original image and the adjacent pixels in the background are similar, and when the target is segmented by the threshold mark of each region, excessive grading and excessive false positive regions are avoided. In order to reduce the misdiagnosis and wrong diagnosis, caused by the fixed threshold, it is intended to introduce an adaptive threshold mechanism to determine the threshold of the layering, according to the change of the gray level. Automatic thresholding is a common method of region of interest (ROI) extracting while minimizing the background noise. The feedback loop is used to optimize the threshold before converting the original grayscale image to the binary one. The threshold of each gray layer is adaptively obtained according to the histogram characteristic, corresponding to the current threshold.
K-means clustering [
23] algorithm is one of the most popular clustering algorithms. Moreover, it is one of the top ten algorithms for data mining. The experiment uses the improved K-means clustering algorithm to measure the similarity between feature values, find the similarity between images and perform specific steps of the algorithm. The conventional K-means algorithm calculates the Euclidean distance from the sample data to each cluster center, it calculates the difference between pixels. The pseudocode is shown in Algorithms 1.
| Algorithm 1: K-means clustering algorithm. |
| Input: number of clusters N; image I(m, n) |
| Output: Threshold of N clusters. |
| 1. Step = max (max (I(m, n) − min (I(m, n)))/Clusters |
| 2. Interval = step |
| 3. For I = 1: N |
| 4. K(I).centroid = interval |
| 5. Interval = interval + step |
| 6. End |
| 7. I(m, n )→K(I).centroid |
| 8. Repeat |
9. While K(I).centroid ≠ update (I)
i. K(I).centroid = update (I)
ii. I(m, n )→K(I).centroid |
| 10. End |
| 11. Until K(I).centroid ≠ update (I) |
| 12. Where K(I).centroid is the cluster center. |
Our algorithm divides pixels into N clusters from the pixel range of the image. Each cell I (m, n) is assigned to the most similar cluster in the initial cluster according to K (I).centroid. Compare to K (I). centroid and update (I). If they are not equal, assign update (I) to new K (I).centroid and assign each cell to the most similar to new K (I).centroid. Until the up K (I).centroid no longer changes, find the calcification location based on the highest mean and extract the calcified region of interest.
Image segmentation is performed using the obtained plurality of threshold values. The calcified image is sharpened by the calcification point and the ROI area is found by the multi-threshold segmentation. The advantage of the threshold segmentation is that it is simple to implement, and it can effectively segment the image when the gray value or other feature values of different types of objects differ greatly. Threshold segmentation is often used as a pre-processing of medical images, which are prepared for other subsequent algorithms. The adaptive multi-threshold segmentation yields the ROI region, but the false positive rates (FPR) are relatively high. It should be indicated that ROI regions use features and classifiers to classify the benign and malignant.
3.3. Feature Extraction
Before SVM classification of ROI, some features need to be extracted from ROI as input to the SVM classifier. The characteristics of the super pixel region are currently described as grayscale feature, shape feature, Histogram of Oriented Gradient (HOG) feature, etc.
Table 1 shows that some feature algorithm.
Researchers use some statistics based on it as the texture classification feature. Choosing the appropriate features can improve the computational efficiency and classification effect. Commonly used texture features for analyzing mammogram image textures are as the following:
(1) Angular Second Moment (ASM)
Local binary pattern (LBP) is a feature used in the field of machine vision for classification. It was first proposed by T. Ojala, M. Pietikäinen and D. Harwood [
24,
25] in 1994 for the texture feature extraction. It has significant advantages, such as rotation and gray invariances. It is a very effective feature that compares each pixel with its neighboring pixels and saves the result as a binary number. Due to its strong discriminative power and simple calculation, the local binary pattern texture operator has been applied in different scenarios. The most important attribute of the LBP is the robustness to grayscale changes, such as illumination changes. Another important feature of it is its simple calculation, which allows it to analyze images in real time. A combination of local binary pattern features and gray level co-occurrence matrix are used in the present study, which can effectively improve the detection effect on some sets. Algorithms 2 shows that, LBP feature algorithm steps. Formulas (6) and (7) are complementary to Algorithm 2, which is more intuitive to understand.
| Algorithm 2: LBP feature algorithm steps. |
| Input: image I(m, n) |
| Output: the feature vector |
| 1. Dividing block 16*16 |
| 2. If Ix, y≥Ix±1, y±1 |
| 3. Ix, y = 0 |
| 4. Else |
| 5. Ix, y = 1 |
| 6. Binary→decimal |
| 7. Normalization of the frequency histogram |
where (
ix),
ip and s are coordinates of the center pixel with gray values, the gray value of the surrounding P Pixel and a symbol function, respectively. The symbol function is defined as:
These two functions are calculated to obtain a binary LBP value.
The HOG feature is a feature descriptor used in computer vision and image processing for object detection. It calculates and statistically analyzes the gradient direction histogram of the local region of the image to form features. In practice, the image is divided into small cells, and each cell unit calculates a gradient direction histogram. In order to have a better sensitivity to calcifications, contrast normalization of the histogram is required, which can be achieved by grouping the cell units into larger pieces and normalizing all the cell units within the block. Combine the HOG descriptors of all blocks in the detection window to form the final eigenvector.
3.4. Adaptive Support Vector Machine
In machine learning, support vector machines (often referred to as SVM) [
26] are supervised learning algorithms that analyze data in classification and regression analysis. Given a set of training data and then the training data is marked as belonging to one or the other of the two categories, the SVM training calculation creates a model that assigns new data to one of the two categories, becoming a non-probabilistic binary linear classification. The SVM model uses so-called kernel functions to map data, which was originally difficult to separate at low latitudes into high-dimensional spaces, separated by distinct intervals of the hyperplane as wide as possible. The SVM method utilizes the statistical learning theory, taking into account the complexity of the model and the learning ability so that the model has the best generalization ability. Since it can reduce the generalization error of the classifier.
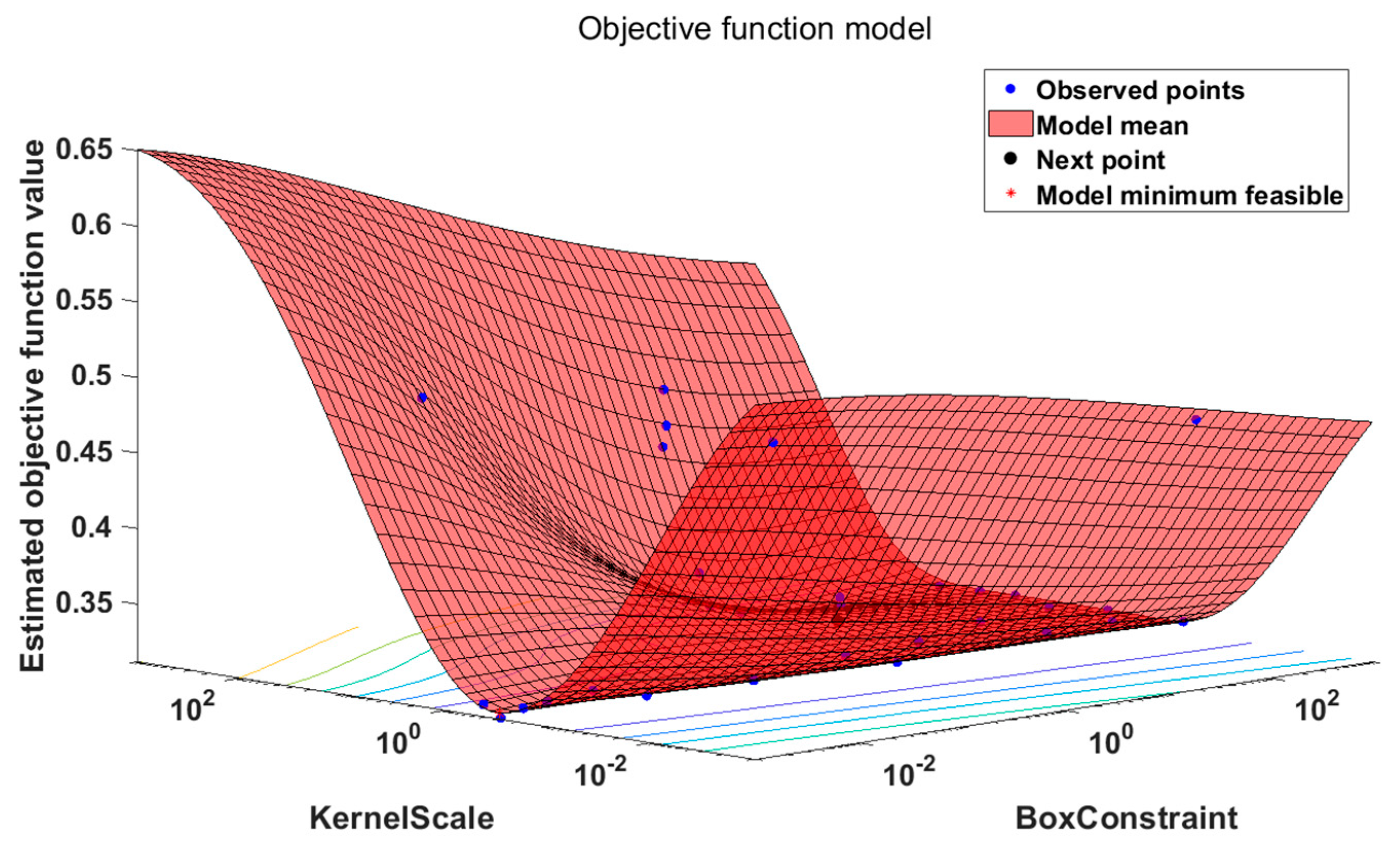
Compared with the traditional fixed SVM kernel function, the kernel function of ASVM is adaptive, it is more flexible and more convenient (See
Figure 3). The algorithm establishes an adaptive incremental sample selection model based on the geometric distance between the original sample and the newly added sample and the current classified hyperplane. The model can effectively screen out boundary samples participating in incremental training. In order to balance the speed and performance of incremental learning, the model sets adjustment coefficients based on spatial distribution similarity for the new sample and the original model sample. Experimental results show that the algorithm improves the performance of the model while speeding up the classification.
The experimental to ASVM is a sparse Bayesian modeling method for parameter adaptive learning. Its biggest feature is that model kernel function parameters are automatically optimized during the training and the model kernel function allows different types of basic functions to be constructed at the same time.
Table 2. ASVM vector machine to find the optimal kernel. In the sixth round of testing, the objective has reached the minimum, ASVM found the optimal kernel.
4. System Performance Evaluation Method
The CAD detection system for breast cancer requires a large-scale mammography database, indicating the location of the lesion. China has not yet established its own public database of breasts. Only a few developed countries in the world have established a standard breast line image database. The DDSM Breast Image database was established in 2009 by the British X-ray Image Analysis Association. The database contains X-ray images of the left and right breasts of 2500 patients. Data include age at the time of the study, American cancer society (ACR) breast density rating, subtlety rating for abnormalities, ACR keyword description of abnormalities. Therefore, all lesion areas have been tested and calibrated by a number of experts. This article uses numbers from the DDSM database. The grayscale resolution of the breast line image in the database is a spatial resolution. Where the size of each image is approximately 3000 × 3000 pixels. The database was marked with calcification, sharply lumped masses, needle-shaped masses, irregular shaped masses, structural distortions, and bilateral tissue asymmetry. In order to verify the accuracy of our algorithm, the results we obtained were compared with two radiologists of different working hours. The accuracy rate of low-grade radiologists 1 who have been diagnosed with mammography for one year is 80%, and that of low-grade attending radiologists 2 who have been diagnosed with mammography for about five years is 85%. In this study, 400 calcified pictures were selected, where 280 images are normal ones and 120 images are calcified pictures. My comparison algorithm is RF (random forest) [
27] and AB (adaptive boosting) [
28], For the RF, the super parameters I set are as follows:
The number of decision trees is 100. More subtrees can make the model perform better, but at the same time make the code slower. The maximum number of features used by a single decision tree is AUTO, simply select all the features, and each tree can use them. The leaf is the end node of the decision tree. Smaller leaves make it easier for the model to capture noise in the training data. I also set the minimum number of leaf nodes to 50. Others I choose the default value. For the AB, the super parameters I set are as follows:
For the base classifier, I set the decision tree and perform boosting based on the classifier. The number of base classifiers lifting, I set 100 times, this value is too large, the model is easy to over-fitting. The value is too small, the model is easy to under-fitting. The learning rate I set is 0.8. After comparison, the convergence speed is optimal. Others I choose the default value. Compares the accuracy of the three algorithms (see
Table 3), our final test results are shown in
Figure 4. The main indicators of the experimental test are sensitivity, specificity and classification accuracy. The best effect in the text is shown in bold.
Breast calcification diagnostic performance indicators include TPR and receiver operating characteristic curve (ROC). When using a breast cancer detection and diagnosis system, for a given lesion (determined by the gold standard), if the algorithm detects it as a lesion, it is called true positive (TP). While the lesion is missed, if the system detects negative, which is called false negative (FN). Moreover, if the non-lesion is detected as a lesion by the detection system, it is called false positive (FP). Furthermore, if the non-lesion is negative by the algorithm, it is true negative (TN) [
29].
TPR is the ratio of true positive to true positive + false negative:
The ideal breast calcification algorithm should have high sensitivity and specificity. In order to fully evaluate the performance of computer-aided detection and diagnostic systems, a receiver operating characteristic (ROC) curve was proposed. With the sensitivity as the abscissa and the specificity as the ordinate axis, these coordinate points are connected to form the ROC curve.
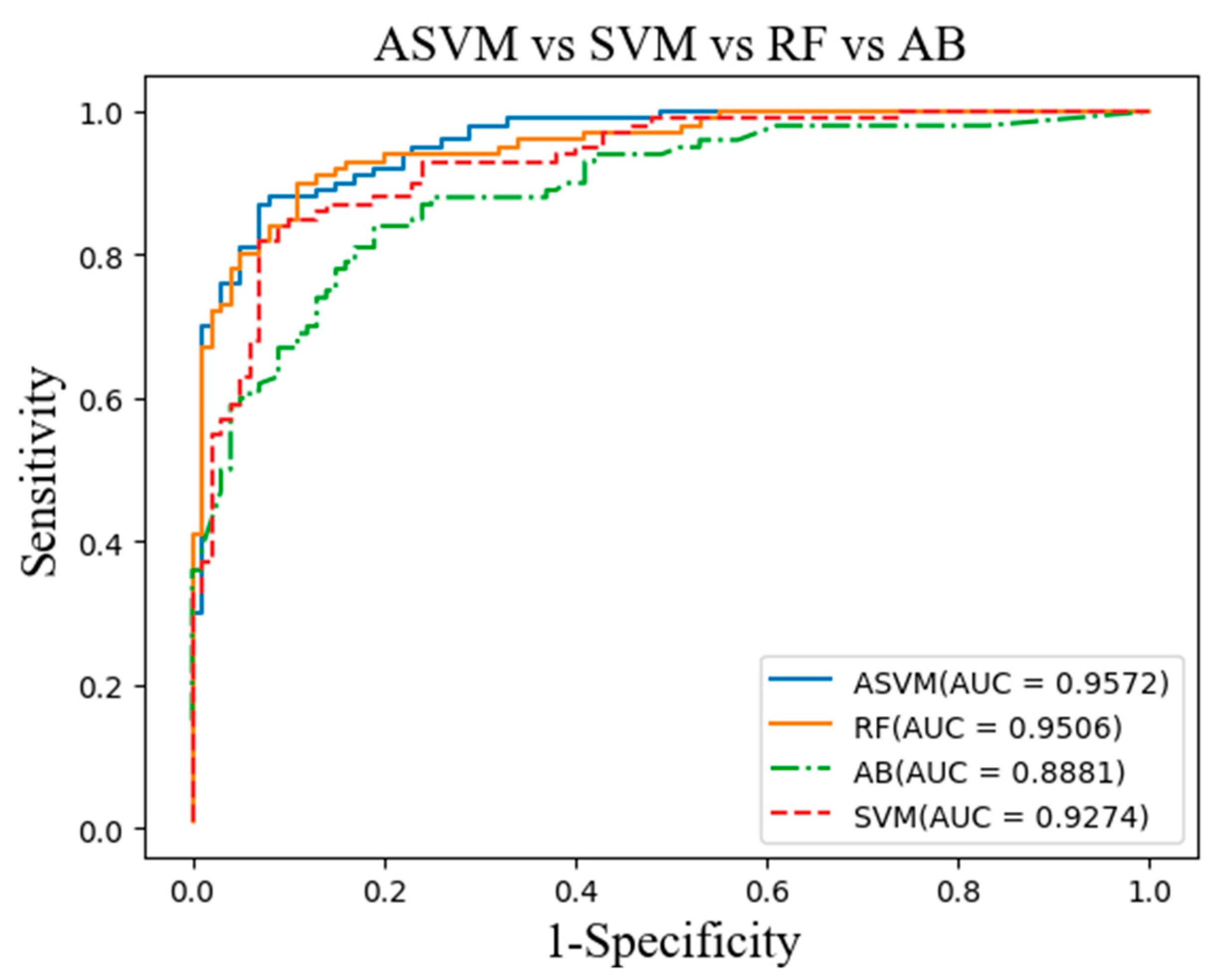
Figure 5 shows ROC distributions obtained by four different methods. The distribution of the sensitivity against the specificity for each method is illustrated with different colors. It is observed that the ASVM algorithm has a higher true positive rate and a lower false positive rate, compared to the AB and RF methods. It is found that as the area under the ROC curve nears to 1, the diagnosis becomes more reliable [
25]. Otherwise, the diagnosis is not reliable. Moreover,
Figure 4 indicates that the ASVM algorithm has the largest area under the ROC curve.
A. Oliver [
30] is based on using local features extracted from a bank of filters to obtain a local description of the microcalcifications morphology. They achieved an AUC value of AZ = 0.918 by using 280 mammograms. Y. Rubio [
31] used a novel methodology based on quantum signal processing and cellular automata to detect microcalcifications in mammograms. They achieved an AUC value of AZ = 0.8297 by using 121 mammograms. X. Liu [
32] integrated the possibilistic fuzzy c-means clustering algorithm and weighted support vector machine for the detection of MC clusters in full-field digital mammograms. The proposed method is evaluated using a database of 410 clinical mammograms and achieved an AUC value of AZ = 0.8676. Our work compared to other similar works that used the DDSM. Our mammograms are enhanced by Contourlet transformation and morphology. The rough ROI is obtained by the improved K-means algorithm, and finally, the adaptive support vector machine (ASVM) is used to obtain an accurate ROI. They achieved an AUC value of AZ = 0.9572 by using 400 mammograms. The difference in the results we get last may be the reason for the amount of data.
5. Conclusions
In the present study, the medical image denoising processing and computer-aided diagnosis of calcification have been discussed and investigated. The medical image processing field has also been further understood and brightness characteristics of breast images are found. It is found that the accuracy of the automatic classification results of the adaptive support vector machine (ASVM) algorithm reaches 94%, and the experimental results are superior to similar algorithms. It is hoped that among further researchers, in addition to the image feature information that can be reflected on the image, information such as the patient’s weight, age, and the like can be utilized as a part of the characteristics of the breast calcification point detection. The introduction of artificial intelligence algorithms, such as machine learning and deep learning into medical diagnosis helps doctors to obtain more accurate diagnostic results. Through analysis of the study, it was found that adaptive support vector machines can be fine-tuned for specific problems, especially in biomedical applications. In summary, deep learning requires a large number of data sets, and the training takes a long time. Our research is suitable for small sample data, and the training takes a relatively short time. The K-means method can detect the breast boundary coarsely and the proposed features are a good description of the calcification area. Combined with the ASVM classification, the classifier has achieved a 94% calcification detection rate, and the large area overlap area, low contrast area has a good detection rate, with a large clinical application value.