An Algorithm for Producing Fuzzy Negations via Conical Sections

Abstract

In this paper we introduced a new class of strong negations, which were generated via conical sections. This paper focuses on the fact that simple mathematical and computational processes generate new strong fuzzy negations, through purely geometrical concepts such as the ellipse and the hyperbola. Well-known negations like the classical negation, Sugeno negation, etc., were produced via the suggested conical sections. The strong negations were a structural element in the production of fuzzy implications. Thus, we have a machine for producing fuzzy implications, which can be useful in many areas, as in artificial intelligence, neural networks, etc. Strong Fuzzy Negations refers to the discrepancy between the degree of difficulty of the effort and the significance of its results. Innovative results may, therefore, derive for use in literature in the specific field of mathematics. These data are, moreover, generated in an effortless, concise, as well as self-evident manner.

1. Introduction

Fuzzy negations play a crucial role in the creation of De Morgan triples and also in the construction of fuzzy implications (c.f. [1,2,3]). As a general admission, the construction of fuzzy negations is the foundation stone of the triples De Morgan construction and fuzzy implications. Gottwald in [4] presented a theoretical approach to fuzzy negations production and one important result ([4], Theorem 5.2.1). A constructive geometrical method of generating strong fuzzy negations, via conical sections has been presented in this paper, followed by the proof of the method and several final remarks, as well as some examples for the strong negations produced via conical sections. It should be particularly emphasized that the specific manner of geometrical construction of strong negations, covers the already known strong negations, such as the Sugeno negations, as well as the classical negation $N\left(x\right)=1-x$ or $N\left(x\right)=\sqrt{1-x^2}$.

It should be noticed that Proposition 3 in paragraph 3 Main Results and particularly Equation (14), constitute new results that might be used in the production of implications, merely from negations (c.f. [2,3]), and by extension in reaching conclusions. In general, the algorithmic approach of negations is virtually non-existent in the applications of fuzzy sets and implications, without any reasons explaining such a gap. This specific new process for producing negations is to address the present gap, since this production is simple and easily understandable. Changing just one parameter in Equation (14), as demonstrated in the examples in paragraph 4. Special Cases, is sufficient to produce a negation which is different from the negations already known, such as the Sugeno or Yager negations. The aforementioned fact led the writers to the extension of their scientific research interests and to the algorithmic approach of their subject matter, namely of the means of application of the present method to real data. The writers were looking forward to a future study on the specific issue.

The key to this effortless production lies in the symmetry of a strong negation, such as the straight line $y=x$, which is an essential attribute of the functions satisfying the condition $N\left(N\left(x\right)\right)=x$. All conical sections with their center at the beginning of the axis, satisfy this symmetry under the condition that they are directed towards π/4 or 3π/4.

The presentation of the authors line of reasoning, along with their methods of proof and their conclusions, follow the aforementioned pattern. The principle definitions and theorems needed to understand the basic theory and proof are set out in paragraph 2 Preliminaries. Then, in paragraph 3 Main Results, the basic propositions and the respective results leading to Proposition 3 are stated and in particular Equation (14) presents the new result. Finally, specific examples of negations through conical sections are presented in the next paragraph, while the study concludes with the remarks and conclusions, as well as the possible applications of the method presented above.

2. Preliminaries

Fuzzy Negation

A fuzzy negation $N$ is a generalization of the classical complement or negation $\neg .$ The fuzzy negation truth table consists of the two conditions: $\neg 1\equiv 0$ and ¬$0\equiv 1$. The fuzzy negation comes to cover the gap between 0 and 1, thus, maintaining the intuitive perspective of negation, as well as the concept of complementarity. The definitions and theorems laid out in this paragraph aim to present the insofar foundation of the fuzzy negation on axioms, by establishing, at the same time, the background of the tools used to support this study. The following definitions and theorems can be found in any introductory text book on Fuzzy logic (see [1,4,5,6,7]).

Definition 1.

A function$N:\left[0,1\left] \to \right[0,1\right]$is called a fuzzy negation if

$$N\left(0\right)=1, N\left(1\right)=0$$

N1

$$Nisdecreasing.$$

N2

Definition 2.

A fuzzy negation$N$is called strict if, in addition,

(1) 

$$Nisastrictlydecreasing,$$

N3

$$Nisacontinuous.$$

N4

(2) 

A fuzzy negation$N$is called strong if the following property is met,

$$N\left(N\left(x\right)\right)=x,\hspace{1em}x\in \left[0,1\right].$$

N5

(3) 

The dual negation based on a fuzzy negation$N$is given by (see [2], p. 124)

$$N^d=1-N\left(1-x\right)$$

Theorem 1.

([1] Theorem 1.4.5). If a function $N:\left[0,1\left] \to \right[0,1\right]$ satisfies (N2) and (N5), then it also satisfies (N1) and (N4). Moreover, N is a bijection, i.e., it satisfies (N3).

Theorem 2.

([1] Lemma 1.4.9). If $N_1$,$N_2$ are fuzzy negations such that $N_1\circ N_2=i{d}_{\left[0,1\right]}$, then

(1) 

$N_1$is a continuous fuzzy negation,

(2) 

$N_2$is a strictly decreasing fuzzy negation,

(3) 

$N_2$is a continuous fuzzy negation if and only if$N_1$is a strictly decreasing fuzzy negation. In both cases$N_1=N_2^{-1}$.

Remark 1.

Both the theorems mentioned above directly lead to the consequence that the${\rm N}5$property is equivalent to the equation$N\left(x\right)={{\rm N}}^{-1}\left(x\right)$. The latter equation leads to the fact that the graphics of the functions${\rm N}$ και ${{\rm N}}^{-1}$ identify with each other, namely in other words, this means that the ${\rm N}$ graphic is symmetrical towards the straight line $y=x$.

Theorem 3.

([1] Theorem 1.4.13) or ([4] Theorem 5.2.1). For a function $N:\left[0, 1\right]\to \left[0,1\right]$ the following statements are equivalent:

(1) 

$N$is a strong negation

$N$is$\Phi -$conjugate with classical negation$N_C$,$\left(N_C\left(x\right)=1-x\right)$there exists$\phi \in \Phi$, such that$N\left(x\right)={\left(N_C\right)}_{\phi }\left(x\right)={\phi }^{-1}\left(1-\phi \left(x\right)\right), x\in \left[0,1\right]$.

Following Theorem 3, the construction of a strong fuzzy negation is a simple case by using the $\phi$ function. Nevertheless, a different mode of construction is attempted in the context of the present study, which involved avoiding the use of the $\phi$ function. The main reasons for adopting the specific procedures were—first and foremost, the creation of negations from parts of the conical sections, the fact that the $\phi$ function might not easily ensure, and secondly the aim to ensure that the mode of constructing the negations shall be based on geometrical methods.

3. Main Results

Production of Fuzzy Negations via Conical Sections

Consider the following special form of conical sections:

$$a{x}^2+b{y}^2+2cxy+dx+ey+f=0 ,x,yϵ\left[0,1\right],$$

(1)

Equation (1) should satisfy the main properties of the negation, namely that ${\rm N}\left(0\right)=1$ and ${\rm N}\left(1\right)=0$. This means that Equation (1) is verified by points ${\rm A}\left(1,0\right),{\rm B}\left(0,1\right)$, while point ${\rm O}\left(0,0\right)$ should not verify it. These considerations led to the following proposal.

Proposition 1.

If (1) satisfies the condition$\left(N1\right)$then takes the form:

$$\alpha x^2+b{y}^2+2cxy+\left(-a-f\right)x+\left(-b-f\right)y+f=0, x,y\in \left[0,1\right], f\ne 0,$$

(2)

Proof of Proposition 1.

Since (1) satisfies the basic property of the negation, the conical section of Equation (1) should pass from points ${\rm A}\left(1,0\right),{\rm B}\left(0,1\right),$ thus, the following relations result

$$b+e+f=0⟹e=-b-f,$$

(3)

$$a+d+f=0⟹d=-a-f.$$

(4)

Furthermore, $f\ne 0$ since point ${\rm O}\left(0,0\right)$ does not verify (1). Simple calculations generate Equation (2). □

An essential element for a part of a conical section to constitute a strong negation pertains to the fact that the basic property $N5$ should be satisfied, namely $N\left(N\left(x\right)\right)=x,x\in \left[0,1\right]$ should be valid. In order to achieve the latter, the conical section defined from Equation (2) should have as an axis of symmetry with the straight line $y=x$, see Remark 1. This statement is used in order to prove the following proposition.

Proposition 2.

The equation:

$$\alpha x^2+\alpha y^2+2cxy+\left(-a-f\right)x+\left(-\alpha -f\right)y+f=0, x,y\in \left[0,1\right], f\ne 0,$$

(5)

is a conical section which has as an axis of symmetry with the straight line$y=x$passing through points${\rm A}\left(1,0\right), {\rm B}\left(0,1\right)$.

Proof of Proposition 2.

In fact, if the conical section of the Equation (2) is to be symmetrical to the straight line $y=x$ the coefficients of the variables $x,y$ should remain the same. This leads to the conclusion that $a=b$, thus Equation (2) becomes:

$$\alpha x^2+\alpha y^2+2cxy+\left(-a-f\right)x+\left(-\alpha -f\right)y+f=0,x,y\in \left[0,1\right],f\ne 0.$$

which is Equation (5). □

Purely for reasons of simplicity and without imposing any restriction on the generalization, in the division of Equation (5) to $f$, the equation transforms to an equivalent one given below in the following form

$$k{x}^2+k{y}^2+2mxy-\left(k+1\right)x-\left(k+1\right)y+1=0, x,y\in \left[0,1\right],$$

(6)

where $k=\frac{a}{f},m=\frac{c}{f}$.

For the remaining part of the paper, Equation (6) shall be used instead of (5). Two cases are derived from Proposition 2 and Equation (6). The first case is for $k=0$. Consequently Equation (6) transforms into

$$2mxy-x-y+1=0$$

(7)

If Equation (7) is solved to $y$ it results, through simple calculations, in the following relation

$$y=\frac{1-x}{1-2mx}, 2m<1.$$

(8)

Due to symmetricity, the solution towards $x$ is given by the same equation

$$x=\frac{1-y}{1-2my}, 2m<1.$$

(9)

The procedure stated above leads to the Sugeno negation, which, as it is known, constitutes a strong fuzzy negation and a general formula, which is

$$N\left(x\right)=\frac{1-x}{1+mx}, m>-1.$$

(10)

The Sugeno negation has been used in many articles (c.f. [8]) and in many applications, a fact that renders its explanation redundant, while the interest it has for the present study refers to the fact that the Sugeno negations form part of the geometrical construction of the conical sections.

The second case is that when $k\ne 0$. In this case, only the symmetry of the conical section with regards to the straight line $y=x$ is to be proved and the central symmetry with regards to ${\rm O}\left(0,0\right)$, namely there is no parallel movement for the axes. The aforementioned are valid only in case that $k=-1$, namely Equation (6) acquires the following form:

$$x^2+y^2-2mxy-1=0, x,y\in \left[0,1\right],$$

(11)

Through easy calculations, Equation (11) becomes, in an equivalent manner

$$x^2+y^2-2mxy-1=0⟺m^2{x}^2-2mxy+y^2=m^2{x}^2-x^2+1,$$

(12)

$$⟺{\left(y-mx\right)}^2=\left(m^2-1\right)x^2+1⟺y=\sqrt{\left(m^2-1\right)x^2+1}+mx,$$

(13)

$$⟺N\left(x\right)=\sqrt{\left(m^2-1\right)x^2+1}+mx, x\in \left[0,1\right], m\le 0 ,$$

(14)

or

$$f\left(x\right)=-\sqrt{\left(m^2-1\right)x^2+1}+mx<0, x\in \left[0,1\right], m\le 0,$$

(15)

for Equation (15) see Remark 2 below.

Once more, due to the symmetry of the conical section to the straight line $y=x$, if Equation (11) is solved for variable $x$, it will generate the same formula of function, namely

$$N^{-1}\left(y\right)=\sqrt{\left(m^2-1\right)y^2+1}+my, y\in \left[0,1\right], m\le 0,$$

(16)

According to Equations (14), και (16), and Remark 1, the equation

$N\left(x\right)=\sqrt{\left(m^2-1\right)x^2+1}+mx,x\in \left[0,1\right],m\le 0$, which is Equation (14), and is a strong fuzzy negation.

In an overview of the results stated above, the following proposition is ensured as a reference to Equation (6).

Proposition 3.

Equation (6) namely

$$k{x}^2+k{y}^2+2mxy-\left(k+1\right)x-\left(k+1\right)y+1=0,x,y\in \left[0,1\right]$$

expresses conical sections, where$k=0$produces strong fuzzy negations with the formula$N\left(x\right)=\frac{1-x}{1+mx}, m>-1$which are known as the Sugeno negations, while for$k=-1$it expresses conical sections, which produce strong fuzzy negations with the formula$N\left(x\right)=\sqrt{\left(m^2-1\right)x^2+1}+mx, x\in \left[0,1\right], m\le 0$, which is Equation (14).

Remark 2.

As far as the$N\left(x\right)$of the aforementioned proposition is concerned, since it forms a part and segment of the conical section, with the beginning of the axes serving as the center of the symmetry, its symmetrical segment for the center of symmetry belongs to the same conical section. The symmetrical segment with the appropriate movement (a single unit upwards and a single unit towards the right) equally constitutes a strong negation and is particularly symmetrical to$N\left(x\right),$with the straight line$y=1-x$as an axis of symmetry. Therefore, it has the following form:$N^d\left(x\right)=1-N\left(1-x\right)$and by Definition 2, it is the dual negation. For instance, if$N\left(x\right)=\sqrt{\left(m^2-1\right)x^2+1}+mx, x\in \left[0,1\right], m\le 0$. Then by Equation (15), we conclude that the function$f\left(x\right)=-\sqrt{\left(m^2-1\right)x^2+1}+mx, x\in \left[0,1\right], m\le 0,$equally constitutes a segment of the conical section, like$N\left(x\right)$, then the$1+f\left(x-1\right)$is nothing more than the dual negation, namely$1+f\left(x-1\right)=N^d\left(x\right)=1-N\left(1-x\right)$.

Certain examples are given below for the explanation and the verification of the aforementioned theoretical results.

4. Special Cases

4.1. Strong Negation via Circle

For $m=0,$ Equation (11) takes the form:

$$x^2+y^2=1⟺N\left(x\right)=\sqrt{1-x^2},\hspace{1em}x\in \left[0,1\right],$$

(17)

which is a negation belonging to the Yager class and is a segment of the unit circle, see Figure 1.

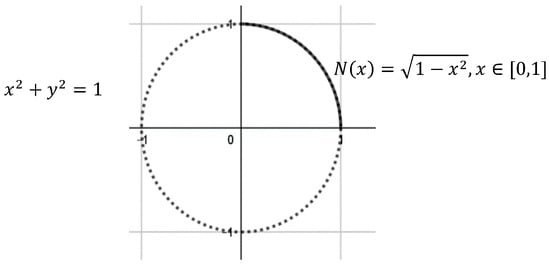
Figure 1. Strong negation via circle.

4.2. Strong Negation via Line

If $m=-1$ then Equation (11) takes the form:

$$x^2+y^2+2xy-1=0\iff N\left(x\right)=1-x,\hspace{1em}x,y\in \left[0,1\right]$$

(18)

which is the classical negation, see Figure 2.

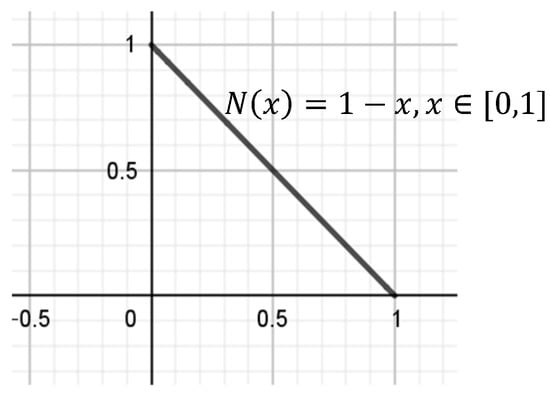
Figure 2. Strong negation via line.

4.3. Strong Negation via Ellipse

If $-1<m<0,$ Equation (11) takes the form:

$$x^2+y^2-2mxy-1=0,\hspace{1em}x,y\in \left[0,1\right]$$

(18)

$$N\left(x\right)=\sqrt{(m^2-1)x^2+1}+mx, -1<m<0,\hspace{1em}x\in \left[0,1\right],$$

(19)

which represents a segment of an ellipse, for example for $m=-\frac{1}{2}$, the below negation is the result, see Figure 3. $N\left(x\right)=\sqrt{-\frac{3}{4}{x}^2+1}-\frac{1}{2}x,x\in \left[0,1\right]$.

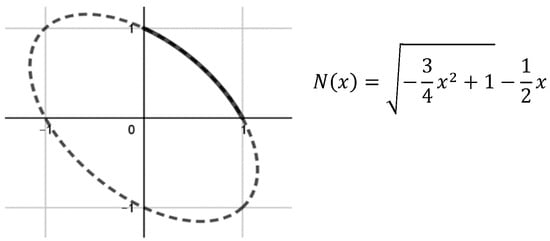
Figure 3. Conical section of ellipse: $x^2+xy+y^2=1$.

4.4. Strong Negation of Hyperbola

If $m<-1,$ Equation (11) takes the form:

$$N\left(x\right)=\sqrt{(m^2-1)x^2+1}+mx,\hspace{1em}m<-1,\hspace{1em}x\in \left[0,1\right],$$

(20)

which represents a segment of the hyperbola, for example for $m=-2$, the below negation is the result, see Figure 4.

$$N\left(x\right)=\sqrt{3x^2+1}-2x, x\in \left[0,1\right]$$

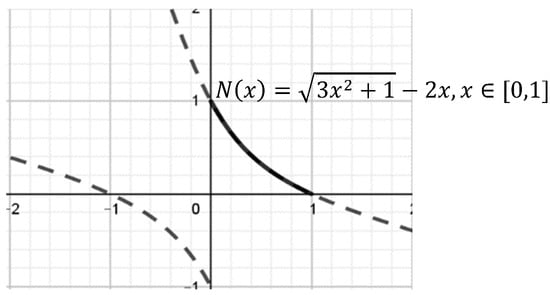
Figure 4. Conical section of hyperbola: $x^2+4xy+y^2-1=0$.

5. Discussion

The purpose of this paper was to propose an algorithm for the production of fuzzy negations, based on which, algorithms for the production of implications might also be proposed. Indeed, an algorithm of producing negations via conical sections has already been found. The last developments in the theory of fuzzy implications (if…X…then…Y…) indicate that fuzzy negation is enough to generate an algorithmic process of production for fuzzy implications, (c.f. [2,3]). For example, supposing that in the context of an application, the fuzzy implication Yager is selected, which is generated in the following way: $I\left(x,y\right)=f^{-1}\left(x·f\left(y\right)\right)$, where $f$ is a decreasing function; if $f$ is replaced by a fuzzy negation, then an algorithm for producing fuzzy implications is automatically generated. If in the place of $f$ we place the negations of Equation (14), then we get the following algorithm,

$${\rm I}\left(x,y\right)=N\left(x·N\left(y\right)\right)=\sqrt{(m^2-1)·x^2·N^2\left(y\right)+1}+m·x·N\left(y\right)\iff$$

$$\begin{gathered} I\left(x,y\right)=\sqrt{(m^2-1)·x^2·{\left(\sqrt{(m^2-1)·y^2+1}+m·y\right)}^2+1} \\ +m·x·\left(\sqrt{(m^2-1)·y^2+1}+m·y\right),x,y\in \left[0,1\right], \end{gathered}$$

(21)

Equation (21) expresses the algorithm of a family of implications for the different values of $m\le 0$.

6. Conclusions

A generation of a new class of fuzzy negations has been enabled by the above procedure. The importance of this relies on the fact that the reasoning process has improved, since for a given application, it is possible to choose the most appropriate implication from a wider class. In most study-applications of fuzzy sets or fuzzy negations, e.g., in the prediction of future events, as well as in the application of fuzzy negations in neural networks, (c.f. [9,10,11]), the classic negation $N\left(x\right)=1-x$ is implicitly used. The replacement of this negation with the negations produced via conical sections offers a new approach in the application of fuzzy implications. It would be important to find out in future—both for the authors and the readers of this paper—whether the aforementioned negations, produced via conical sections and by the extension of the implications introduced, correspond to any kind of application.