Real-time Conflict Resolution Algorithm for Multi-UAV Based on Model Predict Control
Abstract
:1. Introduction
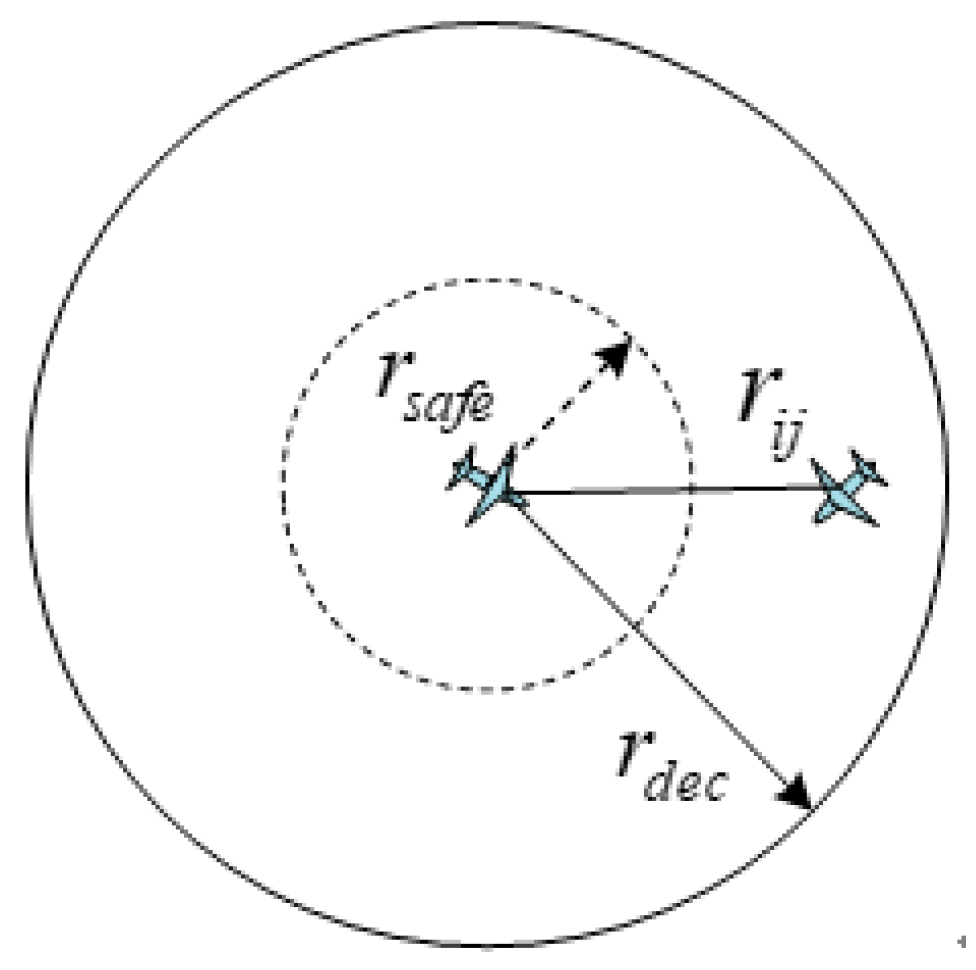
2. Problem Definition
3. Modeling of the Conflict Resolution Problem
3.1. Modeling of UAV
- (1)
- UAV flight performance constraintswhere, , , represent for the maximum speed, overload, angular speed of UAV, represents for the minimum turning radius of UAV.
- (2)
- Collision avoidance constraintDenote the safe flight radius of UAV as , if the distance between any two UAVs () is less than , these two UAVs are considered to collide [17]. So at kth time, the collision avoidance constraint can be given as below:
3.2. Modeling of Conflict Management
| Process 1: |
|
3.3. Conflict Resolution Strategy Based on Synergetic Heading Angle Control Rule
4. Conflict Resolution Algorithm Based on DNMPC
4.1. Performance Indicators for Conflict Resolution
- (1)
- Total flight distance indicator:where, represents for the target of UAV i.
- (2)
- Trajectory adjustment cost indicator:
- (3)
- Conflict penalty function:Rewrite Constraint (5) as a penalty function for conflict:In summary, the entire performance indicator for conflict resolution in period can be given as:where, is the conflict penalty function and is the coefficient for the penalty function.
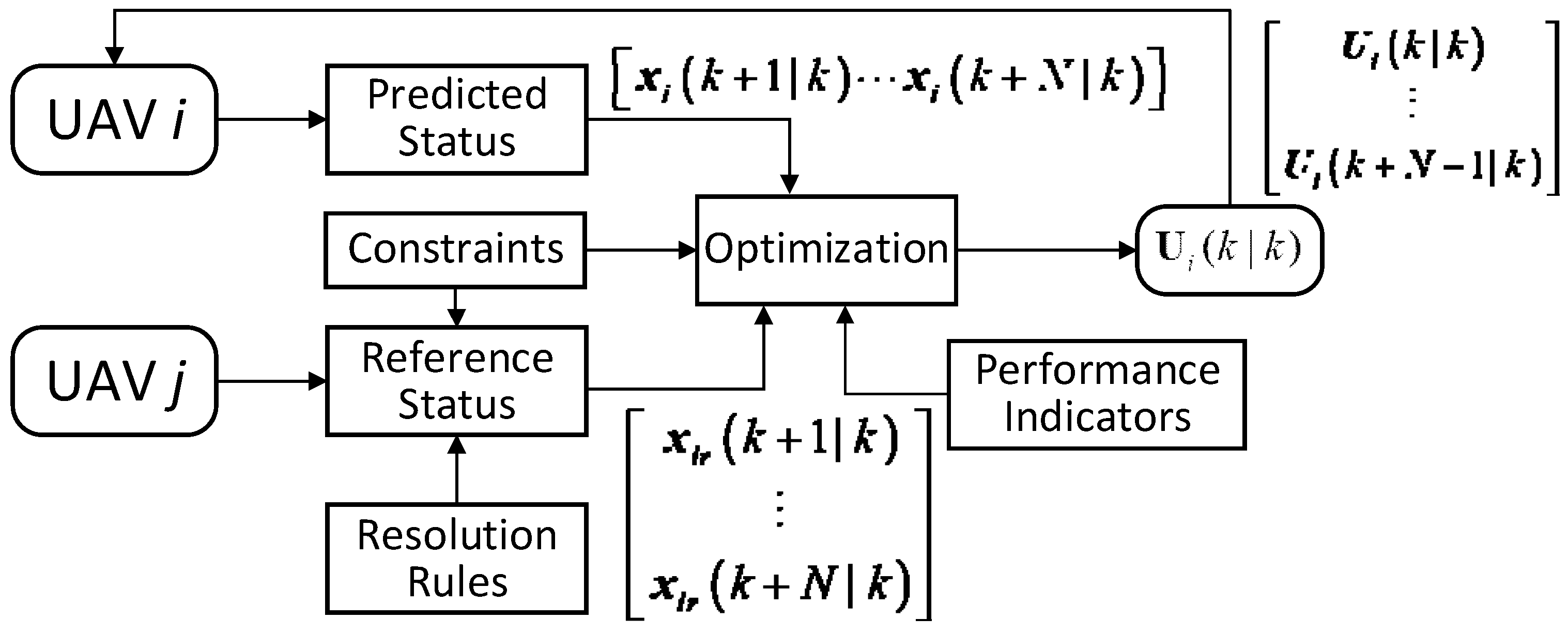
4.2. Controller Design of DNMPC
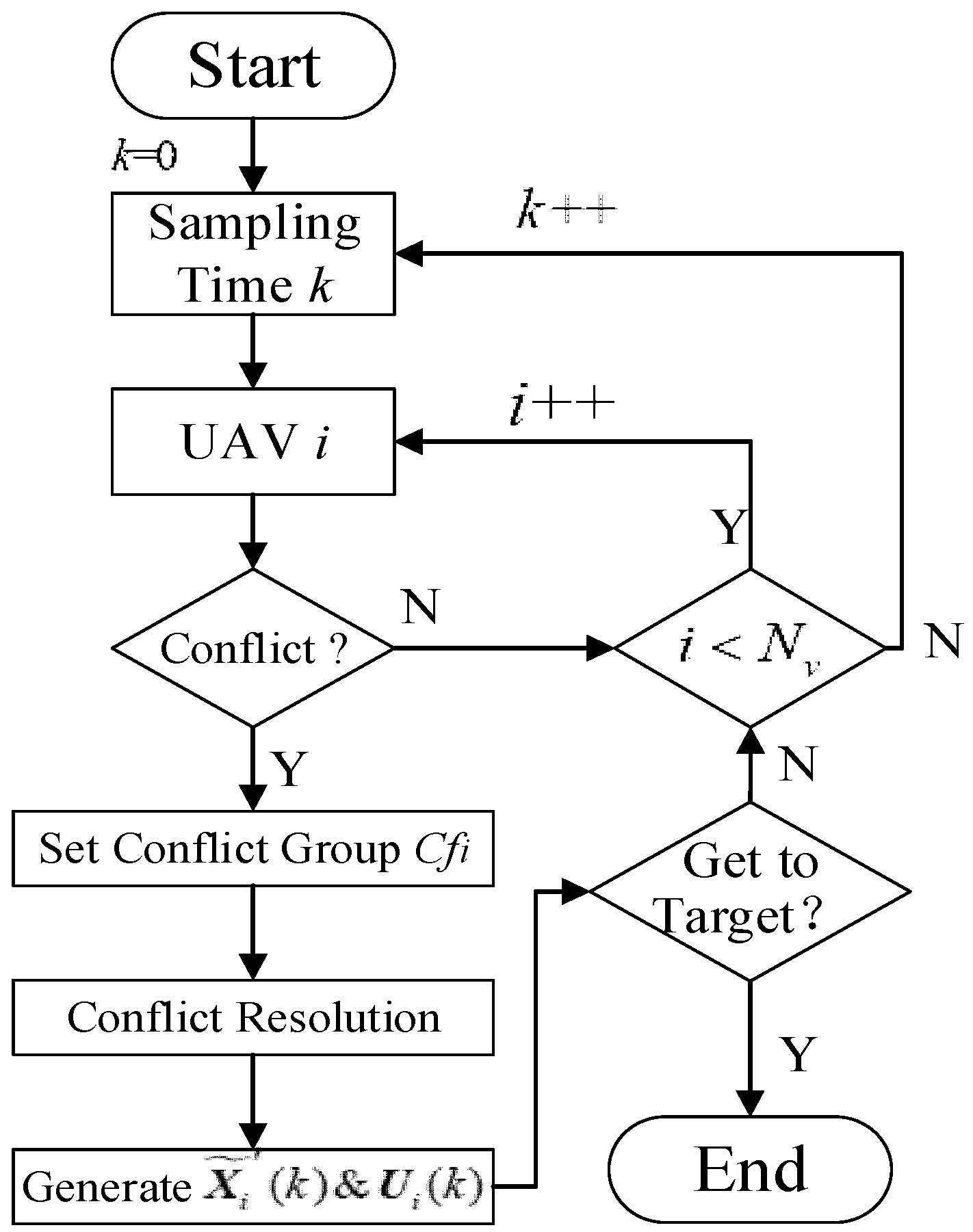
4.3. Algorithm Description for Conflict Resolution
| Algorithm 1: |
|
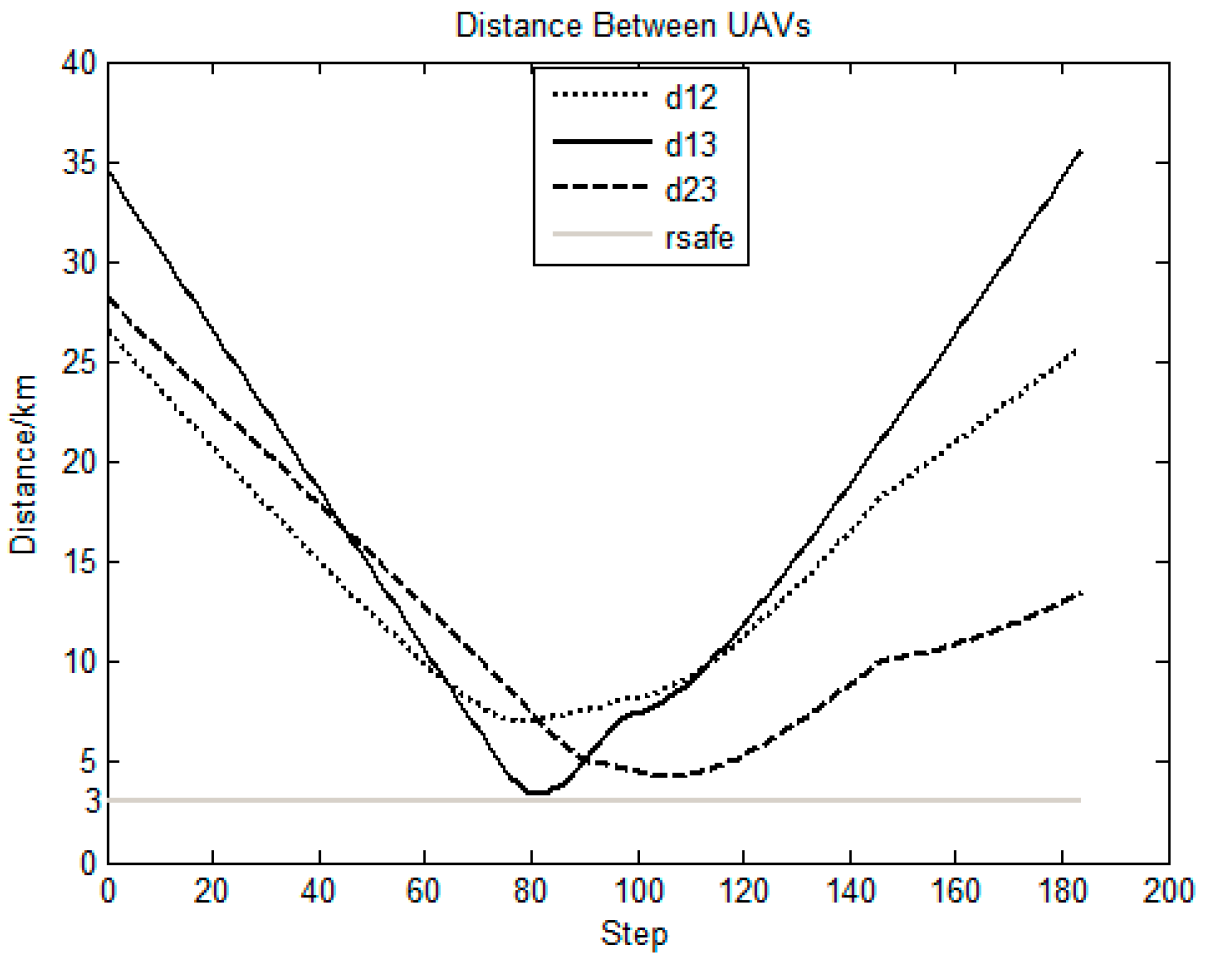
5. Simulation Results and Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability
Acknowledgments
Conflicts of Interest
References
- Cai, G.; Wang, B.; Chen, B.M.; Tong, H.L. Design and Implementation of a Flight Control System for an Unmanned Rotorcraft using. Asian J. Control 2013, 15, 95–119. [Google Scholar] [CrossRef]
- Conde, R.; Alejo, D.; Cobano, J.A.; Viguria, A.; Ollero, A. Conflict Detection and Resolution Method for Cooperating Unmanned Aerial Vehicles. J. Intell. Rob. Syst. 2012, 65, 495–505. [Google Scholar] [CrossRef]
- Pallottino, L.; Feron, E.M.; Bicchi, A. Conflict resolution problems for air traffic management systems solved with mixed integer programming. IEEE Trans. Intell. Transp. Syst. 2002, 3, 3–11. [Google Scholar] [CrossRef]
- Hwang, I.; Kim, J.; Tomlin, C. Protocol-Based Conflict Resolution for Air Traffic Control. Air Traffic Control Q. 2002, 15, 1–34. [Google Scholar] [CrossRef]
- Masci, P.; Tedeschi, A. Modelling and Evaluation of a Game-Theory Approach for Airborne Conflict Resolution in Omnet++. In Proceedings of the International Conference on Dependability, Athens, Glyfada, Greece, 18–23 June 2009; pp. 162–165. [Google Scholar]
- Vela, A.; Solak, S.; Singhose, W.; Clarke, J.-P. A mixed integer program for flight-level assignment and speed control for conflict resolution. In Proceedings of the 48th IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 5219–5226. [Google Scholar]
- Omer, J. A space-discretized mixed-integer linear model for air-conflict resolution with speed and heading maneuvers. Comput. Oper. Res. 2015, 58, 75–86. [Google Scholar] [CrossRef]
- Carbone, C.; Ciniglio, U.; Corraro, F.; Luongo, S. A Novel 3D Geometric Algorithm for Aircraft Autonomous Collision Avoidance. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 1580–1585. [Google Scholar]
- Durand, N.; Alliot, J.M. Ant Colony Optimization for Air Traffic Conflict Resolution. J. Intell. Rob. Syst. 2009. [Google Scholar]
- Lamont, G.B.; Slear, J.N.; Melendez, K. UAV Swarm Mission Planning and Routing using Multi-Objective Evolutionary Algorithms. In Proceedings of the 2007 IEEE Symposium on Computational Intelligence in Multicriteria Decision Making, Honolulu, HI, USA, 1–5 April 2007; pp. 10–20. [Google Scholar]
- Mujumdar, A.; Padhi, R. Reactive Collision Avoidance of Using Nonlinear Geometric and Differential Geometric Guidance. J. Guidance Control Dyn. 2015, 34, 69. [Google Scholar] [CrossRef]
- Chaloulos, G.; Hokayem, P.; Lygeros, J. Hierarchical Control with Prioritized MPC for Conflict Resolution in Air Traffic Control. IFAC Proc. Volumes 2011, 44, 1564–1569. [Google Scholar] [CrossRef]
- Stastny, T.J.; Garcia, G.A.; Keshmiri, S.S. Collision and Obstacle Avoidance in Unmanned Aerial Systems Using Morphing Potential Field Navigation and Nonlinear Model Predictive Control. J. Dyn. Syst. Meas. Control 2015, 137, 014503. [Google Scholar] [CrossRef]
- Chaloulos, G.; Hokayem, P.; Lygeros, J. Distributed hierarchical MPC for conflict resolution in air traffic control. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 3945–3950. [Google Scholar]
- Izadi, H.A.; Gordon, B.W.; Zhang, Y. Rule-Based Cooperative Collision Avoidance Using Decentralized Model Predictive Control. In Proceedings of the Infotech@Aerospace Conference, St. Louis, MO, USA, 29–31 March 2011. [Google Scholar]
- Albaker, B.M.; Rahim, N.A. Unmanned aircraft collision detection and resolution: Concept and survey. In Proceedings of the IEEE Conference on Industrial Electronics and Applications, Taichung, Taiwan, 15–17 June 2010. [Google Scholar]
- Yoo, J.; Devasia, S. Application of provably-safe conflict resolution for air traffic control. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012. [Google Scholar]
- Anderson, R.P.; Milutinovic, D.A. Stochastic Approach to Dubins Vehicle Tracking Problems. IEEE Trans. Autom. Control 2014, 59, 2801–2806. [Google Scholar] [CrossRef]
- Tomlin, C.; Mitchell, I.; Ghosh, R. Safety verification of conflict resolution maneuvers. IEEE Trans. Intell. Transp. Syst. 2001, 2, 110–120. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Kuriki, Y.; Namerikawa, T. Formation Control with Collision Avoidance for a Multi-UAV System Using Decentralized MPC and Consensus-Based Control. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015. [Google Scholar]
- Menon, P.K.; Sweriduk, G.D.; Sridhar, B. Optimal Strategies for Free-Flight Air Traffic Conflict Resolution. J. Guidance Control Dyn. 1999, 22, 202–211. [Google Scholar] [CrossRef]
- Sorcia-Vázquez, F.D.J.; Garcia-Beltran, C.D.; Valencia-Palomo, G.; Guerrero Ramírez, G.; Adam-Medina, M.; Escobar-Jiménez, R. Distributed Model Predictive Control Applied to a Four Interconnected Tank Process. Revista Iberoamericana de Automática eInformática Industrial RIAI. 2015, 12, 365–375. Available online: http://doi.org/10.1016/j.riai.2015.07.002 (accessed on 22 February 2019). (In Spanish).
- Espinosa, J.; Marruedo, D.; Marquardt, W.; Schutter, B.; Valencia, F. A comparative analysis of distributed MPC techniques applied to the HD-MPC four-tank benchmark. J. Process Control 2011, 21, 800–815. [Google Scholar]
- Garriga, J.L.; Soroush, M. Model Predictive Control Tuning Methods: A Review. Ind. Eng. Chem. Res. 2010, 49, 3505–3515. [Google Scholar] [CrossRef]
- Gutiérrez-Urquídez, R.C.; Valencia-Palomo, G.; Rodríguez-Elias, O.M.; Trujillo, L. Systematic selection of tuning parameters for efficient predictive controllers using a multi-objective evolutionary algorithm. Appl. Soft Comput. 2015, 31, 326–338. [Google Scholar] [CrossRef]





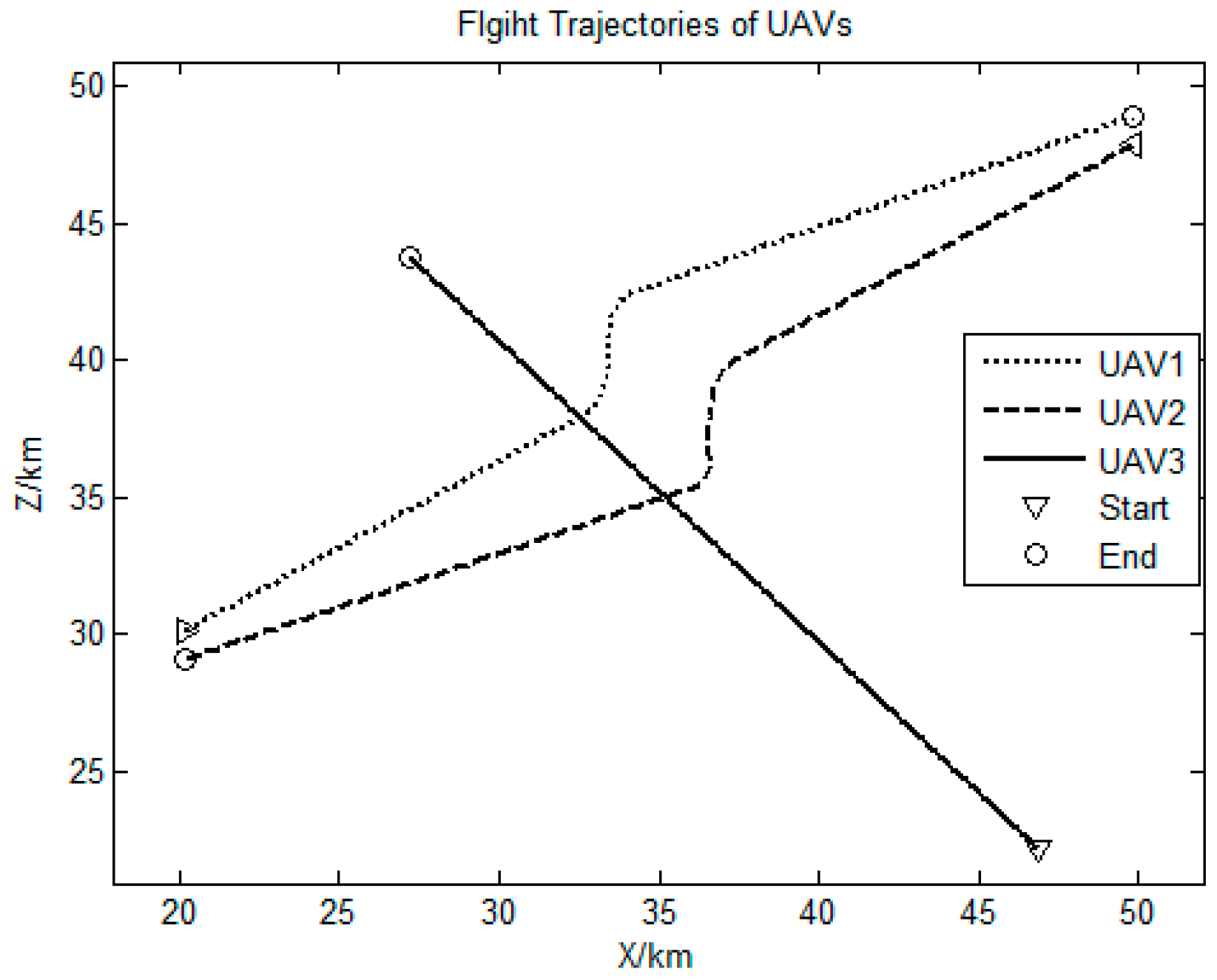



| UAV | Start Points/km | Destination/km | Velocity/m·s−1 | /deg | /deg s−1 |
|---|---|---|---|---|---|
| 1 | (20, 30) | (50, 49) | 180 | 32.5 | (−10,10) |
| 2 | (50, 48) | (20, 29) | 180 | 212.4 | (−10,10) |
| 3 | (45, 20) | (25, 42) | 200 | 132.3 | (−10,10) |
| UAV | Start Points/km | Destination/km | Velocity/m·s−1 | /deg | /deg s−1 | |
|---|---|---|---|---|---|---|
| 1 | (30, 25) | (−31, −26) | 200 | 219.9 | (−10,10) | |
| 2 | (−26, 31) | (25, −30) | 200 | 310.9 | (−10,10) | |
| 3 | (−32, −20) | (28, 31) | 200 | 40.3 | (−10,10) | |
| 4 | (21, −36) | (−30, 23) | 200 | 130.8 | (−10,10) | |
| Indicator | FPI | TRT (s) | TFC (s) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | Best | Worst | Avg. | Best | Worst | Avg. | Best | Worst | Avg. |
| A | 171.6 | 184.2 | 177.1 | 121.9 | 136.5 | 129.7 | 0 | 2 | 0.08 |
| B | 180.4 | 193.1 | 186.3 | 137.6 | 149.9 | 142.4 | 2 | 21 | 5.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.-X.; Nan, Y.; Yang, Y. Real-time Conflict Resolution Algorithm for Multi-UAV Based on Model Predict Control. Algorithms 2019, 12, 47. https://doi.org/10.3390/a12020047
Chen H-X, Nan Y, Yang Y. Real-time Conflict Resolution Algorithm for Multi-UAV Based on Model Predict Control. Algorithms. 2019; 12(2):47. https://doi.org/10.3390/a12020047
Chicago/Turabian StyleChen, Hao-Xiang, Ying Nan, and Yi Yang. 2019. "Real-time Conflict Resolution Algorithm for Multi-UAV Based on Model Predict Control" Algorithms 12, no. 2: 47. https://doi.org/10.3390/a12020047
APA StyleChen, H.-X., Nan, Y., & Yang, Y. (2019). Real-time Conflict Resolution Algorithm for Multi-UAV Based on Model Predict Control. Algorithms, 12(2), 47. https://doi.org/10.3390/a12020047





