A Two-Level Rolling Optimization Model for Real-time Adaptive Signal Control
Abstract
:1. Introduction
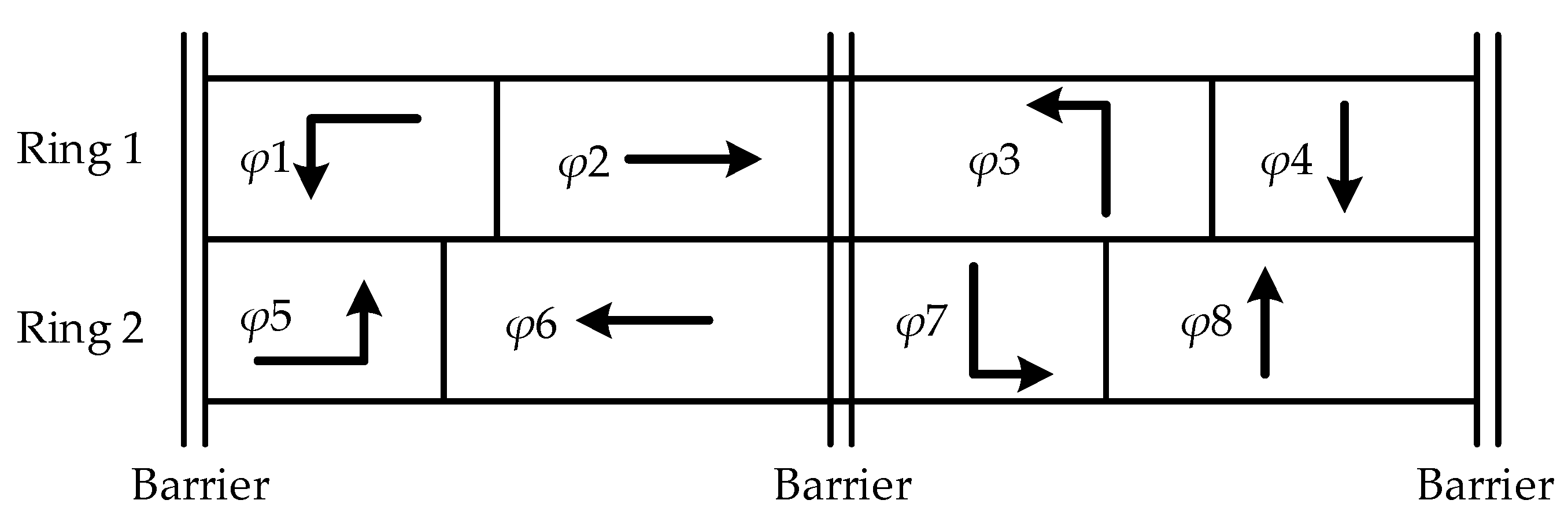
2. Traffic Signal Timing Optimization Algorithm
2.1. Dynamic Programming Algorithm
2.1.1. Forward Recursion
- Step 1:
- Set , and .
- Step 2:
- Calculate .
- Step 3:
- For in {Calculate .record as the optimal solution in Step 2.}.
- Step 4:
- If (), , go to Step 2.Else STOP.
2.1.2. Backward Recursion
- Step 1:
- Set
- Step 2:
- ForRead from the table computed in forward recursion.If (),
2.2. Integer Linear Programming
2.3. Rolling Strategy
3. Case Study and Discussion
4. Conclusions and Future Work
4.1. Conclusions
4.2. Future Work
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Webster, F.V. Traffic Signal Settings. Lond. Road Res. Tech. Pap. 1958, 39, 1–44. [Google Scholar]
- Smith, M.J.; Liu, R.; Mounce, R. Traffic Control and Route Choice: Capacity Maximisation and Stability. Transp. Res. Part B Methodol. 2015, 81, 863–885. [Google Scholar] [CrossRef]
- Liu, R.; Smith, M. Route Choice and Traffic Signal Control: A Study of the Stability and Instability of a New Dynamical Model of Route Choice and Traffic Signal Control. Transp. Res. Part B Methodol. 2015, 77, 123–145. [Google Scholar] [CrossRef]
- Coogan, S.; Flores, C.; Varaiya, P. Traffic Predictive Control from Low-Rank Structure. Transp. Res. Part B Methodol. 2017, 97, 1–22. [Google Scholar] [CrossRef]
- Jiang, Y.S.; Yao, Z.H.; Luo, X.L.; Wu, W.T.; Ding, X.; Khattak, A. Heterogeneous Platoon Flow Dispersion Model Based on Truncated Mixed Simplified Phase-Type Distribution of Travel Speed. J. Adv. Transp. 2016, 50, 2160–2173. [Google Scholar] [CrossRef]
- Yao, Z.H.; Jiang, Y.S.; Han, P.; Luo, X.L.; Xu, T. Traffic Flow Prediction Model Based on Neural Network in Small Time Granularity. J. Transp. Syst. Eng. Inf. Technol. 2017, 17, 67–73. [Google Scholar]
- Yao, Z.H.; Shen, L.; Wu, W.; Jiang, Y.; Huang, L. Heterogeneous Traffic Flow Platoon Dispersion Model Based on Travel Time Distribution. China J. Highw. Transp. 2016, 29, 134–142, 151. [Google Scholar]
- Sims, A.; Dobinson, K. The Sydney Coordinated Adaptive Traffic (SCAT) System Philosophy and Benefits. IEEE Trans. Veh. Technol. 1980, 29, 130–137. [Google Scholar] [CrossRef]
- Hunt, P.; Robertson, D.; Bretherton, R.; Winton, R. SCOOT-A Traffic Responsive Method of Coordinating Signals. Transport and Road Research Laboratory Report LR 1041; Transport and Road Research Laboratory: London, UK, 1981. [Google Scholar]
- Farges, J.L.; Henry, J.J.; Tufal, J. The PRODYN Real-Time Traffic Algorithm. In Proceedings of the 4th IFAC Symposium on Transportation Systems, Baden-Baden, Germany, 20–22 April 1983; pp. 307–312. [Google Scholar]
- Boillot, F.; Midenet, S.; Pierrelée, J.-C. The Real-Time Urban Traffic Control System CRONOS: Algorithm and Experiments. Transp. Res. Part C Emergy Technol. 2006, 14, 18–38. [Google Scholar] [CrossRef]
- Donati, F.; Mauro, V.; Roncoloni, G.; Vallauri, M. A Hierarchical Decentralized Traffic Light Control System-the First Realisation: Progetto Torino. In Proceedings of the 9th World Congress of the International Federation of Automotive Control, Budapest, Hungary, 2–6 July 1984; pp. 2853–2858. [Google Scholar]
- Gartner, N.H. OPAC: A Demand-Responsive Strategy for Traffic Signal Control. In Transportation Research Record: Journal of the Transportation Research Board, No. 906; Transportation Research Board of the National Academies: Washington, DC, USA, 1983; pp. 75–81. [Google Scholar]
- Sen, S.; Head, K.L. Controlled Optimization of Phases at an Intersection. Transp. Sci. 1997, 31, 5–17. [Google Scholar] [CrossRef]
- Mirchandani, P.; Head, L. A Real-time Traffic Signal Control System: Architecture, Algorithms, and Analysis. Transp. Res. Part C Emergy Technol. 2001, 9, 415–432. [Google Scholar] [CrossRef]
- Asthana, R.; Ahuja, N.J.; Darbaari, M.; Shukla, P.K. A Critical Review on the Development of Urban Traffic Models and Control Systems. Int. J. Sci. Eng. Res. 2012, 3, 1–6. [Google Scholar]
- Feng, Y.; Head, L.; Khoshmagham, S.; Zamanipour, M. A Real-Time Adaptive Signal Control in a Connected Vehicle Environment. Transp. Res. Part C Emergy Technol. 2015, 55, 460–473. [Google Scholar] [CrossRef]
- Li, T.; Zhao, D.B.; Yi, J.Q. Adaptive Dynamic Programming for Multi-intersections Traffic Signal Intelligent Control. Intelligent Transportation Systems. In Proceedings of the 11th International IEEE Conference on Intelligent Transportation Systems 2008, Beijing, China, 12–15 October 2008. [Google Scholar]
- Zhuang, H.B.; Zhou, Y.P.; Cao, X.S. Regional Traffic Signal Timing Optimization Based on Genetic Algorithm. J. Transp. Syst. Eng. Inf. Technol. 2012, 12, 57–63. [Google Scholar]
- Ceylan, H.; Bell, M.G.H. Traffic Signal Timing Optimization based on Genetic Algorithm Approach, Including Drivers’ Routing. Transp. Res. Part B Methodol. 2004, 38, 329–342. [Google Scholar] [CrossRef]
- Xu, L.H.; Xi, L.A.; Zhong, L.S. Adaptive Multi-Phase Fuzzy Control of Single Intersection based on Neural Network. China J. Highw. Transp. 2005, 18, 90–93. [Google Scholar]
- Mitsuru, S.; Fan, J. Artificial Neural Network–Based Heuristic Optimal Traffic Signal Timing. Comput.-Aided Civ. Infrastruct. Eng. 2000, 15, 293–307. [Google Scholar]
- Yang, W.C.; Zhang, L.; Zhang, M.; He, Z.C. Rolling Horizon Optimization Based Three Stage Fuzzy Logic Controller for Urban Traffic Signals. J. Tongji Univ. Nat. Sci. 2014, 12, 1846–1853, 1867. [Google Scholar]
- Trabia, M.B.; Kaseko, M.S.; Ande, M. A Two-Stage Fuzzy Logic Controller for Traffic Signals. Transp. Res. Part C: Emergy Technol. 1999, 7, 353–367. [Google Scholar] [CrossRef]
- Yao, Z.H.; Han, P.; Zhao, B.; Jiang, Y.S.; Liu, B.; Du, M.Q. High-Granularity Dynamic Traffic Flow Prediction Model Based on Artificial Neural Network; CD-ROM; Transportation Research Board of the National Academies: Washington, DC, USA, 2017. [Google Scholar]
- Yao, Z.H.; Jiang, Y.S.; Luo, X.L.; Ding, X. Dynamic Traffic Flow Prediction Model for Real-Time Adaptive Signal Control in Vehicle Infrastructure Integration Environment; CD-ROM; Transportation Research Board of the National Academies: Washington, DC, USA, 2017. [Google Scholar]
- Strong, D.W.; Nagui, R.; Courage, K. New Calculation Method for Existing and Extended HCM Delay Estimation Procedure; CD-ROM; Transportation Research Board of the National Academies: Washington, DC, USA, 2006. [Google Scholar]
- PTV AG. VISSIM 5.40 User Manual. Karlsruhe, Germany, 2011. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C50&q=VISSIM+5.40+user+manual&btnG= (accessed on 14 February 2019).




| Variable | Description |
|---|---|
| Phase index in each ring and barrier group, . | |
| Ring index in each barrier group, . | |
| Index of barrier groups/stages. | |
| Last stage calculated by the DP before stopping. | |
| Decision variable denoting the length of barrier group . | |
| State variable denoting the total number of time steps from the start time to barrier group . | |
| A set of state variable . | |
| The total number of discrete time steps in the planning horizon, seconds. | |
| A set of feasible control decisions, given barrier group state . | |
| Performance measure (objective function) at stage , given barrier group state and control variable . | |
| Value function (cumulative value of prior performance measures), given state variable . | |
| Phase change interval which is the total of the yellow change and red clearance times of phase in ring . | |
| Minimum green time of phase in ring . | |
| Maximum green time of phase in ring . | |
| Minimum possible barrier group length of stage . | |
| Maximum possible barrier group length of stage . | |
| Green time of phase in ring . |
| Methods | Phase 1 | Phase 2 | Phase 3 | Phase 4 | Phase 5 | Phase 6 | Phase 7 | Phase 8 | Average | Improvement |
|---|---|---|---|---|---|---|---|---|---|---|
| COP | 43.40 | 34.70 | 53.30 | 39.60 | 38.60 | 48.20 | 50.40 | 37.10 | 43.16 | NA |
| Proposed-6 secs | 41.23 | 32.03 | 51.46 | 38.77 | 36.27 | 46.12 | 50.11 | 34.61 | 41.32 | −4.26% |
| Proposed-4 secs | 38.42 | 30.68 | 50.52 | 36.46 | 36.06 | 43.77 | 48.03 | 34.09 | 39.76 | −7.89% |
| Proposed-2 secs | 36.51 | 30.54 | 48.90 | 34.07 | 35.15 | 41.92 | 45.83 | 31.72 | 38.08 | −11.78% |
| Methods | Phase 1 | Phase 2 | Phase 3 | Phase 4 | Phase 5 | Phase 6 | Phase 7 | Phase 8 | Average | Improvement |
|---|---|---|---|---|---|---|---|---|---|---|
| COP | 35.01 | 24.95 | 44.64 | 30.74 | 28.76 | 38.24 | 40.73 | 29.01 | 34.01 | NA |
| Proposed-6 secs | 32.52 | 24.29 | 43.83 | 27.98 | 28.15 | 37.67 | 39.38 | 26.92 | 32.59 | –4.17% |
| Proposed-4 secs | 31.98 | 23.41 | 43.11 | 27.63 | 25.29 | 36.79 | 36.40 | 26.18 | 31.35 | –7.82% |
| Proposed-2 secs | 29.46 | 23.02 | 42.10 | 25.38 | 24.73 | 34.56 | 34.56 | 24.74 | 29.82 | –12.32% |
| Methods | Phase 1 | Phase 2 | Phase 3 | Phase 4 | Phase 5 | Phase 6 | Phase 7 | Phase 8 | Average | Improvement |
|---|---|---|---|---|---|---|---|---|---|---|
| COP | 25.63 | 15.99 | 36.12 | 21.27 | 19.16 | 30.04 | 31.83 | 20.30 | 25.04 | NA |
| Proposed-6 secs | 22.67 | 13.87 | 33.50 | 19.00 | 18.86 | 27.99 | 29.99 | 17.74 | 22.95 | –8.35% |
| Proposed-4 secs | 20.72 | 12.07 | 30.73 | 17.84 | 18.34 | 26.89 | 29.52 | 17.01 | 21.64 | –13.60% |
| Proposed-2 secs | 19.63 | 11.79 | 28.39 | 17.35 | 17.98 | 25.23 | 28.71 | 15.29 | 20.55 | –17.95% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Z.; Wang, Y.; Xiao, W.; Zhao, B.; Peng, B. A Two-Level Rolling Optimization Model for Real-time Adaptive Signal Control. Algorithms 2019, 12, 38. https://doi.org/10.3390/a12020038
Yao Z, Wang Y, Xiao W, Zhao B, Peng B. A Two-Level Rolling Optimization Model for Real-time Adaptive Signal Control. Algorithms. 2019; 12(2):38. https://doi.org/10.3390/a12020038
Chicago/Turabian StyleYao, Zhihong, Yibing Wang, Wei Xiao, Bin Zhao, and Bo Peng. 2019. "A Two-Level Rolling Optimization Model for Real-time Adaptive Signal Control" Algorithms 12, no. 2: 38. https://doi.org/10.3390/a12020038
APA StyleYao, Z., Wang, Y., Xiao, W., Zhao, B., & Peng, B. (2019). A Two-Level Rolling Optimization Model for Real-time Adaptive Signal Control. Algorithms, 12(2), 38. https://doi.org/10.3390/a12020038






