Pre and Postprocessing for JPEG to Handle Large Monochrome Images
Abstract
:1. Introduction
2. Methodology
2.1. Pre-Processing
- The image size is adjusted to make it divisible to blocks. Let R and C be the image width and length, respectively, then R and C are changed to:where and are divisible by 4, and the image size is adjusted to a blocks.
- To soften the boundaries of the image, padding is added to the image borders with replicated values of the nearest points.
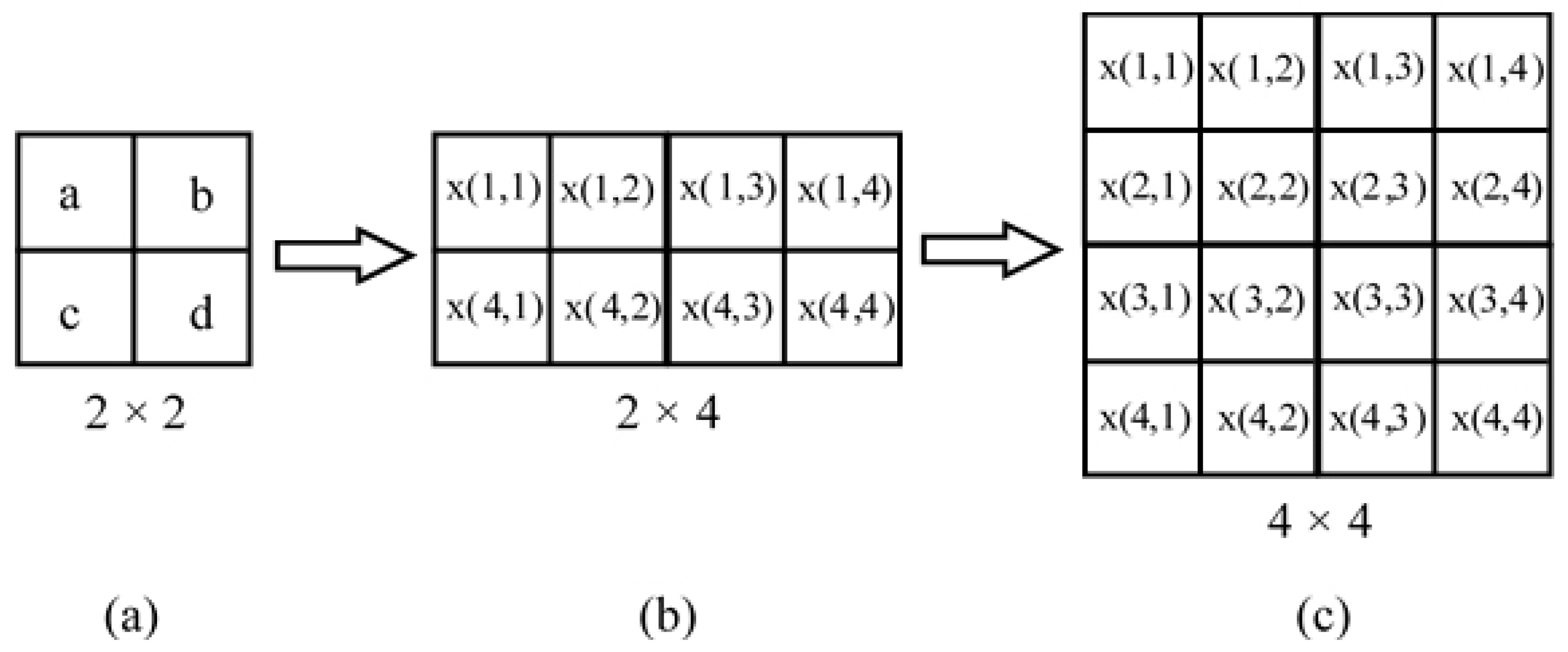
- Next, the image is divided into a non-overlapping blocks.
2.2. Image Compression
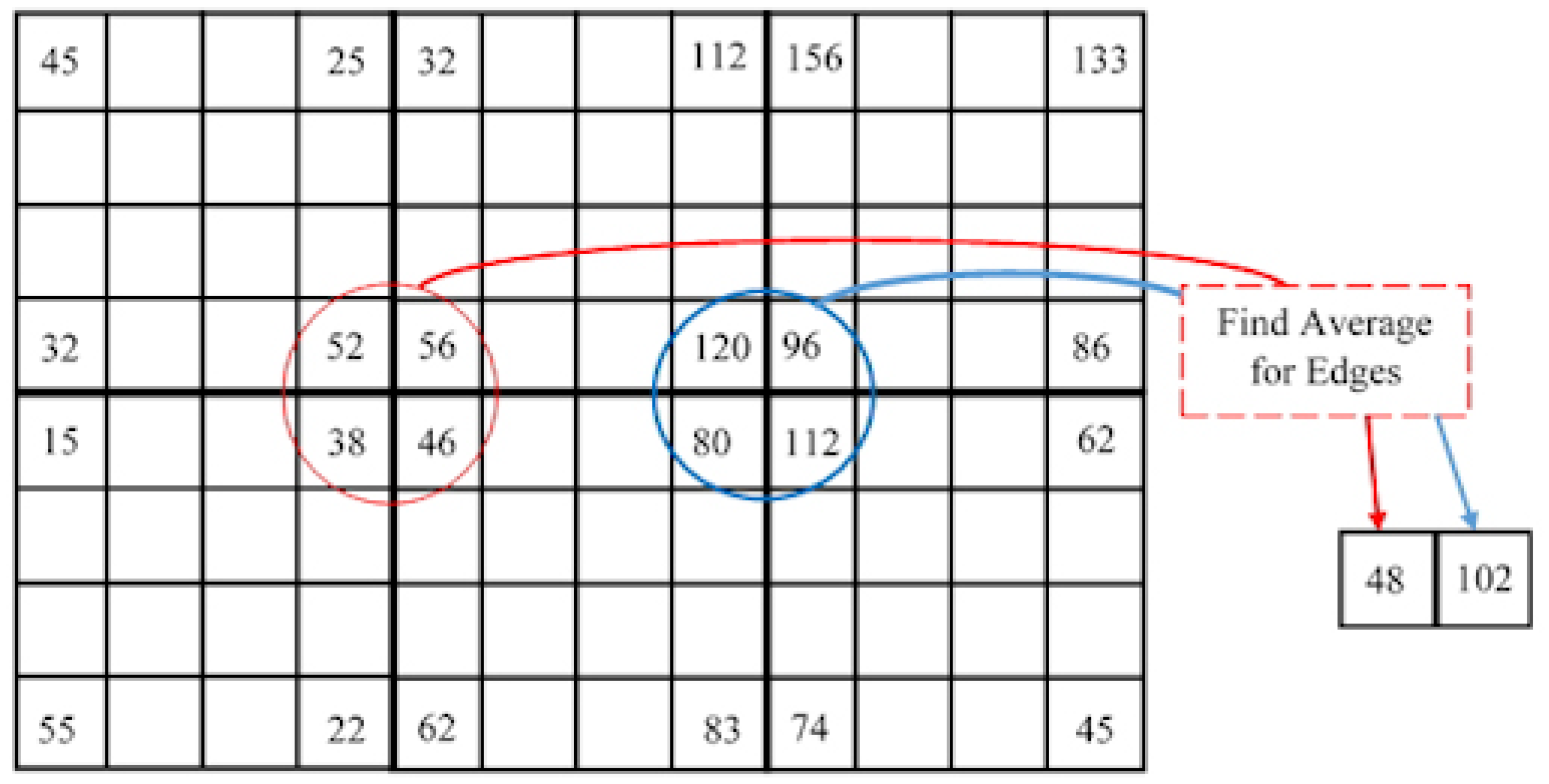
- The four corner points of each non-overlapped blocks of an image are selected.
- The average value for each edge point with the edge points of neighbor blocks is found as shown in Figure 1. Each block is represented by this average value and accordingly a image is compressed to a image.
- The JPEG compression method is carried out for the resultant image from the previous step and further compression is performed.
- The compressed image is stored.
| Algorithm 1: Image Compression |
| Input: Image I of dimensions Output: Compressed Image W of dimension
|
2.3. Image Decompression
- The JPEG decompression method is implemented for the compressed image.
- Let g be the original image, and c be the decompressed image; if , then c is scaled up or down to match g.
- To determine the quality of the decompressed image, PSNR and SSIM have to be calculated.
| Algorithm 2: Image Decompression |
 |
| Algorithm 3: Blocking Effect Removal |
| Input: Original block, reconstructed block. Output: Reconstructed corrected block.
|
2.4. Quality Analysis of the Proposed Approach
3. Experimental Results
3.1. Test 1: Tanh Function Effect
3.2. Test 2: Fixing PSNR
3.3. Test 3: Fixing the Size of the Images
3.4. Test 4
- A
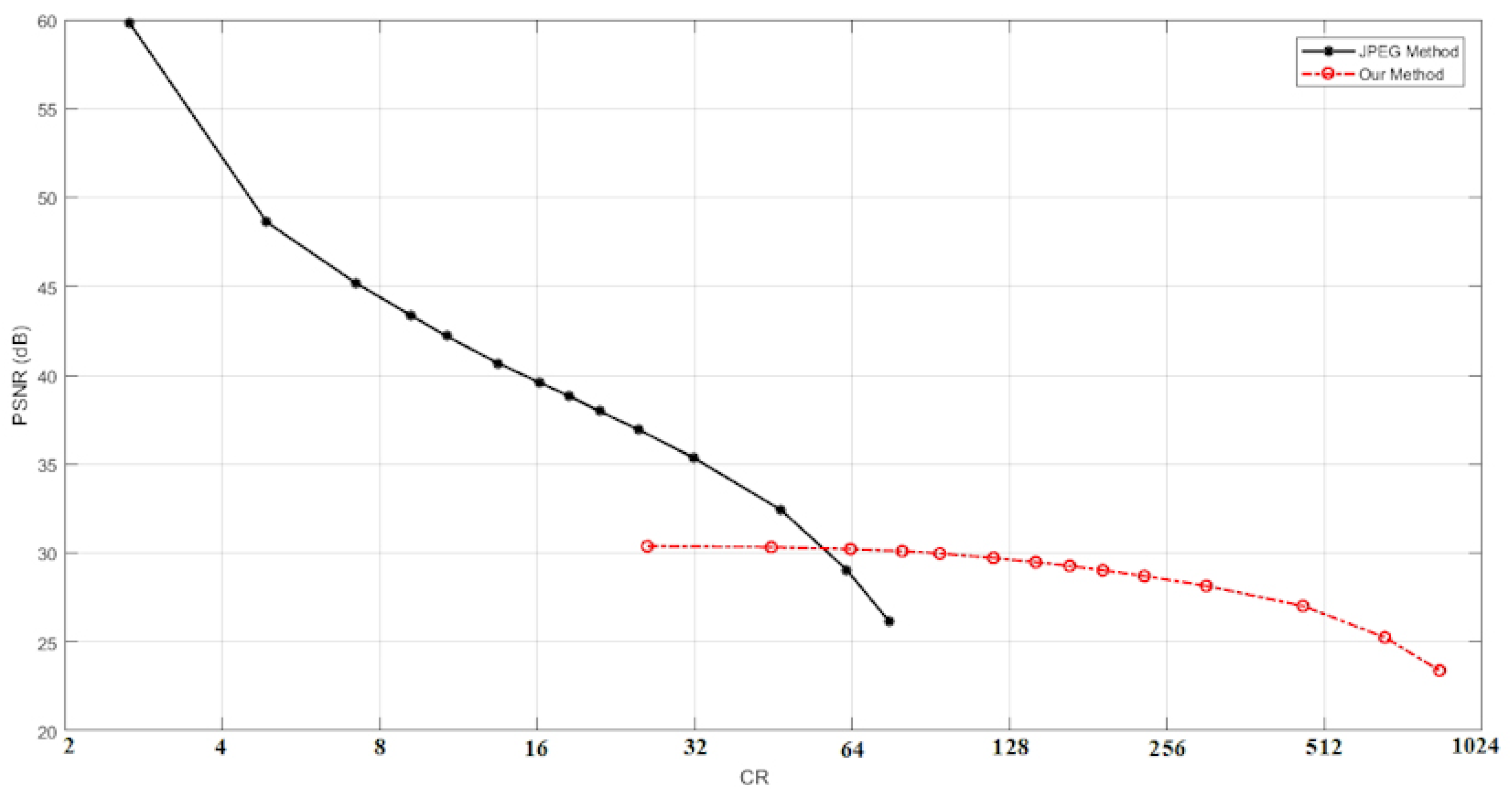
- When Q for the proposed method is high (=88), then the proposed method is +3.7 dB higher than JPEG with the same CR value.
- B
- When Q for the proposed method is low (=20), then the proposed method is +2 dB higher than JPEG and the CR value for the proposed method is more than four times that for JPEG.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CR | Compression Ratio |
| PSNR | Peak Signal-to-Noise Ratio |
| bpp | bits per pixel |
| Q | Image Quality |
| SSIM | Structural Similarity Index |
| JPEG | Joint Photographic Experts Group |
References
- Hussain, A.J.; Al-Fayadh, A.; Radi, N. Image Compression Techniques: A Survey in Lossless and Lossy algorithms. Neurocomputing 2018, 300, 44–69. [Google Scholar] [CrossRef]
- Singh, S. An Algorithm For Improving The Quality Of Compacted JPEG Image By Minimizes The Blocking Artifacts. Int. J. Comput. Graph. Animat. 2012, 2, 17–35. [Google Scholar] [CrossRef]
- Li, H.; Wen-yan, W. Improved Method to Compress JPEG Based on Patent. In Proceedings of the International Conference on Educational and Network Technology, Qinhuangdao, China, 25–27 June 2010; pp. 159–162. [Google Scholar] [CrossRef]
- Dorobantiu, A.; Brad, R. Improving Lossless Image Compression with Contextual Memory. Appl. Sci. 2019, 9, 2681. [Google Scholar] [CrossRef]
- Hu, J.; Deng, J.; Wu, J. Image Compression Based on Improved FFT Algorithm. J. Netw. 2011, 6, 1041–1048. [Google Scholar] [CrossRef]
- Golner, M.; Mikhael, W.; Krishnang, V. Modified jpeg image compression with region-dependent quantization. Circuits Syst. Signal Process. 2002, 21, 163–180. [Google Scholar] [CrossRef]
- Sombutkaew, R.; Chitsobhuk, O.; Prapruttam, D.; Ruangchaijatuporn, T. Adaptive quantization via fuzzy classified priority mapping for liver ultrasound compression. Int. J. Innov. Comput. Inf. Control 2016, 12, 635–649. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2006; ISBN 013168728X. [Google Scholar]
- Hassan, S.A.; Hussain, M. Spatial domain lossless image data compression method. In Proceedings of the International Conference on Information and Communication Technologies, Karachi, Pakistan, 23–24 July 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Sajikumar, S.; Anilkumar, A.K. Image compression using chebyshev polynomial surface fit. Int. J. Pure Appl. Math. Sci. 2017, 10, 15–27. [Google Scholar]
- Khalaf, W.; Zaghar, D.; Hashim, N. Enhancement of Curve-Fitting Image Compression Using Hyperbolic Function. Symmetry 2019, 11, 291. [Google Scholar] [CrossRef]
- Cabeen, K.; Gent, P. Image Compression and the Discrete Cosine Transform. In Math 45; College of the Redwoods: Eureka, CA, USA, 1998; pp. 1–11. [Google Scholar]
- Dagher, I.; Saliba, M.; Farah, R. Combined DCT-Haar Transforms for Image Compression. In Proceedings of the 4th World Congress on World Congress on Electrical Engineering and Computer Systems and Science, Madrid, Spain, 21–23 August 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Doukas, C.N.; Maglogiannis, I.; Kormentzas, G. Medical Image Compression using Wavelet Transform on Mobile Devices with ROI coding support. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 1–4 September 2005; pp. 3779–3784. [Google Scholar]
- Cho, D.; Bui, T.D. Fast image enhancement in compressed wavelet domain. Signal Process. 2014, 98, 295–307. [Google Scholar] [CrossRef]
- Johnston, N.; Vincent, D.; Minnen, D.; Covell, M.; Singh, S.; Chinen, T.; Hwang, S.; Shor, J.; Toderici, G. Improved Lossy Image Compression with Priming and Spatially Adaptive Bit Rates for Recurrent Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4385–4393. [Google Scholar]
- Ding, J.; Huang, Y.; Lin, P.; Pei, S.; Chen, H.; Wang, Y. Two-Dimensional Orthogonal DCT Expansion in Trapezoid and Triangular Blocks and Modified JPEG Image Compression. IEEE Trans. Image Process. 2013, 22, 3664–3675. [Google Scholar] [CrossRef] [PubMed]
- Nosratinia, A. Enhancement of JPEG-Compressed Images by Re-application of JPEG. J. VLSI Signal Process. 2001, 27, 69–79. [Google Scholar] [CrossRef]
- Kacem, H.L.H.; Kammoun, F.; Bouhlel, M.S. Improvement of The Compression JPEG Quality by a Pre-processing Algorithm Based on Denoising. In Proceedings of the 2004 IEEE International Conference on Industrial Technology, Hammamet, Tunisia, 8–10 December 2004; pp. 1319–1324. [Google Scholar] [CrossRef]
- Kohno, K.; Tanaka, A.; Imai, H. A novel criterion for quality improvement of JPEG images based on image database and re-application of JPEG. In Proceedings of the 2012 Asia Pacific Signal and Information Processing Association Annual Summit and Conference, Hollywood, CA, USA, 3–6 December 2012; pp. 1–4. [Google Scholar]
- Cottrell, G.W.; Munro, P.; Zipser, D. Image Compression by Back Propagation: An Example of Extensional Programing. In Advances in Cognitive Science, 2nd ed.; Institute for Cognitive Science, University of California: San Diego, CA, USA, 1987; pp. 208–240. [Google Scholar]
- Hopkins, M.; Mitzenmacher, M.; Wagner-Carena, S. Simulated annealing for jpeg quantization. arXiv 2017, arXiv:1709.00649. [Google Scholar]
- Chiranjeevi, K.; Jena, U.R. Image compression based on vector quantization using cuckoo search optimization technique. Ain Shams Eng. J. 2018, 9, 1417–1431. [Google Scholar] [CrossRef] [Green Version]



| Image (a) | Image (b) | Image (c) | Image (d) | Image (e) | Image (f) | |
|---|---|---|---|---|---|---|
| Original size | 257 K 1 | 257 K | 1 M 2 | 1.97 M | 1.97 M | 1.97 M |
| PSNR of JPEG method | 28.86 | 26.95 | 26.52 | 29.04 | 26.95 | 28.69 |
| PSNR of proposed method | 28.84 | 27.39 | 26.92 | 29.13 | 27.00 | 28.70 |
| SSIM of JPEG method | 0.7957 | 0.7455 | 0.6783 | 0.8135 | 0.6932 | 0.8232 |
| SSIM of proposed method | 0.8246 | 0.8200 | 0.7241 | 0.8371 | 0.6771 | 0.8411 |
| Size using JPEG method | 4.87 k | 4.99 k | 18.6 k | 31.5 k | 30.6 k | 30.5 k |
| Size using proposed method | 2.41 k | 2.91 k | 10.2 k | 10.9 k | 5.49 k | 5.88 k |
| CR using JPEG method | 53 | 52 | 54 | 63 | 66 | 66 |
| CR using proposed method | 107 | 88 | 98 | 181 | 367 | 343 |
| Image (a) | Image (b) | Image (c) | Image (d) | Image (e) | Image (f) | |
|---|---|---|---|---|---|---|
| Original size | 257 K | 257 K | 1 M | 1.97 M | 1.97 M | 1.97 M |
| PSNR of JPEG | 25.66 | 24.93 | 24.65 | 26.14 | 24.93 | 26.66 |
| PSNR of proposed method | 29.71 | 28.15 | 27.59 | 30.15 | 29.60 | 33.19 |
| SSIM of JPEG | 0.7228 | 0.6923 | 0.5911 | 0.7708 | 0.6138 | 0.7851 |
| SSIM of proposed method | 0.8588 | 0.8529 | 0.7638 | 0.8722 | 0.7789 | 0.9301 |
| Size using JPEG | 3.93 k | 4.27 k | 15.4 k | 26.8 k | 26.8 k | 27.7 k |
| Size using proposed | 3.93 k | 4.23 k | 15.4 k | 26.7 k | 26.6 k | 27.8 k |
| CR using JPEG | 76 | 60 | 65 | 73 | 73 | 71 |
| CR using proposed | 76 | 60 | 65 | 74 | 74 | 71 |
| Image (d) | Simulation A | Simulation B |
|---|---|---|
| Original size | 1.97 M | 1.97 M |
| PSNR of JPEG | 26.45 | 26.14 |
| PSNR of proposed method | 30.17 | 28.15 |
| SSIM of JPEG | 0.7797 | 0.7708 |
| SSIM of proposed method | 0.8736 | 0.8147 |
| Size using JPEG | 27.8 k | 26.6 k |
| Size using proposed | 28.1 k | 6.47 k |
| CR using JPEG | 71 | 74 |
| CR using proposed | 70 | 304 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalaf, W.; Al Gburi, A.; Zaghar, D. Pre and Postprocessing for JPEG to Handle Large Monochrome Images. Algorithms 2019, 12, 255. https://doi.org/10.3390/a12120255
Khalaf W, Al Gburi A, Zaghar D. Pre and Postprocessing for JPEG to Handle Large Monochrome Images. Algorithms. 2019; 12(12):255. https://doi.org/10.3390/a12120255
Chicago/Turabian StyleKhalaf, Walaa, Abeer Al Gburi, and Dhafer Zaghar. 2019. "Pre and Postprocessing for JPEG to Handle Large Monochrome Images" Algorithms 12, no. 12: 255. https://doi.org/10.3390/a12120255
APA StyleKhalaf, W., Al Gburi, A., & Zaghar, D. (2019). Pre and Postprocessing for JPEG to Handle Large Monochrome Images. Algorithms, 12(12), 255. https://doi.org/10.3390/a12120255






