Target Image Mask Correction Based on Skeleton Divergence
Abstract
:1. Introduction
2. Materials and Methods
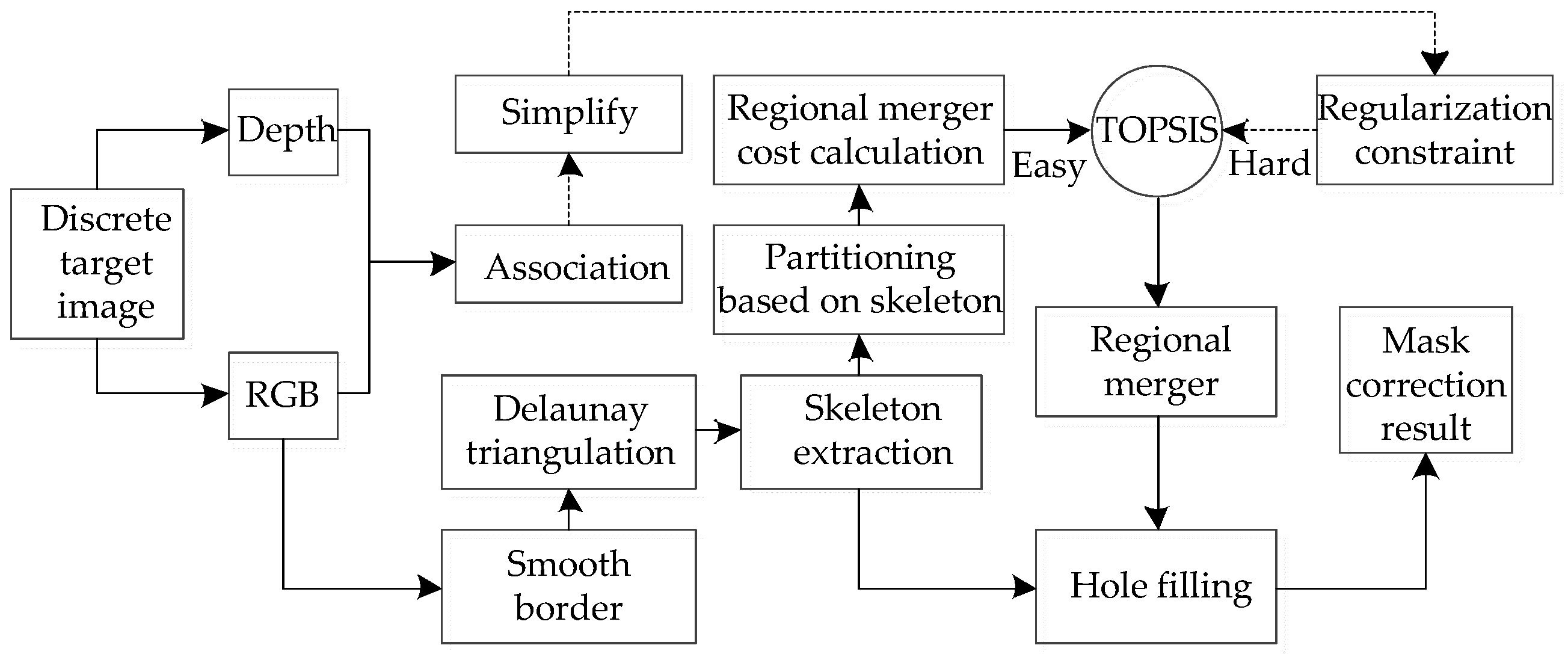
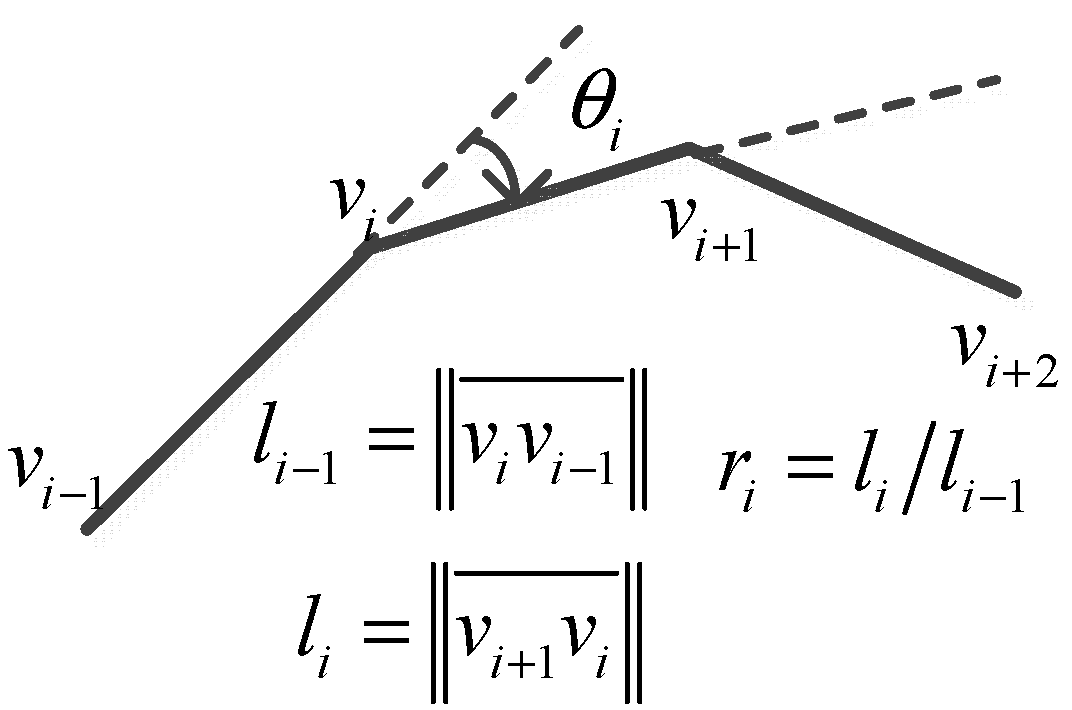
2.1. Mask Optimization Based on Skeleton Divergence
- Delaunay triangulation is performed on the polygons enclosed by the obtained boundary vertices, and the Voronoi diagram is obtained at the same time.
- The watershed algorithm is used to detect the raised points on the boundary.
- With the obtained dual map and raised point information, part of the triangular piece is deleted according to the principle of homotopy equivalence, and the final approximate skeleton is obtained.
2.2. Discrete Pixel Edge Similarity-Guided Merging
2.3. Decision-Based Sparse RGB-Depth Regularization Verification
2.4. Hole Filling
3. Results and Discussion
3.1. Single Target Mask Correction Effect
3.2. Multi-Target Mask Correction Effect
3.3. Multiple Indicator Comparison of Sequence Experimental Results for the Proposed Algorithm and Other Algorithms
3.4. Single Frame Comparison of Experimental Results for the Proposed Algorithm and Other Algorithms
3.5. Effect of the Algorithm on Different Sequences
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brown, M.; Lowe, D.G. Automatic panoramic image stitching using invariant features. Int. J. Comput. Vis. 2007, 74, 59–73. [Google Scholar] [CrossRef]
- Levin, A.; Zomet, A.; Peleg, S.; Weiss, Y. Seamless image stitching in the gradient domain. In Proceedings of the Computer Vision—Proceedings of ECCV 2004, Prague, Czech Republic, 11–14 May 2004; pp. 377–389. [Google Scholar]
- Zhang, F.; Liu, F. Parallax-tolerant image stitching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3262–3269. [Google Scholar]
- Zomet, A.; Levin, A.; Peleg, S.; Weiss, Y. Seamless image stitching by minimizing false edges. IEEE Trans. Image Process. 2006, 15, 969–977. [Google Scholar] [CrossRef] [PubMed]
- Mills, A.; Dudek, G. Image stitching with dynamic elements. Image Vis. Comput. 2009, 27, 1593–1602. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, Y.; Wang, H.; Li, B.; Hu, H.M. A Novel Projective-Consistent Plane based Image Stitching Method. IEEE Trans. Multimed. 2019, 21, 2561–2575. [Google Scholar] [CrossRef]
- Fang, F.; Wang, T.; Fang, Y.; Zhang, G. Color Blending for Seamless Image Stitching. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1115–1119. [Google Scholar] [CrossRef]
- Hu, F.; Li, Y.; Feng, Y. Continuous Point Cloud Stitch based on Image Feature Matching Constraint and Score. IEEE Trans. Intell. Veh. 2019, 4, 363–374. [Google Scholar] [CrossRef]
- Chen, M.; Tang, Y.; Zou, X.; Huang, K.; Li, L.; He, Y. High-accuracy multi-camera reconstruction enhanced by adaptive point cloud correction algorithm. Opt. Lasers Eng. 2019, 122, 170–183. [Google Scholar] [CrossRef]
- Jovanovski, B.L.; Li, J. Image-Stitching for Dimensioning. U.S. Patent Application 16/140,953, 24 January 2019. [Google Scholar]
- Hu, F.; Bai, L.; Li, Y.; Chen, H.; Li, C.; Su, X. Environmental Reconstruction for Autonomous Vehicle Based on Image Feature Matching Constraint and Score. In Proceedings of the PRICAI 2018: Trends in Artificial Intelligence, Nanjing, China, 28–31 August 2018; pp. 140–148. [Google Scholar]
- Ding, C.; Liu, H.; Li, H. Stitching of depth and color images from multiple RGB-D sensors for extended field of view. Int. J. Adv. Robot. Syst. 2019, 16. [Google Scholar] [CrossRef]
- Wang, P.; Liu, J.; Zha, F.; Liu, H.; Sun, L.; Li, M. A fast 3D map building method for indoor robots based on point-line features extraction. In Proceedings of the 2nd International Conference on Advanced Robotics and Mechatronics (ICARM), Hefei and Tai’an, China, 27–31 August 2017; pp. 576–581. [Google Scholar]
- Koller, D.O. Image filtering on 3D objects using 2D manifolds. U.S. Patent 6,756,990, 29 June 2004. [Google Scholar]
- Nanayakkara, C.; Yeoh, W.; Lee, A.; Moayedikia, A. Deciding discipline, course and university through TOPSIS. Stud. High. Educ. 2019, 1–16. [Google Scholar] [CrossRef]
- Feng, L.; Alliez, P.; Busé, L.; Delingette, H.; Desbrun, M. Curved optimal delaunay triangulation. ACM Trans. Graph. (Tog) 2018, 37, 61. [Google Scholar] [CrossRef]
- Robert, L.F.; Gros, N.; Noutary, Y.; Malleus, L.; Fisichella, T.; Lingrand, D.; Precioso, F.; Samoun, L. Keypoint-Based Point-Pair-Feature for Scalable Automatic Global Registration of Large RGB-D Scans. U.S. Patent 10,217,277, 26 February 2019. [Google Scholar]
- Yu, T.; Zheng, Z.; Guo, K.; Zhao, J.; Dai, Q.; Li, H.; Pons-Moll, G.; Liu, Y. Doublefusion: Real-time capture of human performances with inner body shapes from a single depth sensor. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7287–7296. [Google Scholar]
- Murthy, P.A.; Defenu, N.; Bayha, L.; Holten, M.; Preiss, P.M.; Enss, T.; Jochim, S. Quantum scale anomaly and spatial coherence in a 2D Fermi superfluid. Science 2019, 365, 268–272. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.M. Research on Shape Optimization Algorithm of Discrete Curved Surfaces. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2010. (In Chinese). [Google Scholar]
- Shui, P.L.; Zhang, Z.J. Fast SAR image segmentation via merging cost with relative common boundary length penalty. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6434–6448. [Google Scholar] [CrossRef]
- Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.J. Comparing images using the Hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–963. [Google Scholar] [CrossRef]
- Jung, S.; Song, S.; Chang, M.; Park, S. Range image registration based on 2D synthetic images. Comput. Aided Des. 2018, 94, 16–27. [Google Scholar] [CrossRef]
- Zhang, J.; Su, Q.; Liu, P.; Zhu, Q.; Zhang, K. An improved VSLAM algorithm based on adaptive feature map. Acta Autom. Sin. 2019, 45, 553–565. (In Chinese) [Google Scholar] [CrossRef]
- Mitra, N.J.; Gelfand, N.; Pottmann, H.; Guibas, L. Registration of point cloud data from a geometric optimization perspective. In Proceedings of the Eurographics/ACM SIGGRAPH symposium on Geometry Processing, Nice, France, 8–10 July 2004; pp. 22–31. [Google Scholar]
- He, B.; Lin, Z.; Li, Y.F. An automatic registration algorithm for the scattered point clouds based on the curvature feature. Opt. Laser Technol. 2013, 46, 53–60. [Google Scholar] [CrossRef]
- Jiang, J.; Cheng, J.; Chen, X. Registration for 3-D point cloud using angular-invariant feature. Neurocomputing 2009, 72, 3839–3844. [Google Scholar] [CrossRef]
- Goyette, N.; Jodoin, P.M.; Porikli, F.; Konrad, J.; Ishwar, P. A novel video dataset for change detection benchmarking. IEEE Trans. Image Process. 2014, 23, 4663–4679. [Google Scholar] [CrossRef] [PubMed]



| Method | Pr | Re | Sp | FPR | FNR | PWC | F1 |
|---|---|---|---|---|---|---|---|
| Prop | 0.703 | 0.896 | 0.987 | 0.013 | 0.104 | 0.611 | 0.755 |
| GOP [25] | 0.692 | 0.795 | 0.983 | 0.017 | 0.205 | 1.128 | 0.567 |
| CUR [26] | 0.688 | 0.676 | 0.980 | 0.020 | 0.324 | 0.882 | 0.631 |
| IFMCaS [8] | 0.575 | 0.777 | 0.972 | 0.028 | 0.223 | 1.217 | 0.526 |
| AIF [27] | 0.674 | 0.538 | 0.979 | 0.021 | 0.462 | 0.783 | 0.421 |
| Mask Correction Algorithms | Computing Time Cost (s) |
|---|---|
| GOP | 0.532 |
| CUR | 0.618 |
| IFMCaS | 0.471 |
| AIF | 0.672 |
| Prop | 0.301 |
| Sequence | GOP | CUR | IFMCaS | AIF | Prop |
|---|---|---|---|---|---|
| f2/d_p | 28.31 | 27.32 | 28.34 | 27.44 | 29.63 |
| f3/s_h | 27.97 | 26.81 | 27.82 | 28.32 | 28.72 |
| f3/w_h | 27.41 | 28.57 | 28.12 | 27.01 | 28.71 |
| f3/w_r | 26.53 | 26.40 | 27.62 | 26.94 | 28.64 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xu, Z.; Huang, W.; Han, Y.; Jiang, M. Target Image Mask Correction Based on Skeleton Divergence. Algorithms 2019, 12, 251. https://doi.org/10.3390/a12120251
Wang Y, Xu Z, Huang W, Han Y, Jiang M. Target Image Mask Correction Based on Skeleton Divergence. Algorithms. 2019; 12(12):251. https://doi.org/10.3390/a12120251
Chicago/Turabian StyleWang, Yaming, Zhengheng Xu, Wenqing Huang, Yonghua Han, and Mingfeng Jiang. 2019. "Target Image Mask Correction Based on Skeleton Divergence" Algorithms 12, no. 12: 251. https://doi.org/10.3390/a12120251





