1. Introduction
Let
,
, be a system of nonlinear equations. Usually, this kind of problems can not be solved analytically and the approach to a solution is made by means of iterative techniques. The best known iterative algorithm is Newton’s method, with second order of convergence and iterative expression
from an estimation
. This iterative scheme needs the evaluation of the nonlinear function and its associate Jacobian matrix at each iteration. However, sometimes, the size of the system or the specific properties of the problem do not allow to evaluate the Jacobian matrix
, or even its calculation at each iteration (for example, if
F is an error function); in these cases, some approximations of the Jacobian matrix can be used. The most usual one is a divided difference matrix, that is, a linear operator
satisfying condition (see [
1,
2])
In this case, when
in Newton’s method is replaced by
, where
, we obtain the so-called Steffensen’s method [
1], also with order of convergence two. To compute in practice the elements of the divided difference operator, the following first-order divided difference operator
or the symmetric second-order one,
are proposed in [
3].
Let us remark that operator (
4) is symmetric and it can be used to evaluate the divided difference even when the problem is nonsymmetric. However, the number of evaluations of the scalar functions in the computation of (
4) is higher than those in (
3). Moreover, when divided difference (
3) is used as an approximation for the Jacobian matrices appearing in any iterative method, then usually the iterative procedure does not preserve its order of convergence.
The authors in [
4] proposed to replace
in (
2) by
, being
, with
. Then, divided difference
becomes an approximation of
of order
m. It was also shown that, by choosing a suitable value of
m, the order of convergence of any iterative method can be preserved with a reduced computational cost. So, the Jacobian-free variants of Newton’s scheme that we analyze hold the second order of convergence of the original method.
Our aim is to see if, further on the order of convergence of the method, the use of different divided differences to replace the Jacobian matrix in the iterative expression of Newton’s method, can affect the dependence on initial estimations of the modified scheme to converge.
By using Taylor expansion of the divided difference operator (
5), authors in [
4] proved the following results.
Theorem 1. (See [4]) Let F be a nonlinear operator with coordinate functions , and such that . Let us consider the divided difference operator , where , then the order of the divided difference as an approximation of the Jacobian matrix is m. Corollary 1. (See [4]) Under the same assumptions as in Theorem 1, the order of the central divided difference operatoris as an approximation of , being . Based on these results, in [
4] it was presented a new technique to transform iterative schemes for solving nonlinear systems into Jacobian-free ones, preserving the order of convergence in all cases. The key fact of this new approach is the
mth power of the coordinate functions of
, that needs different values depending on the order of convergence of the first step of the iterative method. This general procedure was checked, both theoretical and numerically, showing the preservation of the order of convergence and very precise results when the appropriate values of
m were employed.
Also the authors in [
5] showed that the order of the approximation of
might be improved (in terms of efficiency) by means of the Richardson extrapolation. It can be seen in the following result.
Lemma 1. (See [5]) Divided differencewhich is obtained by Richardson extrapolation of (6) is an approximation of order of . Although the design and convergence analysis of iterative methods for solving nonlinear problems is a successful area of research in the last decades, it has been recently that the study of their stability has become usual (see, for example, [
6,
7,
8,
9,
10]). So, when a method is presented, not only its order of convergence and efficiency are important, but also its dependance on the initial estimations used to converge. This is known as the stability analysis of the iterative scheme.
The study of the stability of an iterative procedure has been mostly made by using techniques from complex discrete dynamics, that are very useful in the scalar case. Nevertheless, it frequently does not provide enough information when systems of nonlinear equations must be solved. This is the reason why the authors in [
11] applied by first time real multidimensional discrete dynamics in order to analyze the performance of vectorial iterative methods on polynomial systems. In this way, it was possible to conclude about their stability properties: their dependence on the initial estimation used and the simplicity or complexity of the sets of convergent initial guesses (known as Fatou set) and their boundaries (Julia set). These procedure have been employed in the last years to analyze new and existing vectorial iterative schemes, see for instance [
5,
12,
13,
14]. We are going to use these techniques in this paper to the vectorial rational functions obtained by applying different Jacobian-free variants of Newton’s method on several low-degree polynomial systems. These vectorial rational functions are called also multidimensional fixed point functions in the literature.
The polynomial systems used in this study are defined by the nonlinear functions:
By using uncoupled systems as
and
and coupled as
, we can generalize the performance of the proposed methods to another nonlinear systems. Moreover, let us remark that these results can be obtained by using similar systems with size
but we analyze the case
in order to use two-dimensional plots to visualize the analytical findings.
In the next section, the dynamical behavior of the fixed point functions of Jacobian-free versions of Newton’s method applied on
,
and
are studied when forward, central and Richardson extrapolation-type of divided differences are used. To get this aim, some dynamical concepts must be introduced.
Definition 1. (See [11]) Let be a vectorial function. The orbit of the point is defined as the set of successive images of by the vectorial function, . The dynamical behavior of the orbit of a point of can be classified depending on its asymptotic behavior. In this way, a point is a fixed point of G if .
The following results are well known results in discrete dynamics and in this paper we use them to study the stability of nonlinear operators.
Theorem 2. (See [15]) Let be . Assume that is a k-periodic point, . Let be the eigenvalues of . - (a)
If all eigenvalues have , then is attracting.
- (b)
If one eigenvalue , then is unstable, that is, a repelling or a saddle point.
- (c)
If all eigenvalues have , then is repelling.
Also, a fixed point is called hyperbolic if for all eigenvalues of , we have . If there exists an eigenvalue such that and an eigenvalue that the hyperbolic point is called saddle point.
Let us note that, the entries of
are the partial derivatives of each coordinate function of the vectorial rational operator that defines the iterative scheme. When the calculation of spectrum of
is difficult the following result which is consistent with the previous theorem, can be used.
Proposition 1. (See [11]) Let be a fixed point of G then, - (a)
If for all , then is attracting.
- (b)
If for all , then is superattracting.
- (c)
If for all , then is unstable and lies at the Julia set.
In this paper, we only use Theorem 2 to investigate the stability of the fixed points. Let us consider an iterative method for finding the roots of a nonlinear systems
. This generates a multidimensional fixed point operator
. A fixed point
of
is called a strange fixed point if it is not a root of the nonlinear function
. The basin of attraction of
(which may be a root of
or a strange fixed point) is the set of pre-images of any order such that
Definition 2. A point is a critical point of if the eigenvalues of are null for all .
The critical points play an important role in this study since a classical result of Julia and Fatou establishes that, in the connected component of any basin of attraction including an attracting fixed point, there is always at least a critical point.
As it is obvious, a superattracting fixed point is also a critical point. A critical point that is not a root of function is called free critical point.
The motivation of this work is to analyze the stability of the Jacobian-free variants of Newton’s method for the most simple nonlinear equations. Certainly, it is known that, in general, divided differences are less stable than Jacobian matrices, but we study how the increasing of the precision in the estimation of the Jacobian matrix affects to the stability of the methods and in the wideness of the basins of attraction of the roots.
2. Jacobian-Free Variants of Newton’s Method
In this section, we study the dynamical properties of Jacobian-free Newton’s method when different divided differences are used. To get this purpose we analyze the dynamical concepts on polynomial systems
,
and
. The dynamical concepts on two dimensional systems can be extended to an
n-dimensional case (see [
11] to notice how the dynamics of a multidimensional iterative method can be analyzed), so for visualizing graphically the analytical results we investigate the two-dimensional case. From now on, the modified Newton’s scheme which results from replacing forward divided difference (
5) instead of Jacobian matrix in Newton’s method, is denoted by FMN
m, for
. In a similar way, when central divided difference (
6) is used to replace Jacobian matrix in Newton’s procedure, the resulting modified schemes are denoted by CMN
m, for
. Also, the modified Newton’s method obtained by using divided difference (
7) is denoted by RMN
m, for
.
Let us remark that Newton’s method has quadratic convergence and, by using the mentioned approximations of the Jacobian matrix, this order is preserved, even in case (in this case, the scheme is known as Steffensen’s method).
We use proposed families FMNm, CMNm and RMNm on the polynomial systems , and . In the following sections, the coordinate functions of the different classes of iterative methods, joint with their fixed and critical points are summarized.
2.1. Second-Degree Polynomial System
Proposition 2. The coordinate functions of the fixed point operator associated to FMNm for on polynomial system are Moreover,
- (a)
For , the only fixed points are the roots of , , , and , that are also superattracting. There is no strange fixed point in this case.
- (b)
The components of free critical points are roots of , provided that k and l are not equal to 1 and , simultaneously.
Remark 1. Except for , that is a case with 12 free critical points, for there exist 32 free critical points of the fixed point operator associated to FMNm. In particular, free critical points for the fixed point function , are
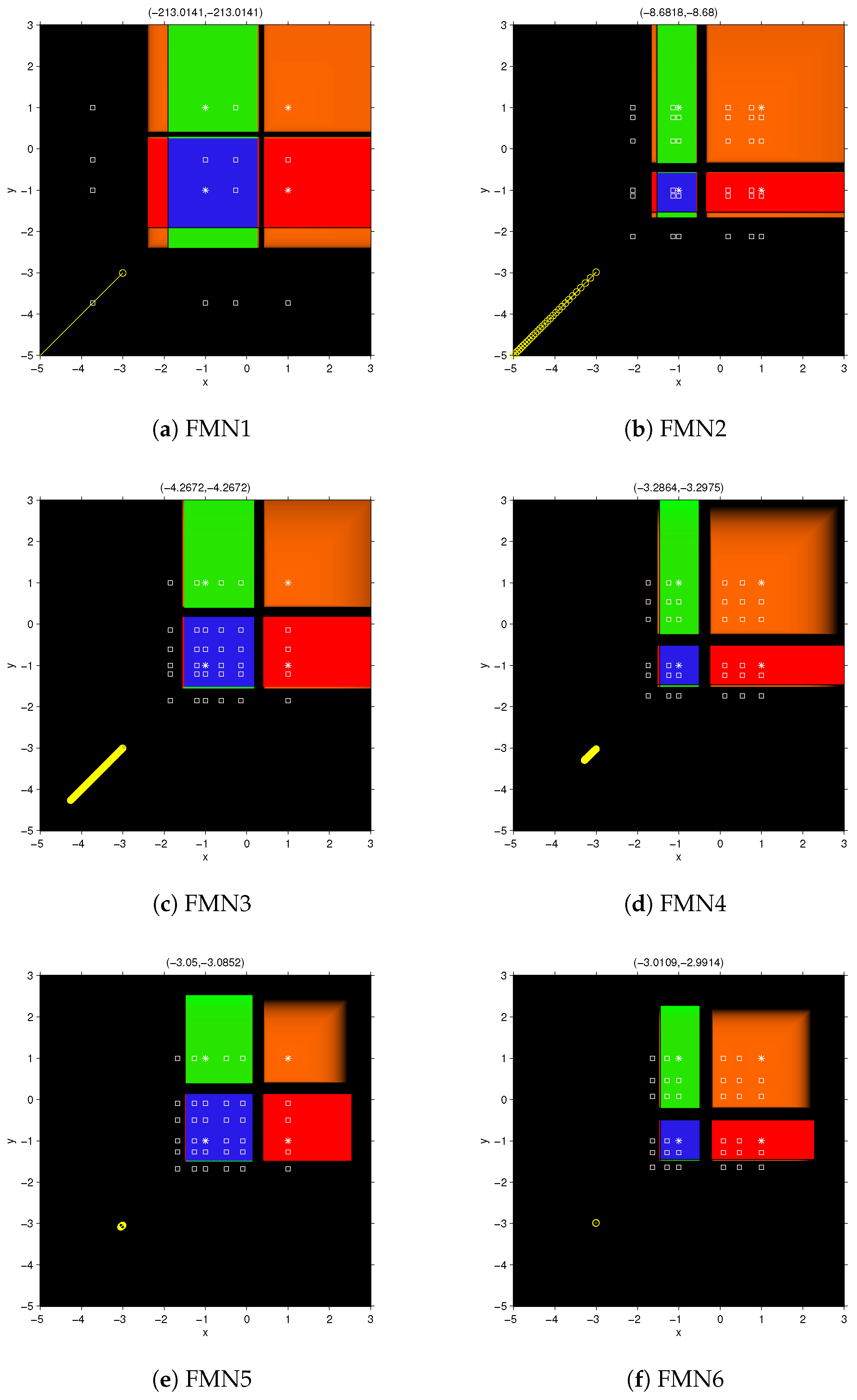
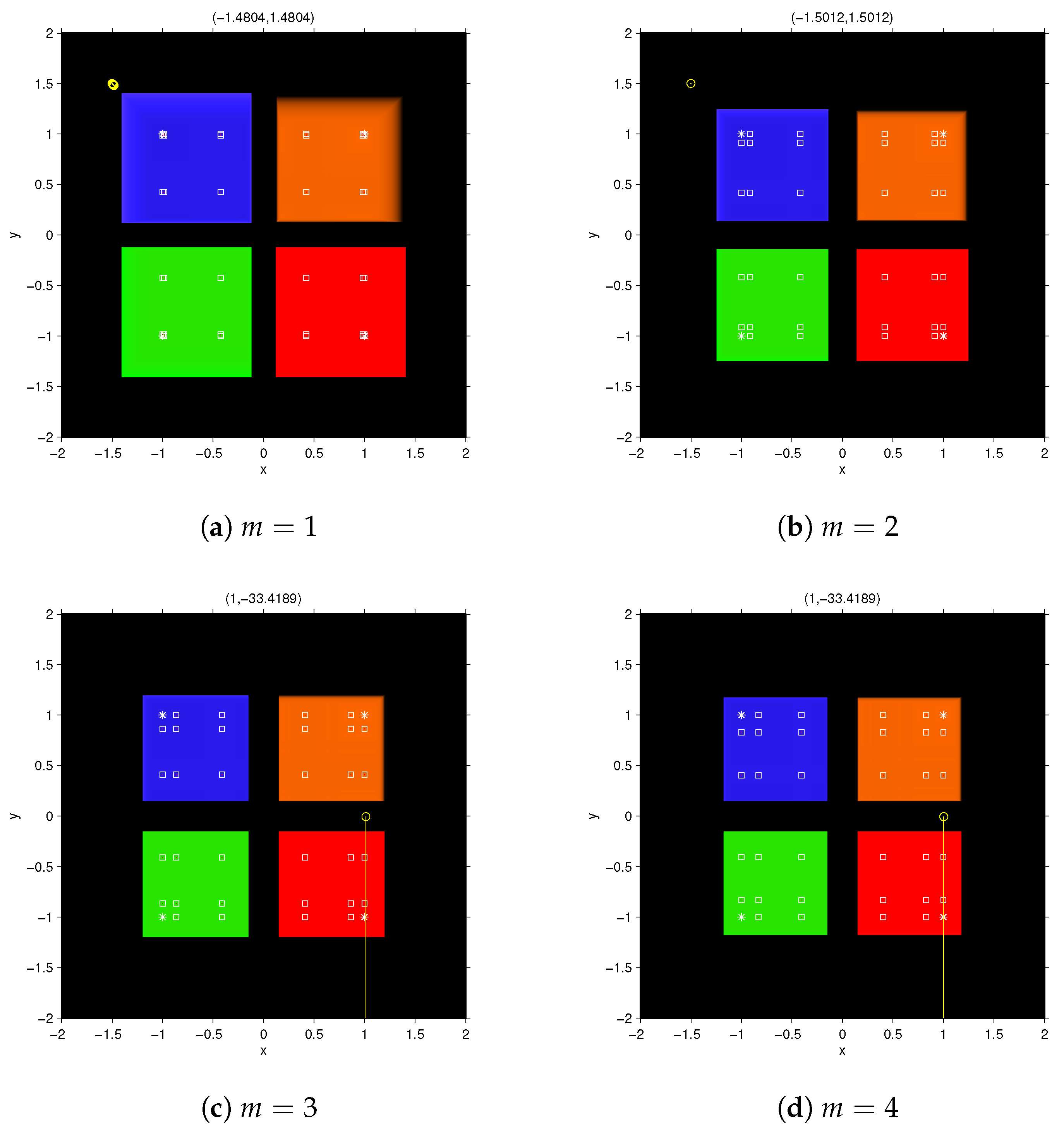
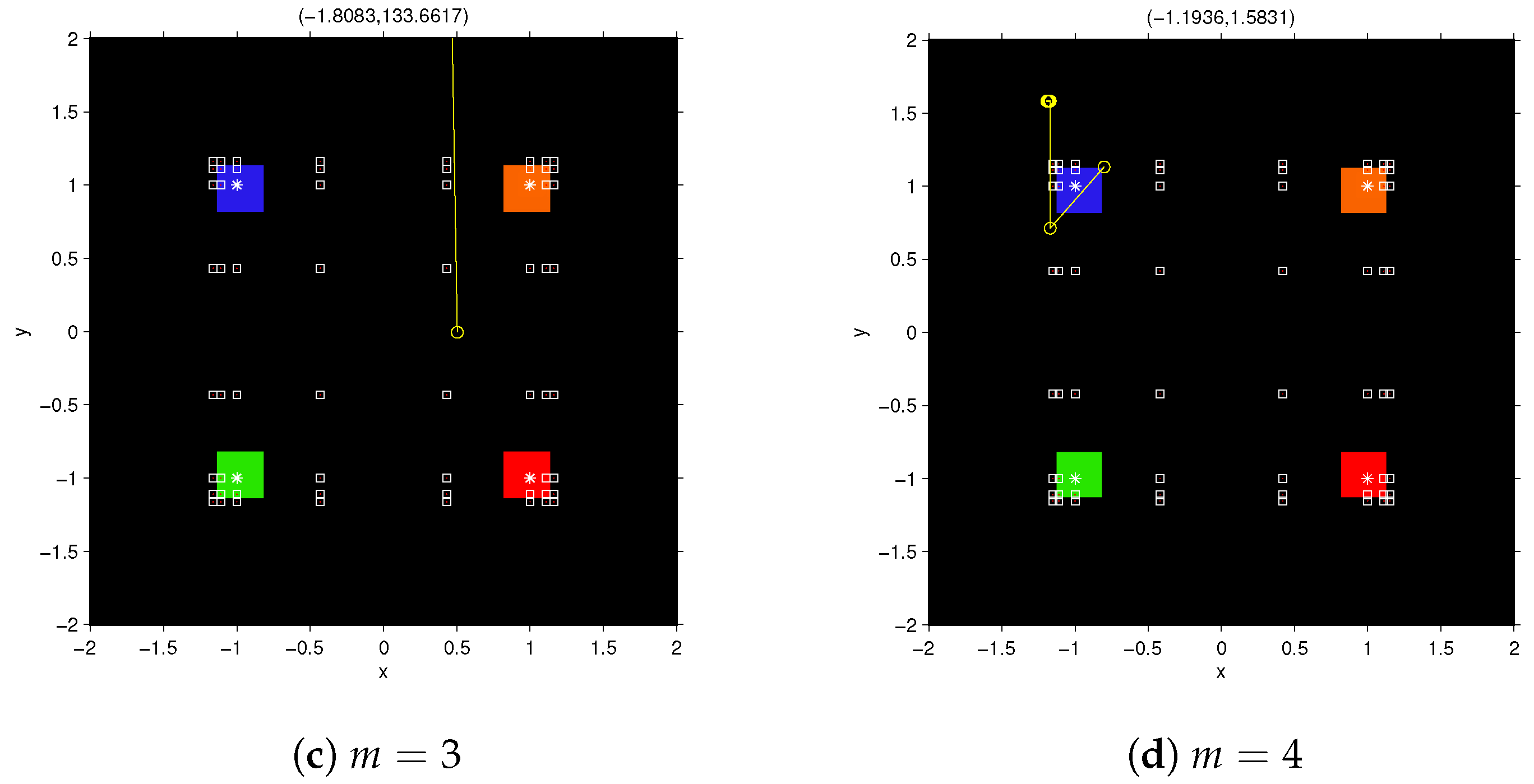
provided that k and l are not equal to 1 and , simultaneously. Figure 1 shows the dynamical behavior of fixed point function
for
. These figures have been obtained by the routines described in [
16]. To draw them, a mesh of
points has been used, 200 was the maximum number of iterations involved and
the tolerance used as stopping criterium. In this paper, we have used a white star to show the roots of the nonlinear polynomial system and a white square for the free critical points.
Figure 1 shows that, as greater
m is, the wideness of basins of attraction decreases, in spite of having a better approximation of the Jacobian matrix. The color assigned to each of the basin of attraction corresponds to one of the roots of the nonlinear system. The black area shows the no convergence in the maximum number of iterations, or divergence.
To see the behavior of the vectorial function in the black area of dynamical planes, we visualize the orbit of the rational function corresponding to the starting point
after 200 iterations. This orbit appears as a yellow circle per each iterate and yellow lines between each pair of consecutive iterates. In
Figure 1a, corresponding to
, its value in the 200th iteration is
.
Figure 1b, which corresponds to
, shows lower rate of divergence (or convergence to infinity), being its value at the 200th iteration
. This effect is higher by increasing
m but, for
it is observed that
The vectors on the top of
Figure 1c–f, corresponds to the last iterate with the starting point
.
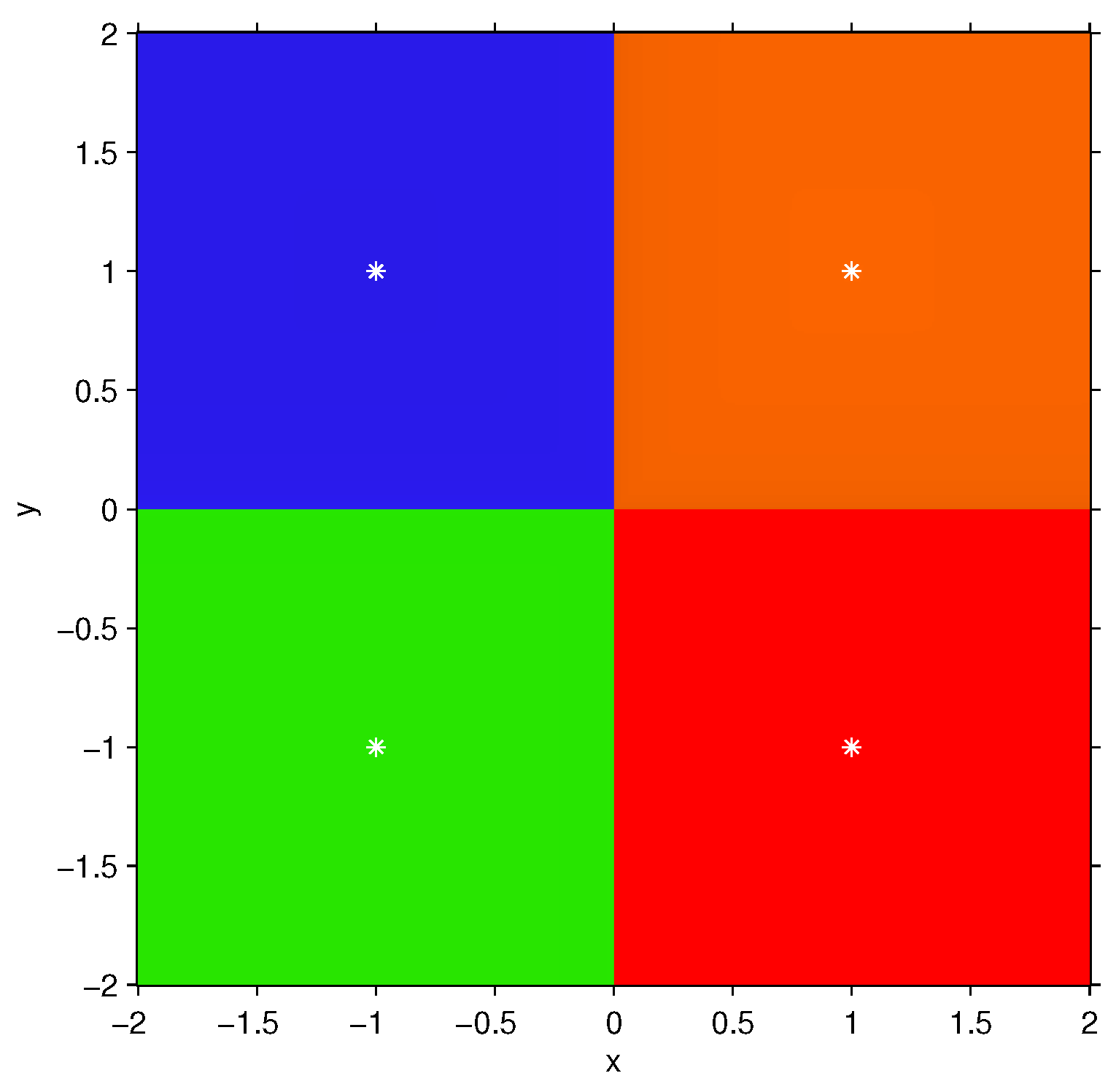
Proposition 3. The coordinates of the fixed point operator associated to CMNm, for , and RMNm, for , on polynomial system arewhich are the same components of the fixed point function of Newton’s method on . Since
is a 2nd-degree polynomial system, the approximations of order equal or higher than 2 of Jacobian matrix are exact and the fixed point function of the CMN
m and RMN
m methods coincide with that of Newton’s method. In this case,
,
,
and
are superattracting fixed points and there are no strange fixed points or free critical points.
Figure 2 shows the resulting dynamical plane, that coincides with that of Newton’s method.
2.2. Sixth-Degree Polynomial System
The corresponding results about FMN
m, CMN
m and RMN
m classes applied on sixth-degree polynomial system
are summarized in the following propositions. They resume, in each case, the iteration function, the fixed and critical points.
Proposition 4. The coordinate functions of the fixed point operator associated to FMNm on , for , areMoreover, - (a)
For the fixed points are , , and that are also superattracting. There are no strange fixed points in this case.
- (b)
The coordinates of free critical points are the roots of the polynomialfor and , provided that k and l are not equal to and 1
simultaneously.
Remark 2. Except for , in which case that the fixed point function has 12
free critical points, the multidimensional rational function FMNm, for , has 32
free critical points. The free critical points in this case are
provided that k and l are not equal to and 1
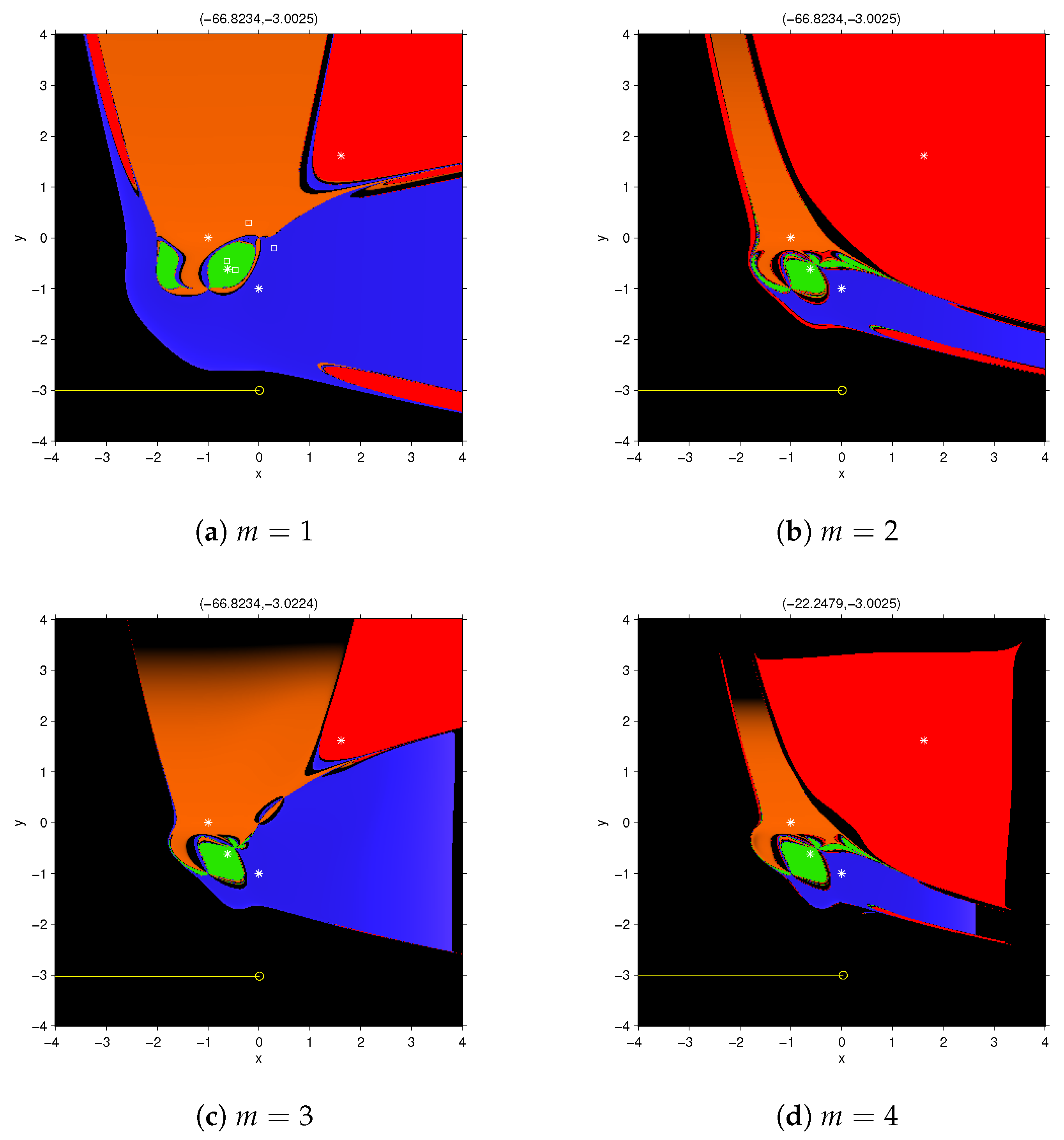
simultaneously. Figure 3 shows the dynamical planes of the fixed point function
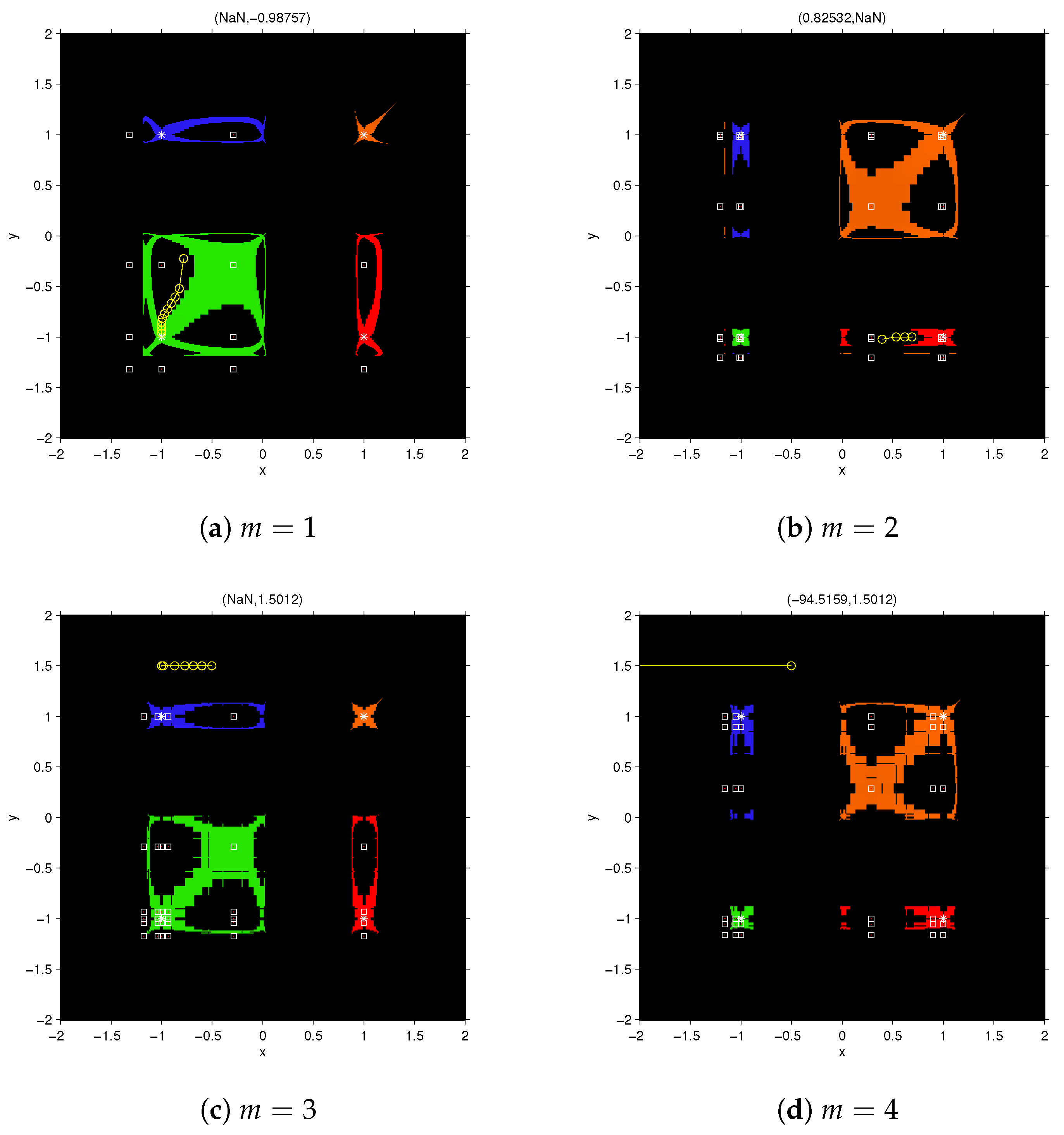
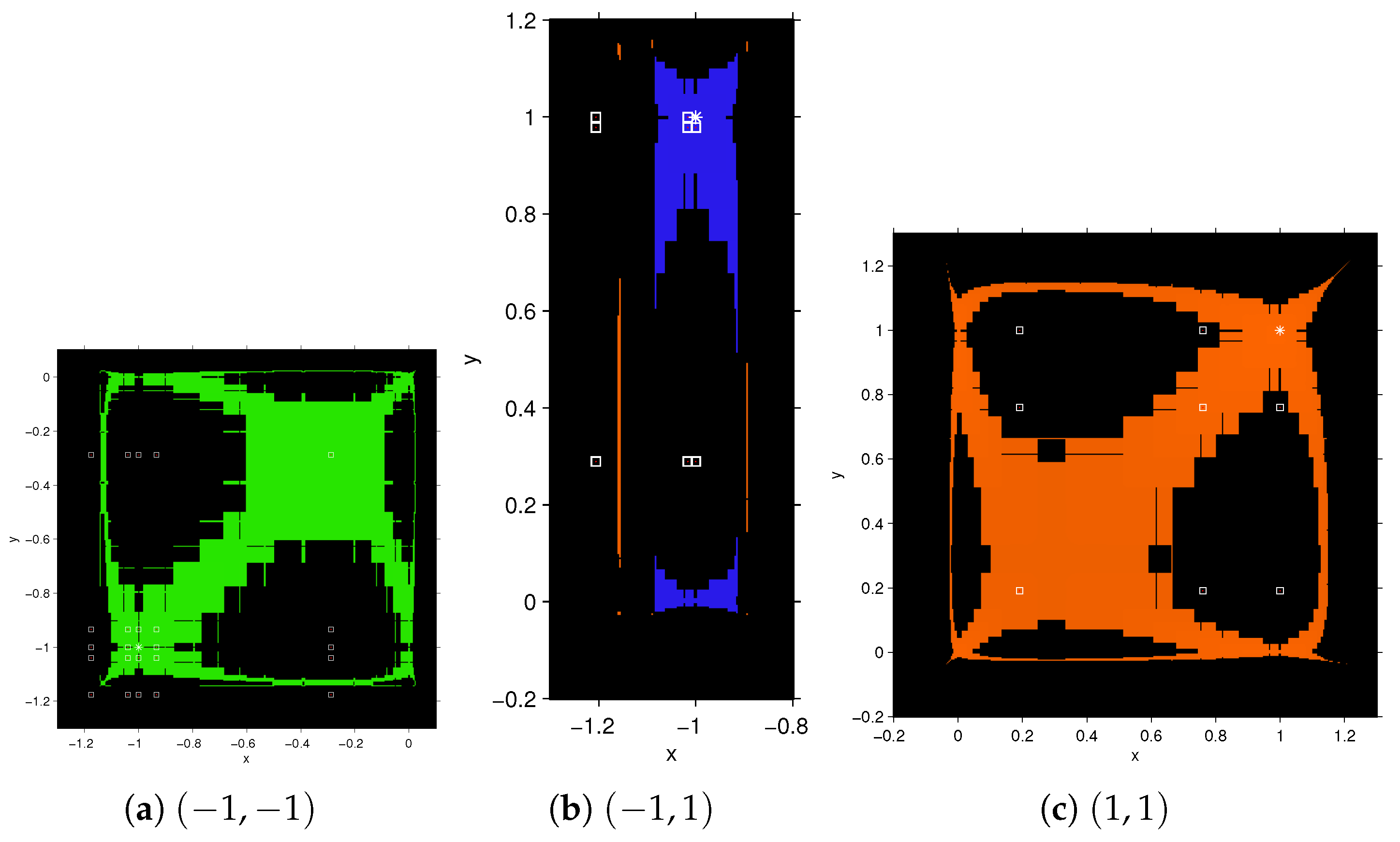
for
. Inside the black areas, there are regions where the orbits tend toward the poles of the rational function (those points that make the denominator of the elements of the rational function null). In fact, the orbits of points in these areas reach very close to the roots, so the vectorial rational function at these points become numerically singular.
Figure 3a,b show two points in these black areas.
Figure 4 and
Figure 5 show details of the dynamical planes of FMN
2 and FMN
3 methods. These figures show the difference between the basins of attraction of an odd member with an even member of the family FMN
m. Because of the symmetry, the transpose of the basin of attraction of
coincide with that of
, so we only depicted one of them.
The analysis for the cases of central divided differences is made in the following result.
Proposition 5. The coordinate functions of the fixed point operator associated to CMNm, for , on are Moreover,
- (a)
The fixed points are , , and that are also superattracting and there are not strange fixed points.
- (b)
The components of free critical points in this case are the roots of the polynomial , provided that , beingwhere k and l are not simultaneously equal to 1
and .
Remark 3. The fixed point rational function , for all m, has 32
free critical points. The free critical points in this case are
provided that k and l are not equal to 1
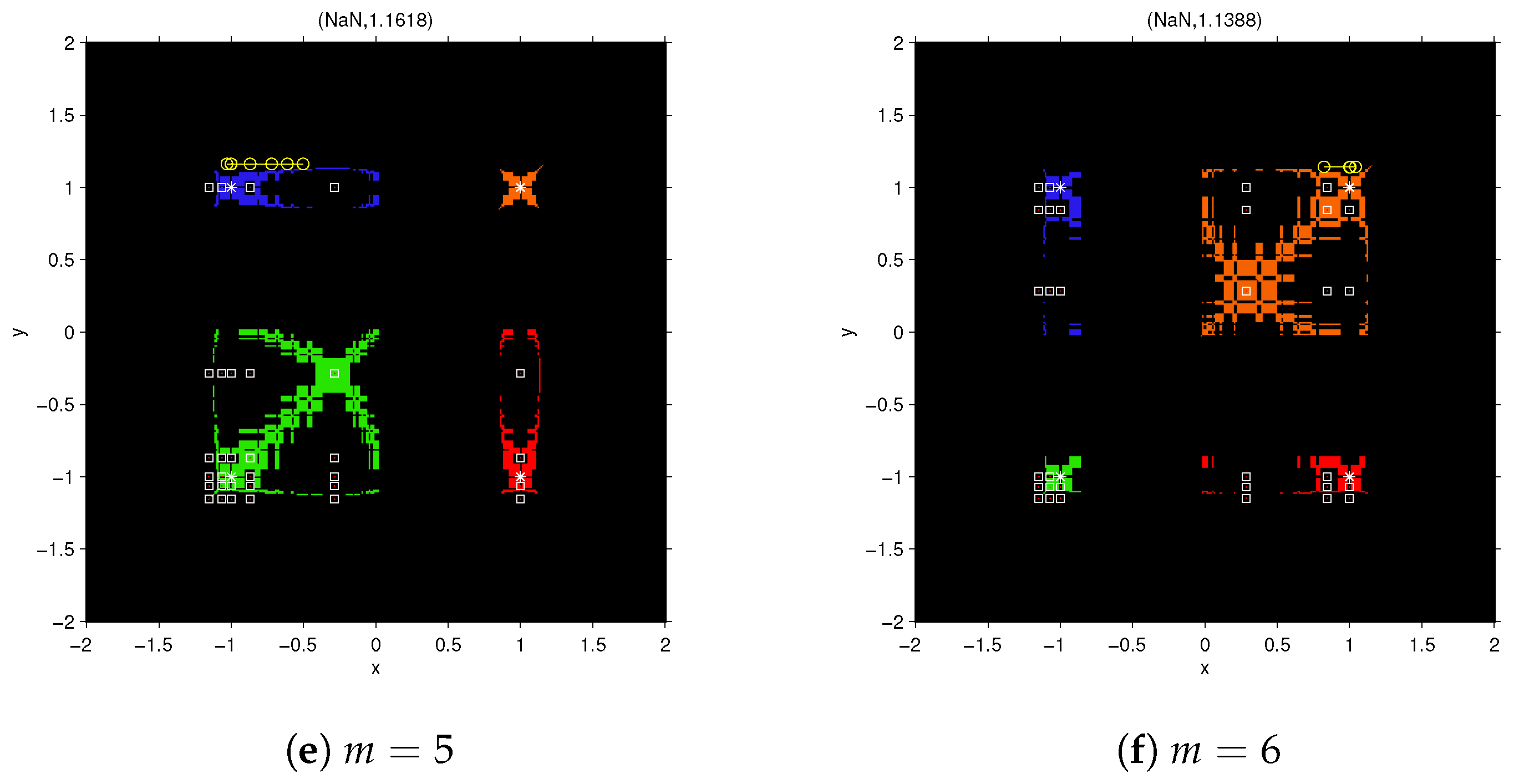
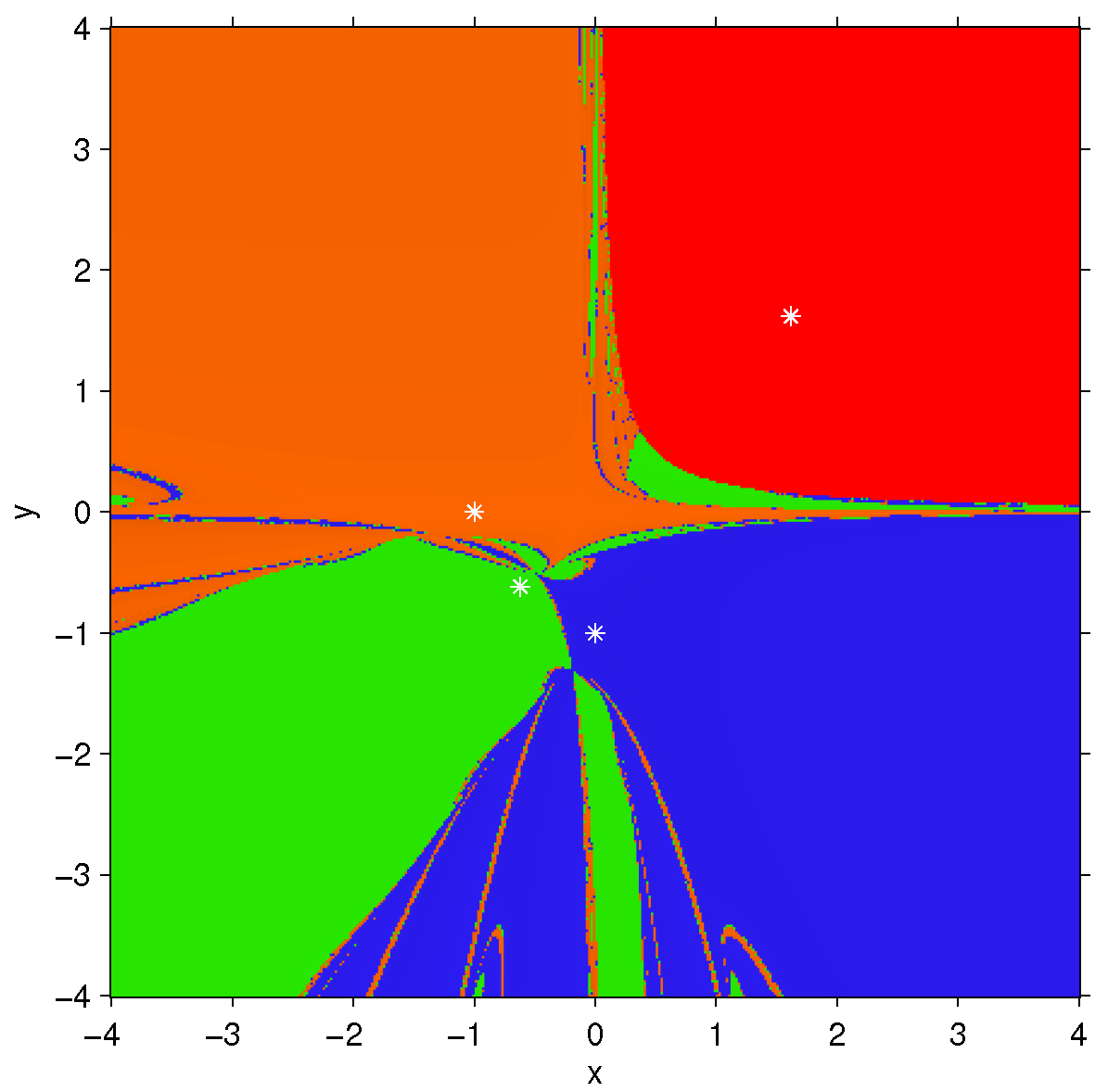
and simultaneously. Central divided differences show very stable behavior. All the free critical points are inside the basins of attraction of the roots. This means that it is not possible other performance than convergence to the roots (or divergence). In fact, the basins of attraction of the roots in this case are much greater than those in the forward divided difference. Black areas near to the boundaries of the basins of attraction are regions of slow convergence or divergence.
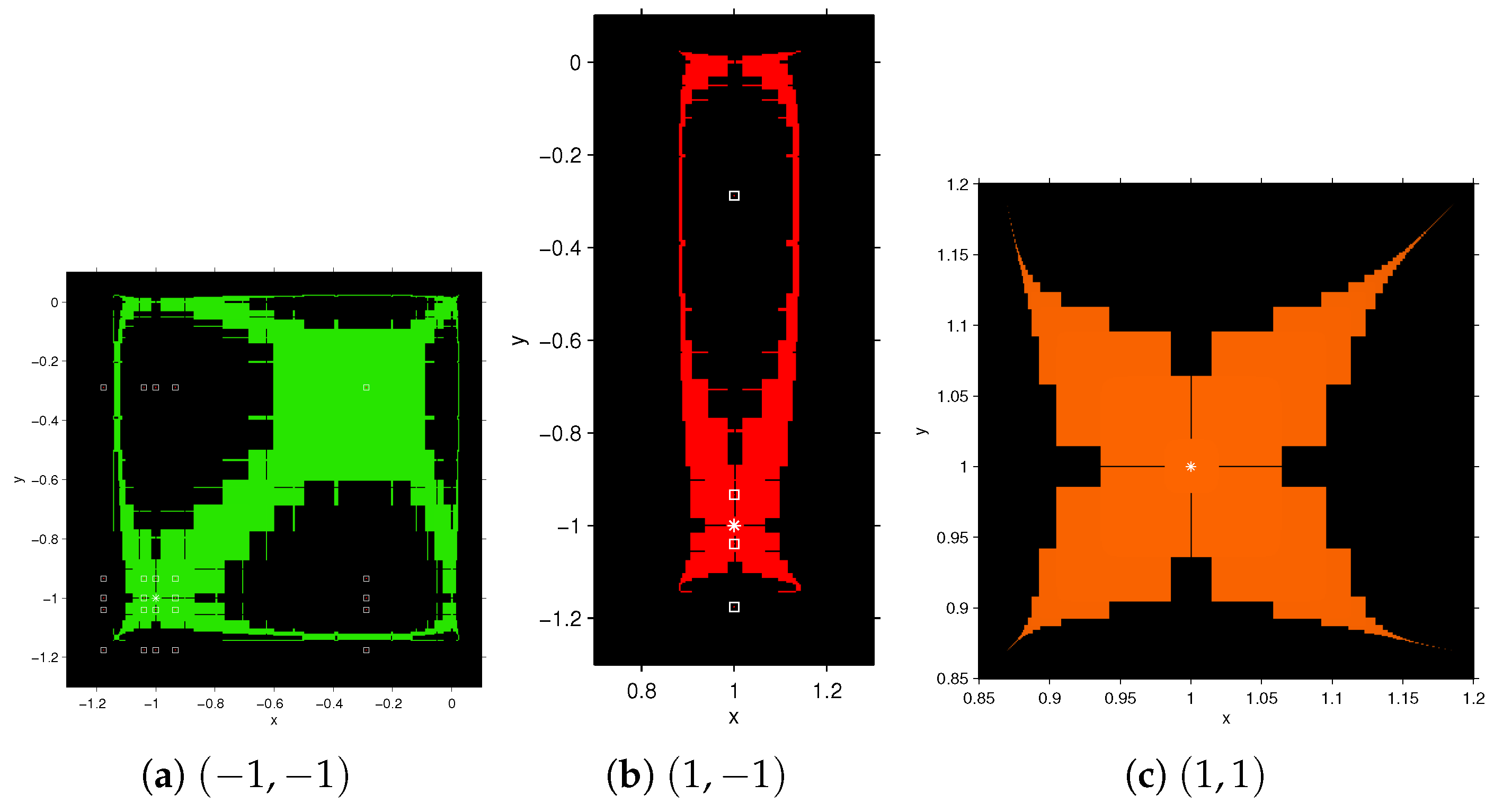
Figure 6a,b shows the slow convergence of the point
towards (−1,1); let us observe that, as for
point
is closer to the boundary so its speed is higher than that for
. The behavior of function
in black area among the basins of attraction and near the axis
x and
y are similar for
. In fact by choosing points in this area the iterative function is slowly divergent (see
Figure 6c,d).
Let us remark that, although this scheme is quite stable, the basins of attraction of the roots are much smaller than those of Newton’s method on , where there are not black regions.
Finally, the following result gives us information about the stability of the sixth-degree system when higher-order estimations of the Jacobian are made.
Proposition 6. The coordinate functions of the fixed point operator associated to RMNm on , for , are - (a)
For , the fixed points are , , and that are also superattracting and there are not strange fixed points in this case.
- (b)
The components of free critical points are the roots of polynomialfor and , provided that and k and l are not simultaneously equal to 1 and .
Remark 4. The fixed point function on for all m has 60
free critical points. The free critical points, for , are
provided that k and l are not equal to 1
and , simultaneously. In this case, we obtain approximations of order
for
, respectively, but nevertheless their basins of attraction are smaller than those of central divided difference (and of course of Newton’s method).
Figure 7 shows the dynamical planes for
. As in the previous cases, in the black area the convergence is very slow (or it diverges).
2.3. Second-Degree Polynomial System
The results about FMN
m, CMN
m and RMN
m classes applied on second-degree polynomial system
are stated in the following propositions. They resume, in each case, the iteration function, the fixed and critical points.
Proposition 7. The coordinate functions of the fixed point operator associated to FMNm on , for , are Moreover,
- (a)
For the only fixed points are the roots , , and , that are superattracting.
- (b)
For , the free critical points are , , and .
The calculation of free critical points of
for
is very complicated hence, so it has been provided only for
.
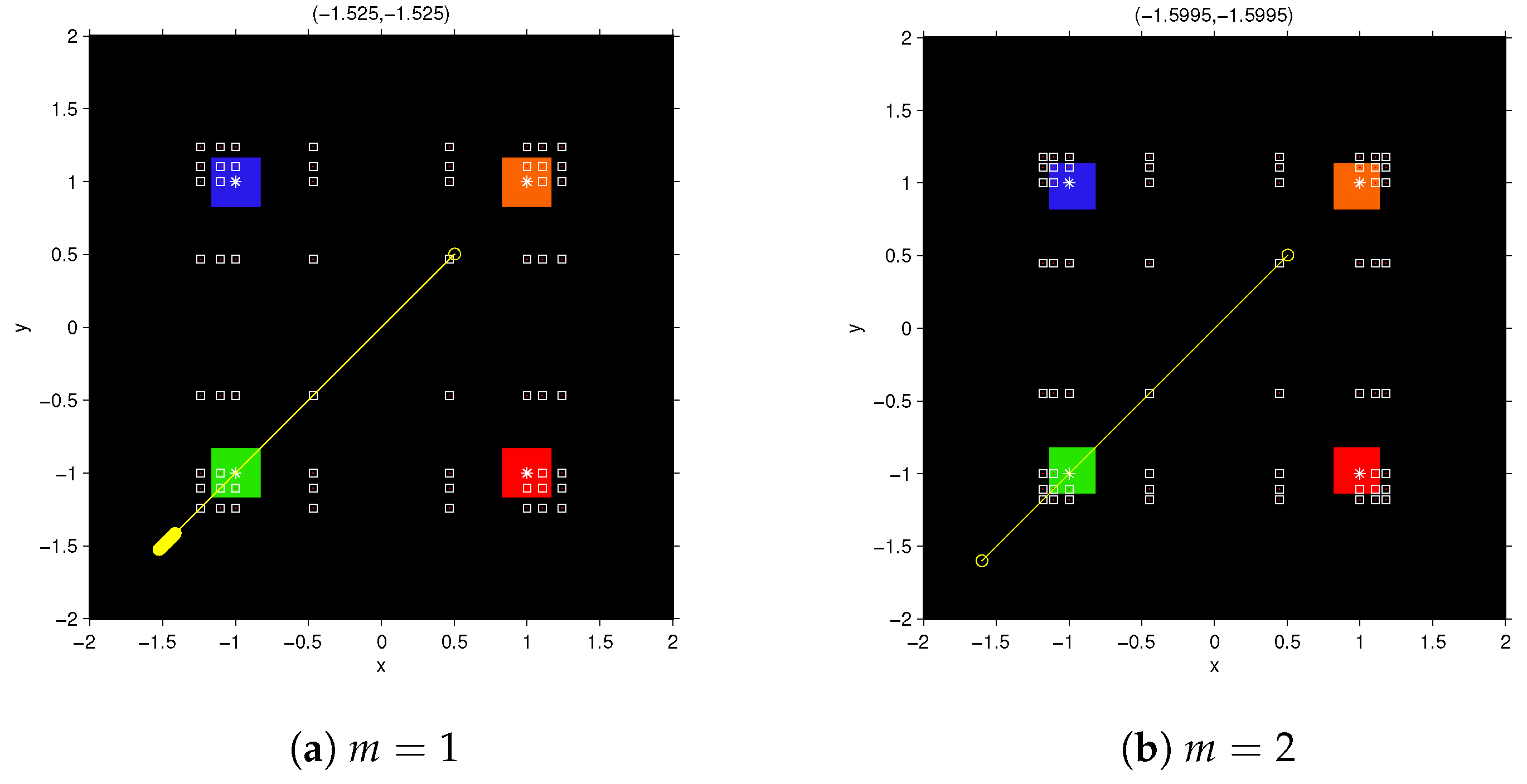
Figure 8 shows the dynamical planes of the fixed point function
for
. Similar results to polynomial system
and
have been obtained in this case, as by increasing
m, the wideness of the basins of attraction decreases. To study the behavior of the vectorial function in the black area of dynamical planes, we visualize the diverging orbits of
with the starting point
, after 200 iterations. The vectors on the top of the
Figure 8a–d, show the last vectorial iterate with the starting point
.
The following proposition shows, that using CMN
m, for
, and RMN
m, for
, on polynomial system
, we obtain, as was the case for the system
, the same fixed point function as the classical Newton’s method.
Proposition 8. The coordinates of the fixed point operator (which is denoted by ) associated to CMNm for and RMNm for on polynomial system arewhich are the same components of the fixed point function of Newton’s method on . Moreover, the fixed points of are the roots , , and that are superattracting. There are no strange fixed points nor free critical points in this case. Figure 9 shows the dynamical plane of the fixed point function
, corresponding to methods CMN
m and RMN
m for any
as well as their original partner, Newton’s scheme.