Enhancing Backtracking Search Algorithm using Reflection Mutation Strategy Based on Sine Cosine
Abstract
:1. Introduction
- A new reflection mutation strategy based on sine cosine is proposed to balance exploration and exploitation ability of BSA. To improve exploration ability, the best global individual is used to guide search direction, while sine and cosine math functions are used to enhance exploitation ability of BSA. Based on the strategy, a novel backtracking search algorithm with reflection mutation strategy based on sine cosine (RSCBSA) is proposed to solve global optimization problems.
- In the above strategy, the center of a unit simplex constructed by three individuals selected randomly is employed to enhance diversity of population, since it considers more information of individuals. In addition, in RSCBSA, crossover operator of BSA is replaced with that of DE.
- A comprehensive experiment is designed to verity the effectiveness of the proposed RSCBSA. In addition, a new parameter in RSCBSA is analyzed to set suitable values so that the performance of RSCBSA is the best.
2. Backtracking Search Optimization Algorithm
3. The Proposed Algorithm
3.1. Initialization
3.2. Reflection Mutation Strategy Based on Sine Cosine
3.3. Crossover Operator
3.4. The Framework of The Proposed Algorithm
| Algorithm 1: Framework of the Proposed Algorithm |
 |
3.5. Complex Analysis of The Proposed Algorithm
4. Experimental Simulations
4.1. Benchmark Test Suit
4.2. Parameter Setting
5. Experimental Results
5.1. Compared with State-of-the-Art Algorithms
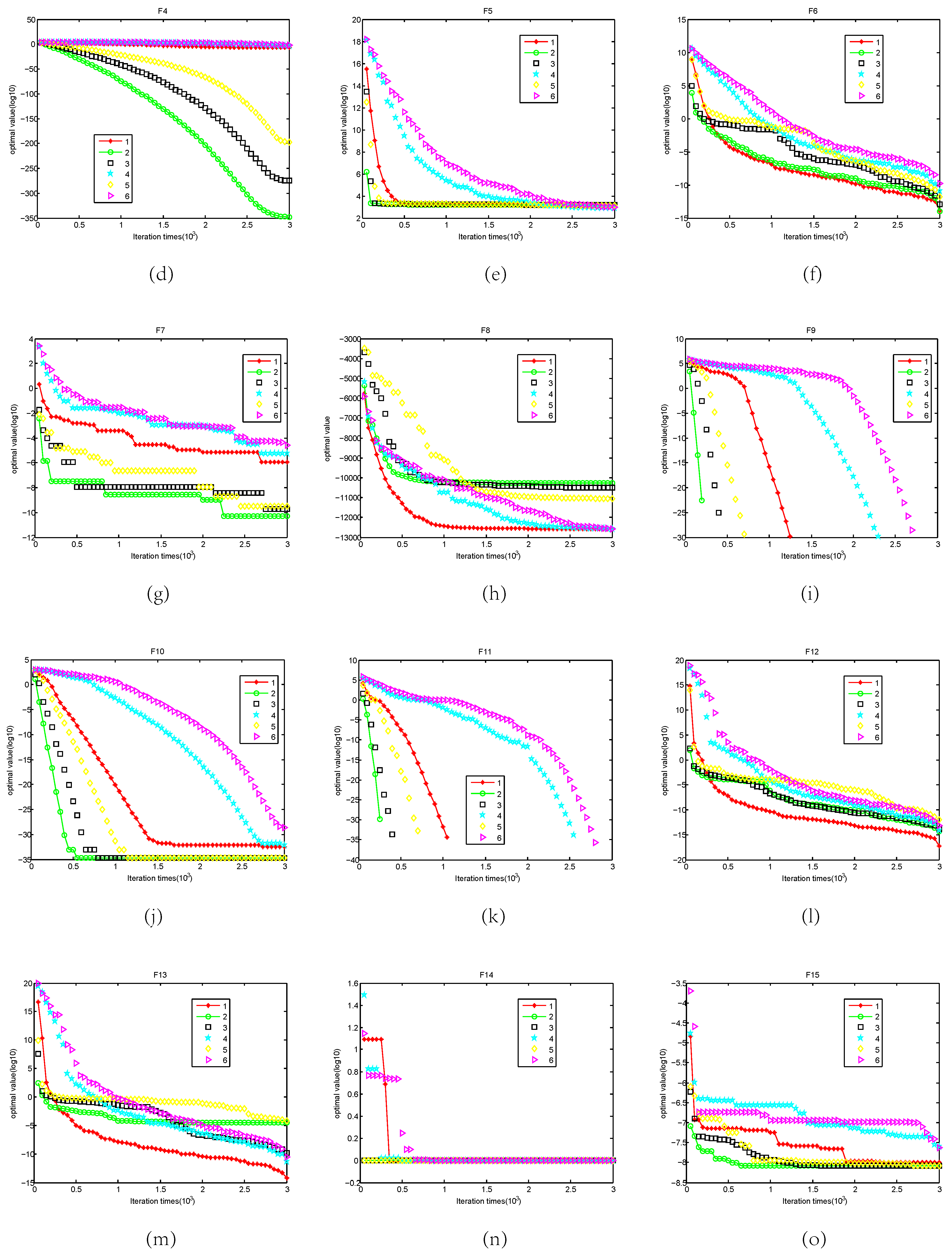
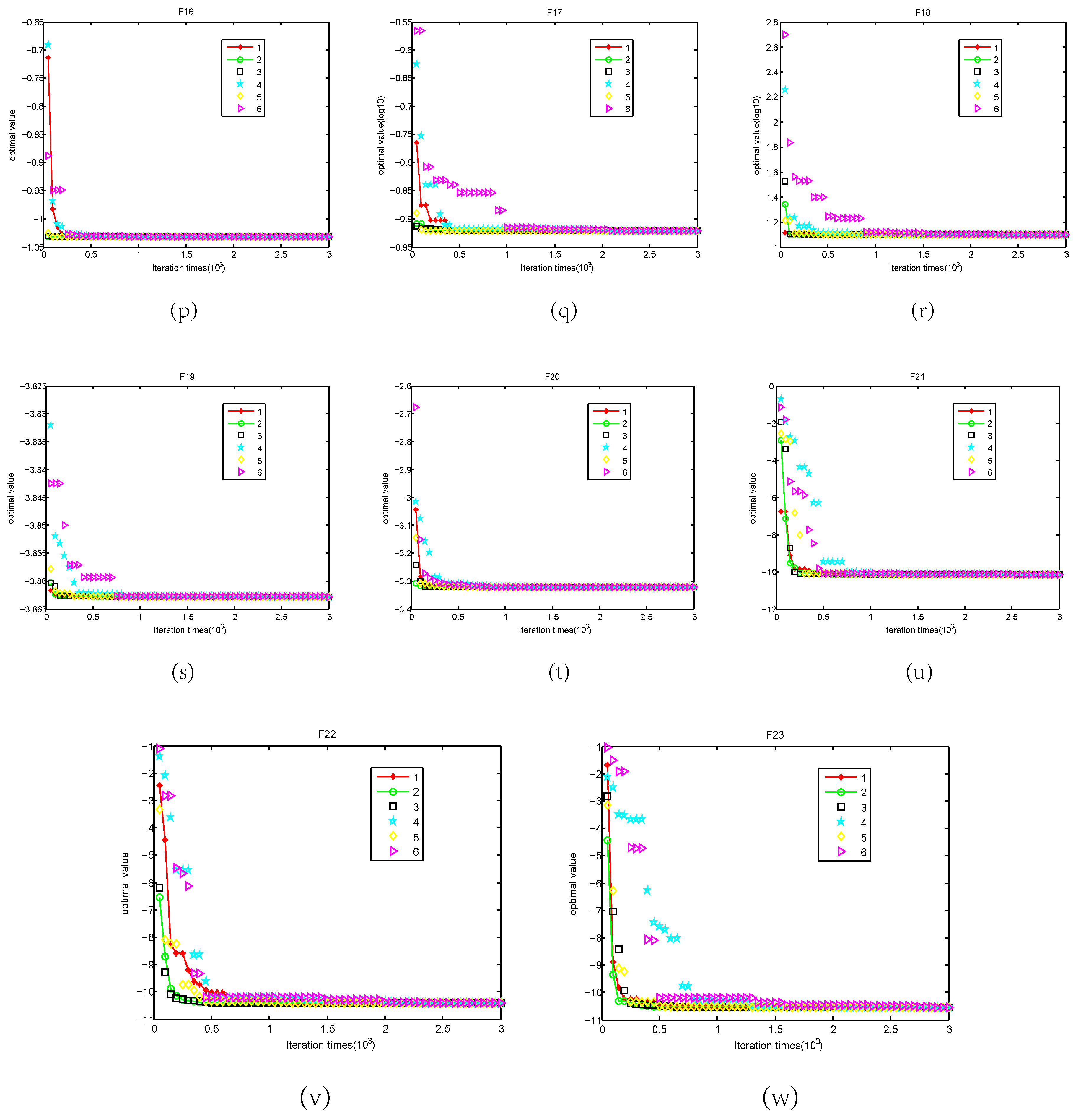
5.2. Convergence Analysis
5.3. Parameter Sensitivity Analysis
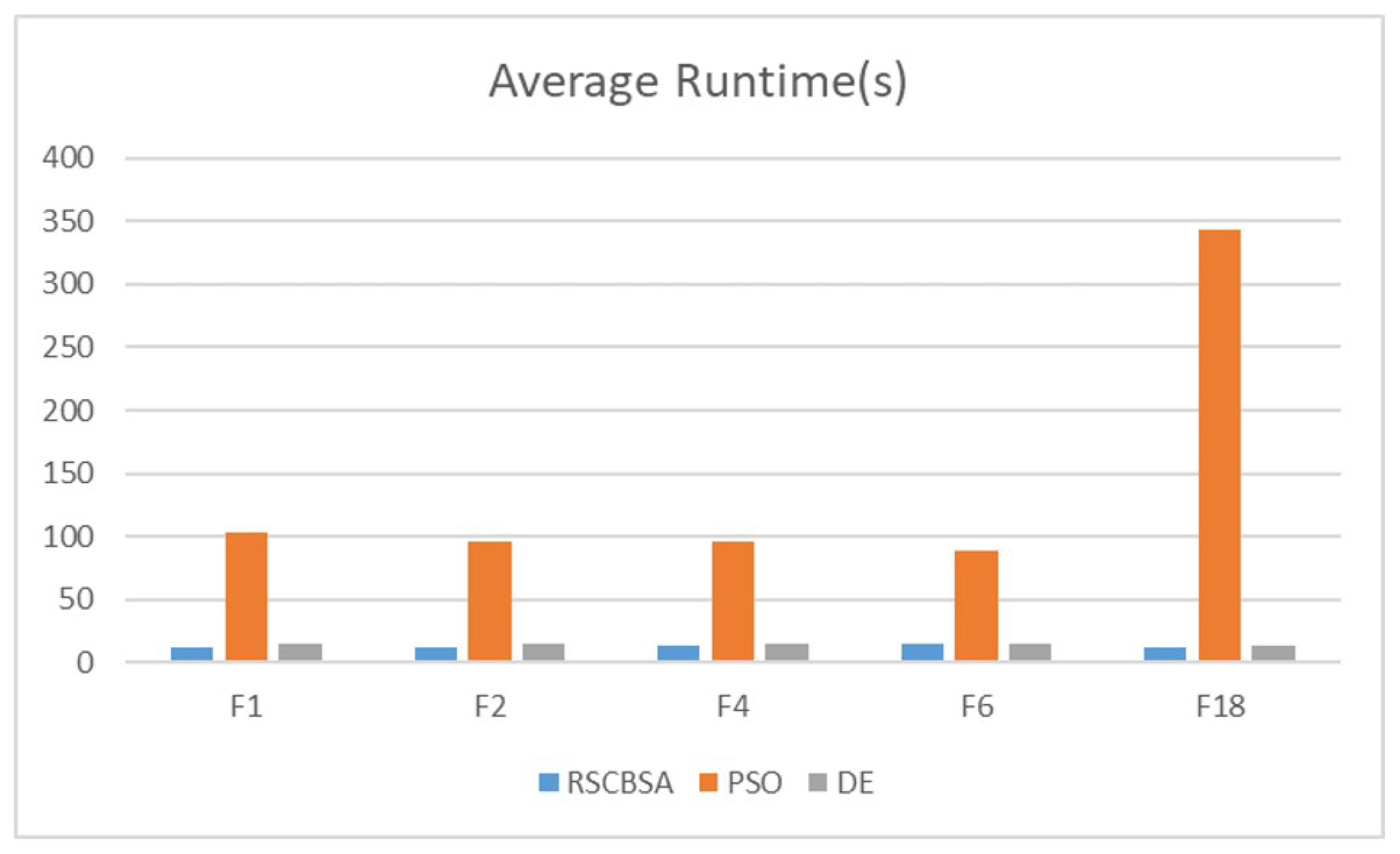
5.4. Runtime Analysis
5.5. Remarks
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Pan, Q.K.; Sang, H.Y.; Duan, J.H.; Gao, L. An improved fruit fly optimization algorithm for continuous function optimization problems. Knowl. Based Syst. 2014, 62, 69–83. [Google Scholar] [CrossRef]
- Soleimanpour-Moghadam, M.; Nezamabadi-Pour, H.; Farsangi, M.M. A quantum inspired gravitational search algorithm for numerical function optimization. Inf. Sci. 2014, 267, 83–100. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Hamzadayi, A.; Köse, S.Y. Testing the performance of teaching–learning based optimization (TLBO) algorithm on combinatorial problems: Flow shop and job shop scheduling cases. Inf. Sci. 2014, 276, 204–218. [Google Scholar] [CrossRef]
- Yaghini, M.; Khoshraftar, M.M.; Fallahi, M. A hybrid algorithm for artificial neural network training. Eng. Appl. Artif. Intell. 2013, 26, 293–301. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Xu, L.; Jia, H.; Lang, C.; Peng, X.; Sun, K. A novel method for multilevel color image segmentation based on dragonfly algorithm and differential evolution. IEEE Access 2019, 7, 19502–19538. [Google Scholar] [CrossRef]
- Goldberg, D. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Reynolds, R.G. An introduction to cultural algorithms. In Evolutionary Programming—Proceedings of the Third Annual Conference; World Scientific: Singapore, 1994; pp. 131–139. [Google Scholar]
- Civicioglu, P. Backtracking search optimization algorithm for numerical optimization problems. Appl. Math. Comput. 2013, 219, 8121–8144. [Google Scholar] [CrossRef]
- Madasu, S.D.; Kumar, M.S.; Singh, A.K. Comparable investigation of backtracking search algorithm in automatic generation control for two area reheat interconnected thermal power system. Appl. Soft Comput. 2017, 55, 197–210. [Google Scholar] [CrossRef]
- Islam, N.N.; Hannan, M.; Shareef, H.; Mohamed, A. An application of backtracking search algorithm in designing power system stabilizers for large multi-machine system. Neurocomputing 2017, 237, 175–184. [Google Scholar] [CrossRef]
- Kolawole, S.O.; Duan, H. Backtracking search algorithm for non-aligned thrust optimization for satellite formation. In Proceedings of the 11th IEEE International Conference on Control & Automation (ICCA), Taichung, Taiwan, 18–20 June 2014; pp. 738–743. [Google Scholar]
- Yuan, X.; Wu, X.; Tian, H.; Yuan, Y.; Adnan, R.M. Parameter identification of nonlinear Muskingum model with backtracking search algorithm. Water Resour. Manag. 2016, 30, 2767–2783. [Google Scholar] [CrossRef]
- Lin, J. Oppositional backtracking search optimization algorithm for parameter identification of hyperchaotic systems. Nonlinear Dyn. 2015, 80, 209–219. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Yin, Y.; Wang, B.; Yi, W.; Yin, Y. An improved backtracking search algorithm for constrained optimization problems. In International Conference on Knowledge Science; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Wang, L.; Zhong, Y.; Yin, Y.; Zhao, W.; Wang, B.; Xu, Y. A hybrid backtracking search optimization algorithm with differential evolution. Math. Probl. Eng. 2015, 2015, 1–16. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Wang, B.; Yin, Y. Best guided backtracking search algorithm for numerical optimization problems. In Knowledge Science, Engineering and Management; Lehner, F., Fteimi, N., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 414–425. [Google Scholar]
- Tian, K. Effective self-learning backtracking search optimization algorithm. Electron. Sci. Tech. 2015, 28, 41. [Google Scholar]
- Wang, P.; Chen, D.; Zou, F.; Li, Z. Guidance and niching backtracking search optimization algorithm. CEA 2017, 53, 126–131. [Google Scholar]
- Chen, D.; Lu, R.; Feng, Z.; Li, S.; Peng, W. A learning and niching based backtracking search optimisation algorithm and its applications in global optimisation and ANN training. Neurocomputing 2017, 266, 579–594. [Google Scholar] [CrossRef]
- Wang, X.; Liu, S.; Tian, W. Improved backtracking search optimization algorithm with new effective mutation scale factor and greedy crossover strategy. J. Comput. Appl. 2014, 34, 2543. [Google Scholar]
- Duan, H.; Luo, Q. Adaptive backtracking search algorithm for induction magnetometer optimization. IEEE Trans. Magn. 2014, 50, 1–6. [Google Scholar] [CrossRef]
- Nama, S.; Saha, A.K.; Ghosh, S. Improved backtracking search algorithm for pseudo dynamic active earth pressure on retaining wall supporting c-Φ backfill. Appl. Soft Comput. 2016, 52, 885–897. [Google Scholar] [CrossRef]
- Chen, X.; Liu, S.; Wang, Y. Emergency resources scheduling based on improved backtracking search optimization algorithm. Comput. Appl. Softw. 2015, 32, 235–238. [Google Scholar]
- Askarzadeh, A.; Coelho, L.D.S. A backtracking search algorithm combined with Burger’s chaotic map for parameter estimation of PEMFC electrochemical model. Int. J. Hydrog. Energy 2014, 39, 11165–11174. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Farrag, S.M. Integrated strategies of backtracking search optimizer for solving reactive power dispatch problem. IEEE Syst. J. 2016, PP, 1–10. [Google Scholar] [CrossRef]
- Ali, A.F. A memetic backtracking search optimization algorithm for economic dispatch problem. Egypt. Comput. Sci. J. 2015, 39, 56–71. [Google Scholar]
- Lin, Q.; Liang, G.; Li, X.; Zhang, C. A hybrid backtracking search algorithm for permutation flow-shop scheduling problem. Comput. Ind. Eng. 2015, 85, 437–446. [Google Scholar] [CrossRef]
- Modiri-Delshad, M.; Kaboli, S.H.A.; Taslimi-Renani, E.; Rahim, N.A. Backtracking search algorithm for solving economic dispatch problems with valve-point effects and multiple fuel options. Energy 2016, 116, 637–649. [Google Scholar] [CrossRef]
- Ayan, K.; Kilic, U. Optimal power flow of two-terminal HVDC systems using backtracking search algorithm. Int. J. Electr. Power Energy Syst. 2016, 78, 326–335. [Google Scholar] [CrossRef]
- Ahandani, M.A.; Ghiasi, A.R.; Kharrati, H. Parameter identification of chaotic systems using a shuffled backtracking search optimization algorithm. Soft Comput. 2017, 1–23. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.; Qu, B.Y.; Zhiping, C.; Heshan, W. Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models. Appl. Energy 2018, 226, 408–422. [Google Scholar] [CrossRef]
- Chu, Z.; Zhou, J.; Li, C.; Fu, W.; Tian, P. A compound structure of ELM based on feature selection and parameter optimization using hybrid backtracking search algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 143, 360–376. [Google Scholar]
- Lin, J.; Wang, Z.J.; Li, X. A backtracking search hyper-heuristic for the distributed assembly flow-shop scheduling problem. Swarm Evol. Comput. 2017, 36, S2210650216305028. [Google Scholar] [CrossRef]
- Su, Z.; Wang, H.; Peng, Y. A hybrid backtracking search optimization algorithm for nonlinear optimal control problems with complex dynamic constraints. Neurocomputing 2016, 186, 182–194. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Qian, W.; Chai, J.; Zhang, Z. Adaptive differential evolution algorithm based on reflective mutation strategy. Comput. Eng. Appl. 2018, 54, 166–173. [Google Scholar]
- Derrac, J.; Garcia, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Introduction to KEEL Software Suite. Available online: https://sci2s.ugr.es/keel/development.php (accessed on 26 October 2019).
- Bergh, F.V.D.; Engelbrecht, A.P. A study of particle swarm optimization particle trajectories. Inf. Sci. 2006, 176, 937–971. [Google Scholar]
- García-Martínez, C.; Gutiérrez, P.D.; Molina, D.; Lozano, M.; Herrera, F. Since CEC 2005 competition on real-parameter optimisation: a decade of research, progress and comparative analysis’s weakness. Soft Comput. 2017, 21, 1–11. [Google Scholar] [CrossRef]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.-P.; Auger, A.; Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization; Technical Report; Nanyang Technological University: Singapore, 2005. [Google Scholar]
- Baioletti, M.; Milani, A.; Santucci, V. Automatic Algebraic Evolutionary Algorithms; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Baioletti, M.; Milani, A.; Santucci, V. Algebraic Particle Swarm Optimization for the permutations search space. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), San Sebastian, Spain, 5–8 June 2017. [Google Scholar]
- He, Y.; Wang, X. Group theory-based optimization algorithm for solving knapsack problems. Knowl. Based Syst. 2018. [Google Scholar] [CrossRef]
- Hansen, N. Covariance matrix adaptation evolution strategy. In Proceedings of the 10th International Conference on Parallel Problem Solving from Nature, Dortmund, Germany, 13–17 September 2008; Springer: Cham, Switzerland, 2008. [Google Scholar]
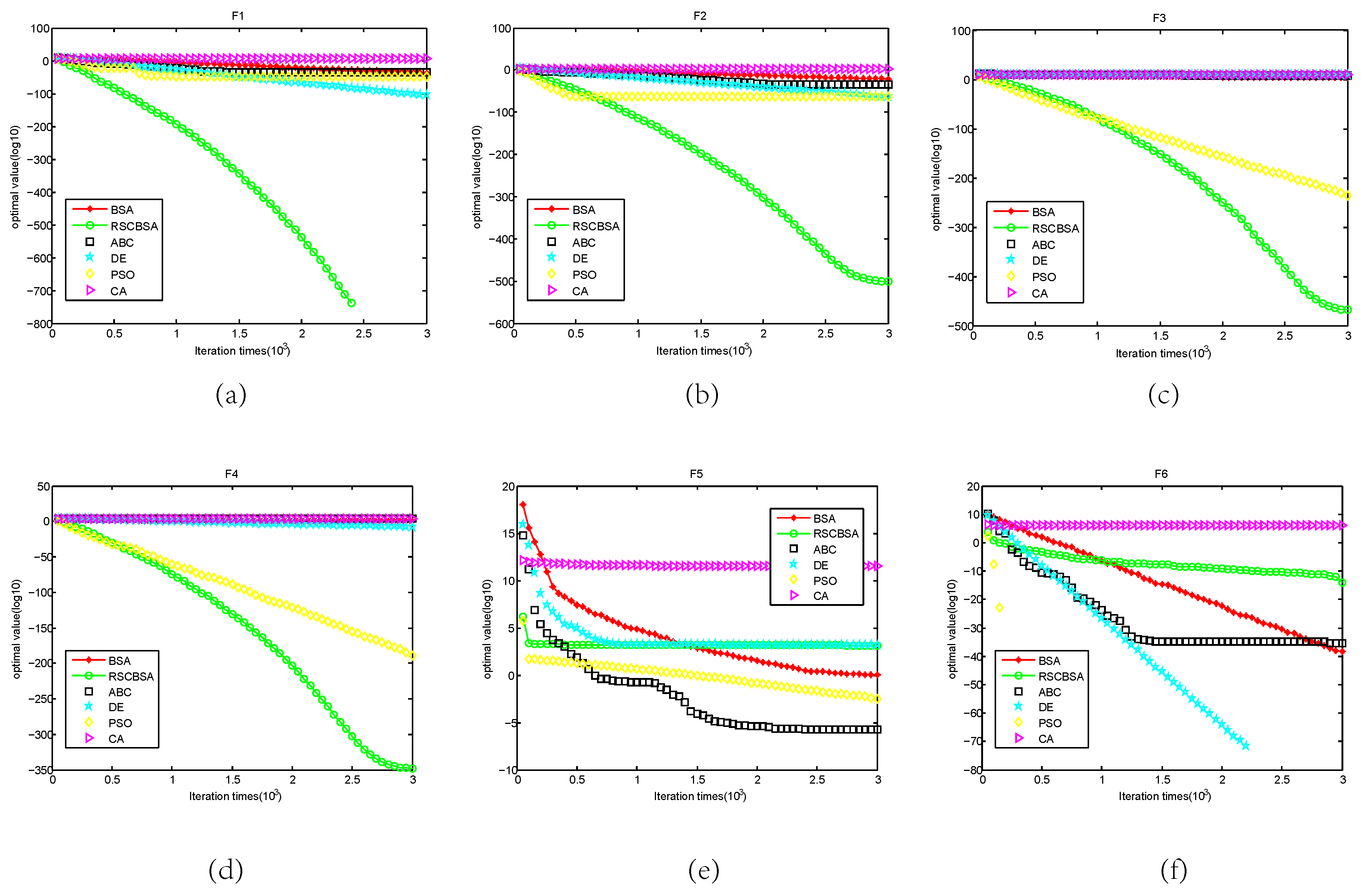
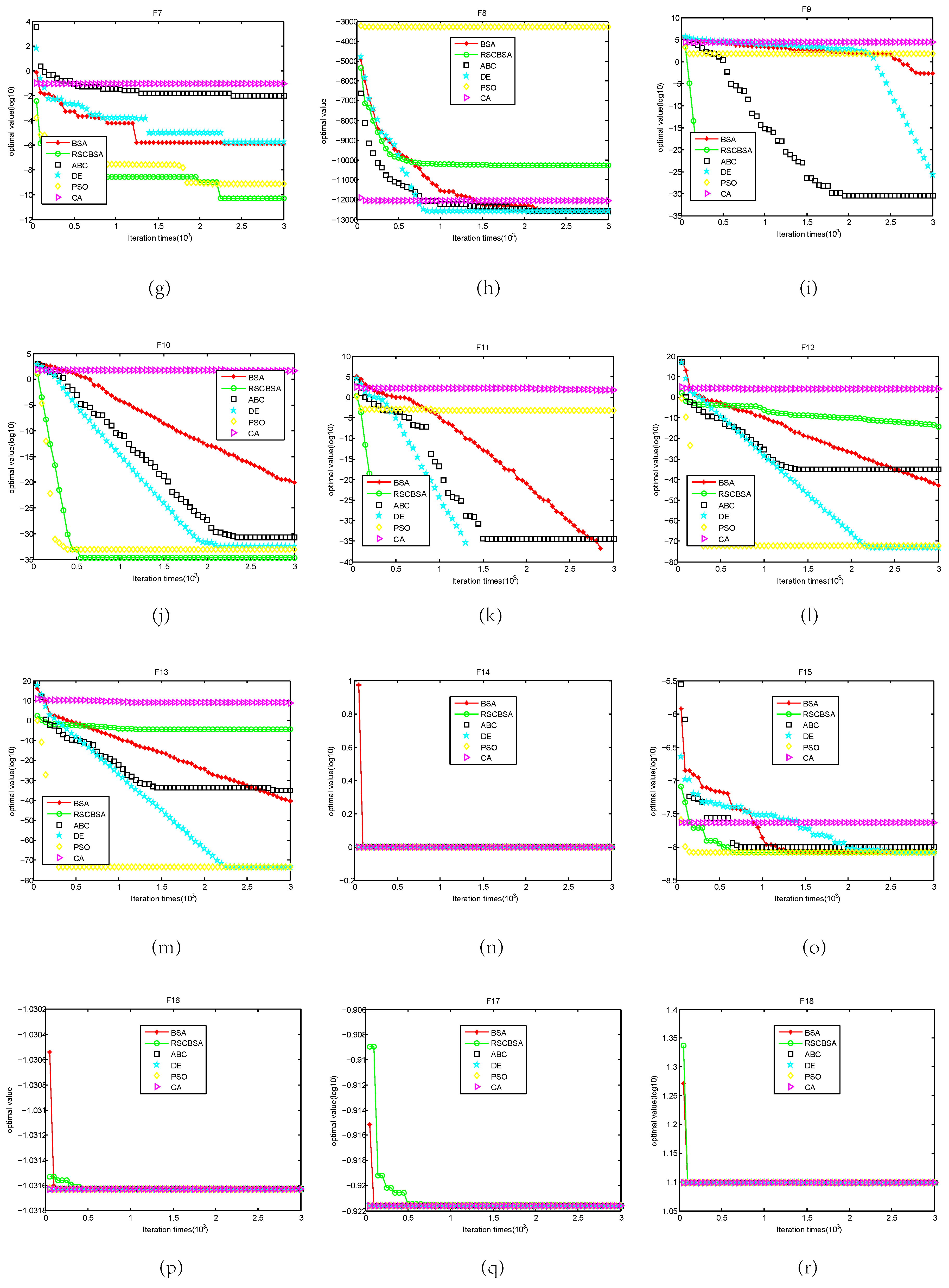
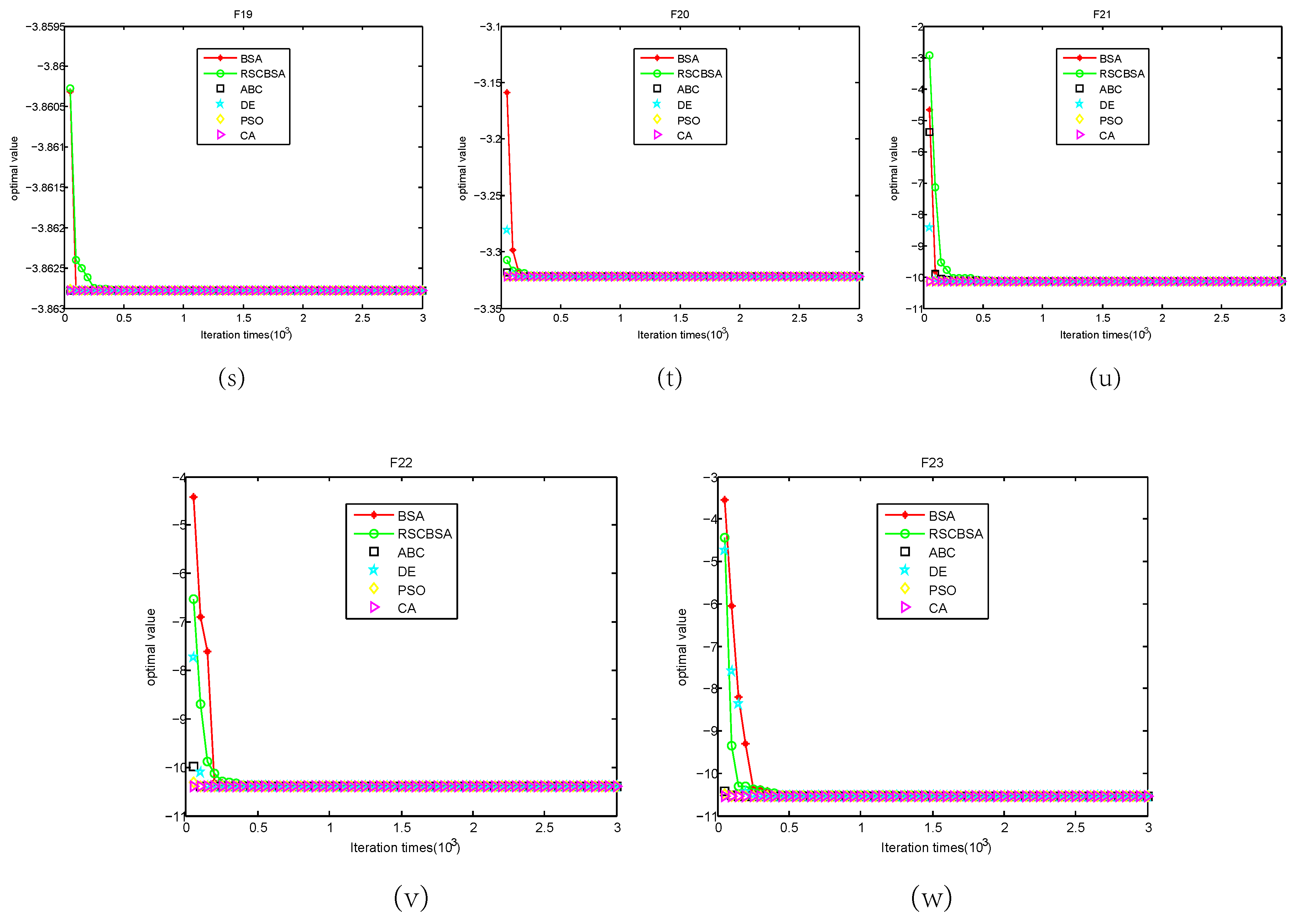
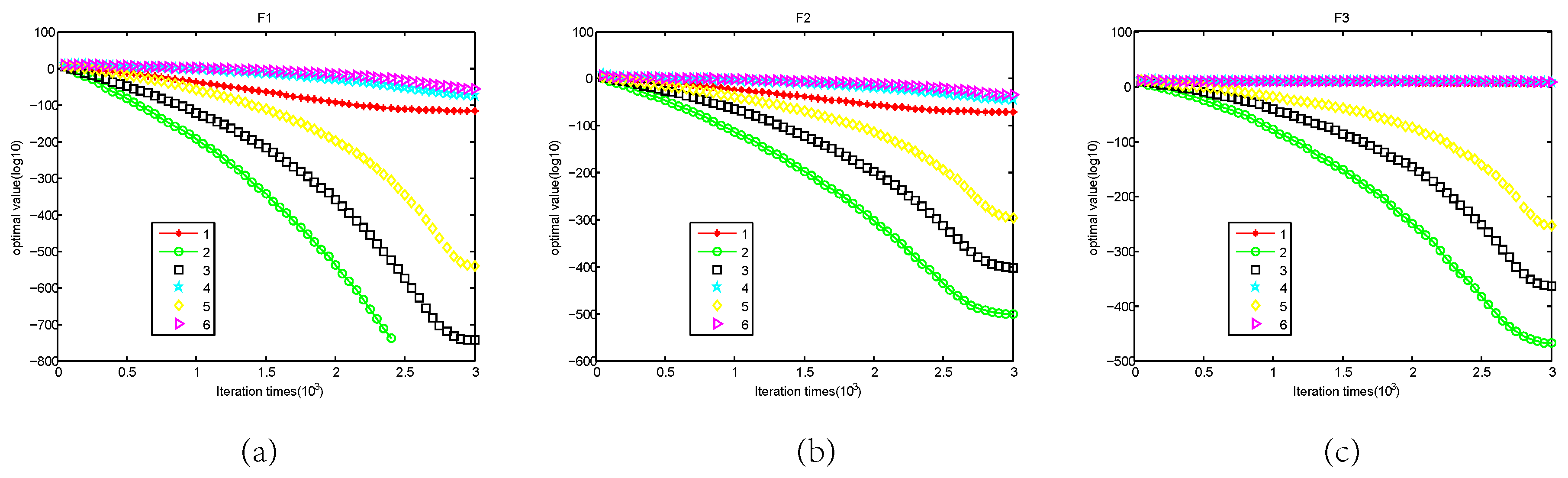
| Benchmark | Function | PSO | ABC | DE | CA | BSA | RSCBSA |
|---|---|---|---|---|---|---|---|
| F1 | best | ||||||
| mean | |||||||
| worst | 3.6505 × 10 | 5.4117 × 10 | 2.4629 × 10 | 4.1270 × 10 | 2.8521× 10 | ||
| std | 1.3868 × 10 | 6.8910 × 10 | 2.6423 × 10 | 9.5577 × 10 | 3.0966 × 10 | ||
| F2 | best | 5.4694 × 10 | 1.6002 × 10 | 4.1335 × 10 | 5.8462 × 10 | 5.0408 × 10 | 4.3459× 10 |
| mean | 1.3657 × 10 | 1.8228 × 10 | 2.0667 × 10 | 2.2100 × 10 | 3.2572 × 10 | 3.9314 × 10 | |
| worst | 1.5274 × 10 | 3.3803 × 10 | 5.6259 × 10 | 6.9183 × 10 | 1.0338 × 10 | 3.1240 × 10 | |
| std | 1.5008 × 10 | 1.6937 × 10 | 1.2307 × 10 | 2.3890 × 10 | 5.5714 × 10 | 0.0000 × 10 | |
| F3 | best | 3.9653 × 10 | 3.5792 × 10 | 7.3893 × 10 | 8.3334 × 10 | 3.0345 × 10 | 8.1950 × 10 |
| mean | 6.4404 × 10 | 5.9449 × 10 | 1.1857 × 10 | 2.0627 × 10 | 1.7266 × 10 | 7.7379 × 10 | |
| worst | 1.5655 × 10 | 1.1140 × 10 | 1.9801 × 10 | 4.0887 × 10 | 3.7642 × 10 | 2.3203 × 10 | |
| std | 8.1160 × 10 | 3.2828 × 10 | 6.0971 × 10 | 7.8083× 10 | 6.6997 × 10 | 0.0000 × 10 | |
| F4 | best | 7.8193 × 10 | 2.8317 × 10 | 5.1221 × 10 | 3.0161 × 10 | 9.0018 × 10 | 8.1338 × 10 |
| mean | 1.5871 × 10 | 3.9440 × 10 | 1.0355 × 10 | 4.6255 × 10 | 2.1297 × 10 | 4.7338 × 10 | |
| worst | 2.4649 × 10 | 5.0921 × 10 | 2.2349 × 10 | 7.9715 × 10 | 3.9292 × 10 | 8.8191 × 10 | |
| std | 2.1488 × 10 | 3.7018 × 10 | 1.5905 × 10 | 1.4438 × 10 | 4.0870 × 10 | 2.6901 × 10 | |
| F5 | best | 7.9093 × 10 | 8.6115 × 10 | 2.3793 × 10 | 1.0168 × 10 | 8.6456 × 10 | 2.3440× 10 |
| mean | 2.2878 × 10 | 5.3359 × 10 | 3.3665 × 10 | 1.2073 × 10 | 5.5375 × 10 | 2.4658 × 10 | |
| worst | 7.0303 × 10 | 1.8079 × 10 | 8.8254 × 10 | 4.4121 × 10 | 8.6258 × 10 | 2.6975 × 10 | |
| std | 3.1431 × 10 | 1.3289 × 10 | 4.0340 × 10 | 1.0354 × 10 | 9.4312 × 10 | 6.2485 × 10 | |
| F6 | best | 0.0000 × 10 | 5.5033 × 10 | 0.0000 × 10 | 4.3707 × 10 | 2.2988 × 10 | 8.6469 × 10 |
| mean | 1.9105 × 10 | 7.4696 × 10 | 0.0000 × 10 | 1.8850 × 10 | 4.8673 × 10 | 1.4989 × 10 | |
| worst | 1.1093 × 10 | 2.5076 × 10 | 0.0000 × 10 | 3.1993 × 10 | 1.9639× 10 | 5.1162× 10 | |
| std | 8.1244× 10 | 1.3274 × 10 | 0.0000 × 10 | 5.4730 × 10 | 2.3180 × 10 | 2.7930 × 10 | |
| F7 | best | 1.1152 × 10 | 9.4208 × 10 | 3.1487 × 10 | 3.5096 × 10 | 4.3966 × 10 | 3.3201 × 10 |
| mean | 7.4359 × 10 | 2.0345 × 10 | 8.2541 × 10 | 1.4979 × 10 | 1.4448 × 10 | 1.7506 × 10 | |
| worst | 2.1471 × 10 | 3.5513 × 10 | 1.2403 × 10 | 3.4948 × 10 | 2.1994 × 10 | 4.4544 × 10 | |
| std | 3.1481 × 10 | 3.7637 × 10 | 4.3611 × 10 | 8.3832 × 10 | 1.6176× 10 | 1.1159 × 10 |
| Algorithm | Ranking |
|---|---|
| PSO | 2.3571 |
| ABC | 3 |
| DE | 3.4286 |
| CA | 6 |
| BSA | 4.0714 |
| RSCBSA | 2.1429 |
| Benchmark | Function | PSO | ABC | DE | CA | BSA | RSCBSA |
|---|---|---|---|---|---|---|---|
| F8 | best | −3.2818 × 10 | −1.2570 × 10 | −1.2570 × 10 | −1.2049 × 10 | −1.2569 × 10 | −1.0278 × 10 |
| mean | −2.4289 × 10 | −1.2541 × 10 | −1.2980 × 10 | −9.8465 × 10 | −1.2569 × 10 | −8.8889 × 10 | |
| worst | −1.6827 × 10 | −1.2209 × 10 | −1.2214 × 10 | −6.9449 × 10 | −1.2569 × 10 | −8.0066 × 10 | |
| std | 9.9518 × 10 | 8.0666 × 10 | −1.2442 × 10 | 3.3642 × 10 | 2.2234 × 10 | 2.3757 × 10 | |
| F9 | best | 5.9698 × 10 | 1.1369 × 10 | 6.8781 × 10 | 7.7160 × 10 | 1.0854 × 10 | 0.0000 × 10 |
| mean | 1.1840 × 10 | 1.4061 × 10 | 5.0229 × 10 | 1.4651 × 10 | 3.3603 × 10 | 0.0000 × 10 | |
| worst | 2.0894 × 10 | 9.9496 × 10 | 2.6971 × 10 | 2.5216 × 10 | 6.6977 × 10 | 0.0000 × 10 | |
| std | 1.5334 × 10 | 6.2573 × 10 | 6.5267 × 10 | 1.8300 × 10 | 3.1008 × 10 | 0.0000 × 10 | |
| F10 | best | 4.4409 × 10 | 4.7074 × 10 | 7.9936 × 10 | 5.5878 × 10 | 2.1721 × 10 | 8.8818 × 10 |
| mean | 3.8505 × 10 | 6.0574 × 10 | 7.9936 × 10 | 1.0163 × 10 | 2.5030 × 10 | 8.8818 × 10 | |
| worst | 1.1552 × 10 | 1.5721 × 10 | 7.9936 × 10 | 1.3951× 10 | 7.7180 × 10 | 8.8818 × 10 | |
| std | 4.2996× 10 | 5.4819 × 10 | 2.2403 × 10 | 3.9939 × 10 | 5.5106 × 10 | 3.8894 × 10 | |
| F11 | best | 3.9319 × 10 | 1.1102 × 10 | 0.0000 × 10 | 5.5845 × 10 | 0.0000 × 10 | 0.0000 × 10 |
| mean | 9.3162 × 10 | 3.5826 × 10 | 0.0000 × 10 | 1.5086 × 10 | 1.6533 × 10 | 0.0000 × 10 | |
| worst | 2.2875 × 10 | 3.5406 × 10 | 0.0000 × 10 | 4.6938 × 10 | 4.9135 × 10 | 0.0000× 10 | |
| std | 1.9610 × 10 | 7.4801 × 10 | 0.0000 × 10 | 8.2619 × 10 | 7.7747 × 10 | 0.0000× 10 | |
| F12 | best | 4.7116 × 10 | 6.1436 × 10 | 1.5705 × 10 | 6.2196 × 10 | 2.8984 × 10 | 6.0657 × 10 |
| mean | 5.1561 × 10 | 7.8009 × 10 | 1.5705 × 10 | 2.7468 × 10 | 2.8011 × 10 | 8.8653 × 10 | |
| worst | 1.2553 × 10 | 5.2760 × 10 | 1.5705 × 10 | 1.7374 × 10 | 4.4505 × 10 | 2.3351 × 10 | |
| std | 2.1613 × 10 | 8.9331 × 10 | 2.9963 × 10 | 1.7490 × 10 | 6.7812 × 10 | 4.6445 × 10 | |
| F13 | best | 1.0987 × 10 | 5.3680 × 10 | 1.3498 × 10 | 6.4179 × 10 | 2.2895 × 10 | 1.1010 × 10 |
| mean | 1.0987× 10 | 8.3837 × 10 | 1.3498 × 10 | 2.6594 × 10 | 3.7103 × 10 | 5.0903 × 10 | |
| worst | 1.0987 × 10 | 2.2538 × 10 | 1.3498 × 10 | 1.2544 × 10 | 2.9765 × 10 | 1.4244 × 10 | |
| std | 1.0865 × 10 | 1.0659 × 10 | 0.0000 × 10 | 1.0542 × 10 | 4.7169 × 10 | 1.0055 × 10 |
| Algorithm | Ranking |
|---|---|
| PSO | 4.5833 |
| ABC | 2.5833 |
| DE | 2.25 |
| CA | 5.6667 |
| BSA | 2.5833 |
| RSCBSA | 3.3333 |
| Benchmark | Function | PSO | ABC | DE | CA | BSA | RSCBSA |
|---|---|---|---|---|---|---|---|
| F14 | best | 9.9800 × 10 | 9.9800 × 10 | 9.9800 × 10 | 9.9800 × 10 | 9.9800 × 10 | 9.9800 × 10 |
| mean | 3.4567× 10 | 9.9800 × 10 | 1.1624 × 10 | 6.6697 × 10 | 9.9800 × 10 | 9.9800 × 10 | |
| worst | 1.2671 × 10 | 9.9800 × 10 | 5.9289 × 10 | 1.6441 × 10 | 9.9800 × 10 | 9.9800 × 10 | |
| std | 9.3179 × 10 | 4.4373 × 10 | 7.8343 × 10 | 1.9194 × 10 | 1.9722 × 10 | 1.9722 × 10 | |
| F15 | best | 3.0749 × 10 | 4.1171 × 10 | 3.0749 × 10 | 4.8171 × 10 | 3.0749 × 10 | 3.0749 × 10 |
| mean | 3.3567 × 10 | 5.5933 × 10 | 4.7100 × 10 | 2.2035 × 10 | 3.0749 × 10 | 3.5056 × 10 | |
| worst | 2.0363 × 10 | 1.0451 × 10 | 7.8431 × 10 | 1.4641 × 10 | 3.0749 × 10 | 1.2232 × 10 | |
| std | 4.4754 × 10 | 1.3891 × 10 | 2.6811 × 10 | 6.8205 × 10 | 1.1755 × 10 | 2.8670 × 10 | |
| F16 | best | −1.0316 × 10 | −1.0316 × 10 | −1.0316 × 10 | −1.0316 × 10 | −1.0316 × 10 | −1.0316 × 10 |
| mean | −1.0316 × 10 | −1.0316 × 10 | −1.0316 × 10 | −1.0316 × 10 | −1.0316 × 10 | −1.0316 × 10 | |
| worst | −1.0316 × 10 | −1.0316 × 10 | −1.0316 × 10 | −1.0316 × 10 | −1.0316 × 10 | −1.0316 × 10 | |
| std | 0.0000 × 10 | 0.0000 × 10 | 0.0000 × 10 | 0.0000 × 10 | 1.9722 × 10 | 1.9722 × 10 | |
| F17 | best | 3.9789 × 10 | 3.9789 × 10 | 3.9789 × 10 | 3.9789 × 10 | 3.9789 × 10 | 3.9789 × 10 |
| mean | 3.9789 × 10 | 3.9789 × 10 | 3.9789 × 10 | 3.9789 × 10 | 3.9789 × 10 | 3.9789 × 10 | |
| worst | 3.9789 × 10 | 3.9789 × 10 | 3.9789 × 10 | 3.9789 × 10 | 3.9789 × 10 | 3.9789 × 10 | |
| std | 2.7733 × 10 | 2.7733 × 10 | 2.7733 × 10 | 2.7733 × 10 | 3.0815 × 10 | 1.9600 × 10 | |
| F18 | best | 3.0000 × 10 | 3.0000 × 10 | 3.0000 × 10 | 3.0000 × 10 | 3.0000 × 10 | 3.0000 × 10 |
| mean | 3.0000 × 10 | 3.0002 × 10 | 3.0000 × 10 | 3.0000 × 10 | 3.0000 × 10 | 3.0000 × 10 | |
| worst | 3.0000 × 10 | 3.0039 × 10 | 3.0000 × 10 | 3.0000 × 10 | 3.0000 × 10 | 3.0000 × 10 | |
| std | 0.0000 × 10 | 5.0468 × 10 | 0.0000 × 10 | 0.0000 × 10 | 0.0000 × 10 | 2.0556 × 10 | |
| F19 | best | −3.8628 × 10 | −3.8628 × 10 | −3.8628 × 10 | −3.8628 × 10 | −3.8628 × 10 | -3.8628 × 10 |
| mean | −3.8370 × 10 | −3.8628 × 10 | −3.8628 × 10 | −3.8628 × 10 | −3.8628 × 10 | −3.8628 × 10 | |
| worst | −3.0898 × 10 | -3.8628 × 10 | −3.8628 × 10 | −3.8628 × 10 | −3.8628 × 10 | −3.8628 × 10 | |
| std | 1.9255 × 10 | 1.9722 × 10 | 1.9722 × 10 | 1.9722 × 10 | 3.1554 × 10 | 3.1554 × 10 | |
| F20 | best | −3.3220 × 10 | −3.3220 × 10 | −3.3220 × 10 | −3.3220 × 10 | −3.3220 × 10 | −3.3220 × 10 |
| mean | −3.2863 × 10 | −3.3220 × 10 | −3.3212 × 10 | −3.2809 × 10 | −3.3220 × 10 | −3.2863 × 10 | |
| worst | −3.2031 × 10 | −3.3220 × 10 | −3.2974 × 10 | −3.1993 × 10 | −3.3220 × 10 | −3.2031 × 10 | |
| std | 2.9688 × 10 | 3.1554 × 10 | 1.9578 × 10 | 3.1319 × 10 | 7.8886 × 10 | 2.9685 × 10 | |
| F21 | best | −1.0153 × 10 | −1.0153 × 10 | −1.0153 × 10 | −1.0153 × 10 | −1.0153 × 10 | −1.0153 × 10 |
| mean | −4.7418 × 10 | −1.0153 × 10 | −9.7358 × 10 | −6.4744 × 10 | −1.0153 × 10 | −1.0153 × 10 | |
| worst | −2.6305 × 10 | −1.0153 × 10 | −2.6829 × 10 | −2.6305 × 10 | −1.0153 × 10 | −1.0153 × 10 | |
| std | 1.0831 × 10 | 1.2622 × 10 | 2.5369 × 10 | 1.1149 × 10 | 1.2622 × 10 | 4.2873 × 10 | |
| F22 | best | −1.0403 × 10 | −1.0403 × 10 | −1.0403 × 10 | −1.0403 × 10 | −1.0403 × 10 | −1.0403 × 10 |
| mean | −6.1650 × 10 | −1.0403 × 10 | −-1.0227 × 10 | −6.7240 × 10 | −1.0403 × 10 | −1.0403 × 10 | |
| worst | −1.8376 × 10 | −1.0403 × 10 | −5.1288 × 10 | −2.7519 × 10 | −1.0403 × 10 | −1.0403 × 10 | |
| std | 1.2604 × 10 | 5.0487 × 10 | 8.9629 × 10 | 1.2263 × 10 | 0.0000 × 10 | 6.5010 × 10 | |
| F23 | best | −1.0536 × 10 | −1.0536 × 10 | −1.0536 × 10 | −1.0536 × 10 | −1.0536 × 10 | −1.0536 × 10 |
| mean | −6.7622 × 10 | −1.0536 × 10 | −1.0536 × 10 | −6.2481 × 10 | −1.0536 × 10 | −1.0133 × 10 | |
| worst | −2.4217E × 10 | −1.0512 × 10 | −1.0536 × 10 | −2.4217 × 10 | −1.0536 × 10 | -3.8354 × 10 | |
| std | 1.4389 × 10 | 1.9658 × 10 | 7.8886 × 10 | 1.4417 × 10 | 2.8399 × 10 | 2.3087 × 10 |
| Algorithm | Ranking |
|---|---|
| PSO | 4.85 |
| ABC | 2.95 |
| DE | 3.3 |
| CA | 4.6 |
| BSA | 2.35 |
| RSCBSA | 2.95 |
| Benchmark | RSCBSA vs. BSA | RSCBSA vs. PSO | RSCBSA vs. ABC | RSCBSA vs. DE | RSCBSA vs. CA | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | p-Value | Winner | H | p-Value | Winner | H | p-Value | Winner | H | p-Value | Winner | H | p-Value | Winner | |
| F1 | 1 | 1.2118 × 10 | + | 1 | 1.2118 × 10 | + | 1 | 1.2118 × 10 | + | 1 | 1.2118 × 10 | + | 1 | 1.2118 × 10 | + |
| F2 | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + |
| F3 | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + |
| F4 | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + |
| F5 | 1 | 1.0763 × 10 | + | 1 | 3.0199 × 10 | − | 1 | 3.0199 × 10 | − | 1 | 1.2493 × 10 | + | 1 | 3.0199 × 10 | + |
| F6 | 1 | 3.0199 × 10 | − | 1 | 2.3692 × 10 | − | 1 | 3.0199 × 10 | − | 1 | 1.2118 × 10 | − | 1 | 3.0199 × 10 | + |
| F7 | 1 | 3.0199 × 10 | + | 1 | 2.0283 × 10 | + | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + | 1 | 3.0199 × 10 | + |
| F8 | 1 | 2.2076 × 10 | − | 1 | 3.0104 × 10 | + | 1 | 1.4248 × 10 | − | 1 | 2.5416 × 10 | − | 1 | 3.8481 × 10 | − |
| F9 | 1 | 1.2118 × 10 | + | 1 | 1.1661 × 10 | + | 1 | 1.0566 × 10 | + | 1 | 1.2118 × 10 | + | 1 | 1.2118 × 10 | + |
| F10 | 1 | 1.2118 × 10 | + | 1 | 1.5702 × 10 | + | 1 | 9.7992 × 10 | + | 1 | 1.6853 × 10 | + | 1 | 1.2118 × 10 | + |
| F11 | 1 | 4.5700 × 10 | + | 1 | 1.2118 × 10 | + | 1 | 1.2078 × 10 | + | 0 | NaN | = | 1 | 1.2118 × 10 | + |
| F12 | 1 | 3.0199 × 10 | − | 1 | 2.4291 × 10 | − | 1 | 3.0199 × 10 | − | 1 | 1.2118 × 10 | − | 1 | 3.0199 × 10 | + |
| F13 | 1 | 3.0199 × 10 | − | 1 | 2.6537 × 10 | − | 1 | 3.0199 × 10 | − | 1 | 1.2118 × 10 | − | 1 | 3.0199 × 10 | + |
| F14 | 0 | NaN | = | 1 | 9.7829 × 10 | + | 1 | 1.6853 × 10 | = | 1 | 2.7085 × 10 | + | 1 | 1.1642 × 10 | + |
| F15 | 1 | 2.1633 × 10 | − | 0 | 9.7028 × 10 | = | 1 | 4.1804 × 10 | + | 1 | 8.8803 × 10 | + | 1 | 1.2050 × 10 | + |
| F16 | 0 | NaN | = | 1 | 1.6853 × 10 | = | 1 | 1.6853 × 10 | = | 1 | 1.6853 × 10 | = | 1 | 1.6853 × 10 | = |
| F17 | 1 | 6.6113 × 10 | = | 1 | 3.8943 × 10 | = | 1 | 3.8943 × 10 | = | 1 | 3.8943 × 10 | = | 1 | 3.8943 × 10 | = |
| F18 | 1 | 4.1865 × 10 | = | 1 | 4.1865 × 10 | = | 0 | 4.6889 × 10 | = | 1 | 4.1865 × 10 | = | 1 | 4.1865 × 10 | = |
| F19 | 0 | NaN | = | 1 | 2.7085 × 10 | + | 1 | 1.6853 × 10 | = | 1 | 1.6853 × 10 | = | 1 | 1.6853 × 10 | = |
| F20 | 1 | 6.2958 × 10 | − | 1 | 5.4952 × 10 | = | 1 | 3.5049 × 10 | − | 1 | 7.8511 × 10 | − | 0 | 9.6974 × 10 | = |
| F21 | 1 | 2.1150 × 10 | = | 1 | 6.7082 × 10 | + | 1 | 2.1150 × 10 | = | 1 | 1.9600 × 10 | + | 1 | 2.5975 × 10 | + |
| F22 | 1 | 1.4331 × 10 | = | 1 | 1.2791 × 10 | + | 1 | 1.4992 × 10 | = | 1 | 1.1131 × 10 | + | 1 | 3.3861 × 10 | + |
| F23 | 1 | 3.1216 × 10 | − | 1 | 2.0775 × 10 | + | 1 | 2.7674 × 10 | − | 1 | 2.7674 × 10 | − | 1 | 6.7273 × 10 | + |
| +/−/= | 9/7/7 | 14/4/5 | 9/7/7 | 12/6/5 | 17/1/5 | ||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, C.; Li, S.; Zhang, Y.; Chen, Z.; Zhang, C. Enhancing Backtracking Search Algorithm using Reflection Mutation Strategy Based on Sine Cosine. Algorithms 2019, 12, 225. https://doi.org/10.3390/a12110225
Zhou C, Li S, Zhang Y, Chen Z, Zhang C. Enhancing Backtracking Search Algorithm using Reflection Mutation Strategy Based on Sine Cosine. Algorithms. 2019; 12(11):225. https://doi.org/10.3390/a12110225
Chicago/Turabian StyleZhou, Chong, Shengjie Li, Yuhe Zhang, Zhikun Chen, and Cuijun Zhang. 2019. "Enhancing Backtracking Search Algorithm using Reflection Mutation Strategy Based on Sine Cosine" Algorithms 12, no. 11: 225. https://doi.org/10.3390/a12110225
APA StyleZhou, C., Li, S., Zhang, Y., Chen, Z., & Zhang, C. (2019). Enhancing Backtracking Search Algorithm using Reflection Mutation Strategy Based on Sine Cosine. Algorithms, 12(11), 225. https://doi.org/10.3390/a12110225





