Abstract
Backtracking Search Algorithm (BSA) is a younger population-based evolutionary algorithm and widely researched. Due to the introduction of historical population and no guidance toward to the best individual, BSA does not adequately use the information in the current population, which leads to a slow convergence speed and poor exploitation ability of BSA. To address these drawbacks, a novel backtracking search algorithm with reflection mutation based on sine cosine is proposed, named RSCBSA. The best individual found so far is employed to improve convergence speed, while sine and cosine math models are introduced to enhance population diversity. To sufficiently use the information in the historical population and current population, four individuals are selected from the historical or current population randomly to construct an unit simplex, and the center of the unit simplex can enhance exploitation ability of RSCBSA. Comprehensive experimental results and analyses show that RSCBSA is competitive enough with other state-of-the-art meta-heuristic algorithms.
1. Introduction
There are many global optimization problems in the real world. These problems are characterized by complexity, multimodality, strong-nonlinearity, dynamic change, and non-differentiality. The traditional optimization algorithms do not show satisfactory performance on such optimization problems. Therefore, many scholars have begun developing new methods to effectively solve the optimization problems. Evolutionary algorithms (EA), which are a kind of population-based global optimization algorithm, have been widely used to solve such problems, like function optimization [1,2,3], combinatorial optimization [4], neural network training [5,6], and image processing [7]. At present, many EAs have been proposed, like Genetic Algorithm (GA) [8], Particle Swarm Optimization (PSO) [9], Differential Evolution (DE) [10], Artificial Bee Colony algorithm (ABC) [1], Grey Wolf Optimizer (GWO) [11], Whale Optimization Algorithm (WOA) [12] and Cultural Algorithms [13].
Backtracking search algorithm (BSA) is a new population-based heuristic method proposed by Civicioglu for solving real-valued numerical optimization problems [14]. BSA has a simple structure and only one control parameter needs to be set, and its performance is insensitive to the initial value of the control parameter [15,16]. BSA uses a historical population which records individuals of the previous generation as the search direction matrix. Due to the historical population, BSA can simultaneously use the current population and previous population to improve the diversity of the population. Meanwhile, BSA owns a mutation operator with strong randomness and double crossover mechanism with probability, which leads to its strong global search ability. Hence, BSA is researched widely by many scholars and many variants are proposed. These variants can be divided roughly into four categories. The first category focuses on improving its initialization. Kolawol et al. [17] proposed chaotic-based BSA, in which random generation of the initial population is replaced with chaotic mapping to enhance the disorder of the initial population. To adequately use the search space, Yuan et al. [18] adopted an orthogonal design method rather than random generation. To enhance the diversity of the initial population, Lin [19] and Xu [7] et al. proposed different BSA variants based on opposition learning, in which the initial population and oppositional initial population are produced simultaneously to select the best candidate solution and the jump-out strategy in the opposition learning is added to update population. The main idea of the second category is that crossover and mutation strategy are improved. Zhao et al. [20] proposed an improved BSA algorithm mixing three mutation strategies, to handle the constrained optimization problem. For slow convergence speed at the late stage and poor exploration ability, Wang et al. [21] proposed a BSA variant embedding mutation strategy of DE, which improves convergence speed without adding complexity of the algorithm. Zhao et al. [22] designed an optimal solution-guided BSA, where the algorithm introduces an experience parameter to divide the overall iteration into two stages. At the earlier stage of the iteration, the algorithm adopts the mutation operator of the original BSA, while at the latter of the iteration, the algorithm employs the optimal solution-guided new mutation operator. Tian et al. [23] developed a new mutation strategy, which does not consider the optimal solution-guided information. This algorithm improves mutation operation though decreasing perturbation to strengthen convergence speed of the algorithm. For the drawbacks of slow convergence speed and falling into local optimum, Wang et al. [24] proposed an improved BSA fusing optimal solution-guided mutation strategy and niche technology. Chen et al. [25] proposed an ensemble learning, niche technology, mutation perturbation-based hybrid BSA and it is successfully applied to neural network training. The third category is improved parameter-based variants. BSA has a crossover probability parameter and an adaptive mutation control parameter F. In [26], Wang et al. proposed an adaptive parameter F strategy which obeys Maxwell Boltzmann distribution since parameter F value influences the convergence speed of the algorithm. Duan et al. [27] introduced a fitness distance-based adaptive parameter F and with experience parameters to accelerate convergence speed. Nama et al. [28] used a fitness information-based feedback mechanism to design a more available adaptive parameter F which can vary in [0.45, 1.99] with the change of fitness. Meanwhile, randomly varied in [0,1] is designed to improve search efficiency of the algorithm. Chen et al. [29] proposed a new adaptive parameter F with experience parameter, which can adaptively reduce with iteration increase of the algorithm, to effectively balance exploration and exploitation of the BSA. Askarzadeh et al. [30] employed burger chaotic mapping to adjust parameter F, but two experience parameters are introduced into the strategy. Shaheen et al. [31] analyzed five different distributions F to impact algorithm performance and select the best available design of F. The fourth category is with the local search mechanisms embedded. To improve local exploitation of BSA and convergence speed, some search mechanisms are embedded into the framework of BSA. A chaotic mapping-based local search is embedded into BSA and combines with another algorithm to solve the hydrothermal generator set problem. Ali et al. [32] added a random walk guided local exploration strategy into BSA after selection-II of BSA, enhancing exploration performance of the algorithm. To solve the displacement flow shop scheduling problem, Lin et al. [33] proposed three different strategies to improve BSA. A new initial generator is constructed to improve the quality of the initial solution. In addition, the selection mechanism accepting a worse solution in the Simulated Annealing (SA) is employed to avoid trapping in local optimum. A local search mechanism randomly inserted is introduced to enhance exploitation ability of BSA. Moreover, due to its flexibility and efficiency, BSA and its variants have been widely applied to a wide range of real-world optimization problems, such as economic dispatch problems [34], optimal power flow [35], parameter identification [36,37], feature selection [38], artificial neural network [25], flow shop scheduling [39], and nonlinear optimal control problem [40].
However, BSA still has some drawbacks and its performance needs to be further improved. The first is that only the historical population information is adopted to guide the search and the information in current population is not used sufficiently, which cannot maintain the population diversity efficiently and thus the exploration ability of BSA is weak. The second is that there is no guidance regarding the approach to the current best individual during the evolution process, which leads to slow convergence speed and poor exploitation ability of BSA.
Based on the above discussion, in this paper, an enhancing backtracking search optimization algorithm with reflection mutation strategy based on sine cosine, named RSCBSA, is proposed. In RSCBSA, inspired by reflection operation in Nelder–Mead method [41] and Sine Cosine Algorithm (SCA) [42], a new reflection mutation strategy based on sine cosine is developed to address the above-mentioned drawbacks, in which the best solution and sine and cosine math models are introduced to balance exploration and exploitation ability of BSA.
The contributions of the paper are listed as follows:
- A new reflection mutation strategy based on sine cosine is proposed to balance exploration and exploitation ability of BSA. To improve exploration ability, the best global individual is used to guide search direction, while sine and cosine math functions are used to enhance exploitation ability of BSA. Based on the strategy, a novel backtracking search algorithm with reflection mutation strategy based on sine cosine (RSCBSA) is proposed to solve global optimization problems.
- In the above strategy, the center of a unit simplex constructed by three individuals selected randomly is employed to enhance diversity of population, since it considers more information of individuals. In addition, in RSCBSA, crossover operator of BSA is replaced with that of DE.
- A comprehensive experiment is designed to verity the effectiveness of the proposed RSCBSA. In addition, a new parameter in RSCBSA is analyzed to set suitable values so that the performance of RSCBSA is the best.
The rest of this paper is organized as follows. Section 2 reviews the classic BSA. Section 3 presents the detail of RSCBSA, including its constituent RSCBSA variants and its framework. The experimental setting and results are reported and analyzed in Section 4 and Section 5. Finally, Section 6 concludes this paper.
2. Backtracking Search Optimization Algorithm
BSA is a young EA which is designed to be a global optimizer. It employs two populations: current population and historical population to search for the optimal solution. As done in other EAs, BSA has simple structure and can be divided into five processes by its functions: initialization, selection-I, mutation, crossover, and selection-II.
Initialization: In the stage, BSA randomly produces the initial population P using Equation (1).
where and is the number of individuals in population. and D is the number of dimension of variables. and are the lower and upper boundaries on the jth variable, respectively. is a random number within [0,1].
Selection-I: In the BSA’s selection-I stage, the initial historical population is generated randomly using Equation (2).
Afterwards, at the beginning of each iteration, is redefined by Equation (3). In addition, Equation (4) is used to randomly update the order of the members in .
where p is a random number within [0,1]. function is a random shuffling function. Through Equation (3), BSA assigns a population randomly selected previous generation as the historical population and saves the historical population until it is changed.
Mutation and Crossover: Mutation and crossover operators aim at producing a new individual. Equation (5) involving historical population and current population is used to generate a trail individual. Then, crossover operator is performed by Equation (6). From Equation (6), a binary integer-value map is employed to guide the crossover direction.
where F is a scale factor and it generally takes value of , where is a random number between 0 and 1. is the value of the jth variable for the ith trial individual.
Selection-II: In the selection-II stage, BSA adopts a greedy selection mechanism to pick out a new solution . For the minimum problem, if the fitness value of the trial individual V is better than that of the current individual , V is selected, as shown in Equation (7);
In the BSA, four above-mentioned processes 2–5 are repeatedly executed until it meets the termination criteria.
3. The Proposed Algorithm
In this section, the proposed algorithm is described in detail.
3.1. Initialization
The initialization stage is similar to that of the origin BSA. The initial population is produced.
where i is the index of individual in population and j is the number of dimension of variables. is a uniformly distributed random number between 0 and 1. and are the upper and low boundary of each jth variable, respectively.
3.2. Reflection Mutation Strategy Based on Sine Cosine
In the proposed algorithm, reflection mutation strategy based on sine cosine is a key operator. Inspired by Nelder–Mead method and SCA, the strategy is proposed. After the operator, a new trial individual is generated to guide the research direction. It is similar to reflection mutation strategy in [43], but the difference is that sine and cosine math functions are introduced into the proposed strategy. First, four individuals are selected from the current population or historical population randomly to construct a unit simplex. The center of the unit simplex is computed using Equations (9) and (10).
where and c are the index of three different individuals randomly selected from population to construct a unit simplex. and are the weights of three vertexes in the unit simplex. and are three vertexes of the unit simplex. is the center of the unit simplex.
Based on the center, the best individual found so far, and sine cosine are introduced into the strategy to balance exploration and exploitation. The best individual provides the better search direction to improve exploration ability of the algorithm, while sine and cosine math models are used to enhance diversity ability and the center of the unit simplex also provides more diversity information. The formulation of the strategy is listed as follows:
where and are random number in [0, 1]. is a random number in [0, 2]. indicates the jth dimension of the best individual. is the jth dimension of the m individual randomly selected from population. t is the current iteration and is the maximum iteration. a is a perturbation parameter and is usually set to 2.0.
3.3. Crossover Operator
To produce better trial individuals, crossover operator is executed. Like the DE, the crossover operator uses two individuals and to generate offspring individual randomly, where is generated by the above mutation strategy and is current individual. The formula of crossover operator is showed as follows:
where , is in [0,1], l is a random integer in [1, D]. is crossover probability and is usually set to 0.9.
3.4. The Framework of The Proposed Algorithm
Based on above description, the framework of the proposed RSCBSA is similar to that of BSA, but the difference is that mutation and crossover stages are replaced with reflection mutation based on sine cosine and crossover operator. The framework of RSCBSA is presented in Algorithm 1.
| Algorithm 1: Framework of the Proposed Algorithm |
 |
3.5. Complex Analysis of The Proposed Algorithm
The proposed algorithm is based on the basic BSA framework. Five processes in the algorithm are implemented: initialization, selection-I, reflection mutation strategy based on sine cosine, crossover operator, and selection-II, where reflection mutation strategy based on sine cosine and crossover operator are the main steps. In the reflection mutation stage, N new individuals are produced, which leads to time complexity, where N is population size and D is the dimension of test problem. Crossover operator needs time complexity for each individual in the trial population. In brief, the time complexity of the proposed algorithm is .
4. Experimental Simulations
In this section, the experimental simulation is listed. In Section 4.1, benchmark test suit used in the experiment is described. Then, the parameter setting is stated in Section 4.2.
4.1. Benchmark Test Suit
The 23 classical benchmark functions used widely by many researchers are used in the experiment to verify performance of the proposed algorithm. These benchmark functions – can be found in [12]. Typically, these functions can be divided into three categories: (1) unimodal benchmark functions, (2) multimodal benchmark functions and (3) fixed-dimension multimodal functions. – belong to unimodal benchmark functions, whose dimension are set to 30 to test the convergence performance of search algorithms. – are multimodal benchmark functions with several local optimum, whose dimension also are set to 30 to verify the convergence performance and avoidance premature convergence of the proposed algorithm, while the other functions with low-dimension are used to deal with small number of local optima. Their function name, expression, dimension, search range and theoretical optimal value can be found in [12]. All of the algorithms are programmed in “Matlab 2014” and implemented on “Windows 10 64bit” environment on a computer with “Intel Core i5” processor and 8 GB memory.
4.2. Parameter Setting
Common parameters of all considered algorithms are set to same size. The maximum number of generations () is equal to 3000. Population size is set to 30. All algorithms are run 30 times independently. The other parameters used in different algorithm are set as follows:
F in DE: random number in [0.2, 0.8];
in DE and RSCBSA: 0.9;
a in RSCBSA: 2.0;
Personal learning coefficient in PSO: 1.5;
Global learning coefficient in PSO: 2.0;
in ABC: 100;
Acceptance Ratio in CA: 0.35.
5. Experimental Results
In this section, five state-of-the-art algorithms are compared with the proposed algorithm, including DE, PSO, ABC, CA and original BSA, to verify the performance of the proposed algorithm. Statistical results on the three categories test problems are reported in Tables 1, 3, and 5, respectively, in which the best value, mean value, the worst value and standard deviation obtained by the six algorithms are listed. To have statistically sound conclusions, the Friedman test with Bonferroni-Dunn’s procedure is employed to achieve the final ranking of different algorithms on the different type benchmark functions. Moreover, the Wilcoxon’s rank-sum test for independent sample at a 0.05 significance level [44], which is a nonparametric statistical test method, is conducted to judge the significance of the results between two algorithms. Signs “+“, “−“ and “=“ indicate that the corresponding comparative algorithm is worse than, better than, and similar to RSCBSA, respectively. Then, convergence behavior of RSCBSA is analyzed and showed. Finally, parameter a in the reflection mutation based on sine cosine is analyzed by taking different value.
5.1. Compared with State-of-the-Art Algorithms
Unimodal Benchmark Problems (–): From Table 1, it is seen that the proposed algorithm is superior to other algorithms considered on the unimodal benchmark functions. The PSO obtains the best performance on 1 () test function. ABC obtains the best solution on 1 () test function. However, RSCBSA can perform the best than other algorithms except 2 ( and ) test functions. The reason maybe that the best global individual is employed to strength the exploration ability which leads to that the algorithm can explore more promising area to find the better solution. In addition, the Friedman rank is implemented based on KEEL software [45], and the results are reported in Table 2. As shown in Table 2, RSCBSA obtains the best place.

Table 1.
Results of unimodal benchmark functions.

Table 2.
Average Rankings of the algorithms (Friedman) on unimodal benchmark functions.
Multimodal Benchmark Problems (–): Experiment results are listed in Table 3 on the multimodal test functions. From Table 3, DE is superior to other five compared algorithms on the 4 ( and –) benchmark functions. RSCBSA can obtain the best solution on the 3 (–) benchmark functions, but on the other functions it does not perform well. ABC and BSA outperform RSCBSA on the 3 ( and –) benchmark functions and CA cannot beat BSA on the any benchmark functions except . Although RSCBSA can get the best on three benchmark functions, accounting for 50%, RSCBSA only gets the third rank in terms of the Friedman rank, as shown in Table 4. DE performs the best than other peer competitors and gets the first rank.

Table 3.
Results of multimodal benchmark functions.

Table 4.
Average Rankings of the algorithms (Friedman) on multimodal benchmark functions.
Fixed-dimension multimodal benchmark functions (–): For the category of benchmark function, the proposed RSCBSA can obtain the best performance on 7 test functions (, – and –) from Table 5. BSA can perform the best than other competitors on the all test functions. The performance of PSO, DE, CA is inferior to that of the BSA and RSCBSA. From Table 6, it is observed that RSCBSA can rank the second place according to the Friedman rank.

Table 5.
Results of fixed-dimension multimodal benchmark functions.

Table 6.
Average Rankings of the algorithms (Friedman) on fixed multimodal benchmark functions.
To further detect the significant differences between the proposed RSCBSA and the five competitors, the Wilcoxon’s rank-sum test is executed. The statistical results are reported in Table 7. It is seen that RSCBSA outperforms 9, 14, 9, 12 and 17 benchmark functions than BSA, PSO, ABC, DE and CA, respectively.

Table 7.
Test statistical results of Wilcoxon rank-sum test.
In summary, the proposed RSCBSA can exhibit very competitive performance than those of the other well-known algorithms, which is able to generate the high-quality solutions and accelerate the convergence speed.
5.2. Convergence Analysis
To analyze the convergence of the proposed RSCBSA, convergence curves of RSCBSA, PSO, DE, ABC, CA and BSA are shown in Figure 1 as iteration increases. In the Figure 1, X axial represents for the total number of iteration and Y axial stands for the logarithm of the function optimal value. It is observed that RSCBSA tends to extensively explore promising areas of design space and exploit the best one. The convergence curve changes abruptly in the early stages of the optimization process and then gradually converge. According to Berg et al. [46], such a behavior can guarantee that a population-based algorithm eventually convergences to a point in a search space. On the unimodal benchmark function, RSCBSA have an obvious advantage than other competitors. However, although RSCBSA does not perform better than other algorithms on the multimodal benchmark function, RSCBSA and other algorithms can converge the global optimal on the almost multimodal benchmark functions. It can be seen that RSCBSA is enough competitive with other state-of-the-art meta-heuristic algorithms.
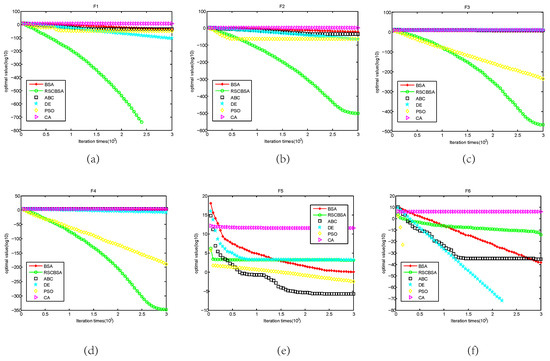
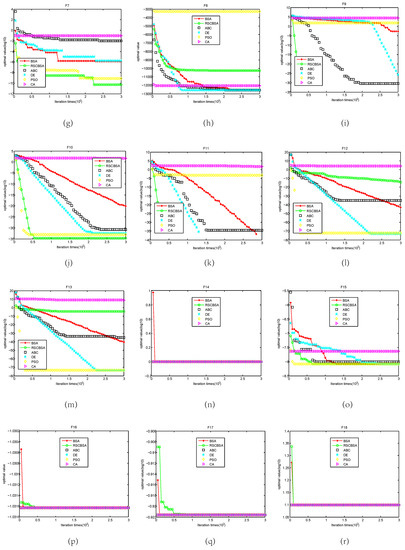
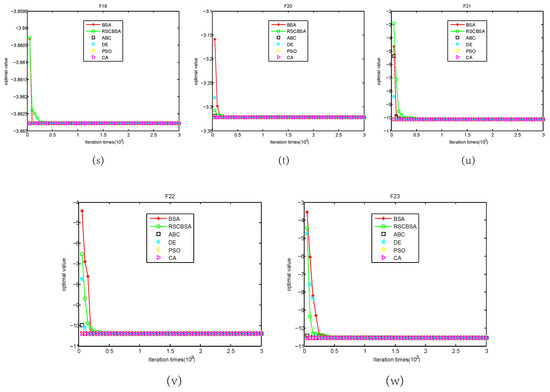
Figure 1.
Convergence figures on test functions F1–F23, where (a–w) indicate the convergence curves
on the functions F1–F23 respectively.
5.3. Parameter Sensitivity Analysis
To investigate the effect of parameter a in the mutation strategy for the proposed algorithm, an experiment is designed. In the experiment, parameter a is set from 1 up to 6 and experiment results are plotted in Figure 2, where X axial represents for the total number of iteration and Y axial stands for the logarithm of the function optimal value. As shown in Figure 2, the performance of the proposed RSCBSA leads to the optimal on the almost test functions when parameter a is set to 2.0.
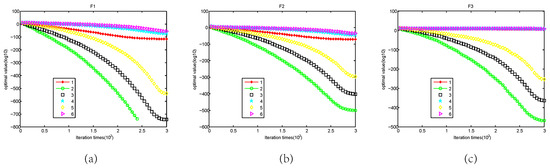
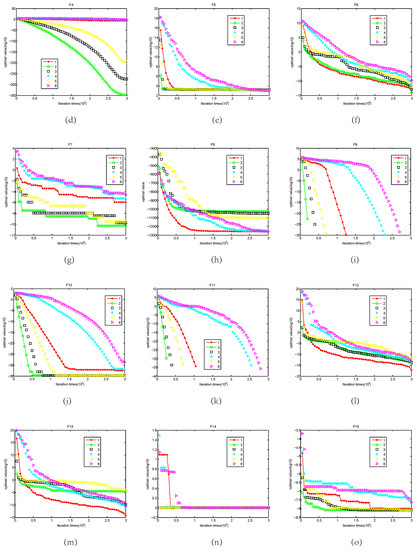
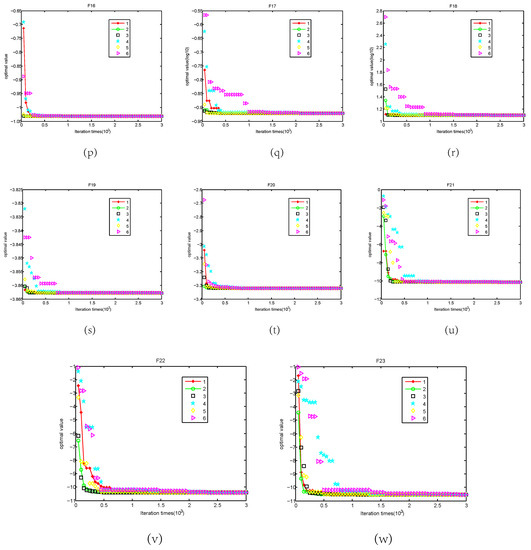
Figure 2.
Convergence curves on test functions F1–F23 for different a values, where (a–w) indicate the convergence curves on the functions F1–F23 respectively.
5.4. Runtime Analysis
To present execution times, RSCBSA, PSO and DE are selected to run 20 times individually and record their runtimes. The average time is computed and showed in the Figure 3. From Figure 3, it is seen that RSCBSA obtains the best execution speed on the five benchmark problems, while DE and PSO rank the second and third place, respectively.
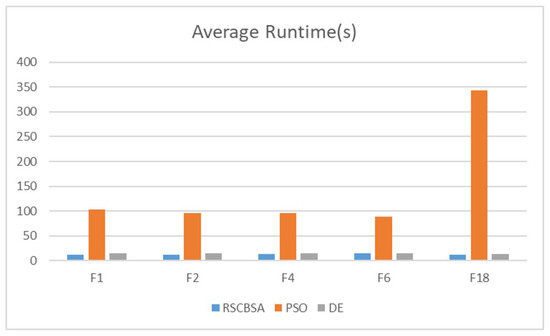
Figure 3.
Runtime(s) of the three algorithms on five test problems.
5.5. Remarks
Based on the above results, some insights can be summarized: (1) RSCBSA can obtain the best performance on the almost unimodal benchmark functions, since in the reflection mutation strategy based on sine cosine, the best individual found so far is employed to improve the exploration ability of the algorithm. In addition, sine cosine math models are introduced to enhance diversity. However, RSCBSA perform badly on the multimodal test function. The reason may be that the crossover operator is weak for enhancing diversity of population. (2) CA is the worst among the six algorithms, but CA can perform the best on the fixed-dimension multimodal benchmark functions from Figure 1, due to strong performance of jump-out local optimal. (3) DE has obvious advantages on the multimodal test functions.
6. Conclusions
This study presented a new backtracking search algorithm, in which a novel reflection mutation strategy based on sine cosine is proposed to balance exploration and exploitation ability of BSA. The proposed algorithm (called RSCBSA) replaces mutation strategy with the proposed reflection mutation strategy based on sine cosine. In the strategy, the best individual found so far is employed to improve convergence speed, while sine cosine and the center of a unit simplex constructed by three individuals selected from population or historical population are used to enhance exploitation ability. Reflection mutation is similar to that in the Nelder–Mead method. To enhance a new trail individual produced by mutation strategy, crossover operator of BSA is replaced with that of DE. In addition, selection-II stage is saved to avoid the loss of the best individual. To verify the performance of RSCBSA, a comprehensive experiment is designed. Experimental results show that the proposed RSCBSA can obtain the best performance on the almost benchmark functions.
In the future, some work should be done to further improve performance of the algorithm. A parameter adaptation strategy can be designed to enhance search ability of RSCBSA. RSCBSA can be tested on some more difficult functions [47,48], to improve the effectiveness of their algorithm. RSCBSA can be extended to discrete/combinatorial spaces using some algebraic-based strategies [49,50,51]. In addition, several other well-studied evolutionary algorithms (EAs), i.e., CMA-ES [52] and WOA [12] can be combined so that the resultant algorithms can effectively complement one another.
Author Contributions
Conceptualization, C.Z. (Chong Zhou) and S.L.; methodology, C.Z. (Chong Zhou); software, S.L.; data curation, S.L. and Y.Z.; writing–original draft preparation, C.Z. (Chong Zhou); writing–review and editing, C.Z. (Cuijun Zhang); project administration, C.Z. (Chong Zhou); funding acquisition, C.Z. (Chong Zhou); resources, Zhikun Chen; computing resources and other analysis tools, C.Z. (Chong Zhou).
Funding
This research was partially funded by Natural Science Youth Foundation of Hebei Province under Grant No. F2019403207, the High-Level Talents Research Projects of Beibu Gulf University under Grant No.2019KYQD27 and Research Fund for the Doctoral Startup Program of Hebei GEO University.
Acknowledgments
The authors thank the anonymous reviewers for their constructive comments. Chong Zhou, Shengjie Li and Cuijun Zhang are equivalent contribution authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Pan, Q.K.; Sang, H.Y.; Duan, J.H.; Gao, L. An improved fruit fly optimization algorithm for continuous function optimization problems. Knowl. Based Syst. 2014, 62, 69–83. [Google Scholar] [CrossRef]
- Soleimanpour-Moghadam, M.; Nezamabadi-Pour, H.; Farsangi, M.M. A quantum inspired gravitational search algorithm for numerical function optimization. Inf. Sci. 2014, 267, 83–100. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Hamzadayi, A.; Köse, S.Y. Testing the performance of teaching–learning based optimization (TLBO) algorithm on combinatorial problems: Flow shop and job shop scheduling cases. Inf. Sci. 2014, 276, 204–218. [Google Scholar] [CrossRef]
- Yaghini, M.; Khoshraftar, M.M.; Fallahi, M. A hybrid algorithm for artificial neural network training. Eng. Appl. Artif. Intell. 2013, 26, 293–301. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Xu, L.; Jia, H.; Lang, C.; Peng, X.; Sun, K. A novel method for multilevel color image segmentation based on dragonfly algorithm and differential evolution. IEEE Access 2019, 7, 19502–19538. [Google Scholar] [CrossRef]
- Goldberg, D. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Reynolds, R.G. An introduction to cultural algorithms. In Evolutionary Programming—Proceedings of the Third Annual Conference; World Scientific: Singapore, 1994; pp. 131–139. [Google Scholar]
- Civicioglu, P. Backtracking search optimization algorithm for numerical optimization problems. Appl. Math. Comput. 2013, 219, 8121–8144. [Google Scholar] [CrossRef]
- Madasu, S.D.; Kumar, M.S.; Singh, A.K. Comparable investigation of backtracking search algorithm in automatic generation control for two area reheat interconnected thermal power system. Appl. Soft Comput. 2017, 55, 197–210. [Google Scholar] [CrossRef]
- Islam, N.N.; Hannan, M.; Shareef, H.; Mohamed, A. An application of backtracking search algorithm in designing power system stabilizers for large multi-machine system. Neurocomputing 2017, 237, 175–184. [Google Scholar] [CrossRef]
- Kolawole, S.O.; Duan, H. Backtracking search algorithm for non-aligned thrust optimization for satellite formation. In Proceedings of the 11th IEEE International Conference on Control & Automation (ICCA), Taichung, Taiwan, 18–20 June 2014; pp. 738–743. [Google Scholar]
- Yuan, X.; Wu, X.; Tian, H.; Yuan, Y.; Adnan, R.M. Parameter identification of nonlinear Muskingum model with backtracking search algorithm. Water Resour. Manag. 2016, 30, 2767–2783. [Google Scholar] [CrossRef]
- Lin, J. Oppositional backtracking search optimization algorithm for parameter identification of hyperchaotic systems. Nonlinear Dyn. 2015, 80, 209–219. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Yin, Y.; Wang, B.; Yi, W.; Yin, Y. An improved backtracking search algorithm for constrained optimization problems. In International Conference on Knowledge Science; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Wang, L.; Zhong, Y.; Yin, Y.; Zhao, W.; Wang, B.; Xu, Y. A hybrid backtracking search optimization algorithm with differential evolution. Math. Probl. Eng. 2015, 2015, 1–16. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Wang, B.; Yin, Y. Best guided backtracking search algorithm for numerical optimization problems. In Knowledge Science, Engineering and Management; Lehner, F., Fteimi, N., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 414–425. [Google Scholar]
- Tian, K. Effective self-learning backtracking search optimization algorithm. Electron. Sci. Tech. 2015, 28, 41. [Google Scholar]
- Wang, P.; Chen, D.; Zou, F.; Li, Z. Guidance and niching backtracking search optimization algorithm. CEA 2017, 53, 126–131. [Google Scholar]
- Chen, D.; Lu, R.; Feng, Z.; Li, S.; Peng, W. A learning and niching based backtracking search optimisation algorithm and its applications in global optimisation and ANN training. Neurocomputing 2017, 266, 579–594. [Google Scholar] [CrossRef]
- Wang, X.; Liu, S.; Tian, W. Improved backtracking search optimization algorithm with new effective mutation scale factor and greedy crossover strategy. J. Comput. Appl. 2014, 34, 2543. [Google Scholar]
- Duan, H.; Luo, Q. Adaptive backtracking search algorithm for induction magnetometer optimization. IEEE Trans. Magn. 2014, 50, 1–6. [Google Scholar] [CrossRef]
- Nama, S.; Saha, A.K.; Ghosh, S. Improved backtracking search algorithm for pseudo dynamic active earth pressure on retaining wall supporting c-Φ backfill. Appl. Soft Comput. 2016, 52, 885–897. [Google Scholar] [CrossRef]
- Chen, X.; Liu, S.; Wang, Y. Emergency resources scheduling based on improved backtracking search optimization algorithm. Comput. Appl. Softw. 2015, 32, 235–238. [Google Scholar]
- Askarzadeh, A.; Coelho, L.D.S. A backtracking search algorithm combined with Burger’s chaotic map for parameter estimation of PEMFC electrochemical model. Int. J. Hydrog. Energy 2014, 39, 11165–11174. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Farrag, S.M. Integrated strategies of backtracking search optimizer for solving reactive power dispatch problem. IEEE Syst. J. 2016, PP, 1–10. [Google Scholar] [CrossRef]
- Ali, A.F. A memetic backtracking search optimization algorithm for economic dispatch problem. Egypt. Comput. Sci. J. 2015, 39, 56–71. [Google Scholar]
- Lin, Q.; Liang, G.; Li, X.; Zhang, C. A hybrid backtracking search algorithm for permutation flow-shop scheduling problem. Comput. Ind. Eng. 2015, 85, 437–446. [Google Scholar] [CrossRef]
- Modiri-Delshad, M.; Kaboli, S.H.A.; Taslimi-Renani, E.; Rahim, N.A. Backtracking search algorithm for solving economic dispatch problems with valve-point effects and multiple fuel options. Energy 2016, 116, 637–649. [Google Scholar] [CrossRef]
- Ayan, K.; Kilic, U. Optimal power flow of two-terminal HVDC systems using backtracking search algorithm. Int. J. Electr. Power Energy Syst. 2016, 78, 326–335. [Google Scholar] [CrossRef]
- Ahandani, M.A.; Ghiasi, A.R.; Kharrati, H. Parameter identification of chaotic systems using a shuffled backtracking search optimization algorithm. Soft Comput. 2017, 1–23. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.; Qu, B.Y.; Zhiping, C.; Heshan, W. Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models. Appl. Energy 2018, 226, 408–422. [Google Scholar] [CrossRef]
- Chu, Z.; Zhou, J.; Li, C.; Fu, W.; Tian, P. A compound structure of ELM based on feature selection and parameter optimization using hybrid backtracking search algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 143, 360–376. [Google Scholar]
- Lin, J.; Wang, Z.J.; Li, X. A backtracking search hyper-heuristic for the distributed assembly flow-shop scheduling problem. Swarm Evol. Comput. 2017, 36, S2210650216305028. [Google Scholar] [CrossRef]
- Su, Z.; Wang, H.; Peng, Y. A hybrid backtracking search optimization algorithm for nonlinear optimal control problems with complex dynamic constraints. Neurocomputing 2016, 186, 182–194. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Qian, W.; Chai, J.; Zhang, Z. Adaptive differential evolution algorithm based on reflective mutation strategy. Comput. Eng. Appl. 2018, 54, 166–173. [Google Scholar]
- Derrac, J.; Garcia, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Introduction to KEEL Software Suite. Available online: https://sci2s.ugr.es/keel/development.php (accessed on 26 October 2019).
- Bergh, F.V.D.; Engelbrecht, A.P. A study of particle swarm optimization particle trajectories. Inf. Sci. 2006, 176, 937–971. [Google Scholar]
- García-Martínez, C.; Gutiérrez, P.D.; Molina, D.; Lozano, M.; Herrera, F. Since CEC 2005 competition on real-parameter optimisation: a decade of research, progress and comparative analysis’s weakness. Soft Comput. 2017, 21, 1–11. [Google Scholar] [CrossRef]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.-P.; Auger, A.; Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization; Technical Report; Nanyang Technological University: Singapore, 2005. [Google Scholar]
- Baioletti, M.; Milani, A.; Santucci, V. Automatic Algebraic Evolutionary Algorithms; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Baioletti, M.; Milani, A.; Santucci, V. Algebraic Particle Swarm Optimization for the permutations search space. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), San Sebastian, Spain, 5–8 June 2017. [Google Scholar]
- He, Y.; Wang, X. Group theory-based optimization algorithm for solving knapsack problems. Knowl. Based Syst. 2018. [Google Scholar] [CrossRef]
- Hansen, N. Covariance matrix adaptation evolution strategy. In Proceedings of the 10th International Conference on Parallel Problem Solving from Nature, Dortmund, Germany, 13–17 September 2008; Springer: Cham, Switzerland, 2008. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).