(Hyper)Graph Embedding and Classification via Simplicial Complexes
Abstract
1. Introduction
- feature generation and feature engineering, where numerical features are ad-hoc extracted from the input patterns
- embedding via information granulation.
2. Information Granulation and Classification Systems
2.1. An Introduction to Simplicial Complexes
- Čech complex:
- for each subset of points, form an -ball (A ball with radius ) centred at each point in S, and include S as a simplex if there is a common point contained in all of the balls created so far.
- Alpha complex:
- for each point , evaluate its Voronoi region (i.e., the set of points closest to it). The set of Voronoi regions forms the widely-known Voronoi diagram and the nerve of the latter is usually referred to as Delaunay complex. By considering an -ball around each point , it is possible to intersect said ball with , leading to a restricted Voronoi region and the nerve of the set of restricted Voronoi regions for all points in is the Alpha complex.
- Vietoris-Rips complex:
- for each subset of points, check whether all of their pairwise distances are below . If so, S is a valid simplex to be included in the Vietoris-Rips complex.
- build the Vietoris-Rips neighbourhood graph where is the set of vertices and is the set of edges, hence and if for any two nodes with
- evaluate all maximal cliques in .
- Clique complex:
- for a given underlying graph , the Clique complex is the simplicial complex formed by the set of vertices of its (maximal) cliques. In other words, a clique of k vertices is represented by a simplex of order .
2.2. Proposed Approach
2.2.1. Embedding
- the match between two simplices (possibly belonging to different simplicial complexes) can be done in an exact manner: two simplices are equal if they have the same order and they share the same set of node labels
- simplicial complexes become multi-sets: two simplices (also within the same simplicial complex) can have the same order and can share the same set of node labels
- the enumeration of different (unique) simplices is straightforward.
2.2.2. Classification
- there is no guarantee that all symbols in are indeed useful for the classification problem at hand
- as introduced in Section 1, it is preferable to have a small, yet informative, alphabet in order to eventually ease an a-posteriori knowledge discovery phase (less symbols to be analysed by field-experts).
- trains the -SVM with regularisation parameter
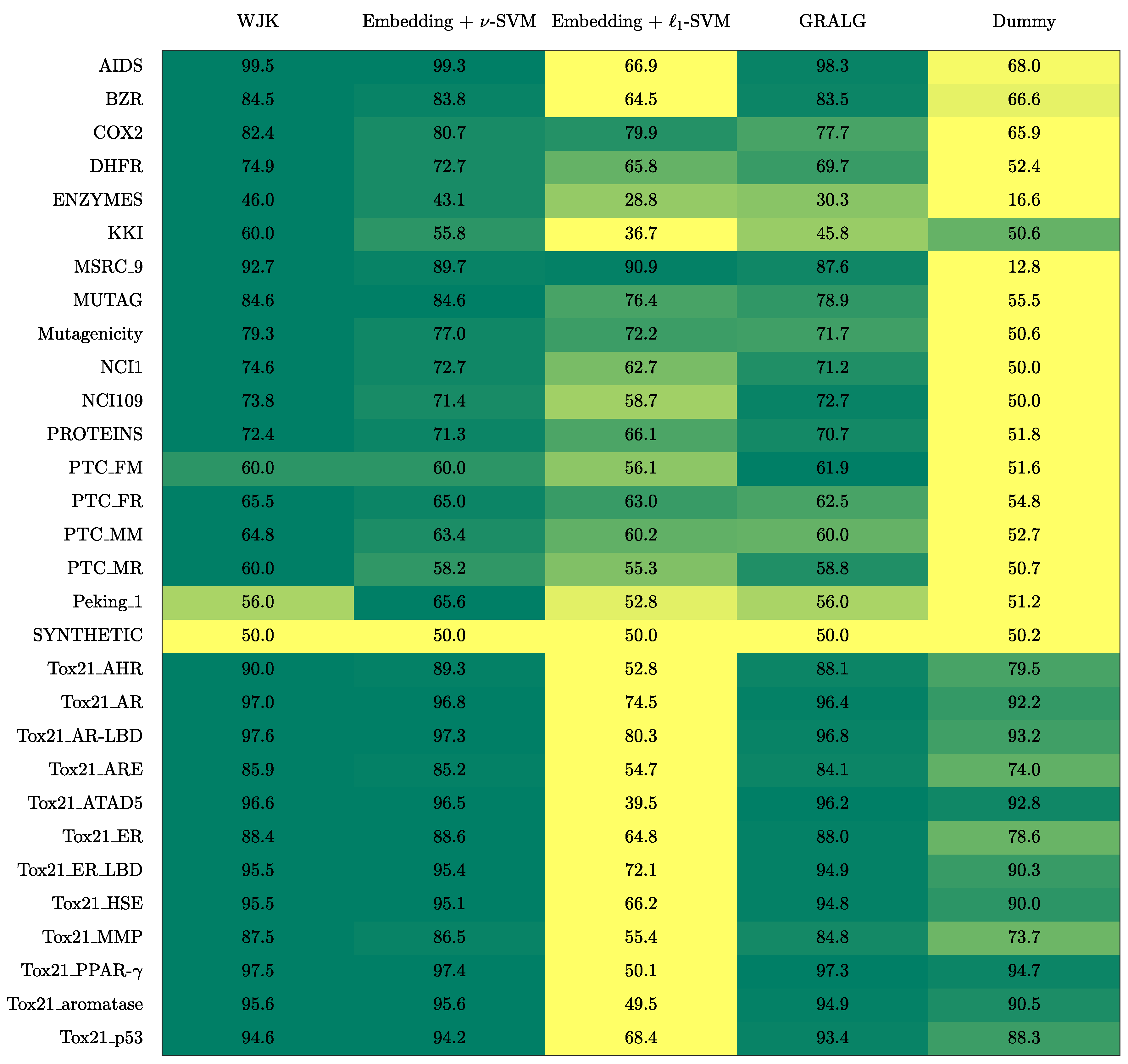
3. Results
3.1. On Benchmark Data
- The Weighted Jaccard Kernel. Originally proposed in Ref. [78], the Weighted Jaccard Kernel (WJK) is an hypergraph kernel working on the top of the simplicial complexes from the underlying graphs. As a proper kernel function, WJK performs an implicit embedding procedure towards a possibly infinite-dimensional Hilbert space. In synthesis, the WJK between two simplicial complexes, say and , is evaluated as follows: after considering the ’simplices-of-node-labels’ rather than the ’simplices-of-nodes’ as described in Section 2.2.1, the set of unique simplices belonging to either or is considered. Then, and are transformed in two vectors, say and , by counting the occurrences of simplices in the unique set within the two simplicial complexes. Finally, . The kernel matrix obtained by evaluating the pairwise weighted Jaccard similarity between any two pairs of simplicial complexes in the available dataset is finally fed to a -SVM.
- GRALG. Originally proposed in Ref. [43] and later used in Refs. [44,79] for image classification, GRALG is a Granular Computing-based classification system for graphs. Despite the fact that it considers network motifs rather than simplices, it is still based on the same embedding procedure by means of symbolic histograms. In synthesis, GRALG extracts network motifs from the training data and runs a clustering procedure on such subgraphs by using a graph edit distance as the core (dis)similarity measure. The medoids (MinSODs [39,40,41,42]) of these clusters form the alphabet on top of which the embedding space is built. Two genetic algorithms take care of tuning the alphabet synthesis and the feature selection procedure, respectively. GRALG, however, suffers from an heavy computational burden which may become unfeasible for large datasets. In order to overcome this problem, the random walk-based variant proposed in Ref. [80] has been used.
3.2. On Real-world Proteomic Data
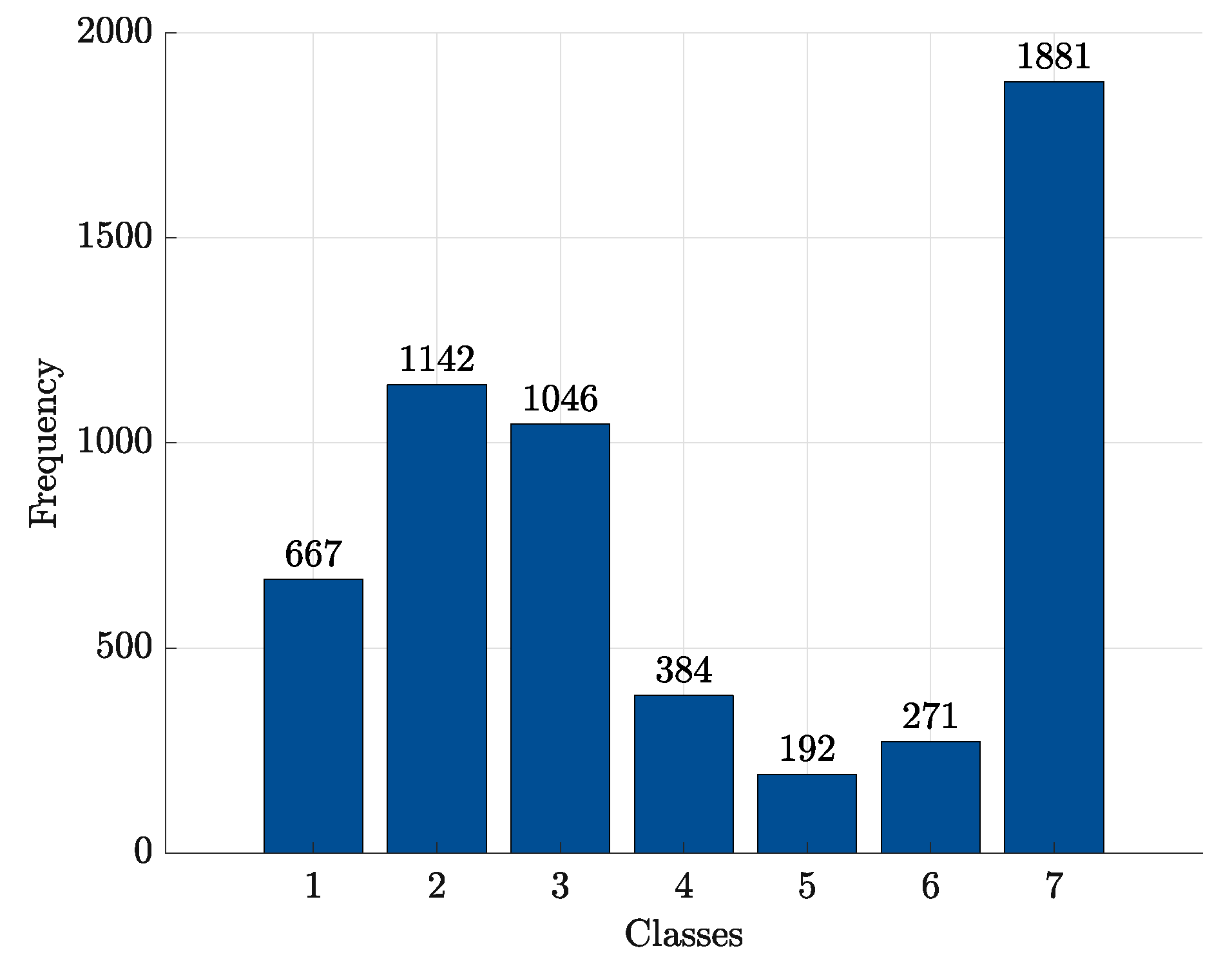
3.2.1. Experiment #1: Protein Function Classification
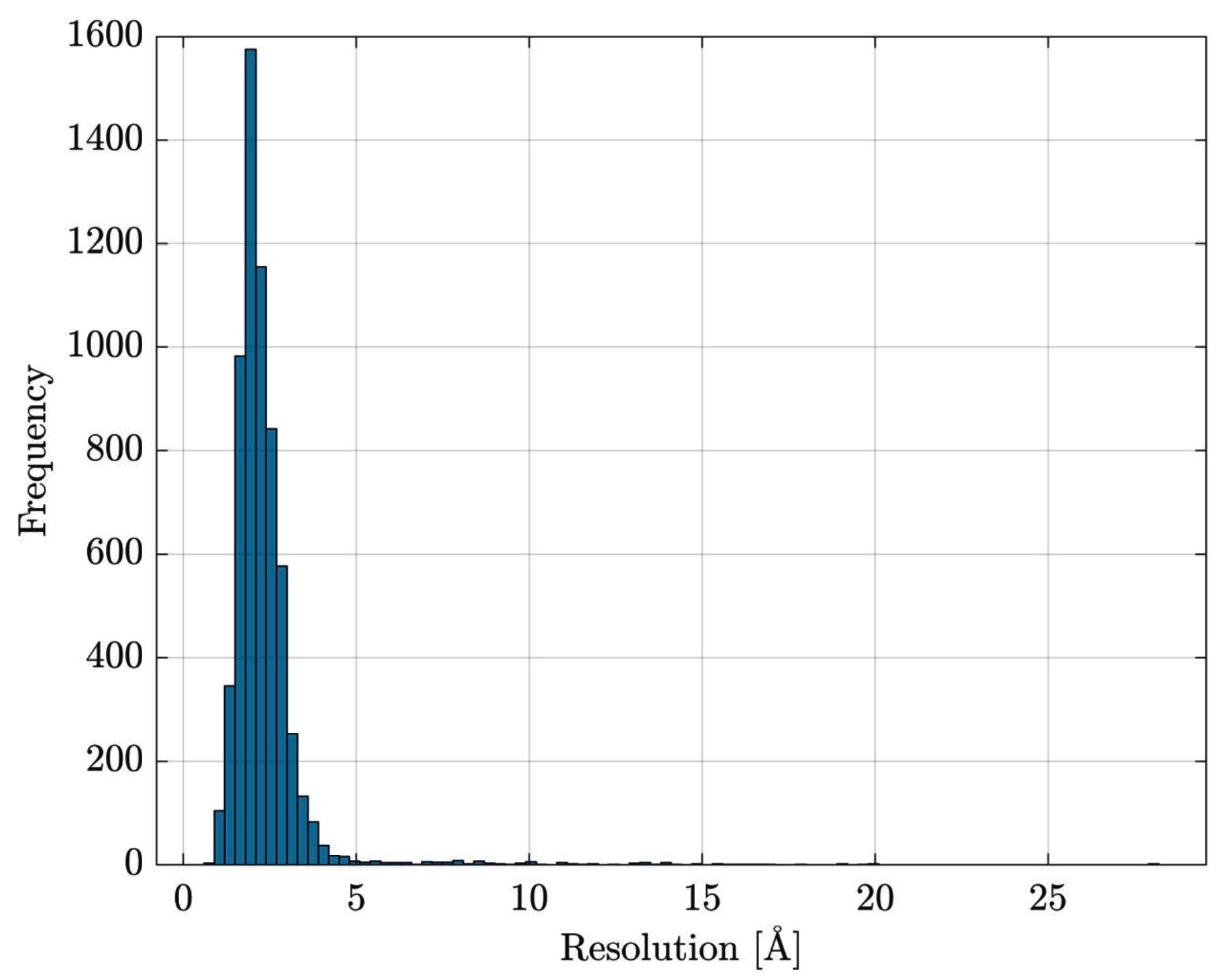
Data Retrieval and Preprocessing
- the entire Escherichia coli (str. K12) list of proteins has been retrieved from UniProt [84]
- the list has been cross-checked with Protein Data Bank [85] in order to download PDB files for resolved proteins
- proteins with multiple EC numbers have been discarded
- in PDB files containing multiple structure models, only the first model is retained; similarly, for atoms having alternate coordinate locations, only the first location is retained.
Computational Results
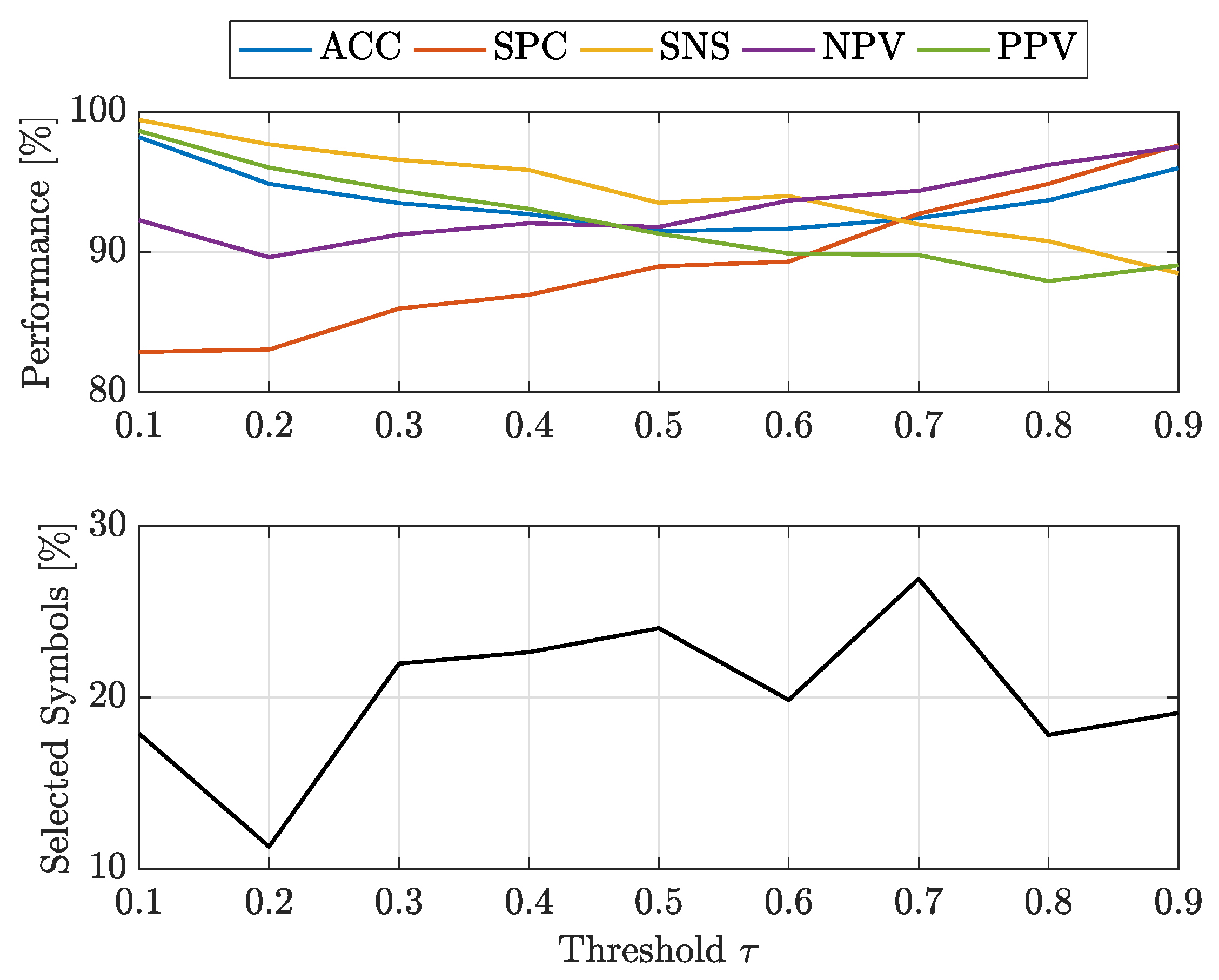
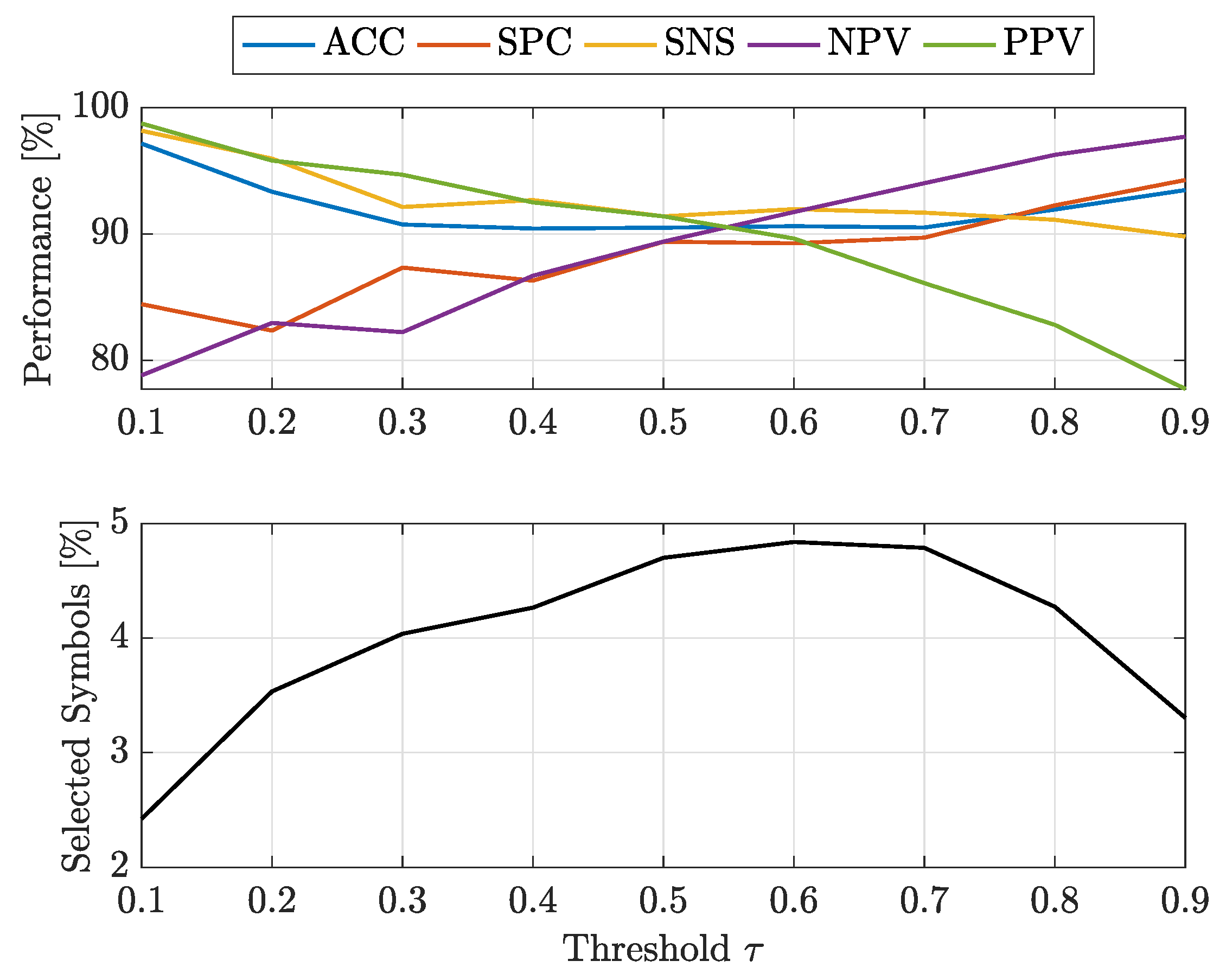
- at : -SVMs outperform the kernelised counterpart in terms of SNS (all classes) and NPV (all classes), whereas -SVMs outperform the former in terms of SPC (all classes) and PPV (all classes). The overall ACC sees -SVMs outperforming -SVMs only for class 7, the two classifiers perform equally for classes 2 and 4 and for the remaining classes -SVMs perform better. Regardless of which performs the best in an absolute manner, the performance shifts are rather small as far as ACC, SPC and NPV are concerned ( or less), whereas interesting shifts include SNS (-SVMs outperforming by on class 4) and PPV (-SVMs outperforming by on class 3 and on class 5);
- at : -SVMs outperform the kernelised counterpart in terms of SNS (all classes) and NPV (all classes), whereas -SVMs outperform the former in terms of SPC (all classes), PPV (all classes) and ACC (all classes). While the performance shifts are rather small for ACC (≈1–2%) and SPC (), there are remarkable shifts regarding PPV (-SVMs outperform up to for class 5) and SNS (-SVMs outperform up to for class 4).
- at : -SVMs select fewer symbols with respect to -SVMs only for classes 1 and 7
- at : -SVMs outperform -SVMs for all classes.
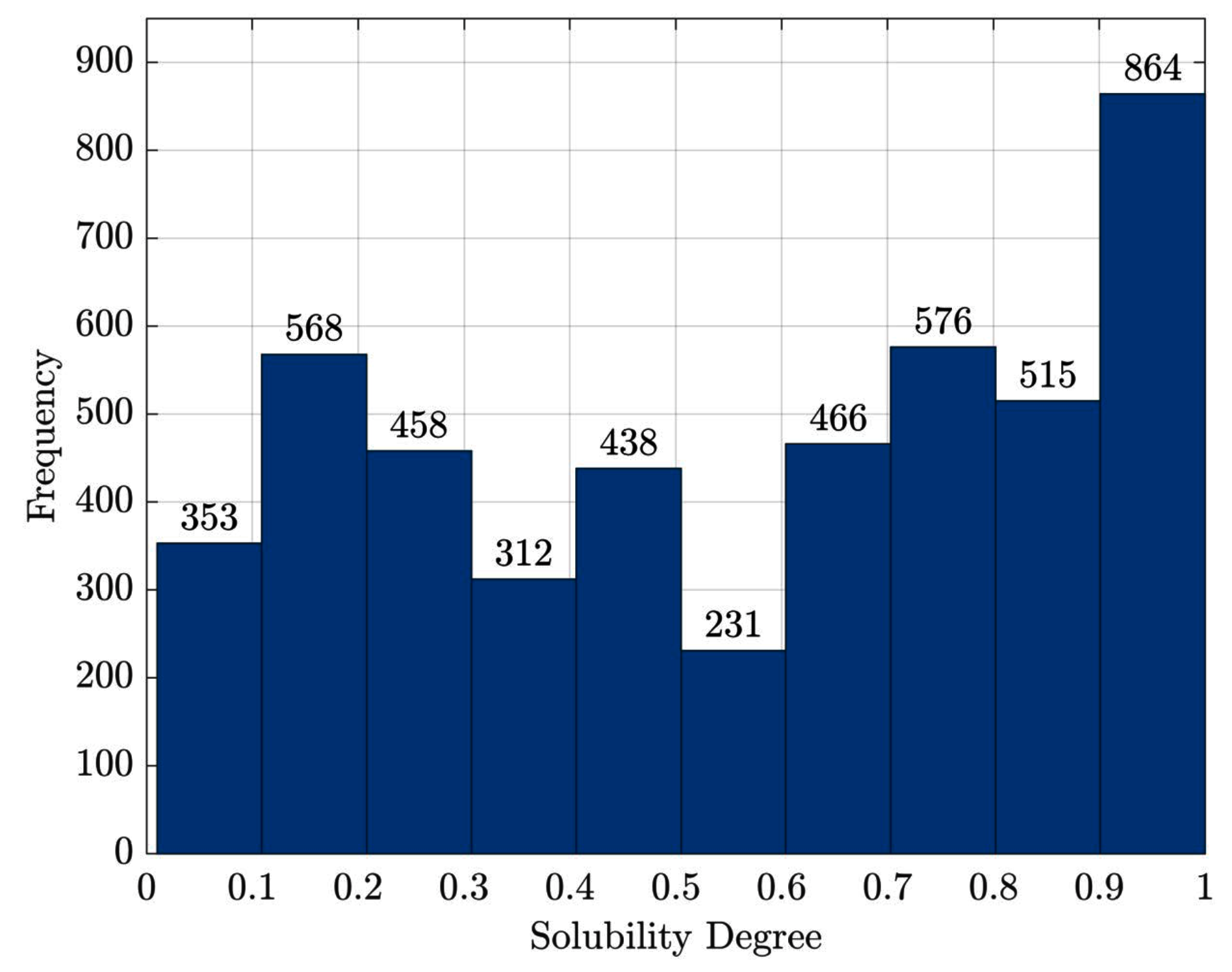
3.2.2. Experiment #2: Protein Solubility Classification
Data Retrieval and Preprocessing
- from the eSOL database (eSOL database http://tp-esol.genes.nig.ac.jp/)) developed in the Targeted Proteins Research Project., containing the solubility degree (in percentage) for the E. coli proteins using the chaperone-free PURE system [87], the entire dump has been collected
- proteins with no information about their solubility degree have been discarded
- in order to enlarge the number of samples (From the entire dump, only 432 proteins had their corresponding PDB ID.), we reversed the JW-to-PDB relation by downloading all structure files (if any) related to each JW entry from eSOL. Each structure will inherit the solubility degree from the JW entry
- inconsistent data (e.g., the same PDB with different solubility values) have been discarded; duplicates have been removed in case of redundant data (e.g., one solubility per PDB but multiple JWs)
- proteins that have a solubility degree greater than have been set as . The (small) deviations from can be ascribed to minor experimental errors. After straightforward normalisation, the solubility degree can be considered a real-valued number in range .
Computational Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ACC | Accuracy |
| EC | Enzyme Commission |
| NPV | Negative Predictive Value |
| PCN | Protein Contact Network |
| PDB | Protein Data Bank |
| PPV | Positive Predictive Value |
| SNS | Sensitivity |
| SPC | Specificity |
| SVM | Support Vector Machine |
References
- Giuliani, A.; Filippi, S.; Bertolaso, M. Why network approach can promote a new way of thinking in biology. Front. Genet. 2014, 5, 83. [Google Scholar] [CrossRef] [PubMed]
- Di Paola, L.; De Ruvo, M.; Paci, P.; Santoni, D.; Giuliani, A. Protein contact networks: An emerging paradigm in chemistry. Chem. Rev. 2012, 113, 1598–1613. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, A.; Zbilut, J.P.; Tomita, M.; Giuliani, A. Proteins as networks: Usefulness of graph theory in protein science. Curr. Protein Pept. Sci. 2008, 9, 28–38. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.; Tombor, B.; Albert, R.; Oltvai, Z.N.; Barabási, A.L. The large-scale organization of metabolic networks. Nature 2000, 407, 651. [Google Scholar] [CrossRef]
- Di Paola, L.; Giuliani, A. Protein–Protein Interactions: The Structural Foundation of Life Complexity. In Encyclopedia of Life Sciences (eLS); John Wiley & Sons: Chichester, UK, 2017; pp. 1–12. [Google Scholar] [CrossRef]
- Wuchty, S. Scale-Free Behavior in Protein Domain Networks. Mol. Biol. Evol. 2001, 18, 1694–1702. [Google Scholar] [CrossRef]
- Davidson, E.H.; Rast, J.P.; Oliveri, P.; Ransick, A.; Calestani, C.; Yuh, C.H.; Minokawa, T.; Amore, G.; Hinman, V.; Arenas-Mena, C.; et al. A Genomic Regulatory Network for Development. Science 2002, 295, 1669–1678. [Google Scholar] [CrossRef]
- Gasteiger, J.; Engel, T. Chemoinformatics: A Textbook; John Wiley & Sons: Haboken, NJ, USA, 2006. [Google Scholar]
- Wasserman, S.; Faust, K. Social Network Analysis: Methods and Applications; Cambridge University Press: New York, NJ, USA, 1994. [Google Scholar]
- Deutsch, A.; Fernandez, M.; Florescu, D.; Levy, A.; Suciu, D. A query language for XML. Comput. Netw. 1999, 31, 1155–1169. [Google Scholar] [CrossRef]
- Weis, M.; Naumann, F. Detecting Duplicates in Complex XML Data. In Proceedings of the 22nd International Conference on Data Engineering (ICDE’06), Atlanta, GA, USA, 3–7 April 2006; p. 109. [Google Scholar] [CrossRef]
- Collins, M.; Duffy, N. Convolution Kernels for Natural Language. In Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic (NIPS’01), Vancouver, BC, Canada, 3–8 December 2001; MIT Press: Cambridge, MA, USA, 2001; pp. 625–632. [Google Scholar]
- Das, N.; Ghosh, S.; Gonçalves, T.; Quaresma, P. Comparison of Different Graph Distance Metrics for Semantic Text Based Classification. Polibits 2014, 51–58. [Google Scholar] [CrossRef]
- Das, N.; Ghosh, S.; Gonçalves, T.; Quaresma, P. Using Graphs and Semantic Information to Improve Text Classifiers. In Advances in Natural Language Processing; Przepiórkowski, A., Ogrodniczuk, M., Eds.; Springer: Cham, Switzerland, 2014; pp. 324–336. [Google Scholar] [CrossRef]
- Livi, L.; Rizzi, A.; Sadeghian, A. Granular modeling and computing approaches for intelligent analysis of non-geometric data. Appl. Soft Comput. 2015, 27, 567–574. [Google Scholar] [CrossRef]
- Livi, L.; Sadeghian, A. Granular computing, computational intelligence, and the analysis of non-geometric input spaces. Granul. Comput. 2016, 1, 13–20. [Google Scholar] [CrossRef]
- Martino, A.; Giuliani, A.; Rizzi, A. Granular Computing Techniques for Bioinformatics Pattern Recognition Problems in Non-metric Spaces. In Computational Intelligence for Pattern Recognition; Pedrycz, W., Chen, S.M., Eds.; Springer: Cham, Switzerland, 2018; pp. 53–81. [Google Scholar] [CrossRef]
- Pękalska, E.; Duin, R.P. The Dissimilarity Representation for Pattern Recognition: Foundations and Applications; World Scientific: Singapore, 2005. [Google Scholar] [CrossRef]
- Livi, L.; Rizzi, A. Graph ambiguity. Fuzzy Sets Syst. 2013, 221, 24–47. [Google Scholar] [CrossRef]
- Livi, L.; Rizzi, A. The graph matching problem. Pattern Anal. Appl. 2013, 16, 253–283. [Google Scholar] [CrossRef]
- Neuhaus, M.; Bunke, H. Bridging the Gap between Graph Edit Distance and Kernel Machines; World Scientific: Singapore, 2007. [Google Scholar] [CrossRef]
- Cinti, A.; Bianchi, F.M.; Martino, A.; Rizzi, A. A Novel Algorithm for Online Inexact String Matching and its FPGA Implementation. Cognit. Comput. 2019. [Google Scholar] [CrossRef]
- Pękalska, E.; Duin, R.P.; Paclík, P. Prototype selection for dissimilarity-based classifiers. Pattern Recognit. 2006, 39, 189–208. [Google Scholar] [CrossRef]
- Livi, L.; Rizzi, A.; Sadeghian, A. Optimized dissimilarity space embedding for labeled graphs. Inf. Sci. 2014, 266, 47–64. [Google Scholar] [CrossRef]
- De Santis, E.; Martino, A.; Rizzi, A.; Frattale Mascioli, F.M. Dissimilarity Space Representations and Automatic Feature Selection for Protein Function Prediction. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Martino, A.; De Santis, E.; Giuliani, A.; Rizzi, A. Modelling and Recognition of Protein Contact Networks by Multiple Kernel Learning and Dissimilarity Representations. Inf. Sci. 2019. Under Review. [Google Scholar]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Massachusetts, MA, USA, 2002. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, MA, USA, 2000. [Google Scholar] [CrossRef]
- Mercer, J. Functions of positive and negative type, and their connection with the theory of integral equations. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1909, 209, 415–446. [Google Scholar] [CrossRef]
- Cover, T.M. Geometrical and statistical properties of systems of linear inequalities with applications in pattern recognition. IEEE Trans. Electron. Comput. 1965, 326–334. [Google Scholar] [CrossRef]
- Li, J.B.; Chu, S.C.; Pan, J.S. Kernel Learning Algorithms for Face Recognition; Springer: New York, NY, USA, 2014. [Google Scholar]
- Bargiela, A.; Pedrycz, W. Granular Computing: An Introduction; Kluwer Academic Publishers: Boston, MA, USA, 2003. [Google Scholar]
- Pedrycz, W.; Skowron, A.; Kreinovich, V. Handbook of Granular Computing; John Wiley & Sons: Haboken, NJ, USA, 2008. [Google Scholar]
- Pedrycz, W.; Homenda, W. Building the fundamentals of granular computing: A principle of justifiable granularity. Appl. Soft Comput. 2013, 13, 4209–4218. [Google Scholar] [CrossRef]
- Yao, Y.; Zhao, L. A measurement theory view on the granularity of partitions. Inf. Sci. 2012, 213, 1–13. [Google Scholar] [CrossRef]
- Yang, J.; Wang, G.; Zhang, Q. Knowledge distance measure in multigranulation spaces of fuzzy equivalence relations. Inf. Sci. 2018, 448, 18–35. [Google Scholar] [CrossRef]
- Ding, S.; Du, M.; Zhu, H. Survey on granularity clustering. Cognit. Neurodyn. 2015, 9, 561–572. [Google Scholar] [CrossRef] [PubMed]
- Martino, A.; Rizzi, A.; Frattale Mascioli, F.M. Efficient Approaches for Solving the Large-Scale k-medoids Problem. In Proceedings of the 9th International Joint Conference on Computational Intelligence—Volume 1: IJCCI; SciTePress: Setúbal, Portugal, 2017; pp. 338–347. [Google Scholar] [CrossRef]
- Del Vescovo, G.; Livi, L.; Frattale Mascioli, F.M.; Rizzi, A. On the problem of modeling structured data with the MinSOD representative. Int. J. Comput. Theory Eng. 2014, 6, 9. [Google Scholar] [CrossRef]
- Martino, A.; Rizzi, A.; Frattale Mascioli, F.M. Efficient Approaches for Solving the Large-Scale k-Medoids Problem: Towards Structured Data. In Computational Intelligence, Proceedings of the 9th International Joint Conference, IJCCI 2017, Funchal-Madeira, Portugal, 1–3 November 2017; Revised Selected Papers; Sabourin, C., Merelo, J.J., Madani, K., Warwick, K., Eds.; Springer: Cham, Switzerland, 2019; pp. 199–219. [Google Scholar] [CrossRef]
- Martino, A.; Rizzi, A.; Frattale Mascioli, F.M. Distance Matrix Pre-Caching and Distributed Computation of Internal Validation Indices in k-medoids Clustering. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Livi, L.; Rizzi, A.; Sadeghian, A. A Granular Computing approach to the design of optimized graph classification systems. Soft Comput. 2014, 18, 393–412. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Scardapane, S.; Rizzi, A.; Uncini, A.; Sadeghian, A. Granular Computing Techniques for Classification and Semantic Characterization of Structured Data. Cognit. Comput. 2016, 8, 442–461. [Google Scholar] [CrossRef]
- Singh, P.K. Similar Vague Concepts Selection Using Their Euclidean Distance at Different Granulation. Cognit. Comput. 2018, 10, 228–241. [Google Scholar] [CrossRef]
- Del Vescovo, G.; Rizzi, A. Automatic classification of graphs by symbolic histograms. In Proceedings of the 2007 IEEE International Conference on Granular Computing (GRC 2007), Fremont, CA, USA, 2–4 November 2007; p. 410. [Google Scholar] [CrossRef]
- Rizzi, A.; Del Vescovo, G.; Livi, L.; Frattale Mascioli, F.M. A new Granular Computing approach for sequences representation and classification. Proceedings ot the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, QLD, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Horak, D.; Maletić, S.; Rajković, M. Persistent homology of complex networks. J. Stat. Mech. Theory Exp. 2009, 2009, P03034. [Google Scholar] [CrossRef]
- Estrada, E.; Rodriguez-Velazquez, J.A. Complex networks as hypergraphs. arXiv 2005, arXiv:physics/0505137. [Google Scholar]
- Carlsson, G. Topology and data. Bull. Am. Math. Soc. 2009, 46, 255–308. [Google Scholar] [CrossRef]
- Wasserman, L. Topological Data Analysis. Annu. Rev. Stat. Its Appl. 2018, 5, 501–532. [Google Scholar] [CrossRef]
- Ramadan, E.; Tarafdar, A.; Pothen, A. A hypergraph model for the yeast protein complex network. In Proceedings of the 18th International Parallel and Distributed Processing Symposium, Santa Fe, NM, USA, 26–30 April 2004; p. 189. [Google Scholar] [CrossRef]
- Gaudelet, T.; Malod-Dognin, N.; Pržulj, N. Higher-order molecular organization as a source of biological function. Bioinformatics 2018, 34, i944–i953. [Google Scholar] [CrossRef] [PubMed]
- Malod-Dognin, N.; Pržulj, N. Functional geometry of protein-protein interaction networks. arXiv 2018, arXiv:1804.04428. [Google Scholar]
- Barbarossa, S.; Sardellitti, S. Topological Signal Processing over Simplicial Complexes. arXiv 2019, arXiv:1907.11577. [Google Scholar]
- Barbarossa, S.; Tsitsvero, M. An introduction to hypergraph signal processing. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 6425–6429. [Google Scholar] [CrossRef]
- Barbarossa, S.; Sardellitti, S.; Ceci, E. Learning from signals defined over simplicial complexes. In Proceedings of the 2018 IEEE Data Science Workshop (DSW), Lausanne, Switzerland, 4–6 June 2018; pp. 51–55. [Google Scholar] [CrossRef]
- Berge, C. Graphs and Hypergraphs; Elsevier: Oxford, UK, 1973. [Google Scholar]
- Zomorodian, A. Topological data analysis. Adv. Appl. Comput. Topol. 2012, 70, 1–39. [Google Scholar]
- Ghrist, R.W. Elementary Applied Topology; Createspace: Seattle, WA, USA, 2014. [Google Scholar]
- Hausmann, J.C. On the Vietoris-Rips complexes and a cohomology theory for metric spaces. Ann. Math. Stud. 1995, 138, 175–188. [Google Scholar]
- Zomorodian, A. Fast construction of the Vietoris-Rips complex. Comput. Graph. 2010, 34, 263–271. [Google Scholar] [CrossRef]
- Bandelt, H.J.; Chepoi, V. Metric graph theory and geometry: A survey. Contemp. Math. 2008, 453, 49–86. [Google Scholar]
- Bandelt, H.J.; Prisner, E. Clique graphs and Helly graphs. J. Comb. Theory Ser. B 1991, 51, 34–45. [Google Scholar] [CrossRef]
- Giusti, C.; Ghrist, R.; Bassett, D.S. Two’s company, three (or more) is a simplex. J. Comput. Neurosci. 2016, 41, 1–14. [Google Scholar] [CrossRef]
- Zomorodian, A.; Carlsson, G. Computing persistent homology. Discret. Comput. Geom. 2005, 33, 249–274. [Google Scholar] [CrossRef]
- Martino, A.; Rizzi, A.; Frattale Mascioli, F.M. Supervised Approaches for Protein Function Prediction by Topological Data Analysis. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Bron, C.; Kerbosch, J. Algorithm 457: Finding All Cliques of an Undirected Graph. Commun. ACM 1973, 16, 575–577. [Google Scholar] [CrossRef]
- Cazals, F.; Karande, C. A note on the problem of reporting maximal cliques. Theor. Comput. Sci. 2008, 407, 564–568. [Google Scholar] [CrossRef]
- Tomita, E.; Tanaka, A.; Takahashi, H. The worst-case time complexity for generating all maximal cliques and computational experiments. Theor. Comput. Sci. 2006, 363, 28–42. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning, 1st ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Schölkopf, B.; Smola, A.J.; Williamson, R.C.; Bartlett, P.L. New support vector algorithms. Neural Comput. 2000, 12, 1207–1245. [Google Scholar] [CrossRef]
- Zhu, J.; Rosset, S.; Tibshirani, R.; Hastie, T.J. 1-norm support vector machines. In Proceedings of the 16th International Conference on Neural Information Processing Systems, Whistler, BC, Canada, 9–11 December 2003; pp. 49–56. [Google Scholar]
- Boser, B.E.; Guyon, I.; Vapnik, V. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From precision, recall and f-measure to roc., informedness, markedness & correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Youden, W.J. Index for rating diagnostic tests. Cancer 1950, 3, 32–35. [Google Scholar] [CrossRef]
- Martino, A.; Rizzi, A. (Hyper)Graph Kernels over Simplicial Complexes. Pattern Recognit. 2019. Under Review. [Google Scholar]
- Bianchi, F.M.; Scardapane, S.; Livi, L.; Uncini, A.; Rizzi, A. An interpretable graph-based image classifier. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 2339–2346. [Google Scholar] [CrossRef]
- Baldini, L.; Martino, A.; Rizzi, A. Stochastic Information Granules Extraction for Graph Embedding and Classification. In Proceedings of the 11th International Joint Conference on Computational Intelligence—Volume 1: NCTA; SciTePress: Vienna, Austria, 2019; pp. 391–402. [Google Scholar] [CrossRef]
- Kersting, K.; Kriege, N.M.; Morris, C.; Mutzel, P.; Neumann, M. Benchmark Data Sets for Graph Kernels. 2016. Available online: http://graphkernels.cs.tu-dortmund.de (accessed on 26 September 2019).
- Di Noia, A.; Martino, A.; Montanari, P.; Rizzi, A. Supervised machine learning techniques and genetic optimization for occupational diseases risk prediction. Soft Comput. 2019. [Google Scholar] [CrossRef]
- Fan, R.E.; Chang, K.W.; Hsieh, C.J.; Wang, X.R.; Lin, C.J. LIBLINEAR: A library for large linear classification. J. Mach. Learn. Res. 2008, 9, 1871–1874. [Google Scholar]
- The UniProt Consortium. UniProt: The universal protein knowledgebase. Nucleic Acids Res. 2017, 45, D158–D169. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Martino, A.; Maiorino, E.; Giuliani, A.; Giampieri, M.; Rizzi, A. Supervised Approaches for Function Prediction of Proteins Contact Networks from Topological Structure Information. In Image Analysis, Proceedings of the 20th Scandinavian Conference, Tromsø, Norway, 12–14 June 2017; Sharma, P., Bianchi, F.M., Eds.; Part I; Springer: Cham, Switzerland, 2017; pp. 285–296. [Google Scholar] [CrossRef]
- Shimizu, Y.; Inoue, A.; Tomari, Y.; Suzuki, T.; Yokogawa, T.; Nishikawa, K.; Ueda, T. Cell-free translation reconstituted with purified components. Nat. Biotechnol. 2001, 19, 751. [Google Scholar] [CrossRef] [PubMed]
- Barley, M.H.; Turner, N.J.; Goodacre, R. Improved descriptors for the quantitative structure–activity relationship modeling of peptides and proteins. J. Chem. Inf. Model. 2018, 58, 234–243. [Google Scholar] [CrossRef] [PubMed]
- Nayar, D.; van der Vegt, N.F.A. Cosolvent effects on polymer hydration drive hydrophobic collapse. J. Phys. Chem. B 2018, 122, 3587–3595. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A. The statistical utilization of multiple measurements. Ann. Eugen. 1938, 8, 376–386. [Google Scholar] [CrossRef]
- Colafranceschi, M.; Colosimo, A.; Zbilut, J.P.; Uversky, V.N.; Giuliani, A. Structure-related statistical singularities along protein sequences: A correlation study. J. Chem. Inf. Model. 2005, 45, 183–189. [Google Scholar] [CrossRef] [PubMed]
| Class | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Class | ACC | SPC | SNS | NPV | PPV | Sparsity | |
|---|---|---|---|---|---|---|---|
| 1 | 0.5 | 95.3 | 96.5 | 87.1 | 98.2 | 77.7 | 3.3 |
| 1 | 97 | 98.4 | 87.3 | 98.3 | 88 | 16 | |
| 2 | 0.5 | 92.7 | 94.2 | 86.7 | 96.5 | 79.6 | 4.5 |
| 1 | 94.5 | 97.3 | 83.8 | 95.9 | 88.9 | 22.7 | |
| 3 | 0.5 | 92.1 | 93.8 | 84.4 | 96.3 | 76.2 | 4 |
| 1 | 93.3 | 95.5 | 83.9 | 96.3 | 81.9 | 17.4 | |
| 4 | 0.5 | 96.6 | 97.7 | 82.5 | 98.7 | 72.9 | 2.8 |
| 1 | 97.3 | 98.6 | 79.8 | 98.5 | 81.6 | 7.8 | |
| 5 | 0.5 | 96.9 | 97.8 | 71.7 | 99 | 56.9 | 1.8 |
| 1 | 97.9 | 98.9 | 70.4 | 98.9 | 75.3 | 5.1 | |
| 6 | 0.5 | 97.5 | 97.9 | 88.8 | 99.4 | 71.5 | 2.2 |
| 1 | 98.7 | 99.4 | 86.2 | 99.3 | 87.8 | 9.6 | |
| 7 | 0.5 | 86.6 | 89.9 | 80.1 | 89.9 | 80.5 | 4.8 |
| 1 | 88.8 | 91.6 | 83.4 | 91.6 | 83.6 | 36.3 |
| Class | ACC | SPC | SNS | NPV | PPV | Sparsity | |
|---|---|---|---|---|---|---|---|
| 1 | 0.5 | 96.8 | 99 | 80.4 | 97.4 | 92 | 9.9 |
| 1 | 97.2 | 99.2 | 81.9 | 97.6 | 93.6 | 11.5 | |
| 2 | 0.5 | 93.9 | 98 | 77.8 | 94.5 | 90.9 | 6.8 |
| 1 | 94.5 | 98.3 | 79.7 | 95 | 92.2 | 26.1 | |
| 3 | 0.5 | 94 | 98.5 | 74.3 | 94.3 | 92.1 | 6.8 |
| 1 | 94.7 | 98.5 | 78.2 | 95.1 | 92.3 | 18.6 | |
| 4 | 0.5 | 97.3 | 99.3 | 69.6 | 97.8 | 88.4 | 12.8 |
| 1 | 97.3 | 99.4 | 69.2 | 97.8 | 89.9 | 19.1 | |
| 5 | 0.5 | 98.5 | 99.8 | 61.3 | 98.6 | 93 | 13.6 |
| 1 | 98.7 | 99.9 | 63.8 | 98.7 | 97.1 | 31.7 | |
| 6 | 0.5 | 98.9 | 99.9 | 80.3 | 99 | 97.1 | 23.3 |
| 1 | 99.1 | 99.9 | 83.5 | 99.2 | 97.2 | 28.7 | |
| 7 | 0.5 | 87.4 | 93 | 76.5 | 88.6 | 84.7 | 6.5 |
| 1 | 87.4 | 93.4 | 75.7 | 88.3 | 85.3 | 6.9 |
| Polarity (avg) | Hydrophilicity (avg) | Polarity (std) | Hydrophilicity (std) | |
|---|---|---|---|---|
| Polarity (avg) | 1 | 0.99818 | −0.01869 | −0.06879 |
| Hydrophilicity (avg) | 0.99818 | 1 | −0.03705 | −0.08582 |
| Polarity (std) | −0.01869 | −0.03705 | 1 | 0.99397 |
| Hydrophilicity (std) | −0.06879 | −0.08582 | 0.99397 | 1 |
| EC1 | EC2 | EC3 | EC4 | EC5 | EC6 | Not Enzymes | |
|---|---|---|---|---|---|---|---|
| 0.0250 | 0.0239 | 0.0212 | 0.0199 | 0.0239 | 0.0170 | 0.0250 | |
| p | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| Hydrophilicity (avg) | Hydrophilicity (std) | |||||
|---|---|---|---|---|---|---|
| Class | t-Value | p | Coefficient | t-Value | p | Coefficient |
| 1 | 11.55 | <0.0001 | −4.17734 | 0.92 | 0.3563 | 0.24438 |
| 2 | 10.52 | <0.0001 | −3.73211 | 0.0647 | 1.85 | 0.47999 |
| 3 | 10.61 | <0.0001 | −3.38981 | 0.0651 | 1.84 | 0.43182 |
| 4 | 11.08 | <0.0001 | −2.98596 | 2.11 | 0.0352 | 0.41574 |
| 5 | 12.13 | <0.0001 | −2.43624 | 2.49 | 0.0127 | 0.36671 |
| 6 | 10.73 | <0.0001 | −2.65512 | 2.57 | 0.01 | 0.46672 |
| 7 | 11.55 | <0.0001 | −4.17734 | 0.92 | 0.3563 | 0.24438 |
| Polarity (avg) | Polarity (std) | |||||
|---|---|---|---|---|---|---|
| Class | t-Value | p | Coefficient | t-Value | p | Coefficient |
| 1 | 11.27 | <0.0001 | 1.51515 | 1.77 | 0.0762 | −0.17376 |
| 2 | 10.26 | <0.0001 | 1.35280 | 2.52 | 0.0118 | −0.24206 |
| 3 | 10.43 | <0.0001 | 1.23898 | 2.62 | 0.0089 | −0.22655 |
| 4 | 10.83 | <0.0001 | 1.08515 | 2.72 | 0.0066 | −0.19836 |
| 5 | 11.84 | <0.0001 | 0.88388 | 3.16 | 0.0016 | −0.17190 |
| 6 | 10.52 | <0.0001 | 0.96768 | 3.14 | 0.0017 | −0.21080 |
| 7 | 11.27 | <0.0001 | 1.51515 | 1.77 | 0.0762 | −0.17376 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martino, A.; Giuliani, A.; Rizzi, A. (Hyper)Graph Embedding and Classification via Simplicial Complexes. Algorithms 2019, 12, 223. https://doi.org/10.3390/a12110223
Martino A, Giuliani A, Rizzi A. (Hyper)Graph Embedding and Classification via Simplicial Complexes. Algorithms. 2019; 12(11):223. https://doi.org/10.3390/a12110223
Chicago/Turabian StyleMartino, Alessio, Alessandro Giuliani, and Antonello Rizzi. 2019. "(Hyper)Graph Embedding and Classification via Simplicial Complexes" Algorithms 12, no. 11: 223. https://doi.org/10.3390/a12110223
APA StyleMartino, A., Giuliani, A., & Rizzi, A. (2019). (Hyper)Graph Embedding and Classification via Simplicial Complexes. Algorithms, 12(11), 223. https://doi.org/10.3390/a12110223






