Image Deblurring under Impulse Noise via Total Generalized Variation and Non-Convex Shrinkage
Abstract
1. Introduction
2. Prerequisite Knowledge
2.1. FTVd Model
2.2. Second-Order TGV Regularization
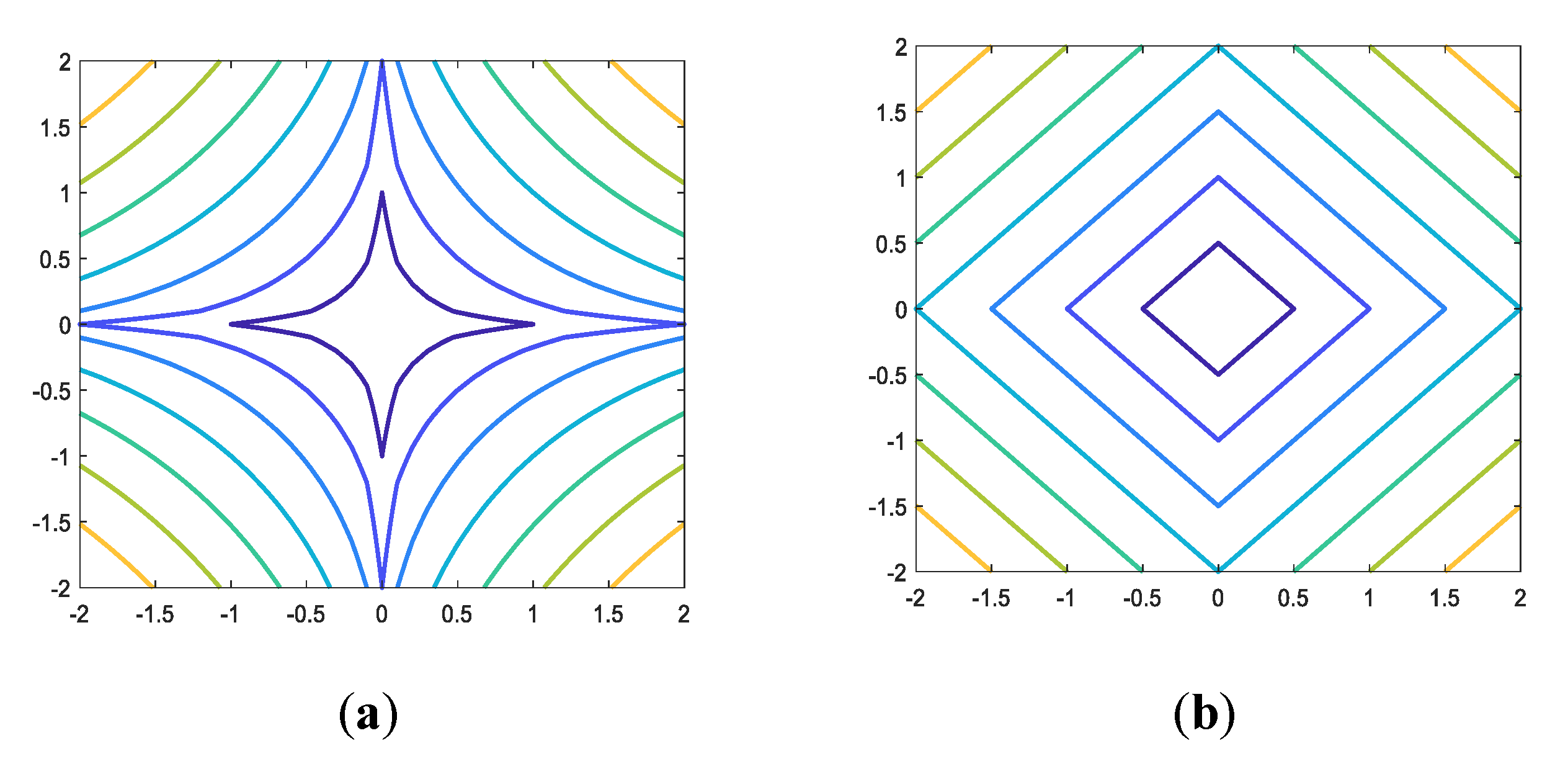
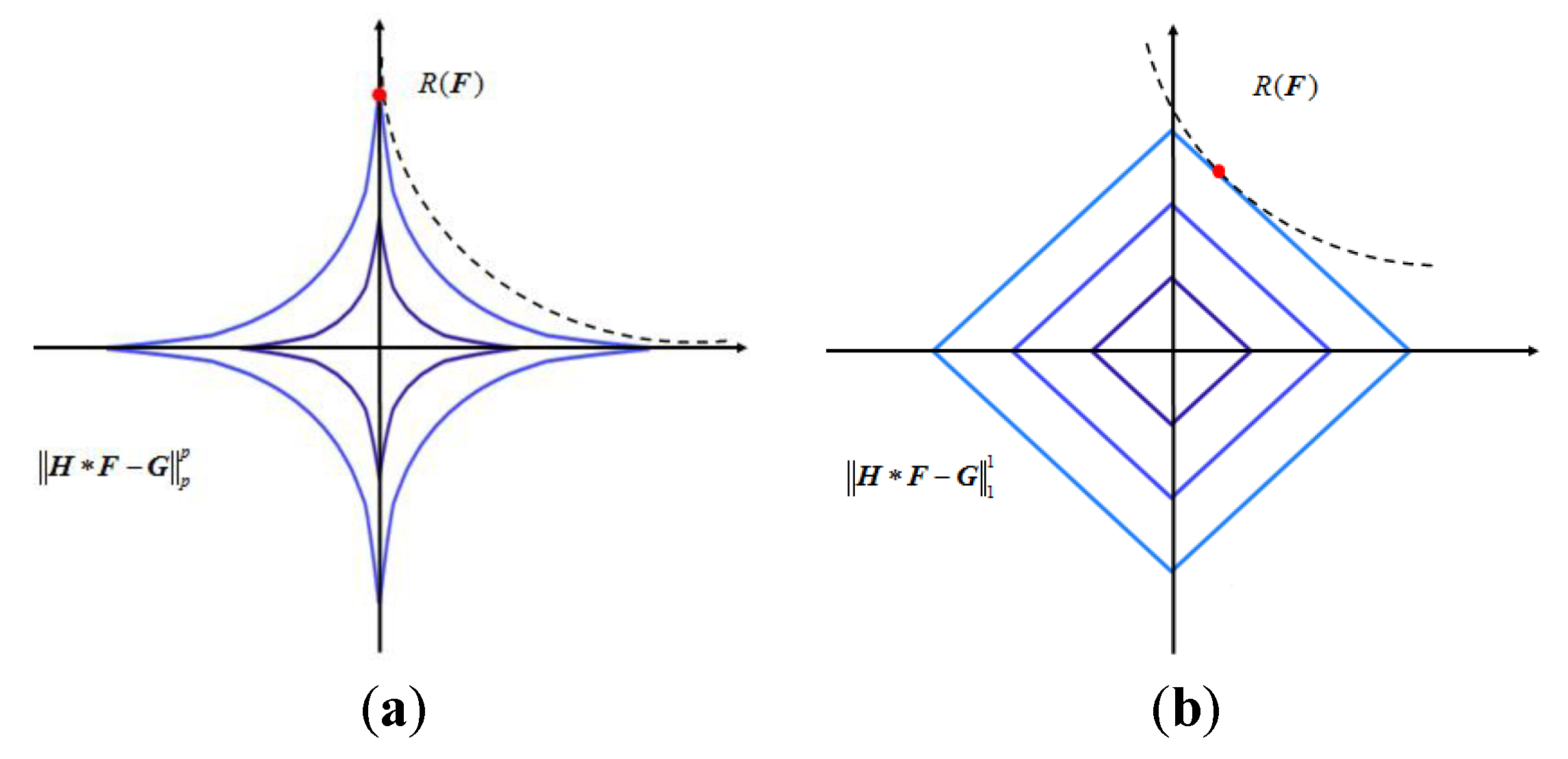
2.3. Lp-Pseudo-Norm
3. Model Proposal and Solution Method
3.1. Proposed Model
3.2. Solution Method
3.2.1. Solving Sub-Problems F, Vh, and Vv
3.2.2. Solving Sub-Problems Containing Intermediate Variables
3.2.3. Solving Sub-Problems Containing Dual Variables
| Algorithm 1. Pseudocode TGV_Lp for image restoration |
| Input:, Output: Initialize: 1: Set as 1; 2: While do 3: Update according to Equation (16); 4: Update according to Equation (18); 5: Update according to Equation (20); 6: k = k + 1; 7: End while 8: Return as . |
4. Numerical Experiments
4.1. Evaluation Indicators and Stopping Criteria
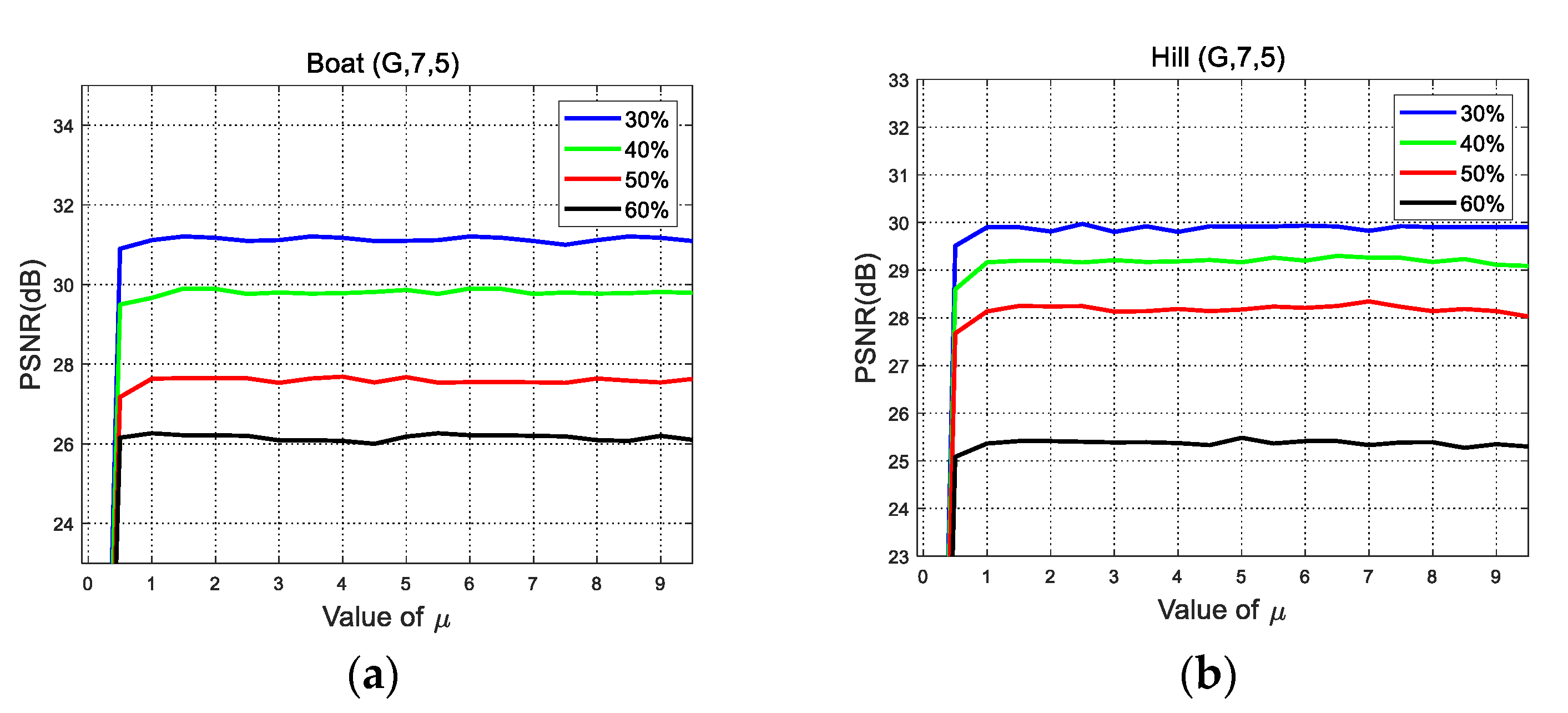
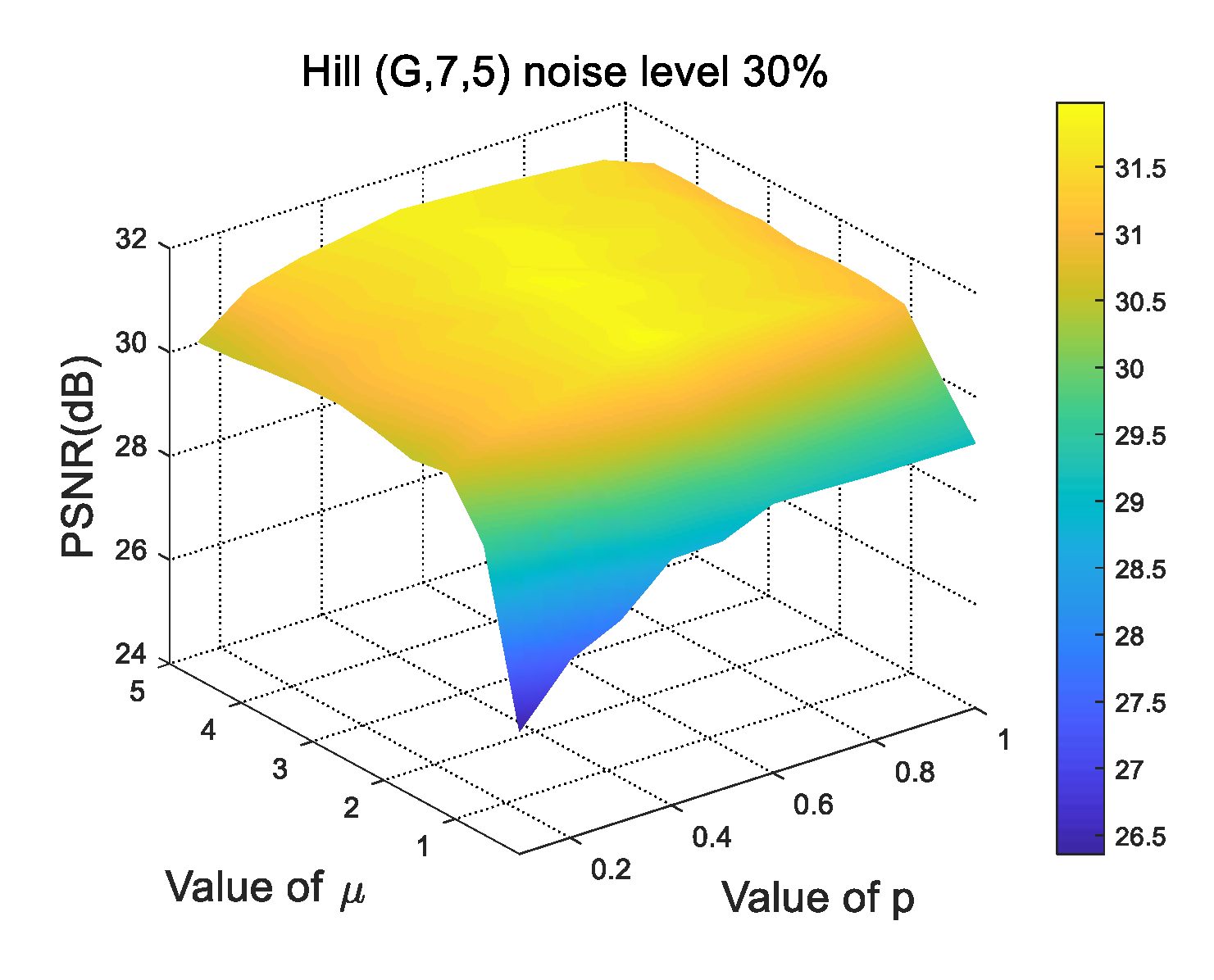
4.2. Parameter Selection and Sensitivity Analysis
4.2.1. Regularization Parameter
4.2.2. Value of p in Lp-Pseudo-Norm
4.3. Numerical Performance Comparison
4.3.1. Numerical Performance Comparison for Image Recovery in the Presence of Gaussian Blur
- All four methods can effectively recover images that were degraded by Gaussian blur and different degrees of impulse noise. The PSNR, SSIM, and SNR values of the proposed method are generally higher than those of other competitive methods, which indicates that the proposed method has better deblurring and denoising effects. In particular, for images with many lines and complex textures, such as “Fingerprint” in Figure 3a, “Butterfly” in Figure 3b, and “Baboon” in Figure 3c, the proposed method performed well, especially at high noise levels. For example, for the “Fingerprint” image of Figure 3a treated with a Gaussian blur kernel and 50% noise, the PSNR value (35.59 dB) of the proposed method was higher by 7.22 dB than that of the FTVd method (28.37 dB), and was higher by 2.55 dB and 1.6 dB than that of the TGV method (33.04 dB) and the OGSTV method (33.99 dB), respectively.
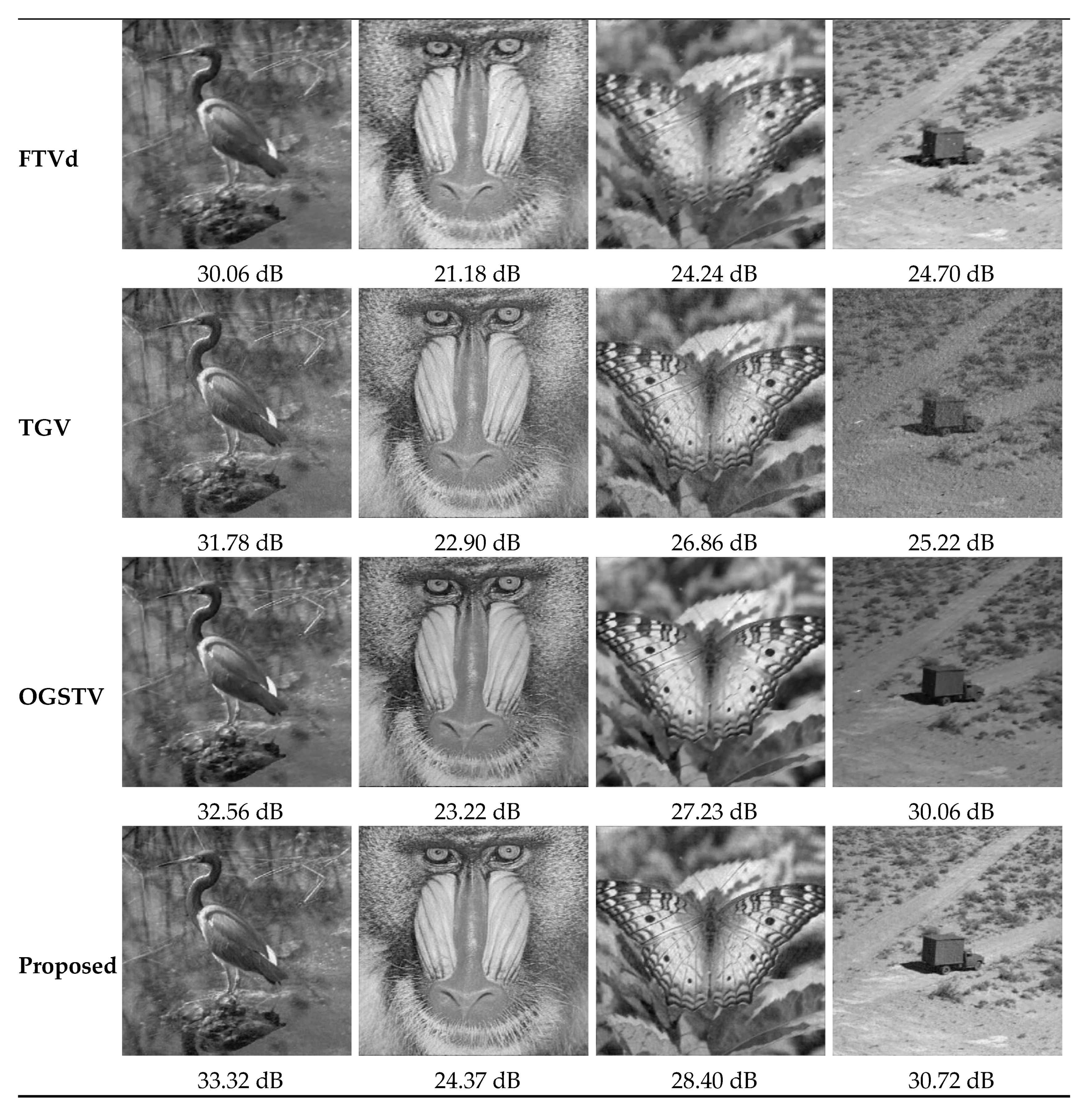
- When restoring the nine degraded images treated with the Gaussian blur kernel and 30–60% impulse noise, the proposed method achieved 0.58–2.85 dB higher PSNR values compared with the TGV method. When restoring the nine degraded images treated with the Gaussian blur kernel and impulse noise, the proposed method achieved 0.45–1.73 dB higher PSNR values compared with the TGV method. For example, for the “Bird” image of Figure 3e treated with the Gaussian blur kernel and two different levels (50% vs. 60%) of noise, the PSNR values of the proposed method (32.31 dB and 29.69 dB) were 2.85 dB and 2.7 dB higher than those of the TGV method (29.46 dB and 26.99 dB), respectively.
- The OGSTV method is an excellent algorithm for image deblurring and impulse noise removal, and it uses the neighborhood gradient information of the image to form a combined gradient for image restoration, which achieves good image restoration performance for smooth image regions but is less satisfactory in recovering image edge regions containing sharp lines and angles. In the test, it was observed that, for smooth images with non-complex textures, such as the “Plane” image of Figure 3h and “Satellite” image of Figure 3i, the OGSTV method had particularly excellent performance, which was slightly better than that of the proposed algorithm in the case of low noise levels. In the case of high noise levels, however, the proposed algorithm was still superior to the OGSTV method. For example, when restoring the “Satellite” image degraded with and 30% noise, the OGSTV method achieved a slightly higher PSNR value of 36.97 dB compared to the proposed method (36.54 dB), with a difference of only 0.43 dB; however, in the cases of 50% and 60% noise, the PSNR values of the OGSTV method were lower than those of the proposed method.
4.3.2. Numerical Performance Comparison for Image Recovery in the Presence of Average Blur
4.3.3. Numerical Performance Comparison for Image Recovery in the Presence of Motion Blur
4.4. Comparison of Visual Effects
4.4.1. Comparison of the Visual Effects of Restored Images in the Case of Gaussian Blur
4.4.2. Visual Effect Comparison for Image Restoration in the Case of Average Blur
4.4.3. Visual Effect Comparison for Image Restoration of Images Degraded with Motion Blur
4.5. Comparison of Computing Time
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tikhonov, A.N.; Goncharsky, A.V.; Stepanov, V.V.; Yagola, A.G. Numerical Methods for the Solution of Ill-Posed Problems; Springer: Berlin, Germany, 1995. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Yin, W.; Zhang, Y. A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imag. Sci. 2008, 1, 248–272. [Google Scholar] [CrossRef]
- Sakurai, M.; Kiriyama, S.; Goto, T.; Hirano, S. Fast algorithm for total variation minimization. In Proceedings of the 2011 18th IEEE International Conference on Image Processing (ICIP), Brussels, Belgium, 11–14 September 2011; pp. 1461–1464. [Google Scholar]
- Ren, Z.; He, C.; Zhang, Q. Fractional order total variation regularization for image super-resolution. Signal Process. 2013, 93, 2408–2421. [Google Scholar] [CrossRef]
- Selesnick, I.W.; Chen, P.-Y. Total variation denoising with overlapping group sparsity. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 5696–5700. [Google Scholar]
- Liu, G.; Huang, T.Z.; Liu, J.; Lv, X.-G. Total variation with overlapping group sparsity for image deblurring under impulse noise. PLoS ONE 2015, 10, e0122562. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Huang, T.Z.; Liu, G.; Wang, S.; Lv, X.-G. Total variation with overlapping group sparsity for speckle noise reduction. Neurocomputing 2016, 216, 502–513. [Google Scholar] [CrossRef]
- Bredies, K.; Kunisch, K.; Pock, T. Total generalized variation. SIAM J. Imag. Sci. 2010, 3, 492–526. [Google Scholar] [CrossRef]
- Knoll, F.; Bredies, K.; Pock, T.; Stollberger, R. Second order total generalized variation (TGV) for MRI. Magn. Reson. Med. 2011, 65, 480–491. [Google Scholar] [CrossRef] [PubMed]
- Kong, D.; Peng, Z. Seismic random noise attenuation using shearlet and total generalized variation. J. Geophys. Eng. 2015, 12, 1024–1035. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, Z.; Li, M.; Yu, F.; Lin, F. Seismic signal denoising using total generalized variation with overlapping group sparsity in the accelerated ADMM framework. J. Geophys. Eng. 2019, 16, 30–51. [Google Scholar] [CrossRef]
- Donoho, D.L.; Elad, M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization. Proc. Natl. Acad. Sci. USA 2003, 100, 2197–2202. [Google Scholar] [CrossRef] [PubMed]
- Woodworth, J.; Chartrand, R. Compressed sensing recovery via nonconvex shrinkage penalties. Inverse Probl. 2016, 32, 75004–75028. [Google Scholar] [CrossRef]
- Zheng, L.; Maleki, A.; Weng, H.; Wang, X.; Long, T. Does ℓp-minimization outperform ℓ1-minimization? IEEE Trans. Inform. Theory 2017, 63, 6896–6935. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Yan, B.; Li, L.; Cai, A.; Hu, G. Constrained total generalized p-variation minimization for few-view x-ray computed tomography image reconstruction. PLoS ONE 2016, 11, e0149899. [Google Scholar] [CrossRef] [PubMed]
- Chartrand, R. Shrinkage mappings and their induced penalty functions. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 1026–1029. [Google Scholar]
- Chen, Y.; Peng, Z.; Gholami, A.; Yan, J.; Li, S. Seismic signal sparse time–frequency representation by Lp-quasinorm constraint. Digit. Signal Process. 2019, 87, 43–59. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Y.; Lin, F.; Chen, Y.; Yu, F.; Cai, Z. Impulse noise denoising using total variation with overlapping group sparsity and Lp-pseudo-norm shrinkage. Appl. Sci. 2018, 8, 2317. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers; Foundations and Trends® in Machine Learning: Boston, FL, USA, 2011; Volume 3, pp. 1–122. [Google Scholar]
- Yang, J.; Zhang, Y.; Yin, W. An efficient TVL1 algorithm for deblurring multichannel images corrupted by impulsive noise. SIAM J. Sci. Comput. 2009, 31, 2842–2865. [Google Scholar] [CrossRef]
- Yang, J.; Yin, W.; Zhang, Y.; Wang, Y. A fast algorithm for edge-preserving variational multichannel image restoration. SIAM J. Imag. Sci. 2009, 2, 569–592. [Google Scholar] [CrossRef]
- Gonzalez, R.C. Digital Image Processing, 3rd ed.; Pearson Prentice hall: New Jersey, NJ, USA, 2016. [Google Scholar]
- Guo, W.; Qin, J.; Yin, W. A new detail-preserving regularization scheme. SIAM J. Imag. Sci. 2014, 7, 1309–1334. [Google Scholar] [CrossRef]
- Nikolova, M. A variational approach to remove outliers and impulse noise. J. Math. Imag. Vis. 2004, 20, 99–120. [Google Scholar] [CrossRef]
- Emory University Image Database. Available online: http://www.mathcs.emory.edu/~nagy/RestoreTools/ (accessed on 15 March 2018).
- CVG-UGR (Computer Vision Group, University of Granada) Image Database. Available online: http://decsai.ugr.es/cvg/dbimagenes/index.php (accessed on 15 March 2018).
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]







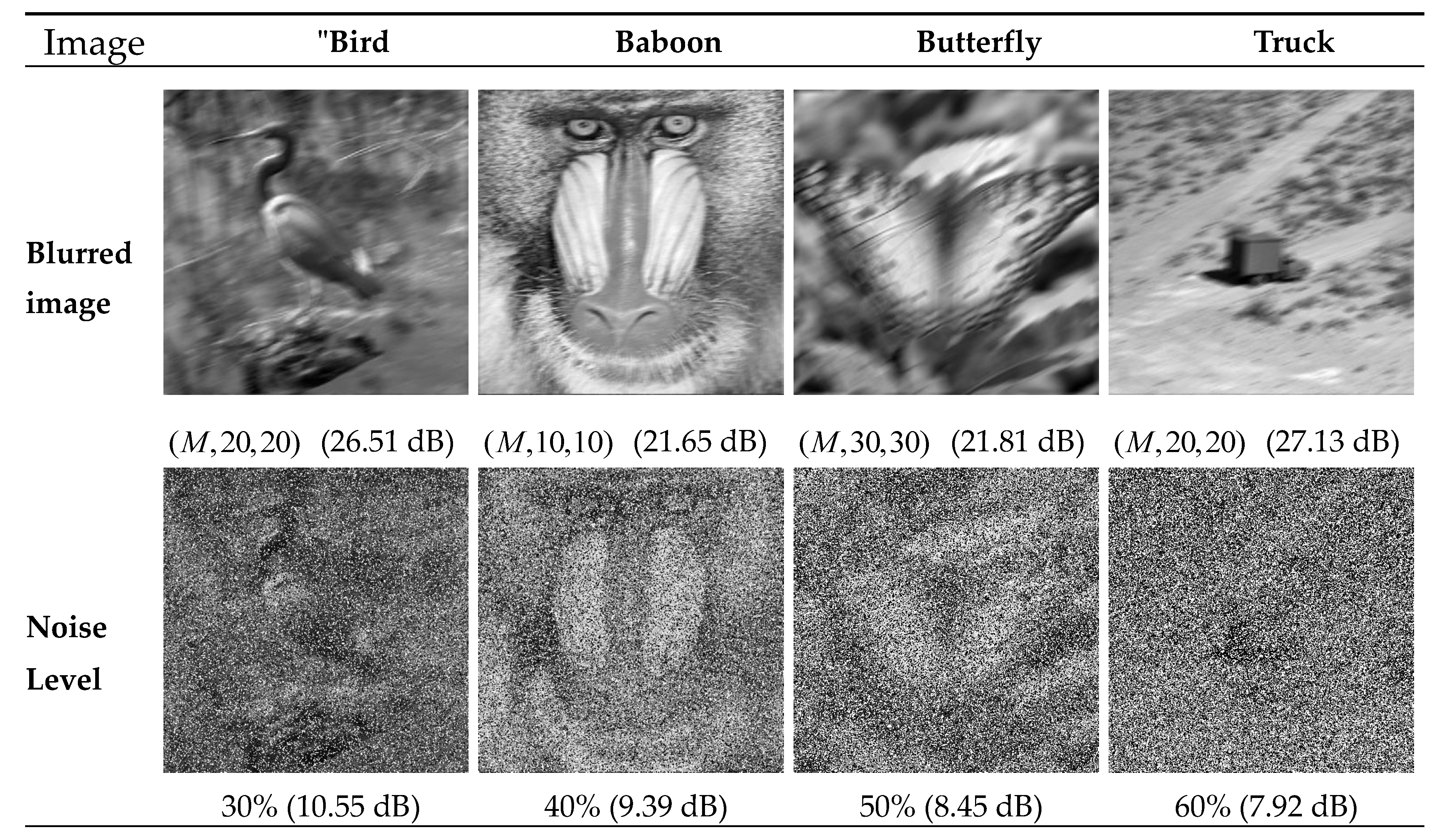
| Noise Level | Fingerprint | Butterfly | Baboon | Boat | Bird | Hill | Truck | Plane | Satellite |
|---|---|---|---|---|---|---|---|---|---|
| 30% | 0.30 | 0.45 | 0.50 | 0.35 | 0.50 | 0.55 | 0.50 | 0.55 | 0.75 |
| 40% | 0.30 | 0.45 | 0.50 | 0.35 | 0.50 | 0.55 | 0.50 | 0.55 | 0.75 |
| 50% | 0.30 | 0.45 | 0.50 | 0.35 | 0.50 | 0.55 | 0.50 | 0.55 | 0.75 |
| 60% | 0.25 | 0.50 | 0.50 | 0.35 | 0.50 | 0.55 | 0.55 | 0.55 | 0.75 |
| Images | Noise Level | FTVd | TGV | OGSTV | Proposed | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | SNR | PSNR | SSIM | SNR | PSNR | SSIM | SNR | PSNR | SSIM | SNR | ||
| Finger | 30 | 30.49 | 0.950 | 21.90 | 36.13 | 0.980 | 27.39 | 36.21 | 0.980 | 27.68 | 38.63 | 0.989 | 30.08 |
| 40 | 29.16 | 0.913 | 19.84 | 35.32 | 0.976 | 26.79 | 35.64 | 0.981 | 26.4 | 37.44 | 0.983 | 28.90 | |
| 50 | 28.37 | 0.866 | 19.51 | 33.04 | 0.959 | 24.5 | 33.99 | 0.957 | 24.56 | 35.59 | 0.970 | 27.05 | |
| 60 | 25.74 | 0.831 | 16.27 | 28.89 | 0.915 | 20.35 | 28.84 | 0.906 | 19.32 | 30.60 | 0.923 | 22.07 | |
| Butterfly | 30 | 28.21 | 0.894 | 21.96 | 30.37 | 0.919 | 24.17 | 30.84 | 0.932 | 24.59 | 32.17 | 0.946 | 25.92 |
| 40 | 27.36 | 0.875 | 21.11 | 29.58 | 0.901 | 23.33 | 30.46 | 0.926 | 24.21 | 30.99 | 0.931 | 24.74 | |
| 50 | 25.42 | 0.825 | 19.17 | 28.45 | 0.869 | 22.2 | 28.83 | 0.895 | 22.45 | 29.96 | 0.912 | 23.71 | |
| 60 | 24.06 | 0.734 | 14.47 | 26.48 | 0.804 | 20.24 | 26.61 | 0.818 | 20.27 | 28.99 | 0.898 | 22.75 | |
| Baboon | 30 | 21.29 | 0.628 | 15.83 | 22.93 | 0.756 | 17.47 | 23.15 | 0.765 | 17.69 | 24.01 | 0.806 | 18.55 |
| 40 | 21.06 | 0.608 | 15.60 | 22.56 | 0.730 | 17.10 | 22.93 | 0.756 | 17.46 | 23.39 | 0.779 | 17.93 | |
| 50 | 20.62 | 0.572 | 15.15 | 22.08 | 0.693 | 16.63 | 21.90 | 0.702 | 16.44 | 22.66 | 0.738 | 17.20 | |
| 60 | 20.27 | 0.525 | 14.43 | 21.23 | 0.627 | 15.77 | 20.57 | 0.546 | 15.12 | 22.23 | 0.710 | 16.77 | |
| Boat | 30 | 27.25 | 0.840 | 21.92 | 29.05 | 0.894 | 23.71 | 29.45 | 0.906 | 24.11 | 31.46 | 0.932 | 26.11 |
| 40 | 26.49 | 0.802 | 21.16 | 28.33 | 0.873 | 22.99 | 29.06 | 0.898 | 23.71 | 30.28 | 0.914 | 24.94 | |
| 50 | 25.65 | 0.789 | 20.30 | 27.25 | 0.839 | 21.91 | 27.23 | 0.836 | 21.88 | 28.47 | 0.884 | 23.12 | |
| 60 | 23.90 | 0.756 | 18.56 | 25.13 | 0.766 | 19.80 | 26.30 | 0.780 | 21.06 | 27.37 | 0.849 | 21.78 | |
| Bird | 30 | 31.03 | 0.914 | 21.97 | 32.82 | 0.934 | 23.76 | 33.49 | 0.947 | 24.43 | 34.54 | 0.957 | 25.47 |
| 40 | 29.71 | 0.890 | 20.65 | 31.84 | 0.915 | 22.77 | 33.03 | 0.941 | 23.97 | 33.39 | 0.943 | 24.32 | |
| 50 | 26.73 | 0.831 | 17.67 | 29.46 | 0.874 | 20.39 | 30.45 | 0.882 | 21.38 | 32.31 | 0.930 | 23.24 | |
| 60 | 22.75 | 0.722 | 13.69 | 26.99 | 0.797 | 17.93 | 27.85 | 0.813 | 18.77 | 29.69 | 0.898 | 20.62 | |
| Hill | 30 | 28.24 | 0.859 | 21.87 | 30.27 | 0.898 | 23.91 | 30.71 | 0.908 | 24.35 | 31.98 | 0.925 | 25.62 |
| 40 | 27.24 | 0.831 | 20.88 | 29.48 | 0.878 | 23.11 | 30.29 | 0.899 | 23.93 | 30.94 | 0.909 | 24.57 | |
| 50 | 25.57 | 0.802 | 19.68 | 28.39 | 0.845 | 22.03 | 28.25 | 0.865 | 21.92 | 29.72 | 0.887 | 23.36 | |
| 60 | 24.87 | 0.760 | 18.51 | 26.16 | 0.773 | 19.79 | 27.03 | 0.845 | 20.69 | 28.52 | 0.855 | 21.74 | |
| Truck | 30 | 29.50 | 0.887 | 22.23 | 32.79 | 0.926 | 25.52 | 33.48 | 0.939 | 26.22 | 34.22 | 0.946 | 26.96 |
| 40 | 28.70 | 0.828 | 21.73 | 31.85 | 0.908 | 24.58 | 33.06 | 0.932 | 25.79 | 33.14 | 0.933 | 25.87 | |
| 50 | 27.26 | 0.794 | 19.99 | 30.42 | 0.873 | 23.15 | 31.17 | 0.905 | 23.90 | 32.50 | 0.923 | 25.23 | |
| 60 | 26.13 | 0.620 | 19.18 | 29.06 | 0.860 | 21.80 | 30.48 | 0.865 | 23.11 | 31.05 | 0.903 | 23.79 | |
| Plane | 30 | 32.37 | 0.902 | 29.18 | 33.96 | 0.948 | 30.77 | 36.33 | 0.975 | 33.15 | 36.23 | 0.974 | 33.05 |
| 40 | 31.68 | 0.898 | 28.49 | 33.00 | 0.929 | 29.82 | 35.20 | 0.961 | 31.37 | 35.30 | 0.965 | 32.11 | |
| 50 | 30.42 | 0.831 | 27.24 | 31.43 | 0.892 | 28.25 | 32.71 | 0.901 | 29.52 | 33.90 | 0.951 | 30.72 | |
| 60 | 27.90 | 0.730 | 24.72 | 29.73 | 0.764 | 26.04 | 30.07 | 0.805 | 26.89 | 31.96 | 0.927 | 28.78 | |
| Satellite | 30 | 31.80 | 0.925 | 18.12 | 34.17 | 0.959 | 20.49 | 36.97 | 0.989 | 23.20 | 36.54 | 0.985 | 23.05 |
| 40 | 30.38 | 0.910 | 16.70 | 33.39 | 0.945 | 19.72 | 36.00 | 0.983 | 22.32 | 35.76 | 0.980 | 22.08 | |
| 50 | 29.08 | 0.883 | 15.41 | 31.37 | 0.910 | 17.70 | 32.32 | 0.926 | 18.64 | 32.61 | 0.975 | 18.92 | |
| 60 | 27.99 | 0.830 | 14.31 | 29.54 | 0.855 | 15.86 | 30.05 | 0.904 | 16.38 | 30.21 | 0.944 | 16.72 | |
| Images | Degrada -tion | FTVd | TGV | OGSTV | Proposed | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | SNR | PSNR | SSIM | SNR | PSNR | SSIM | SNR | PSNR | SSIM | SNR | ||
| Fingerprint | Blur: Noise level: 30% | 27.31 | 0.877 | 18.78 | 29.89 | 0.935 | 21.36 | 30.09 | 0.934 | 21.55 | 30.72 | 0.970 | 22.18 |
| Butterfly | 24.91 | 0.705 | 18.67 | 26.96 | 0.861 | 20.72 | 27.05 | 0.864 | 20.80 | 27.47 | 0.873 | 21.22 | |
| Baboon | 19.89 | 0.481 | 14.43 | 20.99 | 0.597 | 15.53 | 21.09 | 0.603 | 15.62 | 21.72 | 0.645 | 16.27 | |
| Boat | 24.73 | 0.679 | 19.20 | 25.63 | 0.815 | 20.29 | 26.37 | 0.835 | 21.02 | 26.86 | 0.851 | 21.82 | |
| Bird | 28.15 | 0.741 | 19.08 | 29.60 | 0.885 | 20.54 | 29.81 | 0.892 | 20.75 | 30.05 | 0.906 | 20.91 | |
| Hill | 25.98 | 0.690 | 19.68 | 27.37 | 0.830 | 21.01 | 27.41 | 0.832 | 21.05 | 28.01 | 0.840 | 21.65 | |
| Truck | 27.56 | 0.707 | 20.29 | 29.42 | 0.862 | 22.16 | 29.57 | 0.866 | 22.31 | 30.30 | 0.872 | 23.01 | |
| Plane | 29.76 | 0.815 | 26.58 | 30.67 | 0.904 | 27.65 | 31.34 | 0.938 | 28.15 | 31.82 | 0.948 | 28.64 | |
| Satellite | 28.20 | 0.821 | 14.52 | 29.66 | 0.900 | 15.98 | 31.47 | 0.963 | 17.79 | 31.39 | 0.962 | 17.71 | |
| Images | Blur Size | Noise Level | TGV | OGSTV | Proposed | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | SNR | PSNR | SSIM | SNR | PSNR | SSIM | SNR | |||
| Fingerprint | 30 | 36.46 | 0.983 | 27.91 | 36.73 | 0.980 | 29.19 | 38.31 | 0.989 | 29.77 | |
| 60 | 28.74 | 0.905 | 20.20 | 29.30 | 0.907 | 21.24 | 30.11 | 0.910 | 21.57 | ||
| Butterfly | 30 | 30.40 | 0.918 | 24.15 | 30.99 | 0.933 | 24.74 | 32.21 | 0.947 | 25.97 | |
| 60 | 25.83 | 0.784 | 19.59 | 26.45 | 0.803 | 20.66 | 28.59 | 0.895 | 22.35 | ||
| Baboon | 30 | 23.01 | 0.761 | 17.54 | 23.29 | 0.778 | 17.83 | 24.11 | 0.814 | 18.65 | |
| 60 | 21.14 | 0.622 | 15.68 | 21.51 | 0.657 | 16.10 | 22.31 | 0.715 | 16.85 | ||
| Boat | 30 | 29.11 | 0.894 | 23.77 | 29.60 | 0.907 | 24.26 | 31.50 | 0.933 | 26.16 | |
| 60 | 25.11 | 0.755 | 19.77 | 26.24 | 0.776 | 20.52 | 27.22 | 0.855 | 21.88 | ||
| Bird | 30 | 32.75 | 0.933 | 23.67 | 33.53 | 0.948 | 24.47 | 34.53 | 0.957 | 25.46 | |
| 60 | 27.05 | 0.785 | 17.99 | 29.06 | 0.853 | 20.35 | 30.19 | 0.899 | 21.13 | ||
| Hill | 30 | 30.33 | 0.899 | 23.97 | 30.85 | 0.910 | 24.49 | 32.07 | 0.927 | 25.71 | |
| 60 | 25.96 | 0.757 | 19.60 | 26.10 | 0.762 | 20.07 | 27.96 | 0.852 | 21.60 | ||
| Truck | 30 | 32.79 | 0.925 | 25.52 | 33.61 | 0.940 | 26.34 | 34.32 | 0.947 | 27.06 | |
| 60 | 27.25 | 0.780 | 19.97 | 30.28 | 0.848 | 22.32 | 31.38 | 0.904 | 24.12 | ||
| Plane | 30 | 33.87 | 0.945 | 30.68 | 36.45 | 0.975 | 33.27 | 36.37 | 0.969 | 33.08 | |
| 60 | 28.15 | 0.793 | 24.97 | 31.87 | 0.922 | 28.69 | 32.31 | 0.926 | 29.13 | ||
| Satellite | 30 | 33.95 | 0.956 | 20.28 | 36.85 | 0.989 | 23.18 | 36.52 | 0.981 | 23.10 | |
| 60 | 28.06 | 0.814 | 14.38 | 28.52 | 0.933 | 14.84 | 28.54 | 0.933 | 14.87 | ||
| Images | Blur Size | Noise Level | FTVd | TGV | OGSTV | Proposed |
|---|---|---|---|---|---|---|
| Baboon | 30 | 21.7921 | 24.0100 | 22.0647 | 24.8964 | |
| 40 | 21.1785 | 22.9020 | 23.2183 | 24.3687 | ||
| 30 | 21.0863 | 23.0958 | 22.8402 | 23.6167 | ||
| 40 | 20.7721 | 22.4554 | 22.3522 | 23.2369 | ||
| Butterfly | 30 | 26.0616 | 28.7070 | 28.4671 | 29.3110 | |
| 40 | 25.3602 | 27.9250 | 27.8820 | 28.9013 | ||
| 50 | 24.2406 | 26.8643 | 27.2269 | 28.3973 | ||
| 60 | 22.4797 | 25.2250 | 26.4264 | 27.7279 | ||
| Bird | 30 | 30.0618 | 31.7805 | 32.5596 | 33.3166 | |
| 40 | 28.7341 | 30.3195 | 31.8788 | 32.6383 | ||
| 50 | 26.2732 | 28.2106 | 31.1538 | 31.7443 | ||
| 60 | 22.9536 | 25.2543 | 30.1680 | 30.3756 | ||
| Truck | 30 | 30.3177 | 31.8087 | 32.3495 | 33.3499 | |
| 40 | 29.1381 | 30.3154 | 31.7592 | 32.7189 | ||
| 50 | 27.5260 | 28.4093 | 31.1104 | 31.9235 | ||
| 60 | 24.7013 | 25.2220 | 30.0642 | 30.7173 |
| Images | Blur Type | Noise Level | FTVd | TGV | OGSTV | Proposed |
|---|---|---|---|---|---|---|
| Fingerprint 256 × 256 | 30 | 0.86 | 1.47 | 0.81 | 1.19 | |
| 40 | 0.92 | 1.48 | 0.98 | 1.17 | ||
| 30 | 0.81 | 1.47 | 1.09 | 1.22 | ||
| 60 | 0.84 | 1.48 | 1.47 | 1.17 | ||
| Plane 512 × 512 | 30 | 3.28 | 6.03 | 6.20 | 5.31 | |
| 40 | 3.42 | 6.17 | 5.98 | 5.36 | ||
| 30 | 3.61 | 6.28 | 6.78 | 5.33 | ||
| 60 | 3.27 | 6.36 | 4.16 | 5.36 | ||
| Satellite 512 × 512 | 30 | 3.36 | 7.11 | 3.11 | 5.27 | |
| 40 | 3.50 | 6.20 | 2.66 | 5.34 | ||
| 30 | 3.31 | 6.22 | 3.59 | 5.16 | ||
| 60 | 3.23 | 6.23 | 4.09 | 5.14 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, F.; Chen, Y.; Chen, Y.; Yu, F. Image Deblurring under Impulse Noise via Total Generalized Variation and Non-Convex Shrinkage. Algorithms 2019, 12, 221. https://doi.org/10.3390/a12100221
Lin F, Chen Y, Chen Y, Yu F. Image Deblurring under Impulse Noise via Total Generalized Variation and Non-Convex Shrinkage. Algorithms. 2019; 12(10):221. https://doi.org/10.3390/a12100221
Chicago/Turabian StyleLin, Fan, Yingpin Chen, Yuqun Chen, and Fei Yu. 2019. "Image Deblurring under Impulse Noise via Total Generalized Variation and Non-Convex Shrinkage" Algorithms 12, no. 10: 221. https://doi.org/10.3390/a12100221
APA StyleLin, F., Chen, Y., Chen, Y., & Yu, F. (2019). Image Deblurring under Impulse Noise via Total Generalized Variation and Non-Convex Shrinkage. Algorithms, 12(10), 221. https://doi.org/10.3390/a12100221





