2. Related Work
There has been some research into wireless communication systems with energy-harvesting equipment. For a time-invariant channel, in [
3], the optimal offline power allocation policies are proposed to minimize the transmission completion time under energy causality for two kinds of data arrival scenarios. In [
4], the optimal power allocation policies are derived when the capacity of the battery is limited. In [
5], for a sensor networks scenario, the problem of maximizing the throughput of the system is firstly studied, and then the problem of minimizing the average delay is solved. In addition, wireless transmission with a time-varying channel is also studied. In [
6], directional water-filling algorithm is proposed to solve throughput maximization question and the proving of optimality is given. The authors next use stochastic dynamic programming to tackle the optimal online policy with causal channel information and propose a low-complexity near-optimal algorithm. In [
7], structural results for the optimal energy allocation are obtained by using dynamic programming and optimization theory; then, the staircase water-filling algorithm is obtained based on the conventional water-filling algorithm when considering that the capacity of a battery has no limit. In [
8], a geometric water-filling (GWF) algorithm is proposed in place of the conventional water-filling algorithm with a sum power constraint. Then, the recursively geometric water-filling (RGWF) algorithm is obtained by taking energy causality into account.
All the energy collected in [
3,
4,
5,
6,
7,
8] is used for transmission and other losses are ignored, which is too idealistic. In [
9], the authors analyze the problem of optimizing system throughput in the case of imperfect batteries: the batteries will leak over time or the upper limit of the battery capacity decreases with time. In [
10], for a time-invariant channel, taking the circuit consumption factor into account and considering both energy efficiency (EE) and spectrum efficiency (SE), the EE–SE two-phase algorithm is proposed to solve the problem of the optimization of throughput. In [
11], circuit consumption is also considered for both time-invariant and time-varying channels, and the optimal solution is given to maximize the throughput. In [
12], three questions are studied: throughput maximization, the minimization of energy consumption when data transmission is completed, and the minimization of data transmission completion time. Inspired by the offline optimal algorithm of the above problems, an online power allocation algorithm with low complexity is proposed. The losses of energy in the storage process are studied in [
13], where the conditions of time-invariant and time-varying channels, infinite and limited battery capacity, single users and broadcast channels are discussed, respectively. Then, an optimal power allocation algorithm with a double-threshold structure is proposed. Besides the above-mentioned studies, there has also been some research into power allocation in other scenarios. For example, [
14] develops distributed methods to efficiently use harvested energy in a sensor network while [
15] considers power and server allocation in a multibeam satellite downlink.
Some of the above references do not consider the additional energy losses and some consider only the single energy losses, while there would be more than one kind of energy loss problem in the actual scene. This paper aims to study the scenario where not only circuit consumption generated in the process of transmission but also the energy losses in the storage process are considered. These two factors are considered as restrictive conditions in the optimization problem for time-invariant and time-varying channels, respectively. We discuss the offline optimal power allocation strategies to solve the throughput maximization problems and then propose an online power allocation policy with low complexity.
The contents are as follows:
Section 3 shows the establishment of the system model;
Section 4 solves the optimization problem for the time-invariant channel and proposes a power allocation algorithm with a three-threshold structure;
Section 5 presents the optimal power allocation strategy in view of the time-varying channel;
Section 6 puts forward the online power allocation algorithm with low complexity and adaptive thresholds;
Section 7 gives the simulation results and analysis; and
Section 8 and
Section 9 are a discussion and a summary of this paper, respectively.
3. System Model
The model of a wireless transmission system with an energy harvesting transmitter is shown in
Figure 1. Supposing that the data transmission time has
time slots, the length of each time slot is unit 1, the transmitter will harvest
units of energy at the beginning of time slot
. The energy
collected at each time slot is independent and obeys uniform distribution. The transmit power in time slot
is
; when
, the circuit consumption power is
mW, and the total power consumed is
In (1),
is defined as
where
(
) is the actual transmission time,
is the amount of energy stored in the battery,
is the amount of energy extracted from the battery and
is the consumption.
There are energy losses when the energy is stored in the battery, supposing that the storage efficiency is
(
). If the energy collected by the time slot is used up to transmit the data, there are no energy storage losses; if the collected energy is not used up at the current time slot, the remaining energy
is stored in the battery, the amount of energy loss is
, and only
units of energy can be used for future. The amount of energy in the battery in time slot
can be written as
For the additive white Gaussian noise channel, the instantaneous transmission rate
is
In (4),
is the channel fading coefficient in time slot
.
In this paper, the average throughput of the system is maximized by optimizing the transmit power of each time slot and the factors such as energy arrivals, channel states, circuit consumption and storage losses are considered comprehensively.
4. Optimal Offline Power Allocation for the Time-Invariant Channel
We first study the time-invariant channel scene where
and the energy arrivals are
. The instantaneous transmission rate is (4); then, the optimization problem P1 can be described as
The condition in (6) means that the amount of energy in the battery is nonnegative, which reflects the energy causality. The condition in (7) means the power is nonnegative.
Observing this optimization problem, it can be found that
is concave in
and all conditions are linear, so P1 is a convex optimization problem and the Lagrange multiplier method and KKT conditions can be used. The Lagrange function is
where
are nonnegative Lagrange multipliers for the restrictive conditions.
Taking the derivatives with respect to
, we can obtain
where
.
The remaining KKT conditions are
Putting (10), (11) and (12) in order:
If
,
; If
,
and
, (16) and (17) can be written as
We first analyze (18). Since the system exhibits storage losses, the optimal solution cannot be achieved by using a conventional water-filling algorithm or the DWF (Directional Water-Filling) algorithm in [
6]. Reference [
13] defines two thresholds according to (18):
Obviously,
, and the two thresholds have the following relationship:
In [
13], the authors have analyzed
, which means that the optimal power should be between two thresholds. If
is greater than
, the part of the energy which exceeds
should be stored in the battery, so
is called the storage threshold; if
is less than
, the system needs to retrieve energy from the battery, so
is called the retrieval threshold. According to Lemma 3 in [
13], the threshold should be monotonically increasing and its value changes only when the battery is empty. Combined with the analysis of [
13] and the restrictions of this paper, the optimal power should satisfy the following conditions:
Then, we analyze (19) and firstly propose a new optimization problem, P2:
In (25), , P2 aims to maximize the throughput in time slot with units of energy, and the length of time slot has no limit.
Taking the derivative of (25), we can obtain
It is obvious that (26) is similar to (19), and the only difference is the parameter
which corresponds to the condition
. Supposing that
is the optimal solution of P2, if the circuit consumption
and the channel fading coefficient
are determined,
is determined. It has been analyzed in [
12] that the optimal power allocation for P2 adding the condition
should satisfy the following:
According to the above analysis, in our optimization problem,
and
should satisfy the following:
In addition, the last time slot should use up all the energy harvested and that remaining in the battery. Comprehensively considering the above analyses, finally, and should satisfy the following situations:
(1) When , then . We first set , if , ; if , ; if , .
(2) When , assume that . If , , ; if , , , ; if , , , .
(3) When , we can obtain from (23) and .
No matter what the situation is, the power allocation in the last time slot should be
It can be found from the above discussion that power allocation mainly depends on , and ; thus, Algorithm 1 next proposed is called the three-threshold algorithm:
| Algorithm 1. Optimal solution for the time-invariant channel |
1) Calculate , initialize:
, , ;
2) for :1: do
Linear search the largest and which can make feasible in (23), (24) and the condition should be satisfied;
for
if ( is an arbitrarily small value) or
for
are decided by and ;
;
; ;
end for
; ;
break;
end if
end for
end for
3) for
Compare the value of with and , then adjust and calculate ;
end for
4) ; . |
5. Optimal Offline Power Allocation for Time-Varying Channel
Now we consider the time-varying channel scenario, and the instantaneous transmission rate is still (4), so the optimization problem P3 is
P3 is still a convex optimization problem, and so we can also use the Lagrange multiplier method and the KKT conditions:
Other KKT conditions are the same as in (10), (11) and (12).
From (37) and (38), we can see that
where
is the water level and can be written as
For (41), we still use the definitions in [
13]:
In (42) and (43),
and
are two water-level thresholds and the function of them is similar with those of
and
. Obviously,
Like the time-invariant channel, the optimal solution should satisfy
Unlike the time-invariant channel, the channel may be in a very bad situation in some time slots where
. If this happens, the power allocation should be
The analysis of (39) is similar to the previous one, but the difference is that the value of
changes with
, and so
and
should satisfy
In addition, the policy in the last time slot should be
According to the above analyses, the optimal power allocation algorithm also has a three-threshold structure and depends on the values of , , and . Algorithm 2 is as follows:
| Algorithm 2. Optimal solution for the time-varying channel |
1) Calculate , initialize:
, , ;
2) for :1: do
Linear search the largest and which can make feasible in (45), (46) or in (47) and the condition should be satisfied;
for
if ( is an arbitrarily small value) or
for
are decided by and ;
;
; ;
end for
; ;
break;
end if
end for
end for
3) for
;
;
end for
4) ; . |
6. Online Power Allocation Policies
Inspired by the offline optimal algorithm, the online algorithm should have similar structural features. The offline optimal solution can calculate
,
,
and
exactly by the full information about the energy arrivals and channel states; then, the optimal power allocation is decided by these thresholds and
or
. However, when considering the online policies, we only know the information of the present moment and past moment, and so these thresholds need to be predicted. The prediction equations in [
13] are
In (52), is the probability density function of . In (53), is the probability density function of , is the joint probability density function of and , and because the two variables are independent of each other.
The disadvantage of this prediction method is that the calculated thresholds are fixed, which is not feasible for all time slots and
. Based on the solution of Equations (52) and (53), an adaptive-threshold algorithm is proposed in this paper. For the time-invariant channel, we first get
from (52); then, the adaptive threshold should be
In (54), two factors will affect the threshold: the storage efficiency
and time slot
. Obviously, the value of the threshold will increase when
becomes smaller or
becomes larger, and the strategy is reasonable because the transmitter should use more energy instead of storage when a time slot is close to the end or the storage efficiency
is small. In addition,
is calculated by (22), according to the analysis in the offline part; then, the online power allocation policy should be
For the time-varying channel, we first get
and then
is calculated by (44) and the online power allocation method is
7. Simulation Results and Analysis
The simulation tool is MATLAB 2014a in this paper (part of our MATLAB code is available in the
Supplementary File). The system model is as shown in
Figure 1 in part 3. The additive white Gaussian noise (AWGN) channel is adopted and we assume that the noise spectral density
, the bandwidth is 1 MHz and the path loss
between the transmitter and the receiver is -100 dB for the time-invariant channel. For the time-varying channel, the
obeys exponential distribution with
. The energy arrival of each time slot is independent and obeys the uniform distribution. We consider 10 time slots, and the length of each of time slot is 1 second.
and the capacity of the battery has no limit. The circuit consumption power is set to be 5 mW.
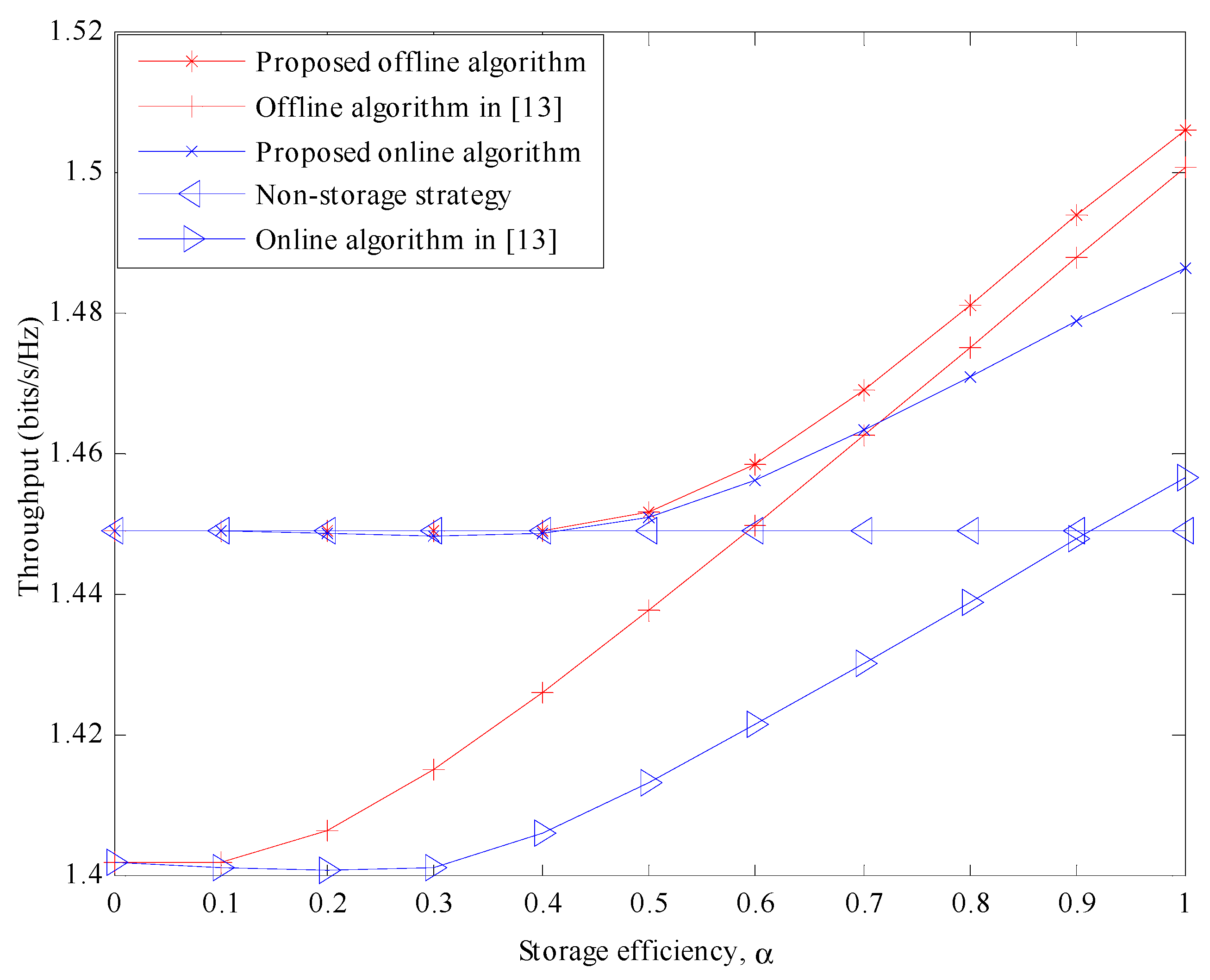
Figure 2 shows the performance changes of each algorithm as the storage efficiency of the battery is changed when the channel is time-invariant. The energy arrivals obey the uniform distribution of [5, 15] mJ. The non-storage strategy means that the energy of the current slot is completely expended in the slot and the power allocation policy is as in (27) and (28). It can be seen from the figure that the algorithm proposed in this paper is obviously superior to the algorithm in [
13] because compared with the algorithm in [
13], the factor of circuit consumption is considered in our optimization process. The curve of the adaptive-threshold online algorithm proposed in this paper is close to the offline optimal strategy curve while the gap between the double-threshold offline algorithm in [
13] and its corresponding fixed-threshold online algorithm is larger, which shows that the adaptive-threshold is more beneficial to improve the throughput. From
Figure 2, it can be also found that under the low storage efficiency, the strategy of non-storage has a great advantage, and with the increasing of storage efficiency, the disadvantage of non-storage strategy is gradually reflected.
Figure 3 shows the performance of each algorithm when the energy arrivals obey the uniform distribution of [5, 20] mJ and the channel is time-invariant. It can be found that the overall change trend of each algorithm is similar to
Figure 2. However, because of the increasing average value of energy arrivals, the overall throughput is obviously improved and the gap between the various algorithms gets larger. It is worth noting that with the improvement of storage efficiency, the double-threshold algorithm curve in [
13] is closer to the curve of the offline algorithm proposed in this paper. This is due to the improvements of the mean of the energy arrivals and the storage efficiency; the energy used in the transmission increases, while the circuit consumption is constant, which makes the influence of circuit consumption smaller.
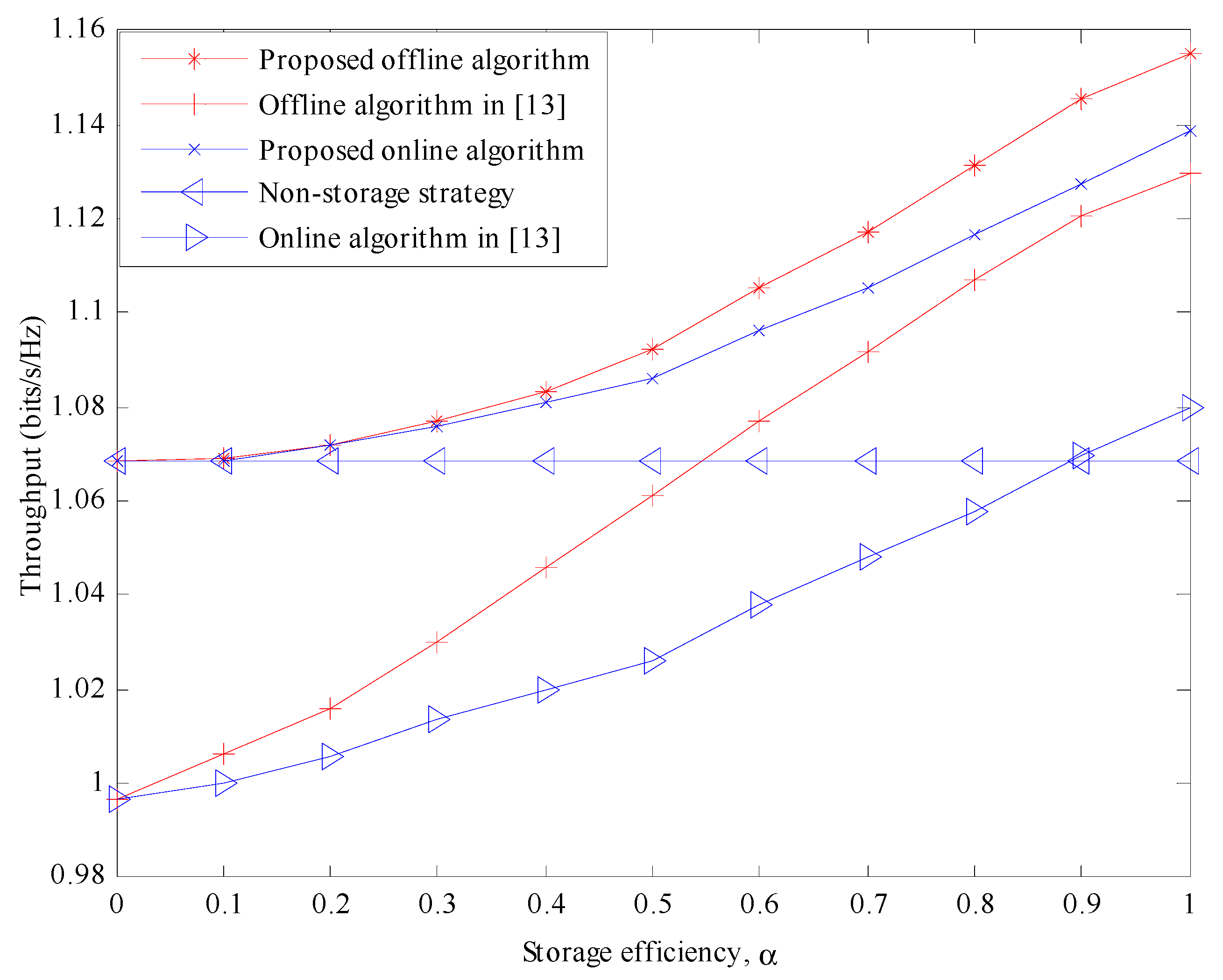
As shown in
Figure 4 and
Figure 5, the performance of each algorithm varies with the change of storage efficiency under the time-varying channel when the energy arrivals obey the uniform distribution of [5, 15] mJ and [5, 20] mJ, respectively. As can be seen from the pictures, the algorithm proposed in this paper is still superior to the algorithm in [
13]. However, the performance of the strategy of non-storage is not ideal, because the channel state is changing all the time and the strategy of non-storage may still transmit data when the channel is in a very poor state. As with the time-invariant channel scene, the adaptive-threshold online algorithm curve proposed in this paper is close to the curve of the offline algorithm. When the mean of energy arrival gets larger and the storage efficiency increases, the influence of circuit consumption decreases, and so the performance of the double-threshold algorithm in [
13] will be closer to the algorithm in this paper.
By changing the
, we get three curves in
Figure 6. It can be seen that the channel state plays a vital role and the performance of the proposed offline algorithm increases more obviously when the channel state improves.
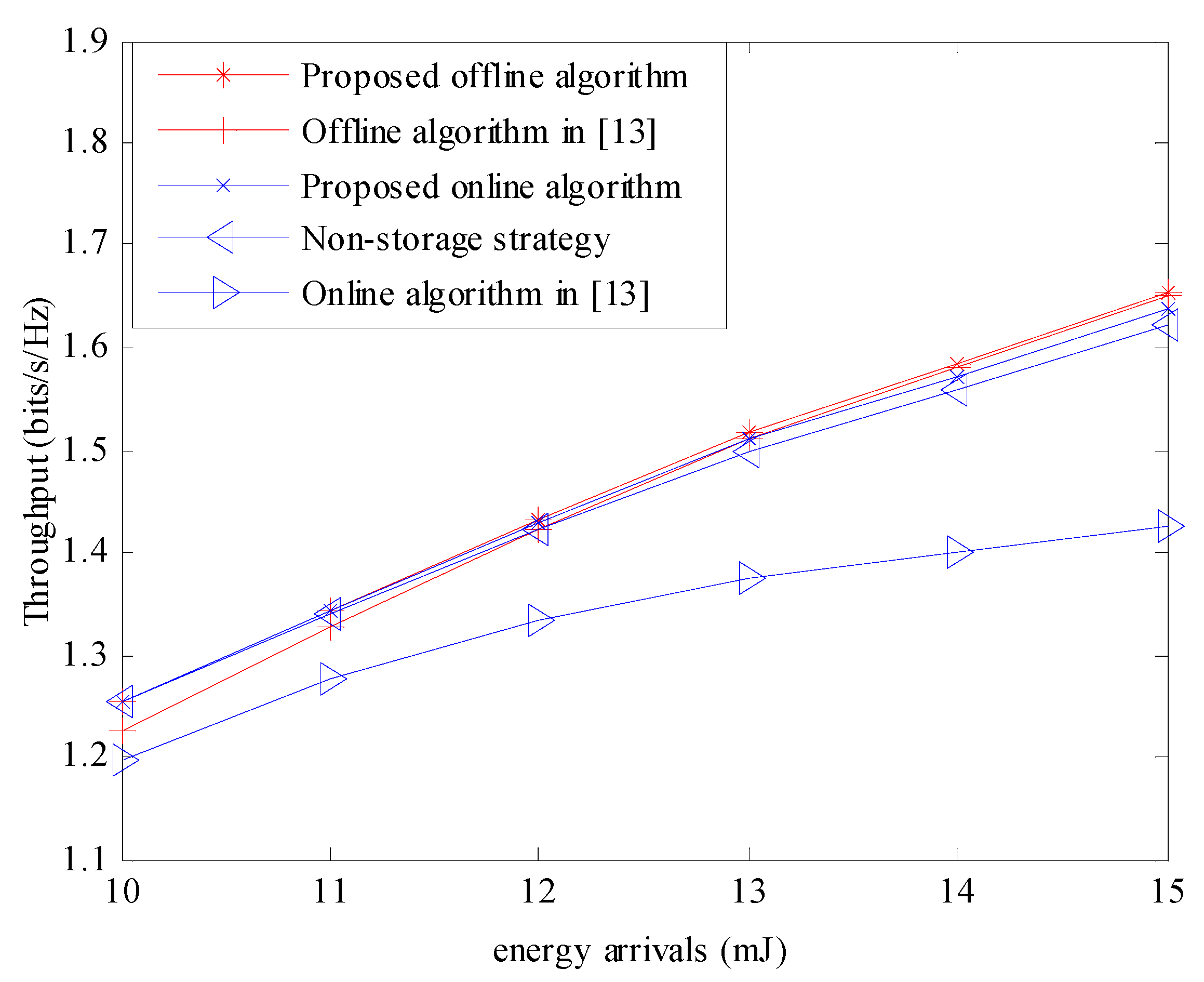
Figure 7 shows the performance of each algorithm when the storage efficiency is 60% and the channel is time-invariant. The performance of the online algorithm in [
13] is the worst, while the proposed offline algorithm in this paper is still the best.