Research on Fault Diagnosis of a Marine Fuel System Based on the SaDE-ELM Algorithm
Abstract
1. Introduction
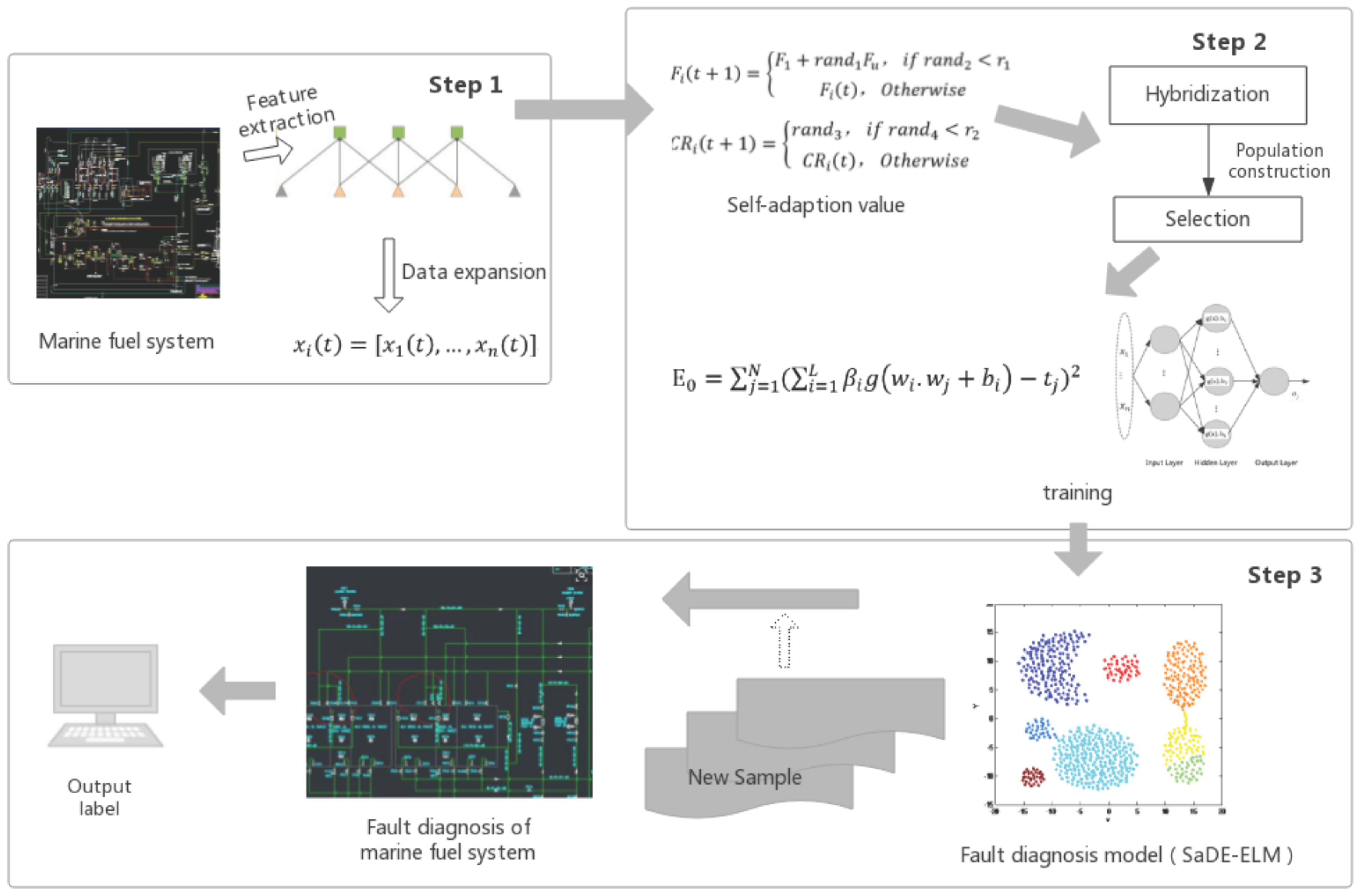
2. Research Framework
- (1)
- Extract the feature vectors of the state of the marine fuel system and use Gaussian white noise to expand the data samples;
- (2)
- A differential evolution algorithm is used to adaptively acquire the extreme learning initialization parameters, and the fault diagnosis model for marine fuel system is constructed for different types of data, and the minimum value of the objective function is estimated;
- (3)
- Get the test model with SaDE-ELM training and diagnose the most probable state of the marine fuel system according to the new sample.
3. Proposed Algorithm
- (1)
- The convergence of learning efficiency and algorithm is a positive relationship; that is, with the improvement of learning efficiency, the convergence of the algorithm is stronger, but when the learning efficiency is large enough, the stability of the algorithm will be worse, thus affecting the performance of the overall algorithm;
- (2)
- The algorithm is easy to fall into a local minimum, so when the algorithm finishes running, the operation ends at a distance far from the global minimum;
- (3)
- The training process of the algorithm can easily lead to the reduction of the overall generalization ability of the algorithm and thus affect the experimental accuracy of the algorithm;
- (4)
- The learning rules in the network are time-consuming and not conducive to the acquisition of real-time information.
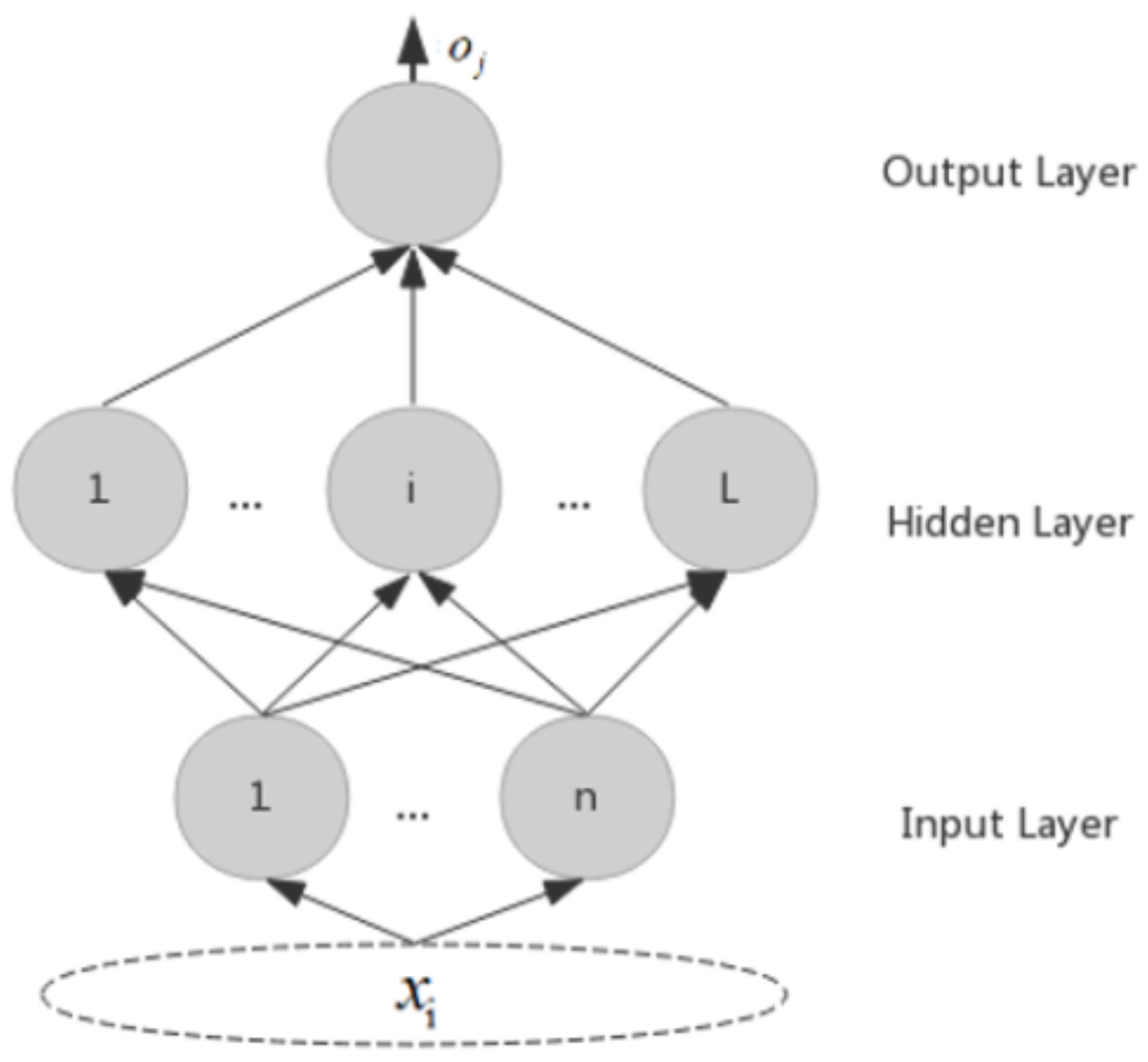
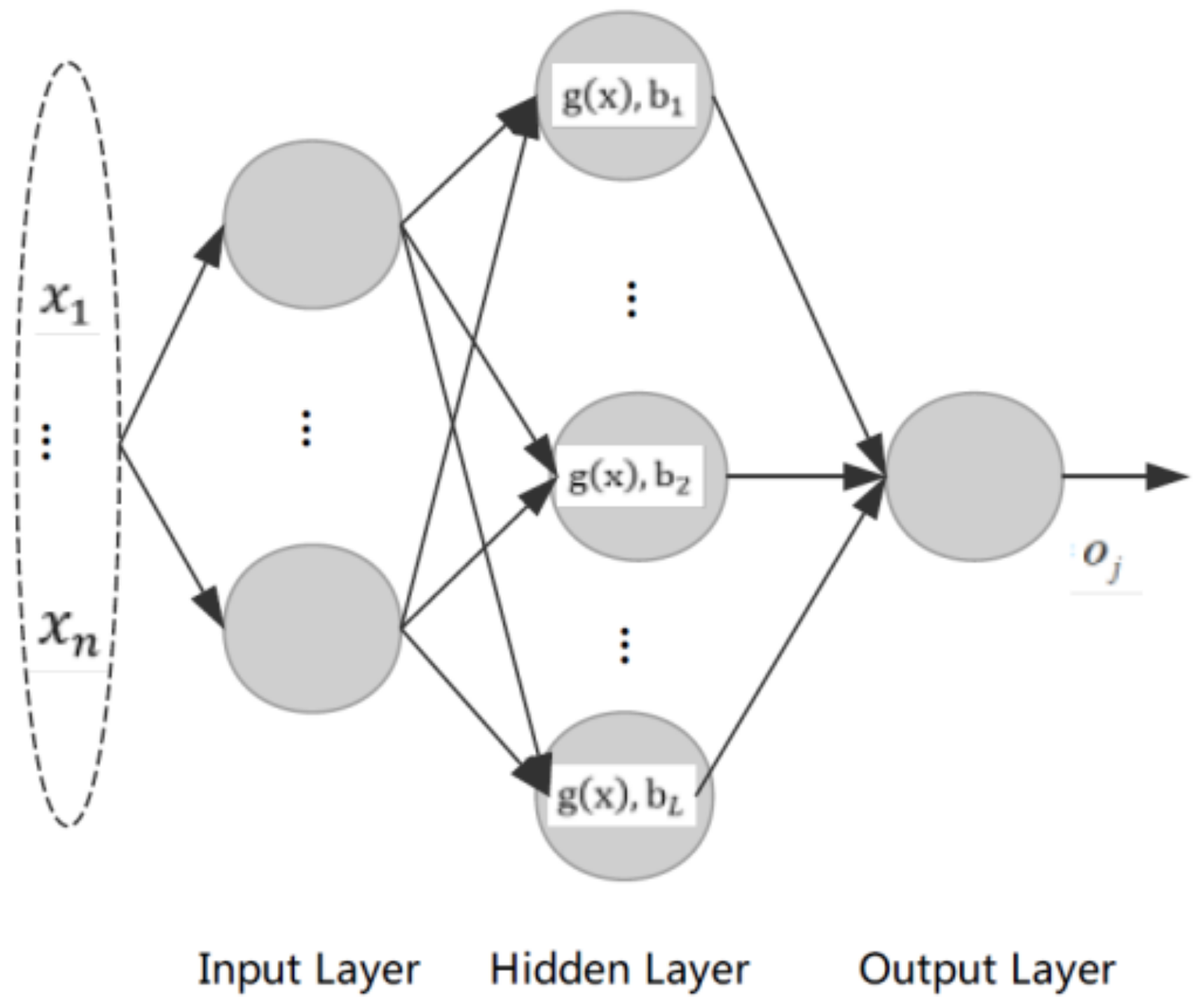
3.1. ELM Algorithm
- (1)
- Ease of use. The model does not have to set a large number of parameters, and the training speed does not need to intervene and also can obtain better experimental results;
- (2)
- Fast learning. The learning time of the model is quite short, which is more conducive to the user’s real-time information acquisition;
- (3)
- Generalization performance is high, and the ELM algorithm has a better generalization performance for different data types;
- (4)
- Activation function selection is flexible. Alternative types of activation function in ELM algorithms are adequate.
3.2. The Differential Evolution (DE) Algorithm
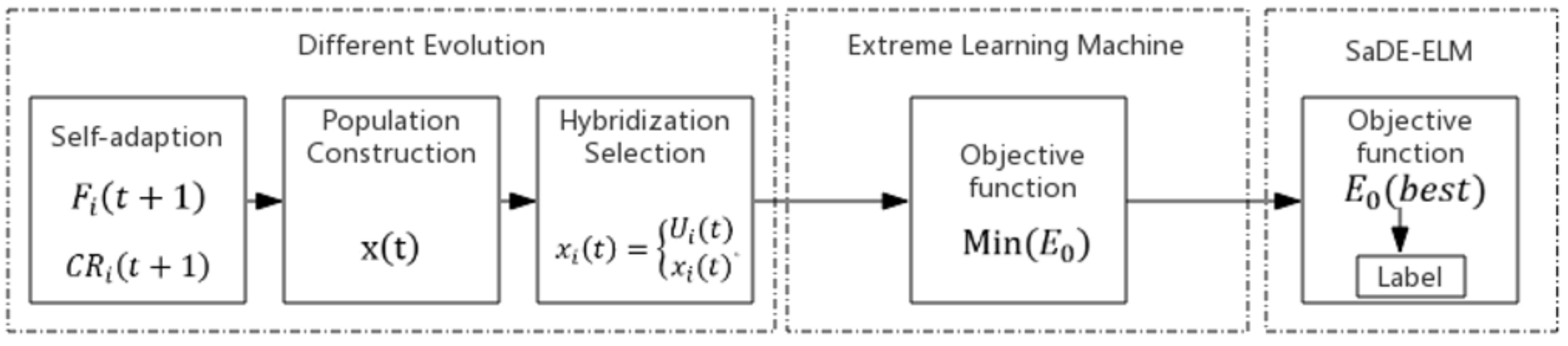
3.3. SaDE-ELM
- (1)
- The main parameters of SaDE-ELM: Scale factor F and hybrid probability CR. The parameters F and CR have a great influence on the convergence, stability and convergence speed of the DE algorithm. SaDE-ELM is proposed. The adjustment process of parameters F and CR is as follows:is the adaptive acquisition scaling factor. is the adaptive acquisition of hybrid probability and is an evenly distributed random number within the interval ; are evenly distributed random numbers within the interval . are adjustment parameters.
- (2)
- Construct groups. Based on adaptive acquisition parameters, construct new groups . Each sample is the state of feature matrix of the marine fuel system, namely .
- (3)
- Individuals of the groups are crossed and selected. The final choice of highly competitive individuals is as follows:represents the minimum value in the objective function, namely the objective function value of each individual in groups.
- (4)
- Define iteration errors. According to the defined number of iterations to determine whether the iteration is terminated, if you continue to step (2) within the iteration range, otherwise go to the next step.
- (5)
- Output the best iteration result, and corresponding hidden layer weight .
- (6)
- Output ELM algorithm of fault diagnosis results for a marine system.
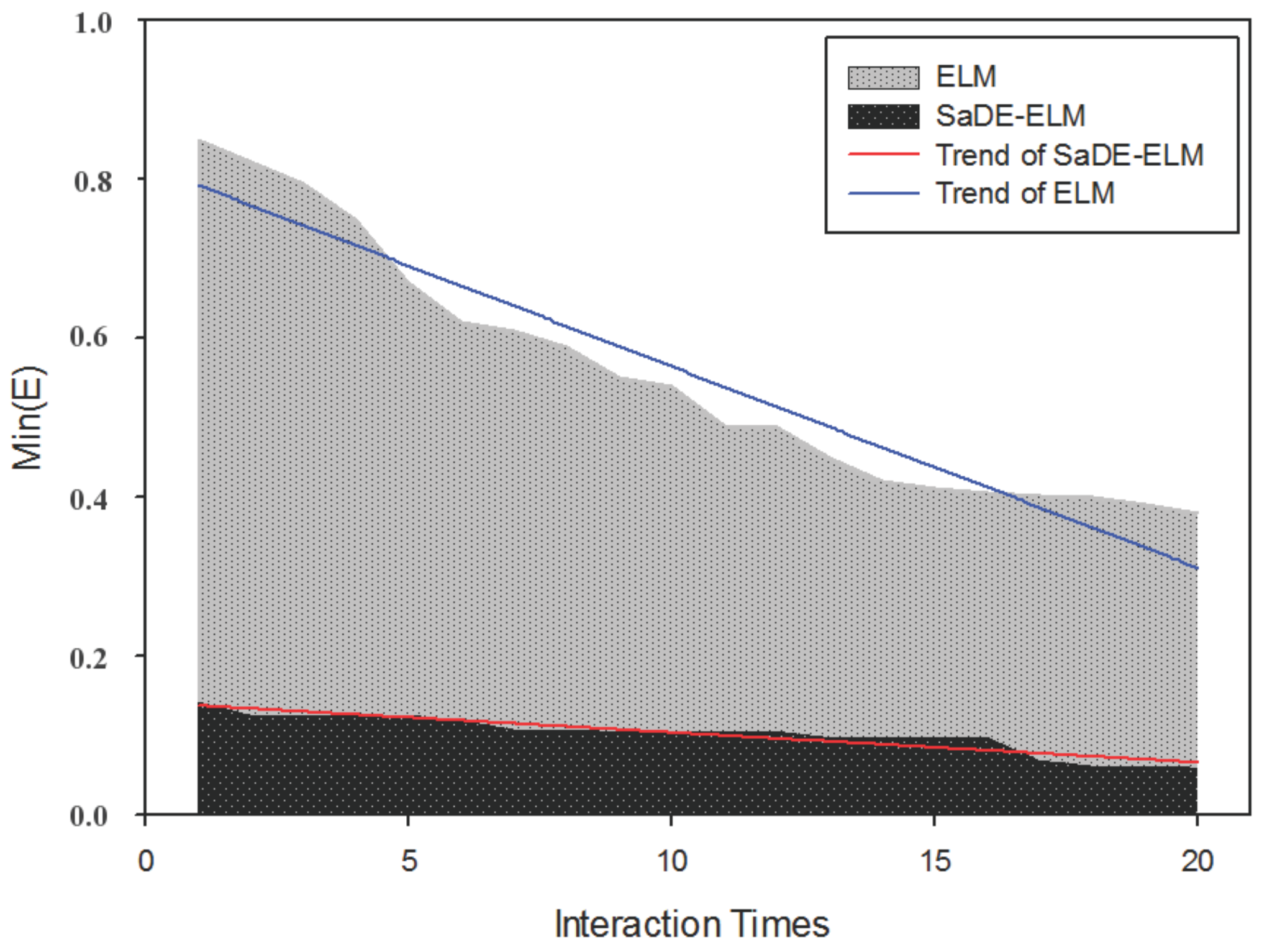
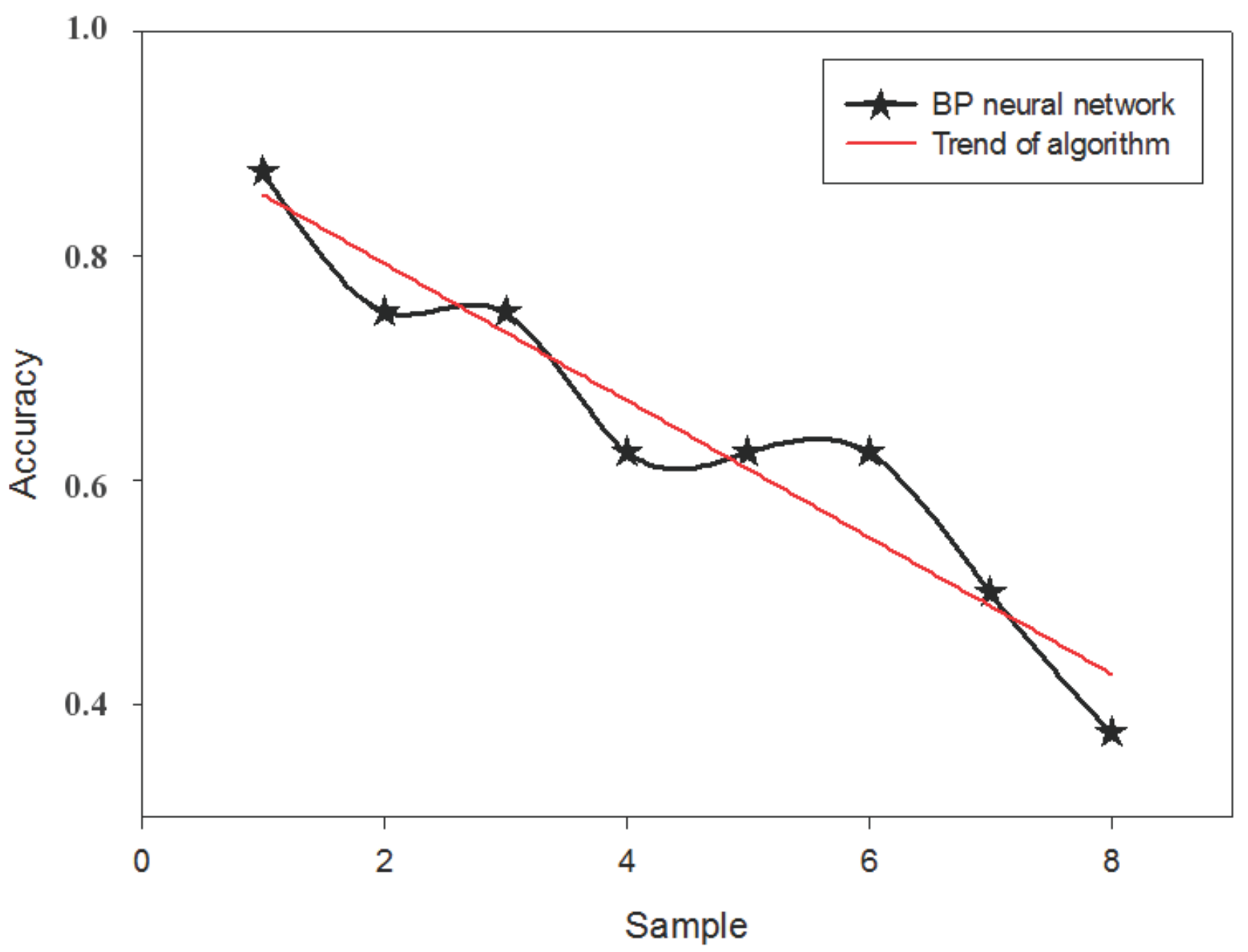
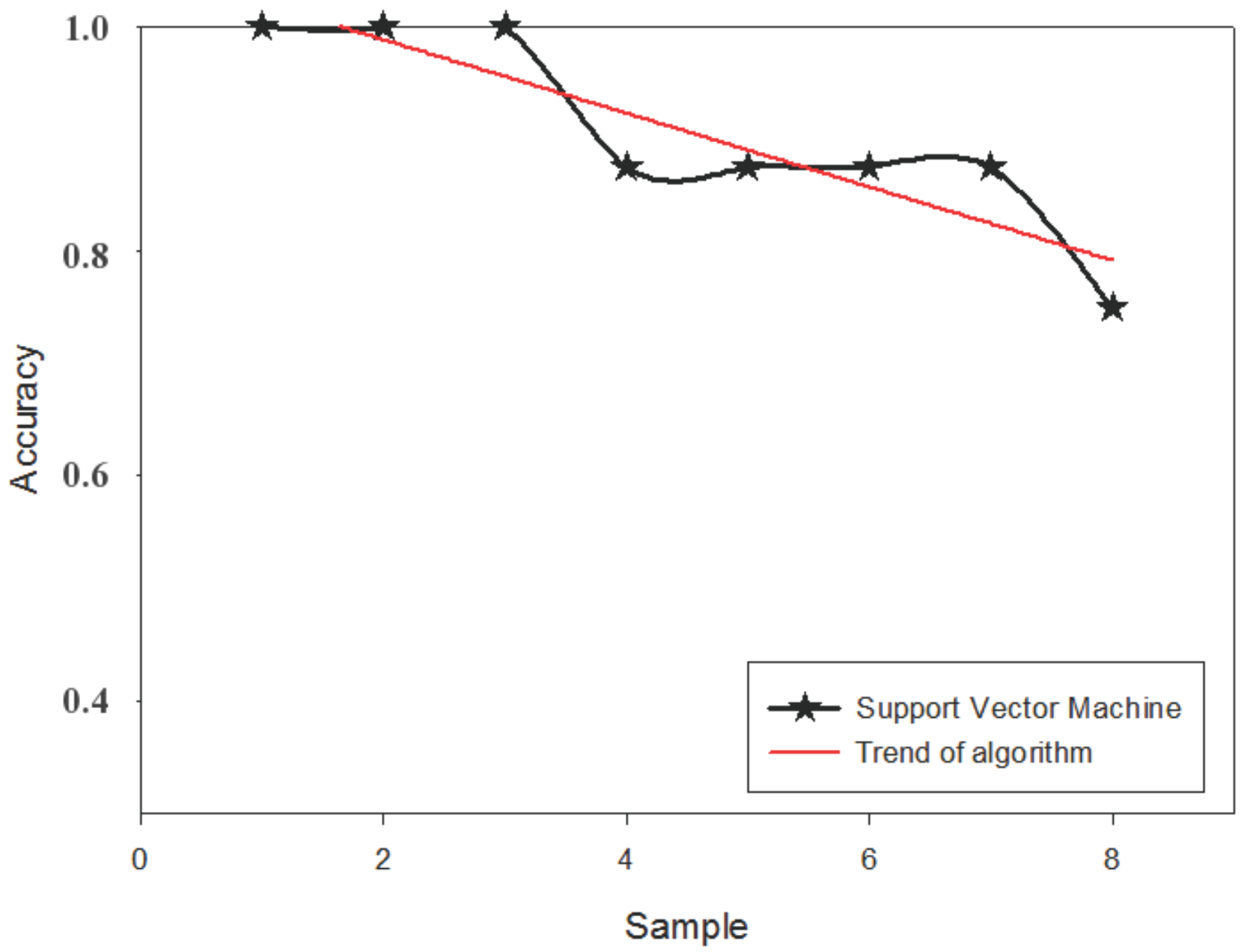
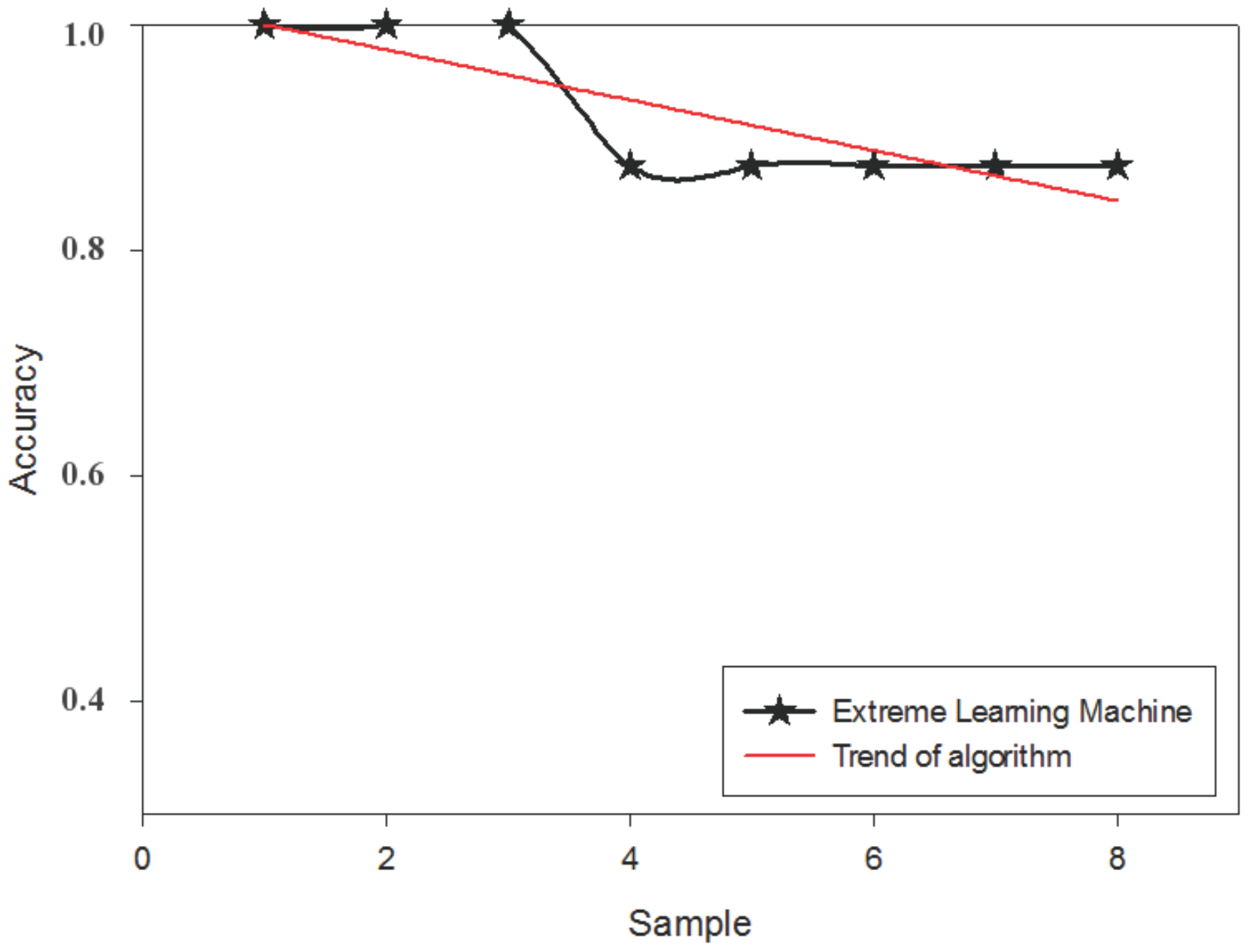
4. Model Construction and Simulation Experiment Results
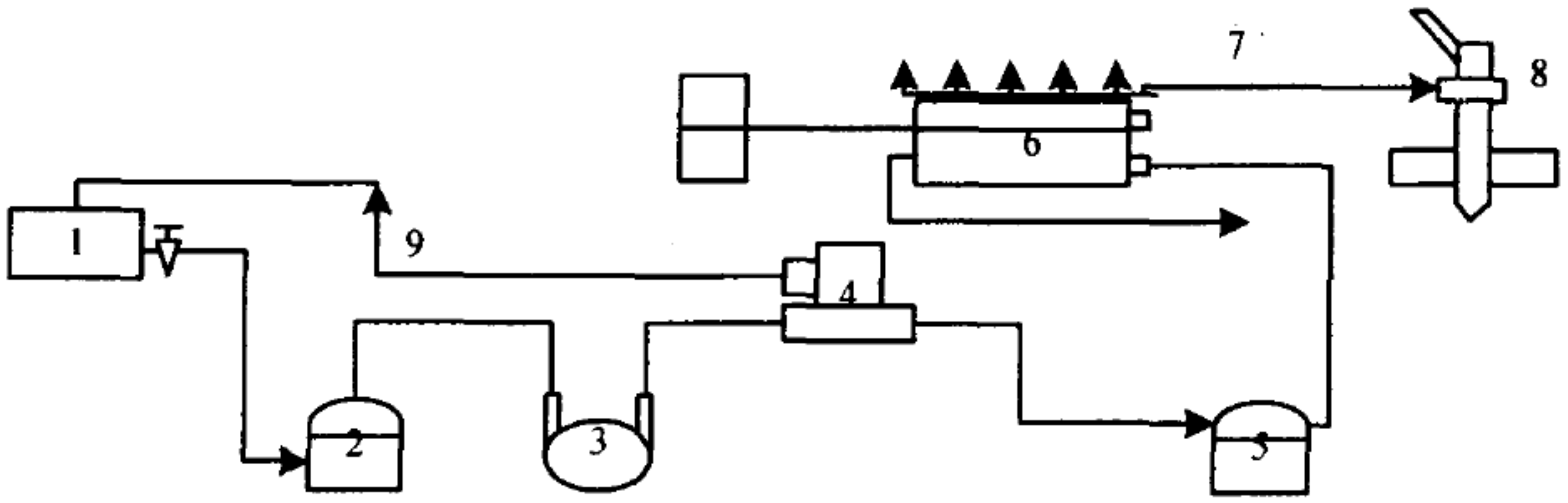
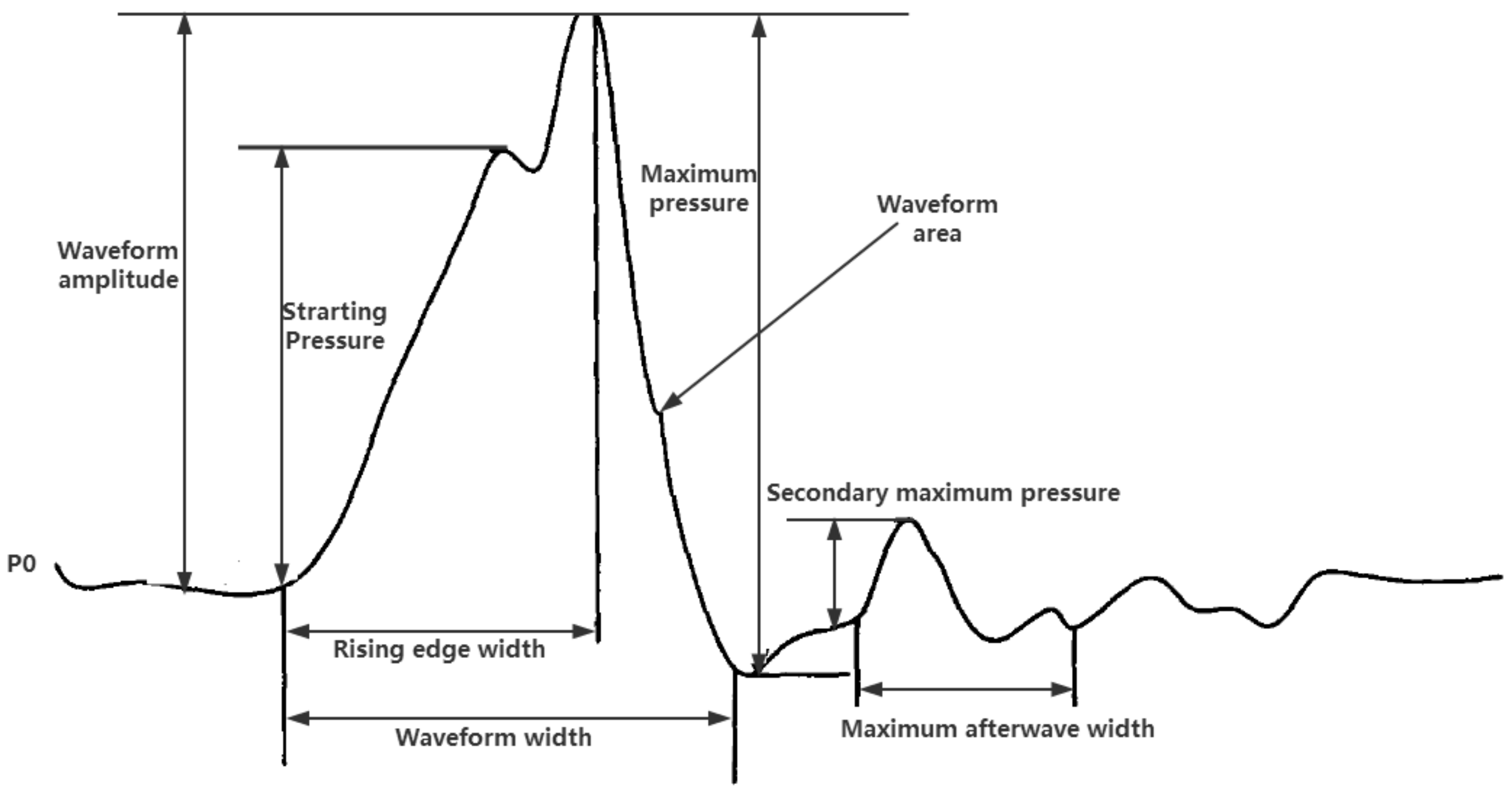
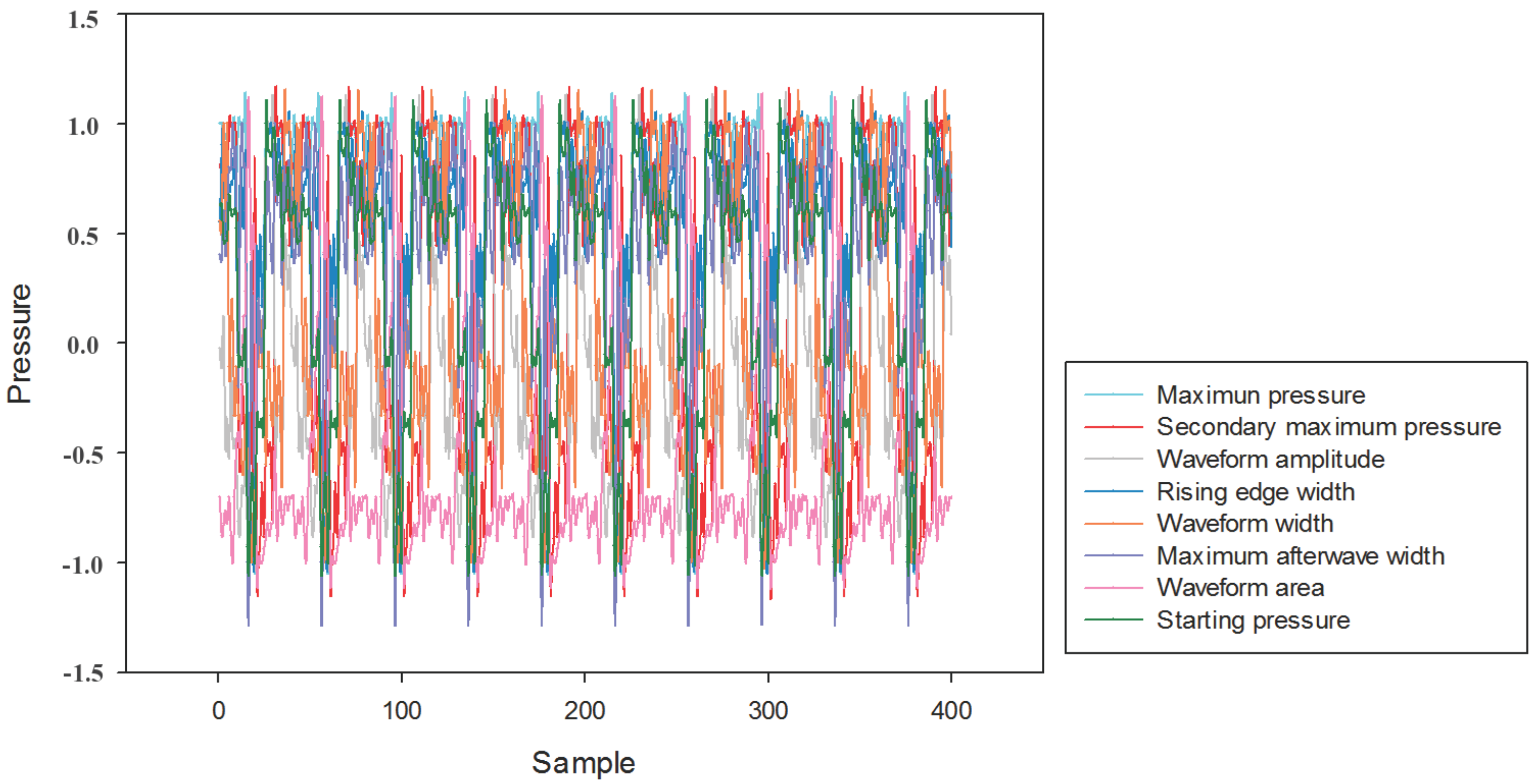
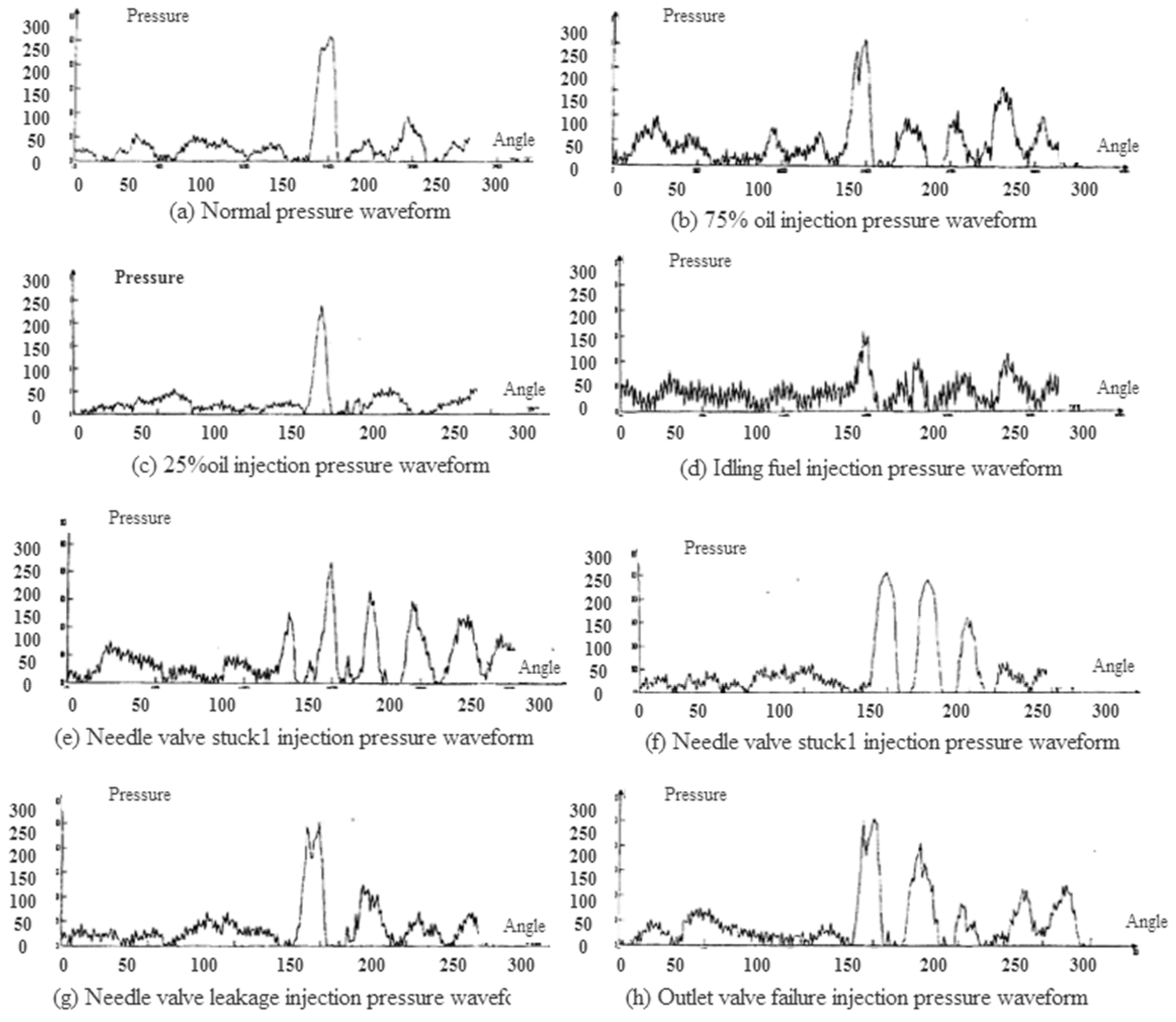
4.1. Extraction of Fault Feature for Marine Fuel System
4.2. Model Construction
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Han, L. Intelligent Fault Diagnosis Technology of Diesel Engine; National Defense Industry Press: Beijing, China, 2005. [Google Scholar]
- Liu, Y.; Zhang, J.; Qin, K.; Xu, Y. Diesel engine fault diagnosis using intrinsic time-scale decomposition and multistage Adaboost relevance vector machine. Proc. Inst. Mech. Eng. Part C 2018, 232, 881–894. [Google Scholar] [CrossRef]
- Govindaraj, T.; Su, Y.L.D. A model of fault diagnosis performance of expert marine engineers. Int. J. Man-Mach. Stud. 1988, 29, 1–20. [Google Scholar] [CrossRef]
- Autar, R.K. An automated diagnostic expert system for diesel engines. J. Eng. Gas Turbines Power 1996, 118, 673–679. [Google Scholar] [CrossRef]
- Cai, C.; Weng, X.; Zhang, C. A novel approach for marine diesel engine fault diagnosis. Clust. Comput. 2017, 20, 1691–1702. [Google Scholar] [CrossRef]
- Jiang, W.; Hu, W.; Xie, C. A new engine fault diagnosis method based on multi-sensor data fusion. Appl. Sci. 2017, 7, 280. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man. Cybern. B Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Jin, C.; Zhao, W.; Liu, Z.; Lee, J.; He, X. A vibration-based approach for diesel engine fault diagnosis. In Proceedings of the 2014 IEEE Conference on Prognostics and Health Management (PHM), Cheney, WA, USA, 22–25 June 2014; pp. 1–9. [Google Scholar]
- Widodo, A.; Yang, B.S. Support vector machine in machine condition monitoring and fault diagnosis. Mech. Syst. Signal Process. 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xu, Y.J. Fault Diagnosis for Diesel Engine Cylinder Head Based on Genetic-SVM Classifier. In Applied Mechanics and Materials; Trans Tech Publications: Zürich, Switzerland, 2014; Volume 590, pp. 390–393. [Google Scholar]
- Wang, Y.M.; Cui, T.; Zhang, F.J.; Dong, T.; Li, S. Fault diagnosis of diesel engine lubrication system based on PSO-SVM and centroid location algorithm. In Proceedings of the 2016 International Conference on Control, Automation and Information Sciences (ICCAIS), Ansan, Korea, 27–29 October 2016; pp. 221–226. [Google Scholar]
- Zhang, Z.; Guo, H. Research on Fault Diagnosis of Diesel Engine Based on PSO-SVM. In Proceedings of the 6th International Asia Conference on Industrial Engineering and Management Innovation, Tianjin, China, 25–26 July 2015; Atlantis Press: Paris, France, 2016; pp. 509–517. [Google Scholar]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M.; Schröder, J. Diagnosis and Fault-Tolerant Control; Springer: Berlin, Germany, 2006. [Google Scholar]
- Padma, K.; Vaisakh, K. Oposition-based modified differential evolution algorithm with SSVR device under different load conditions. In Proceedings of the IEEE Power, Communication and Information Technology Conference, Bhubaneswar, India, 15–17 October 2015; pp. 935–940. [Google Scholar]
- Li, Y.; Guo, P.; Li, X. Short-Term Load Forecasting Based on the Analysis of User Electricity Behavior. Algorithms 2016, 9, 80. [Google Scholar] [CrossRef]
- Tang, J.; Deng, C.; Huang, G.B. Extreme Learning Machine for Multilayer Perceptron. IEEE Trans. Neural Netw. Learn. Syst. 2017, 27, 809–821. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Lin, S.; Fang, J.; Xu, Z. Is extreme learning machine feasible? A theoretical assessment (part I). IEEE Trans. Neural Netw. Learn. Syst. 2017, 26, 7–20. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, D. Evolutionary Cost-Sensitive Extreme Learning Machine. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 3045–3060. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Dai, W.; Tang, L. A novel decomposition ensemble model with extended extreme learning machine for crude oil price forecasting. Eng. Appl. Artif. Intell. 2016, 47, 110–121. [Google Scholar] [CrossRef]
- Li, S.; You, Z.H.; Guo, H.; Luo, X.; Zhao, Z.Q. Inverse-Free Extreme Learning Machine with Optimal Information Updating. IEEE Trans. Cybern. 2016, 46, 1229. [Google Scholar] [CrossRef] [PubMed]
- Teo, T.T.; Logenthiran, T.; Woo, W.L. Forecasting of photovoltaic power using extreme learning machine. In Proceedings of the IEEE Innovative Smart Grid Technologies—Asia, Bangkok, Thailand, 3–6 November 2015; pp. 1–6. [Google Scholar]
- Sajjadi, S.; Shamshirband, S.; Alizamir, M.; Yee, L.; Mansor, Z.; Manaf, A.A.; Mostafaeipour, A. Extreme learning machine for prediction of heat load in district heating systems. Energy Build. 2016, 122, 222–227. [Google Scholar] [CrossRef]
- Sivalingam, K.C.; Mahendran, S.; Natarajan, S. Forecasting Gold Prices Based on Extreme Learning Machine. Int. J. Comput. Commun. Control 2016, 11, 372. [Google Scholar] [CrossRef]
- Liu, Z.X.; Zhen-Yu, L.U.; Huang, P.F. Parameter Identification of Space Robot Based on Recursive Different Evolution Algorithm. J. Astronaut. 2014, 35, 1127–1134. [Google Scholar]
- Naji, S.; Keivani, A.; Shamshirband, S.; Alengaram, U.J.; Jumaat, M.Z.; Mansor, Z.; Lee, M. Estimating building energy consumption using extreme learning machine method. Energy 2016, 97, 506–516. [Google Scholar] [CrossRef]
- Al-Yaseen, W.L.; Othman, Z.A.; Nazri, M.Z.A. Multi-level hybrid support vector machine and extreme learning machine based on modified K-means for intrusion detection system. Expert Syst. Appl. 2017, 67, 296–303. [Google Scholar] [CrossRef]
- Zhong, H.; Miao, C.; Shen, Z.; Feng, Y. Comparing the learning effectiveness of BP, ELM, I-ELM, and SVM for corporate credit ratings. Neurocomputing 2014, 128, 285–295. [Google Scholar] [CrossRef]
- Liu, Y. Research Progress on Different Evolution Algorithm. Sci. Mosaic 2013, 3, 004. [Google Scholar]
- Lu, Q.; Zhang, X.; Wen, S.; Lan, C. Comparison Four Different Probability Sampling Methods based on Differential Evolution Algorithm. J. Adv. Inf. Technol. 2012, 3, 206–214. [Google Scholar] [CrossRef]
- Fu-Heng, Q.U.; Ya-Ting, H.U.; Yang, Y.; Sun, S.Z.; Yuan, L.H. Differential evolution algorithm with different strategies and control parameters. J. Comput. Appl. 2011, 31, 3097–3100. [Google Scholar]
- Lin, J.L.; Tsai, Y.H.; Yu, C.Y.; Li, M.S. Interaction Enhanced Imperialist Competitive Algorithms. Algorithms 2012, 5, 433–448. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Corallo, A.; Margherita, A.; Pascali, G. Digital Mock-up to Optimize the Assembly of a Ship Fuel System. J. Model. Simul. Syst. 2010, 1, 4–12. [Google Scholar]


| Hidden Layer Number | Training Time | Training Error | Test Error | |||
|---|---|---|---|---|---|---|
| ELM | SaDE-ELM | ELM | SaDE-ELM | ELM | SaDE-ELM | |
| 1 | 0.121 | 3.791 | 0.875 | 0.8 | 1 | 1 |
| 5 | 1.342 | 6.522 | 0.275 | 0.125 | 0.275 | 0 |
| 10 | 2.527 | 11.357 | 0.125 | 0.1 | 0.125 | 0 |
| 15 | 3.712 | 11.388 | 0.075 | 0.05 | 0.075 | 0 |
| 20 | 3.855 | 18.767 | 0.065 | 0.05 | 0.065 | 0 |
| 25 | 4.521 | 19.032 | 0.025 | 0 | 0.025 | 0 |
| Algorithm | Training Time | Training Error | Test Error |
|---|---|---|---|
| BP neural network | 12.531 | 0.5 | 0.625 |
| SVM | 10.012 | 0.25 | 0.25 |
| SaDE-ELM | 19.032 | 0 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Yue, Y. Research on Fault Diagnosis of a Marine Fuel System Based on the SaDE-ELM Algorithm. Algorithms 2018, 11, 82. https://doi.org/10.3390/a11060082
Wei Y, Yue Y. Research on Fault Diagnosis of a Marine Fuel System Based on the SaDE-ELM Algorithm. Algorithms. 2018; 11(6):82. https://doi.org/10.3390/a11060082
Chicago/Turabian StyleWei, Yi, and Yaokun Yue. 2018. "Research on Fault Diagnosis of a Marine Fuel System Based on the SaDE-ELM Algorithm" Algorithms 11, no. 6: 82. https://doi.org/10.3390/a11060082
APA StyleWei, Y., & Yue, Y. (2018). Research on Fault Diagnosis of a Marine Fuel System Based on the SaDE-ELM Algorithm. Algorithms, 11(6), 82. https://doi.org/10.3390/a11060082





