A Novel Design of Sparse Prototype Filter for Nearly Perfect Reconstruction Cosine-Modulated Filter Banks
Abstract
:1. Introduction
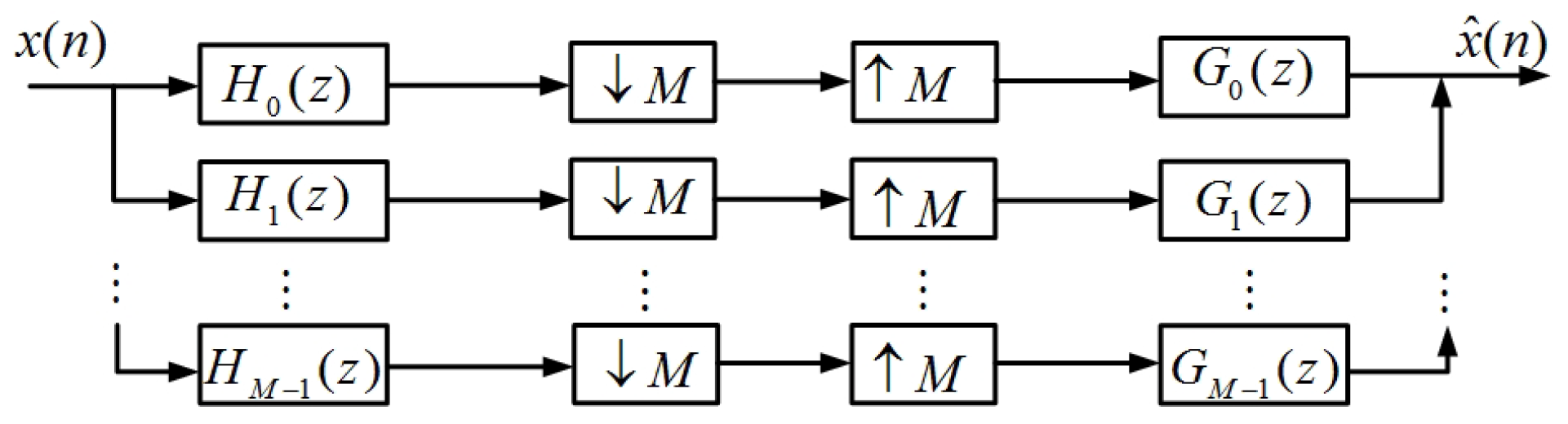
2. Perfect-Reconstruction Cosine-Modulated Filter Banks
3. The Design of Sparse Linear Phase FIR Prototype Filter of NPR Cosine-Modulated Filter Banks
4. Examples
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| NPR | Nearly Perfect-Reconstruction |
| WCLS | Weighted Constrained Least Square |
| QBPSO | Quantum-Behaved Particle Swarm Optimization |
| GI | gradient information |
| OMP | orthogonal matching pursuit |
References
- Hang, S.; Tian, L.; Ma, X.; Wei, Y. A reconfigurable sound wave decomposition filter bank for hearing aids based on nonlinear transformation. IEEE Tran. Biomed. Circuits Syst. 2016, 10, 487–496. [Google Scholar] [CrossRef] [PubMed]
- Ling, B.W.; Ho, C.Y.; Teo, K.; Siu, W.; Cao, J.; Dai, Q. Optimal design of cosine modulated nonuniform linear phase FIR filter bank via both stretching and shifting frequency response of single prototype filter. IEEE Trans. Signal Proc. 2014, 62, 2517–2530. [Google Scholar] [CrossRef]
- Kyochi, S.; Ikehara, M. A class of near shift-invariant and orientation-selective transform based on delay-less oversampled even-stacked cosine-modulated filter banks. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2010, E93.A, 724–733. [Google Scholar] [CrossRef]
- Zhao, N.; Pu, F.; Xu, X.; Chen, N. Cognitive wideband spectrum sensing using cosine-modulated filter banks. Int. J. Electron. 2015, 102, 1890–1901. [Google Scholar] [CrossRef]
- Sakiyama, A.; Watanabe, K.; Tanaka, Y. Spectral graph wavelets and filter banks with low approximation error. IEEE Trans. Signal Inf. Proc. Over Netw. 2016, 2, 230–245. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, G.K.; Anand, R.S. A simple design method for the cosine-modulated filter banks using weighted constrained least square technique. J. Frankl. Inst. Geophys. 2011, 348, 606–621. [Google Scholar] [CrossRef]
- Tan, F.; Zhang, T.; Gao, C.; Huang, L. Optimal design of cosine modulated filter banks using quantum-behaved particle swarm optimization algorithm. Image Signal Proc. 2011, 5, 2280–2284. [Google Scholar] [CrossRef]
- Zhang, Z.J. Efficient design of cosine modulated filter banks based on gradient information. IEEE Signal Proc. Lett. 2007, 14, 940–943. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Bube, K.P. Hybrid l1/l2 minimization with applications to tomography. Geophysics 1997, 62, 1183. [Google Scholar] [CrossRef]
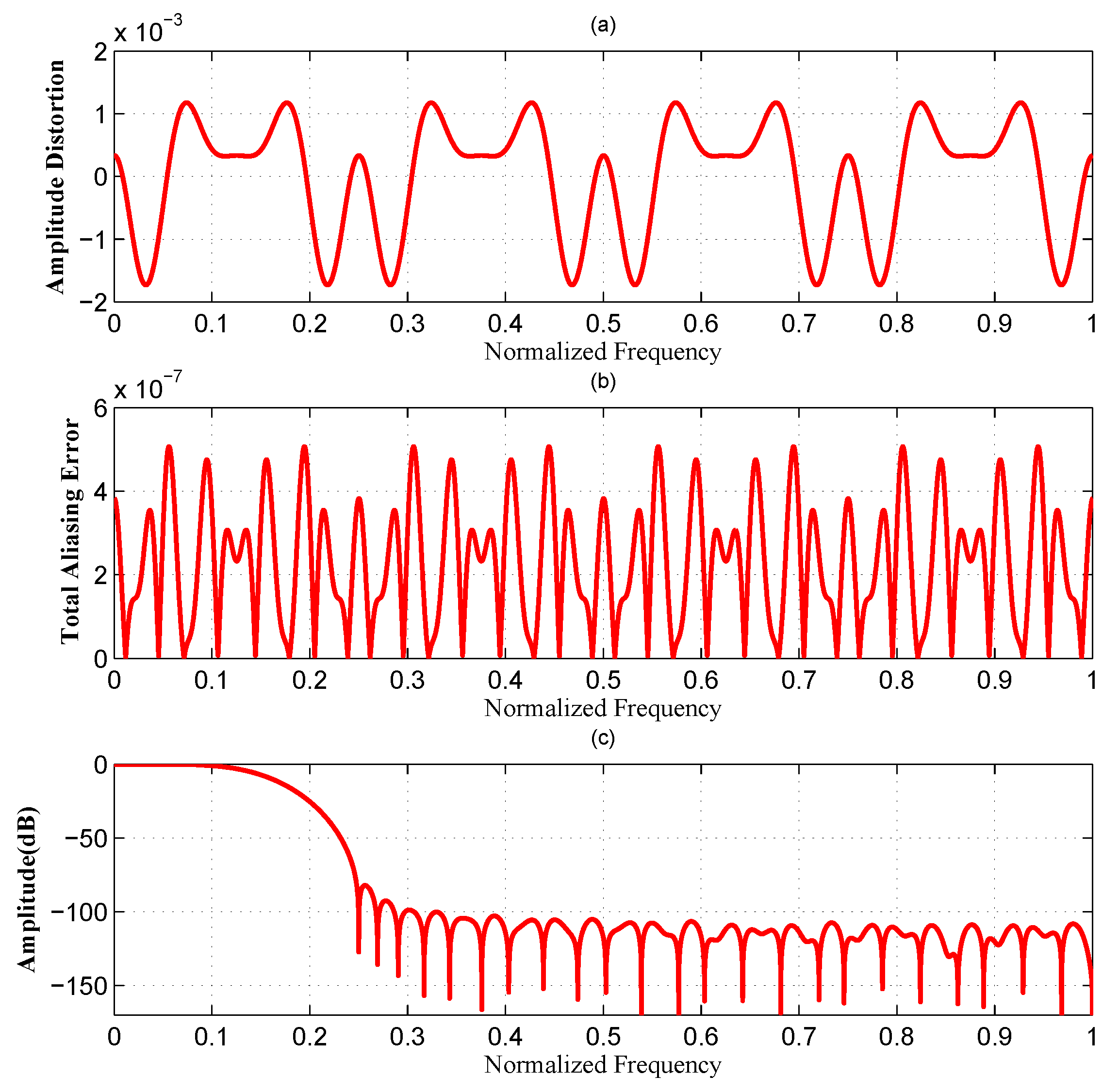
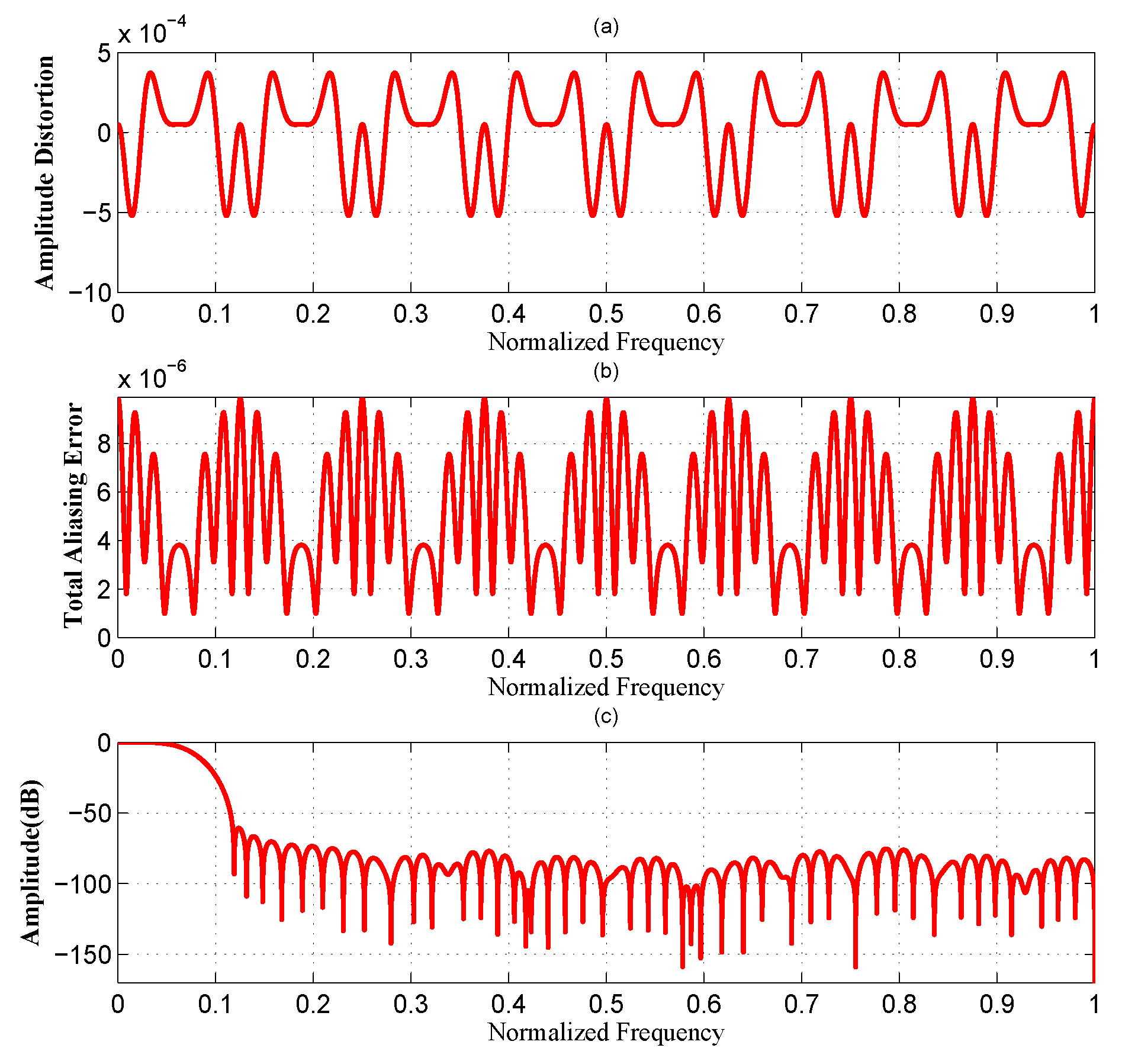
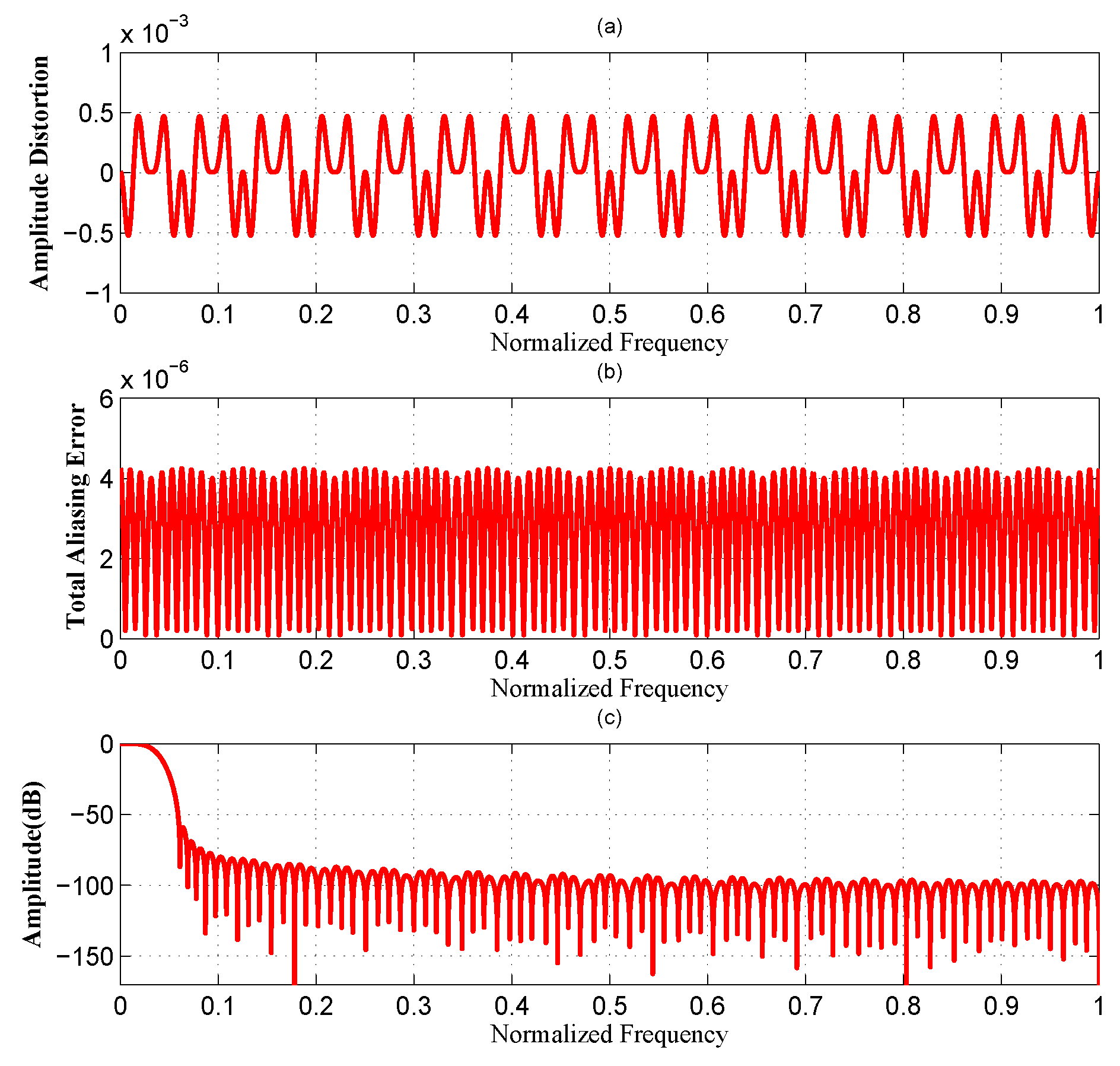
| M | Design Method | Filter Order | Number of Nonzero Taps | Amplitude Distortion | Total Aliasing Error |
|---|---|---|---|---|---|
| WCLS | 80 | 80 | |||
| 4 | QBPSO | 80 | 80 | ||
| Proposed Method | 140 | 62 | |||
| WCLS | 144 | 144 | |||
| 8 | GI | 132 | 132 | ||
| Proposed Method | 160 | 98 | |||
| WCLS | 224 | 224 | |||
| 16 | QBPSO | 256 | 256 | ||
| Proposed Method | 254 | 166 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Li, Y.; Miao, J.; Zhao, J.; Gao, X. A Novel Design of Sparse Prototype Filter for Nearly Perfect Reconstruction Cosine-Modulated Filter Banks. Algorithms 2018, 11, 77. https://doi.org/10.3390/a11050077
Xu W, Li Y, Miao J, Zhao J, Gao X. A Novel Design of Sparse Prototype Filter for Nearly Perfect Reconstruction Cosine-Modulated Filter Banks. Algorithms. 2018; 11(5):77. https://doi.org/10.3390/a11050077
Chicago/Turabian StyleXu, Wei, Yi Li, Jinghong Miao, Jiaxiang Zhao, and Xin Gao. 2018. "A Novel Design of Sparse Prototype Filter for Nearly Perfect Reconstruction Cosine-Modulated Filter Banks" Algorithms 11, no. 5: 77. https://doi.org/10.3390/a11050077
APA StyleXu, W., Li, Y., Miao, J., Zhao, J., & Gao, X. (2018). A Novel Design of Sparse Prototype Filter for Nearly Perfect Reconstruction Cosine-Modulated Filter Banks. Algorithms, 11(5), 77. https://doi.org/10.3390/a11050077





