A New Oren–Nayar Shape-from-Shading Approach for 3D Reconstruction Using High-Order Godunov-Based Scheme
Abstract
1. Introduction
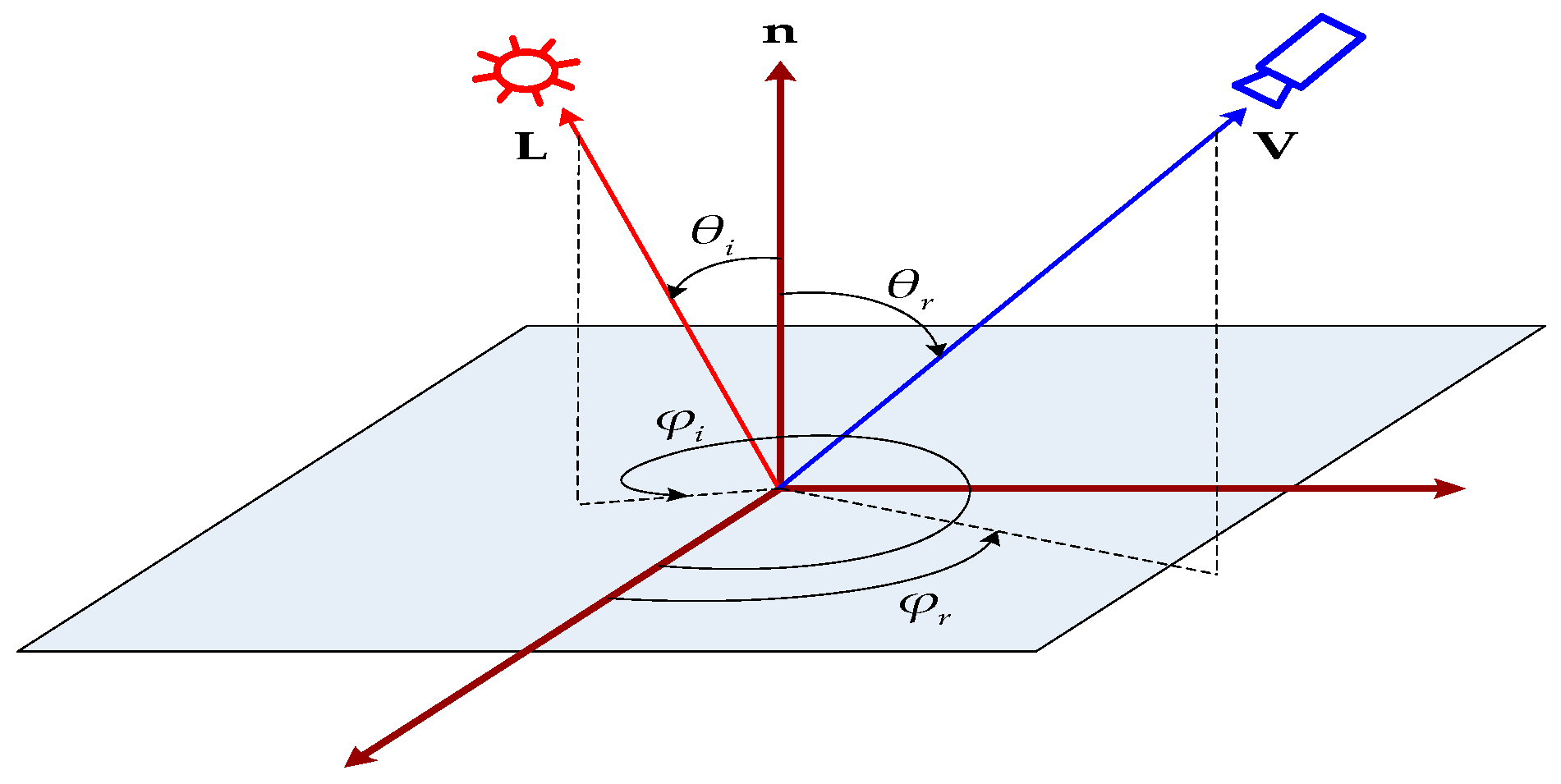
2. IIR for Oren–Nayar Reflectance
3. Numerical Algorithm for Solving the Resulting Eikonal PDE
3.1. High-Order Godunov-Based Scheme
3.2. Alternating Sweeping Strategy for Godunov-Based Scheme
- (1)
- Initialization: On the boundary we set the grid points to be accurate values, i.e., , which are unchanged during the iterations of the scheme. The approximated solution from the first-order Godunov-based scheme is applied as the initial guess for all other grid points.
- (2)
- Iterations with Alternating Sweepings Orderings: We calculate at th iteration, updated by the rules (19) using Gauss–Seidel iterations with the following four alternating sweepings orderings:
- ●
- ;
- ●
- ;
- ●
- ;
- ●
- .
- (3)
- Convergence Test: If , where is a known threshold value, the scheme stops and converges, or else comes back to (2). In this paper, is taken.
4. Experimental Results
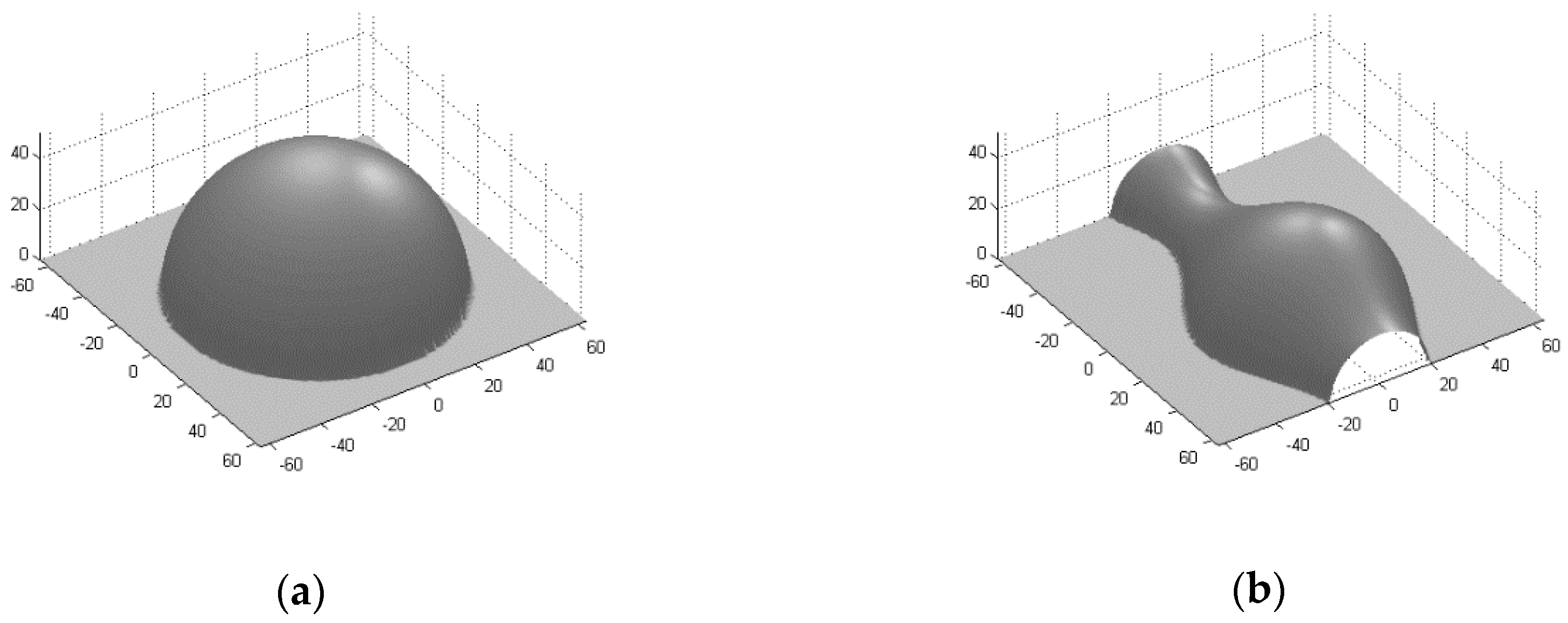
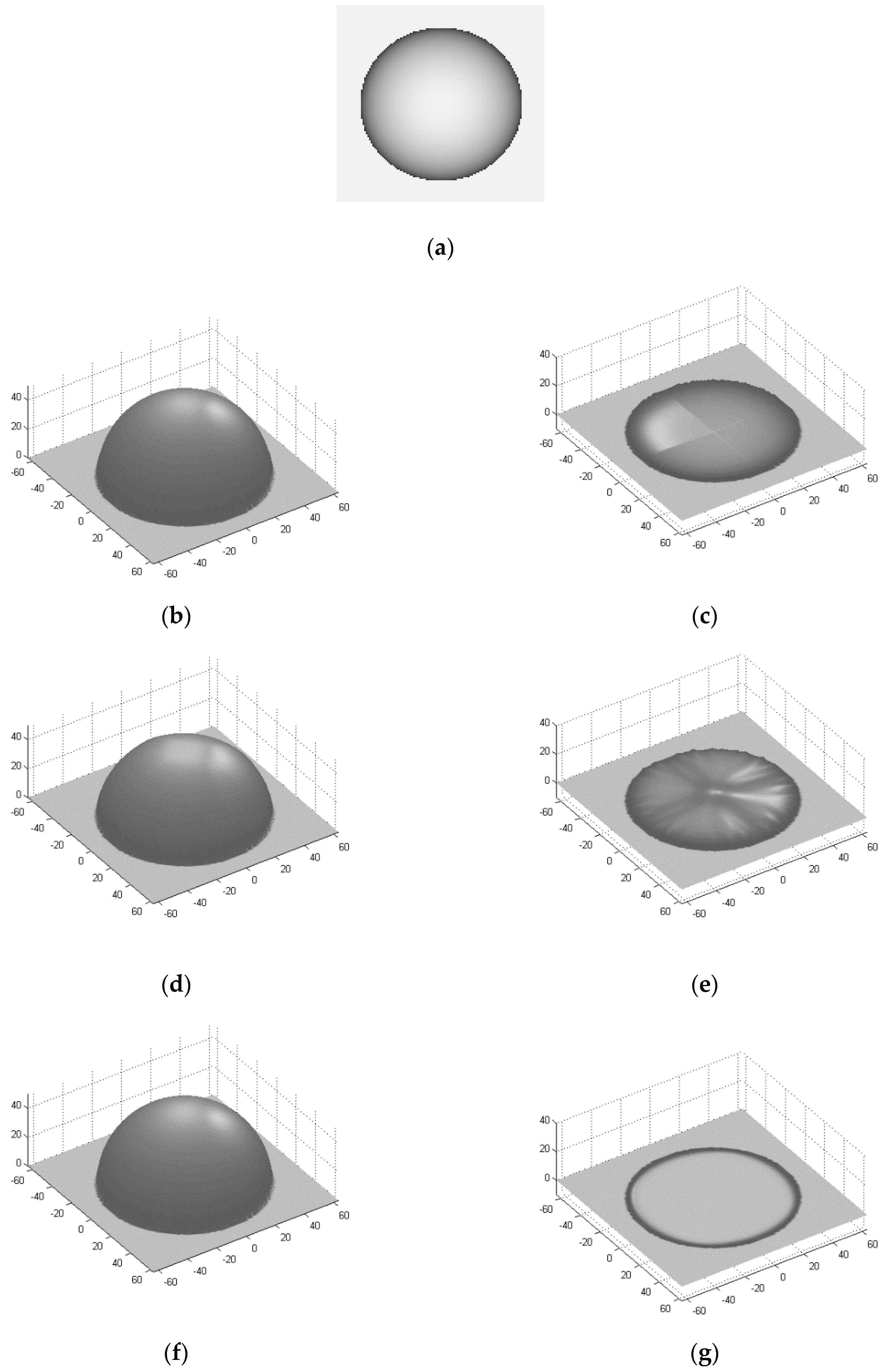
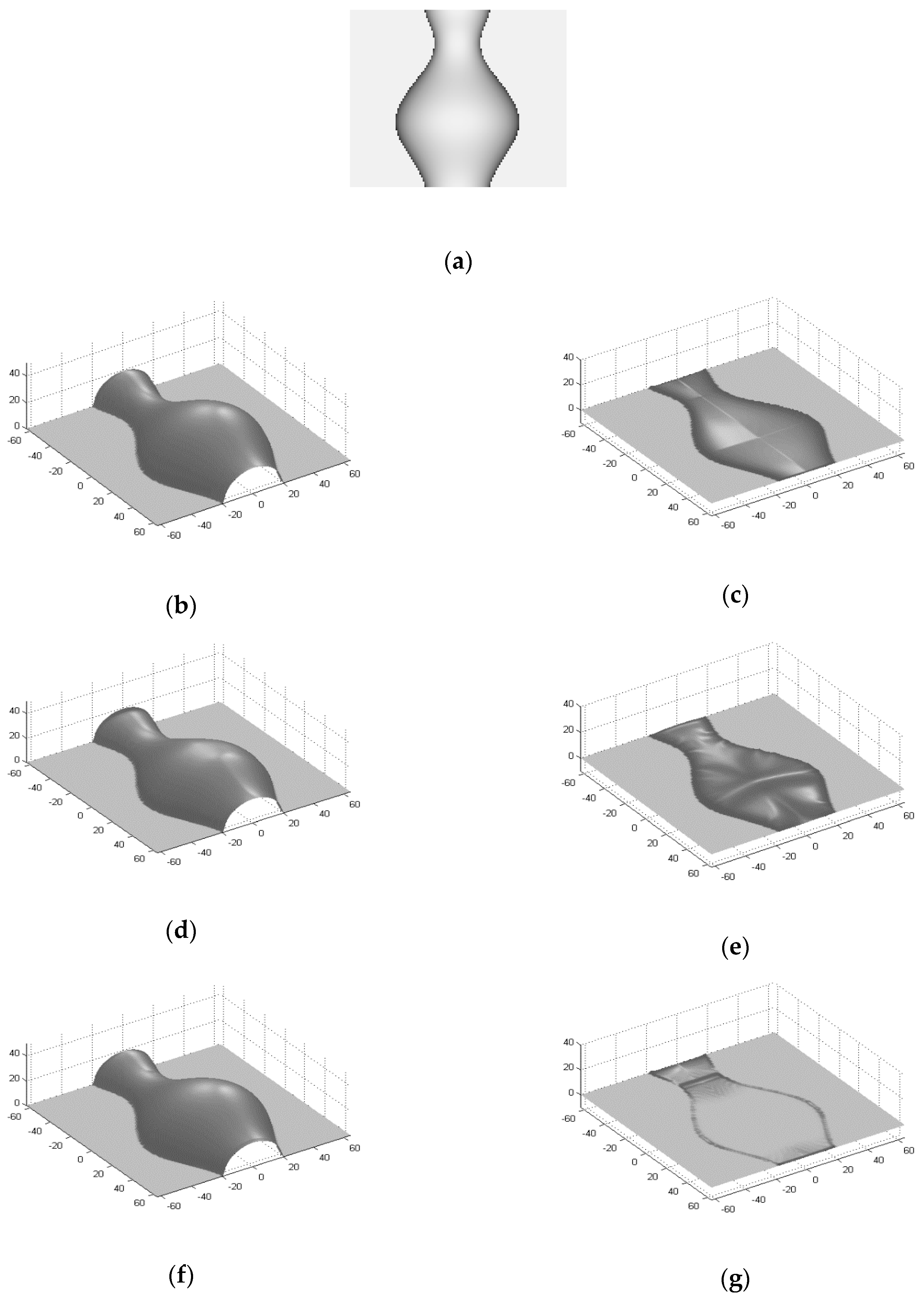
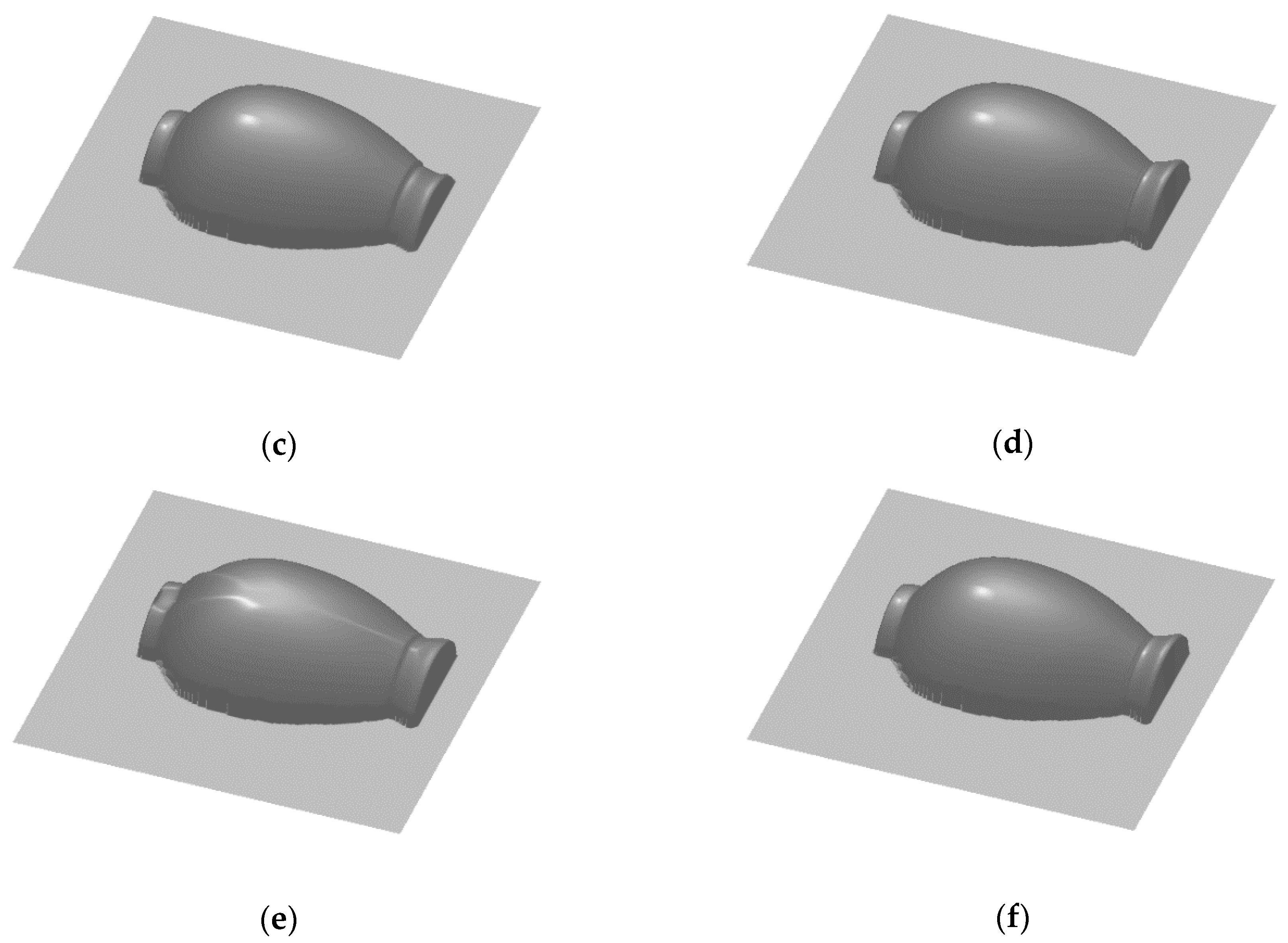
4.1. Experimental Results on Synthetic Images
4.2. Experimental Results on Real-World Image
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Horn, B.K.P. Shape from Shading: A Method for Obtaining the Shape of a Smooth Opaque Object from One View. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1970. [Google Scholar]
- Horn, B.K.P.; Brooks, M.J. The variational approach to shape from shading. Comput. Vis. Graph. Image Process. 1986, 33, 174–208. [Google Scholar] [CrossRef]
- Horn, B.K.P.; Brooks, M.J. Shape from Shading; MIT Press: Cambridge, MA, USA, 1989; ISBN 978-0-262-08183-2. [Google Scholar]
- Zhang, R.; Tsai, P.-S.; Cryer, J.E.; Shah, M. Shape from shading: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 690–706. [Google Scholar] [CrossRef]
- Durou, J.-D.; Falcone, M.; Sagona, M. Numerical methods for shape-from-shading: A new survey with benchmarks. Comput. Vis. Image Underst. 2008, 109, 22–43. [Google Scholar] [CrossRef]
- Tozza, S.; Falcone, M. Analysis and approximation of some shape-from-shading models for non-Lambertian surfaces. J. Math. Imaging Vis. 2016, 55, 153–178. [Google Scholar] [CrossRef]
- Rouy, E.; Tourin, A. A viscosity solutions approach to shape-from-shading. SIAM J. Numer. Anal. 1992, 29, 867–884. [Google Scholar] [CrossRef]
- Kimmel, R.; Sethian, J.A. Optimal algorithm for shape from shading and path planning. J. Math. Imaging Vis. 2001, 14, 237–244. [Google Scholar] [CrossRef]
- Prados, E.; Camilli, F.; Faugeras, O. A unifying and rigorous shape from shading method adapted to realistic data and applications. J. Math. Imaging Vis. 2006, 25, 307–328. [Google Scholar] [CrossRef]
- Breuß, M.; Cristiani, E.; Durou, J.-D.; Falcone, M.; Vogel, O. Numerical algorithms for perspective shape from shading. Kybernetika 2010, 46, 207–225. [Google Scholar]
- Breuß, M.; Cristiani, E.; Durou, J.-D.; Falcone, M.; Vogel, O. Perspective shape from shading: Ambiguity analysis and numerical approximations. SIAM J. Imaging Sci. 2012, 5, 311–342. [Google Scholar] [CrossRef]
- Sethian, J.A. Fast marching methods. SIAM Rev. 1999, 41, 199–235. [Google Scholar] [CrossRef]
- Lee, K.M.; Kuo, C.-C.J. Shape from shading with perspective projection. Comput. Vis. Graph. Image Process. 1994, 59, 202–212. [Google Scholar] [CrossRef]
- Courteille, F.; Crouzil, A.; Durou, J.-D.; Gurdjos, P. 3D-spline reconstruction using shape from shading: Spline from shading. Image Vis. Comput. 2008, 26, 466–479. [Google Scholar] [CrossRef]
- Quéau, Y.; Mélou, J.; Castan, F.; Cremers, D.; Durou, J.-D. A variational approach to shape-from-shading under natural illumination. In Proceedings of the International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition (EMMCVPR 2017), Venice, Italy, 30 October–1 November 2017; Pelillo, M., Hancock, E., Eds.; Springer International Publishing AG: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Scheffler, R.; Yarahmadi, A.M.; Breuß, M.; Köhler, E. A graph theoretic approach for shape from shading. In Proceedings of the International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition (EMMCVPR 2017), Venice, Italy, 30 October–1 November 2017; Pelillo, M., Hancock, E., Eds.; Springer International Publishing AG: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Oren, M.; Nayar, S.K. Generalization of the Lambertian model and implications for machine vision. Int. J. Comput. Vis. 1995, 14, 227–251. [Google Scholar] [CrossRef]
- Samaras, D.; Metaxas, D. Incorporating illumination constraints in deformable models for shape from shading and light direction estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 247–260. [Google Scholar] [CrossRef]
- Ragheb, H.; Hancock, E.R. Surface radiance correction for shape from shading. Pattern Recognit. 2005, 38, 1574–1595. [Google Scholar] [CrossRef]
- Ahmed, A.H.; Farag, A.A. Shape from shading under various imaging conditions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2007), Minneapolis, MN, USA, 17–22 June 2007; IEEE Press: Piscataway, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Kao, C.-Y.; Osher, S.; Qian, J. Lax-Friedrichs sweeping scheme for static Hamilton-Jacobi equations. J. Comput. Phys. 2004, 196, 367–391. [Google Scholar] [CrossRef]
- Ahmed, A.H.; Farag, A.A. A new formulation for shape from shading for non-Lambertian surfaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2006), New York, NY, USA, 17–22 June 2006; IEEE Press: Piscataway, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Ju, Y.C.; Tozza, S.; Breuß, M.; Bruhn, A.; Kleefeld, A. Generalised perspective shape from shading with Oren-Nayar reflectance. In Proceedings of the 24th British Machine Vision Conference (BMVC 2013), Bristol, UK, 9–13 September 2013; Burghardt, T., Damen, D., Mayol-Cuevas, W., Mirmehdi, M., Eds.; BMVA Press: Durham, UK, 2013. [Google Scholar] [CrossRef]
- Galliani, S.; Ju, Y.C.; Breuß, M.; Bruhn, A. Generalised perspective shape from shading in spherical coordinates. In Proceedings of the International Conference on Scale Space and Variational Methods in Computer Vision (SSVM 2013), Leibnitz, Austria, 2–6 June 2013; Kuijper, A., Bredies, K., Pock, T., Bischof, H., Eds.; Springer Press: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Wang, G.; Liu, S.; Han, J.; Zhang, X. A novel shape from shading algorithm for non-Lambertian surfaces. In Proceedings of the 3rd International Conference on Measuring Technology and Mechatronics Automation (ICMTMA 2011), Shangshai, China, 6–7 January 2011; IEEE Press: Piscataway, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Tozza, S.; Falcone, M. A comparison of non-Lambertian models for the shape-from-shading problem. In New Perspectives in Shape Analysis; Breuß, M., Bruckstein, A., Maragos, P., Wuhrer, S., Eds.; Springer International Publishing AG: Cham, Switzerland, 2016; pp. 15–42. ISBN 978-3-319-24724-3. [Google Scholar] [CrossRef]
- Zhang, Y.-T.; Zhao, H.-K.; Qian, J. High order fast sweeping methods for static Hamilton-Jacobi equations. J. Sci. Comput. 2006, 29, 25–56. [Google Scholar] [CrossRef]
- Tsai, Y.-H.R.; Cheng, L.-T.; Osher, S.; Zhao, H.-K. Fast sweeping algorithms for a class of Hamilton-Jacobi equations. SIAM J. Numer. Anal. 2003, 41, 673–694. [Google Scholar] [CrossRef]
- Zhao, H.-K. A fast sweeping method for eikonal equations. Math. Comput. 2005, 74, 603–627. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Chu, Y. A New Oren–Nayar Shape-from-Shading Approach for 3D Reconstruction Using High-Order Godunov-Based Scheme. Algorithms 2018, 11, 75. https://doi.org/10.3390/a11050075
Wang G, Chu Y. A New Oren–Nayar Shape-from-Shading Approach for 3D Reconstruction Using High-Order Godunov-Based Scheme. Algorithms. 2018; 11(5):75. https://doi.org/10.3390/a11050075
Chicago/Turabian StyleWang, Guohui, and Yuanbo Chu. 2018. "A New Oren–Nayar Shape-from-Shading Approach for 3D Reconstruction Using High-Order Godunov-Based Scheme" Algorithms 11, no. 5: 75. https://doi.org/10.3390/a11050075
APA StyleWang, G., & Chu, Y. (2018). A New Oren–Nayar Shape-from-Shading Approach for 3D Reconstruction Using High-Order Godunov-Based Scheme. Algorithms, 11(5), 75. https://doi.org/10.3390/a11050075





