Single Machine Scheduling Problem with Interval Processing Times and Total Completion Time Objective
Abstract
1. Introduction
2. Problem Setting and the Related Results
3. The Optimality Box
3.1. An Example of the Problem
3.2. Properties of a Job Permutation Based on Blocks
| Algorithm 1 |
| Input: Segments for the jobs . The permutation . |
| Output: The optimality box for the permutation . |
| Step 1: FOR to n DO set , END FOR |
| set , |
| Step 2: FOR to n DO |
| IF THEN set ELSE set END FOR |
| Step 3: FOR to 1 STEP DO |
| IF THEN set ELSE set END FOR |
| Step 4: Set , |
| Step 5: FOR to n DO set , |
| END FOR |
| Step 6: Set STOP. |
3.3. The Largest Relative Perimeter of the Optimality Box
4. An Algorithm for Constructing a Job Permutation with the Largest Relative Perimeter of the Optimality Box
| Algorithm 2 |
| Input: Segments for the jobs . |
| Output: The permutation with the largest relative perimeter . |
| Step 1: IF the condition of Theorem 3 holds |
| THEN for any permutation STOP. |
| Step 2: IF the condition of Theorem 4 holds |
| THEN construct the permutation such that |
| using Procedure 2 described in the proof of Theorem 4 STOP. |
| Step 3: ELSE determine the set B of all blocks using the |
| -Procedure 1 described in the proof of Lemma 1 |
| Step 4: Index the blocks according to increasing |
| left bounds of their cores (Lemma 3) |
| Step 5: IF THEN problem is called problem |
| (Theorem 5) set GOTO step 8 ELSE set |
| Step 6: IF there exist two adjacent blocks and such |
| that ; let r denote the minimum of the above index |
| in the set THEN decompose the problem P into |
| subproblem with the set of jobs and subproblem |
| with the set of jobs using Lemma 4; |
| set , , GOTO step 7 ELSE |
| Step 7: IF THEN GOTO step 9 ELSE |
| Step 8: Construct the permutation with the largest relative perimeter |
| using Procedure 3 described in the proof of |
| Theorem 5 IF or GOTO step 12 ELSE |
| Step 9: IF there exists a block in the set B containing more than one |
| non-fixed jobs THEN construct the permutation with the |
| largest relative perimeter for the problem |
| using Procedure 5 described in Section 4.1 GOTO step 11 |
| Step 10: ELSE construct the permutation with the largest relative |
| perimeter for the problem using |
| -Procedure 4 described in the proof of Theorem 6 |
| Step 11: Construct the optimality box for the permutation |
| using Algorithm 1 IF and THEN |
| set , , , |
| GOTO step 6 ELSE IF THEN GOTO step 8 |
| Step 12: IF THEN set , determine the permutation |
| and the optimality box |
| GOTO step 13 |
| ELSE |
| Step 13: The optimality box has the largest value of |
| STOP. |
4.1. Procedure 5 for the Problem with Blocks Including More Than One Non-Fixed Jobs
4.2. The Application of Procedure 5 to the Small Example
5. An Approximate Solution to the Problem
| Algorithm 3 |
| Input: Segments for the jobs . |
| Output: The permutation and optimality box , which provide |
| the minimal value of the error function . |
| Step 1: IF the condition of Theorem 3 holds |
| THEN for any permutation |
| and the equality holds STOP. |
| Step 2: IF the condition of Theorem 4 holds |
| THEN using Procedure 2 construct |
| the permutation such that both equalities |
| and hold STOP. |
| Step 3: ELSE determine the set B of all blocks using the |
| -Procedure 1 described in the proof of Lemma 1 |
| Step 4: Index the blocks according to increasing |
| left bounds of their cores (Lemma 3) |
| Step 5: IF THEN problem is called problem |
| (Theorem 5) set GOTO step 8 ELSE set |
| Step 6: IF there exist two adjacent blocks and such |
| that ; let r denote the minimum of the above index |
| in the set THEN decompose the problem P into |
| subproblem with the set of jobs and subproblem |
| with the set of jobs using Lemma 4; |
| set , , GOTO step 7 ELSE |
| Step 7: IF THEN GOTO step 9 ELSE |
| Step 8: Construct the permutation with the minimal value of |
| the error function using Procedure 3 |
| IF or GOTO step 12 ELSE |
| Step 9: IF there exists a block in the set B containing more than one |
| non-fixed jobs THEN construct the permutation with |
| the minimal value of the error function for the problem |
| using Procedure 5 GOTO step 11 |
| Step 10: ELSE construct the permutation with the minimal value of the |
| error function for the problem using Procedure 3 |
| Step 11: Construct the optimality box for the permutation |
| using Algorithm 1 IF and THEN |
| set , , , |
| GOTO step 6 ELSE IF THEN GOTO step 8 |
| Step 12: IF THEN set , determine the permutation |
| and the optimality box: |
| GOTO step 13 |
| ELSE |
| Step 13: The optimality box has the minimal value |
| of the error function STOP. |
6. Computational Results
7. Concluding Remarks
Author Contributions
Conflicts of Interest
References
- Davis, W.J.; Jones, A.T. A real-time production scheduler for a stochastic manufacturing environment. Int. J. Prod. Res. 1988, 1, 101–112. [Google Scholar] [CrossRef]
- Pinedo, M. Scheduling: Theory, Algorithms, and Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Daniels, R.L.; Kouvelis, P. Robust scheduling to hedge against processing time uncertainty in single stage production. Manag. Sci. 1995, 41, 363–376. [Google Scholar] [CrossRef]
- Sabuncuoglu, I.; Goren, S. Hedging production schedules against uncertainty in manufacturing environment with a review of robustness and stability research. Int. J. Comput. Integr. Manuf. 2009, 22, 138–157. [Google Scholar] [CrossRef]
- Sotskov, Y.N.; Werner, F. Sequencing and Scheduling with Inaccurate Data; Nova Science Publishers: Hauppauge, NY, USA, 2014. [Google Scholar]
- Pereira, J. The robust (minmax regret) single machine scheduling with interval processing times and total weighted completion time objective. Comput. Oper. Res. 2016, 66, 141–152. [Google Scholar] [CrossRef]
- Grabot, B.; Geneste, L. Dispatching rules in scheduling: A fuzzy approach. Int. J. Prod. Res. 1994, 32, 903–915. [Google Scholar] [CrossRef]
- Kasperski, A.; Zielinski, P. Possibilistic minmax regret sequencing problems with fuzzy parameteres. IEEE Trans. Fuzzy Syst. 2011, 19, 1072–1082. [Google Scholar] [CrossRef]
- Özelkan, E.C.; Duckstein, L. Optimal fuzzy counterparts of scheduling rules. Eur. J. Oper. Res. 1999, 113, 593–609. [Google Scholar] [CrossRef]
- Braun, O.; Lai, T.-C.; Schmidt, G.; Sotskov, Y.N. Stability of Johnson’s schedule with respect to limited machine availability. Int. J. Prod. Res. 2002, 40, 4381–4400. [Google Scholar] [CrossRef]
- Sotskov, Y.N.; Egorova, N.M.; Lai, T.-C. Minimizing total weighted flow time of a set of jobs with interval processing times. Math. Comput. Model. 2009, 50, 556–573. [Google Scholar] [CrossRef]
- Sotskov, Y.N.; Lai, T.-C. Minimizing total weighted flow time under uncertainty using dominance and a stability box. Comput. Oper. Res. 2012, 39, 1271–1289. [Google Scholar] [CrossRef]
- Graham, R.L.; Lawler, E.L.; Lenstra, J.K.; Kan, A.H.G.R. Optimization and Approximation in Deterministic Sequencing and Scheduling. Ann. Discret. Appl. Math. 1979, 5, 287–326. [Google Scholar]
- Smith, W.E. Various optimizers for single-stage production. Nav. Res. Logist. Q. 1956, 3, 59–66. [Google Scholar] [CrossRef]
- Lai, T.-C.; Sotskov, Y.N.; Egorova, N.G.; Werner, F. The optimality box in uncertain data for minimising the sum of the weighted job completion times. Int. J. Prod. Res. 2017. [CrossRef]
- Burdett, R.L.; Kozan, E. Techniques to effectively buffer schedules in the face of uncertainties. Comput. Ind. Eng. 2015, 87, 16–29. [Google Scholar] [CrossRef][Green Version]
- Goren, S.; Sabuncuoglu, I. Robustness and stability measures for scheduling: Single-machine environment. IIE Trans. 2008, 40, 66–83. [Google Scholar] [CrossRef]
- Kasperski, A.; Zielinski, P. A 2-approximation algorithm for interval data minmax regret sequencing problems with total flow time criterion. Oper. Res. Lett. 2008, 36, 343–344. [Google Scholar] [CrossRef]
- Kouvelis, P.; Yu, G. Robust Discrete Optimization and Its Application; Kluwer Academic Publishers: Boston, MA, USA, 1997. [Google Scholar]
- Lu, C.-C.; Lin, S.-W.; Ying, K.-C. Robust scheduling on a single machine total flow time. Comput. Oper. Res. 2012, 39, 1682–1691. [Google Scholar] [CrossRef]
- Yang, J.; Yu, G. On the robust single machine scheduling problem. J. Comb. Optim. 2002, 6, 17–33. [Google Scholar] [CrossRef]
- Harikrishnan, K.K.; Ishii, H. Single machine batch scheduling problem with resource dependent setup and processing time in the presence of fuzzy due date. Fuzzy Optim. Decis. Mak. 2005, 4, 141–147. [Google Scholar] [CrossRef]
- Allahverdi, A.; Aydilek, H.; Aydilek, A. Single machine scheduling problem with interval processing times to minimize mean weighted completion times. Comput. Oper. Res. 2014, 51, 200–207. [Google Scholar] [CrossRef]
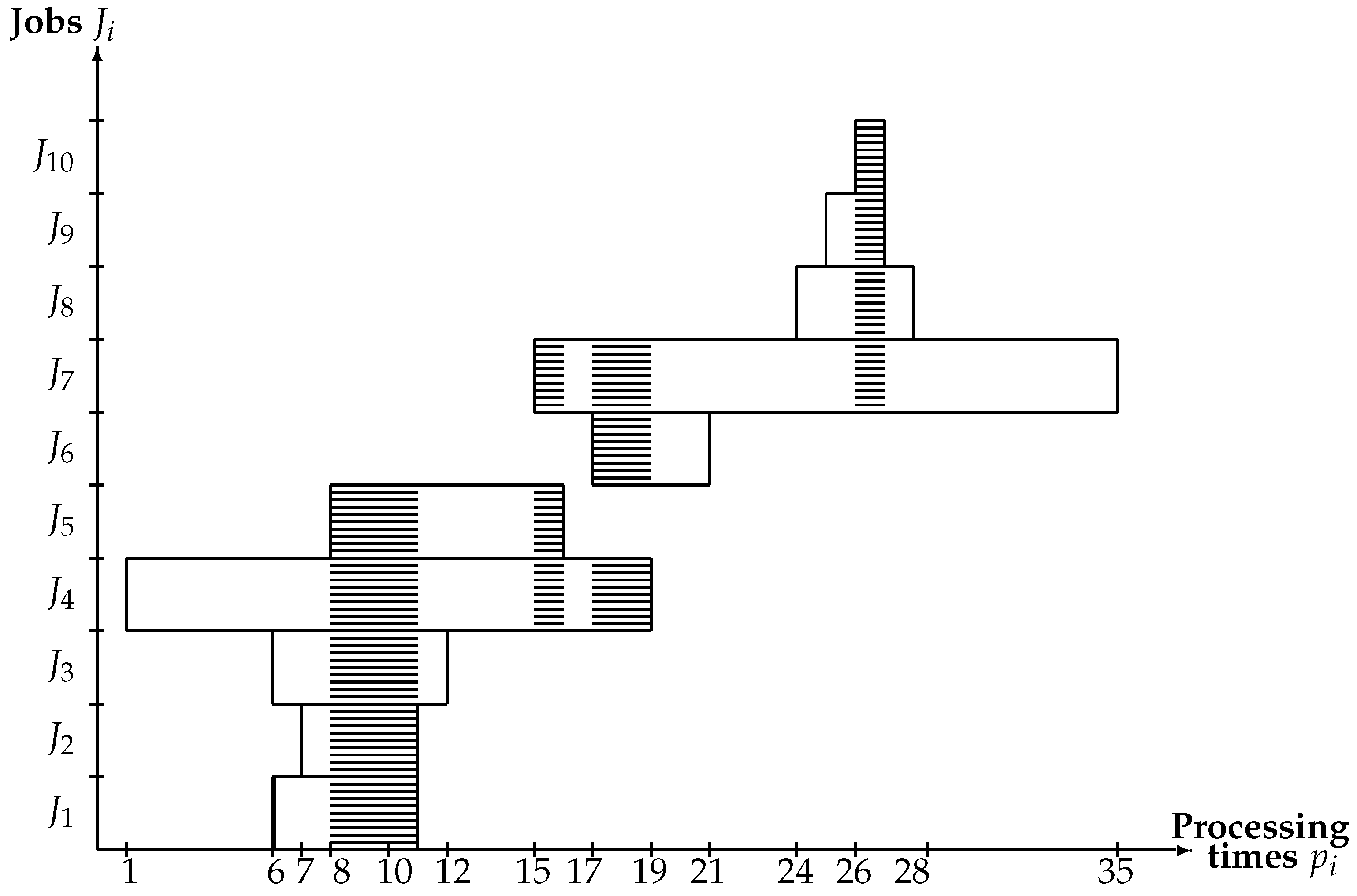
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 7 | 6 | 1 | 8 | 17 | 15 | 24 | 25 | 26 | |
| 11 | 11 | 12 | 19 | 16 | 21 | 35 | 28 | 27 | 27 |
| n | / | / | CPU-Time (s) | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 100 | 1 | 0.08715 | 0.197231 | 1.6 | 2.263114 | 1.27022 | 0.046798 |
| 100 | 5 | 0.305088 | 0.317777 | 1.856768 | 1.041589 | 1.014261 | 0.031587 |
| 100 | 10 | 0.498286 | 0.500731 | 1.916064 | 1.001077 | 1.000278 | 0.033953 |
| 500 | 1 | 0.095548 | 0.208343 | 1.6 | 2.18052 | 1.0385 | 0.218393 |
| 500 | 5 | 0.273933 | 0.319028 | 1.909091 | 1.164623 | 1.017235 | 0.2146 |
| 500 | 10 | 0.469146 | 0.486097 | 1.948988 | 1.036133 | 1.006977 | 0.206222 |
| 1000 | 1 | 0.093147 | 0.21632 | 1.666667 | 2.322344 | 1.090832 | 0.542316 |
| 1000 | 5 | 0.264971 | 0.315261 | 1.909091 | 1.189795 | 1.030789 | 0.542938 |
| 1000 | 10 | 0.472471 | 0.494142 | 1.952143 | 1.045866 | 1.000832 | 0.544089 |
| 5000 | 1 | 0.095824 | 0.217874 | 1.666667 | 2.273683 | 1.006018 | 7.162931 |
| 5000 | 5 | 0.264395 | 0.319645 | 1.909091 | 1.208965 | 1.002336 | 7.132647 |
| 5000 | 10 | 0.451069 | 0.481421 | 1.952381 | 1.06729 | 1.00641 | 7.137556 |
| 10,000 | 1 | 0.095715 | 0.217456 | 1.666667 | 2.271905 | 1.003433 | 25.52557 |
| 10,000 | 5 | 0.26198 | 0.316855 | 1.909091 | 1.209463 | 1.003251 | 25.5448 |
| 10,000 | 10 | 0.454655 | 0.486105 | 1.952381 | 1.069175 | 1.003809 | 25.50313 |
| Minimum | 0.08715 | 0.197231 | 1.6 | 1.001077 | 1.000278 | 0.031587 | |
| Average | 0.278892 | 0.339619 | 1.827673 | 1.489703 | 1.033012 | 6.692502 | |
| Maximum | 0.498286 | 0.500731 | 1.952381 | 2.322344 | 1,27022 | 25.5448 | |
| n | N-Fix Jobs | Laws | Per | / | / | CPU-Time (s) | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Class 2 | |||||||||
| 50 | 1 | 0 | 1.2.3 | 1.023598 | 2.401925 | 1.027 | 2.346551 | 1,395708 | 0,020781 |
| 100 | 1 | 0 | 1.2.3 | 0.608379 | 0.995588 | 0.9948 | 1.636461 | 1.618133 | 0.047795 |
| 500 | 1 | 0 | 1.2.3 | 0.265169 | 0.482631 | 0.9947 | 1.820092 | 1.630094 | 0.215172 |
| 1000 | 1 | 0 | 1.2.3 | 0.176092 | 0.252525 | 0.9952 | 1.434053 | 1.427069 | 0.535256 |
| 5000 | 1 | 0 | 1.2.3 | 0.111418 | 0.14907 | 0.9952 | 1.33793 | 1.089663 | 7.096339 |
| 10,000 | 1 | 0 | 1.2.3 | 0.117165 | 0.13794 | 0.9948 | 1.177313 | 1.004612 | 25.28328 |
| Minimum | 0.111418 | 0.13794 | 0.9947 | 1.177313 | 1.004612 | 0.020781 | |||
| Average | 0.383637 | 0.736613 | 0.99494 | 1.6254 | 1.399944 | 5.533104 | |||
| Maximum | 1.023598 | 2.401925 | 0.9952 | 2.346551 | 1.630094 | 25.28328 | |||
| Class 3 | |||||||||
| 50 | 3 | 1 | 1.2.3 | 0.636163 | 0.657619 | 1.171429 | 1.033727 | 1.004246 | 0.047428 |
| 100 | 3 | 1 | 1.2.3 | 1.705078 | 1.789222 | 1.240238 | 1.049349 | 1.009568 | 0.066329 |
| 500 | 3 | 1 | 1.2.3 | 0.332547 | 0.382898 | 1.205952 | 1.151412 | 1.138869 | 0.249044 |
| 1000 | 3 | 1 | 1.2.3 | 0.286863 | 0.373247 | 1.400833 | 1.301132 | 1.101748 | 0.421837 |
| 5000 | 3 | 1 | 1.2.3 | 0.246609 | 0.323508 | 1.380833 | 1.311825 | 1.140728 | 2.51218 |
| 10,000 | 3 | 1 | 1.2.3 | 0.26048 | 0.338709 | 1.098572 | 1.300324 | 1.095812 | 5.46782 |
| Minimum | 0.246609 | 0.323508 | 1.098572 | 1.033727 | 1.004246 | 0.047428 | |||
| Average | 0.577957 | 0.644201 | 1.249643 | 1.191295 | 1.0818286 | 1.460773 | |||
| Maximum | 1.705078 | 1.789222 | 1.400833 | 1.311825 | 1.140728 | 5.46782 | |||
| Class 4 | |||||||||
| 50 | 3 | 1 | 1 | 0.467885 | 0.497391 | 1.17369 | 1.063064 | 1.035412 | 0.043454 |
| 100 | 3 | 1 | 1 | 0.215869 | 0.226697 | 1.317222 | 1.05016 | 1.031564 | 0.067427 |
| 500 | 3 | 1 | 1 | 0.128445 | 0.15453 | 1.424444 | 1.203083 | 1.17912 | 0.256617 |
| 1000 | 3 | 1 | 1 | 0.111304 | 0.118882 | 1.307738 | 1.068077 | 1.042852 | 0.50344 |
| 5000 | 3 | 1 | 1 | 0.076917 | 0.085504 | 1.399048 | 1.111631 | 1.046061 | 2.612428 |
| 10,000 | 3 | 1 | 1 | 0.067836 | 0.076221 | 1.591905 | 1.123606 | 1.114005 | 4.407236 |
| Minimum | 0.067836 | 0.076221 | 1.17369 | 1.05016 | 1.031564 | 0.043454 | |||
| Average | 0.178043 | 0.193204 | 1.369008 | 1.10327 | 1.074836 | 1.3151 | |||
| Maximum | 0.467885 | 0.497391 | 1.591905 | 1.203083 | 1.17912 | 4.407236 | |||
| Class 5 | |||||||||
| 50 | 3 | 2 | 1.2.3 | 1.341619 | 1.508828 | 1.296195 | 1.124632 | 1.035182 | 0.049344 |
| 100 | 3 | 2 | 1.2.3 | 0.700955 | 0.867886 | 1.271976 | 1.238149 | 1.037472 | 0.070402 |
| 500 | 3 | 2 | 1.2.3 | 0.182378 | 0.241735 | 1.029 | 1.32546 | 1.296414 | 0.255463 |
| 1000 | 3 | 2 | 1.2.3 | 0.098077 | 0.11073 | 1.473451 | 1.129006 | 1.104537 | 0.509969 |
| 5000 | 3 | 2 | 1.2.3 | 0.074599 | 0.084418 | 1.204435 | 1.131624 | 1.056254 | 2.577595 |
| 10,000 | 3 | 2 | 1.2.3 | 0.064226 | 0.074749 | 1.359181 | 1.163846 | 1.042676 | 5.684847 |
| Minimum | 0.064226 | 0.074749 | 1.029 | 1.124632 | 1.035182 | 0.049344 | |||
| Average | 0.410309 | 0.481391 | 1.272373 | 1.185453 | 1.095422 | 1.524603 | |||
| Maximum | 1.341619 | 1.508828 | 1.473451 | 1.32546 | 1.296414 | 5.684847 | |||
| Class 6 | |||||||||
| 50 | 4 | 2 | 1.2.3 | 0.254023 | 0.399514 | 1.818905 | 1.57275 | 1.553395 | 0.058388 |
| 100 | 4 | 2 | 1.2.3 | 0.216541 | 0.260434 | 1.868278 | 1.202704 | 1.03868 | 0.091854 |
| 500 | 4 | 2 | 1.2.3 | 0.081932 | 0.098457 | 1.998516 | 1.201691 | 1.1292 | 0.365865 |
| 1000 | 4 | 2 | 1.2.3 | 0.06145 | 0.067879 | 1.933984 | 1.104622 | 1.061866 | 0.713708 |
| 5000 | 4 | 2 | 1.2.3 | 0.050967 | 0.060394 | 1.936453 | 1.184953 | 1.048753 | 3.602502 |
| 10,000 | 4 | 2 | 1.2.3 | 0.045303 | 0.05378 | 2.332008 | 1.187101 | 1.038561 | 7.426986 |
| Minimum | 0.045303 | 0.05378 | 1.818905 | 1.104622 | 1.038561 | 0.058388 | |||
| Average | 0.118369 | 0.156743 | 1.981357 | 1.242304 | 1.1450756 | 2.043217 | |||
| Maximum | 0.254023 | 0.399514 | 2.332008 | 1.57275 | 1.553395 | 7.426986 | |||
| Class 7 | |||||||||
| 50 | 2 | 2–4 | 1.2.3 | 4.773618 | 6.755918 | 0.262946 | 1.415262 | 1.308045 | 0.039027 |
| 100 | 2 | 2–4 | 1.2.3 | 3.926612 | 4.991843 | 0.224877 | 1.271285 | 1.160723 | 0.059726 |
| 500 | 2 | 2–6 | 1.2.3 | 3.811794 | 4.600017 | 0.259161 | 1.206785 | 1.132353 | 0.185564 |
| 1000 | 2 | 2–8 | 1.2.3 | 3.59457 | 4.459855 | 0.337968 | 1.24072 | 1.08992 | 0.474514 |
| 5000 | 2 | 2–8 | 1.2.3 | 3.585219 | 4.297968 | 0.261002 | 1.198802 | 1.031319 | 2.778732 |
| 10,000 | 2 | 2–8 | 1.2.3 | 3.607767 | 4.275581 | 0.299311 | 1.185105 | 1.013096 | 5.431212 |
| Minimum | 3.585219 | 4.275581 | 0.224877 | 1.185105 | 1.013096 | 0.039027 | |||
| Average | 3.883263 | 4.896864 | 0.274211 | 1.252993 | 1.122576 | 1.494796 | |||
| Maximum | 4.773618 | 6.755918 | 0.337968 | 1.415262 | 1.308045 | 5.431212 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sotskov, Y.N.; Egorova, N.G. Single Machine Scheduling Problem with Interval Processing Times and Total Completion Time Objective. Algorithms 2018, 11, 66. https://doi.org/10.3390/a11050066
Sotskov YN, Egorova NG. Single Machine Scheduling Problem with Interval Processing Times and Total Completion Time Objective. Algorithms. 2018; 11(5):66. https://doi.org/10.3390/a11050066
Chicago/Turabian StyleSotskov, Yuri N., and Natalja G. Egorova. 2018. "Single Machine Scheduling Problem with Interval Processing Times and Total Completion Time Objective" Algorithms 11, no. 5: 66. https://doi.org/10.3390/a11050066
APA StyleSotskov, Y. N., & Egorova, N. G. (2018). Single Machine Scheduling Problem with Interval Processing Times and Total Completion Time Objective. Algorithms, 11(5), 66. https://doi.org/10.3390/a11050066





