An Optimal Online Resource Allocation Algorithm for Energy Harvesting Body Area Networks
Abstract
:1. Introduction
- By using energy harvesting technology, the lifetime of the system is greatly prolonged. Energy harvesting technology is very important to the BAN system. Sensors harvest energy from the renewable sources. We propose a framework to characterize the stochastic nature of the energy harvesting and energy consumption, we do not need any a priori knowledge of these stochastic processes.
- We propose an optimization problem to maximize the user utility. We use Lyapunov optimization approach to decompose the user utility optimization problem into three sub-problems, i.e., battery management, collecting rate control and transmission power allocation. We propose an optimal online resource allocation algorithm that makes decisions at the beginning of each time slot and then updates queues, and achieves close-to-optimal time average user utility.
2. Related Works
3. System Model
3.1. Collecting Rate and Utility
3.2. Data Transmission
3.3. Energy Consumption Model
3.4. Queues Dynamic Model
3.5. Optimization Problem Formulation
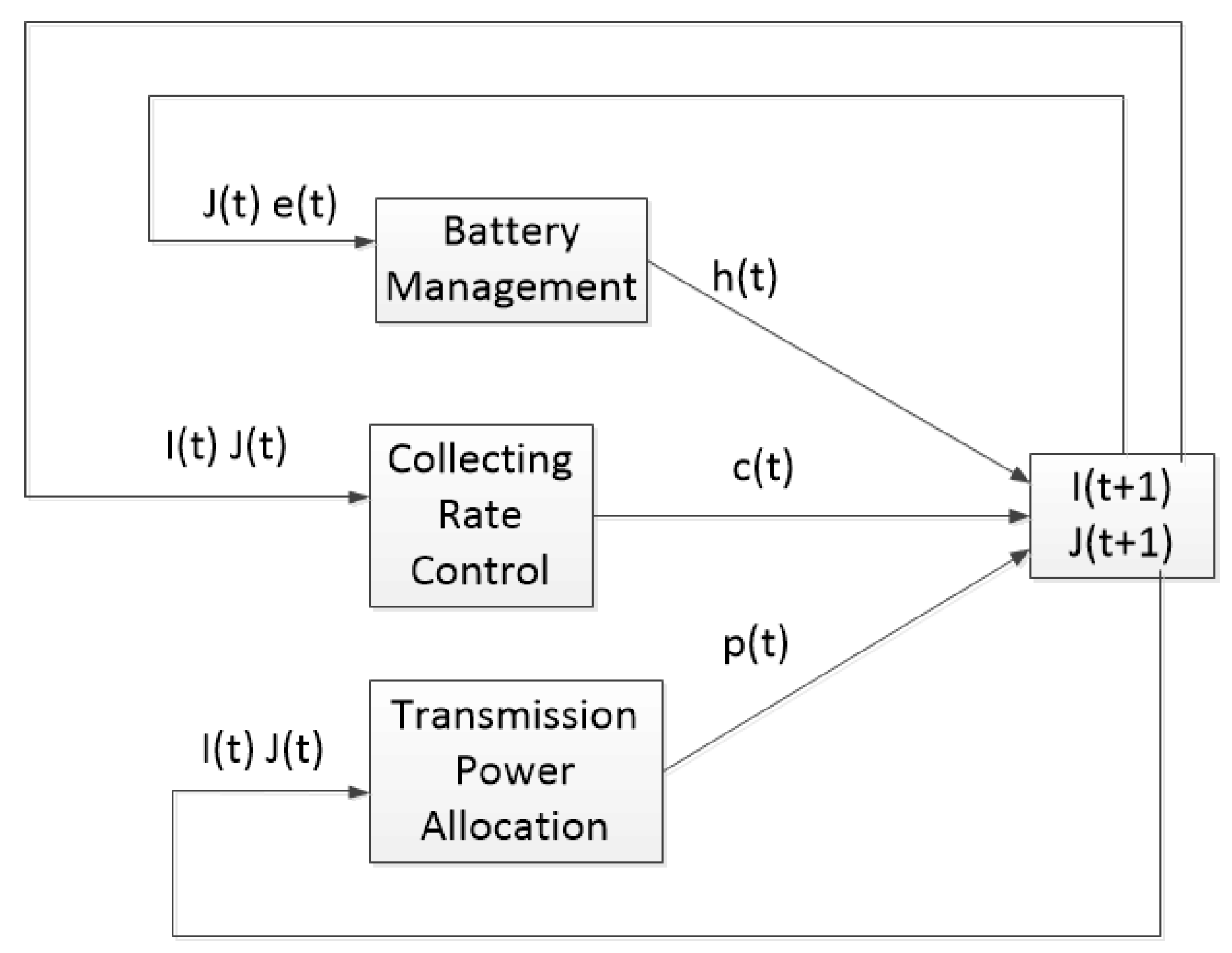
4. Resource Allocation Algorithm
4.1. Lyapunov Optimization
4.2. Sub-Problem Solution
- Battery ManagementThe sensor should harvest energy as much as possible for data collection and data transmission. The system is stable only if the energy in the system is sufficient enough. In this sub-problem, we need to optimize energy harvesting rate . To keep the BAN system running, we should try to charge the battery of sensor n carried by patient as much as possible. For each sensor , combining the first term of with the constraint Equation (9), we have the optimization problem of as follows:The problem is linear of . In time slot t, we can get the value of energy queue occupancy . Thus, minimize the optimization problem just to maximize the with the constraints. If the battery of sensor n carried by patient is full, equals 0, and we do not need to harvest energy, . If the battery is not full, and , we need to harvest energy as much as possible, . According to the above, we can get
- Collecting Rate ControlIn this sub-problem, we consider data scheduling of sensor n carried by patient in BAN. We optimize the second part of while ensuring the constraint Equation (1). We have the optimization problem of as follows:In time slot t, we can get the values of energy queue occupancy and data queue occupancy . and V are constants. Thus, minimize the optimal problem just need to optimize the collection rate . According to Section 3.1, we can get that the utility function is a concave function; thus, the problem is convex. According to the convex optimization, let the collecting rate be the unique optimal solution, and we can get:
- Transmission Power AllocationIn this sub problem, we consider transmission power allocation of sensor n carried by the patient. We optimize the third part of to get the optimal transmission power. Combining the third term of with the constraint Equation (2), we have the optimization problem of as follows:where , . Substituing the expression of into . According to the nature of logarithmic function, we can getWe can get the value of in time slot t, and is a constant. Thus, the minimization problem can transform toIn time slot t, we can get the values of energy queue occupancy , data queue occupancy , and . They are constants in time slot t. Thus, minimization of the optimal problem just needs to optimize the transmission power , and the logarithmic function is concave. Thus, the problem is convex. Let the transmission power rate be the optimal solution, and we have:
4.3. Proposed Algorithm
| Algorithm 1: Online Resource Allocation Algorithm. |
 |
5. Performance Analysis
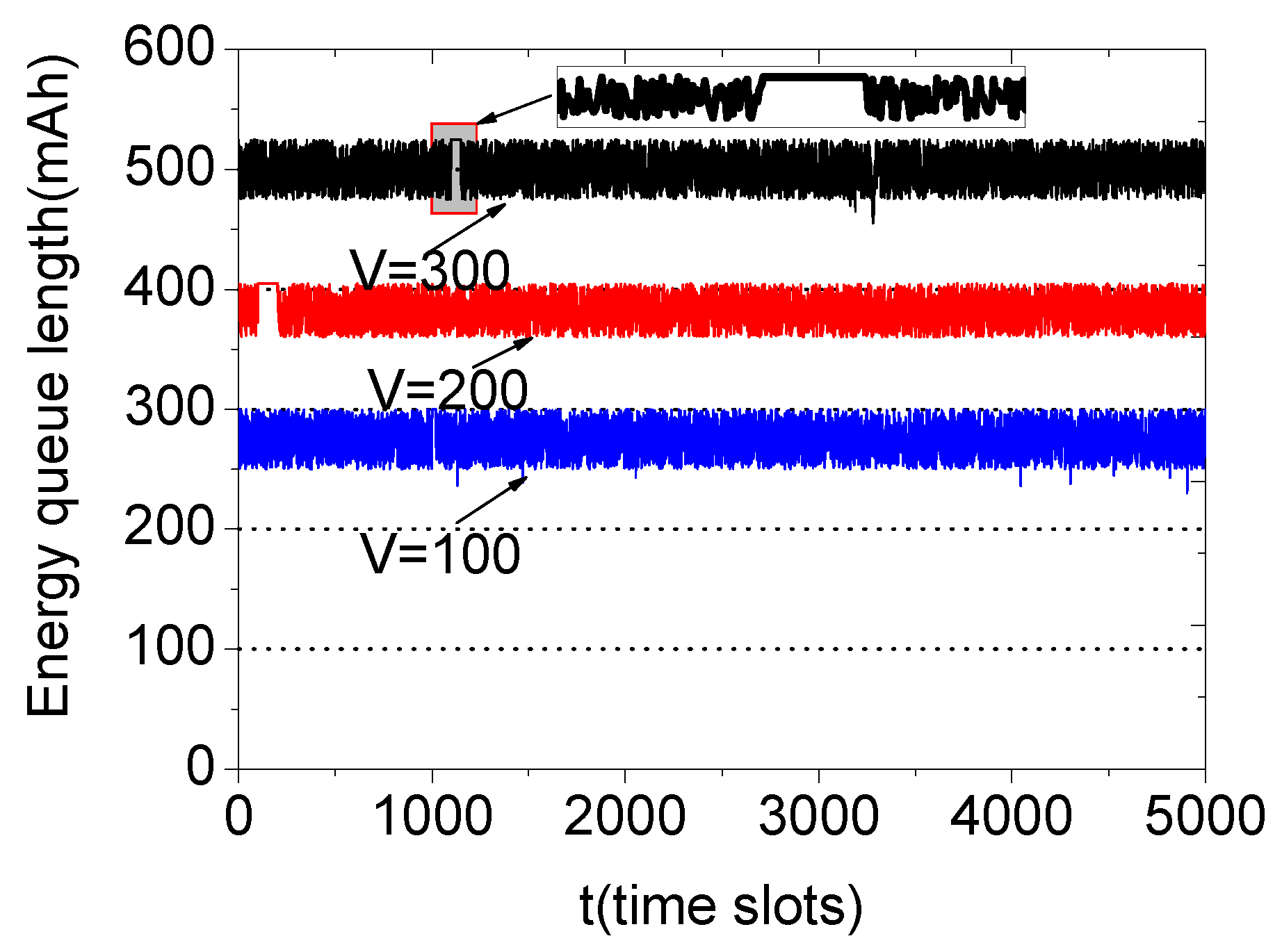
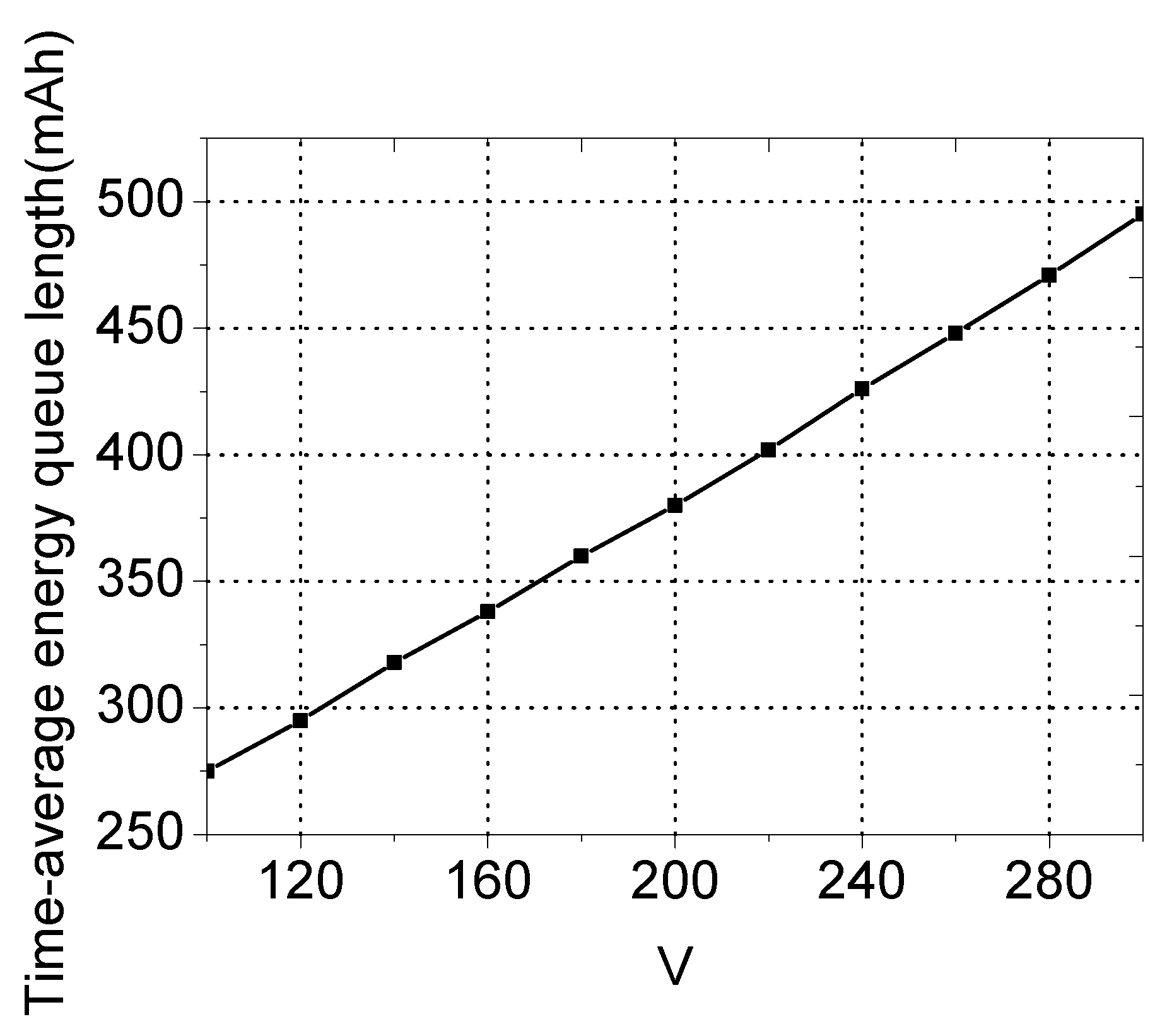
5.1. Required Battery Capacity
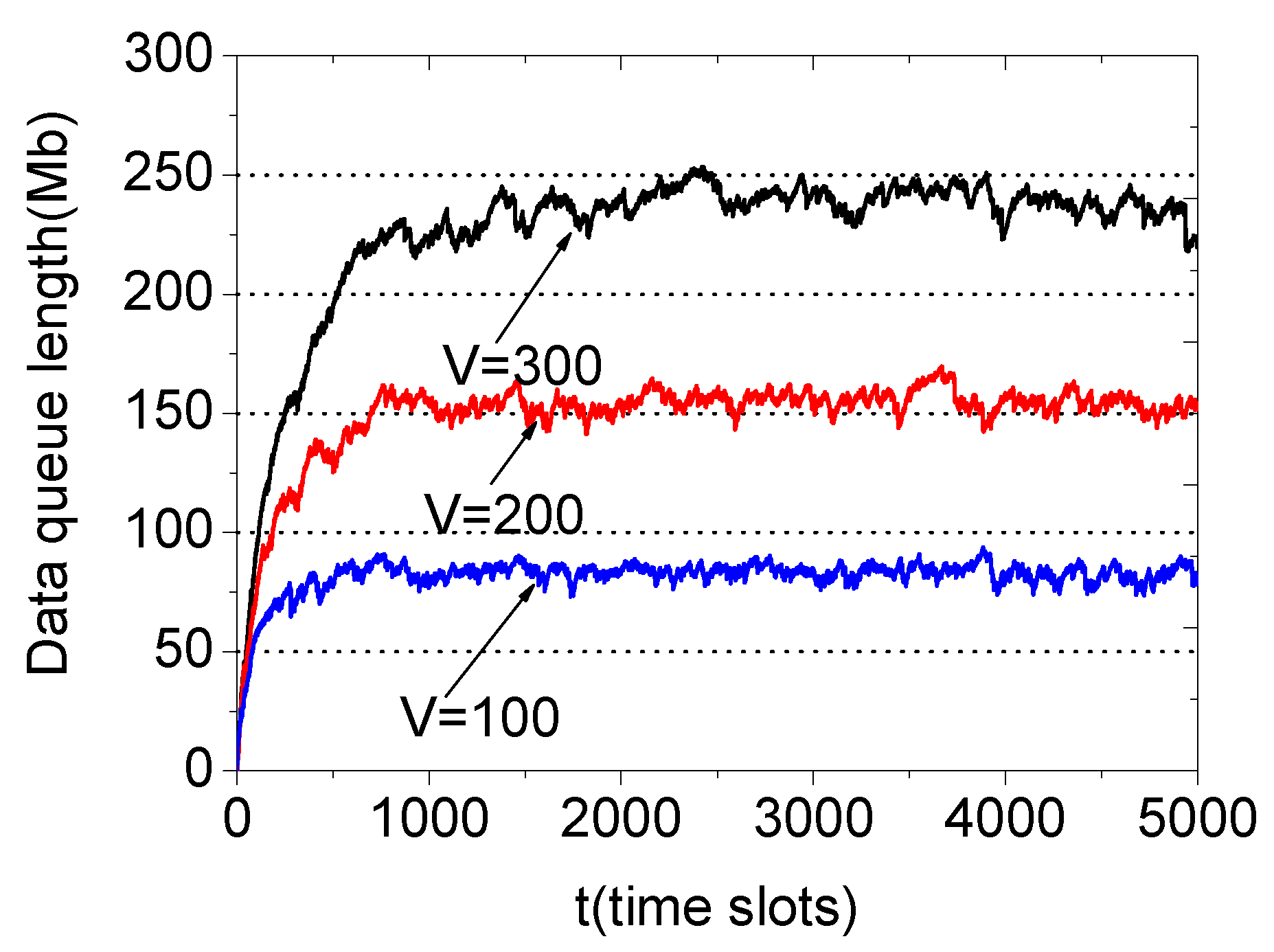
5.2. Bounded Data Queues
5.3. Optimality of the Proposed Algorithm
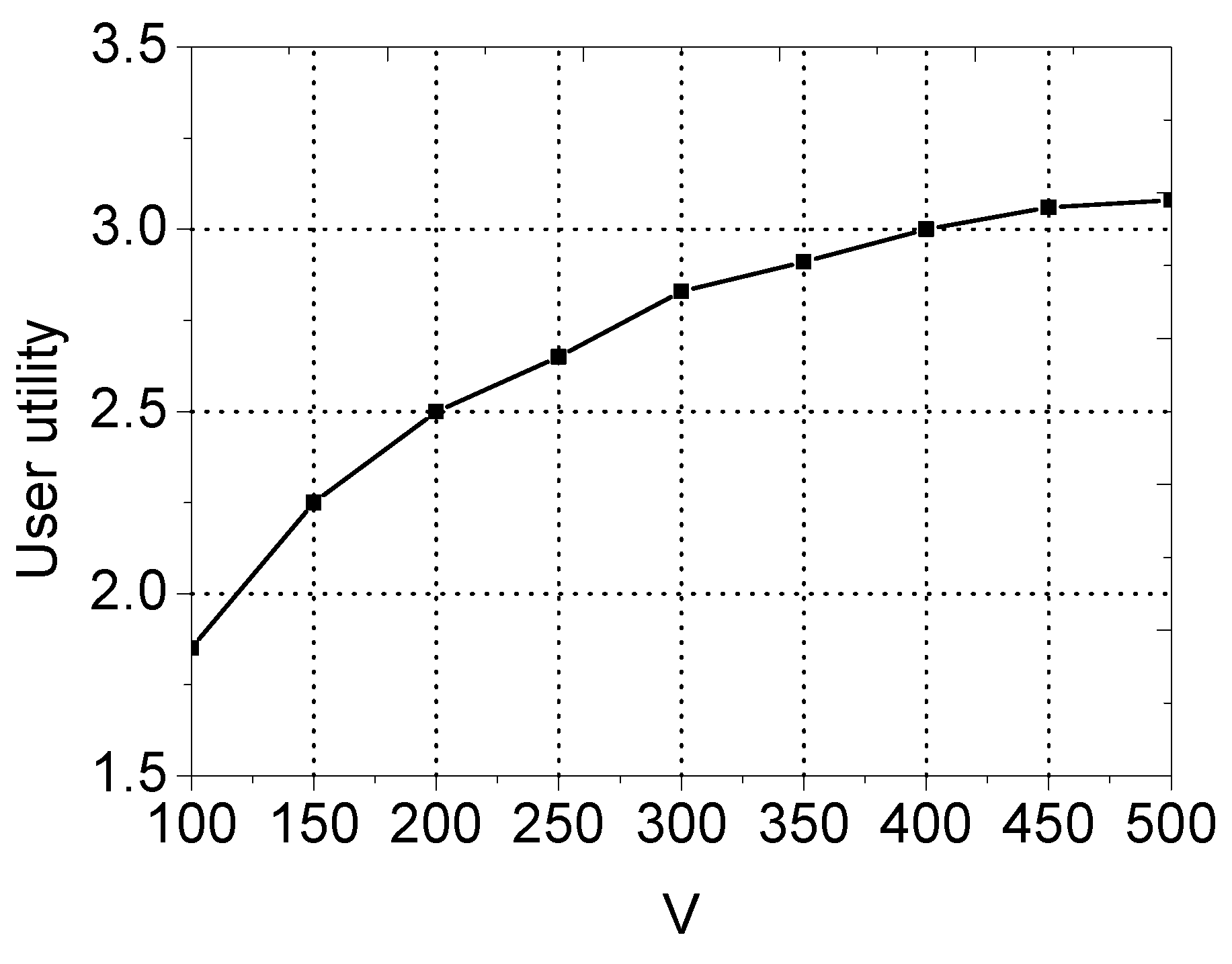
6. Simulation Results
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 2
Appendix C. Proof of Theorem 3
- (1)
- If , i.e., sensor n does not collect data, we can get .
- (2)
- If sensor n collect data with rate , we have , , so . is the maximum of the user utility function, . Furthermore, , and we have .
Appendix D. Proof of Theorem 4
References
- Sumita, M. Communique of the National Bureau of Statistics of People’s Republic of China on Major Figures of the 2010 Population Census(No.2). China Popul. Today 2011, 6, 24–25. [Google Scholar]
- Latre, B.; Braem, B.; Moerman, I.; Blondia, C.; Demeester, P. A survey on wireless body area networks. Wirel. Netw. 2011, 17, 1–18. [Google Scholar] [CrossRef]
- Cao, H.; Leung, V.; Chow, C.; Chan, H. Enabling technologies for wireless body area networks: A survey and outlook. IEEE Commun. Mag. 2009, 47, 84–93. [Google Scholar] [CrossRef]
- Qi, X.; Wang, K.; Yue, D.; Shu, L.; Liu, Y.; Zhao, H. Adaptive TDMA-based MAC protocol in energy harvesting wireless body area network for mobile health. In Proceedings of the IEEE 41st Annual Conference on Industrial Electronics Society, IECON 2015, Yokohama, Japan, 9–12 November 2016; pp. 4175–4180. [Google Scholar]
- Chen, M.; Gonzalez, S.; Vasilakos, A.; Cao, H.; Leung, V.C. Body Area Networks: A Survey. Mob. Netw. Appl. 2011, 16, 171–193. [Google Scholar] [CrossRef]
- Liu, B.; Yu, S.; Chang, W.C. Optimal resource allocation in energy harvesting-powered body sensor networks. In Proceedings of the International Symposium on Future Information and Communication Technologies for Ubiquitous Healthcare, Beijing, China, 28–30 May 2015; pp. 1–5. [Google Scholar]
- Elias, J. Optimal Design of Energy-Efficient and Cost-Effective Wireless Body Area Networks; Elsevier Science Publishers: Amsterdam, The Netherlands, 2014; pp. 560–574. [Google Scholar]
- Yick, J.; Mukherjee, B.; Ghosal, D. Wireless sensor network survey. Comput. Netw. 2008, 52, 2292–2330. [Google Scholar] [CrossRef]
- Jemili, I.; Belghith, A. Wireless Body Area Networks: Applications and Technologies. In Proceedings of the 2nd International Workshop on Recent Advances on Machine-To-Machine Communications, Madrid, Sapin, 9 May 2016; pp. 1274–1281. [Google Scholar]
- Elias, J.; Paris, S.; Krunz, M. Cross-Technology Interference Mitigation in Body Area Networks: An Optimization Approach. IEEE Trans. Veh. Technol. 2015, 64, 4144–4157. [Google Scholar] [CrossRef]
- Cavallari, R.; Martelli, F.; Rosini, R.; Buratti, C. A Survey on Wireless Body Area Networks: Technologies and Design Challenges. IEEE Commun. Surv. Tutor. 2014, 16, 1635–1657. [Google Scholar] [CrossRef]
- D’Andreagiovanni, F.; Krolikowski, J.; Pulaj, J. A fast hybrid primal heuristic for multiband robust capacitated network design with multiple time periods. Appl. Soft Comput. 2015, 26, 497–507. [Google Scholar] [CrossRef]
- D’Andreagiovanni, F.; Nardin, A.; Natalizio, E. A Fast ILP-Based Heuristic for the Robust Design of Body Wireless Sensor Networks. In Applications of Evolutionary Computation, EvoApplications 2017; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2017; Volume 10199, pp. 234–250. [Google Scholar]
- Wu, J.; Chen, Z. Data Decision and Transmission Based on Mobile Data Health Records on Sensor Devices in Wireless Networks. Wirel. Pers. Commun. 2016, 90, 2073–2087. [Google Scholar] [CrossRef]
- Movassaghi, S.; Abolhasan, M.; Lipman, J.; Smith, D.; Jamalipour, A. Wireless Body Area Networks: A Survey. IEEE Commun. Surv. Tutor. 2014, 16, 1658–1686. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.C. Wearable Sensors for Human Activity Monitoring: A Review. IEEE Sens. J. 2014, 15, 1321–1330. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, T.; Song, L.; Zhang, Q. Energy Efficiency Optimization by Resource Allocation in Wireless Body Area Networks. In Proceedings of the IEEE Vehicular Technology Conference (VTC Spring), Seoul, Korea, 18–21 May 2014; pp. 1–6. [Google Scholar]
- Zhang, D.; Chen, Z.; Ren, J.; Zhang, N.; Awad, M.; Zhou, H.; Shen, X. Energy Harvesting-Aided Spectrum Sensing and Data Transmission in Heterogeneous Cognitive Radio Sensor Network. IEEE Trans. Veh. Technol. 2016, 66, 831–843. [Google Scholar] [CrossRef]
- Hoang, D.C.; Tan, Y.K.; Chng, H.B.; Panda, S.K. Thermal energy harvesting from human warmth for wireless body area network in medical healthcare system. In Proceedings of the International Conference on Power Electronics and Drive Systems, Taipei, Taiwan, 2–5 November 2009; pp. 1277–1282. [Google Scholar]
- Panatik, K.Z.; Kamardin, K.; Shariff, S.A.; Yuhaniz, S.S.; Ahmad, N.A.; Yusop, O.M.; Ismail, S.A. Energy harvesting in wireless sensor networks: A survey. In Proceedings of the IEEE International Symposium on Telecommunication Technologies, Kuala Lumpur, Malaysia, 28–30 November 2016; pp. 53–58. [Google Scholar]
- D’Andreagiovanni, F.; Nardin, A. Towards the fast and robust optimal design of Wireless Body Area Networks. Appl. Soft Comput. 2015, 37, 971–982. [Google Scholar] [CrossRef]
- Liu, S.; Wang, K.; Guo, J.; Wang, Y.; Qi, X. Review on MAC Protocols in Energy-Harvesting Wireless Body Area Networks. In Proceedings of the International Conference on Identification, Information, and Knowledge in the Internet of Things, Beijing, China, 22–23 October 2015; pp. 303–304. [Google Scholar]
- Zhang, D.; Chen, Z.; Awad, M.K.; Zhang, N.; Zhou, H.; Shen, X.S. Utility-Optimal Resource Management and Allocation Algorithm for Energy Harvesting Cognitive Radio Sensor Networks. IEEE J. Sel. Areas Commun. 2016, 34, 3552–3565. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, Z.; Cai, L.X.; Zhou, H.; Ren, J.; Shen, X. Resource Allocation for Green Cloud Radio Access Networks Powered by Renewable Energy. In Proceedings of the Global Communications Conference, Washington, DC, USA, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Akhtar, F.; Rehmani, M.H. Energy Harvesting for Self-Sustainable Wireless Body Area Networks. IT Prof. 2017, 19, 32–40. [Google Scholar] [CrossRef]
- Liu, R.S.; Sinha, P.; Koksal, C.E. Joint energy management and resource allocation in rechargeable sensor networks. In Proceedings of the Conference on Information Communications, San Diego, CA, USA, 14–19 March 2010; pp. 902–910. [Google Scholar]
- Zhang, Y.; He, S.; Chen, J. Data gathering optimization by dynamic sensing and routing in rechargeable sensor networks. In Proceedings of the Sensor, Mesh and Ad Hoc Communications and Networks, New Orleans, LA, USA, 24–27 June 2013; pp. 273–281. [Google Scholar]
- Ghosh, A.; Meenakshi; Khalid, S.; Harigovindan, V.P. Performance analysis of wireless body area network with thermal energy harvesting. In Proceedings of the Communication Technologies, Thuckalay, India, 23–24 April 2015; pp. 916–920. [Google Scholar]
- Zhang, Y.; He, S.; Chen, J.; Sun, Y.; Shen, X.S. Distributed Sampling Rate Control for Rechargeable Sensor Nodes with Limited Battery Capacity. IEEE Trans. Wirel. Commun. 2013, 12, 3096–3106. [Google Scholar] [CrossRef]
- Huang, L.; Neely, M.J. Utility optimal scheduling in energy-harvesting networks. IEEE/ACM Trans. Netw. 2010, 21, 1117–1130. [Google Scholar] [CrossRef]
- Li, Y.; Shi, R. An intelligent solar energy-harvesting system for wireless sensor networks. Eurasip J. Wirel. Commun. Netw. 2015, 2015, 179. [Google Scholar] [CrossRef]
- Rao, S.; Mehta, N.B. Hybrid energy harvesting wireless systems: Performance evaluation and benchmarking. In Proceedings of the Wireless Communications and Networking Conference, Shanghai, China, 7–10 April 2013; pp. 4244–4249. [Google Scholar]
- Natalizio, E.; Loscri, V.; Viterbo, E. Optimal Placement of Wireless Nodes for Maximizing Path Lifetime. IEEE Commun. Lett. 2008, 12, 362–364. [Google Scholar] [CrossRef]
- Tsouri, G.R.; Alvaro, P.; Nikhil, A. On Increasing Network Lifetime in Body Area Networks Using Global Routing with Energy Consumption Balancing. Sensors 2012, 12, 13088–13108. [Google Scholar] [CrossRef] [PubMed]
- Elias, J.; Mehaoua, A. Energy-aware topology design for wireless body area networks. In Proceedings of the IEEE International Conference on Communications, Ottawa, ON, Canada, 10–15 June 2012; pp. 3409–3410. [Google Scholar]
- Chai, R.; Wang, P.; Huang, Z.; Su, C. Network lifetime maximization based joint resource optimization for Wireless Body Area Networks. In Proceedings of the IEEE International Symposium on Personal, Indoor, and Mobile Radio Communication, Washington, DC, USA, 2–5 September 2014; pp. 1088–1092. [Google Scholar]
- Khan, A.W.; Khan, A.A.; Basit, A.; Siddiqui, S.; Salam, A. Achieving energy efficiency in Body Area Networks (BAN’s) through avoiding spatially correlated contention. In Proceedings of the International Conference on Information and Communication Technologies, Karachi, Pakistan, 12–13 December 2016; pp. 1–5. [Google Scholar]
- Singh, K.; Singh, R.K. An energy efficient fuzzy based adaptive routing protocol for Wireless Body Area Network. In Proceedings of the Electrical Computer and Electronics, Allahabad, India, 4–6 December 2016; pp. 1–6. [Google Scholar]
- Movassaghi, S.; Majidi, A.; Jamalipour, A.; Smith, D.; Abolhasan, M. Enabling interference-aware and energy-efficient coexistence of multiple wireless body area networks with unknown dynamics. IEEE Access 2016, 4, 2935–2951. [Google Scholar] [CrossRef]
- Neely, M. Stochastic Network Optimization with Application to Communication and Queueing Systems; Synthesis Lectures on Communication Networks; Morgan and Claypool Publishers: San Rafael, CA, USA, 2010; Volume 3, p. 211. [Google Scholar]
- Shen, Q.; Zhuang, W. Energy efficient scheduling for delay constrained communication in wireless body area networks. In Proceedings of the IEEE Global Communications Conference, Anaheim, CA, USA, 3–7 December 2012; pp. 262–267. [Google Scholar]
- Kennington, J.; Olinick, E.; Rajan, D. Wireless Network Design: Optimization Models and Solution Procedures; Springer: New York, NY, USA, 2010; pp. 179–184. [Google Scholar]
- Resende, M.G.C.; Pardalos, P.M. Handbook of Optimization in Telecommunications; Springer: New York, NY, USA, 2006. [Google Scholar]
- D’Andreagiovanni, F.; Mannino, C.; Sassano, A. GUB Covers and Power-Indexed formulations for Wireless Network Design. Manag. Sci. 2013, 59, 142–156. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.; Chen, Z.; Guo, L.; Wu, J. An Optimal Online Resource Allocation Algorithm for Energy Harvesting Body Area Networks. Algorithms 2018, 11, 14. https://doi.org/10.3390/a11020014
Wu G, Chen Z, Guo L, Wu J. An Optimal Online Resource Allocation Algorithm for Energy Harvesting Body Area Networks. Algorithms. 2018; 11(2):14. https://doi.org/10.3390/a11020014
Chicago/Turabian StyleWu, Guangyuan, Zhigang Chen, Lin Guo, and Jia Wu. 2018. "An Optimal Online Resource Allocation Algorithm for Energy Harvesting Body Area Networks" Algorithms 11, no. 2: 14. https://doi.org/10.3390/a11020014
APA StyleWu, G., Chen, Z., Guo, L., & Wu, J. (2018). An Optimal Online Resource Allocation Algorithm for Energy Harvesting Body Area Networks. Algorithms, 11(2), 14. https://doi.org/10.3390/a11020014





