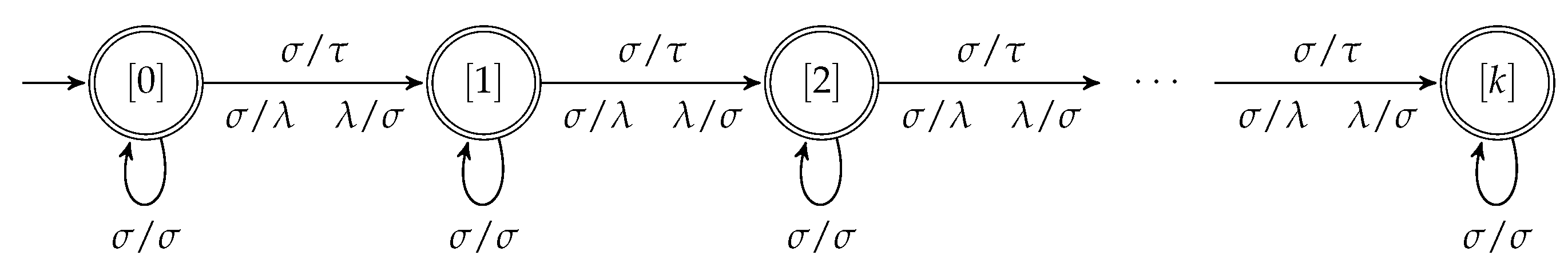Efficient Algorithms for Computing the Inner Edit Distance of a Regular Language via Transducers

Abstract

The concept of edit distance and its variants has applications in many areas such as computational linguistics, bioinformatics, and synchronization error detection in data communications. Here, we revisit the problem of computing the inner edit distance of a regular language given via a Nondeterministic Finite Automaton (NFA). This problem relates to the inherent maximal error-detecting capability of the language in question. We present two efficient algorithms for solving this problem, both of which execute in time $O(r^2{n}^{2}d)$, where r is the cardinality of the alphabet involved, n is the number of transitions in the given NFA, and d is the computed edit distance. We have implemented one of the two algorithms and present here a set of performance tests. The correctness of the algorithms is based on the connection between word distances and error detection and the fact that nondeterministic transducers can be used to represent the errors (resp., edit operations) involved in error-detection (resp., in word distances).

1. Introduction

The concept of edit distance and its variants has applications in many areas such as computational linguistics [1], bioinformatics [2], and synchronization error detection in data communications [3]. The edit distance of a language L with at least two words—also referred to as inner edit distance of L—is the minimum edit distance between any two different words in L. In [4], the author considers the problem of computing the edit distance of a regular language, which is given via a Nondeterministic Finite Automaton (NFA), or a Deterministic Finite Automaton (DFA). For a given automaton $\mathbf{a}$ with n transitions and an alphabet of r symbols, the algorithm proposed in [4] has worst-case time complexity

$$O(r^2{n}^2{q}^2(q+r)),$$

(1)

where q is either the number of states in $\mathbf{a}$ (if $\mathbf{a}$ is a DFA), or the square of the number of states in $\mathbf{a}$ (if $\mathbf{a}$ is an NFA). If the size of the alphabet is ignored and the automaton in question has only states that can be reached from the start state, then the number of states is $O(n)$ and the worst-case time complexity shown in Label (1) can be written as

$$O(n^5)\mathrm{for}\mathrm{DFAs},\mathrm{and}O(n^8)\mathrm{for}\mathrm{NFAs}.$$

(2)

In this paper, we present two efficient algorithms to compute the inner edit distance of a regular language given via an NFA with n transitions—see Theorems 1 and 3. Both algorithms, which are called DistErrDetect and DistInpAlter, have the same worst-case time complexity

$$O(n^{2}d{r}^2),$$

(3)

where d is the computed distance, which is a significant improvement over the original algorithm in [4].

Our first algorithm, DistErrDetect, is based on the general method of [5] for computing distances via the error-detection property. Now, however, we have an efficient way of realizing algorithmically that general method using an incremental construction of a (nondeterministic) transducer and the test of [6] for partial identity for transducers. In our second algorithm, DistInpAlter, the idea is to model the edit operations of the desired distance using an efficient, in terms of size, input-altering transducer (a transducer whose output is always different from the input used). Please see subsequent sections for definitions of terms. For clarity of presentation, we give in detail not only the new algorithms, but also their preliminary versions PrelimDistErrDetect and PrelimDistInpAlter that could possibly be applied to other types of distances. We have implemented the preliminary and final versions of the second algorithm (PrelimDistInpAlter and DistInpAlter) in Python using the well maintained, open source package FAdo for automata [7]. We have also tested our implementation experimentally, and we present in this paper the outcomes of the tests.

We note that some related problems involving distances between words and languages can be found in [8,9] (edit distance between a word and a language), and in [10,11,12,13,14] (various distances between two languages). Also in [15], the newer concept of edit distance with moves is investigated. The problem considered here is technically different, however, as the desired distance involves different words within the same language. More specifically, if we used directly the tools of [10,11], for instance, to compute an edit string with minimal number of errors between the given language and itself, then that string would simply be an edit string of zero errors, as the edit distance between any word and itself is zero. We also note that the inner prefix distance of a regular language, which is quite different from the inner edit distance, is considered in [16] and computed in time $O(n^2\log n)$.

The paper is organized as follows. The next section contains basic notions on languages, word relations, finite-state machines and edit-strings. Section 3 describes the approach of computing the desired edit distance via the concept of error-detection and presents the preliminary version PrelimDistErrDetect of the first algorithm. Then, Section 4 explains the improved and final version DistErrDetect of the first algorithm. In Section 5, it is shown that the edit distance is definable via an efficient input-altering transducer—see Theorem 2—and then the second algorithm DistInpAlter is presented. Section 6 discusses the implementation and testing of the second algorithm and its preliminary version. The last section contains a few concluding remarks. The appendix contains the proofs of two technical lemmata.

2. Notation, Background and Preliminary Results

This section contains basic terminology about formal languages, automata, transducers, and edit strings. Most of the basic notions presented here can be found in various texts such as [17,18,19,20,21].

2.1. Sets, Words, Languages, Channels

The set of positive integers is denoted by $\mathbb{N}$. Then, ${\mathbb{N}}_0=\mathbb{N}\cup \{0\}$. If S is any set, the expression $\left|S\right|$ denotes the cardinality of S. We use standard basic notation and terminology for alphabets, words and languages—see [22], for instance. For example, $\Sigma$ denotes an alphabet, ${\Sigma }^{+}$ the set of nonempty words, $\lambda$ the empty word, ${\Sigma }^{\ast }={\Sigma }^{+}\cup \{\lambda \}$, $\left|w\right|$ the length of the word w. We write $u{\le }_{p}w$ to indicate that the word u is a prefix of w, that is, $w=uv$ for some word v. Then, $u{<}_{p}w$ means that u is a proper prefix, that is, $u{\le }_{p}w$ and $u\ne w$. We use the concepts of (formal) language and concatenation between words, or languages, in the usual way. We say that w is an L-word if $w\in L$ and L is a language.

A binary word relation $\rho$ on ${\Sigma }^{\ast }$ is any subset of ${\Sigma }^{\ast }\times {\Sigma }^{\ast }$. The domain of $\rho$ is $\{u\mid (u,v)\in \rho \mathrm{for}\mathrm{some}v\in {\Sigma }^{\ast }\}$. A channel $\gamma$ is a binary relation on ${\Sigma }^{\ast }$ that is input-preserving; that is, $\gamma \subseteq {\Sigma }^{\ast }\times {\Sigma }^{\ast }$ and $(w,w)\in \gamma$ for all words w in the domain of $\gamma$. When $(u,v)\in \gamma$, we say that u can be received as v via the channel $\gamma$, or v is a possible output of $\gamma$ when u is used as input. If $v\ne u$, then we say that u can be received (via $\gamma$) with errors. Here, we only consider the channel $\mathrm{sid}(k)$, for some $k\in \mathbb{N}$, such that $(u,v)\in \mathrm{sid}(k)$ if and only if v can be obtained by applying at most k errors in u, where an error could be a deletion of a symbol in u, a substitution of a symbol in u with another symbol, or an insertion of a symbol in u—see further below for a more rigorous definition via edit-strings.

2.2. NFAs and Transducers

A Nondeterministic Finite Automaton with empty transitions, λ-NFA for short, or just automaton, is a quintuple $\mathbf{a}=(Q,\Sigma ,T,s,F)$ such that Q is the finite set of states, $\Sigma$ is the alphabet, $s\in Q$ is the start (or initial) state, $F\subseteq Q$ is the set of final states, and $T\subseteq Q\times (\Sigma \cup \{\lambda \})\times Q$ is the finite set of transitions or edges. Let $(p,x,q)$ be a transition of $\mathbf{a}$. Then, x is called the label of the transition, and we say that the transition goes out of p. We also use the notation

$$p\stackrel{x}{\to }q$$

for a transition $(p,x,q)$. The $\lambda$-NFA $\mathbf{a}$ is called an NFA, if no transition label is empty, that is, $T\subseteq Q\times \Sigma \times Q$. A Deterministic Finite Automaton, DFA for short, is a special type of NFA in which, for each state p, there are no two transitions with equal labels going out of p.

A path of $\mathbf{a}$ is a finite sequence of consecutive transitions:

$$(p_0,x_1,p_1)(p_1,x_2,p_2)\cdots (p_{\ell -1},x_{\ell },p_{\ell }),$$

(4)

for some nonnegative integer ℓ, where we use concatenation of these transitions to denote the path. Then, if $P_1$ and $P_2$ are two paths such that the last state of $P_1$ is equal to the first state of $P_2$,

$P_1{P}_2$ denotes the path resulting by concatenating the transitions of $P_1$ and $P_2$.

The word $x_1\cdots x_{\ell }$ is called the label of the path in Label (4). We write $p_0\stackrel{x}{\to }{}^{\ast }{p}_{\ell }$ to indicate that there is a path with label x from $p_0$ to $p_{\ell }$. A path as above is called a computation of $\mathbf{a}$ if $p_0$ is the start state. It is called an accepting path/computation if $p_0$ is the start state and $p_{\ell }$ is a final state. The language accepted by $\mathbf{a}$, denoted as $L(\mathbf{a})$, is the set of labels of all the accepting paths of $\mathbf{a}$. The automaton $\mathbf{a}$ is called trim, if every state appears in some accepting path of $\mathbf{a}$.

A (finite nondeterministic) transducer [17,20] is a quintuple (In the literature, a transducer also has an output alphabet $\Gamma$, but we consider here that $\Gamma$ is the same as the input alphabet $\Sigma$. Without further mention all transducers considered here are nondeterministic.) $\mathbf{t}=(Q,\Sigma ,T,s,F)$ such that $Q,s,F$ are exactly the same as those in $\lambda$-NFAs, $\Sigma$ is the alphabet, and $T\subseteq Q\times (\Sigma \cup \{\lambda \})\times (\Sigma \cup \{\lambda \})\times Q$ is the finite set of transitions or edges. We write $(p,x/y,q)$, or $p\stackrel{x/y}{\to }q$ for a transition—the label here is $(x/y)$, with x being the input and y being the output label of the transition. The concepts of path, computation, accepting path, and trim transducer are similar to those in $\lambda$-NFAs. However, the label of a transducer path $(p_0,x_1/y_1,p_1)\cdots (p_{\ell -1},x_{\ell }/y_{\ell },p_{\ell })$ is the pair $(x_1\cdots x_{\ell },y_1\cdots y_{\ell })$ of the two words consisting of the concatenations of the input and output labels in the path, respectively. The relation realized by the transducer $\mathbf{t}$, denoted by $R(\mathbf{t})$, is the set of labels in all the accepting paths of $\mathbf{t}$. We write $\mathbf{t}(u)$ for the set of possible outputs of $\mathbf{t}$ on input u, that is,

$$v\in \mathbf{t}(u)\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}(u,v)\in R(\mathbf{t}).$$

The transducer $\mathbf{t}$ is called functional, if the relation $R(\mathbf{t})$ is a function, that is, $\mathbf{t}(u)$ consists of at most one word, for all input words u. We say that $\mathbf{t}$ realizes a partial identity, if $v\in \mathbf{t}(u)$ implies that $v=u$.

If $\mathbf{m}$ is an automaton or a transducer, then the size of $\mathbf{m}$, denoted by $\left|\mathbf{m}\right|$, is the number of states plus the number of transitions in $\mathbf{m}$. We shall write

$$Q_{\mathbf{m}},T_{\mathbf{m}}\mathrm{for}\mathrm{the}\mathrm{sets}\mathrm{of}\mathrm{states}\mathrm{and}\mathrm{transitions}\mathrm{of}\mathbf{m},\mathrm{respectively}.$$

If $\mathbf{m}$ is trim then $|Q_{\mathbf{m}}|\le |T_{\mathbf{m}}|+1$; thus,

$$\mathrm{if}\mathbf{m}\mathrm{is}\mathrm{trim}\mathrm{then}\left|\mathbf{m}\right|=O(|T_{\mathbf{m}}|).$$

We recall that making an automaton or transducer $\mathbf{m}$ trim can be done in linear time $O(|\mathbf{m}|)$.

2.3. Edit Strings and Edit Distance

The alphabet $E_{\Sigma }$ of the (basic) edit operations, which depends on the alphabet $\Sigma$ of ordinary symbols, consists of all symbols $(x/y)$ such that $x,y\in \Sigma \cup \{\lambda \}$ and at least one of x and y is in $\Sigma$. If $(x/y)\in E_{\Sigma }$ and x is not equal to y, then $(x/y)$ is called an error [23]. The edit operations $(a/b)$, $(\lambda /a)$, $(a/\lambda )$, where $a,b\in \Sigma -\{\lambda \}$ and $a\ne b$, are called substitution, insertion, deletion, respectively. We write $(\lambda /\lambda )$ for the empty word over the alphabet $E_{\Sigma }$. We note that $\lambda$ is used as a formal symbol in the elements of $E_{\Sigma }$. For example, if $a,b\in \Sigma$, then $(\lambda /a)(b/b)\ne (b/a)(\lambda /b)$. The elements of $E_{\Sigma }^{\ast }$ are called edit strings. The weight of an edit string h, denoted by $\mathrm{weight}(h)$, is the number of errors occurring in h. For example, for

$$g=(a/a)(a/\lambda )(b/b)(b/a)(b/b),$$

(5)

$\mathrm{weight}(g)=2$. The input and output parts of an edit string $h=(x_1/y_1)\cdots (x_n/y_n)$ are the words (over $\Sigma$) $x_1\cdots x_n$ and $y_1\cdots y_n$, respectively. We write $\mathrm{inp}(h)$ for the input part and $\mathrm{out}(h)$ for the output part of h. For example, for the g shown above, $\mathrm{inp}(g)=aabbb$ and $\mathrm{out}(g)=abab$. The inverse of an edit string h is the edit string resulting by inverting the order of the input and output parts in every edit operation in h. For example, the inverse of g shown above is

$$(a/a)(\lambda /a)(b/b)(a/b)(b/b).$$

The channel $\mathrm{sid}(k)$ can be defined more rigorously via edit strings:

$$\mathrm{sid}(k)=\{(u,v)\mid u=\mathrm{inp}(h),v=\mathrm{out}(h),\mathrm{for}\mathrm{some}h\in E_{\Sigma }^{\ast }\mathrm{with}\mathrm{weight}(h)\le k\}.$$

The edit (or Levenshtein) distance [24] between two words u and v, denoted by $\delta (u,v)$, is the smallest number of errors (substitutions, insertions and deletions) that can be used to transform u to v. More formally,

$$\delta (u,v)=\min \{\mathrm{weight}(h)\mid h\in E_{\Sigma }^{\ast },\mathrm{inp}(h)=u,\mathrm{out}(h)=v\}.$$

We say that an edit string h realizes the edit distance between two words u and v, if $\mathrm{weight}(h)=\delta (u,v)$ and, either $\mathrm{inp}(h)=u$ and $\mathrm{out}(h)=v$, or $\mathrm{inp}(h)=v$ and $\mathrm{out}(h)=u$. For example, for $\Sigma =\{a,b\}$, we have that $\delta (ababa,babbb)=3$ and the edit string

$$h=(a/\lambda )(b/b)(a/a)(b/b)(a/b)(\lambda /b)$$

realizes $\delta (ababa,babbb)$. Note that several edit strings can realize the distance $\delta (u,v)$. If L is a language containing at least two words, then the edit distance of L is

$$\delta (L)=\min \{\delta (u,v)\mid u,v\in L\mathrm{and}u\ne v\}.$$

Testing whether a given NFA accepts at least two words is not a concern in this paper, but we note that this can be done efficiently (in linear time via a breadth first search type algorithm) [25].

The next lemma comes from [4]. The bound $D_{\mathbf{a}}$ is always less than or equal to the number of states in the NFA $\mathbf{a}$. Moreover, there are NFAs for which this bound is tight—see Section 6.

Lemma 1.

For every NFA $\mathbf{a}$ accepting at least two words, we have that

$$\delta (L(\mathbf{a}))\le D_{\mathbf{a}},$$

where $D_{\mathbf{a}}$ is the number of states in the longest path in $\mathbf{a}$ from the start state having no repeated state.

However, the bound $D_{\mathbf{a}}$ is of no use in our context, as the problem of determining the length of a longest path in a given automaton, or a graph in general, is NP-complete since an algorithm solving this problem can be used to decide the existence of a Hamiltonian path; see for example [26]. There are many ways to obtain an efficiently computable upper bound on the edit distance of $L(\mathbf{a})$ that is always at most equal to the number of states in $\mathbf{a}$. For example, that distance is always less than or equal to the distance of the two shortest accepted words. We agree to use this as a working upper bound:

Lemma 2.

For every NFA $\mathbf{a}$ accepting at least two words, we have that

$$\delta (L(\mathbf{a}))\le B_{\mathbf{a}},$$

where $B_{\mathbf{a}}$ is the edit distance of two shortest words in $L(\mathbf{a})$.

3. Edit Distance via Error-Detection

In [5], the authors discuss a conceptual method for computing integral distances of regular languages—integral means that all distance values are nonnegative integers—via the property of error-detection. In this section, we review that method and produce a concrete preliminary algorithm for computing the edit distance of a regular language.

A language L is error-detecting for a channel $\gamma$, [27], if no L-word can be received as a different L-word via $\gamma$; that is (The definition of error-detection in [27] uses $L\cup \{\lambda \}$ instead of L in Formula 6. This slight change makes the presentation here simpler and has no bearing on any existing results regarding error-detecting languages.), for any words u and v,

$$u,v\in L\mathrm{and}(u,v)\in \gamma \to u=v.$$

(6)

Remark 1.

The error-detection method of [5] for computing inner distances of regular languages is based on the following observations, where $\mathbf{a}$ is an NFA and $\mathbf{t}$ is an input-preserving transducer.

1.

A language L is error-detecting for $\mathrm{sid}(m)$, if and only if $\delta (L)>m$.

2.

$\delta (L)$ is equal to the positive integer k such that L is error-detecting for $\mathrm{sid}(k-1)$ and L is not error-detecting for $\mathrm{sid}(k)$.

3.

We have the following facts from [27]. A language L is error-detecting for a channel γ if and only if the following relation is a function

$$\gamma \cap (L\times {\Sigma }^{\ast })\cap ({\Sigma }^{\ast }\times L).$$

(7)

Moreover, if $\mathbf{a}$ accepts L and $\mathbf{t}$ realizes γ, then a transducer $(\mathbf{t}\downarrow \mathbf{a})$ realizing $\gamma \cap (L\times {\Sigma }^{\ast })$ can be constructed in time $O(|\mathbf{t}\left|\right|\mathbf{a}|)$ and, analogously, a transducer $(\mathbf{t}\uparrow \mathbf{a})$ realizing $\gamma \cap ({\Sigma }^{\ast }\times L)$ can be constructed in time $O(|\mathbf{t}\left|\right|\mathbf{a}|)$. Both constructions are cross-product constructions. In each case, the resulting transducer has $O(|Q_{\mathbf{a}}\left|\right|Q_{\mathbf{t}}|)$ states and $O(|T_{\mathbf{a}}\left|\right|T_{\mathbf{t}}|)$ transitions. Thus, the transducer

$$(\mathbf{t}\downarrow \mathbf{a}\uparrow \mathbf{a})$$

realizes relation (7) and can be constructed in time $O(|\mathbf{t}\left|\right|\mathbf{a}{|}^2)$.

4.

There is an $O(|T_{\mathbf{s}}{|}^2+r|Q_{\mathbf{s}}{|}^2)$ time algorithm that decides whether a given transducer $\mathbf{s}$ is functional [6,28], where r is the size of the alphabet.

Using the above observations, we present first a preliminary error-detection-based algorithm for computing the desired edit distance.

    Algorithm PrelimDistErrDetect

0.

Input: NFA $\mathbf{a}$    

1.

Let $B_{\mathbf{a}}$ be the edit distance bound in Lemma 2

2.

Let $\min \leftarrow 1$ and $\max \leftarrow B_{\mathbf{a}}-1$

Perform binary search to find the largest k in $\{\min ,\dots ,\max \}$

for which $L(\mathbf{a})$ is error-detecting for $\mathrm{sid}(k)$ as follows:

while ($\min \le \max$)

a)

Let $k\leftarrow \lfloor (\min +\max )/2\rfloor$

b)

Construct transducer ${\mathbf{sid}}_k$ realizing the channel $\mathrm{sid}(k)$—see Figure 1

c)

Construct the transducer ${\mathbf{t}}_k^{\prime }\leftarrow ({\mathbf{sid}}_k\downarrow \mathbf{a}\uparrow \mathbf{a})$

d)

If $L(\mathbf{a})$ is error-detecting for $\mathrm{sid}(k)$, let $\min \leftarrow k+1$

Else let $\max \leftarrow k-1$

4.

return min

Remark 2.

Step (3d) of the above algorithm can be computed using the transducer functionality algorithm on ${\mathbf{t}}_k^{\prime }$, which leads again to a polynomial but expensive algorithm. It turns out, however, using standard logical arguments, that

$$Condition(6)isequivalenttowhether(\mathbf{t}\downarrow \mathbf{a}\uparrow \mathbf{a})realizesapartialidentity,$$

when $\mathbf{t}$ realizes γ—in the above algorithm, $\mathbf{t}$ is ${\mathbf{sid}}_k$. Moreover, [6], there is an

$$O(|T_{\mathbf{t}}|+r|Q_{\mathbf{t}}|)$$

time algorithm that tests whether a given transducer $\mathbf{t}$ realizes a partial identity, where r is the size of the alphabet.

Corollary 1.

Consider the algorithm PrelimDistErrDetect. Using the partial identity test for ${\mathbf{t}}_k^{\prime }$ in step 3d, the algorithm computes the edit distance of a language given via a trim NFA $\mathbf{a}$ in time

$$O(n^2{r}^2{B}_{\mathbf{a}}\log B_{\mathbf{a}}),$$

where r is the cardinality of the alphabet used in $T_{\mathbf{a}}$, and $n=|T_{\mathbf{a}}|$.

Proof. 

The correctness of the algorithm follows from Remarks 1 and 2. For the time complexity, the whole loop will perform $O(\log B_{\mathbf{a}})$ iterations. In each iteration, the value k is used to construct the transducer ${\mathbf{sid}}_k$ shown in Figure 1 with alphabet being the set of alphabet symbols appearing in the definition of $\mathbf{a}$. Then, the transducer ${\mathbf{t}}_k^{\prime }$ is constructed having $O(k|Q_{\mathbf{a}}{|}^2)$ states and $O(k{r}^2|T_{\mathbf{a}}^2|)$ transitions. Then, the partial identity of ${\mathbf{t}}_k^{\prime }$ is tested in time $O(|T_{\mathbf{a}}{|}^{2}k{r}^2)$. As $k<B_{\mathbf{a}}$, it follows that the total time complexity is as required. □

We note that, in the worst case, $B_{\mathbf{a}}$ is of order $O(n)$ and, assuming a fixed alphabet, the above algorithm operates in time $O(n^3\log n),$ which is asymptotically better than the time complexity of the algorithm in [4], even when the given automaton is a DFA.

4. An $\mathit{O}\mathbf{\left(}{\mathit{n}}^{\mathbf{2}}\mathit{d}\mathbf{\right)}$ Algorithm for Edit Distance via Error-Detection

In this section, we observe that the algorithm of the previous section repeats a lot of computations, and we eliminate those repeated computations to arrive at an improved algorithm that computes the edit distance d of a trim NFA $\mathbf{a}$ in time $O(n^{2}d{r}^2)$, where r is the cardinality of the alphabet used in $T_{\mathbf{a}}$, and $n=|T_{\mathbf{a}}|$. The improved algorithm is based on the following two observations:

• The previous algorithm starts the binary search loop by constructing the transducer ${\mathbf{t}}_{\lfloor B_{\mathbf{a}}/2\rfloor }^{\prime }$, but the edit distance might be much smaller than $\lfloor B_{\mathbf{a}}/2\rfloor$. It turns out that it is more efficient in the end to construct in turn ${\mathbf{t}}_1^{\prime },{\mathbf{t}}_2^{\prime },\dots$ until the first ${\mathbf{t}}_d^{\prime }$ that does not realize a partial identity.
• If ${\mathbf{t}}_k^{\prime }$ is constructed and tested that does not realize a partial identity, then the transducer ${\mathbf{t}}_{k+1}^{\prime }$ is constructed from scratch and the partial identity test is repeated for the part of ${\mathbf{t}}_{k+1}^{\prime }$ that corresponds to ${\mathbf{t}}_k^{\prime }$. We shall define the transducer ${\mathbf{t}}_{k+1}^{″}$ to be the part that is added to ${\mathbf{t}}_k^{\prime }$ in order to obtain ${\mathbf{t}}_{k+1}^{\prime }$, plus some initial state. Moreover, we shall show that, if ${\mathbf{t}}_k^{\prime }$ realizes a partial identity, then ${\mathbf{t}}_{k+1}^{\prime }$ realizes a partial identity if and only if ${\mathbf{t}}_{k+1}^{″}$ does so. Thus, the partial identity test in each step will apply only to the new part that is added to the transducer of the previous step.

We proceed with details based on the above observations.

Product construction of trim ${\mathbf{t}}^{\prime }=\mathbf{t}\downarrow \mathbf{a}\uparrow \mathbf{a}$, given transducer $\mathbf{t}$ and NFA $\mathbf{a}$. As usual in cross product constructions, the states of ${\mathbf{t}}^{\prime }$ are triples of the form $(\phi ,q,q^{\prime })$, where $\phi$ is a state of $\mathbf{t}$, and q, $q^{\prime }$ are states of $\mathbf{a}$. The initial state of ${\mathbf{t}}^{\prime }$ is $({\phi }_0,q_0,q_0)$, where ${\phi }_0$ is the initial state of $\mathbf{t}$ and $q_0$ is the initial state of $\mathbf{a}$. The construction is incremental, starting with the creation of $({\phi }_0,q_0,q_0)$; then:

• If state $(\phi ,q,q^{\prime })$ has been created, and there are transitions $\phi \stackrel{x/y}{\to }\psi ,q\stackrel{x}{\to }r,q^{\prime }\stackrel{y}{\to }{r}^{\prime }$ of $\mathbf{t}$, ${\mathbf{a}}^{\lambda }$ and ${\mathbf{a}}^{\lambda }$, respectively, then the transition

  $$(\phi ,q,q^{\prime })\stackrel{x/y}{\to }(\psi ,r,r^{\prime })$$

  is added in ${\mathbf{t}}^{\prime }$. Here, ${\mathbf{a}}^{\lambda }$ is the $\lambda$-NFA that results if we add in $\mathbf{a}$ the loop transitions $(q,\lambda ,q)$ to all states q of $\mathbf{a}$.

The final states of ${\mathbf{t}}^{\prime }$ are those constructed triples consisting of final states in $\mathbf{t}$ and $\mathbf{a}$. In the end, we also make ${\mathbf{t}}^{\prime }$ trim.

Optimized construction of ${\mathbf{t}}_{k+1}^{″}$ and ${\mathbf{t}}_{k+1}^{\prime }$ from the trim ${\mathbf{t}}_k^{\prime }$. Suppose that ${\mathbf{t}}_k^{\prime }$ has been constructed, where initially ${\mathbf{t}}_1^{\prime }={\mathbf{sid}}_1\downarrow \mathbf{a}\uparrow \mathbf{a}$. Constructing ${\mathbf{t}}_{k+1}^{\prime }$ using ${\mathbf{t}}_k^{\prime }$ will be done again incrementally. The first phase of the incremental construction is to add the new transitions

$$(\left[k\right],q,q^{\prime })\stackrel{x/y}{\to }([k+1],r,r^{\prime }),$$

(8)

where $x/y$ is an error and $q\stackrel{x}{\to }r,q^{\prime }\stackrel{y}{\to }{r}^{\prime }$ are transitions in ${\mathbf{a}}^{\lambda }$. There will be no new transitions of the form $(\left[i\right],q,q^{\prime })\stackrel{x/y}{\to }([k+1],r,r^{\prime })$ for $i<k$, because the transducer ${\mathbf{sid}}_{k+1}$ has no transitions from any state $\left[i\right]$ with $i<k$ to state $[k+1]$. Note that the numbers of new transitions and new states created as in (8) are $O(|T_{\mathbf{a}}{|}^2{r}^2)$ and $O(|Q_{\mathbf{a}}{|}^2)$, respectively.

After the first phase, the incremental construction proceeds from the new states $([k+1],r,r^{\prime })$ in (8). Any new transition must be of the form

$$([k+1],q,q^{\prime })\stackrel{\sigma /\sigma }{\to }([k+1],r,r^{\prime }),$$

(9)

where $\sigma \in \Sigma$. This is because the transducer ${\mathbf{sid}}_{k+1}$ has only transitions of the form $[k+1]\stackrel{\sigma /\sigma }{\to }[k+1]$ going out of the state $[k+1]$. The process ends when no new states are created. The transitions and final states of the transducer ${\mathbf{t}}_{k+1}^{\prime }$ are those in ${\mathbf{t}}_k^{\prime }$ plus the newly created ones, after removing any new states that cannot reach a final state (thus, also ${\mathbf{t}}_{k+1}^{\prime }$ is trim). The transducer ${\mathbf{t}}_{k+1}^{″}$ has as transitions and final states only the newly created ones, and has as initial state a new state $[-1]$ with transitions $[-1]\stackrel{\lambda /\lambda }{\to }(\left[k\right],q,q^{\prime })$, for all states of the form $(\left[k\right],q,q^{\prime })$. □

Lemma 3.

Suppose the trim transducer ${\mathbf{t}}_k^{\prime }$ realizes a partial identity.

• If $C_1$ is a computation of ${\mathbf{t}}_k^{\prime }$ ending at a state of the form $(\left[k\right],p,p^{\prime }),$ then the label of $C_1$ is of the form $(w_1,w_1)$.
• ${\mathbf{t}}_{k+1}^{\prime }$ realizes a partial identity if and only if ${\mathbf{t}}_{k+1}^{″}$ does so.

Proof. 

For the first statement, consider any computation $C_1$ of ${\mathbf{t}}_k^{\prime }$ having some label $(w_1,w_1^{\prime })$ and ending at a state of the form $(\left[k\right],p,p^{\prime })$. We show that $w_1=w_1^{\prime }$. If the state $(\left[k\right],p,p^{\prime })$ is final, then $C_1$ is an accepting computation, which implies $w_1=w_1^{\prime }$, as ${\mathbf{t}}_k^{\prime }$ realizes a partial identity. If $(\left[k\right],p,p^{\prime })$ is not a final state, then, as ${\mathbf{t}}_k^{\prime }$ is trim, there is a path $C_1^{\prime }$ from $(\left[k\right],p,p^{\prime })$ to a final state of ${\mathbf{t}}_k^{\prime }$, where all states of that path are of the form $(\left[k\right],r,r^{\prime })$ and all labels of that path are of the form $\sigma /\sigma$—this is because any transition of ${\mathbf{sid}}_k$ from state $\left[k\right]$ can only go to state $\left[k\right]$ and can only have a label of the form $\sigma /\sigma$. Thus, there is an accepting path of ${\mathbf{t}}_k^{\prime }$ of the form $C_1{C}_1^{\prime }$ with label $(w_{1}z,w_1^{\prime }z)$ for some nonempty word z. Then, as ${\mathbf{t}}_k^{\prime }$ realizes a partial identity, we have that $w_{1}z=w_1^{\prime }z$, which implies $w_1=w_1^{\prime }$, as required.

For the ‘only if’ part of the second statement, assume that ${\mathbf{t}}_{k+1}^{\prime }$ realizes a partial identity. Consider any accepting computation $C_2$ of ${\mathbf{t}}_{k+1}^{″}$ with some label $(w_2,w_2^{\prime })$. We show that $w_2=w_2^{\prime }$. Let $[-1]\stackrel{\lambda /\lambda }{\to }(\left[k\right],p,p^{\prime })$ be the first transition of $C_2$. Let $C_2^{\prime }$ be the path that results when we remove the first transition of $C_2$. By the construction of ${\mathbf{t}}_{k+1}^{\prime }$, there is a computation $C_1$ of ${\mathbf{t}}_k^{\prime }$ that ends at state $(\left[k\right],p,p^{\prime })$. Let $(w_1,w_1)$ be the label of $C_1$. Then, $C_1{C}_2^{\prime }$ is an accepting computation of ${\mathbf{t}}_{k+1}^{\prime }$ with label $(w_1{w}_2,w_1{w}_2^{\prime })$. As ${\mathbf{t}}_{k+1}^{\prime }$ realizes a partial identity, $w_1{w}_2=w_1{w}_2^{\prime }$, which implies $w_2=w_2^{\prime }$, as required.

For the ‘if’ part of the second statement, assume that ${\mathbf{t}}_{k+1}^{″}$ realizes a partial identity. Consider any accepting computation C of ${\mathbf{t}}_{k+1}^{\prime }$. We show that the label of C must be of the form $(w,w)$. If C is already a computation of ${\mathbf{t}}_k^{\prime }$, then this holds, as ${\mathbf{t}}_k^{\prime }$ realizes a partial identity. Now suppose that $C=C_1{C}_2$ such that $C_1$ is a computation of ${\mathbf{t}}_k^{\prime }$ and $C_2$ is a path in ${\mathbf{t}}_{k+1}^{\prime }$ that starts with a transition as in (8) and then uses transitions as in (9). Let $(\left[k\right],p,p^{\prime })$ be the last state of $C_1$, which is also the first state of $C_2$. Then, $C_1$ has some label $(w_1,w_1)$. In addition, the path

$$([-1]\stackrel{\lambda /\lambda }{\to }(\left[k\right],p,p^{\prime }))C_2$$

is an accepting computation of ${\mathbf{t}}_{k+1}^{″}$, which implies that it has some label $(w_2,w_2)$. Hence, the label of C is $(w_1{w}_2,w_1{w}_2)$ and, therefore, ${\mathbf{t}}_k^{\prime }$ realizes a partial identity.

The improved algorithm is shown next:

    Algorithm DistErrDetect

0.

Input: NFA $\mathbf{a}$    

1.

Construct the transducer ${\mathbf{sid}}_1$ realizing the channel $\mathrm{sid}(1)$—see Figure 1

2.

Construct the trim transducer ${\mathbf{t}}_1^{\prime }={\mathbf{sid}}_1\downarrow \mathbf{a}\uparrow \mathbf{a}$

3.

Let $k\leftarrow 1$

4.

Let $\mathbf{s}\leftarrow {\mathbf{t}}_1^{\prime }$

5.

while ($\mathbf{s}$ realizes a partial identity)

a)

Construct ${\mathbf{t}}_{k+1}^{″}$ and ${\mathbf{t}}_{k+1}^{\prime }$ from ${\mathbf{t}}_k^{\prime }$ using the optimized construction

b)

Let $\mathbf{s}\leftarrow {\mathbf{t}}_{k+1}^{″}$

c)

Let $k\leftarrow k+1$

6.

returnk

Theorem 1.

Algorithm DistErrDetect computes the edit distance of a language given via a trim NFA $\mathbf{a}$ in time

$$O(n^{2}d{r}^2),$$

where d is the computed edit distance, $n=|T_{\mathbf{a}}|$, and r is the cardinality of the alphabet used in $T_{\mathbf{a}}$.

Proof. 

The correctness of the algorithm follows from the optimized construction and the above lemma. For the time complexity of the algorithm, we note the following. First, ${\mathbf{t}}_1^{\prime }$ is constructed in time $O(|\mathbf{a}{|}^2{r}^2)$. Then, ${\mathbf{t}}_2^{″},\dots ,{\mathbf{t}}_d^{″}$ are constructed according to the optimized construction. Each of these is constructed in time $O(|\mathbf{a}{|}^2{r}^2)$ and has $O(|Q_{\mathbf{a}}{|}^2)$ states and $O(|T_{\mathbf{a}}{|}^2{r}^2)$ transitions. In addition, each ${\mathbf{t}}_k^{″}$ is tested for partial identity in time $O(|T_{\mathbf{a}}{|}^2{r}^2+{\left|Q_{\mathbf{a}}\right|}^{2}r)$, which is $O(|\mathbf{a}{|}^2{r}^2)$.

5. An $\mathit{O}\mathbf{\left(}{\mathit{n}}^{\mathbf{2}}\mathit{d}\mathbf{\right)}$ Algorithm for Edit Distance via Input-Altering Transducers

In this section, we present another algorithm for computing the desired edit distance via input-altering transducers—see Theorem 3 and the associated algorithm. A transducer $\mathbf{t}$ is called input-altering, if

$$w\notin \mathbf{t}(w),\mathrm{for}\mathrm{all}\mathrm{words}w,$$

that is, the output of $\mathbf{t}$ is never equal to the input used.

We explain now how input-altering transducers are related to edit-distance and error-detection. Let $\mathbf{t}$ be a transducer. A language L is $\mathbf{t}$-independent, 29,30], if

$$u,v\in L\mathrm{and}u\in \mathbf{t}(v)\to u=v.$$

(10)

Of course, when $R(\mathbf{t})$ is input-preserving, then $\mathbf{t}$-independence is the same as error-detection for the channel $R(\mathbf{t})$, and condition (10) can be tested as explained in Remark 2. On the other hand, if the transducer $\mathbf{t}$ is input-altering, then [30], condition (10) is equivalent to

$$\mathbf{t}(L)\cap L=\varnothing .$$

(11)

If L is accepted by some NFA $\mathbf{a}$, then the above condition can be tested using two product constructions: first, construct an NFA $\mathbf{b}$ accepting $\mathbf{t}(L)$, then construct an NFA $\mathbf{c}$ by intersecting $\mathbf{b}$ with $\mathbf{a}$, and then test whether there is a path from the start to a final state of $\mathbf{c}$. Thus, condition (11) can be tested in time

$$O(|\mathbf{a}{|}^2\left|\mathbf{t}\right|).$$

(12)

Certain types of input-altering transducers are useful in constructing maximal $\mathbf{t}$-independent languages [30]. In Theorem 2, we show how an input-altering transducer can be used to model the edit operations used in the definition of the edit distance.

5.1. An Input-Altering Transducer for Edit-Distance

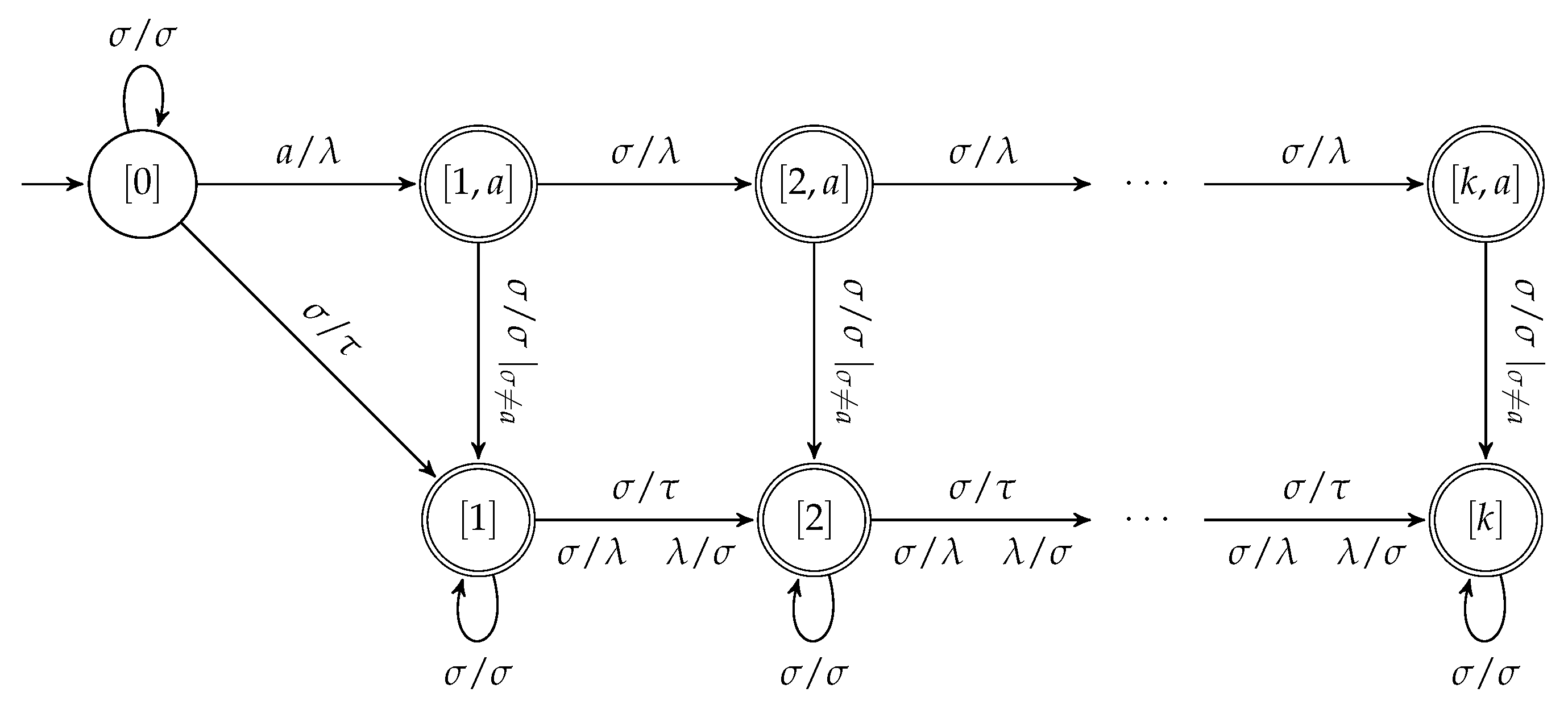
We shall define the input-altering transducer ${\mathbf{ia}}_k$, which is partially shown in Figure 2. The value i in a state $\left[i\right]$ or $[i,a]$ is called the error counter, meaning that any path from $\left[0\right]$ to a state with error counter i has to be labeled $uv$ such that $\delta (u,v)\le i$. More precisely, we will define the edges such that a state $[i,a]$ can be reached from $\left[0\right]$ via a path with label $uv$ if and only if $u=vax$ for some word x and $i=\left|ax\right|$, thus, v is a proper prefix of u and state $[i,a]$ remembers the left-most letter of u that occurs after its prefix v. A state $\left[i\right]$ with $i\ge 1$ can only be reached via a path labeled $uv$ from $\left[0\right]$ if $1\le \delta (u,v)\le i$, thus, $u\ne v$. Furthermore, we make sure that for $u\ne v$ such that neither $u{\le }_{p}v$ nor $v{\le }_{p}u$ there is a path from $\left[0\right]$ to $[\delta (u,v)],$ which is labeled by $uv$ or $vu$.

Definition 1.

The transducer

$${\mathbf{ia}}_k=(Q,\Sigma ,E,\left[0\right],F)$$

is defined as follows. The set of states is

$$Q=\left\{\left[i\right]\left|\phantom{\left[i\right]}\phantom{0\le i\le k}\right.0\le i\le k\right\}\cup \left\{[i,a]\left|\phantom{[i,a]}\phantom{1\le i\le k,a\in \Sigma }\right.1\le i\le k,a\in \Sigma \right\}$$

with all but the initial state $\left[0\right]$ being final states:

$$F=Q\backslash \left\{\left[0\right]\right\}.$$

The transitions in ${\mathbf{ia}}_k$ can be divided into the four sets of edges $E=E_0\cup E_s\cup E_i\cup E_d$. The transitions from $E_0$ do not introduce any error, edges from the other sets model one substitution ($E_s$), insertion ($E_i$), or deletion ($E_d$):

$$\begin{array}{cc}\hfill E_0=& \left\{\left[i\right]\stackrel{\sigma /\sigma }{\to }\left[i\right]\sigma \in \Sigma ,0\le i\le k\right\}\cup ,\hfill \end{array}$$

(13)

$$\begin{array}{cc}& \left\{[i,a]\stackrel{\sigma /\sigma }{\to }\left[i\right]a,\sigma \in \Sigma ,a\ne \sigma ,1\le i\le k\right\},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill E_s=& \left\{\left[i\right]\stackrel{\sigma /\tau }{\to }[i+1]\sigma ,\tau \in \Sigma ,\sigma \ne \tau ,0\le i<k\right\},\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill E_i=& \left\{\left[i\right]\stackrel{\lambda /\sigma }{\to }[i+1]\sigma \in \Sigma ,1\le i<k\right\},\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill E_d=& \left\{\left[0\right]\stackrel{a/\lambda }{\to }[1,a]a\in \Sigma \right\}\cup ,\hfill \end{array}$$

(17)

$$\begin{array}{cc}& \left\{\left[i\right]\stackrel{\sigma /\lambda }{\to }[i+1]\sigma \in \Sigma ,1\le i<k\right\}\cup ,\hfill \end{array}$$

(18)

$$\begin{array}{cc}& \left\{[i,a]\stackrel{\sigma /\lambda }{\to }[i+1,a]a,\sigma \in \Sigma ,1\le i<k\right\}.\hfill \end{array}$$

(19)

Terminology. If $\mathbf{t}=(Q,\Sigma ,T,q_0,F)$ is a transducer in standard form, then, we write ${\mathbf{t}}^{\mathrm{e}}$ for the NFA

$${\mathbf{t}}^{\mathrm{e}}=(Q,E_{\Sigma },T,q_0,F)$$

over the edit alphabet $E_{\Sigma }$, where the labels of the transitions in $\mathbf{t}$ are viewed as elements of $E_{\Sigma }$. Note that, the label of a path P in $\mathbf{t}$ is a pair of words $(u,v)$, whereas the label of the corresponding path in ${\mathbf{t}}^{\mathrm{e}}$, which we denote as $P^{\mathrm{e}}$, is an edit string h such that $\mathrm{inp}(h)=u$ and $\mathrm{out}(h)=v$. This type of NFA is called an eNFA in [23].

Definition 2.

An edit string h of nonzero weight is calledreduced, if (a) the first error in h is not an insertion, and (b) if the first error in h is a deletion of the form $(a/\lambda )$, then the first non-deletion edit operation that follows $(a/\lambda )$ in h (if any) is of the form $\sigma /\sigma$ with $\sigma \in \Sigma \backslash \{a\}$.

Example. The edit string $(a/a)(a/b)(a/\lambda )(\lambda /a)$ is reduced as its first error is a substitution. The edit string $(a/a)(a/\lambda )(b/b)(b/a)$ is reduced as well. The edit string $(\lambda /a)(a/a)$ is not reduced as it starts with an insertion, and the edit string $(a/\lambda )(b/a)(b/b)$ is not reduced either.

The proofs of the next two lemmata are given in the appendix.

Lemma 4.

Let $x,y,u,v$ be words. The following statements hold true:

1.

$\delta (xuy,xvy)=\delta (u,v)$.

2.

If $v{<}_{p}u$ then $\delta (u,v)=\left|u\right|-\left|v\right|$.

3.

If $u\ne v$, then there is a reduced edit string h realizing $\delta (u,v)$.

Lemma 5.

Let $k\in \mathbb{N}$ and let $u,v$ be words. The following statements hold true with respect to the transducer ${\mathbf{ia}}_k$.

1.

In ${\mathbf{ia}}_k^{\mathrm{e}}$, every path from the start state $\left[0\right]$ to any state $\left[i\right]$ or $[i,a]$ has as label a reduced edit string whose weight is equal to i.

2.

If $1\le \delta (u,v)\le k$ and h is a reduced edit string realizing $\delta (u,v)$, then h is accepted by ${\mathbf{ia}}_k^{\mathrm{e}}$.

3.

If $v\in {\mathbf{ia}}_k(u)$, then $1\le \delta (u,v)\le k$.

Theorem 2.

For each $k\in \mathbb{N}$, the transducer ${\mathbf{ia}}_k$ is input-altering and of size $O(k{r}^2)$, where r is the cardinality of the alphabet, and satisfies the following condition, for any language L containing at least two words

$${\mathbf{ia}}_k(L)\cap L=\varnothing ifandonlyif\delta (L)>k.$$

(20)

Proof. 

By construction, it follows that ${\mathbf{t}}_k$ is trim and has $O(rk)$ states and $O(k{r}^2)$ transitions. Hence, it is indeed of size $O(k{r}^2)$. The third statement of Lemma 5 implies that the transducer is input-altering. Next, we show that (20) is true for all languages L containing at least two words.

First, for the ‘if’ part, assume $\delta (L)>k$ and consider any words $u,v\in L$. We need to prove $v\notin {\mathbf{ia}}_k(u)$. If $u=v$, then this holds as ${\mathbf{ia}}_k$ is input-altering. Else, it follows from the third statement of Lemma 5. Now, for the ‘only if’ part, assume

$${\mathbf{ia}}_k(L)\cap L=\varnothing ,$$

(21)

but, for the sake of contradiction, suppose there are different words $u,v\in L$ such that $1\le \delta (u,v)\le k$. Let h be a reduced edit string realizing $\delta (u,v)$. By the second statement of Lemma 5, h is accepted by ${\mathbf{ia}}_k^{\mathrm{e}}$ via some path $P^{\mathrm{e}}$ and, therefore, either of $(u,v)$ and $(v,u)$ is the label of the path P of ${\mathbf{ia}}_k$, that is, we have $u\in {\mathbf{ia}}_k(v)$ or $v\in {\mathbf{ia}}_k(u)$, which contradicts (21). □

Corollary 2.

For each NFA $\mathbf{a}$ accepting at least two words and for each transducer ${\mathbf{ia}}_k$, with $k\in \mathbb{N}$, the following condition is satisfied:

$$R\left({\mathbf{ia}}_k\downarrow \mathbf{a}\uparrow \mathbf{a}\right)=\varnothing ifandonlyif\delta \left(L(\mathbf{a})\right)>k.$$

(22)

Proof. 

The statement follows from the above theorem and the fact (based on standard logic arguments) that $R\left({\mathbf{ia}}_k\downarrow \mathbf{a}\uparrow \mathbf{a}\right)=\varnothing$ is equivalent to ${\mathbf{ia}}_k\left(L(\mathbf{a})\right)\cap L(\mathbf{a})=\varnothing$. □

The reason why condition $R\left({\mathbf{ia}}_k\downarrow \mathbf{a}\uparrow \mathbf{a}\right)=\varnothing$ is preferred to the equivalent one in Theorem 2 is explained further below in the remark that follows Theorem 3.

5.2. The Second $O(n^{2}d)$ Algorithm for Edit Distance

Here, we use the results of the previous subsection to arrive at the second algorithm for computing the desired edit distance. Corollary 2 implies that the preliminary algorithm PrelimDistInpAlter shown below correctly computes the desired edit distance. Moreover, by reasoning as in the proof of Corollary 1, it follows that this algorithm also executes in time $O(n^2{r}^2{B}_{\mathbf{a}}\log B_{\mathbf{a}})$, where r is the cardinality of the alphabet used in $T_{\mathbf{a}}$, and $n=|T_{\mathbf{a}}|$.

    Algorithm PrelimDistInpAlter

0.

Input: NFA $\mathbf{a}$    

1.

Let $B_{\mathbf{a}}$ be the bound in Lemma 2

2.

Let $\min \leftarrow 1$ and $\max \leftarrow B_{\mathbf{a}}-1$

3.

Perform binary search to find the largest k in $\{\min ,\dots ,\max \}$

for which $L(\mathbf{a})$ is error-detecting for $\mathrm{sid}(k)$ as follows:

while ($\min \le \max$)

a)

Let $k\leftarrow \lfloor (\min +\max )/2\rfloor$

b)

Construct the transducer ${\mathbf{ia}}_k$ (see Figure 2)

c)

Construct the transducer ${\mathbf{t}}_k^{\prime }\leftarrow {\mathbf{ia}}_k\downarrow \mathbf{a}\uparrow \mathbf{a}$

d)

If $\left(R({\mathbf{t}}_k^{\prime })=\varnothing \right)$ let $\min \leftarrow k+1$

Else let $\max \leftarrow k-1$

4.

return min

We discuss now how to improve the above algorithm. The two observations we made at the beginning of Section 4 apply here as well if, instead of partial identity of ${\mathbf{t}}_k^{\prime }$, we talk about the emptiness of ${\mathbf{t}}_k^{\prime }$. Thus, we want the improved algorithm to construct in turn ${\mathbf{t}}_1^{\prime },{\mathbf{t}}_2^{\prime },\dots$ until the first ${\mathbf{t}}_d^{\prime }$ with $R({\mathbf{t}}_d^{\prime })\ne \varnothing$. Moreover, when ${\mathbf{t}}_k^{\prime }$ has been constructed and realizes ∅, we continue in the next step with new transitions added to ${\mathbf{t}}_k^{\prime }$ in order to get ${\mathbf{t}}_{k+1}^{\prime }$.

Optimized construction of ${\mathbf{t}}_{k+1}^{\prime }$ from the trim ${\mathbf{t}}_k^{\prime }$. Suppose that the trim ${\mathbf{t}}_k^{\prime }$ has been constructed, where initially ${\mathbf{t}}_1^{\prime }\leftarrow {\mathbf{ia}}_1\downarrow \mathbf{a}\uparrow \mathbf{a}$. Constructing ${\mathbf{t}}_{k+1}^{\prime }$ using ${\mathbf{t}}_k^{\prime }$ will be done again incrementally. The first phase of the incremental construction is to add two sets of new transitions: the new transitions

$$(\left[k\right],q,q^{\prime })\stackrel{x/y}{\to }([k+1],r,r^{\prime }),$$

(23)

where $x/y$ is an error and $q\stackrel{x}{\to }r,q^{\prime }\stackrel{y}{\to }{r}^{\prime }$ are transitions in ${\mathbf{a}}^{\lambda }$; and the new transitions

$$([k,a],q,q^{\prime })\stackrel{\sigma /\lambda }{\to }([k+1,a],r,r^{\prime }),$$

(24)

where $a,\sigma \in \Sigma$, and $q\stackrel{\sigma }{\to }r,q^{\prime }\stackrel{\lambda }{\to }{r}^{\prime }$ are transitions in ${\mathbf{a}}^{\lambda }$. Note that the total numbers of new transitions and states created in the first phase are $O(|T_{\mathbf{a}}{|}^2{r}^2)$ and $O(|Q_{\mathbf{a}}{|}^{2}r)$, respectively.

After the first phase, the incremental construction proceeds from the new states $([k+1],r,r^{\prime })$ and $([k+1,a],r,r^{\prime })$. Any new transition must be of the form

$$([k+1],r,r^{\prime })\stackrel{\sigma /\sigma }{\to }([k+1],t,t^{\prime })\mathrm{or}([k+1,a],r,r^{\prime })\stackrel{\sigma /\sigma }{\to }([k+1],t,t^{\prime }),$$

(25)

where $\sigma \in \Sigma$ and, in the second case above, $\sigma \ne a$. This is because the transducer ${\mathbf{ia}}_{k+1}$ has only transitions of the form $[k+1]\stackrel{\sigma /\sigma }{\to }[k+1]$ and $[k+1,a]\stackrel{\sigma /\sigma }{\to }[k+1]$, with $\sigma \ne a$, going out of the state $[k+1]$. The incremental process ends when no new states are created. The transitions and final states of the transducer ${\mathbf{t}}_{k+1}^{\prime }$ are those in ${\mathbf{t}}_k^{\prime }$ plus the newly created ones, after removing any new states that cannot reach a final state (thus, also ${\mathbf{t}}_{k+1}^{\prime }$ is trim). □

Remark 3.

If the trim transducer ${\mathbf{t}}_k^{\prime }$ has no final states, then ${\mathbf{t}}_{k+1}^{\prime }$ has no final states if and only if none of the new created states in the optimized construction is a final state.

    Algorithm DistInpAlter

0.

Input: NFA $\mathbf{a}$    

1.

Construct the transducer ${\mathbf{ia}}_1$—see Figure 2

2.

Construct the trim transducer ${\mathbf{t}}_1^{\prime }\leftarrow {\mathbf{ia}}_1\downarrow \mathbf{a}\uparrow \mathbf{a}$

3.

Let $k\leftarrow 1$

4.

Let $\mathbf{s}\leftarrow$ the set of states of ${\mathbf{t}}_1^{\prime }$

5.

while ($\mathbf{s}$ contains no final states)

a)

Construct ${\mathbf{t}}_{k+1}^{\prime }$ from ${\mathbf{t}}_k^{\prime }$ using the optimized construction

b)

Let $\mathbf{s}$ be the set of new states in the optimized construction

c)

Let $k\leftarrow k+1$

6.

returnk

Theorem 3.

Algorithm DistInpAlter computes the edit distance of the language given via a trim NFA $\mathbf{a}$ in time

$$O(n^{2}d{r}^2),$$

where d is the computed edit distance, $n=|T_{\mathbf{a}}|$, and r is the cardinality of the alphabet used in $T_{\mathbf{a}}$.

Proof. 

The correctness of the algorithm follows from the above optimized construction and Corollary 2. For the time complexity of the algorithm, we note the following: first, ${\mathbf{t}}_1^{\prime }$ is constructed in time $O(|\mathbf{a}{|}^2{r}^2)$. Then, ${\mathbf{t}}_2^{\prime },\dots ,{\mathbf{t}}_d^{\prime }$ are constructed according to the optimized construction. Each of these is constructed in time $O(|\mathbf{a}{|}^2{r}^2)$ and has $O(|Q_{\mathbf{a}}{|}^{2}r)$ states and $O(|T_{\mathbf{a}}{|}^2{r}^2)$ transitions. In addition, each ${\mathbf{t}}_k^{\prime }$ is tested for final states in linear time. □

Remark 4.

When a final state f, say, of ${\mathbf{t}}_k^{\prime }$ is created, then we know that there is an accepting path of ${\mathbf{ia}}_k\downarrow \mathbf{a}\uparrow \mathbf{a}$ ending at f. The label of that path is a word pair $(u,v)$ such that $\delta (u,v)=k$. Thus, the above algorithm can be modified to return not only the edit distance of $L(\mathbf{a})$, but also a witness pair for that distance.

6. Implementation and Testing

As both algorithms DistErrDetect and DistInpAlter have the same theoretical complexity, we chose to implement one of the two. We chose to implement DistInpAlter because it requires a simpler test for each constructed transducer (although ${\mathbf{ia}}_k$ is slightly more complex than ${\mathbf{sid}}_k$, the test for partial identity, [6], is more sophisticated than testing merely for existence of final states). We have also implemented the preliminary algorithm PrelimDistInpAlter.

Our implementation uses the FAdo package for automata, version 1.3.5.1, [7], which is well maintained and provides several useful tools for manipulating automata. We have performed several tests (All tests were performed on a laptop with the following specification. Make: Apple, Model: MacBook Pro, Processor 2.5 GHz Intel Core i7, Memory (RAM): 16.00 GB, Operating System: macOS High Sierra Version 10.13.6.) for the correctness of these algorithms, as well as two sets of tests for the time complexity, which confirm the theoretical result that DistInpAlter is indeed faster than PrelimDistInpAlter. 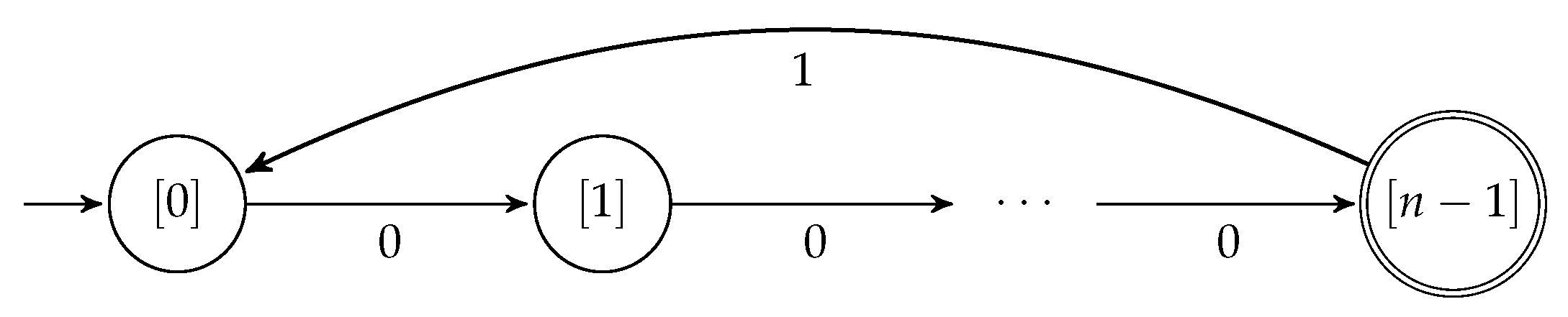The two sets of tests correspond to two lists of DFAs, $({\mathbf{a}}_n)$ and $({\mathbf{b}}_n)$, shown in Figure 3 and Figure 4. The first test set is such that the desired distance is equal to n, for each DFA ${\mathbf{a}}_n$, that is, the distance grows with n and, in fact, it is a worst-case scenario where the distance is equal to the number of states of the automaton. The second test set is such that the desired distance is fixed, equal to 2, for all n.

Table 1. Outcomes of performance tests on the automata $({\mathbf{a}}_n)$.

DFA	d	${\mathit{B}}_{{\mathbf{a}}_{\mathit{n}}}$	PrelimDistInpAlter	DistInpAlter
${\mathbf{a}}_{28}(28)$	28	28	0.696s	0.078s
${\mathbf{a}}_{41}(41)$	41	41	3.977s	0.267s
${\mathbf{a}}_{56}(56)$	56	56	12.811s	0.691s
${\mathbf{a}}_{76}(76)$	76	76	52.086s	1.885s
${\mathbf{a}}_{100}(100)$	100	100	159.370s	4.841s
${\mathbf{a}}_{124}(124)$	124	124	354.306s	10.643s
${\mathbf{a}}_{152}(152)$	152	152	998.438s	21.991s
${\mathbf{a}}_{184}(184)$	184	184	2294.636s	43.484s

shows the actual running times (in seconds) of the two algorithms on the DFAs ${\mathbf{a}}_{28},{\mathbf{a}}_{41},{\mathbf{a}}_{56},{\mathbf{a}}_{76},{\mathbf{a}}_{100},{\mathbf{a}}_{124},{\mathbf{a}}_{152},{\mathbf{a}}_{184}$. The number in parentheses next to each ${\mathbf{a}}_n$ indicates the number of transitions in ${\mathbf{a}}_n$. The column d shows the computed edit distance, and the column $B_{{\mathbf{a}}_n}$ shows the computed upper bound on the edit distance (used in algorithm PrelimDistInpAlter).

Table 2. Outcomes of performance tests on the automata $({\mathbf{b}}_n)$.

DFA	d	${\mathit{B}}_{{\mathbf{b}}_{\mathit{n}}}$	PrelimDistInpAlter	DistInpAlter
${\mathbf{b}}_6(28)$	2	3	0.112s	0.076s
${\mathbf{b}}_7(41)$	2	3	0.302s	0.196s
${\mathbf{b}}_8(56)$	2	4	0.731s	0.436s
${\mathbf{b}}_9(76)$	2	3	1.621s	0.927s
${\mathbf{b}}_{10}(100)$	2	3	3.223s	1.844s
${\mathbf{b}}_{11}(124)$	2	4	5.673s	3.238s
${\mathbf{b}}_{12}(152)$	2	5	61.416s	5.892s
${\mathbf{b}}_{13}(184)$	2	4	16.624s	9.272s

shows the actual running times (in seconds) of the two algorithms on the DFAs ${\mathbf{b}}_6,\dots ,{\mathbf{b}}_{13}$. Again, the number in parentheses next to each ${\mathbf{b}}_n$ indicates the number of transitions in ${\mathbf{b}}_n$.

In both test sets, the empirical outcomes confirm the asymptotic outcome that the improved algorithm based on the optimized construction is faster than the preliminary one.

7. Conclusions

This paper represents a significant improvement in the time complexity of computing the inner edit distance of a given regular language. The performance tests of the implemented algorithm show that in practice the algorithm is reasonably fast for moderate size automata. As discussed in [4], this problem is related to the inherent capability of a language to detect substitution, insertion, and deletion errors.

The two preliminary algorithms can be applied to different distances as long as these distances can be related to appropriate transducers. For some of those distances, the idea in the optimized algorithms can also be used. For example, one can construct a transducer similar to ${\mathbf{sid}}_k$ for insertion/deletion only errors. A direction for future research is to investigate to what extent the methods used here can be extended to compute inner weighted distances or the inner edit distance with moves.