Variable Selection Using Adaptive Band Clustering and Physarum Network
Abstract
:1. Introduction
2. Theory
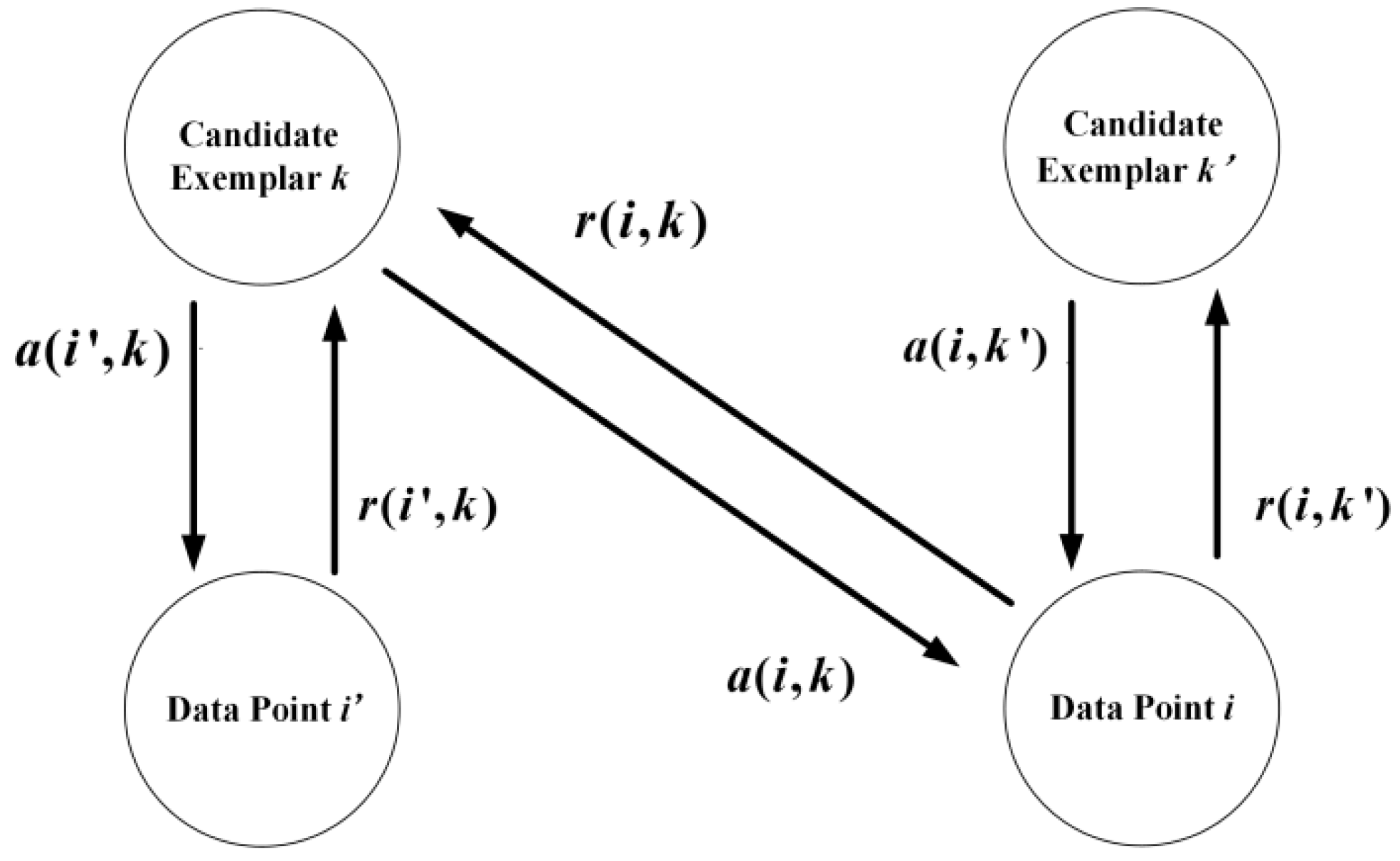
2.1. AP Algorithm
2.2. Variable Selection Based on AP-PN
- Calculate the similarity matrix according to the Formula (7);
- Set as a value between 0 to 1, staring from 0.00001 and updating by using ;
- Set , ;
- Calculate the responsibility information and availability information, and update them according to the Formulas(1)–(6);
- Determine the clusters, and go to step 2 until all are tried;
- Determine the according to Formula (8) and the corresponding clusters and exemplars;
- Bring the calculated clustering results into the PN for variable selection.
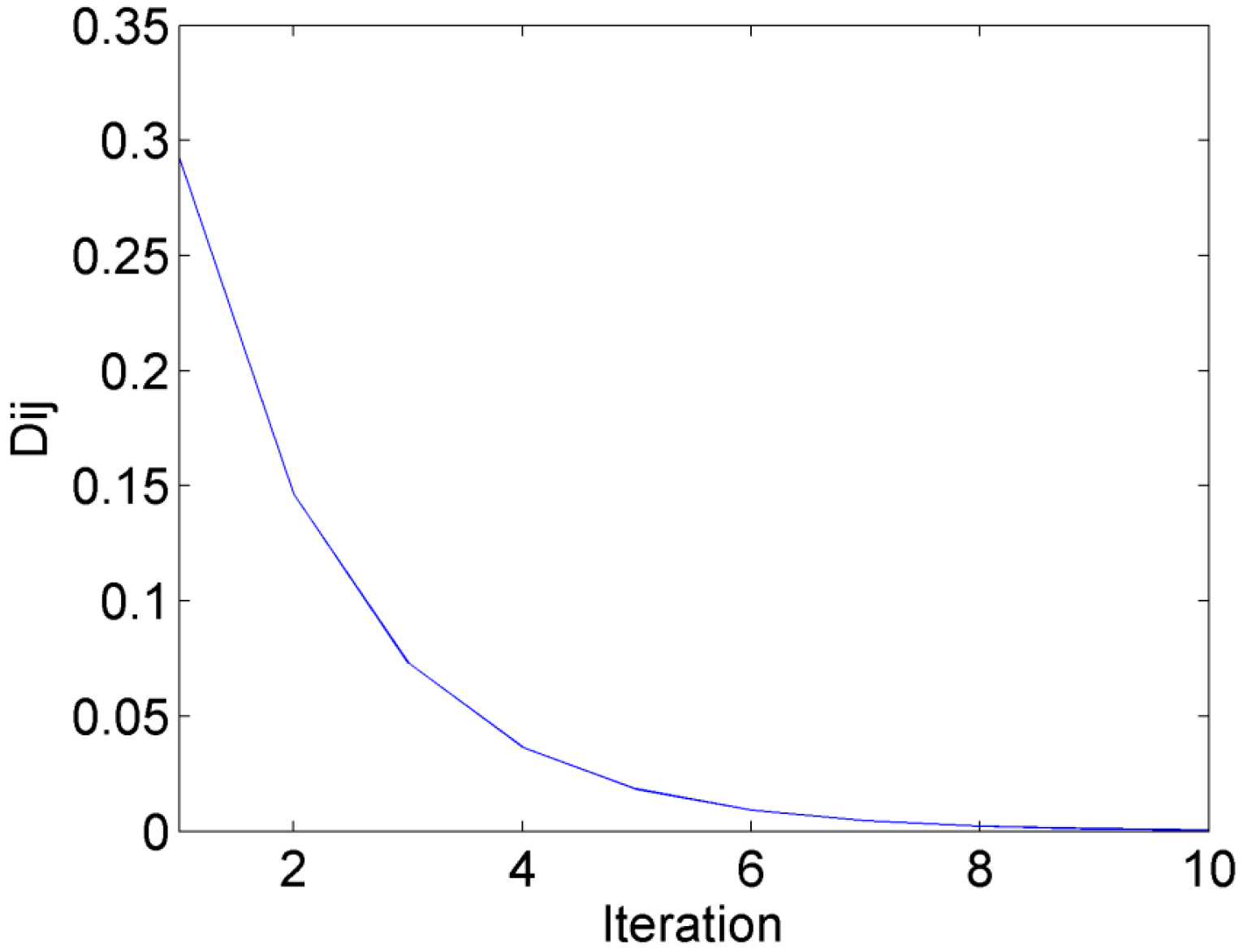
2.3. Complexity Analysis of AP-PN
3. Experiment
3.1. Corn Data Set
3.1.1. Data Set
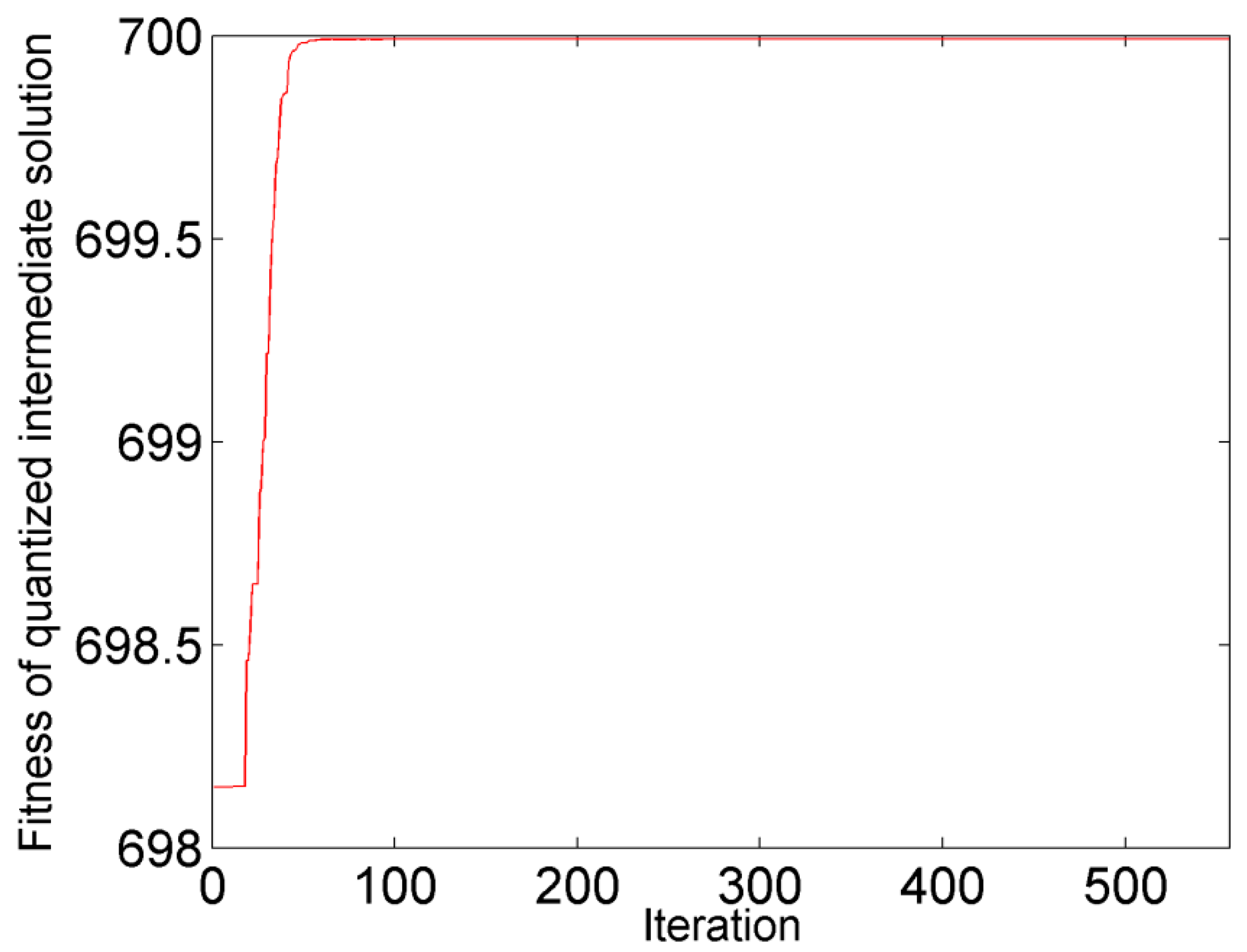
3.1.2. Data Analysis
3.2. Diesel Data Set
3.2.1. Data Set
3.2.2. Data Analysis
3.3. Sweet Orange Leaves Data Set
3.3.1. Data Set
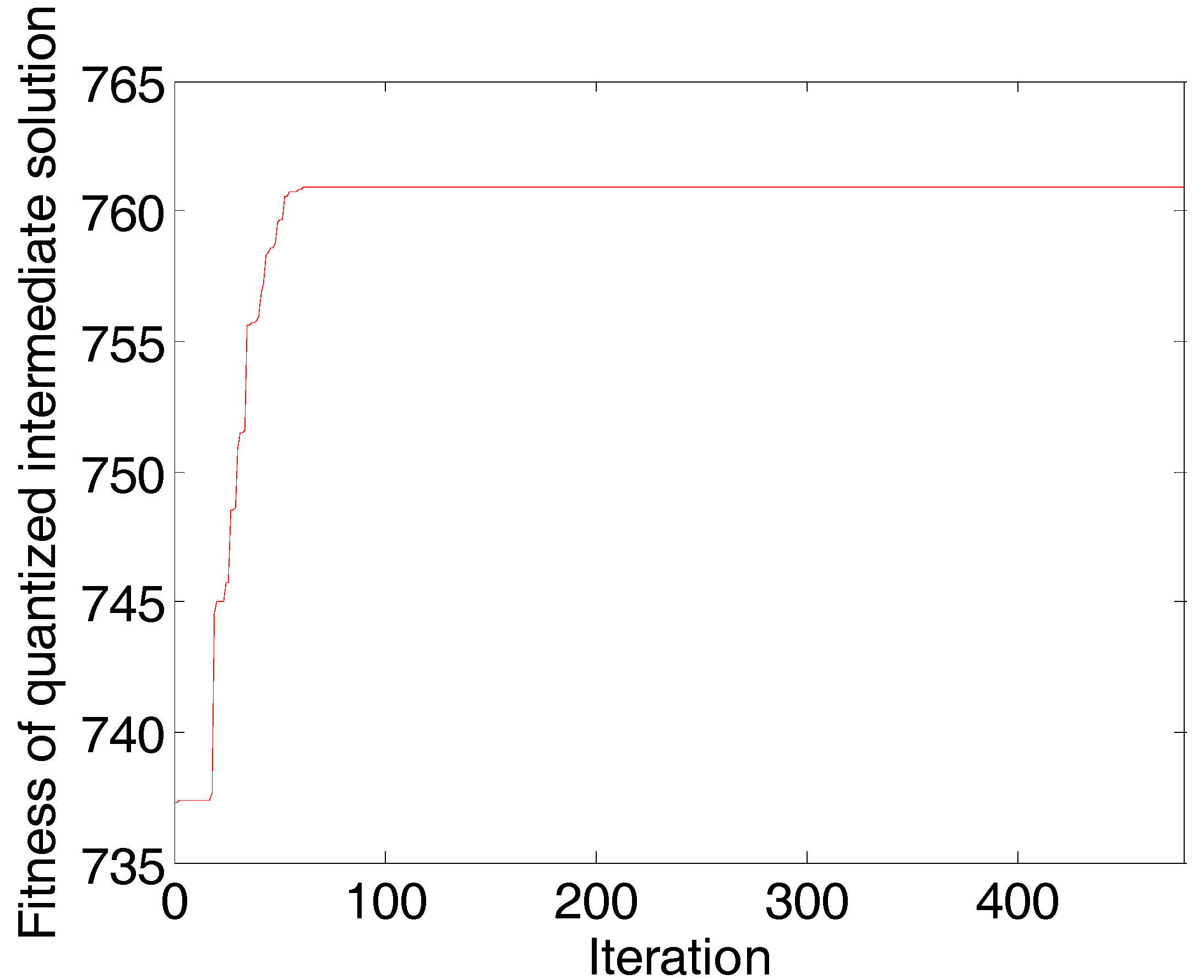
3.3.2. Data Analysis
4. Results and Discussion
4.1. Corn Data Set
4.2. Diesel Data Set
4.3. Sweet Orange Leaves Data Set
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Burges, C.J. Dimension reduction: Aguided tour. Found. Trends Mach. Learn. 2010, 2, 275–365. [Google Scholar] [CrossRef]
- Zou, X.; Zhao, J.; Povey, M.J.; Holmes, M.; Mao, H. Variables selection methods in near-infrared spectroscopy. Anal. Chim. Acta 2010, 667, 14–32. [Google Scholar]
- Leardi, R.; Gonzalez, A.L. Genetic algorithms applied to feature selection in PLS regression: How and when to use them. Chemom. Intell. Lab. Syst. 1998, 41, 195–207. [Google Scholar] [CrossRef]
- Ghasemi, J.; Niazi, A.; Leardi, R. Genetic-algorithm-based wavelength selection in multicomponent spectrophotometric determination by PLS: Application on copper and zinc mixture. Talanta 2003, 59, 311–317. [Google Scholar] [CrossRef]
- Durand, A.; Devos, O.; Ruckebusch, C.; Huvenne, J.P. Genetic algorithm optimization combined with partial least squares regression and mutual information variable selection procedures in near- infrared quantitative analysis of cotton–viscose textiles. Anal. Chim. Acta 2007, 595, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Haaland, D.M.; Thomas, E.V. Partial least-squares methods for spectral analyses. 1. Relation to other quantitative calibration methods and the extraction of qualitative information. Anal. Chem. 1988, 60, 1193–1202. [Google Scholar]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in partial least squares regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Soh, C.S.; Raveendran, P.; Mukundan, R. Mathematical models for prediction of active substance content in pharmaceutical tablets and moisture in wheat. Chemom. Intell. Lab. Syst. 2008, 93, 63–69. [Google Scholar] [CrossRef]
- Roger, J.M.; Bellon-Maurel, V. Using genetic algorithms to select wavelengths in near-infrared spectra: Application to sugar content prediction in cherries. Appl. Spectrosc. 2000, 54, 1313–1320. [Google Scholar] [CrossRef]
- Leardi, R.; Seasholtz, M.B.; Pell, R.J. Variable selection for multivariate calibration using a genetic algorithm: Prediction of additive concentrations in polymer films from Fourier transform-infrared spectral data. Anal. Chim. Acta 2002, 461, 189–200. [Google Scholar] [CrossRef]
- Van, D.B.; Wienke, D.; Melssen, W.J.; Buydens, L.M.C. Optimal wavelength range selection by a genetic algorithm for discrimination purposes in spectroscopic infrared imaging. Appl. Spectrosc. 1997, 51, 1210–1217. [Google Scholar]
- Chen, T.; Zhao, X.C.; Zhou, H.; Liu, G.-Y. Selecting variables with the least correlation based on physarum network. Chemom. Intell. Lab. Syst. 2016, 153, 33–39. [Google Scholar] [CrossRef]
- Bonifaci, V.; Mehlhorn, K.; Varma, G. Physarum can compute shortest paths. J. Theor. Biol. 2012, 309, 121–133. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Song, Y.; Zhang, H.; Ma, H.; Vasilakos, A.V. Physarum optimization: A biology-inspired algorithm for the steiner tree problem in networks. IEEE Trans. Comput. 2015, 64, 818–831. [Google Scholar]
- Song, Y.; Liu, L.; Ma, H.; Vasilakos, A.V. A biology-based algorithm to minimal exposure problem of wireless sensor networks. IEEE Trans. Netw. Serv. Manag. 2014, 11, 417–430. [Google Scholar] [CrossRef]
- Cheng, J.H.; Sun, D.W.; Wei, Q. Enhancing Visible and Near-Infrared Hyperspectral Imaging Prediction of TVB-N Level for Fish Fillet Freshness Evaluation by Filtering Optimal Variables. Food Anal. Methods 2016, 1–11. [Google Scholar] [CrossRef]
- Zhang, X.; Chan, F.T.S.; Adamatzky, A.; Mahadevan, S.; Yang, H.; Zhang, Z.; Deng, Y. An intelligent physarum solver for supply chain network design under profit maximization and oligopolistic competition. Int. J. Prod. Res. 2017, 55, 244–263. [Google Scholar] [CrossRef]
- Frey, B.J.; Dueck, D. Clustering by passing messages between data points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; Yao, F.; Jia, S. Band selection for hyperspectral imagery using affinity propagation. IET Comput. Vis. 2009, 3, 213–222. [Google Scholar] [CrossRef]
- Shi, X. Parallelizing Affinity Propagation Using Graphics Processing Units for Spatial Cluster Analysis over Big Geospatial Data. Adv. Geocomput. 2017, 355–369. [Google Scholar] [CrossRef]
- Clarke, R.; Ressom, H.W.; Wang, A.; Xuan, J.; Liu, M.C.; Gehan, E.A.; Wang, Y. The properties of high-dimensional data spaces: Implications for exploring gene and protein expression data. Nat. Rev. Cancer 2008, 8, 37–49. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.X.; Can, H.; Qu, L.Y. Hyperspectral Image Compression Based on Adaptive Band Clustering PCA. Sci. Technol. Eng. 2015, 15, 86–91. [Google Scholar]
- Dueck, D.; Frey, B.J. Non-metric affinity propagation for unsupervised image categorization. In Proceedings of the IEEE 11th International Conferenceon Computer Vision (ICCV), Rio de Janeiro, Brazil, 14–21 October 2007. [Google Scholar]
- Vlasblom, J.; Wodak, S.J. Markov clustering versus affinity propagation for the partitioning of protein interaction graphs. BMC Bioinform. 2009, 10, 99. [Google Scholar] [CrossRef] [PubMed]
- Givoni, I.E.; Frey, B.J. A binary variable model for affinity propagation. Neural Comput. 2009, 21, 1589–1600. [Google Scholar] [CrossRef] [PubMed]
- NIR of Corn Samples for Standardization Benchmarking. Available online: http://www.eigenvector.com/data/Corn/ (accessed on 26 June 2017).
- Near Infrared Spectra of Diesel Fuels. Available online: http://www.eigenvector.com/data/SWRI/index.html (accessed on 26 June 2017).
- Lichtenthaler, H.K. Chlorophylls and carotenoids: pigments of photosynthetic biomembranes. Methods Enzymol. 1987, 148, 350–382. [Google Scholar]
- Burns, D.A.; Ciurczak, E.W. Handbook of Near-Infrared Analysis, 3rd ed.; CRC Press: New York, NY, USA, 2016. [Google Scholar]
- Shen, Y.J. Effects of Polycyclic Aromatic Hydrocarbons on Diesel Particulate Matter Emission. Pet. Prod. Appl. Res. 2006, 3, 85–87. [Google Scholar]
- Zscheile, F.P.; Comar, C.L. Influence of preparative procedure on the purity of chlorophyll components as shown by absorption spectra. Bot. Gaz. 1941, 102, 463–481. [Google Scholar] [CrossRef]




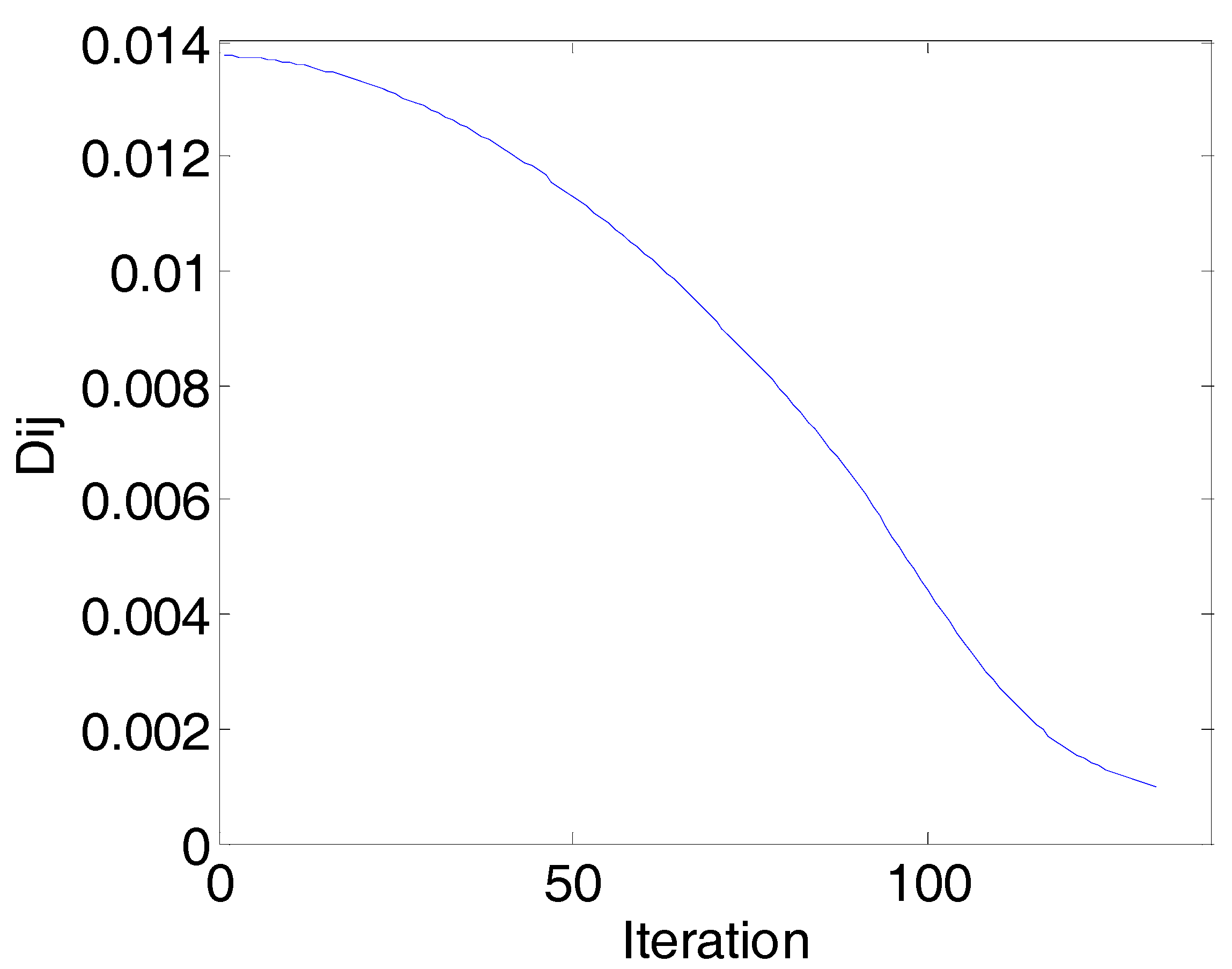
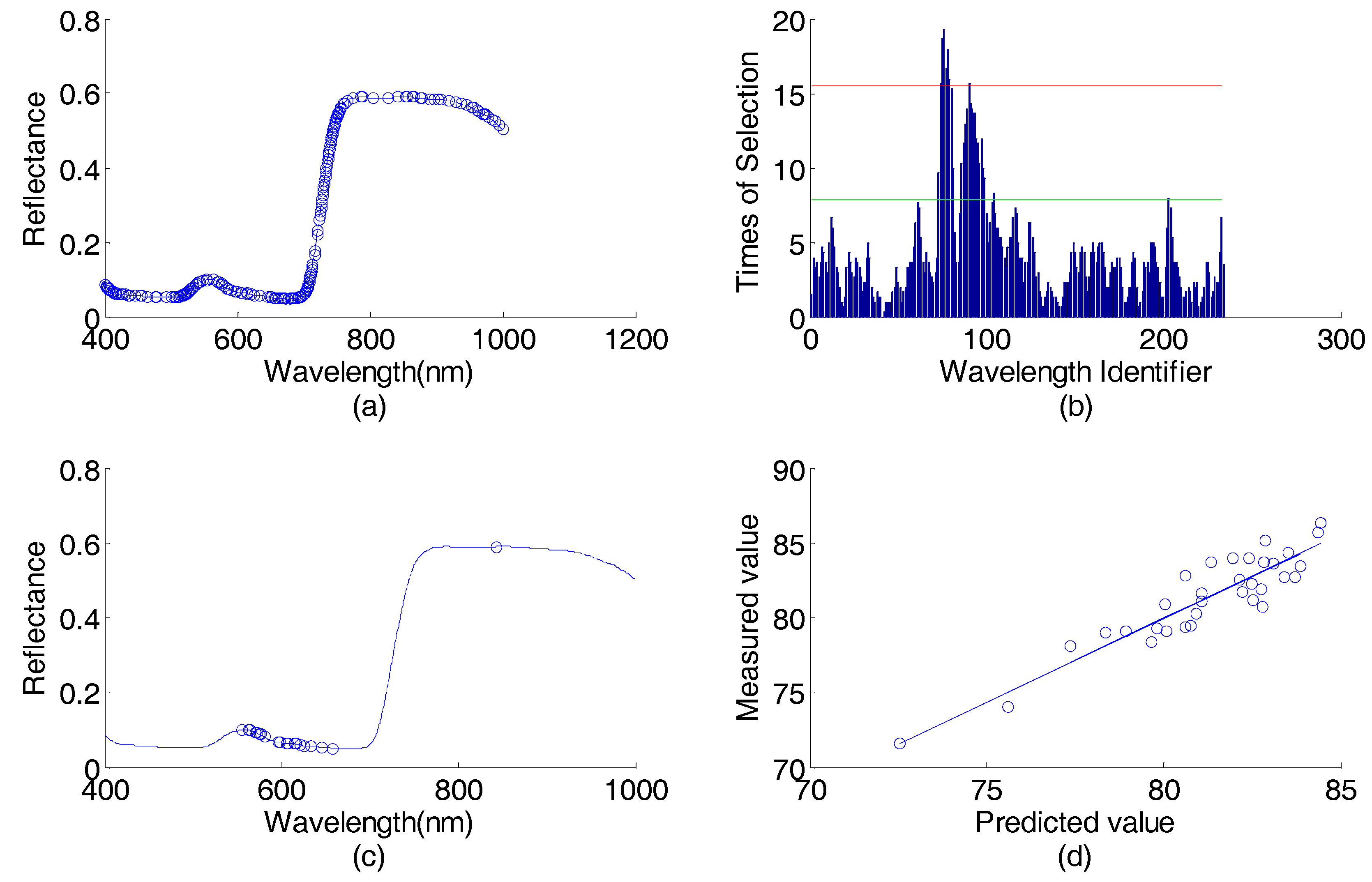
| 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
| Number of groups | 184 | 184 | 184 | 184 | 184 |
| 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
| Number of groups | 120 | 120 | 120 | 120 | 120 |
| 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
| Number of groups | 234 | 234 | 234 | 234 | 234 |
| Method | Number of Input Wavelengths | Number of Selected Wavelengths | R | RMSEP(%) |
|---|---|---|---|---|
| PLS | 700 | 700 | 0.9832 | 0.0902 |
| GA-PLS | 700 | 67 | 0.9989 | 0.0431 |
| PN-GA-PLS | 700 | 35 | 0.9960 | 0.0597 |
| AP-GA-PLS | 700 | 39 | 0.9941 | 0.0643 |
| AP-PN-GA-PLS | 700 | 25 | 0.9970 | 0.0397 |
| Method | Number of Input Wavelengths | Number of Selected Wavelengths | R | RMSEP(%) |
|---|---|---|---|---|
| PLS | 401 | 401 | 0.9716 | 0.1370 |
| GA-PLS | 401 | 142 | 0.9739 | 0.1203 |
| PN-GA-PLS | 401 | 40 | 0.9727 | 0.1404 |
| AP-GA-PLS | 401 | 66 | 0.9722 | 0.1356 |
| AP-PN-GA-PLS | 401 | 26 | 0.9744 | 0.1167 |
| Method | Number of Input Wavelengths | Number of Selected Wavelengths | R | RMSEP (%) |
|---|---|---|---|---|
| PLS | 761 | 761 | 0.9025 | 1.4124 |
| GA-PLS | 761 | 125 | 0.9069 | 1.4998 |
| PN-GA-PLS | 761 | 49 | 0.9110 | 1.3206 |
| AP-GA-PLS | 761 | 56 | 0.9034 | 1.4226 |
| AP-PN-GA-PLS | 761 | 27 | 0.9220 | 1.2436 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Chen, T.; Zhang, Z.; Liu, G. Variable Selection Using Adaptive Band Clustering and Physarum Network. Algorithms 2017, 10, 73. https://doi.org/10.3390/a10030073
Chen H, Chen T, Zhang Z, Liu G. Variable Selection Using Adaptive Band Clustering and Physarum Network. Algorithms. 2017; 10(3):73. https://doi.org/10.3390/a10030073
Chicago/Turabian StyleChen, Huanyu, Tong Chen, Zhihao Zhang, and Guangyuan Liu. 2017. "Variable Selection Using Adaptive Band Clustering and Physarum Network" Algorithms 10, no. 3: 73. https://doi.org/10.3390/a10030073
APA StyleChen, H., Chen, T., Zhang, Z., & Liu, G. (2017). Variable Selection Using Adaptive Band Clustering and Physarum Network. Algorithms, 10(3), 73. https://doi.org/10.3390/a10030073





