The system has been designed as a client-server solution. The smartphone acts as the client and runs the semi-automatic part of the system. Building on our previous work, we complete the processing cycle addressing all of the main practical and theoretical issues related with food volume estimation.
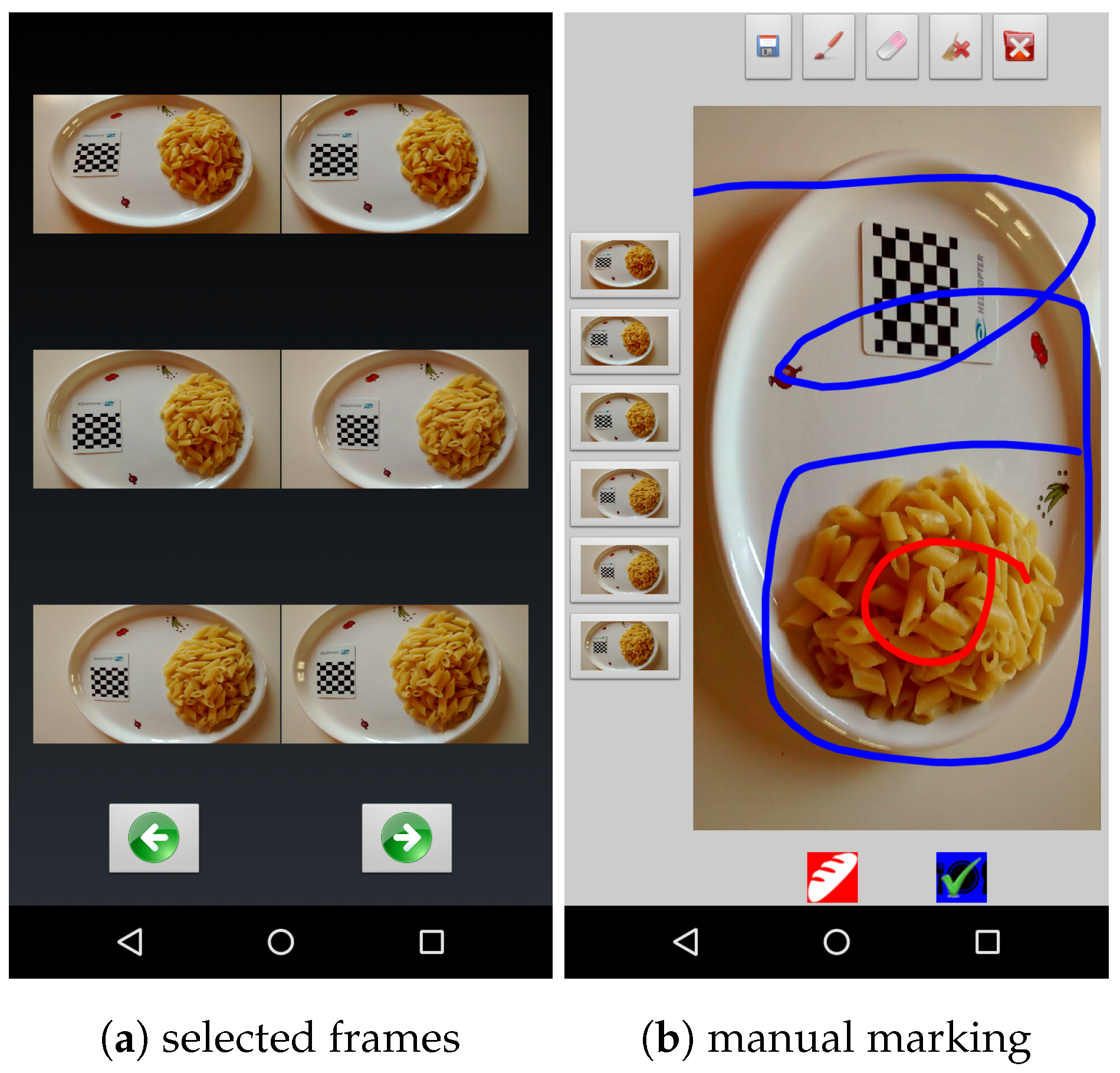
In the system described in this paper, as a first step, the user is asked to take a short video of the food. Then, a subset of the frames is automatically extracted from the video to provide relevant views of the food from all sides. Next, the user marks some food and non-food parts in one of the selected frames of the video. A mobile application that we developed facilitates this part (see
Figure 1). The segmentation process, which is performed on the server side, is seeded by the user’s marks. The segmented images are then fed into a customized image-based process that builds a 3D model of the food items. This model is finally used to calculate the volume of the food. A small checkerboard is used as the size and ground reference for the modeling process.
2.1. Image Acquisition
Reconstructing the 3D model of an object from a set of input images requires the availability of relevant visual information about the whole object. Usually, as happens in [
9,
10], the reconstruction is based on two or three images taken from different viewpoints. The main problem with these approaches is that such a small number of images is usually not enough to acquire the necessary information from all sides of objects and may lead to an incomplete reconstruction. This problem is particularly relevant for methods that include steps, like feature matching or fundamental-matrix estimation, which are very sensitive to noise or lack of information.
Thus, our method relies on information drawn from a larger number of images to obtain a better coverage of the whole object. This also allows it to achieve satisfying results using relatively low-resolution images.
Acquiring a larger number of images is usually avoided because, in that situation, the user should be skilled enough to choose the best viewpoints, while the goal of the app is to limit user intervention at most to a few purely mechanical gestures that do not require any problem-specific knowledge. In our approach, the user takes a short video of the object by moving the camera around it for a few seconds to make sure that images of the object are acquired from virtually all possible viewpoints. Then, the application automatically selects six frames that optimize object coverage based on the orientation of the smartphone during filming. The frame selection process is performed almost in real time, so one can use the application smoothly.
Figure 2 provides an example of the output of this step, showing the six viewpoints that have been automatically selected by the application.
The built-in sensors of the mobile device are used for the selection process. Most modern smartphones are equipped with different kinds of sensors, among which accelerometer and geomagnetic field sensors are very common. These sensors can provide enough data to detect the orientation of the smartphone in each moment. The orientation of the device is defined by three values (pitch, roll, and azimuth), which, respectively, correspond to the rotation angles around the x-axis, y-axis, and z-axis. The application records the time-tag of the frames that coincide with the min/max values of pitch, roll, and azimuth recorded while taking the movie. Algorithm 1 reports the pseudo code of the function used to detect the proper frames. Later, six frames presenting the min/max rotational moments are chosen as the input of the modeling process. Thus, the user neither needs to take several images nor should worry about choosing proper camera viewpoints. Moreover, the Graphical User Interface (GUI) of the app allows the user to remove one of the images or to replace it with some other frame just by tapping on the screen.
Figure 1 shows two snapshots of the mobile application.
| Algorithm 1 Choosing six frames to obtain a good coverage of the object |
function onSensorChanged(SensorEvent event) if event.sensors include [ACCELEROMETER, MAGNETIC_ FIELD] then if pitch is new min/max then end if if roll is new min/max then end if if azimuth is new min/max then end if end if end function
|
2.2. Segmentation
The objective of the segmentation step is to detect the exact location of the food items in the images. Food image segmentation can be very challenging. There are very different ways of cooking the same kind of food and of arranging food on a dish. These problems and many other factors cause food appearance to vary dramatically. Some studies impose constraints when taking pictures of food, in order to make segmentation easier. For example, Zhu [
13] assumes that food lies on a dish that is brighter than the table cloth. Several other studies [
14,
15,
16] impose that the dish, or the container where the food lies, has a pre-specified shape.
Recently, attention has been paid to semi-automatic methods. In [
17,
18], the user is requested to draw a bounding box around the food items, while in [
19], the user must mark the initial seeds before starting to grow segments. In this work, a semi-automatic method is designed which can be run on smartphones in a user-friendly manner.
The method is based on a customized interactive version of the graph-cut (GC) algorithm [
20], which deals with image segmentation as a pixel-labeling problem. The graph-cut algorithm assigns a “foreground” (food) or “background” (not food) label to each pixel.
We evaluated the general effectiveness of this method in a previous work [
11]. In our customized version of GC, the user imposes some hard constraints by marking some food and non-food areas in one of the images. The application provides a user-friendly environment for marking images by simply touching the screen (see
Figure 1).
Algorithm 2 reports the pseudo-code of this process. The marked parts of the image are fed into a Gaussian Mixture Model (GMM) algorithm [
21] that estimates the distribution of the Red-Green-Blue (RGB) values for the image foreground (food) and background (not food). The K-means algorithm is then used to divide the data from each RGB channel into ten clusters that are assumed to follow a normal distribution. Then, the GMM estimates the distribution by combining the normal models. Next, a value is assigned to every pixel, which denotes the likelihood of its belonging to the foreground or the background, based on the distribution estimated by the GMM. These likelihood values are used to seed the graph-cut algorithm, which produces the final segmentation. However, if the user is dissatisfied with the segmentation output, he/she can repeat the marking step to improve the result.
| Algorithm 2 Segmentation of a marked image using GMM and graph-cut |
function Segmentation(OriginalImage, MarkedImage) return Segments end function
|
Although the input to the segmentation method we propose consists of the six images which are automatically extracted from the short video, the user needs to mark only one of them. The segmentation for such an image obtained based on the marked pixels is then used to extend the process to the other images by recomputing the GMM on the whole segmented image and using such a more accurate estimate as the model used in segmenting the others. This is based on the primary assumption that the images acquired are characterized by a similar color distribution.
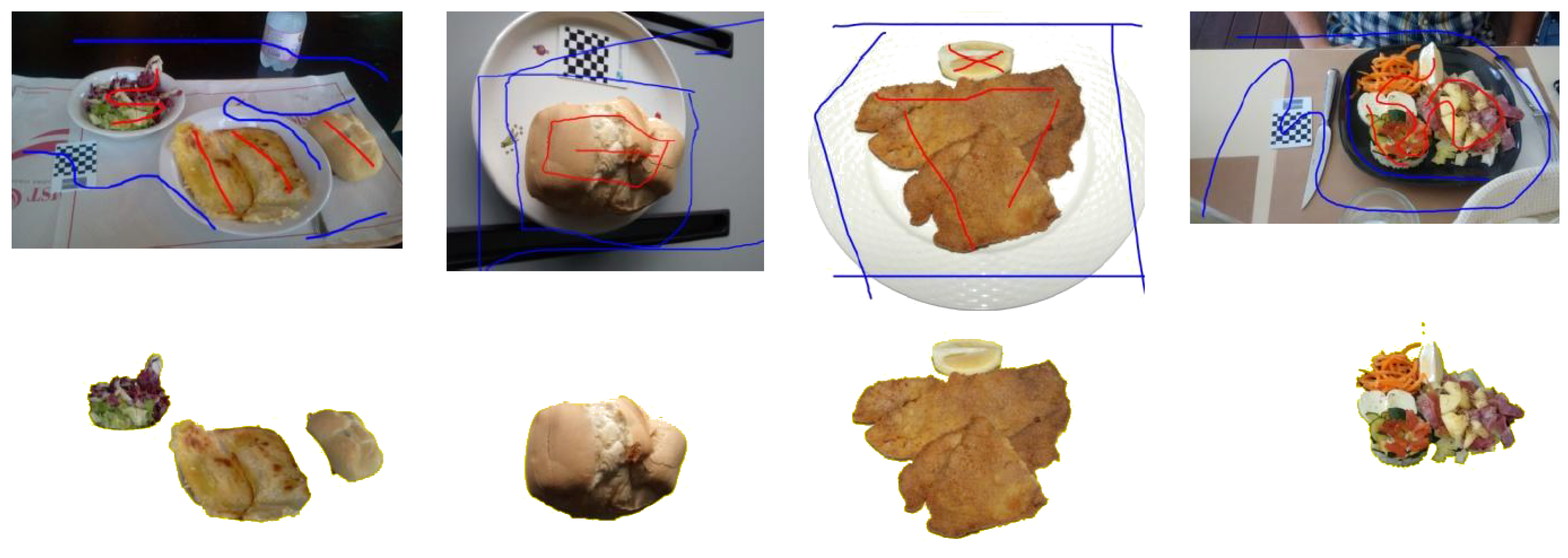
Figure 3 shows the segmentation of four food images obtained by our method.
Being based on six images, a small segmentation error in one image can be recovered by the results obtained on the other images. In fact, if the errors are not very large, the object part corresponding to an under/over-segmentation of one item might be correctly segmented in others. This gives more flexibility to the method and minimizes processing time because every part needs to be marked as the foreground in at least two images to be taken into consideration in the modeling process.
2.3. Size/Ground Reference Localization
Volume can be estimated from images using several different procedures, but results are computed only up to a scale factor. Therefore, in many studies, an object of known size is used as a reference for volume estimation. In [
8], for instance, the user puts his/her finger besides the dish. In [
6], a specific pattern of known size printed on a card is used as a reference. Many studies have followed the same idea using a checkerboard as a reference [
13,
22] because of the simplicity of the checkerboard pattern and the existence of effective algorithms to detect it. Nevertheless, off-the-shelf checkerboard detection algorithms are usually designed to be means for camera calibration or pose-detection processes. They are usually tuned for specific situations like: flat checkerboards, a big checkerboard that is often the only object in the image, etc. Thus, for applications that do not satisfy these requirements, different algorithms, or modified versions of available ones, are needed. Checkerboards that are used as size references usually consist of few squares and occupy a relatively small region of the image. This makes detecting them hard for ‘standard’ checkerboard detectors.
Figure 4 shows three examples in which the checkerboard detection algorithms provided by the open software package OpenCV 3.1.0 [
23] and Matlab R2014b (The MathWorks Inc., Natick, MA, USA) fail.
In [
12], we have introduced a method to locate a small checkerboard in an image. We used a
checkerboard, printed on a Polyvinyl Chloride (PVC) card, as a size reference. The method consists of two main steps: locating the checkerboard in the image and then detecting the checkerboard corners in the located area.
The procedure that we adopt estimates the pose of an object based on a 3D model and can be utilized with any projection system and any general object model.
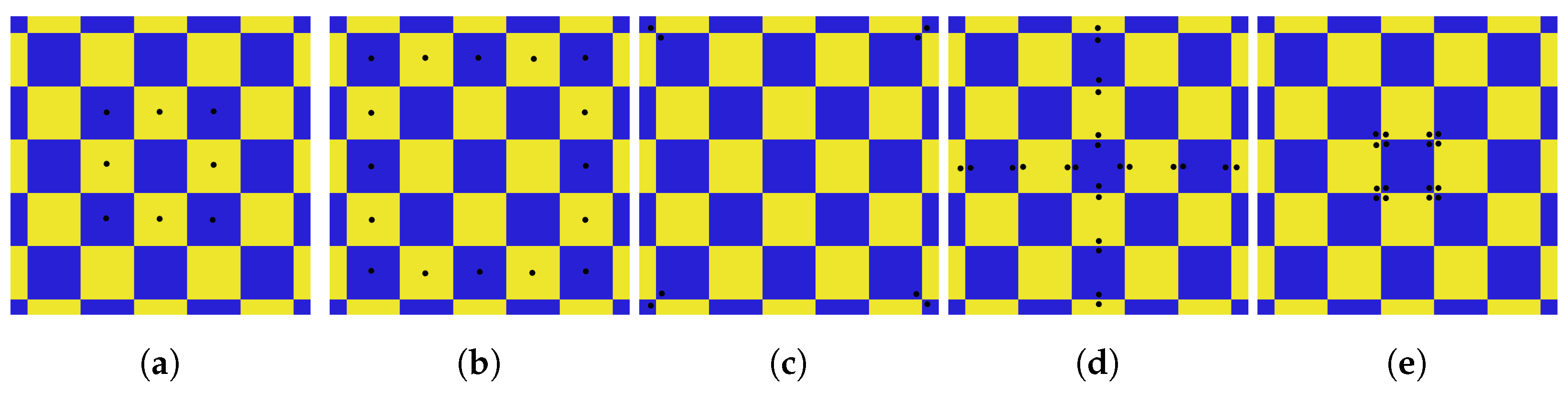
Figure 5 shows the model that we use to detect the checkerboard. It consists of 73 key points corresponding to the center, edges and corners of each square.
In this method, a hypothesis of checkerboard location can be evaluated by rigidly transforming a model of the checkerboard and then projecting it onto the image according to a perspective transform. The likelihood of the hypothesis is evaluated using a similarity measure between the projected model and the actual content of the image region onto which the pattern is projected.
This procedure allows one to turn checkerboard detection into an optimization problem, in which the parameters to be optimized are the coefficients of the rigid transformation and of the projection. In this work, Differential Evolution (DE) [
24] is employed for optimization as described in [
25]. Algorithm 3 reports the pseudo-code of the fitness function used to evaluate each hypothesis. In the algorithm, each step presented in
Figure 5 is implemented as a separate function. One of the advantages of using a stochastic algorithm like DE is having a chance of success in the next try if an attempt to find the checkerboard fails.
| Algorithm 3 Fitness Function |
function FitnessFunction(PoseVector) Calc Rotation & Translation matrices from PoseVector if Score > 6 then end if if Score & the center is black then end if if Score > 23 then end if return Score end function
|
Based on this estimated checkerboard location, the corners of the checkerboard are then precisely detected as described in [
12]. This allows the algorithm to estimate the checker size and, consequently, the scale factor, which is to be applied to estimate food volume.
Additionally, the checkerboard can be assumed as a reference for the ground surface, whose orientation is represented by the plane having the smallest squared distance from the checkerboard corners.
If we term
n the vector normal to the ground plane and
a
matrix in which the columns are the detected corners’ coordinates, the plane can be found by calculating the Singular Value Decomposition (SVD) of
, where
c is a point belonging the plane [
26]. We set
c equal to the centroid of the columns of
P and set
n as the left singular vector of the SVD [
26].
This use of the checkerboard is valuable during 3D-modeling to extract more information about the lower parts of the object, which could be invisible in the video taken from above, as well as to remove noise.
The approach requires that the checkerboard be at the same height as the food, which might raise some concerns about the practicality of the method. However, the procedure could still be useful, especially since one can estimate the average thickness of the dishes where users commonly eat and print the pattern on top of a box, in order to lift it at more or less the same level and compensate for the thickness of the dish. The use of the checkerboard as ground-reference mainly helps to eliminate noise and outliers from the model’s point-cloud. These outliers are usually located below the surface, at a very large distance from it. Therefore, the method only requires that the checkerboard be ’almost’ on the same level as the dish bottom surface.
2.4. Image-Based Modeling
In this step, a 3D model of the food item in the form of a point-cloud is generated based on a Structure from Motion (SfM) algorithm. We followed the same approach described in [
27,
28], properly adapting it to this work. In fact, the base approaches have been designed to build a model based on many (up to a few thousands) images. Our algorithm is customized for using a lower number of images (six, in our case) and address processing time-related concerns. Algorithm 4 reports the pseudo-code of the method, while
Figure 6 shows three examples of the reconstructed models.
| Algorithm 4 3D modeling algorithm |
|
| ▹ Prepare Matches |
|
| ▹ Start Modeling |
while there is more un-processed image do end while
|
| ▹ Find Checkerboard |
|
| ▹ Refine PointCloud |
|
First, Speeded Up Robust Features (SURF) [
29] of the images are extracted and their Binary Robust Invariant Scalable Keypoints (BRISK) [
30] description is used to find matches between image pairs. A pair is considered to be relevant if it produces at least 30 matches, in which case the corresponding points are added to the point-cloud. There are 15 possible pairs in total to be taken into consideration for six images, which is generally a large number, which could affect the total processing time significantly. Therefore, only a limited number of image pairs, configurable by the user, are actually used instead of all possible pairs.
Then, the Fundamental Matrix [
31] is calculated for all image pairs using an 8-point Random Sample Consensus (RANSAC) [
32]. The RANSAC outliers threshold is set to
of the maximum image dimension (i.e., the largest between height and width) and the level of confidence is set to
. The results of RANSAC are therefore also used to “clean” the point-cloud by removing outliers.
In the next step, the best image pair is chosen as the starting point for the 3D reconstruction, using the results of a homographic transformation as a selection criterion. Homography is the mathematical term for mapping points on one surface to points on another. The transformation between images of each pair is calculated using the RANSAC with the outliers threshold set to
of the largest image dimension. This method, besides finding the transformation, classifies the matching features into inliers and outliers. The pair with the largest inlier rate is chosen to start the reconstruction. The quality of the selected image pair is further evaluated by checking the validity of its Essential Matrix [
31]. If the selected pair fails the test, the next best pair is chosen as the baseline of the 3D reconstruction.
Then, the 2D coordinates of the matching points belonging to the selected images are used to calculate the corresponding 3D coordinates. Assuming
to be the camera matrix of the
image and
and
the 2D coordinates of two matching points in the
and
image, the relationships
and
hold, where
X denotes the 3D coordinate of the projected point. Moreover, for every point that is not too close to the camera or at infinity, one can say
, where
t is the scaling factor. This creates an inhomogeneous linear system of the form
. The least-squares solution of this equation can be found by using the Singular Value Decomposition (SVD). Unfortunately, this method is not very accurate. The method introduced by Hartley and Sturm [
33] iteratively re-calculates
X by updating
A and
B based on the results of the previous step. This allows one to refine the estimate and to significantly increase accuracy.
The other images are then successively taken into consideration in the triangulation process. Since the 3D coordinates can be estimated only up to a scaling factor t, the 3D points belonging to different image pairs might have a different scale factor, and it may be therefore impossible to build a consistent 3D reconstruction. The other issue is the order in which the different views are taken into account. Taking into account a lower image-quality view before the others may affect the final model negatively. In order to tackle these issues, we first choose the best view among the remaining ones by calculating, for each view, the number of features that produce successful matches with the images that have been previously processed, and selecting the one for which it is largest. Then, the camera position for the selected view is estimated based on the previously reconstructed points. This is a classic Perspective-n-Point problem (PnP), which determines the position and orientation of a camera given its intrinsic parameters and a set of n correspondences between 3D points and their 2D projections. The function, provided by OpenCV, which finds the pose that minimizes the reprojection error, is used to solve it. The use of RANSAC makes the function robust to outliers. This approach also ensures that the 3D points added to the point-cloud based on the new images share the same scaling factor as the previous ones.
Bundle Adjustment [
34] is also applied to the triangulation output in order to refine the results. It is an optimization step that provides a maximum-likelihood estimation of the positions of both the 3D points and the cameras [
34]. This result is obtained by finding the parameters of the camera view
and the 3D points
, which minimize the reprojection error, i.e., the sum of squared distances between the observed image points
and the reprojected image points
[
31].
In the next step, all of the non-object points are removed from the point-cloud based on the output of the segmentation stage. The requirement by which a 3D point must appear in at least two images compensates for some segmentation errors that might have occurred in some images.
Finally, outliers are removed from the point-cloud. Since the ground surface has been determined based on the checkerboard location, it is possible to apply restrictions to the maximum acceptable height of the food item (we set such limit to 20 cm). The point-cloud usually also includes isolated outliers that are relevantly far from the other points. To deal with this problem, we remove from the point-cloud the points whose distance from the closest neighbor is larger than a threshold. In practice, for each point, four types of distances are defined: the Euclidean distance and the distances along the three coordinate axes. Acceptable points should be no farther from their nearest neighbor than one standard deviation for each of the measures taken into consideration.
Moreover, if an isolated set of less than five points is too far from its neighbors, it will be removed as well.