Seismic Signal Compression Using Nonparametric Bayesian Dictionary Learning via Clustering
Abstract
:1. Introduction
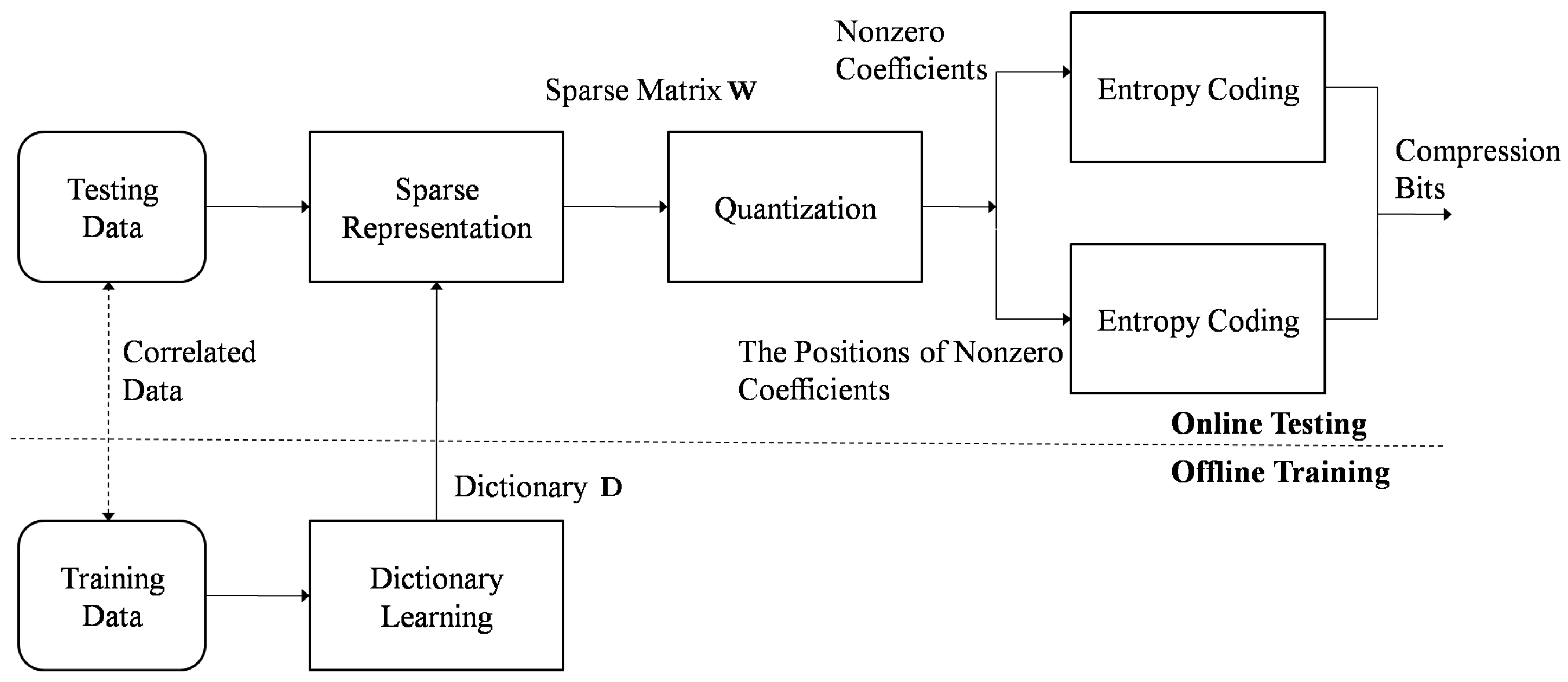
2. Seismic Signal Compression Based on Offline Dictionary Learning
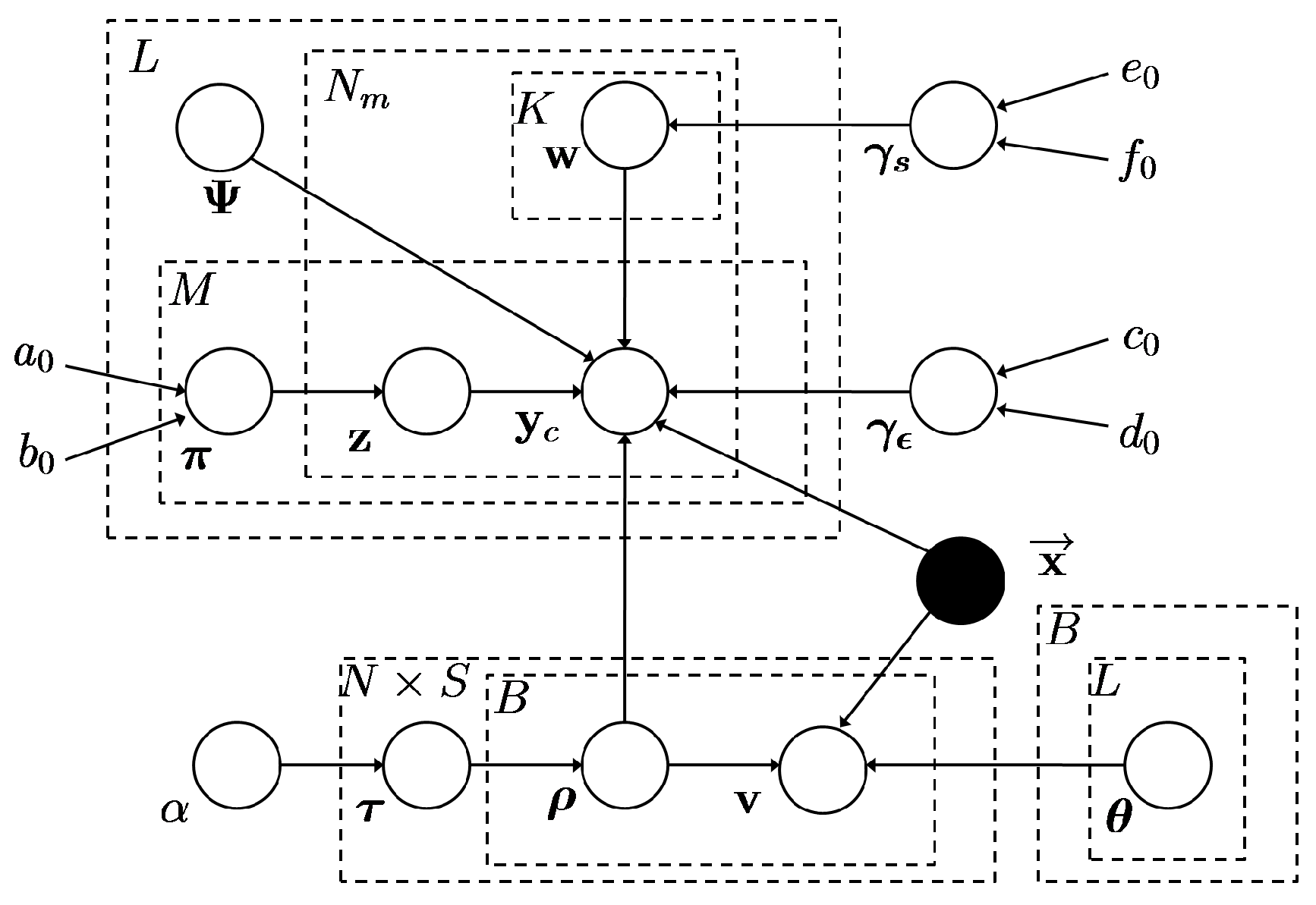
3. Seismic Signal Compression Using Nonparametric Bayesian Dictionary Learning via Clustering
3.1. Online Training
- (1)
- Feature dimension reduction by principal component analysis (PCA)
- (2)
- Clustering via MMNB
- (a)
- E step:
- (b)
- M step:
- (3)
- Dictionary learning via BPFA
| Algorithm 1: Cluster Merging |
 |
3.2. Online Testing
- (1)
- Online clustering and sparse representation
- (2)
- Quantization and entropy coding
| Algorithm 2: Online Training Algorithm Based on MMNB and BPFA |
 |
| Algorithm 3: Online Testing Algorithm Based on MMNB and BPFA |
 |
3.3. Performance Analysis
4. Experimental Results
4.1. Clustering Experiment
4.2. Dictionary Learning Experiment
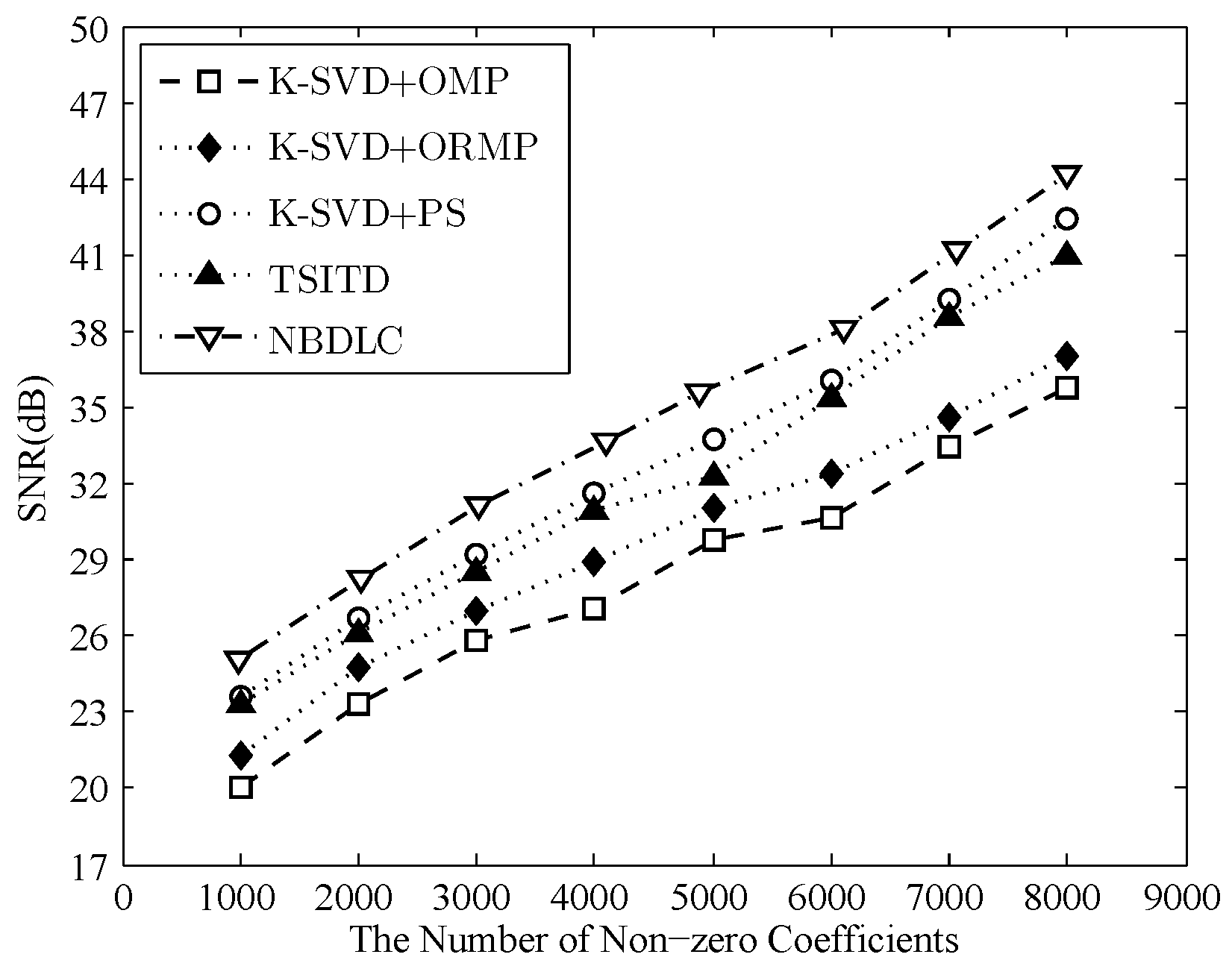
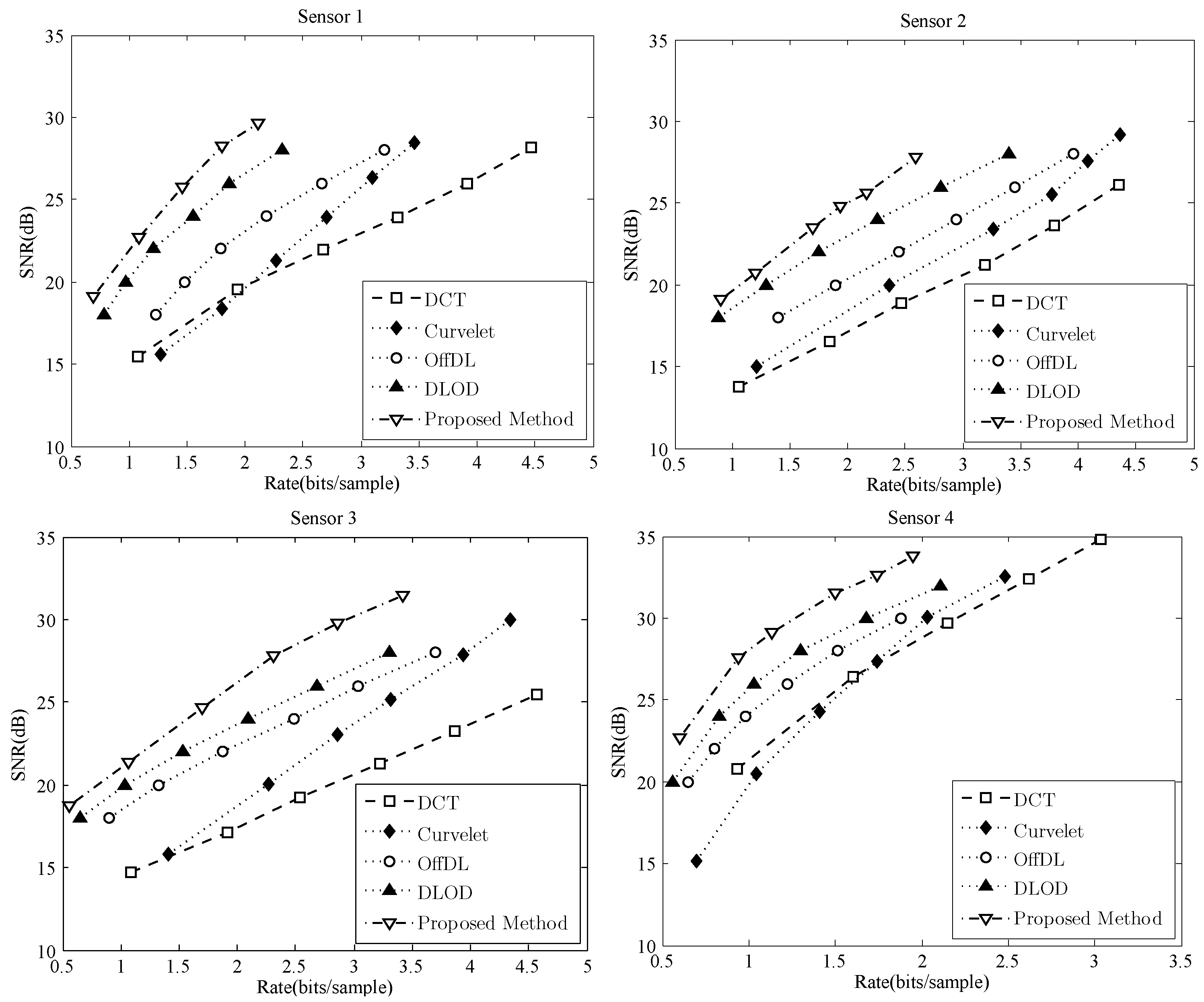
4.3. Comparison of Compression Performance
5. Conclusions
Supplementary Materials
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yunusa-Kaltungo, A.; Sinha, J.K.; Nembhard, A.D. Use of composite higher order spectra for faults diagnosis of rotating machines with different foundation flexibilities. Measurement 2015, 70, 47–61. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K. Sensitivity analysis of higher order coherent spectra in machine faults diagnosis. Struct. Health Monit. 2016, 15, 555–567. [Google Scholar] [CrossRef]
- Spanias, A.S.; Jonsson, S.B.; Stearns, S.D. Transform Methods for Seismic Data Compression. IEEE Trans. Geosci. Remote Sens. 1991, 29, 407–416. [Google Scholar] [CrossRef]
- Aparna, P.; David, S. Adaptive Local Cosine transform for Seismic Image Compression. In Proceedings of the 2006 International Conference on Advanced Computing and Communications, Surathkal, India, 20–23 December 2006. [Google Scholar]
- Douma, H.; de Hoop, M. Leading-order Seismic Imaging Using Curvelets. Geophysics 2007, 72, S231–S248. [Google Scholar] [CrossRef]
- Herrmann, F.J.; Wang, D.; Hennenfent, G.; Moghaddam, P.P. Curvelet-based seismic data processing: A multiscale and nonlinear approach. Geophysics 2008, 73, A1–A5. [Google Scholar] [CrossRef]
- Skretting, K.; Engan, K. Image compression using learned dictionaries by RLS-DLA and compared with K-SVD. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 1517–1520. [Google Scholar]
- Nejati, M.; Samavi, S.; Karimi, N.; Soroushmehr, S.M.R.; Najaran, K. Boosted multi-scale dictionaries for image compression. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 1130–1134. [Google Scholar]
- Zhan, X.; Zhang, R. Complex SAR Image Compression Using Entropy-Constrained Dictionary Learning and Universal Trellis Coded Quantization. Chin. J. Electron. 2016, 25, 686–691. [Google Scholar] [CrossRef]
- Horev, I.; Bryt, O.; Rubinstein, R. Adaptive image compression using sparse dictionaries. In Proceedings of the 2012 19th International Conference on Systems, Signals and Image Processing (IWSSIP), Vienna, Austria, 11–13 April 2012; pp. 592–595. [Google Scholar]
- Sun, Y.; Xu, M.; Tao, X.; Lu, J. Online Dictionary Learning Based Intra-frame Video Coding. Wirel. Pers. Commun. 2014, 74, 1281–1295. [Google Scholar]
- Adler, J.; Rao, B.D.; Kreutz-Delgado, K. Comparison of basis selection methods. In Proceedings of the Conference Record of the Thirtieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 1996; pp. 252–257. [Google Scholar]
- Skretting, K.; Håkon Husøy, J. Partial Search Vector Selection for Sparse Signal Representation; NORSIG-03; Stavanger University College: Stavanger, Norway, 2003. [Google Scholar]
- Engan, K.; Aase, S.O.; Håkon Husøy, J. Method of optimal directions for frame design. In Proceedings of the 1999 IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP99 (Cat. No. 99CH36258), Phoenix, AZ, USA, 15–19 March 1999; pp. 2443–2446. [Google Scholar]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Zepeda, J.; Guillemot, C.; Kijak, E. Image Compression Using Sparse Representations and the Iteration-Tuned and Aligned Dictionary. IEEE J. Sel. Top. Signal Process. 2011, 5, 1061–1073. [Google Scholar] [CrossRef]
- Paisley, J.; Zhou, M.; Sapiro, G.; Carin, L. Nonparametric image interpolation and dictionary learning using spatially-dependent Dirichlet and beta process priors. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 1869–1872. [Google Scholar]
- Zhou, M.; Chen, H.; Paisley, J.; Ren, L.; Li, L.; Xing, Z.; Dunson, D.; Sapiro, G.; Carin, L. Nonparametric Bayesian Dictionary Learning for Analysis of Noisy and Incomplete Images. IEEE Trans. Image Process. 2012, 21, 130–144. [Google Scholar] [CrossRef] [PubMed]
- Shan, H.; Banerjee, A. Mixed-membership naive Bayes models. Data Min. Knowl. Discov. 2011, 23, 1–62. [Google Scholar] [CrossRef]
- Stramer, O. Monte Carlo Statistical Methods. J. Am. Stat. Assoc. 2001, 96, 339–355. [Google Scholar] [CrossRef]
- Masmoudi, A.; Masmoudi, A.; Puech, W. An efficient adaptive arithmetic coding for block-based lossless image compression using mixture models. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 5646–5650. [Google Scholar]
- UTAM Seismic Data Library. Available online: http://utam.gg.utah.edu/SeismicData/SeismicData.html (accessed on 21 May 2009).
- Santafe, G.; Lozano, J.A.; Larranaga, P. Bayesian Model Averaging of Naive Bayes for Clustering. IEEE Trans. Syst. Man Cybern. Part B 2006, 36, 1149–1161. [Google Scholar] [CrossRef]
- Dhillon, I.S.; Mallela, S.; Modha, D.S. Information-theoretic Co-clustering. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’03), New York, NY, USA, 24–27 August 2003; pp. 89–98. [Google Scholar]


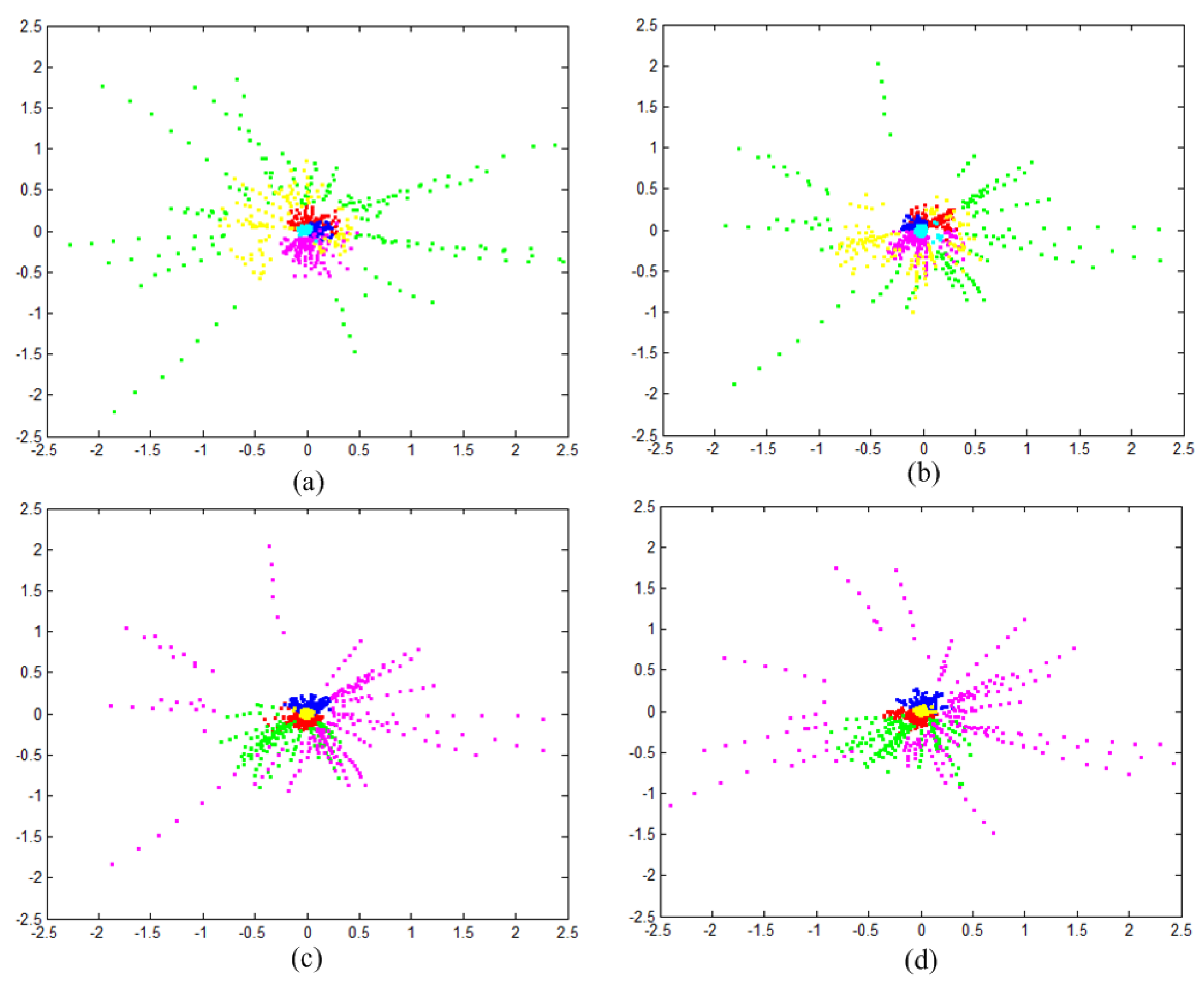
| Training Data | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| NB | ||||||
| MMNB |
| Training Data | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| NB | ||||||
| MMNB |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, X.; Li, S. Seismic Signal Compression Using Nonparametric Bayesian Dictionary Learning via Clustering. Algorithms 2017, 10, 65. https://doi.org/10.3390/a10020065
Tian X, Li S. Seismic Signal Compression Using Nonparametric Bayesian Dictionary Learning via Clustering. Algorithms. 2017; 10(2):65. https://doi.org/10.3390/a10020065
Chicago/Turabian StyleTian, Xin, and Song Li. 2017. "Seismic Signal Compression Using Nonparametric Bayesian Dictionary Learning via Clustering" Algorithms 10, no. 2: 65. https://doi.org/10.3390/a10020065
APA StyleTian, X., & Li, S. (2017). Seismic Signal Compression Using Nonparametric Bayesian Dictionary Learning via Clustering. Algorithms, 10(2), 65. https://doi.org/10.3390/a10020065






