1. Introduction
Clustering is an important research direction in data analysis. This method does not make any statistical hypothesis on data and, thus, is called unsupervised learning in pattern recognition and data mining. Clustering is mainly used in text clustering [
1], search engine optimization [
2], landmark selection [
3], face recognition [
4], and medicine and biology [
5].
Clustering is one of the most difficult and challenging problems in machine learning. The variety of clustering algorithms is roughly divided into three main types, namely, overlapping (so-called non-exclusive) [
6], partitional [
7], and hierarchical [
8]. Regardless of the type of clustering algorithm applied, the main goal is to maximize homogeneity within each cluster and heterogeneity among different clusters. In other words, objects that belong to the same cluster should be more similar to each other than objects that belong to different clusters.
Although present algorithms have their own advantages, they are sensitive to the initialization parameters and it is difficult to find their optimal clusters. In recent years, optimization methods inspired by natural phenomena have provided new ways to solve clustering problems. A swarm of individuals are employed to explore the search space and obtain an optimal solution, such as genetic algorithms (GA) [
9], particle swarm optimization algorithms (PSO) [
10], and ant colony optimization (ACO) [
11], among others. Other novel swarm intelligence algorithms have been proposed, such as harmony search (HS) [
12], honeybee mating optimization algorithm (HBMO) [
13], artificial fish swarm algorithm (AFSA) [
14], artificial bee colony (ABC) [
15], firefly algorithm (FA) [
16], monkey algorithm (MA) [
17], bat algorithm (BA) [
18], and many others.
The krill herd algorithm (KHA) [
19] is a novel swarm algorithm that is based on the simulation of the herding behavior of krill individuals and the minimum distances of each individual krill from food and from the highest density of the herd, which are considered as the objective functions for krill movement. Although proposed recently, KHA has quickly been applied to multiple scenarios. Amudhavel et al. [
20] used KHA to optimize a peer-to-peer network. KHA is applied in a smartphone ad hoc network [
21]. Kowalski et al. [
22] used KHA for learning an artificial neural network. In [
23], KHA demonstrated better performance compared with well-known algorithms, such as PSO and GA. Gandomi and Alavi [
19] illustrated that KHA with a crossover operator is superior to other well-known algorithms, including differential evolution (DE) [
24], biogeography-based optimization (BBO) [
25], and ACO.
Although KHA outperforms many other swarm intelligent algorithms [
19], the algorithm cannot search globally particularly well [
26]. In [
27], a free search KHA for function optimization was proposed to improve the feasibility and effectiveness of KHA. An improved KHA with a linear decreasing step was proposed by Li et al. [
28]. Furthermore, a new KHA that improved the original genetic operator by modifying the mutation mechanism and adding a new updated scheme will be demonstrated in our paper.
In this paper, we apply KHA as an optimization means to transform clustering into an optimization problem. In other words, we use individual krill to represent K cluster centers (K is the number of clusters), and KHA is used to search for the optimal clustering center. According to the principle of minimum distance of centers, all of the objects of the dataset are divided into different clusters, which leads to obtaining clustering results.
The rest of the paper is organized as follows: In
Section 2, details of KHA are introduced.
Section 3 briefly explains the improved KHA. In
Section 4 clustering with the IKHA approach is proposed.
Section 5 presents the experimental results of our proposed algorithm. Finally, the summary and future works are provided in
Section 6.
2. Introduction to Krill Herd Algorithm
KHA is based on the simulation of the herding of krill swarms in response to specific biological and environmental processes. Nearly all necessary coefficients for KHA are obtained from real-world empirical studies [
19].
In nature, the adaptability of an individual is judged by its distance to food and the maximum density of the krill population. Thus, based on the assumption of an imaginary distance, the fitness is the value of the objective function. Within a two-dimensional space, the specific location of the individual krill varies with time depending on the following three actions [
19]:
KHA uses the Lagrangian model to extend the search space to an
n-dimensional decision space as:
where
is the motion of the
ith krill induced by other krill individuals,
represents the foraging activity, and
denotes the physical diffusion of the krill individuals.
The explanations for basic KHA are given as follows:
(1) Motion induced by other krill individuals
According to theoretical arguments, individual krill maintain a high density and move due to mutual effects. The direction of motion induced,
, is estimated from the local swarm density (local effect), target swarm density (target effect), and repulsive swarm density (repulsive effect). For an individual krill, the motion can be defined as:
where:
is the maximum induced speed,
is the inertia weight of the motion induced in the range [0, 1]s,
is the last motion induced,
is the local effect provided by the neighbors, and
is the target direction effect provided by the best individual krill. According to the measured values of the maximum induced speed (
),
is taken as 0.01 (ms
−1) in [
19].
Different strategies can be used in choosing the neighbor. Based on the actual behavior of krill individuals, a sensing distance () should be determined around a krill individual and the neighbors should be found.
The sensing distance for each krill individual can be determined by using different heuristic methods. Here, the sensing distance is determined by using the following formula for each iteration:
where
is the sensing distance for the
ith krill individual and
N is the number of the krill individuals, and
represents the related positions of
ith krill. If the distance of
and
is less than the defined sensing distance (
),
is a neighbor of
.
(2) Foraging motion
This movement is intended to comply with two criteria. The first is food location, and the second is previous experience about the food location. For the
ith krill, the foraging motion can be expressed as:
where:
where
is foraging speed,
is inertia weight of the foraging motion in the range [0, 1],
is the attractive food, and
is the effect of the best fitness of the
ith krill so far. According to measured values of the foraging speed,
is taken as 0. 02 ms
−1 in [
19].
Food effect is defined in terms of its location. The center of food should be found and then formulated for food attraction. This solution cannot be determined, but can be estimated. In this study, the virtual center of food concentration is estimated according to the fitness distribution of krill individuals, which is inspired by the "center of mass" concept. The center of food for each iteration is formulated as:
where
is the objective function value of the
ith krill individual.
(3) Physical diffusion
The physical diffusion of the krill individuals is considered a random process. This motion can be expressed in terms of a maximum diffusion speed and a random directional vector. The formula is as follows:
where
is the maximum diffusion speed, and
is the random directional vector and its arrays are random values between −1 and 1.
is the actual iteration number and
is the maximum number of iterations.
(4) Motion process of KHA
Defined motions regularly change the krill position toward the best fitness. The foraging motion and motion induced by other krill individuals contain two local (
) and two global strategies (
), which work simultaneously and create a powerful algorithm. Using diverse operative parameters of the motion throughout the time, the position vector of a krill individual during interval
to
is expressed by the following equation:
where
represents the updated krill individual position, and
represents the current position. Note that
is considered the most important constant and should be tuned carefully based on the optimization problem. This is because this parameter works as a scale factor of the speed vector, and
can be obtained from the following formula:
where
is the total number of variables, and
and
are the lower and upper bounds of the
jth variables (
), respectively. Therefore, the absolute of their subtraction shows the search space. It is empirically found that
is a constant number between [0, 2]. It is also obvious that low values of
let the krill individuals search the space carefully.
(5) Genetic operators
Crossover operation is the use of a binomial crossover scheme to update the
mth components of the
ith krill by the following formula:
where
Cr is crossover probability, which is a random number between 0 and 1,
. Mutation is controlled by mutation probability (
). The adaptive mutation scheme used is formulated as
where
and
is a number between 0 and 1. In
, the nominator is
. Based on this new mutation probability, the mutation probability for the global best is equal to zero, which increases as fitness decreases.
3. Improved KHA
The KHA algorithm considers various motion characteristics of individual krill, as well as the global exploration and local exploitation ability. Through simulation and experiments [
19], the performance of the algorithm is better than that of the majority of swarm intelligence algorithms. However, recent studies show that the KHA algorithm has excellent local exploitation ability, but global exploration ability is not as strong, especially in the treatment of high-dimensional multimodal function optimization [
29], because the algorithm cannot always converge rapidly. To solve the problem, selection and crossover operators are added to the basic KHA in [
29], and [
30] used a local search to explore around the solution obtained by the KHA. Inspired by these developments, we propose the improved KHA algorithm (IKHA) based on a modified mutation scheme and a new updated mechanism.
The main ideas of IKHA are as follows: First, we sorted the individuals of each generation according to the fitness value in ascending order. The first part included individuals with good fitness (individuals with fitness value among the top 10%, but apart from the global best), and the rest comprised the second part. For the first part, which we call sub-optimal individuals, the fitness value was close to the optimal individual, but worse than the optimal solution. In the process of optimization of this part, the individual does not have much effect. Another noteworthy point, based on Equatio (14) in the previous section, is that mutation probability () for the global best is equal to zero and increases with decreasing fitness. In other words, the smaller the fitness value, the higher the probability of mutation. Thus, we can improve the mutation mechanism to use this part of the individual and allow them to find the potential solution in the vicinity of the optimal solution.
For the first part of the sub-optimal individuals, we use the individual’s own neighbors
(a neighbor of
) to optimize the mutation program instead of the original stochastic selection
. Specific operations observed the following formula, where SN is the abbreviation of sub-optimal individuals and
is a number between 0 and 1:
For the second part of the individuals, we only had to use good individuals to guide them toward a better direction of evolution. Therefore, we chose sub-optimal individuals to optimize the mutation program. The specific formula is as follows:
where
∈ {SN | SN} are sub-optimal individuals.
Beyond the modified mutation mechanism, an updated operator is added in our approach. After many iterations, the KHA tends to stagnate. To avoid premature convergence in the early run phase, we added an updated mechanism to overstep the local extremum. In our approach, a parameter, the maximum number of stalls (
), is added. Suppose that the
(the fitness value of the global best individual of the population) remains unchanged, and
(the number of unchanged iterations) is greater than
, then the updated formula is shown as follows:
where
is the average position of the
SN, and
is a number between 0 and 1. If the fitness value of
or
is less than
, we replace the old position with the new position.
, which is defined as follows, and is a positive integer greater than zero and decreases with the increase of the iteration number:
In IKHA, the optimized mutation scheme abandons the original randomly-selected individuals for mutations, and uses different mutations for individuals with different fitness values. With such a divide-and-rule strategy, we take full advantage of all individuals, as opposed to the KHA. For example, sub-optimal individuals can be used to find potentially better values, thereby preventing the algorithm from falling into a local optimum. For the remaining individuals, excellent individuals could guide them, thereby speeding up optimization. The purpose of the updated operation is to find the potential for the escape from the local solution at the later run phase of the process.
The time computational complexity of IKHA is the same as KHA, and the analysis is as follows: In KHA, for each krill in an iteration, the time complexity of calculating the sensing distance is , so KHA’s time computational complexity is ; in IKHA, the added updated operating is mainly according to Equations (17) and (18), and time computational complexity is . Moreover, with the improved mutation mechanism, we need to sort the individuals according to their fitness value, and we use a quick sort algorithm, whose time computational complexity is in the average case, or in the worst case, but for every generation, one sorting operation is added, thus, the time computational complexity of IKHA is still .
To test IKHA further, we conducted the following experiments by using the Ackley function [
31]. The Ackley function is defined as follows and its graph is shown in
Figure 1:
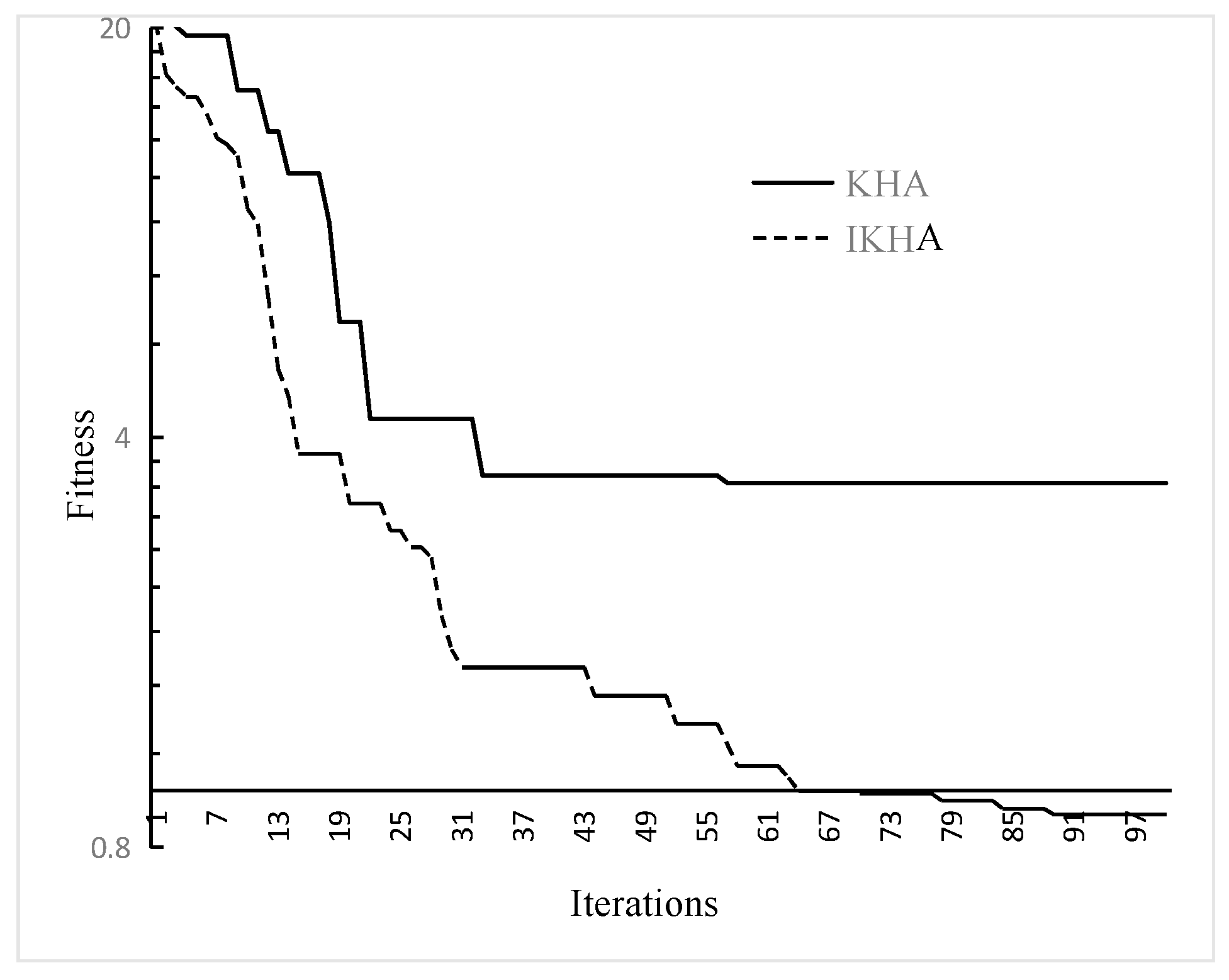
The convergence graphs for the Ackley function is drawn in
Figure 2. In our experiment, the number of iterations is set to 100, the population size is 50, and the results are obtained after 50 trials. For the KHA and the proposed IKHA, we set the same parameters
= 0.01,
= 0.02,
= 0.005,
= 5, and
= 0.5 at the beginning and these parameters linearly decreased to 0.1 at the end in IKHA [
32,
33]. Regarding the convergence behavior of KHA and IKHA, both IKHA and KHA converged quickly in the early run phase, but IKHA converged faster than KHA. During the latter run, KHA began to stagnate after rapid convergence, but IKHA continued to find a better value. Thus, IKHA can quickly converge in the early iterations and jump out of the local optimum to find a better solution.
5. Simulation and Experiment
To investigate the performance of IKHCA, five clustering algorithms, namely, K-means [
34], ACO [
35], PSO [
36], KHCA I in [
30], and KHCA II, were compared. KHCA II is a clustering algorithm based on KHA [
19]. Five datasets obtained from UCI Machine Learning Repository [
37] were used in our experiment. The details of the data sets, including the name, number of classes, attributes, and records are presented in
Table 1. Our experiments were conducted on Eclipse 4.6.0 with Windows 7 environment using Intel Core i7, 3.40 GHz, and 4 GB RAM.
Before the experiment, the setting of the parameters and the selection of the objective functions in KHCA II and IKHCA were specified. In KHCA II and IKHCA, we used the sum of squared error (
) as the objective function directly, the formula is indicated in Equation (25). The low value of
, the higher the quality of the clustering is
The parameters are set in accordance with [
19,
38]:
= 0.01;
= 0.02; and
= 0.005.
Here, Ct is set to 0.5, and the inertia weights are equal to 0.9 at the beginning of the search, and linearly decreased to 0.1 at the end to encourage exploitation. The size of the population is set to 25, , = 0.5 at the beginning, and linearly decreased to 0.1 at the end in IKHCA.
We compared the performance of different clustering algorithms from two aspects. First, we compared the objective function value of the different clustering algorithms in
Table 2, and then we compared the accuracy of different clustering algorithms in
Table 3. Accuracy is specifically expressed as follows:
Table 2 lists the best and worst means of the solution, and ranks the algorithms based on the mean values for all datasets in
Table 1. As compared, algorithm results are directly taken from [
30]. KHCA II and IKHCA algorithms were executed 100 times independently with the same parameters described in this paper, except that the maximum number of generations was set to 200. As shown in
Table 2, IKHCA obtained better solutions for the best and worse than other algorithms on the Wine, Glass, Cancer, and CMC datasets, but not on Iris. KHCA II obtained the first solution for best on the Iris dataset. However, KHCA II generated a poor solution for the worst with respect to the Iris dataset. Then, we observed that IKHCA achieved the best solutions from mean values on all datasets, except Glass. However, IKHCA is very close to the results obtained by the KHCA II algorithm on the Glass dataset. From the experimental results, our proposed algorithm achieved better optimal solutions with improved stability in a limited number of iterations. IKHCA ranked first in all algorithms.
In
Table 3, the clustering accuracies of IKHCA and other clustering algorithms are given, and part of the results were obtained directly from [
30], with the bold font indicating the best results. At a glance, one can easily see that the last three clustering algorithms (KHCA I, KHCA II, and IKHCA) by using KHA are obviously better than the K-means, ACO, and PSO algorithms. It can be seen that the introduction of KHA into the clustering problem is reasonable and effective. Based on these results, IKHCA is proved to be the best algorithm with respect to objective function value and accuracy.
6. Conclusions and Future Work
KHA is a good swarm intelligent heuristic algorithm that could be gradually applied to address real-world problems. For the original KHA algorithm that could not always converge rapidly and search globally particularly well, we proposed IKHA, which improved the original mutation mechanism to provide two different mutation schemes and introduced an updated mechanism. In IKHA, we were in accordance with the fitness of individuals, set different mutation schemes according to their own conditions, made outstanding individuals look for better solutions, and the rest moved closer to the good individual. Then, through the updated mechanism, optimal individuals looked for potential solutions in the surrounding space to avoid being stuck in the local optimal zone. Experimental results showed that IKHA performed better than KHA.
Several clustering algorithms depend highly on the initial states and always converge to the nearest local optimum from the starting position of the search. In order to find the optimal clustering center, we applied the IKHA to solve an actual clustering problem and proposed the improved krill-herd clustering algorithm (IKHCA). According to the experiments, the IKHCA had better efficiency than, and outperformed, other well-known clustering approaches. Moreover, the results of the experiments show that the IKHA can successfully be introduced in clustering problems and perform best in almost all experimental datasets. In the future, there are several issues the can be further studied, such as utilizing the optimization ability of the IKHA to find the optimal cluster number and apply the IKHA to other scenarios to solve a wide range of real-world problems.