Reliable Portfolio Selection Problem in Fuzzy Environment: An mλ Measure Based Approach
Abstract
:1. Introduction
2. Problem Statement and Mathematical Models
- S: total number of involved securities;
- s: index of involved securities, ;
- : return of the s-th security;
- : the investment ratio for security s, which is a decision variable.
2.1. Measure and Expected Value Operator
- (a)
- ;
- (b)
- ;
- (c)
- if , then and ;
- (d)
- if , then and .
2.2. New Reliable Models
3. Property Analysis
- The procedure of simulating :Step 1. Randomly generate crisp vectors from the -level set of fuzzy vector , respectively, where is a sufficiently small number and ;Step 2. Let for where is the membership function of ;Step 3. Return the following value:
- The procedure of simulating :Step 1. Set ;Step 2. Randomly generate crisp vectors from the -level set of fuzzy vector , respectively, where is a sufficiently small number and ;Step 3. Set and ;Step 4. Randomly generate r in interval ;Step 5. If , let ; otherwise, let ;Step 6. Repeat Step 4 to Step 5 for a total of N times;Step 7. .
4. Solution Method
4.1. Solution Representation
- Step 1. Randomly generate a sequence of nonnegative real numbers , , …, ;
- Step 2. Let , .
- Step 1. Let ;
- Step 2. If or , go to Step 4; otherwise, go to Step 3;
- Step 3. Randomly find an index with ; let , ;
- Step 4. If , let , go to Step 3; otherwise, stop.
4.2. Selection Operation
4.3. Crossover Operation
4.4. Mutation Operation
- Procedure of the genetic algorithm:With the technical details designed above, the framework of the genetic algorithm can be summarized in the following.Step 1. Determine the parameters for the algorithm, including population size , fitness value parameter , crossover probability , mutation probability , number of generation M, etc.;Step 2. Initialize the population, in which a total of feasible individuals should be produced;Step 3. Implement the selection operation based on the objective functions of different chromosomes;Step 4. Implement the crossover operation with crossover probability ;Step 5. Implement the mutation operation with mutation probability ;Step 6. Repeat Step 3 to Step 5 for M times;Step 7. Output the best individual found in this procedure as the near-optimal solution to the proposed model.
5. Numerical Examples
- (1)
- Steadiness of the proposed algorithmWith the above-mentioned decision data, we implement this experiment by the genetic algorithm in C++ software, in which the relevant model parameters are set as , . The computational results are listed in Table 3. Specifically, we randomly choose the critical parameters in the algorithm, including the crossover probability, mutation probability and population size, to test the steadiness of the algorithmic implementation. The algorithm terminated after 500 cycles, i.e., , and a total of ten tests is finally executed. To further show the performance of the computational results, we compute the relatively errors among different results with respect to the best objective function (i.e., 80.23) according to the following equation,Typically, among all of these experiments, the relative errors are not greater than , which implies the steadiness of the proposed algorithm with respect to these critical parameters. For the parameter setting , and , we can find the near-optimal solution with objective value 80.23, and the corresponding optimal solution is , , .
- (2)
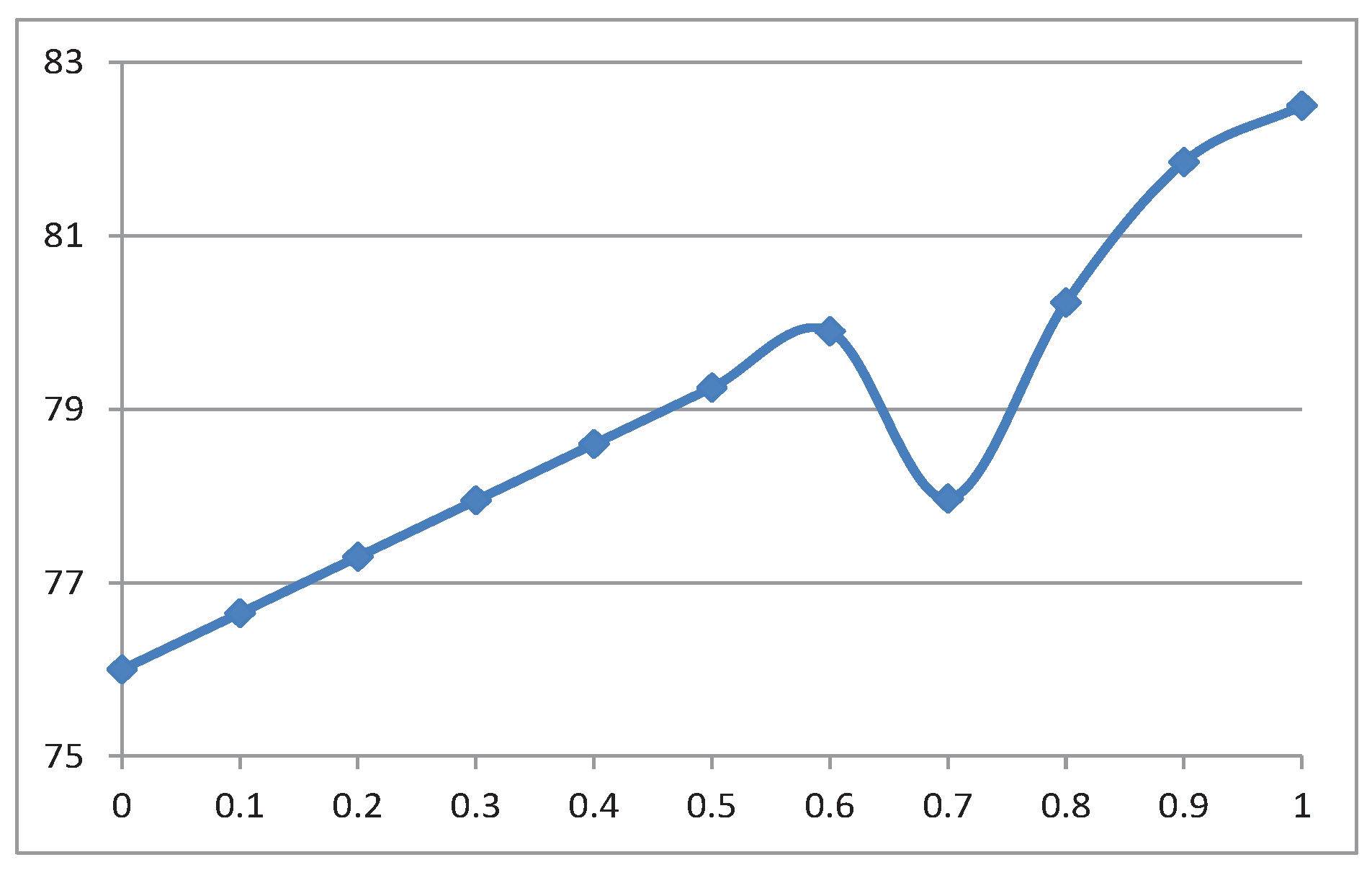
- Sensitivity w.r.t parameterIn the proposed model, we use the measure to characterize the feature of the involved decision makers. Then, we are particularly interested in investigating the sensitivity analysis of the near-optimal solution with respect to parameter . In detail, we discretize this parameter into the following numbers, i.e., , , , , , , , , , , , and the critical parameters in the genetic algorithm are taken as follows: , and . We list the computational results in Table 4. In particular, to further show a straightforward overview, we also give Figure 2 to show the variation of the objective function with respect to different parameters . Typically, in the experimental results, the returned optimal objective values take almost an increasing tendency when we enhance the parameter except for at which an opposite tendency occurs in comparison to the adjacent values. As expected, when we take different parameters , the optimal solutions can be different. For instance, when ; the optimal solution turns out to be , , , ; if , the optimal solution is changed to , , , , which is typically different from the solution of .
- (3)
- Sensitivity w.r.t parameterIn our proposed variance-constrained Model (9), the parameter is regarded as the upper bound of variance to denote the risk-averse degree in the decision-making process. Practically, since the variance can be used to denote the risk of an investment strategy, a small parameter corresponds to a risk-averse decision. In order to show the influence of this parameter on the optimal solution, we here especially implement a set of experiments to test this performance. Specifically, we take a total of ten cases for parameter , i.e., . In addition, we set in the measure, and , , in the genetic algorithm. The computational results are listed in Table 5. Clearly, different parameters might produce different optimal solutions. For instance, if we take , the optimal solution turns out to be , , ; on the other hand, when we set , the outputted optimal solution is , , .
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio Selection: Efficient Diversification of Investments; John Wiley & Sons: New York, NY, USA, 1959. [Google Scholar]
- Shen, Y. Mean-variance portfolio selection in a complete market with unbounded random coefficients. Automatica 2015, 55, 165–175. [Google Scholar] [CrossRef]
- Lv, S.; Wu, Z.; Yu, Z. Continuous-time mean-variance portfolio selection with random horizon in an incomplete market. Automatica 2016, 69, 176–180. [Google Scholar] [CrossRef]
- He, F.; Qu, R. A two-stage stochastic mixed-integer program modelling and hybrid solution approach to portfolio selection problems. Inf. Sci. 2014, 289, 190–205. [Google Scholar] [CrossRef]
- Najafi, A.A.; Mushakhian, S. Multi-stage stochastic mean-semivariance-CVaR portfolio optimization under transaction costs. Appl. Math. Comput. 2015, 256, 445–458. [Google Scholar] [CrossRef]
- Low, R.K.Y.; Faff, R.; Aas, K. Enhancing mean-variance portfolio selection by modeling distributional asymmetries. J. Econ. Bus. 2016, 85, 49–72. [Google Scholar] [CrossRef]
- Shi, Y.; Cui, X.; Li, D. Discrete-time behavioral portfolio selection under cumulative prospect theory. J. Econ. Dyn. Control 2015, 61, 283–302. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, X.; Siu, T.K. Mean-variance portfolio selection under a constant elasticity of variance model. Oper. Res. Lett. 2014, 42, 337–342. [Google Scholar] [CrossRef]
- Kim, M.J.; Lee, Y.; Kim, J.H.; Kim, W.C. Sparse tangent portfolio selection via semi-definite relaxation. Oper. Res. Lett. 2016, 44, 540–543. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, P. Mean-variance portfolio selection with regime switching under shorting prohibition. Oper. Res. Lett. 2016, 44, 658–662. [Google Scholar] [CrossRef]
- Chiu, M.C.; Wong, H.Y. Mean-variance portfolio selection with correlation risk. J. Comput. Appl. Math. 2014, 263, 432–444. [Google Scholar] [CrossRef]
- Fulga, C. Portfolio optimization with disutility-based risk measure. Eur. J. Oper. Res. 2016, 251, 541–553. [Google Scholar] [CrossRef]
- Alexander, G.J.; Baptista, A.M.; Yan, S. Mean-variance portfolio selection with ‘at-risk’ constraints and discrete distributions. J. Bank. Financ. 2007, 31, 3761–3781. [Google Scholar] [CrossRef]
- Villena, M.J.; Reus, L. On the strategic behavior of large investors: A mean-variance portfolio approach. Eur. J. Oper. Res. 2016, 254, 679–688. [Google Scholar] [CrossRef]
- Maillet, B.; Tokpavi, S.; Vaucher, B. Global minimum variance portfolio optimisation under some model risk: A robust regression-based approach. Eur. J. Oper. Res. 2015, 244, 289–299. [Google Scholar] [CrossRef]
- Huang, X. Portfolio selection with a new definition of risk. Eur. J. Oper. Res. 2008, 186, 351–357. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, W. Multiperiod mean absolute deviation fuzzy portfolio selection model with risk control and cardinality constraints. Fuzzy Sets Syst. 2014, 255, 74–91. [Google Scholar] [CrossRef]
- Li, J.; Xu, J. Multi-objective portfolio selection model with fuzzy random returns and a compromise approach-based genetic algorithm. Inf. Sci. 2013, 220, 507–521. [Google Scholar] [CrossRef]
- Gupta, P.; Inuiguchi, M.; Mehlawat, M.K.; Mittal, G. Multiobjective credibilistic portfolio selection model with fuzzy chance-constraints. Inf. Sci. 2013, 229, 1–17. [Google Scholar] [CrossRef]
- Mehlawat, M.K. Credibilistic mean-entropy models for multi-period portfolio selection with multi-choice aspiration levels. Inf. Sci. 2016, 345, 9–26. [Google Scholar] [CrossRef]
- Huang, X.; Di, H. Uncertain portfolio selection with background risk. Appl. Math. Comput. 2016, 276, 284–296. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, T. Mean-chance model for portfolio selection based on uncertain measure. Insur. Math. Econ. 2014, 59, 243–250. [Google Scholar] [CrossRef]
- Bermudeza, J.D.; Segurab, J.V.; Vercher, E. A multi-objective genetic algorithm for cardinality constrained fuzzy portfolio selection. Fuzzy Sets Syst. 2012, 188, 16–26. [Google Scholar] [CrossRef]
- Rebiasz, B. Selection of efficient portfolios-probabilistic and fuzzy approach, comparative study. Comput. Ind. Eng. 2013, 64, 1019–1032. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Xu, W. A possibilistic mean-semivariance-entropy model for multi-period portfolio selection with transaction costs. Eur. J. Oper. Res. 2012, 222, 341–349. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, X.; Hao, F. A new Chance-Variance optimization criterion for portfolio selection in uncertain decision systems. Expert Syst. Appl. 2012, 39, 6514–6526. [Google Scholar] [CrossRef]
- Bhattacharyya, R.; Hossain, S.A.; Kar, S. Fuzzy cross-entropy, mean, variance, skewness models for portfolio selection. J. King Saud Univ. Comput. Inf. Sci. 2014, 26, 79–87. [Google Scholar] [CrossRef]
- Saborido, R.; Ruiz, A.B.; Bermudez, J.D.; Vercher, E.; Luque, M. Evolutionary multi-objective optimization algorithms for fuzzy portfolio selection. Appl. Soft Comput. 2016, 39, 48–63. [Google Scholar] [CrossRef]
- Yang, L.; Iwamura, K. Fuzzy chance-constrained programming with linear combination of possibility measure and necessity measure. Appl. Math. Sci. 2008, 2, 2271–2288. [Google Scholar]
- Nahmias, S. Fuzzy variable. Fuzzy Sets Syst. 1978, 1, 97–110. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.K. Expected value of fuzzy variable and fuzzy expected value model. IEEE Trans. Fuzzy Syst. 2002, 10, 445–450. [Google Scholar]
- Dai, C.; Cai, Y.P.; Li, Y.P.; Sun, W.; Wang, X.W.; Guo, H.C. Optimal strategies for carbon capture, utilization and storage based on an inexact mλ-measure fuzzy chance-constrained programming. Energy 2014, 78, 465–478. [Google Scholar] [CrossRef]
- Li, Z.; Huang, G.; Zhang, Y.; Li, Y. Inexact two-stage stochastic credibility constrained programming for water quality management. Resour. Conserv. Recycl. 2013, 73, 122–132. [Google Scholar] [CrossRef]
- Liu, B. Theory and Practice of Uncertain Programming; Physica-Verlag: Heidelberg, Germany, 2002. [Google Scholar]
- Xing, T.; Zhou, X. Finding the most reliable path with and without link travel time correlation: A Lagrangian substitution based approach. Transp. Res. Part B 2011, 45, 1660–1679. [Google Scholar] [CrossRef]
- Sen, S.; Pillai, R.; Joshi, S.; Rathi, A.K. A Mean-Variance Model for Route Guidance in Advanced Traveler Information Systems. Transp. Sci. 2001, 35, 37–49. [Google Scholar] [CrossRef]
- Wang, L.; Yang, L.; Gao, Z. The Constrained Shortest Path Problem with Stochastic Correlated Link Travel Times. Eur. J. Oper. Res. 2016, 255, 43–57. [Google Scholar] [CrossRef]
- Wang, L.; Yang, L.; Gao, Z.; Li, S.; Zhou, X. Evacuation Planning for Disaster Responses: A Stochastic Programming Framework. Transp. Res. Part C Emerg. Technol. 2016, 69, 150–172. [Google Scholar] [CrossRef]

| λ | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp. | 115.00 | 117.5 | 120.00 | 122.50 | 125.00 | 127.50 | 130.00 | 132.50 | 135.00 | 137.50 | 140.00 |
| Sim. | 115.17 | 117.63 | 120.10 | 122.57 | 125.04 | 127.51 | 129.97 | 132.44 | 134.91 | 137.38 | 139.85 |
| Security Index | Fuzzy Return | Security Index | Fuzzy Return |
|---|---|---|---|
| 1 | (35, 45, 50) | 11 | (45, 53, 70) |
| 2 | (54, 80, 90) | 12 | (44, 60, 70) |
| 3 | (44, 60, 65) | 13 | (33, 45, 50) |
| 4 | (35, 40, 50) | 14 | (43, 54, 70) |
| 5 | (55, 70, 75) | 15 | (45, 66, 70) |
| 6 | (63, 70, 80) | 16 | (44, 50, 60) |
| 7 | (45, 54, 60) | 17 | (35, 50, 55) |
| 8 | (72, 80, 85) | 18 | (28, 40, 50) |
| 9 | (66, 73, 90) | 19 | (33, 40, 45) |
| 10 | (35, 40, 50) | 20 | (45, 50, 55) |
| Test Index | Expected Value | Variance | Optimal Objective | Relative Error | |||
|---|---|---|---|---|---|---|---|
| 1 | 0.4 | 0.3 | 30 | 78.52 | 35.23 | 78.52 | 2.13% |
| 2 | 0.4 | 0.4 | 50 | 78.12 | 38.64 | 78.12 | 2.63% |
| 3 | 0.5 | 0.6 | 40 | 78.54 | 34.68 | 78.54 | 2.11% |
| 4 | 0.5 | 0.5 | 50 | 78.59 | 37.14 | 78.59 | 2.04% |
| 5 | 0.6 | 0.7 | 40 | 80.23 | 39.83 | 80.23 | 0.00% |
| 6 | 0.6 | 0.5 | 50 | 78.00 | 38.60 | 78.00 | 2.78% |
| 7 | 0.7 | 0.6 | 40 | 78.08 | 36.59 | 78.08 | 2.68% |
| 8 | 0.6 | 0.7 | 50 | 77.42 | 37.27 | 77.42 | 3.50% |
| 9 | 0.7 | 0.7 | 60 | 78.28 | 35.91 | 78.28 | 2.43% |
| 10 | 0.8 | 0.7 | 50 | 78.05 | 36.30 | 78.05 | 2.72% |
| 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Opti.Obj | 76.00 | 76.65 | 77.30 | 77.95 | 78.60 | 79.25 | 79.90 | 77.97 | 80.23 | 81.85 | 82.50 |
| 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Opti.Obj | 80.23 | 77.98 | 76.58 | 77.88 | 78.66 | 77.22 | 77.03 | 77.05 | 78.34 | 78.13 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Wang, L.; Liu, X. Reliable Portfolio Selection Problem in Fuzzy Environment: An mλ Measure Based Approach. Algorithms 2017, 10, 43. https://doi.org/10.3390/a10020043
Feng Y, Wang L, Liu X. Reliable Portfolio Selection Problem in Fuzzy Environment: An mλ Measure Based Approach. Algorithms. 2017; 10(2):43. https://doi.org/10.3390/a10020043
Chicago/Turabian StyleFeng, Yuan, Li Wang, and Xinhong Liu. 2017. "Reliable Portfolio Selection Problem in Fuzzy Environment: An mλ Measure Based Approach" Algorithms 10, no. 2: 43. https://doi.org/10.3390/a10020043
APA StyleFeng, Y., Wang, L., & Liu, X. (2017). Reliable Portfolio Selection Problem in Fuzzy Environment: An mλ Measure Based Approach. Algorithms, 10(2), 43. https://doi.org/10.3390/a10020043





