RGloVe: An Improved Approach of Global Vectors for Distributional Entity Relation Representation
Abstract
:1. Introduction
- RQ1
- How to learn the distributional entity representations only by using the statistical information of entity-entity co-occurrences?
- RQ2
- How to build, store and query the relationships between entities without extracting the predefined relation types or vocabulary?
2. Related Work
2.1. Entity Relation Extraction
2.2. Distributional Word Representation
3. Methods
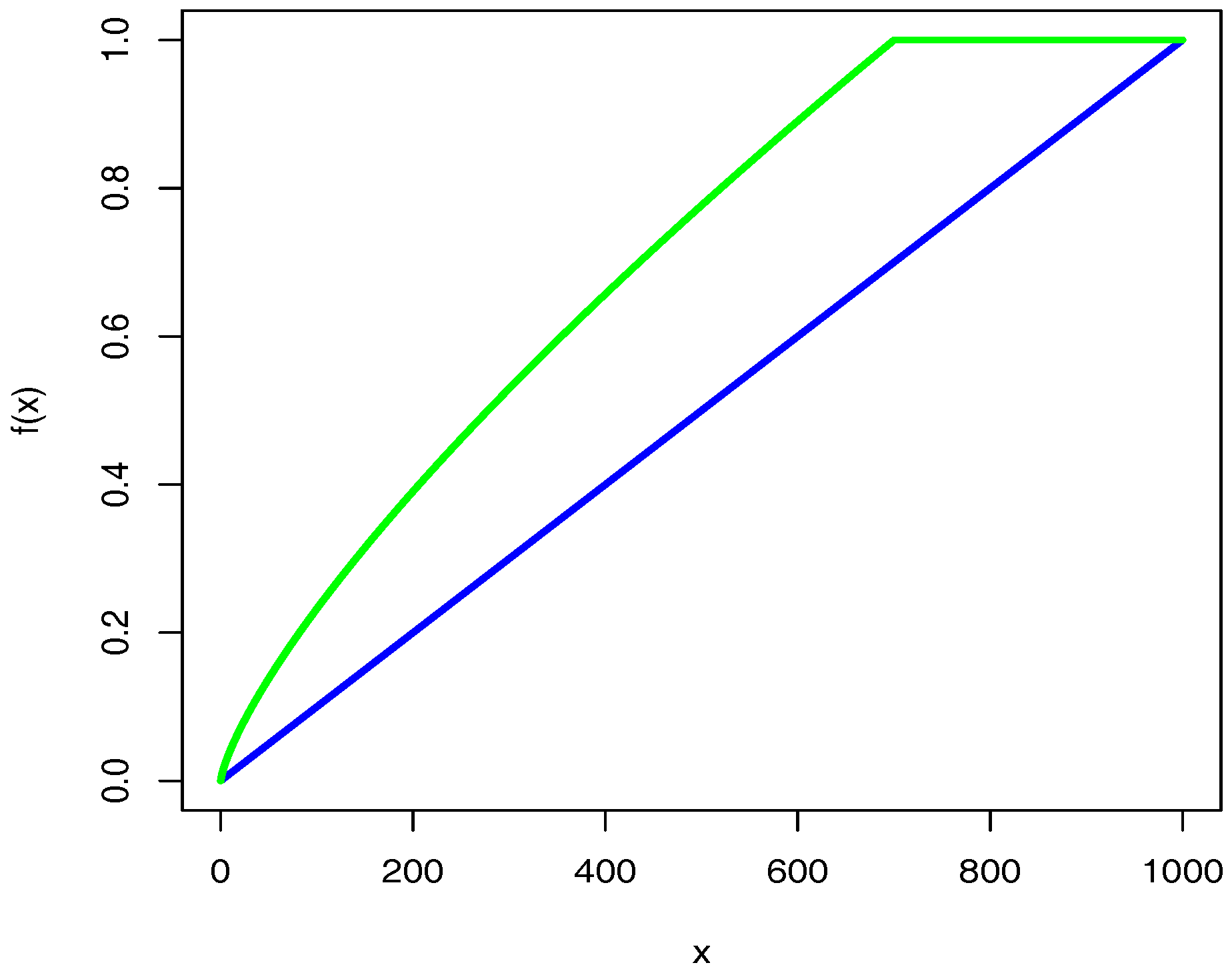
3.1. Co-Occurrence Matrix
3.2. Distributional Entityrepresentation of RGloVe
3.2.1. Brief Review of Global Vectors
3.2.2. Global Vectors for Distributional Relation Representation
3.2.3. Training by AdaGrad
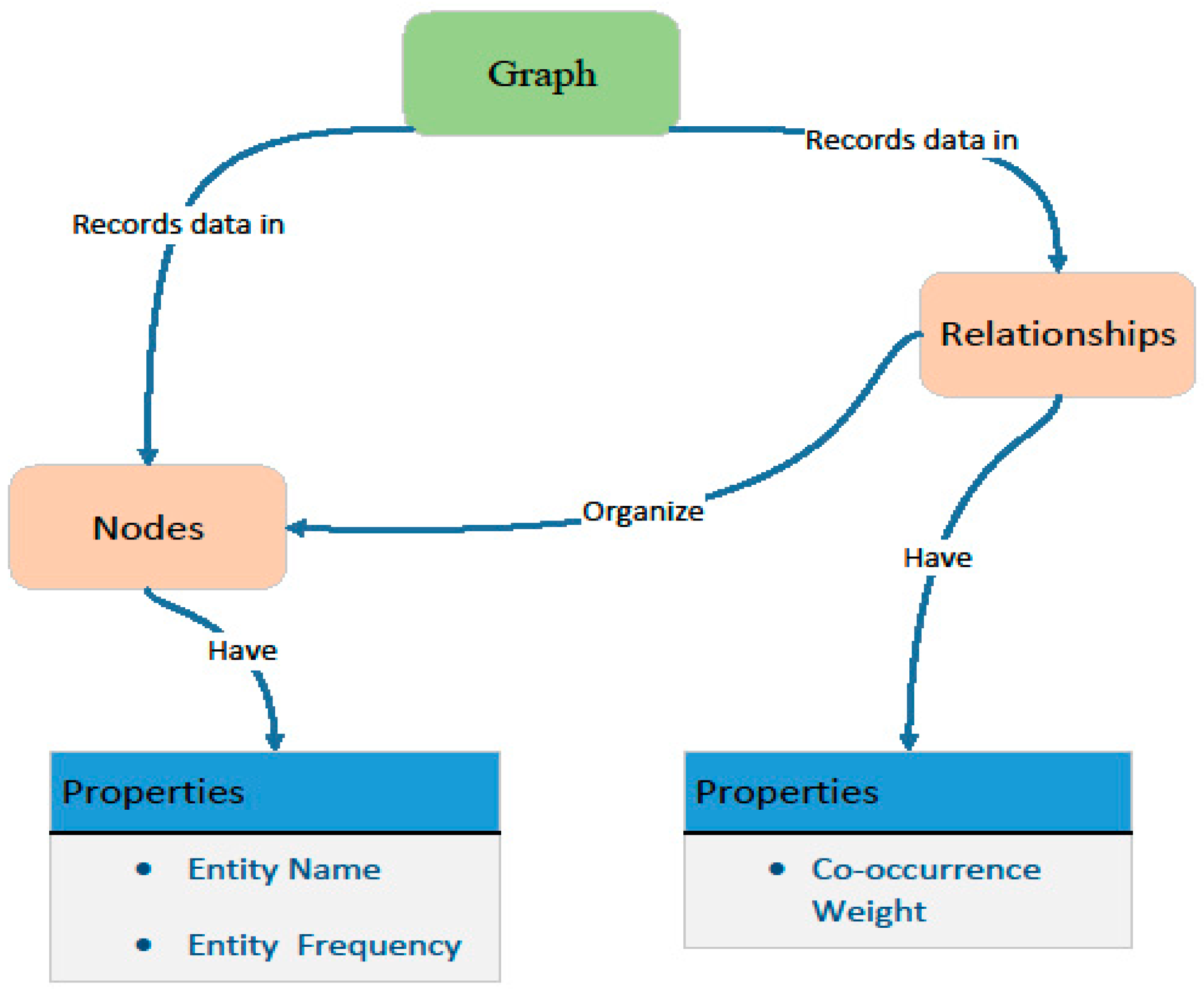
3.3. Entity Relational Storage of Neo4j
4. Experiments
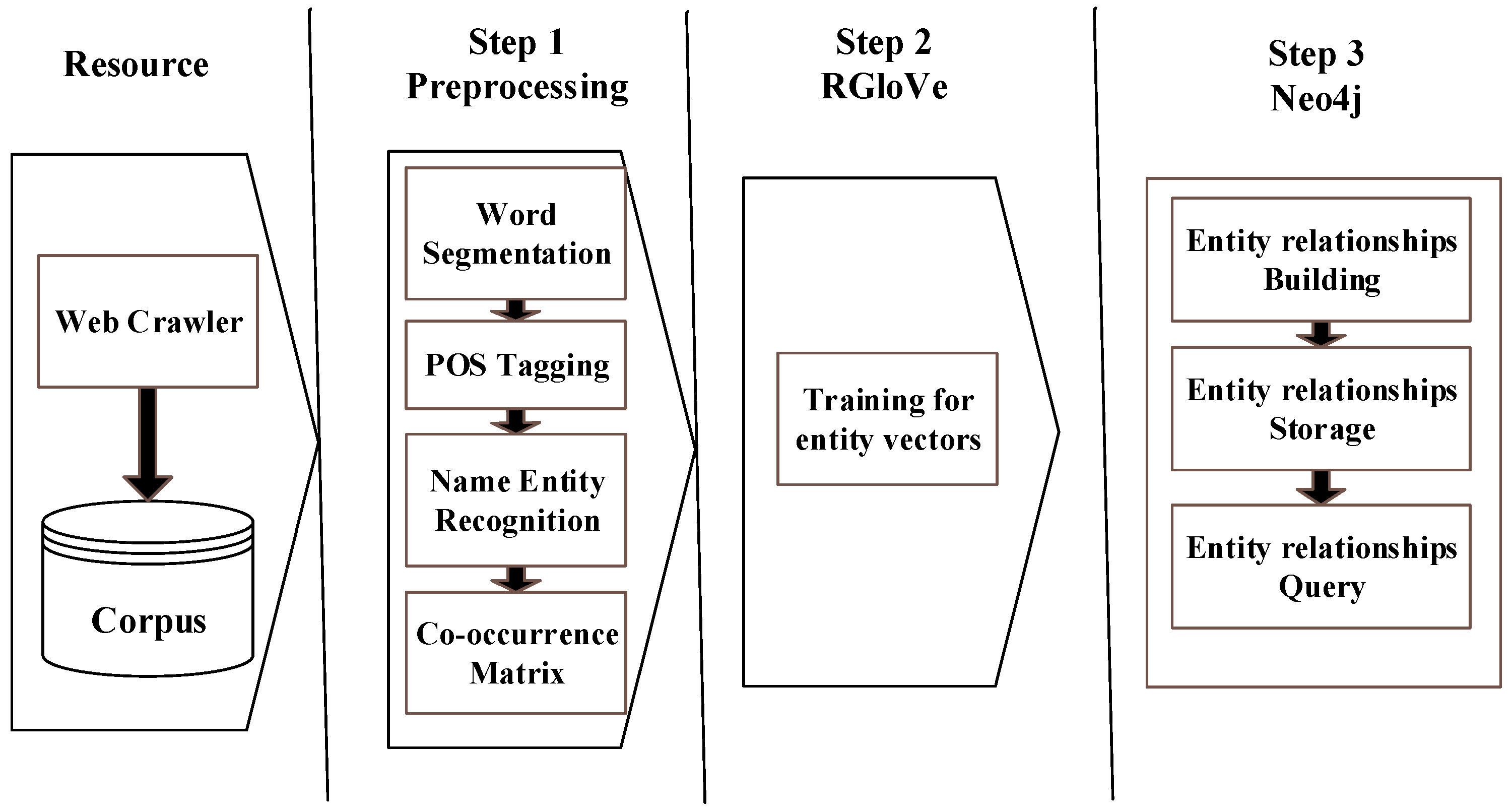
4.1. Data Set and Experimental Settings
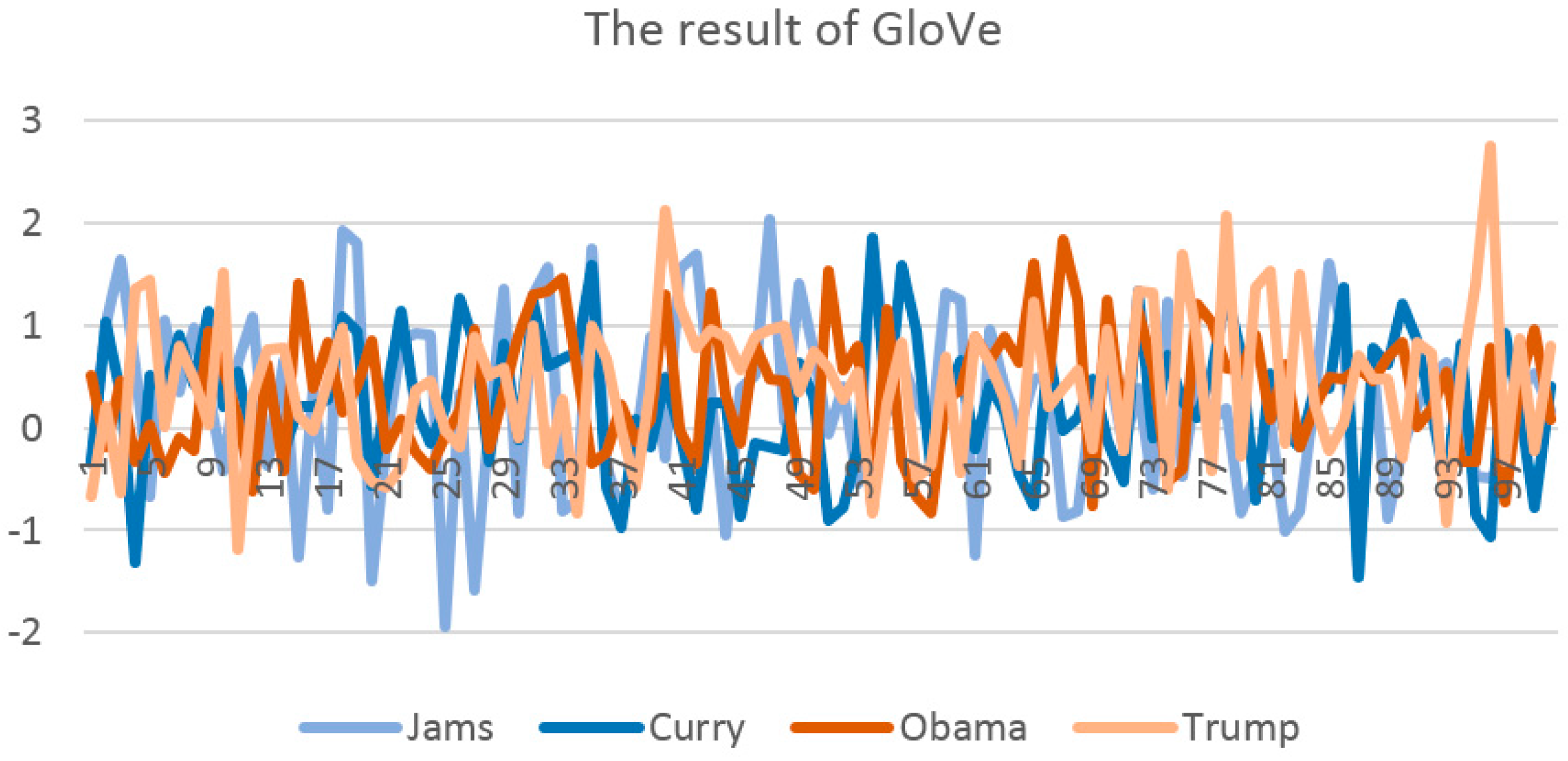
4.2. Entity Vectors Presentation
4.3. Quantitative Representation Result and Discussion
4.3.1. Error Rate
4.3.2. Top N Precision
4.3.3. Average Accuracy of Relationship Classification
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Doddington, G.; Mitchell, A.; Przybocki, M.; Ramshaw, L.; Strassel, S.; Weischedel, R. The automatic content extraction (ACE) program-tasks, data, and evaluation. LREC 2004, 2, 837–840. [Google Scholar]
- Banko, M.; Etzioni, O.; Center, T. The Tradeoffs between Open and Traditional Relation Extraction. In Proceedings of the 46th Annual Meeting of the Association for Computational Linguistics, Columbus, OH, USA, 15–20 June 2008; pp. 28–36. [Google Scholar]
- Etzioni, O.; Banko, M.; Soderland, S.; Weld, D.S. Open information extraction from the web. Commun. ACM 2008, 51, 68–74. [Google Scholar] [CrossRef]
- Etzioni, O.; Fader, A.; Christensen, J.; Soderland, S.; Mausam, M.I. Open Information Extraction: The Second Generation. In Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; pp. 3–10. [Google Scholar]
- Banko, M.; Cafarella, M.J.; Soderland, S.; Broadhead, M.; Etzioni, O. Open Information Extraction for the Web. In Proceedings of the 20th International Joint Conference on Artifical Intelligence, Hyderabad, India, 6–12 January 2007; pp. 2670–2676. [Google Scholar]
- Kalyanpur, A.; Murdock, J.W. Unsupervised Entity-Relation Analysis in IBM Watson. In Proceedings of the Third Annual Conference on Advances in Cognitive Systems ACS, Atlanta, GA, USA, 28–31 May 2015; p. 12. [Google Scholar]
- Fader, A.; Soderland, S.; Etzioni, O. Identifying Relations for Open Information Extraction. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Edinburgh, UK, 27–31 July 2011; pp. 1535–1545. [Google Scholar]
- Tseng, Y.-H.; Lee, L.-H.; Lin, S.-Y.; Liao, B.-S.; Liu, M.-J.; Chen, H.-H.; Etzioni, O.; Fader, A. Chinese Open Relation Extraction for Knowledge Acquisition. In Proceedings of the 14th Conference of the European Chapter of the Association for Computational Linguistics, Gothenburg, Sweden, 26–30 April 2014; pp. 12–16. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C.D. Glove: Global Vectors for Word Representation. In Proceedings of the Empiricial Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Zhou, G.; Zhang, M. Extracting relation information from text documents by exploring various types of knowledge. Inf. Process. Manag. 2007, 43, 969–982. [Google Scholar] [CrossRef]
- Khayyamian, M.; Mirroshandel, S.A.; Abolhassani, H. Syntactic Tree-Based Relation Extraction Using a Generalization of Collins and Duffy Convolution Tree Kernel. Proceedings of Human Language Technologies: The 2009 Annual Conference of the North American Chapter of the Association for Computational Linguistics, Boulder, CO, USA, 31 May–5 June 2009; pp. 66–71. [Google Scholar]
- Choi, M.; Kim, H. Social relation extraction from texts using a support-vector-machine-based dependency trigram kernel. Inf. Process. Manag. 2013, 49, 303–311. [Google Scholar] [CrossRef]
- Choi, S.-P.; Lee, S.; Jung, H.; Song, S.-K. An intensive case study on kernel-based relation extraction. Multimed. Tools Appl. 2014, 71, 741–767. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, W.; Gao, S.; Guo, J. A Bottom-Up Kernel of Pattern Learning for Relation Extraction. In Proceedings of the Chinese Spoken Language Processing (ISCSLP), Singapore, 12–14 September 2014; pp. 609–613. [Google Scholar]
- Nguyen, T.H.; Plank, B.; Grishman, R. Semantic Representations for Domain Adaptation: A Case Study on the Tree Kernel-Based Method for Relation Extraction. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing of the Asian Federation of Natural Language Processing, Beijing, China, 27–31 July 2015; pp. 635–644. [Google Scholar]
- Zhou, G.; Qian, L.; Zhu, Q. Label propagation via bootstrapped support vectors for semantic relation extraction between named entities. Comput. Speech Lang. 2009, 23, 464–478. [Google Scholar]
- Sun, A.; Grishman, R.; Sekine, S. Semi-Supervised Relation Extraction with Large-Scale Word Clustering. In Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, Portland, OR, USA, 19–24 June 2011; pp. 521–529. [Google Scholar]
- Fukui, K.-I.; Ono, S.; Megano, T.; Numao, M. Evolutionary Distance Metric Learning Approach to Semi-Supervised Clustering with Neighbor Relations. In Proceedings of the 2013 IEEE 25th International Conference on Tools with Artificial Intelligence (ICTAI), Herndon, VA, USA, 4–6 November 2013; IEEE Computer Society: Washington, DC, USA, 2013; pp. 398–403. [Google Scholar]
- Maziero, E.; Hirst, G.; Pardo, T. Semi-Supervised Never-Ending Learning in Rhetorical Relation Identification. Proceeding of the Recent Advances in Natural Language Processing, Hissar, Bulgaria, 5–11 September 2015; pp. 436–442. [Google Scholar]
- Min, B.; Shi, S.; Grishman, R.; Lin, C.-Y. Ensemble Semantics for Large-Scale Unsupervised Relation Extraction. In Proceedings of the 2012 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning, Jeju Island, Korea, 12–14 July 2012; pp. 1027–1037. [Google Scholar]
- Wang, J.; Jing, Y.; Teng, Y.; Li, Q. A Novel Clustering Algorithm for Unsupervised Relation Extraction. In Proceedings of the Seventh International Conference Digital Information Management (ICDIM), Macau, Macao, 22–24 August 2012; pp. 16–21. [Google Scholar]
- De Lacalle, O.L.; Lapata, M. Unsupervised Relation Extraction with General Domain Knowledge. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Seattle, Washington, USA, 18–21 October 2013; pp. 415–425. [Google Scholar]
- Takase, S.; Okazaki, N.; Inui, K. Fast and large-scale unsupervised relation extraction. Proceedings of 29th Pacific Asia Conference on Language, Information and Computation, Shanghai, China, 30 October–1 November 2015; pp. 96–105. [Google Scholar]
- Remus, S. Unsupervised Relation Extraction of In-Domain Data From Focused Crawls. In Proceedings of the Student Research Workshop at the 14th Conference of the European Chapter of the Association for Computational Linguistics, Gothenburg, Sweden, 26–30 April 2014; pp. 11–20. [Google Scholar]
- Alicante, A.; Corazza, A.; Isgrò, F.; Silvestri, S. Unsupervised entity and relation extraction from clinical records in Italian. Comput. Biol. Med. 2016, 72, 263–275. [Google Scholar] [CrossRef] [PubMed]
- Landauer, T.K.; Dumais, S.T. A solution to plato’s problem: The latent semantic analysis theory of acquisition, induction, and representation of knowledge. Psychol. Rev. 1997, 104, 211–240. [Google Scholar] [CrossRef]
- Turney, P.D. Similarity of semantic relations. Comput. Linguist. 2006, 32, 379–416. [Google Scholar] [CrossRef]
- Sebastian; Lapata, M. Dependency-based construction of semantic space models. Comput. Linguist. 2007, 33, 161–199. [Google Scholar]
- Gamallo, P.; Bordag, S. Is singular value decomposition useful for word similarity extraction? Lang. Resour. Eval. 2011, 45, 95–119. [Google Scholar] [CrossRef]
- Bengio, Y.; Ducharme, R.; Vincent, P.; Janvin, C. A neural probabilistic language model. Mach. Learn. Res. 2003, 3, 1137–1155. [Google Scholar]
- Collobert, R.; Weston, J.; Bottou, L.; Karlen, M.; Kavukcuoglu, K.; Kuksa, P. Natural language processing (almost) from scratch. Mach. Learn. Res. 2011, 12, 2493–2537. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv, 2013; arXiv:1301.3781. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Zhang, H.-P.; Liu, Q.; Cheng, X.-Q.; Zhang, H.; Yu, H.-K. Chinese Lexical Analysis Using Hierarchical Hidden Markov Model. In Proceedings of the second SIGHAN workshop on Chinese language processing, Sapporo, Japan, 11–12 July 2003; pp. 63–70. [Google Scholar]
- Fleiss, J.L. Measuring nominal scale agreement among many raters. Psychol. Bull. 1971, 76, 378. [Google Scholar] [CrossRef]
| Word2Vec (%) | GloVe (%) | RGloVe (%) | |
|---|---|---|---|
| error rate | 16.76 | 13.68 | 4.09 |
| Word2Vec (%) | GloVe (%) | RGloVe (%) | |
|---|---|---|---|
| N = 1000 | 0.18 | 0.2 | 4.7 |
| N = 5000 | 0.65 | 0.7 | 12.4 |
| N = 10,000 | 1.13 | 1.24 | 15.98 |
| SVM (%) | Word2Vec (%) | GloVe (%) | RGloVe (%) | |
|---|---|---|---|---|
| average accuracy | 90.7 | 75.6 | 76.8 | 79.3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Huang, Y.; Liang, Y.; Wang, Y.; Fu, X.; Fu, K. RGloVe: An Improved Approach of Global Vectors for Distributional Entity Relation Representation. Algorithms 2017, 10, 42. https://doi.org/10.3390/a10020042
Chen Z, Huang Y, Liang Y, Wang Y, Fu X, Fu K. RGloVe: An Improved Approach of Global Vectors for Distributional Entity Relation Representation. Algorithms. 2017; 10(2):42. https://doi.org/10.3390/a10020042
Chicago/Turabian StyleChen, Ziyan, Yu Huang, Yuexian Liang, Yang Wang, Xingyu Fu, and Kun Fu. 2017. "RGloVe: An Improved Approach of Global Vectors for Distributional Entity Relation Representation" Algorithms 10, no. 2: 42. https://doi.org/10.3390/a10020042
APA StyleChen, Z., Huang, Y., Liang, Y., Wang, Y., Fu, X., & Fu, K. (2017). RGloVe: An Improved Approach of Global Vectors for Distributional Entity Relation Representation. Algorithms, 10(2), 42. https://doi.org/10.3390/a10020042





