Backtracking-Based Iterative Regularization Method for Image Compressive Sensing Recovery
Abstract
:1. Introduction
2. Compressive Sensing and IST Algorithm
| Algorithm 1 IST [11] |
| Input: y, A, , c, x0 = 0 for k = 1 to K do (a) (b) end for |
3. Image CS Recovery via Backtracking-Based Adaptive IST
3.1. New Objective Function
3.2. BAIST Algorithm for Solving the New Objective Function
| Algorithm 2 IST with Adaptive Nonlocal Regularization |
| Input: y, A, s, c, x0 = 0 for k = 1 to K do (a) (b) end for |
| Algorithm 3 Backtracking-Based Adaptive IST |
| Input: y, A, b1, b2, …, bB, s, c, x0 = 0 for k = 1 to K do (a) (b) end for |
4. Experiments
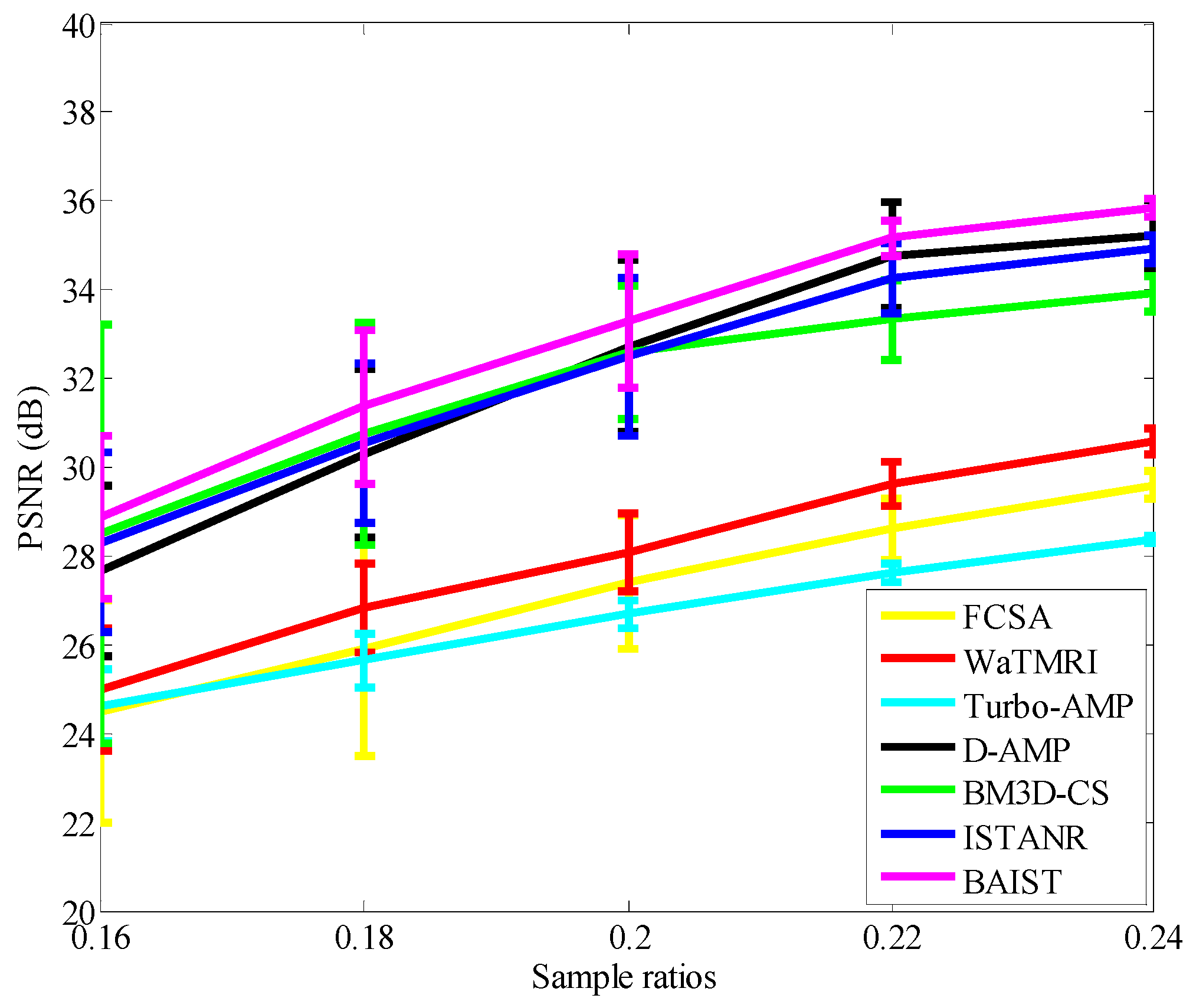
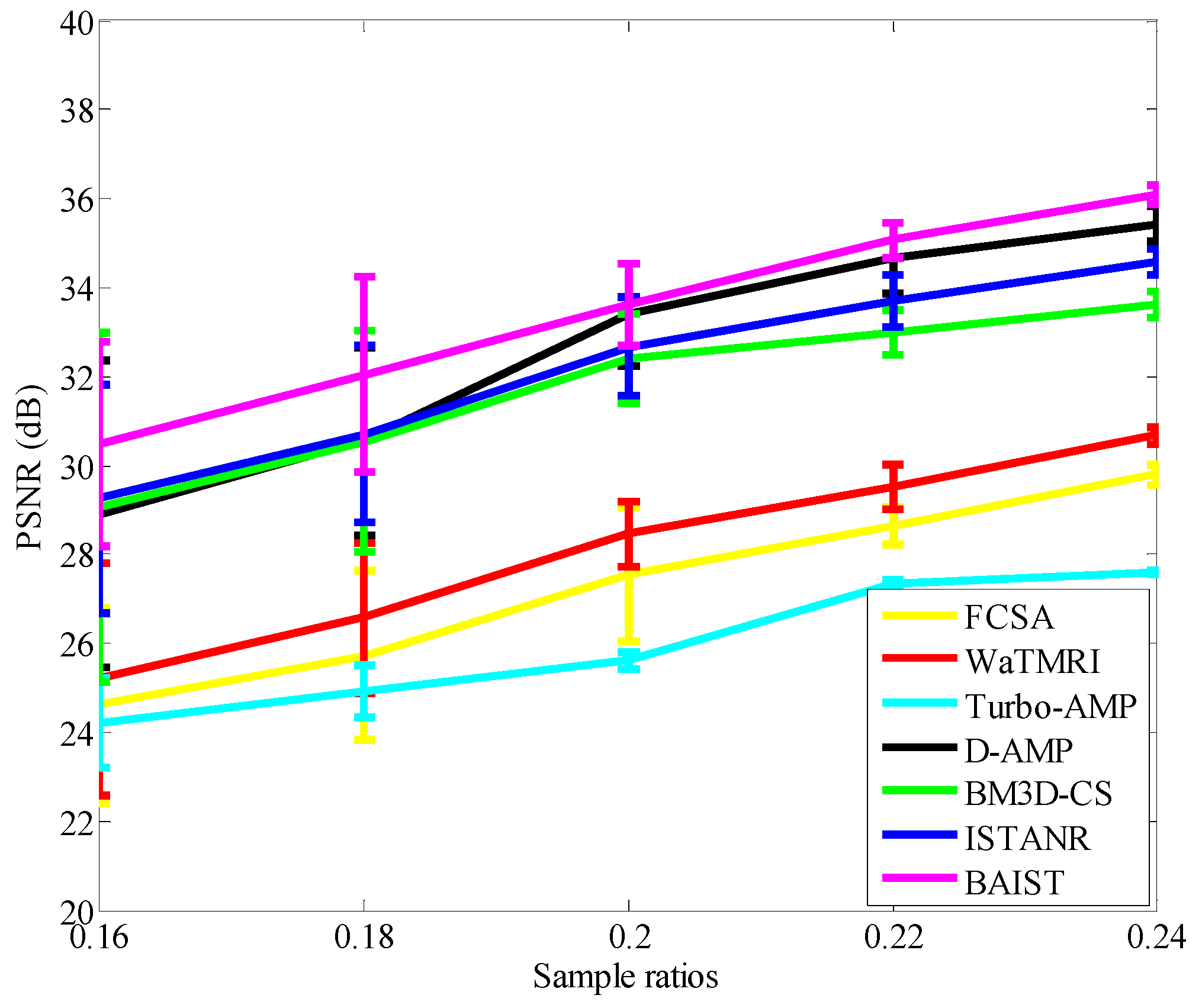
4.1. Average PSNR Evaluation
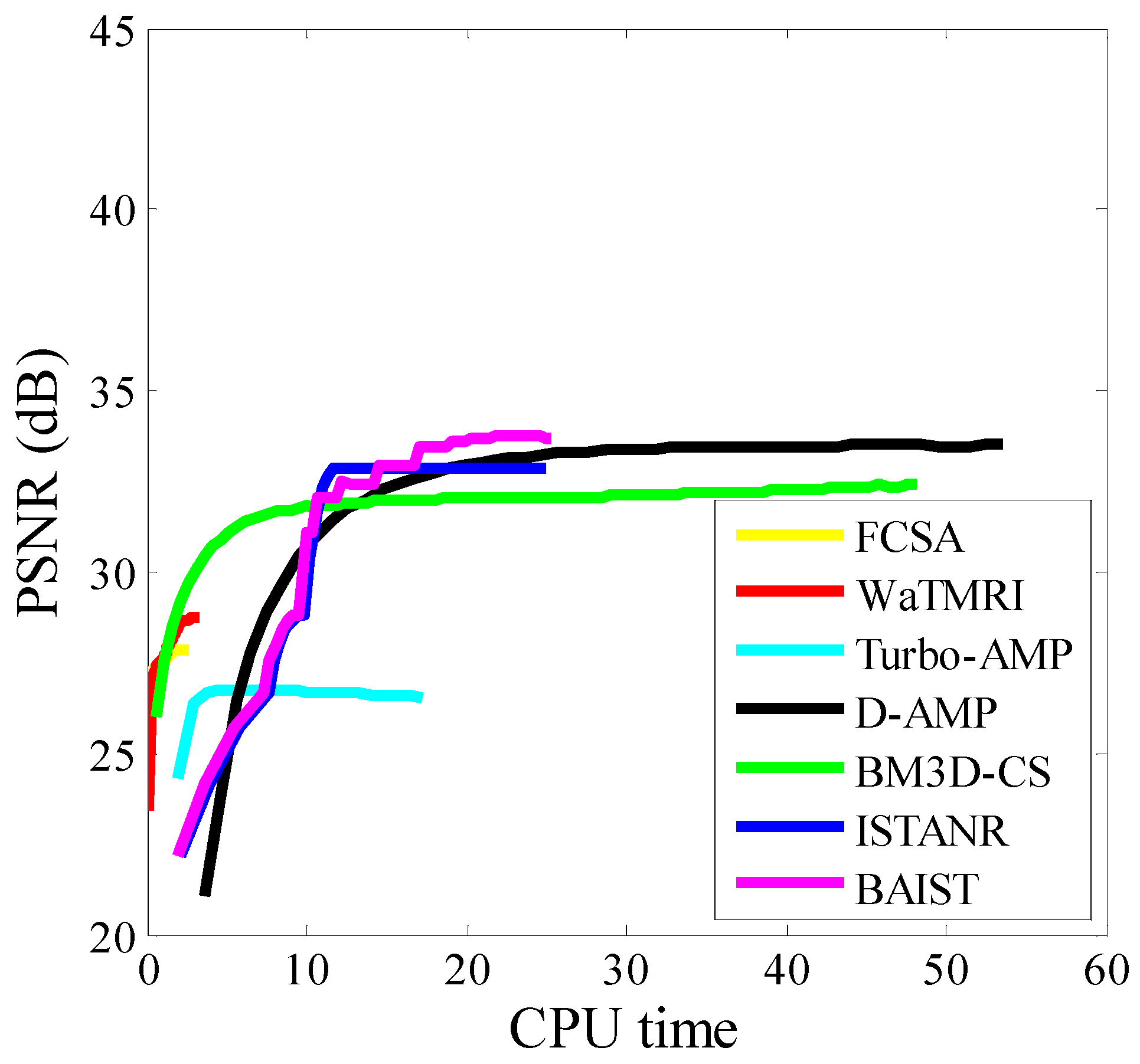
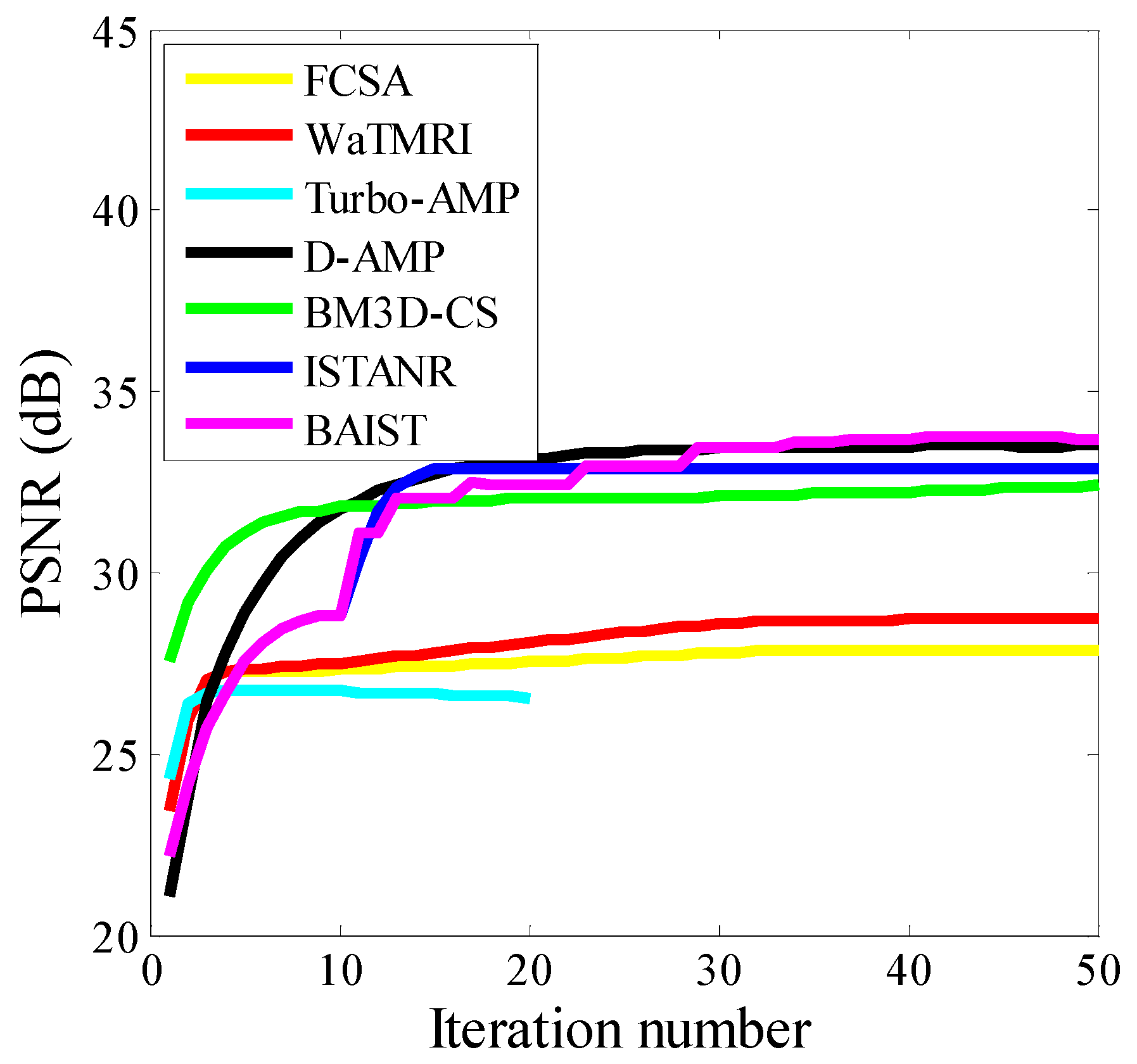
4.2. Visual Quality and Runtime Evaluation on Boat Image
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Huang, J.; Zhang, S.; Metaxas, D. Efficient MR Image Reconstruction for Compressed MR Imaging. Med. Image Anal. 2011, 15, 670–679. [Google Scholar] [CrossRef] [PubMed]
- Mahrous, H.; Ward, R. Block Sparse Compressed Sensing of Electroencephalogram (EEG) Signals by Exploiting Linear and Non-Linear Dependencies. Sensors 2016, 16, 201. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Huang, J. Exploiting the wavelet structure in Compressed Sensing MRI. Magn. Reson. Imaging 2014, 32, 1377–1389. [Google Scholar] [CrossRef] [PubMed]
- Burns, B.L.; Wilson, N.E.; Thomas, M.A. Group Sparse Reconstruction of Multi-Dimensional Spectroscopic Imaging in Human Brain in Vivo. Algorithms 2014, 7, 276–294. [Google Scholar] [CrossRef]
- Som, S.; Schniter, P. Compressive imaging using approximate message passing and a markov-tree prior. IEEE Trans. Signal Process. 2012, 60, 3439–3448. [Google Scholar] [CrossRef]
- Dong, W.; Shi, G.; Li, X.; Ma, Y.; Huang, F. Compressive sensing via nonlocal low-rank regularization. IEEE Trans. Image Process. 2014, 23, 3618–3632. [Google Scholar] [CrossRef] [PubMed]
- Metzler, C.; Maleki, A.; Baraniuk, R.G. From denoising to compressed sensing. IEEE Trans. Inf. Theory 2016, 62, 5117–5144. [Google Scholar] [CrossRef]
- Egiazarian, K.; Foi, A.; Katkovnik, V. Compressed sensing image reconstruction via recursive spatially adaptive filtering. In Proceedings of the IEEE International Conference on Image Processing (ICIP), San Antonio, TX, USA, 16–19 September 2007; pp. I-549–I-552.
- Shi, J.; Zheng, X.; Yang, W. Robust sparse representation for incomplete and noisy data. Information 2015, 6, 287–299. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Bioucas-Dias, J.; Figueiredo, M. A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Cheng, L. Reweighted fast iterative shrinkage thresholding algorithm with restarts for l1-l1, minimisation. IET Signal Process. 2016, 10, 28–36. [Google Scholar] [CrossRef]
- Daubechies, I.; Defriese, M.; DeMol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Afonso, M.; Bioucas-Dias, J.; Figueiredo, M. Fast image recovery using variable splitting and constrained optimization. IEEE Trans. Image Process. 2010, 19, 2345–2356. [Google Scholar] [CrossRef] [PubMed]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Xie, Z.; Feng, J. Backtracking-Based Iterative Regularization Method for Image Compressive Sensing Recovery. Algorithms 2017, 10, 7. https://doi.org/10.3390/a10010007
Liu L, Xie Z, Feng J. Backtracking-Based Iterative Regularization Method for Image Compressive Sensing Recovery. Algorithms. 2017; 10(1):7. https://doi.org/10.3390/a10010007
Chicago/Turabian StyleLiu, Lingjun, Zhonghua Xie, and Jiuchao Feng. 2017. "Backtracking-Based Iterative Regularization Method for Image Compressive Sensing Recovery" Algorithms 10, no. 1: 7. https://doi.org/10.3390/a10010007
APA StyleLiu, L., Xie, Z., & Feng, J. (2017). Backtracking-Based Iterative Regularization Method for Image Compressive Sensing Recovery. Algorithms, 10(1), 7. https://doi.org/10.3390/a10010007





