Pressure Control for a Hydraulic Cylinder Based on a Self-Tuning PID Controller Optimized by a Hybrid Optimization Algorithm

Abstract

In order to improve the performance of the hydraulic support electro-hydraulic control system test platform, a self-tuning proportion integration differentiation (PID) controller is proposed to imitate the actual pressure of the hydraulic support. To avoid the premature convergence and to improve the convergence velocity for tuning PID parameters, the PID controller is optimized with a hybrid optimization algorithm integrated with the particle swarm algorithm (PSO) and genetic algorithm (GA). A selection probability and an adaptive cross probability are introduced into the PSO to enhance the diversity of particles. The proportional overflow valve is installed to control the pressure of the pillar cylinder. The data of the control voltage of the proportional relief valve amplifier and pillar pressure are collected to acquire the system transfer function. Several simulations with different methods are performed on the hydraulic cylinder pressure system. The results demonstrate that the hybrid algorithm for a PID controller has comparatively better global search ability and faster convergence velocity on the pressure control of the hydraulic cylinder. Finally, an experiment is conducted to verify the validity of the proposed method.

1. Introduction

The complexity of the dynamic system makes it generally urgent to develop process control technology. Numerous control methods have been proposed, such as fuzzy control [1], neural control [2] and adaptive control [3]. Among these, the proportion integration differentiation (PID) controller is the most popular. Thanks to its simple structure, easy implementation and robust performance, the PID controller was widely used in many different fields, including process control [4], flight control [5], motor drives [6] and instrumentation [7]. Modern industrial systems often suffered from problems of high orders, nonlinearities and time delays [8,9]. In order to improve the control accuracy of systems, many intelligence methods were researched and compared [10]. The main object of the PID controller is to adjust the response signals to be as close as possible to the drive signals. Thus, it is important to optimally adjust the controller’s parameters.

The past decades have witnessed the proposal of many methods to improve the capacity of parameters’ optimization. The first classical tuning method was proposed by Ziegler and Nichols (Z-N). However, the performance of Z-N on the practical engineering was poor [11]. In recent decades, artificial intelligence algorithms have developed and play an important role in optimization fields, such as artificial neural network (ANN) [12], genetic algorithm (GA) [13], fuzzy logic [1] and neural-fuzzy system [2]. Due to the poor performance of the Z-N method, intelligence algorithms were put into use for tuning the PID controller. The above theoretical tuning methods were proven to have better applications in acquiring optimal parameters.

Particle swarm optimization (PSO) was an evolutionary computation derived from the behavior of birds flocking, insects swarming and fish schooling [14]. All particles were updated by their positions and velocities during iterations [15]. The optimal solution was searched for in particles’ cooperation and information sharing. Thanks to its high capacity for acquiring the optimal solution within shorter iteration time and stable convergence property, PSO was widely applied in the areas of system identification [16], feature selection [17], function optimization [18], neural network training [19] and fuzzy systems control [20]. Thus, PSO is an excellent method for solving the problem of self-tuning the PID controller. As for the particular weaknesses and advantages of different algorithms, many researches proposed the theory of algorithm fusion to increase the optimization efficiency [21,22]. GA had outstanding global search ability on account of the genetic operation [23]. Similar to other optimization algorithms, PSO was easily trapped in the local optimum [24,25]. In order to improve the global search ability and convergence characteristics, this paper combined GA and PSO for self-tuning the PID controller. The simulation and experiment were conducted on a hydraulic cylinder pressure system. The results showed the obvious improvement in optimizing the parameters of the PID controller.

The paper is organized as follows. Section 2 describes the related work about the PID controller and PSO algorithm. The basic theories of the PID controller and PSO are presented in Section 3. The specific process for tuning PID parameters and the flow of pressure control for the hydraulic cylinder are described in Section 4. Section 5 shows the simulation and experiment results. Finally, a brief conclusion is illustrated in Section 6.

2. Literature Review

Publications relevant to this paper can be divided into two research streams: proportion integration differentiation controller and particle swarm optimization algorithm.

2.1. Proportion Integration Differentiation Controller

As the superior control performance on industrial process control, the PID controller was used as the most domain form of control [26]. More than 90% of the controllers were PID type [27]. The tuning of the parameter was a complex problem for the PID controller [28]. The vast majority of research work has been conducted in this field.

The methods for parameter tuning mainly consist of two types. One is the practical tuning method. Since 1942, when Ziegler-Nichols (Z-N) straightforward tuning was proposed, many improved methods, based on the Z-N, have been studied [29,30,31,32,33]. Another is the intelligence algorithm for tuning parameters tuning. In [34], GA was used as an optimal method for the parameters of the PID controller. Through the comparison of simulation results, GA was more efficient than practical Z-N tuning in tuning parameters. In [35], a self-tuning PID controller combining GA and fuzzy logic was proposed for anti-lock braking systems. The paper utilized three decoupled modules for PID parameters. The optimal selection of the fuzzy modules was obtained using a modified GA. The PSO algorithm was introduced into the PID controller to acquire the optimal parameters. The simplicity and convenience of PSO made the controller quickly seek out the optimal output value [36]. In [37], four intelligent methods including fuzzy logic, artificial neural network, adaptive neural fuzzy inference system and GA for tuning the PID controller were compared. Simulation results showed the merits of each method in different characteristics of PID optimization.

2.2. Particle Swarm Optimization Algorithm

The PSO algorithm was developed in 1995 by Kennedy and Eberhart [38]. Although PSO had an effective application in optimization problems in a variety of fields, some problems still exist, such as a low convergence rate in the later period of evolution and its likelihood of falling into the local optimum [39,40]. To overcome these shortages, various methods were proposed. In 1999, Shi and Eberhart proposed the linear inertia factor to improve the exploration and exploitation capacities of the PSO algorithm [41]. In [42], an improved particle swarm optimization based on the D-cent chaotic model was proposed to improve the convergence rate and reduce the iterative time. An adaptive particle swarm optimization (APSO) was proposed for identifying system parameters [11]. Each particle dynamically adjusted inertia weight according to the feedback taken from the best memories of particles. The simulation result showed that APSO achieved faster convergence speed and better solution accuracy. To improve the diversity of swarm so as to prevent premature convergence, Par et al. [43] proposed a variant PSO (PSOS) using a novel evolutionary strategy to improve particles’ local and global best positions information. In [44], a chaotic particle swarm optimization (CPSO) that combined the chaotic logistic dynamics, hierarchical inertia weight, enhancement learning strategy, mutation mechanism and a PID controller, was proposed. The chaotic logistic map was applied to substitute random parameters for accelerating the convergence rate. The hierarchical inertia weight coefficients were determined by the present fitness value of the best local position in order to adaptively expand the search space. A mutation mechanism was employed to increase the diversity of particles in a bid to avoid the local optimum. In [45], a nominal average position of the swarm was introduced into an improved PSO (IPSO). The IPSO algorithm was proven to have stable convergence characteristics and good computational ability by simulating five well-known benchmark functions. In [46], a new factor, the best particle of each sub-population, was proposed for the velocity updating formula in developed PSO. The improved algorithm enhanced the search capacity, robustness and applicability.

2.3. Discussion

Based on the above reviews on tuning parameters of the PID controller, the practical tuning methods rely too much on experience and the adjustment process takes a long time. Nowadays, many industrial systems are non-linear and unstable. Single algorithm or theoretical analysis methods have difficulty in acquiring the optimal parameters. Thus, this paper combines two algorithms to accelerate the optimization speed and improve optimization performance.

Although many methods have been proposed to improve the PSO algorithm, some problems still need to be solved. Firstly, the strategy of population diversity is utilized to substitute a random selection of particles. While this method can enlarge the diversity of particles, particles with the high fitness value might be replaced and the optimization capacity be affected. Then, the crossover operation of selected particles is determined with a crossover probability. The probability is stable but not adaptive to the search capacity.

In order to solve the above problems, this paper introduces a hybrid algorithm that combines PSO and GA. The number of crossover particles is determined with the selection probability. The selection of crossover particles is in accordance with the order of particles’ fitness values. Moreover, the cross coefficient is adaptively changed with particles’ fitness level. Several simulations based on different methods are provided and the results show that the hybrid algorithm has high search capacity and effective application in parameters’ optimization.

3. Background

3.1. PID Controller

The PID control is the most common control method of industrious automation. As a linear controller, it constitutes the deviation $e\left(t\right)$ derived from the set point $r\left(t\right)$ and the actual output value $y\left(t\right)$. Through the calculation of proportion, integration and differentiation operation in the continuous time domain, the output value $u\left(t\right)$ is computed by the following formula: where $K_p$ is the proportion coefficient, $K_i$ is the integration coefficient, $K_d$ is the differentiation coefficient.

$$e\left(t\right)=r\left(t\right)-y\left(t\right)$$

(1)

$$u(t)=K_{p}e(t)+K_i{{\displaystyle \int }}_0^{t}e(t)\mathrm{d}t+K_d\frac{\mathrm{d}e\left(t\right)}{\mathrm{d}t}$$

(2)

In order to induce the calculated quantity, the sampling instant $kT$ replaces the continuous time t. The integral item and differentiation item are discretized. Through the transformation, the incremental PID controller is presented as:

$$\begin{array}{r}\hfill \mathrm{\Delta }u\left(k\right)=K_p\left[e\left(k\right)-e\left(k-1\right)\right]+K_{i}e\left(k\right)+K_d\left[e\left(k\right)-2e\left(k-1\right)+e\left(k-2\right)\right]\\ \hfill =\left(K_p+K_i+K_d\right)e\left(k\right)-\left(K_p+2K_d\right))e\left(k-1\right)+K_d\left(k-2\right)\end{array}$$

(3)

$$u\left(k\right)=u(k-1)+\mathrm{\Delta }u\left(k\right)$$

(4)

where $\mathrm{\Delta }u\left(k\right)$ is the control increment, $u\left(k\right)$ is the output value of $kT$ time.

3.2. Particle Swarm Optimization

In PSO, each particle representing a candidate solution is associated with the velocity. The velocity of each particle is adjusted according to the response of its own and its companions’ experience. The positions of particles are compared to determine the local and global best position. Particles fly through the search space and move towards better solution areas. Finally, the particle with the best global position is the most optimal solution.

Assuming that the optimal solution is searched for in an N-dimension space, a particle swarm is initiated with a random position and velocity. The position of the $ith$ particle at the $tth$ iteration is presented as $X_i^t=\left(x_1^t,x_2^t,\dots ,x_N^t\right)$ and the velocity $ith$ of the particle at $tth$ iteration is presented as$V_i^t=\left(v_1^t,v_2^t,\dots ,v_N^t\right)$. The local best position is presented as $pbest$ and the global best position is presented as$gbest$. The fitness value of each particle is computed by the objective function to compare with the $pbest$ and $gbest$ value. The best position is achieved according to the compared result. Then, the information of particles is updated through the following formula:

$$V_i^{t+1}=\omega V_i^t+c_1\times rand()\times \left(pbes{t}_i^t-x_i^t\right)+c_2\times rand()\times \left(gbes{t}_i^t-x_i^t\right)$$

(5)

$$X_i^{t+1}=X_i^t+V_i^{t+1}$$

(6)

where $c_1,c_2$ are the learning factors, usually$c_1=c_2$, $\omega$ is the inertia weight,$rand()$ is a random value in the range of 0 and 1.

In order to balance the global search capacity and local search capacity, the algorithm selects the inertia coefficient of linear change. The changing formula is:

$$\omega ={\omega }_{max}-t\times \frac{{\omega }_{max}-{\omega }_{min}}{t_{max}}$$

(7)

where ${\omega }_{max}$ is the biggest inertia weight while ${\omega }_{min}$ is the smallest, $t_{max}$ is the biggest iteration and t is the present iteration.

The specific iterative process of the PSO algorithm can be presented as follows:

Step 2.1: Randomly initialize the particles including the search position and velocity. Define all PSO algorithm parameters, such as inertia weight ${\omega }_{max},{\omega }_{min},\omega$, learning factors$c_1,c_2$, swarm size$N$, maximum iterations $t_{max}$, etc.

Step 2.2: Calculate the value of each particle using the evaluation function. In this paper, the integrated time and absolute error (ITAE) are adopted for the performance criteria. The formula is defined as:

$$\mathrm{J}={{\displaystyle \int }}_0^{\infty }t\left|e\left(t\right)\right|dt$$

(8)

Step 2.3: Update the value of the inertia weight using Equation (7).

Step 2.4: Update the $pbest$ particles by comparing the fitness value with the experience of each individual. The best evaluation value among all $pbest$is the$gbest$.

Step 2.5: Modify the velocity and position of each particle according to Equations (5) and (6). The inertia weight is determined by step 2.3.

Step 2.6: If the number of iterations reaches the maximum$t_{max}$, then stop. The latest$gbest$is the optimal controller parameter. Otherwise go back to step 2.2.

3.3. Genetic Algorithm

GA is a global optimization algorithm based on the natural selection mechanism. A search framework is supplied by GA to solve the complex issues. The search space consisted of all the solutions presented as chromosomes. Each chromosome is described by the gene with characteristic value. The process of optimization is conducted through the basic individual operations, including encoding, selection, crossover and mutation.

Encoding is utilized to transform the practical solutions to the coding area. GA has binary encoding and real encoding. Real coding uses the actual value of variable as the individual. Compared with binary encoding, real encoding is simple and easy. In order to ensure that the superior chromosome with a high fitness value is inherited by the offspring, the selection operator is the main method for survival of the fittest. The selection probability is determined by the individual fitness and the total fitness value. When the crossover probability is above the random value between 0 and 1, crossover is operated to reconstruct two selected parents. Then, the new offspring is produced to enlarge the global search capacity. If the crossover probability is below the random value, the new generations totally copy the parents. Assuming that $X_m$and$X_n$are the selected parents, the crossover is performed at the $tth$ iteration. The formula of hybrid operation is presented as:

$$\{\begin{array}{c}{X}_m\left(t+1\right)=\alpha \times X_m\left(t\right)+\left(1-\alpha \right)\times X_n\left(t\right)\\ X_n\left(t+1\right)=\alpha \times X_n\left(t\right)+\left(1-\alpha \right)\times X_m\left(t\right)\end{array}$$

(9)

where $\alpha$is a random value in the range of$\left(0,1\right)$.

The mutation operator changes the gene values of chromosomes to acquire new properties of chromosomes. If the optimal solution is approaching, then mutation can enhance the local optimization capacity as the mutation probability is small. A relatively big mutation probability can avoid the premature convergence.

4. The Proposed Method

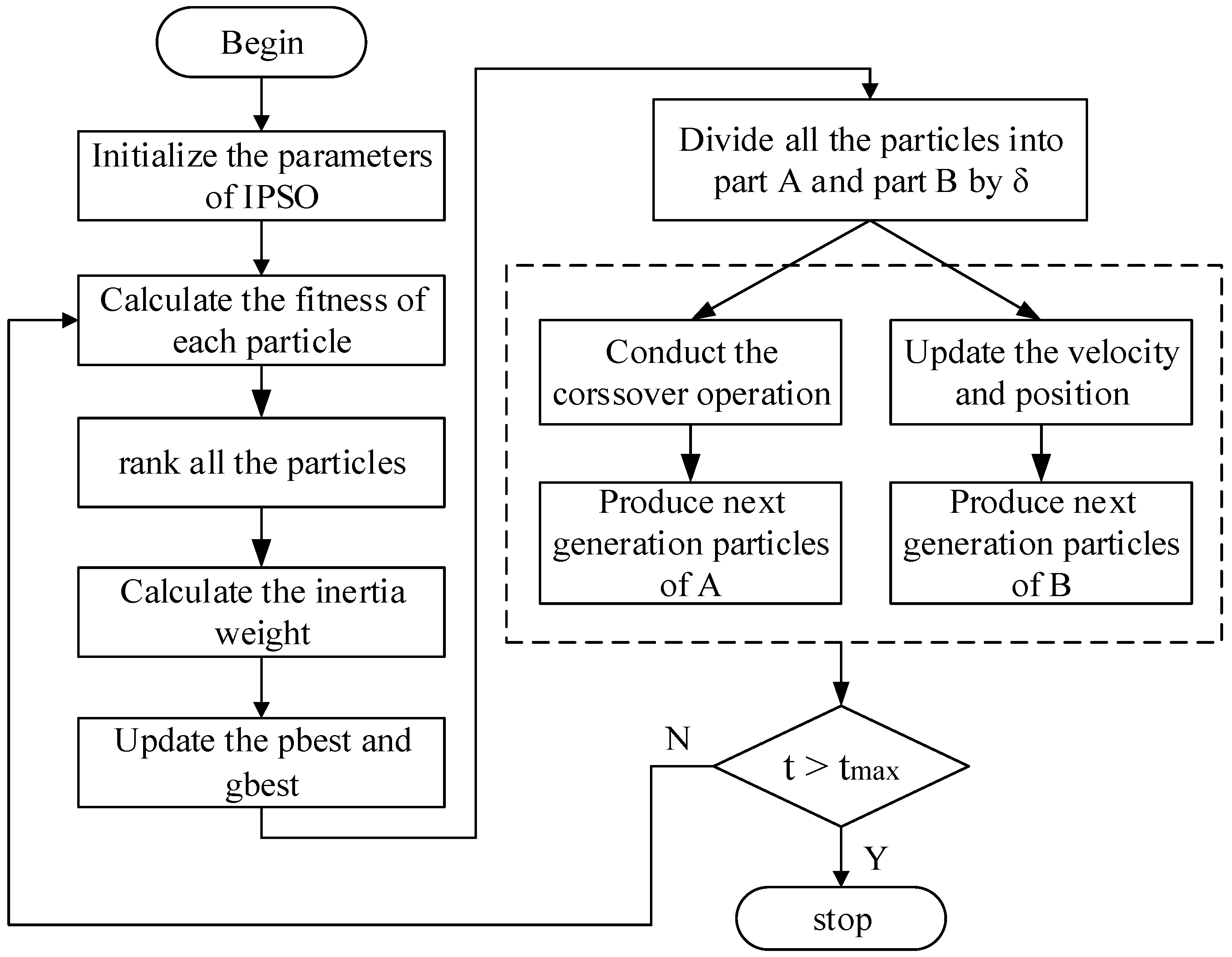
4.1. Hybrid Optimization Algorithm

While standard PSO has a fast rate of convergence, it is easy to fall into the local optimum. In order to ensure the diversity of particles, this paper introduces selection and crossover operations into PSO by quoting the principles of GA. After calculating the fitness values of individuals, the values are ranked and divided into part $A$and part $B$. At each iteration, part $A$ with low fitness is selected for random crossover to produce new generations. The amount of the offspring is the same as the parents. Part $B$ is undated by the PSO algorithm. The amount of hybrid individuals is determined by the selection probability$\delta$.

In order to avoid destroying the individual with a high fitness value as well as accelerating the convergence speed, the paper adopts the adaptive crossover probability. The crossover probability depends on the compared value between fitness values of selected individuals and the average value. The formula is presented as:

$$P=\{\begin{array}{c}{P}_1,f<f_{avg}\\ P_1-\frac{\left(P_1-P_2\right)\left(f-f_{avg}\right)}{f_{max}-f_{avg}},f\ge f_{avg}\end{array}$$

(10)

where $f_{max}$ is the biggest fitness value among the particles; $f_{avg}$ is the average fitness value; $f$ is the bigger fitness value among the two hybrid individuals; $P_1,P_2$ are the range of cross probability.

The step of PSO is modified as follows:

Step 1.1: Randomly initialize the particles including the search position and velocity. Define all PSO algorithm parameters such as inertia weight${\omega }_{max},{\omega }_{min},\omega$, learning factors$c_1,c_2$, swarm size$N$, maximum iterations $t_{max}$, etc.

Step 1.2: Calculate the fitness of each particle using the evaluation function. All the particles are ranked according to the fitness values. In this paper, ITAE is adopted for the performance criteria.

Step 1.3: Update the value of inertia weight using Equation (7).

Step 1.4: Update the $pbest$ particles by comparing each individual fitness value with its experience. The best value among all $pbest$is the$gbest$.

Step 1.5: Divide the particles into part $A$and part$B$according to the selection probability$\delta$. The particles with low fitness presented as part $A$are randomly conducted in the crossover operation. The crossover probability $P$ is calculated with Equation (10). If the crossover probability of two selected particles is above the random value in the range of$\left(0,1\right)$, then, the crossover is performed using Equation (9). Otherwise, the selected particles are copied by the next generation. Part $B$ is undated by the conventional PSO algorithm. The velocity and position of particles are modified according to Equations (5) and (6). The inertia weight is determined by step 1.3.

Step 1.6: After updating all the particles, the iteration number reaching the maximum is judged. If the termination condition of the algorithm is achieved, the latest$gbest$is the optimal controller parameter. Otherwise go back to step 1.2.

The flowchart of the hybrid algorithm is presented in Figure 1.

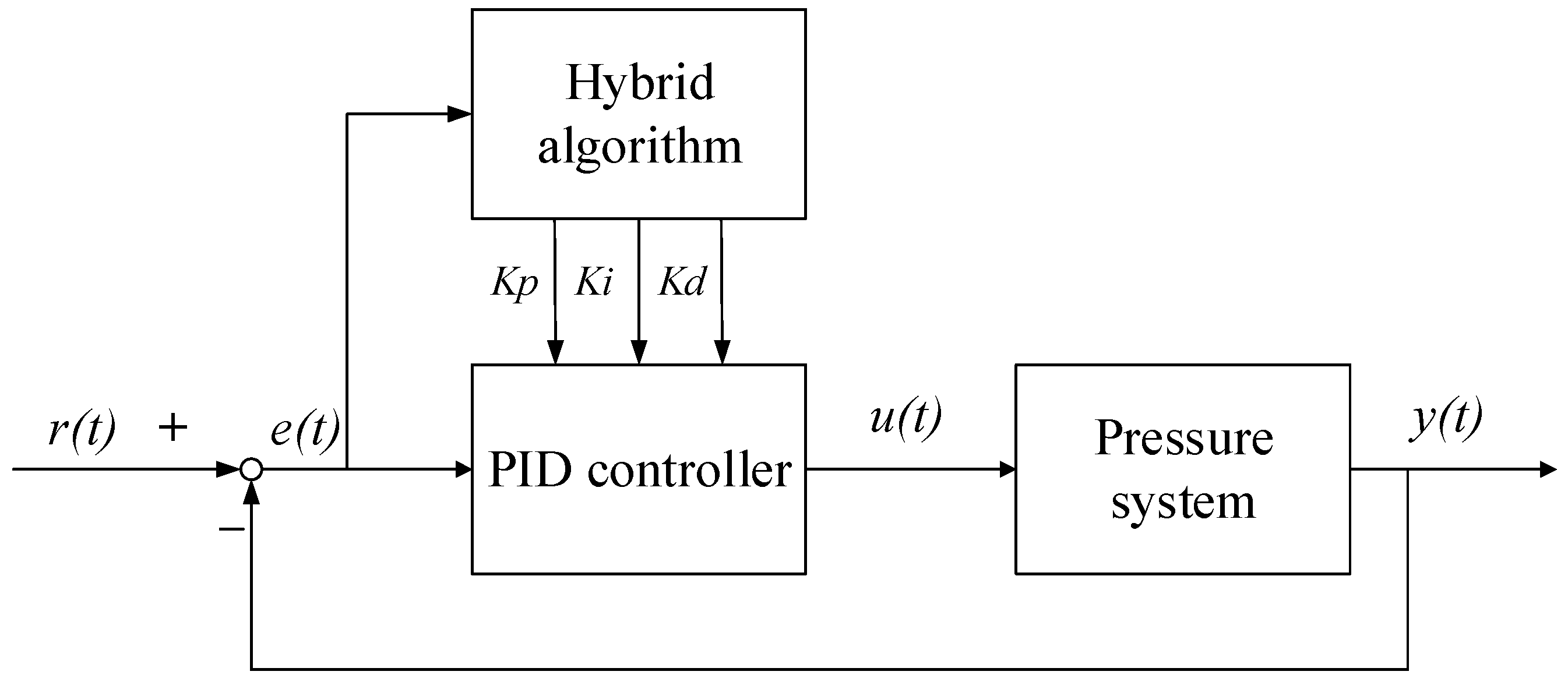
4.2. The Process of Pressure Control on the Hydraulic Cylinder

In order to imitate the actual pressure of the hydraulic cylinder, the proportional overflow valve is utilized to control the pressure. The data, containing the control voltage of the proportional relief valve amplifier and pillar pressure, are collected. The incremental PID controller and hybrid algorithm are applied in the paper. The flow of the control process is shown as follows:

Step 2.1: Acquiring the system transfer function. Before solving the issues with the control strategy, the mathematical model of the controlled project needs to be built. The hydraulic cylinder pressure system is a coupled system with more disturbances. In addition, the leak problem of the hydraulic system is unavoidable. Thus, it is difficult to build the mathematical model through theoretic calculation.

This paper uses the system identification toolbox of MATLAB. Two sets of data are collected during the normal system operation. One set of data is used for system identification, and another is used for detection. Firstly, the data are put into the system identification toolbox. Then, the start time and sampling frequency are set. According to the characteristics of the system, data are preprocessed to eliminate the disturbing signals. The process model is selected under the menu of the estimate. After completing the setting of the pole, zero and delay parameters, the system model is estimated. Finally, the identification result is checked and the fitting rate of data is tested.

Step 2.2: Tuning parameters. Three-parameters tuning is the core content in the PID controller. The coefficients $\left(K_p,K_i,K_d\right)$ are defined as the particles $N$. All the alternatives $K=\left(K_p,K_i,K_d\right)$compose the search space. The above hybrid algorithm is utilized to select the optimal coefficients so as to make the output values meet the terminal condition. Figure 2 illustrates the PID controller design using the hybrid algorithm with PSO and GA.

Step 2.3: Terminal condition. If the iteration number reaches$t_{max}$, terminate the iterative process. Otherwise, continue the optimization.

5. Simulation and Analysis

Since the hydraulic support electro-hydraulic control system (HSEHCS) serves as the crucial device of the hydraulic support, its property needs to be tested by a platform. This test platform contains a supervision system and a hydraulic support analog system. Specifically, the HSEHCS consists of the hydraulic support controllers, multi- function hydraulic oil sources, control console, electrical control cabinets and Win-CC monitoring host. The distribution of the HSEHCS is shown in Figure 3.

The pillar is an important part of the hydraulic support; the motoring and adjustment of the pillar pressure directly affect the entire work statement of the hydraulic support. As the pressure of the pillar was one of the most important data for the HSEHCS, the pressure control strategy of the pillar cylinder was investigated in this paper. In the HSEHCS test platform, S7-300 PLC was the core hardware of the control system located in electrical control cabinets. The Win-CC upper computer communicated with the programmable logic controller (PLC) via a transmission control protocol/internet protocol (TCP/IP) channel unit. The multi-function hydraulic oil source output flow and outlet pressure were controlled through the man–machine interface. Meanwhile, the distributed input/output (I/O) modules in the electric control box were arranged to control the pillar pressure. The overflow pressure of the proportional overflow valve was controlled in order to change the back-pressure of the hydraulic cylinder of the HSEHCS test platform. The above hybrid algorithm for the PID controller was employed to control the overflow pressure with the purpose of imitating the actual pillar pressure.

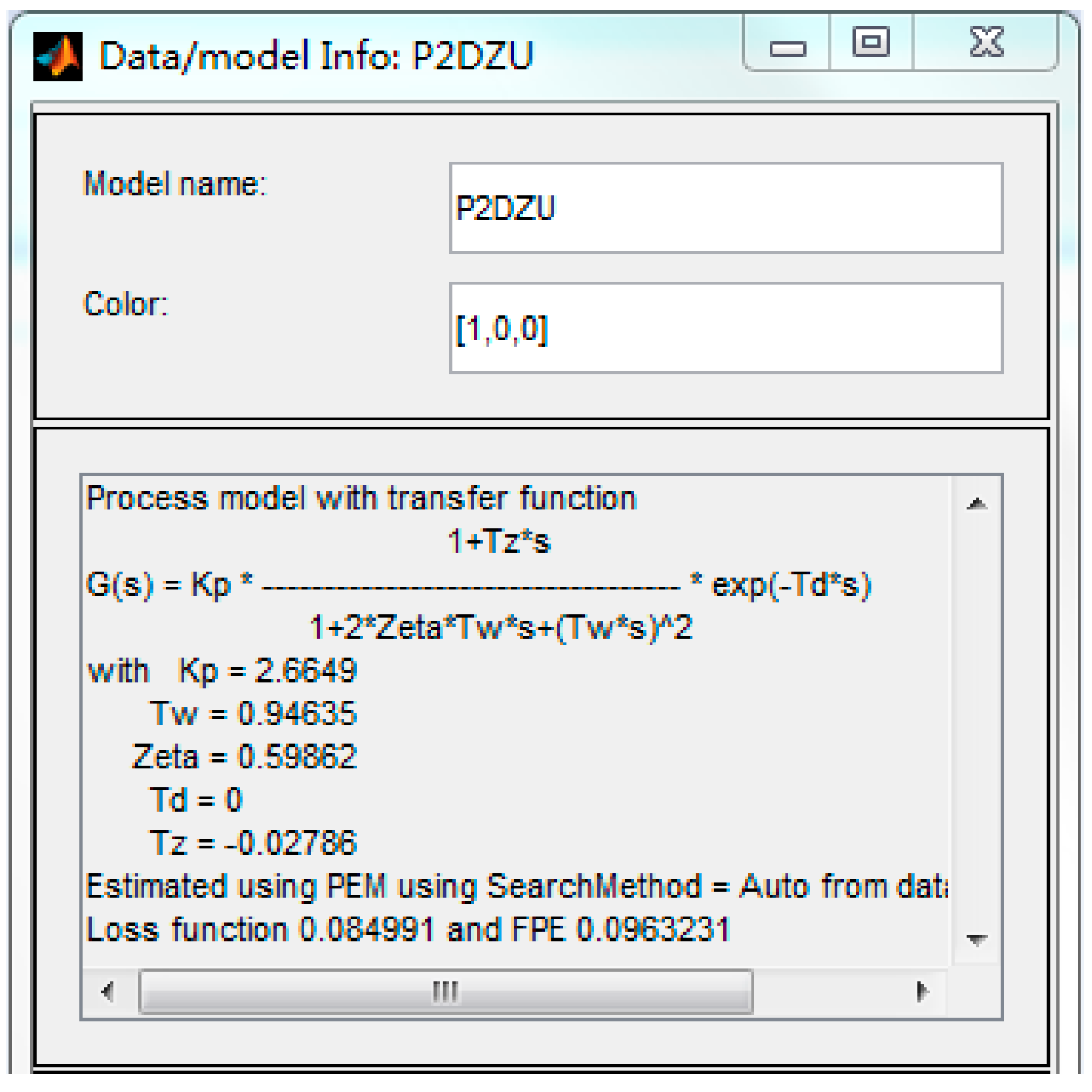
5.1. Acquiring the System Transfer Function

After collecting the data of the control voltage of the proportional relief valve amplifier and pillar pressure in the time domain, the system transfer function was acquired through the above step 2.1 in Section 4. The result of the system identification was shown in Figure 4. The best fit was 94.56% and the system model can be represented as:

$$G\left(s\right)=K_p\times \frac{1+T_z\times s}{1+2\times Zeta\times T_w\times s+{\left(T_w\times s\right)}^2}exp\left(-T_d\times s\right)$$

(11)

where $K_p=2.6649,T_w=0.94635,Zeta=0.59862,T_d=0,T_i=-0.02786$.

After the compilation of the above equation, the mathematical model of the system was described as:

$$G\left(s\right)=\frac{2.6649-0.0742s}{0.8956s^2+1.133s+1}$$

(12)

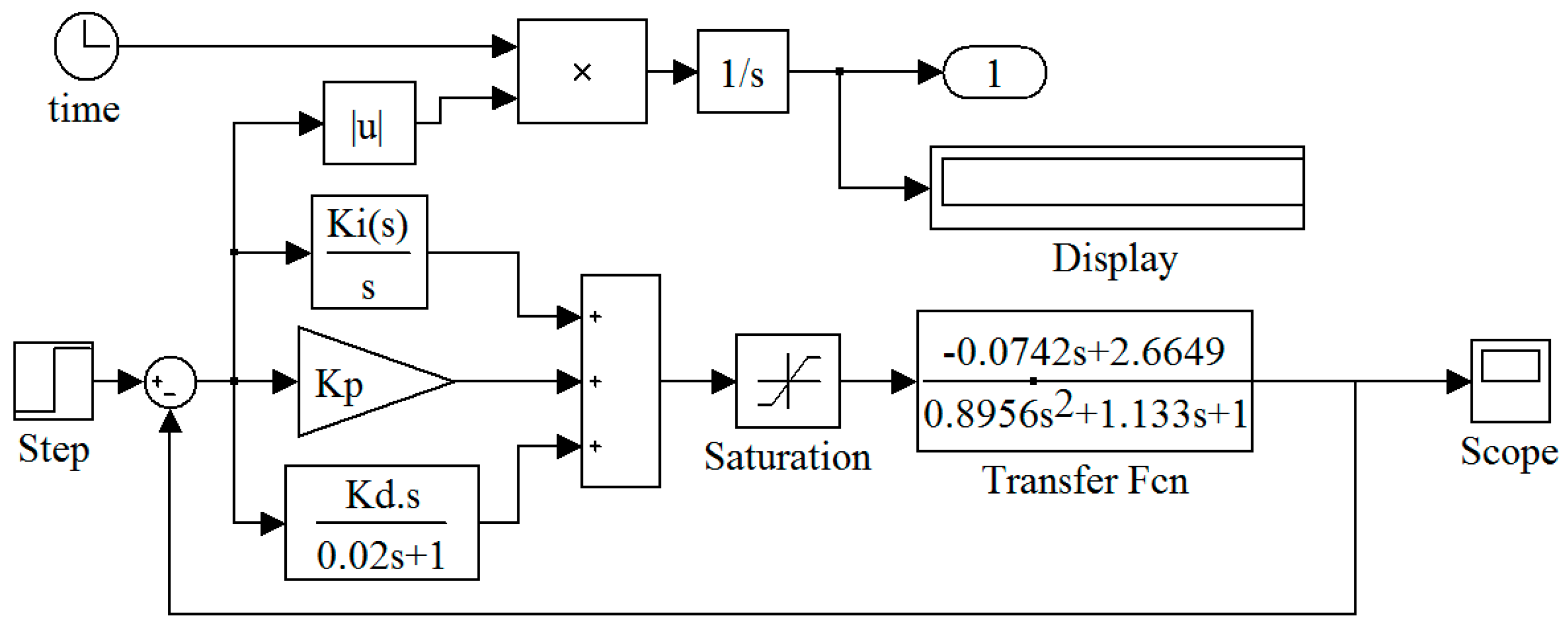
5.2. Parameters Setting and Simulation

According to the achieved mathematical model of the system, the model (Figure 5) was built in the Simulink software. In order to validate the superiority of the proposed method, the conventional tuning method Z-N, PSO, and improved PSO were applied in the PID controller to compare the simulation results. The improved PSO algorithm referred to three types: the inertia weight of PSO is linearly changed (WPSO); a hybrid algorithm combining GA, PSO and the cross probability is stable (SPSO) and a hybrid algorithm combining GA, PSO and the cross probability is adaptive (APSO). In the conventional PID controller, three parameters were determined: $K_p=40,K_i=0.4,K_d=4.5$, by constant adjustments and examinations,

Under the same parameters, simulations by the above methods were performed to compare the convergence characteristics. In the PSO algorithm, the parameters were set as follows:

Inertia weight$\omega =0.6$, learning factors $c_1=c_2=2$, search dimension$D=3$, swarm size $N=100$, maximum iteration $t_{max}=100$.

In the WPSO, the bound of inertia weight was set as${\omega }_{max}=0.9,{\omega }_{min}=\mathrm{0.4.}$; the inertia value was calculated with Equation (7) at each iteration. Other parameters were the same with the PSO algorithm.

In the SPSO, the stable crossover probability was set as $P=0.6$, the selection probability $\mathsf{\delta }=0.3,;$other parameters were the same with the WPSO algorithm.

In the APSO, the bound of crossover probability was set as$P_1=0.9,P_2=\mathrm{0.6.}$; other parameters were the same with the SPSO algorithm.

After setting the parameters, the steady state time, overshoot, fitness value, convergence iteration, running time and the PID parameters for the five optimization methods were illustrated in

Table 1. Simulation results using Ziegler–Nichols (Z-N), particle swarm algorithm (PSO), linearly changed weight for particle swarm algorithm (WPSO), stable cross probability for particle swarm algorithm (SPSO), adaptively cross probability for particle swarm algorithm (APSO).

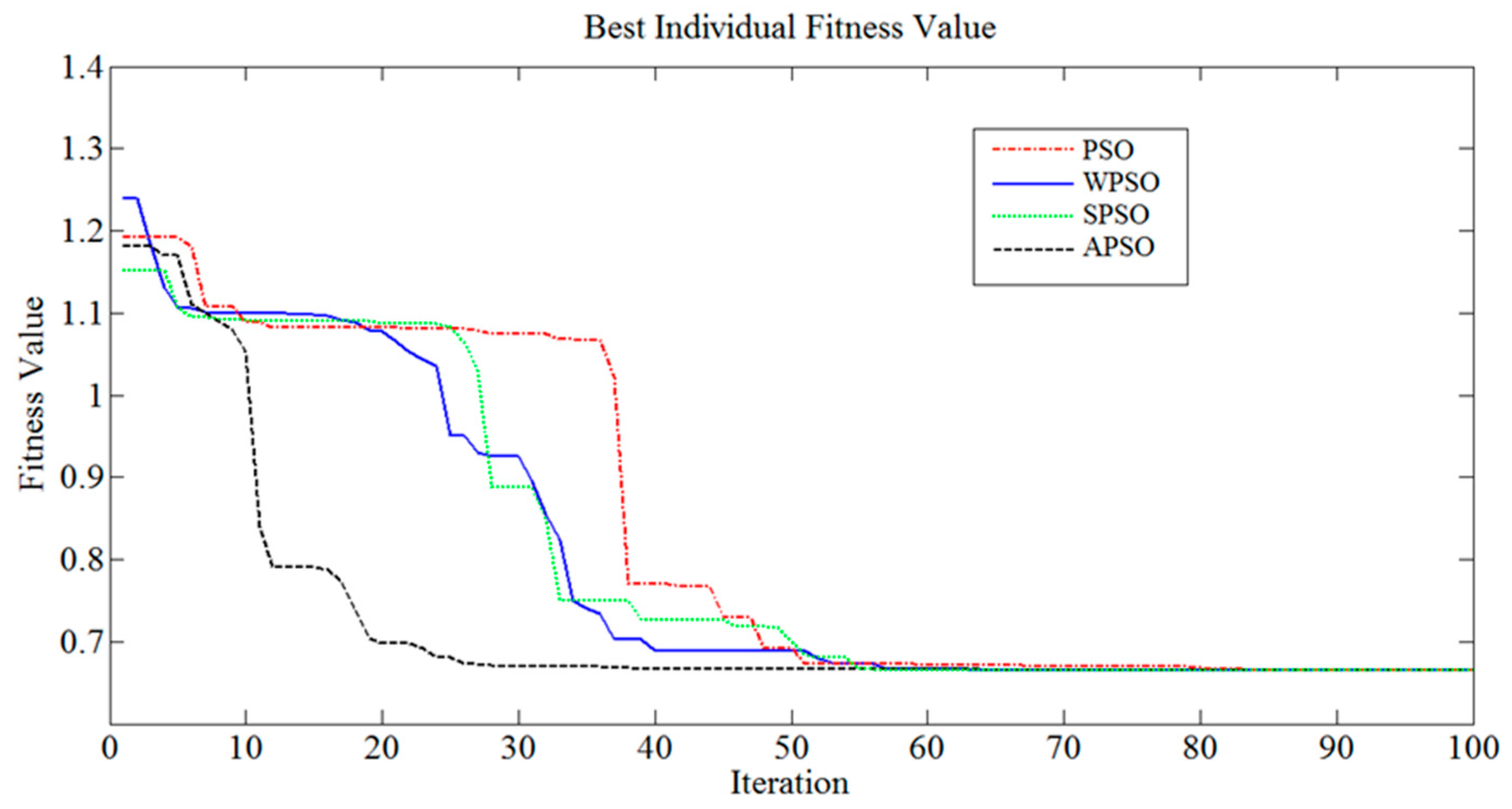
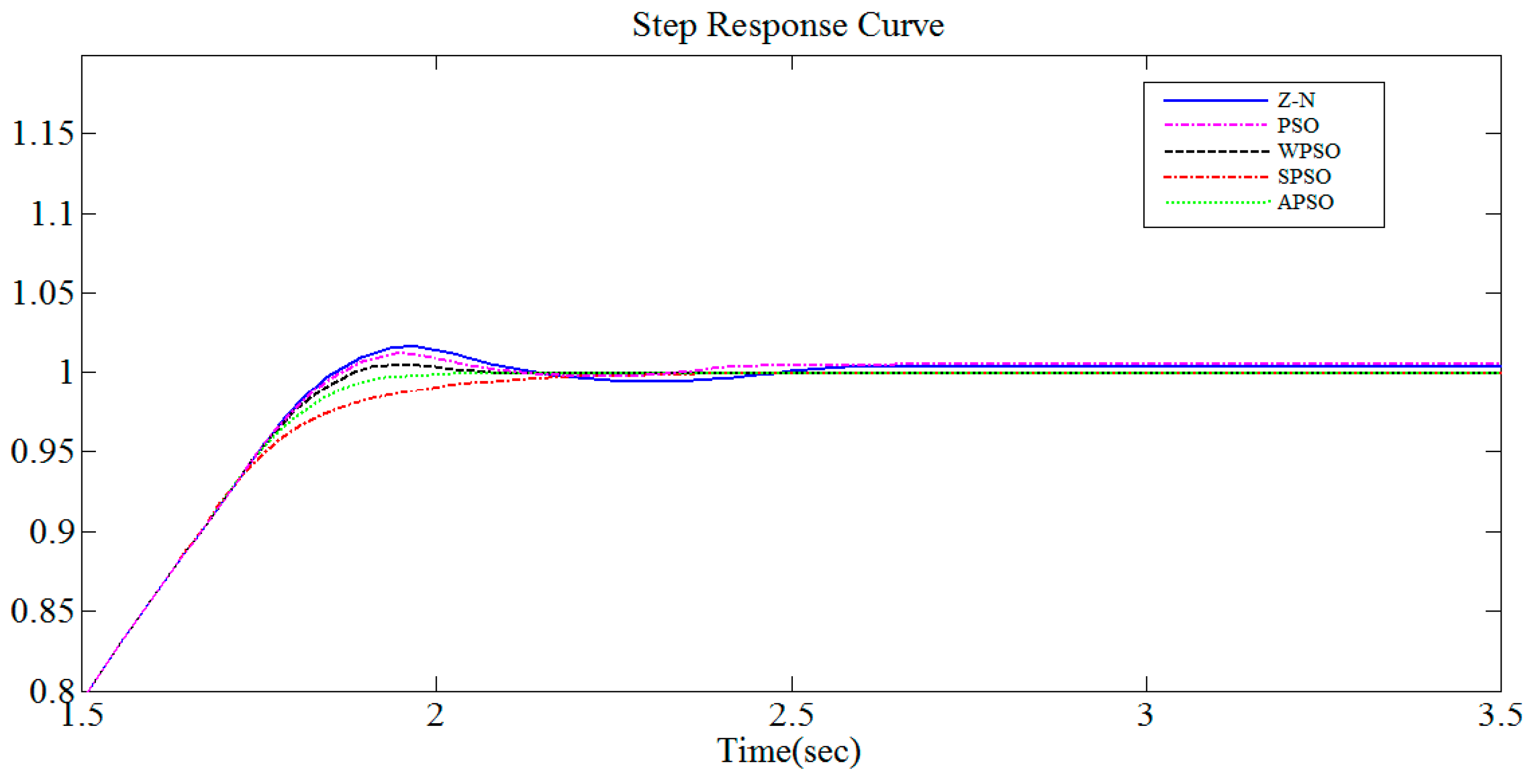
Tuning Method	${\mathit{K}}_{\mathit{p}}$	${\mathit{K}}_{\mathit{i}}$	${\mathbf{K}}_{\mathit{d}}$	Convergence Iteration	Overshoot (%)	Steady State Time (sec)	Running Time (sec)
Z–N	40	0.5	4.5	——	1.64	3.0294	——
PSO	31.3072	0.3540	3.5556	82	1.12	2.6472	12.16
WPSO	29.4390	0.3540	4.2422	60	0.52	2.4286	12.57
SPSO	25.7658	0.3540	4.2677	56	0	2.8785	13.83
APSO	22.3045	0.3523	3.4870	40	0	2.3192	16.78

. Figure 6 showed the fitness curves of simulations and Figure 7 was the partial enlarged view of the response curves derived from the step input. From Table 1 and Figure 7, it was easy to find that the steady state time of APSO was the shortest. In addition, the system overshoots of APSO decreased 164% while the steady state time reduced 23.4% compared with the Z–N tuning method. The dynamic characteristic was improved by APSO. From Figure 6, the response curve of APSO declined most quickly. Thus, the convergence velocity of APSO was obviously the fastest compared with other methods. Furthermore, the convergence iteration of APSO was at 40 iteration and far smaller than the 82 iteration in the case of PSO. From the response and convergence curves, the proposed method not only avoided the premature convergence but also accelerated the convergence velocity. Due to the complexity of the hybrid algorithm, the running time was 38% longer than PSO. However, with the improvement of computer configuration, the running time can be further reduced. In conclusion, the simulation results showed that the APSO algorithm conducted efficient performance on the parameters’ optimization of the PID controller compared with Z-N, PSO, WPSO and SPSO.

6. Conclusions

In order to imitate the actual pressure of the hydraulic support, a hybrid algorithm with PSO and GA was proposed to optimize the PID controller. The data of the control voltage of the proportional relief valve amplifier and pillar pressure were collected to acquire the system transfer function using the system identification toolbox of MATLAB. The selection and crossover operations were introduced into the PSO algorithm to avoid the local optimization and to improve the convergence velocity. Several simulations with different methods were performed to compare the optimization capacity. Finally, the experiment on the HSEHCE test platform was conducted to validate the efficiency of the proposed method. The simulation and experiment results showed that the APSO algorithm for the PID controller can acquire better steady-state and dynamic response characteristics as well as satisfy the control requirements of the HSEHCS test platform.

However, there are also some limitations and bugs in this paper listed as follows: (1) parameter selections for the hybrid algorithm rely on extensive simulations; (2) the optimization process takes a long time and the real-time control has response delay in the pressure system; (3) the proposed method is not applied to other industrial fields to demonstrate its superiority. In future research, the authors will focus on improving the algorithm further to increase the optimization time. More effective methods will be introduced to enhance the intelligence of the pressure control system, such as adaptively setting the parameter, faster response and better applications in other fields.