Machine Learning: A Crucial Tool for Sensor Design

Abstract

Sensors have been widely used for disease diagnosis, environmental quality monitoring, food quality control, industrial process analysis and control, and other related fields. As a key tool for sensor data analysis, machine learning is becoming a core part of novel sensor design. Dividing a complete machine learning process into three steps: data pre-treatment, feature extraction and dimension reduction, and system modeling, this paper provides a review of the methods that are widely used for each step. For each method, the principles and the key issues that affect modeling results are discussed. After reviewing the potential problems in machine learning processes, this paper gives a summary of current algorithms in this field and provides some feasible directions for future studies.

1. Introduction

Sensors have been applied to a variety of fields such as environmental quality monitoring [1], non-invasive disease diagnosis [2], food quality control [3], and industrial process analysis [4], because of the following advantages: (1) ability to function in a harsh environment, (2) ability to operate continuously and automatically, and (3) high accuracy and sensitivity. In general, developing a sensor depends on two major components: analytical instruments and data analysis techniques. Novel analytical instruments allow producing a great amount of information (data) and also permit the exploration of new fields.

However, these generated sensor data may contain irrelevant information and moreover the principles of the new fields could be very complex and even totally unknown, so reliable sensor systems are becoming increasingly reliant on sophisticated data processing techniques.

Figure 1. Flowchart of a machine learning process for electric sensor systems.

Figure 1. Flowchart of a machine learning process for electric sensor systems.

As a powerful tool for advanced data processing, machine learning has become a core technique for novel sensor development, aiming to discover the hidden rules that control complex systems. As shown in Figure 1, a complete machine learning process is composed of three steps: data pre-processing, feature extraction and dimension reduction, and system modeling. Data pre-processing comprises noise filtering, data normalization, signal alignment, and other related data treatments. Sensor signals are usually composed of a large number of variables, so in the second step feature extracting methods are used to transfer sensor signals from their original high dimensional space to a low dimensional feature space or to select “representative” (pertinent) variables to characterize an entire system. Given a good feature expression, the last step of machine learning is to establish system models either for classification problems such as pollutant detection and disease diagnosis or quantitative estimation problems like chemical concentration prediction.

Any of these three steps can play a key role in controlling machine learning effects. There have been some good review papers and books about pattern recognition techniques for either general industrial applications or specific fields like food science [5, 6]. This paper will provide a review of the algorithms that are currently used in each step, compare their individual properties, and discuss future perspectives of machine learning methods for sensor development, covering the applications to both classification and quantitative estimation.

2. Data Preprocessing

Data pre-treatment is important and also the first step for establishing a machine learning model, as raw sensor signals usually (even unavoidably) have some problems that could be harmful for modeling effects.

2.1 Noise Removal

Noise removal is a basic procedure for signal enhancement. Many sensor signals are composed of time series data, so a variety of digital signal processing and time series analysis techniques have been applied for signal enhancement. Different from Fourier analysis which only focuses on frequency domain, wavelet analysis examines data in both time and frequency domains. It has become a powerful noise filtering method, decomposing original signal into low and high frequency domains [7]. The high frequency domain contains more noise information from the original data, so modifying the wavelet coefficients in the high frequency domain by setting up a threshold is a simple but effective method for sensor signal enhancement [8]. Auto-regressive (AR) analysis is another noise filtering technique, generating AR coefficients to represent and reconstruct original signal. It has been successfully used for chromatographic signal enhancement [9, 10].

2.2 Baseline Removal

Baseline removal is another important pre-treatment for signal enhancement. A conventional baseline removal process for spectral or time series data consists of three major steps [11]: (1) to determine baseline key points in spectrum, (2) to build a baseline model for the whole spectrum using the detected baseline points, and (3) to correct the signal by subtracting the baseline from original signal. Recently, some new algorithms have been developed, such as an adaptive learning algorithm for electrocardiogram (ECG) baseline removal [12] and a selective filter for ECG baseline correction [13].

2.3 Signal Alignment

Signal shifting is a potential problem for data series. Chromatography/spectral instrument based sensors are a typical place where this problem often occurs. It is no doubt that shifted signals can result in a failure of sensor analysis. In general, for chromatography data, time alignment begins with locating the peaks that correspond to the same chemicals in a selected template chromatography profile. Then, after getting these peaks aligned, a linear or nonlinear interpolation process is applied for chromatography profile registration. Spline functions are an efficient nonlinear interpolation method [14]. Figure 2 shows a significant improvement on the separation of two groups of gas chromatography mass spectrometry (GC/MS) data before and after time alignment process [14], by employing a clustering tool called principal component analysis. The details of this tool will be discussed in the next section. As an extension of one-dimensional alignment, two dimensional alignment can be applied to the three dimensional spectral data, such as gas chromatography differential mobility spectrometry (GC/DMS) data [15].

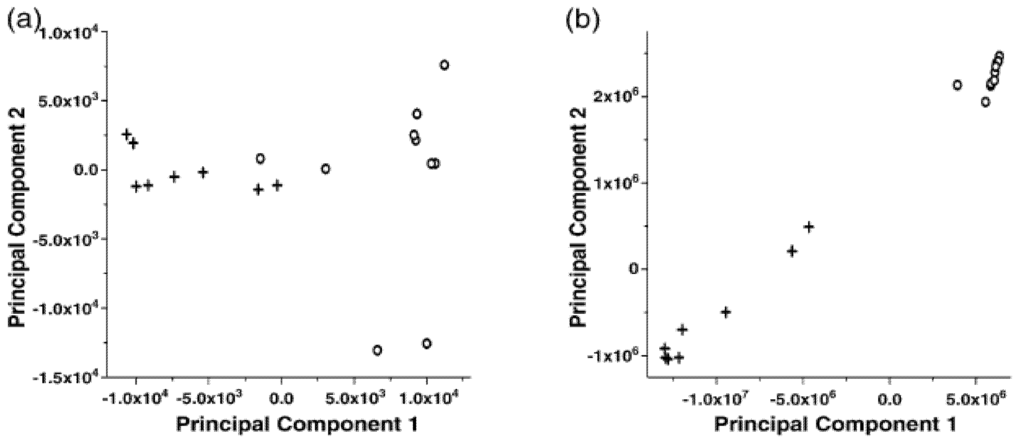
Figure 2. Principal component analysis of total ion chromatograms resulting from GC–MS analysis of headspace above plasma samples from two donors (Donor A: +, Donor B: o). (a) before and (b) after alignment.

Figure 2. Principal component analysis of total ion chromatograms resulting from GC–MS analysis of headspace above plasma samples from two donors (Donor A: +, Donor B: o). (a) before and (b) after alignment.

2.4 Outlier Detection

To have a reliable and automated sensor system, data pre-treatment also needs to detect possible outliers that could influence modeling effects. Unlike noise, an outlier is an observation that disobeys the distribution of the rest of the data [16]. Outliers can also be called “questionable data”, “strange points”, or “doubtable observations”, and are often caused by confounding system mechanisms or instrument error [17]. Outliers may cause damage to a modeling system to which they do not belong, so a broad range of techniques have been applied for outlier detection. Statistical analysis methods are widely used to detect outliers in linear systems, estimating the standardized residual of each observation in the regression model [17, 18]. Self-organizing map (SOM) was introduced to detect outliers in nonlinear systems, based on the distance between data points [19]. However, in some cases, distance is not a proper criterion for outlier verification, because some normal data may deviate more from the majority of the data than outliers, especially for highly nonlinear systems. A method integrating a linear outlier detection strategy with radial basis function neural networks (RBFNN) was proposed to detect outliers in complex nonlinear systems [20]. Outliers are not noise, so simply excluding outliers from analysis may be not beneficial to the discovery of the hidden mechanisms and rules.

2.5 Data Normalization

Normalization usually is the final step for data pre-treatment. In terms of data characteristics, this step can be divided into local normalization and global normalization. A typical local normalization process is unit scaling, which is widely used for spectral data. The similarity of two spectral samples is represented by the dot product of their unit spectral vectors. Global normalization aims to make sensor variables comparable, preventing some variables with lower magnitudes from being overwhelmed by others with higher magnitudes. However, in some cases, global optimization can amplify the noise or the information of irrelevant sensor variables, which might be harmful for modeling.

3. Feature extraction and dimension reduction

The development of novel instruments has produced sensors that generate data with extremely high dimensions, which provides an opportunity to carry out an extensive system investigation. However, analyzing these copious amounts of data depends on sophisticated techniques to extract pertinent features from original data. Generally, feature extraction and dimension reduction aim to create a map from a high dimensional space to a low dimensional space $f:R^m\to R^n(n<<m)$. This step not only unloads heavy computational burdens from the subsequent system modeling step but also excludes irrelevant and noise signals from analysis.

3.1 Traditional multivariate analysis methods

Multivariate statistical analysis is a very efficient strategy for feature extraction. Principal component analysis (PCA) is the most widely used method for this purpose. PCA is a linear transformation that transforms original data to a new coordinate system where the greatest variance of the data lies on the first coordinate (called the first principal component), the second greatest variance on the second coordinate, and so forth. In other words, PCA is an eigenvector-based multivariate analysis method, providing a map from an original data space to a new space with much lower dimensions [21]. With the abilities to remove co-linearity in variables, condense information of original data, and enhance signal quality, PCA has been extensively applied for sensor signal analysis such as fungal growth detection in bakery products [22], olive oil discrimination [23], and environmental quality monitoring [24]. As extension of PCA, independent component analysis (ICA) is another effective feature extraction method, extracting statistically independent components from original data space [25, 26]. Different from PCA that solely de-correlates the data, ICA has obtained great applications to sensor design [27, 28].

Linear discrimination analysis (LDA) and partial least square regression (PLSR) are also widely used as statistical feature extraction methods for sensor development [29, 30]. Different from PCA, the extractions based on LDA and PLSR are embedded in a classification or regression process that requires both independent data X and dependent data Y. The principles of these two methods will be discussed in the following “System modeling” section.

Positive matrix factorization is another important feature extraction method, especially in the cases where the generated “loading” and “score” matrixes should only have positive values to ensure their physical meanings. A positive matrix factorization (PMF) method based on least square regression has been extensively applied to air quality analysis and control [31, 32, 33], with potential applications to a variety of environmental sensor design.

3.2 Digital signal processing based methods

In many cases, sensor output signal is a time series, such as a chromatogram, or an image, such as mass spectrometry – mass spectrometry (MS/MS) data, so digital signal processing and time series analysis have become powerful feature extraction methods for sensor signals.

3.2.1 Wavelet analysis

In contrast to the traditional fast Fourier transformation, wavelet analysis is able to examine the signal simultaneously in both time and frequency domains, so it is an excellent tool to analyze non-periodic, noisy, and intermittent signals and has spawned a number of wavelet-based methods for signal analysis and interrogation [7]. Basically, wavelet transformation aims to represent an arbitrary function by superposing a group of wavelets which are generated from a mother wavelet Ψ through dilations and translations. A wavelet function generated at scale a and location b can be described as,

$${\Psi }_{a,b}(x)=\frac{1}{\sqrt{a}}\Psi \left(\frac{x-b}{a}\right)$$

(1)

Proposed by Mallet for digital signal processing, wavelet analysis was substantially developed for various application fields after Daubechies constructed a set of wavelet orthonormal basis functions [34, 35]. In a recent study of sensor selection for machine olfaction design [36], discrete wavelet transformation not only significantly reduced the number of sensor variables but also yielded an almost 100% accuracy for the classification of two types of odor (coffee and soda). Wavelet transformation coupled with artificial neural networks was also successfully used for electronic tongue design [37] and environmental variable monitoring [38]. To ensure the feature extraction effect of wavelet analysis, a couple of things should be taken into account including wavelet type and decomposition level. The coefficients of an overly-deep decomposition level might not have enough signal information, while those of a low decomposition level may still contain much noise. Determining how many levels of wavelet coefficients are needed and whether the coefficients in both low and high frequency domains are useful is case-dependent.

3.2.2 Auto-regressive modeling

Auto-regressive (AR) analysis is an efficient feature extraction tool for time series data, widely used for speech analysis [39, 40]. As an all pole model (filter), a p-order AR model can be expressed as:

$$x_n=a_0+{\displaystyle \sum _{i=1}^p{a}_i{x}_{n-i}}+{\epsilon }_n$$

(2)

where x is time series data, a_i (i=1, … ,p) are AR coefficients, a₀ is a constant, and ${\epsilon }_n$ is an error estimate. Briefly, using AR coefficients, we can represent the nth value x_n with its previous p values: x_n-1, x_n-2, … , x_n-p. The goal of an AR model is to estimate the AR coefficients that can fit the original data series as closely as possible through an optimization process.

AR coefficients systematically characterize a changing trend in the data series, so in addition to the common effects of signal treatment, such as noise removal and dimension reduction, the AR model shows its significant advantage in dealing with mild signal shifts in the time series (such as chromatograph data). AR modeling can permit us to directly work on time shifted chromatograph data without using time alignment as a preprocessing step. This advantage has recently been proven in a GC/MS based sensor design for bacterial identification [41].

3.3 Feature subset selection

The output of sensor array or even a single sensor can be composed of a high dimensional vector, with each element representing a physical variable or a chemical compound. However, it is very likely that only some of these variables contain pertinent information, so feature subset selection not only reduces signal dimension but also excludes irrelevant variables from system modeling. More importantly, the selected feature subset can provide the most direct and pertinent information for system analysis. For example, detecting biomarkers from the signals of a biosensor designed for disease diagnosis can provide the kernel information for pathology research.

In general, selecting a feature subset is an optimization problem which aims to find a subset that can yield an optimal solution such as the highest classification accuracy. Because the objective function could be represented by nontraditional models like neural network models, stochastic optimization methods such as genetic algorithms [42], differential evolution [43], and simulated annealing [44] are popularly used in this aspect.

3.3.1 Genetic algorithm (GA)

GA is a powerful optimization method that mimics natural evolution principles, consisting of three major operators: selection, crossover, and mutation [45, 46]. By employing an objective function constructed by selected variables, GA attempts to provide an optimal feature subset. In this optimization problem, a binary vector indicating which variables are selected into the feature subset is used as chromosome for the evolution process in GA and the objective function represented by classification or predication accuracy is used as a fitness function to evaluate chromosome quality.

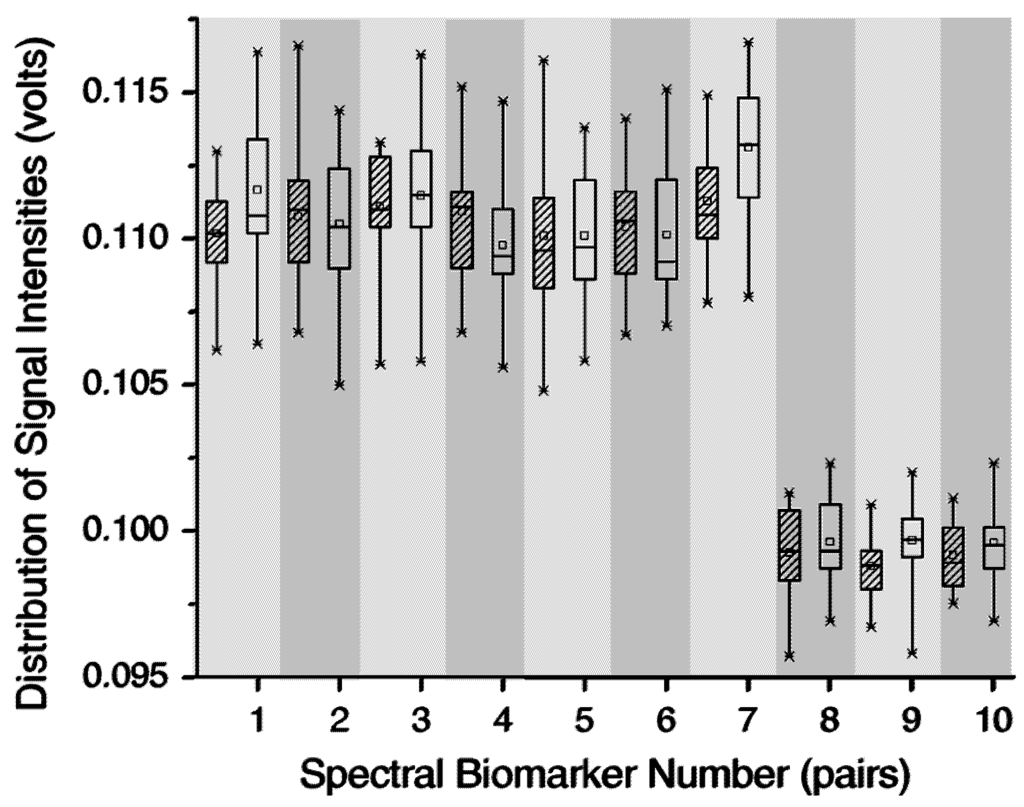
Figure 3. Amplitude distributions between pairs of 10 detected biomarkers that distinguish T4 bacteriophage (blank box) from Bovine serum albumin protein (shaded box).

Figure 3. Amplitude distributions between pairs of 10 detected biomarkers that distinguish T4 bacteriophage (blank box) from Bovine serum albumin protein (shaded box).

Figure 3 shows 10 biomarkers that were detected by GA to differentiate protein and virus from the output signals of a gas chromatography differential mobility spectrometry (GC/DMS) based sensor [47]. Using a PCA and neural network integrated classification model, these 10 biomarkers yielded 94% classification accuracy. The GA- driven feature subset selection approach was also applied for DMS based bacterial identification and Bacillus spore detection [48, 49] and MS based electric nose design [50]. Although GA can theoretically provide a global optimal solution, for a high dimensional optimization problem, GA is very likely to fall into local optima, which usually indicates a premature solution. It is therefore a key issue to define proper cross-over and mutation rates, although it can be difficult in some cases.

3.3.2 Differential evolution (DE)

DE is a novel parallel optimal searching method proposed in the mid-1990s [43]. The main concept of DE is a scheme to generate population vectors. Basically, DE employs three population vectors to generate a new population vector. The weighted difference between two selected population vectors is added to the third vector, which is then crossed-over with the target vector g to generate a new vector v. If v has a better quality than g, it will replace g for the next generation, otherwise, v will be discarded and g will survive [51]. This “family” generation process is different from that of GA, where two randomly selected members are used to generate a member for the next generation.

Using a probabilistic neural network (PNN) model as the cost function, DE was applied for the wavelength selection to develop a surface acoustic wave sensor for food quality monitoring [51]. In this study, a comparison between the results of DE and GA shows that although both methods significantly reduced data dimensions by 50%, DE achieved a better average performance than GA, reaching the minimal misclassification rate of 0.0175.

3.3.3 Simulated annealing (SA)

Simulated annealing (SA) is another global searching approach motivated by statistical thermodynamics [44]. During an optimization process, SA algorithms replace the current solution with a random neighbor solution based on a probability p which is a function of current “annealing” temperature (T). This replacement can help prevent searching processes from falling into local optima. SA has been applied to detect “representative” mass spectrometry fragments for an E-nose based food classification [50]. The key for SA is to establish a proper “annealing” temperature (T) decrease function. In some cases, it could be challenging to design a proper decreasing process of T and also SA could require prohibitively long periods of time to follow this process.

4. System modeling

With the data preprocessing and feature extraction steps done, a machine learning process is moving to the final step, a real learning process called system modeling. In terms of learning strategies, the learning processes can be divided into two categories, supervised leaning and unsupervised learning.

4.1 Supervised learning methods

Assuming the sensor output signals of the analyzed samples are X and the corresponding information (e.g., class memberships or chemical concentrations) are Y, supervised learning process aims to establish a function f: Y = f(X) to describe the relationship between X and Y and make a prediction for a new sample. Most supervised learning methods can be used for both classification problems like vapor identification and quantitative estimation problems like vapor concentration prediction, while some can be used only for classification problems.

4.1.1 Principal component regression (PCR)

As a simple machine learning method, least square (LS) regression is the most popular method to create a map from independent variables X to dependent variables Y. The major problems for ordinary LS methods are that (1) the sample number must be equal to or larger than the number of model parameters (i.e., the number of independent variables) and (2) possible co-linearity in the independent variables could result in the ill-condition of a regression matrix and eventually lead to an unreliable solution. One feasible way to solve these problems is to create a regression model based on principal components, called PCR [21]. Thus, the regressors are decorrelated and the number of regressors is also significantly reduced. However, the extraction of principal components is solely reliant on the independent variables (sensor signals), so the direction of maximal variance in PCA is not related with the dependent variables, which usually results in the modeling effect of PCR being a little poorer than the effect of a model to be discussed next.

4.1.2 Partial least square regression (PLSR)

PLSR is another modified LSR, extracting uncorrelated latent variables from the original data. The difference between PLSR and PCR is the extraction of latent variables in PLSR not only employs independent variables X but also take into account dependent variables Y.

A general linear model is $Y=XB+E$, where B is the regression coefficients and E is the residual matrix. PLSR generates a transforming matrix W to transform X to T ($T=XW$, called score matrix or PLS components). Let Λ = WB, then the PLS regression model turns to be Y = TΛ + E. Thus, the regression of X against Y becomes the regression of PLS components T against Y. One standard PLS algorithm is nonlinear iterative partial least squares (NIPALS). The details of this algorithm are discussed in the literature [52].

Both PCR and PLSR were designed for quantitative estimation problems and classification problems as well. As an effective linear function approximation tool, PLSR has been widely applied to E-nose design [53, 54, 55].

4.1.3 Linear discrimination analysis (LDA)

LDA is a linear classifier that expects to find the best separating line or plane between two groups of samples. Figure 4 shows a schematic LDA based separation of two groups. Assuming a sensor output vector is x, a general equation for LDA can be expressed as:

$$f(x)=w^{T}x+w_0$$

(3)

where w is a weight vector and w₀ is a constant (threshold value). The decision rule for a two-class problem is based on the positivity or negativity of the function value of f(x).

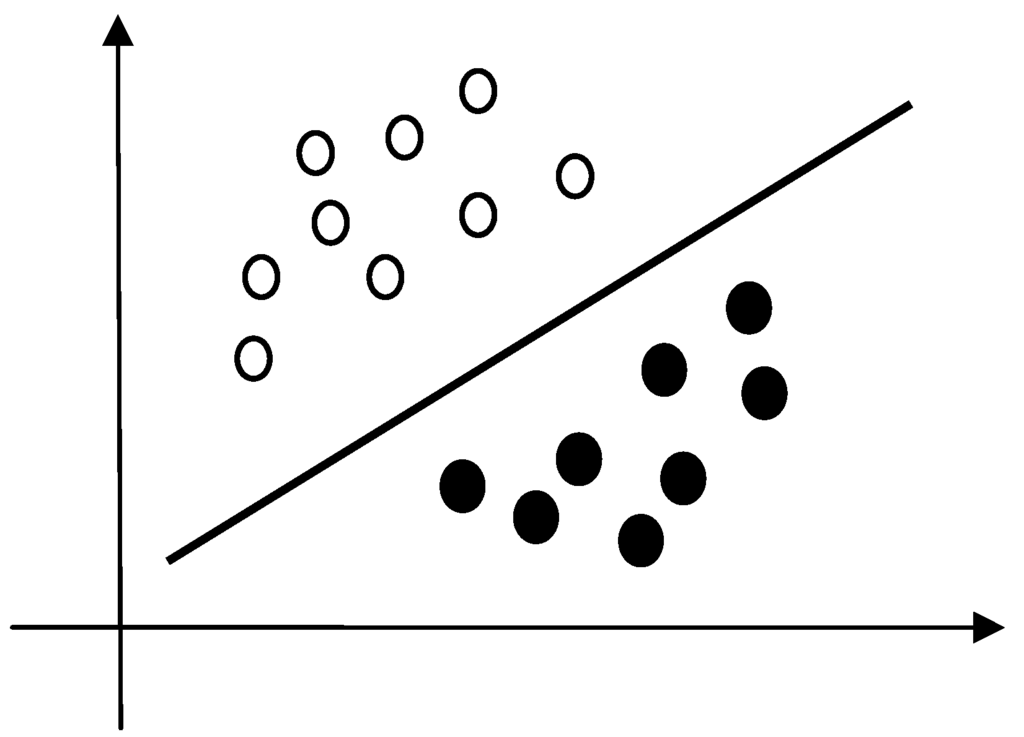
Figure 4. A schematic illustration of a two-class linear separation.

Figure 4. A schematic illustration of a two-class linear separation.

The key for designing a LDA classifier is to obtain the best separation line or plane (i.e., the best w and w₀) from the training samples. Fisher discrimination [56] is the most canonical strategy for finding the best parameters w and w₀. Given the between- and within-covariance matrices ($S_B$ and $S_W$) of two sample groups, Fisher discrimination is to maximize the ratio of the between-to-within variability through the following optimization problem.

$$\max J(w)=\frac{w^T{S}_{B}w}{w^T{S}_{W}w}$$

(4)

The above classification strategy can be extended to a multiple-class separation problem. Stepwise linear discrimination functions are a feasible tool for such an extension. LDA has also been extensively used in E-nose applications such as wine classification [57] and green tea grade identification [58].

4.1.4 Bayes classifier

Bayes classifier is a maximal probability rule based classification method, aiming to minimize the “expected risk” caused by misclassification [59]. Assuming there are N classes (1,2,.., N), the posterior probability of class h for sample x is:

$$P(h/x)=\frac{{\lambda }_{h}P(x/h)}{{\displaystyle {\sum }_{j=1}^N{\lambda }_{j}P(x/j)}}$$

(5)

where, ${\lambda }_j$ is the priori probability of class j and $P(x/j)$ is the conditional probability of x given class j. The Bayes decision rule is:

$$x=\underset{h}{\arg \max }\left[P(h/x)\right](h=1,2,\mathrm{...},N)$$

(6)

The priori probability ${\lambda }_h$ can be estimated as the ratio of the number of the samples in Class h to the number of all the samples. In most cases, the conditional probability $P(x/h)$ can be replaced by a continuous probability density function $f(x/h)$ and usually can be estimated by two methods, namely the parametric approach and non-parametric approach [59]. A Bayes classifier based on parametric approach can also be called quadratic discrimination (QD) process while non-parametric approaches generally apply kernel functions to estimate $f(x/h)$.

Bayes classifier was successfully applied to classify the bacterial infections in a hospital environment [59]. In this study, using an adaptive kernel function based probability density function, the Bayes classifier reached an excellent bacterial classification accuracy of 99.8%.

4.1.5 k-nearest neighbors (k-NN)

k-NN is a relatively straightforward pattern recognition method for sensor design [60, 61]. Assuming there are N samples belonging to C classes, in order to classify a new sample, k-NN needs to find k nearest neighbors of this new sample from the N samples based on distance or similarity. Let the k nearest samples be composed of k₁ from class 1, k₂ from class 2, …, and k_C from class C. Thus, the decision rule is:

$$x=\underset{j}{\arg \max }:k_j(j=1,2,\mathrm{...},C)$$

(7)

The new sample belongs to the class that has the most neighbors of this sample. The key parameter for this method is k. A larger value of k could reduce the influence of outlier or noise but could generate clouded class boundaries. Usually small k values (3 or 5) are preferred [6].

The advantages of k-NN are (1) mathematical simplicity and (2) no need for statistical assumptions for sample distribution. However, k-NN may not work well when the sample numbers of each class are not comparable. In such cases, using weighted distance for clustering is a feasible choice. Meanwhile, considering the determination of k could be empirical and arbitrary, an adaptive k-NN was recently proposed to provide a robust categorization result [1], where the categorization of a new sample is not solely based on the number of its neighbors in each class. This adaptive k-NN approach presented a good application in detecting air pollutants with a sensor array [1].

4.1.6 Back-propagation neural network (BPNN)

From this subsection on, the discussion of supervised learning methods will focus on artificial neural network (ANN) models. Some modifications of linear learning methods such as stepwise functions and polynominal regression can be applied for non-linear systems, but they do not work for highly nonlinear modeling problems. Presenting a good mimic of human brain cognition process, ANN has been extensively used for machine learning tasks. A variety of ANN models have been developed for sensor design, but this paper will focus on three most widely used ANN models, since many of others can be considered derivatives of these versions.

BPNN is one of the most widely used neural network models, with extensive applications in function approximation (classification is also a type of function approximation problem). Typically BPNN is composed of three layers: input, hidden, and output. A sigmoid function is a standard nonlinear activation function for each hidden and output neuron. Given the error between the stipulated and predicted results for the kth sample, E_k, the learning process (i.e., the adjusting process for connecting weights) based on the gradient descent algorithm can be represented as:

$$\Delta v=-\alpha \left[\frac{\partial E_k}{\partial v}\right]\mathrm{and}\Delta w=-\beta \left[\frac{\partial E_k}{w}\right]$$

(8)

where, $\alpha$ and $\beta$ are the learning rates, v and w are the connecting weight vectors between hidden and input layers and between output and hidden layers, respectively. This learning process is repeated for all the training samples, which is called one iteration. This iteration process continues until a convergence criterion is reached.

BPNN has been used for developing various E-nose systems including bacterial infected illness diagnosis and warfare agent stimulants classification [62, 63, 64, 65]. A three-layer BPNN with sufficient hidden neurons has proven able to approximate any classification boundaries [66], but a possible over-fitting problem will lead to a failure in the prediction of new samples. A constructive approach for building BPNN could be either starting with a small structure followed by a gradual increase of hidden neurons or using pruning strategies to remove extra hidden neurons from a big initial model structure.

Possible overlong learning time and local optima are two major problems for BPNN. Adaptive learning strategies can help BPNN reach a convergence and jump out of local optima, but designing such a self-adjusting process is empirical and difficult.

4.1.7 Radial basis function neural network (RBFNN)

RBFNN is another widely used neural network model. The basic concept of RBFNN is a radial function-based interpolation process, seeking a function $f\left(x_i\right)=y_i$ to create a map from sample set $\left\{x_i\right\}$ to their corresponding outputs $\left\{y_i\right\}$. The typical structure of RBFN is also a three-layer forward structure. The hidden layer performs a nonlinear transformation to transform the input space into a high dimensional transitional space through radial basis functions. Gaussian kernel functions are a typical choice of radial basis functions.

$$\phi \left(x,c_j\right)=\exp (-{\Vert x-c_j\Vert }^2/{\sigma }_j^2)$$

(9)

where x is a learning sample vector, c_j is the radial basis vector of the jth hidden node, ${\sigma }_j$ is the Gaussian width of the jth hidden node. With the weights connecting the output node and the hidden nodes, the output layer produces a linear summation of all the hidden layer outputs. RBFNN can avoid long training time, performing a one-step learning strategy.

RBFNN was successfully applied for bacteria classification [67], yielding a 98% classification accuracy for six bacteria species. RBFNN was also used to develop sensors for odor classification [68] and fragrance discrimination [69].

The major hindrance of building up an RBFNN model is to estimate the radial basis vectors and their corresponding Gaussian widths. A conventional strategy to determine the radial basis vector is to use K-means algorithm to group training samples into a number of clusters and then use the cluster center vectors as the radial basis vectors [70]. However the possible local optima of K-means algorithm could make the cluster centers unable to correctly reflect the data space distribution. In the early 1990’s, orthogonal least squares (OLS) was introduced to construct RBFNN, using a Gram-Schmidt scheme to select regressors (i.e., radial basis vectors) from the training data [71]. Genetic algorithms were also applied to determine which training samples could be used as radial basis vectors by minimizing the training error [72], but the searching process may take a very long time and can be stuck in local optima. Integrating RBFNN with multivariate analysis methods is another effective strategy for radial basis vector construction [73]. In the RBF-PLSR approach, all the training samples are used as radial basis vectors and then PLSR is applied for the linear regression between the hidden and output layers. This method statistically solves the construction of radial basis vectors and has been used for mass spectrometry calibration [74] and GC/MS based bacterial classification [41].

4.1.8 Support vector machine (SVM)

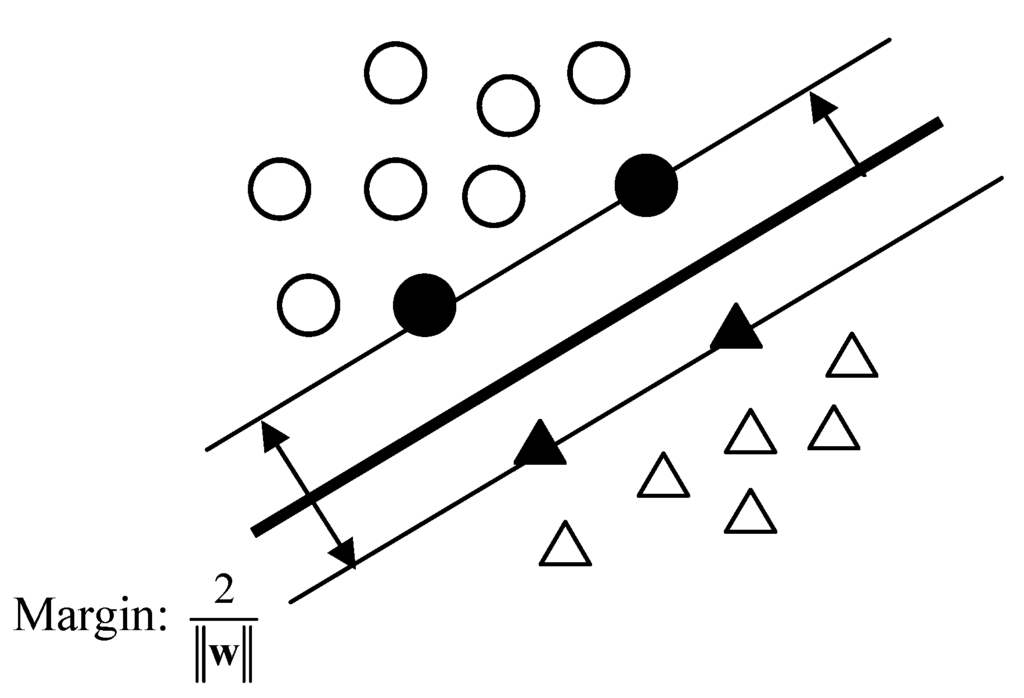
The principle for SVM was proposed in the 1960’s, but extensive studies and applications of SVM began in the 1990’s. Principally SVM is a statistical method, but in many cases it can be categorized in the neural network field, as it has the same structure as RBFNN. In contrast to BPNN which requires defining a number of hidden neurons before training, the structure of SVM is adaptively determined during a learning process. Figure 5 shows a schematic linear classification based on support vectors. The black circles and triangles are the support vectors of two classes, respectively. Basically, SVM is to find a discrimination function as shown in eq. (10), which is the same as LDA, but the calculation of the weight vector is only based on the support vectors.

$$f(x_i)=w^T{x}_i+b$$

(10)

where x_i is a sample vector, w is the weight vector and b is a threshold value.

Assuming support vectors have been determined, the optimal separation plane is the one that can maximize the margin between two classes, which is proved to be $2/\Vert w\Vert$ [75]. Introducing Lagrange multipliers to this quadratic optimization problem can yield,

$$\min :L(w,b,\alpha )=\frac{1}{2}{w}^{T}w-{\displaystyle \sum _i{\alpha }_i\{y_i[w{x}_i+b]-1\}}$$

(11)

Figure 5. Support vectors based classification system.

Figure 5. Support vectors based classification system.

where ${\alpha }_i$ are Lagrange multipliers. The optimal solution is $w^{opt}={\displaystyle \sum _i{\alpha }_i^{opt}{y}_i{x}_i}$. $b^{opt}$ can be easily calculated by any support vector using $w^{opt}$. Support vectors are the samples whose ${\alpha }_i\ne 0$. The separation process can be extended to multiple-class problems.

Using Gaussian kernel functions to transform the original input space to a linear transitional space, the linear separation process of SVM can be easily extended to nonlinear systems. Gaussian kernel functions are also a key issue for RBFNN, so in some cases SVM for nonlinear systems can also be considered as a specific modification of RBFNN where only the support vectors (samples) are used for constructing a classifier.

SVM has obtained successful applications in many fields such as E-nose based vapor detection for environmental monitoring [76] and alcohol identification [77]. Using Gaussian kernel function for signal space transformation, SVM also presents some inherent problems including the determination of a proper Gaussian width for each kernel function.

In addition to the above three ANN models, probability neural network (PNN) is also popularly used for sensor signal analysis. Basically, PNN has the same principle as Bayes classifier. PNN also used kernel functions for signal space transformation, so PNN can be considered another specific modification of RBFNN or a neural network implementation of Bayes classifier. Kernel functions have been also integrated with PLS and PCA to extend the application fields of these two classical machine learning tools from linear problems to nonlinear problems. RBF-PLS discussed above is a typical kernel PLS model.

4.2 Unsupervised learning methods

Unsupervised learning is used to examine how the data are organized. In contrast to supervised learning processes, unsupervised learning processes are only given unlabeled samples. In other words, learners only have independent information X but no corresponding information Y. Cluster analysis is a major topic for unsupervised learning methods. For sensor signal analysis, unsupervised learning methods can not only display the distribution and the grouping of the data but also provide concentrated information for supervised learning processes.

PCA can be considered as the simplest unsupervised learning method, providing a visual data grouping result. Another simple but effective unsupervised learning method is K-means algorithm. The basic concept of this algorithm is to minimize the sum of the distances between all the samples to their cluster centers (i.e., total intra-cluster variance) through an iteration process. K-means algorithm has been widely used as a tool for system resolution and feature extraction. For example, K-means is a practical method to determine radial basis vectors for RBFNN and center vectors for PNN. The major drawbacks of K-means are that (1) the global convergence of this algorithm largely depends on the initial sample order and (2) the algorithm may have a skewed clustering result, if the cluster number estimate is incorrect. Therefore in this section, we will review a couple of adaptive unsupervised learning methods.

4.2.1 Self-organizing map (SOM)

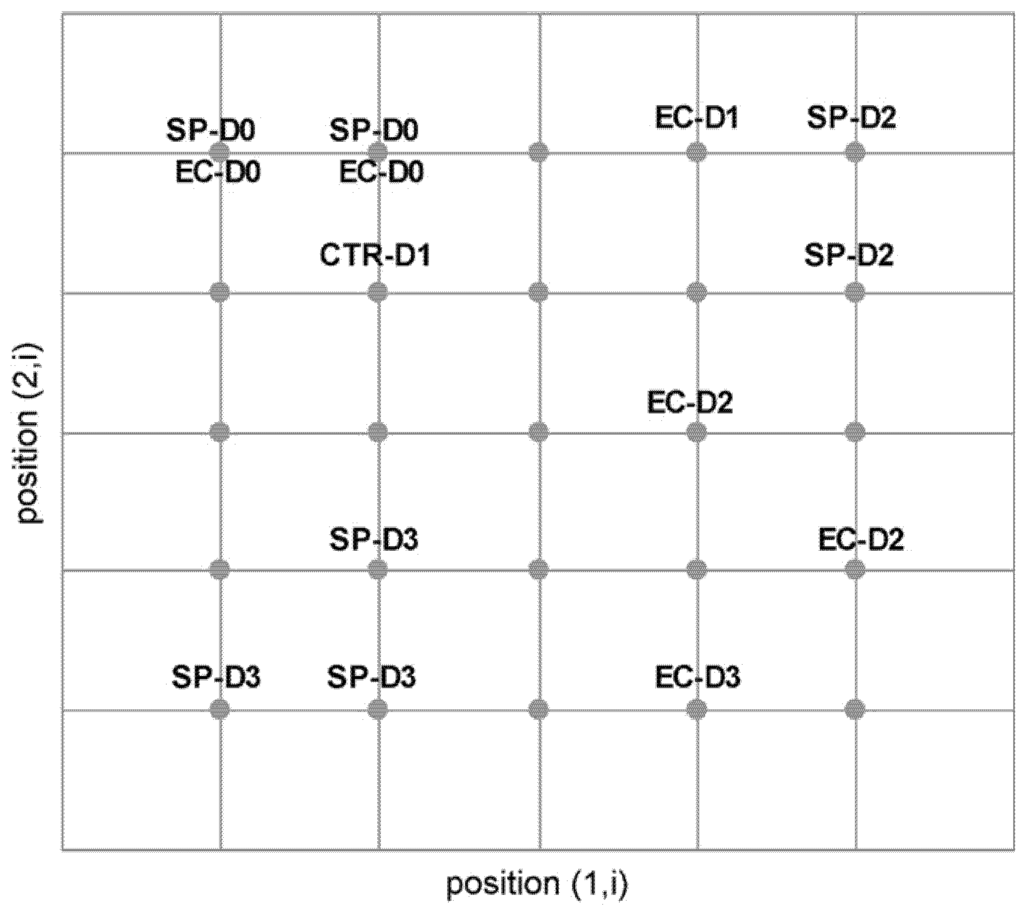
Figure 6. Self-organizing map of sensor responses on a 5×5 rectangular grid with clusters indicating the sample subgroups labeled using the following scheme: SP-D0, SP-D1, SP-D2 and SP-D3 are packaged vegetable kept at 10°C for 0–3 days, respectively; EC-D0, EC-D1, EC-D2 and EC-D3 are packaged vegetable inoculated with E. coli on the first day of inoculation and after stored at 10°C for 1–3 days, respectively. (Reprinted with the permission from Elsevier).

Figure 6. Self-organizing map of sensor responses on a 5×5 rectangular grid with clusters indicating the sample subgroups labeled using the following scheme: SP-D0, SP-D1, SP-D2 and SP-D3 are packaged vegetable kept at 10°C for 0–3 days, respectively; EC-D0, EC-D1, EC-D2 and EC-D3 are packaged vegetable inoculated with E. coli on the first day of inoculation and after stored at 10°C for 1–3 days, respectively. (Reprinted with the permission from Elsevier).

SOM is an unsupervised learning neural network. The most significant advantage of SOM is its capability to project a high-dimensional space onto a two-dimensional space while preserving the topology property of high-dimensional data. In terms of structure, SOM is a one-layer neural network. The learning process of SOM is based on a competitive algorithm which can be separated into three major steps: (1) locating the winner neuron whose weight vector is the closest to an input training vector, (2) adjusting the winner weight vector towards the input vector, and (3) updating the weight vectors of the neurons within a neighboring area of the winner neuron. These three steps reflect the mechanisms of the electric signal transfer among the brain neurons.

SOM was recently applied to detect the pathogen contaminated packaged fresh vegetables [78]. Figure 6 shows a SOM based grouping result for the fresh vegetables with and without E. coli contamination. SOM has also been used for E-nose based S. aureus infection identification in hospital environment [79].

4.2.2 Adaptive resonance theory based neural network – type 2a (ART-2a)

As an unsupervised learning method, ART-2a is mainly used for cluster analysis. Different from K-means algorithm where the number of clusters needs to predefined, ART-2a shows its advantageous ability to add a new cluster without disturbing the existing clusters [80], so it has a potential to be used for real-time sensor data analyses. ART-2a has become the most widely used method for mass spectrometry (MS) data cluster analysis, calibration modeling, and their applications for environmental quality studies [74, 81, 82, 83].

Given the initial cluster center vectors which usually are randomly selected from the sample set, the learning process of ART-2a can be divided into 4 steps:

• Randomly select an input sample vector and scale it to unit length.
• Find the neuron whose cluster vector has the largest resonance to this input vector and call this neuron the “winner”. The resonance is estimated by the dot product of the input sample vector and the cluster vector.
• If the resonance of the winner neuron is larger than a predefined vigilance factor (VF), ρ_vig, adjust the cluster vector of the winner neuron toward the input sample vector. Otherwise, create a new cluster for this sample vector.
• Repeat the above steps for all the sample vectors, which is defined as one cycle. Continue this process, until a stopping criterion is reached.

Clearly, the number of clusters is adaptively determined by ART-2a, which makes the cluster analysis more robust and flexible. It can be seen that the vigilance factor is a key parameter to control the cluster number. An overly large vigilance factor could result in an “overly fine” clustering result (the extreme case is one cluster for one mass spectral sample) by generating many homogeneous small clusters, while an overly small vigilance would result in an “overly coarse” result [81]. In ART-2a, a sample that does not belong to any currently existing clusters is classified into a new cluster. However, during the subsequent training process, this new cluster will only expand but never be merged with its neighbor clusters, even if this new cluster becomes very similar to its neighbor clusters. Therefore, some clusters generated by ART-2a could have a significant overlap among their sample distribution spaces, especially in cases with high vigilance factors. A possible remedy for this problem is to regroup the ART-2a clusters with the same vigilance factor.

4.2.3 Density-based clustering of application with noise (DBSCAN)

DBSCAN presents a very unique clustering process. Different from many other cluster analysis methods including ART-2a, DBSCAN performs a cluster territory expansion process by examining the density and continuity of sample distribution. The entire clustering process is controlled by two parameters: neighbor number (k) and neighborhood radius (ε). Briefly, the clustering process starts with a randomly selected sample and a cluster is set up for this sample. Controlled by the two predefined parameters, k and ε, the process will expand the territory of this cluster and examine if the cluster can be further expanded. If not, a new cluster will be generated. This searching process will continue until all the samples are clustered. DBSCAN presents a one-step clustering process based on a recursive procedure. The details can be found in the literature [84, 85, 86].

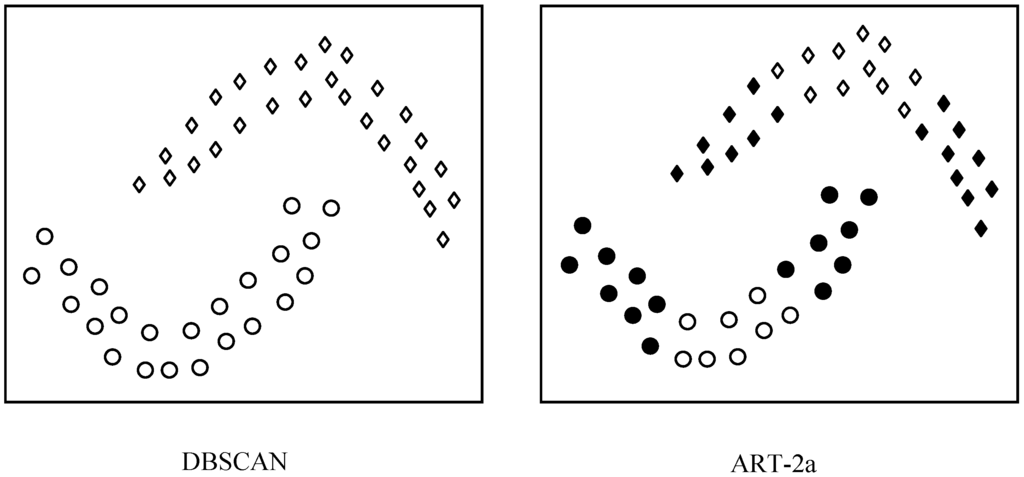
Figure 7. A schematic illustration of the difference between the clustering principles of DBSCAN and ART-2a.

Figure 7. A schematic illustration of the difference between the clustering principles of DBSCAN and ART-2a.

Figure 7 shows a schematic illustration of the difference between the clustering principles of ART-2a and DBSCAN. DBSCAN is able to cluster the samples that have a continuous distribution into one group, while ART-2a and other methods such as K-means divide each group into a couple of small groups based on the sample similarity (distance). With this advantage, DBSCAN surpasses many clustering methods including ART-2a in clustering the data with continuous and irregular distributions.

A comparison study of the clustering effects of DBSCAN and ART-2a on MS data [81, 87] indicates that a proper vigilance factor can produce a reasonable ART-2a clustering result, but an overly fine or ‘‘crashed’’ clustering result for an ART-2a with a high vigilance factor can be recovered by a post-processing strategy. DBSCAN seems to be more effective and robust in the post-processing step than conventional regrouping analysis [81].

5. Discussion

After reviewing the methods for each step of a complete machine learning process, this section will discuss some potential problems and feasible suggestions to help ensure machine learning effects. Outlier detection is one of the key issues for data pre-treatment. Because (1) outliers may contain the important information and (2) it can be difficult to detect and confirm outliers in real-time analyses, it is necessary to establish robust models to resist the disturbance of possible outliers. Using weighting functions to adaptively determine the “contribution” of each sample to the modeling effect based on their space or probability distribution is a feasible choice for real-time sensor analyses.

Optimization methods like GA, DE, and SA have been widely used for system feature extraction. As an objective driven searching process, they can adaptively locate different “representative” features or variables for different tasks such as classification or chemical concentration estimation. The key issue in the searching process is to use a proper function (model) to evaluate the fitness and quality of the selected features. It is likely that a set of less “representative” features can also yield a high quality if there is a “super-powerful” model. Therefore, if the feature selection is not only for a high modeling accuracy but also for subsequent mechanism studies such as pathological studies, it is suggested to employ a relatively straightforward model as a fitness evaluation function to ensure (1) the high fitness is mainly due to the selected features and (2) these features may have sufficient physical meaning.

Another important issue for establishing a reliable supervised learning strategy and preventing over-fitting is to properly make use of the available samples. For a case where there are sufficient samples, a feasible way is to divide the data into three subsets: training, validating, and testing. The training set is used to obtain the model parameters, the validating set is to verify modeling effects and finalize the model construction, and the testing set is used to formally and finally evaluate the modeling effects. For a case with quite limited samples, k-fold cross-validating is good choice for model construction and testing. The extreme case of k-fold cross-validating process is leave-one-out (LOO) strategy, which seems to be the minimum for sample sufficiency requirements. Assuming there are m samples, the LOO method repeats a training-testing process, in which one sample is left out for testing and m-1 samples for training, for m times to cover a small sample set.

Machine learning methods aim to discover the hidden rules that control complex systems. Since the physical laws of these complex systems are not yet clear, a machine learning process based on these statistical and artificial intelligence methods should be a continuously self-adjusting process. In other words, for real applications, we need to be cautious to the results generated by these “grey box” and “black box” models. A validating process and a possible model parameter updating process are always suggested for a reliable model.

6. Conclusion

This paper has provided a review of the methods that are popularly used in the machine learning step for sensor design. With the increased complexity of sensor systems and their application fields, any of the three steps (data pre-treatment, feature extraction, and system modeling) can be a key factor for a successful machine learning process. Especially, feature extraction and system modeling more and more work together as a system, serving each other, to obtain a good final result. Selecting “good” features can yield a nice modeling effect and a proper model can help detect “good” features. Integration of linear and nonlinear methods such as RBF-PLS and PCA-BPNN is becoming a popular machine learning method. Gaussian kernel functions are the fundamental element for a group of neural networks including RBFNN, SVM, and PNN. A constructive method to determine the parameters of Gaussian kernel function will lead to an essential improvement of properties of these neural networks. Training time, accuracy, adaptability, stability, and plasticity are the major issues for machine learning processes. There may be a trade-off among them, so integration of the methods with different advantages is a promising direction for the machine learning section of sensor design. Developing transferrable machine learning models is another attractive direction for novel sensor design, as it can prevent a complete retraining for a new system or environment. Certainly, instrumentation analysis improvements are a vital force to develop novel machine learning algorithms for sensor design.