Deformation Behavior of Recycled Concrete Aggregate during Cyclic and Dynamic Loading Laboratory Tests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material and Sample Preparation
2.2. Physical Properties Analysis
2.3. The Static Tests
2.4. Torsional Shear Test
2.5. Static and Long-Term Cyclic Triaxial Tests
3. Results and Discussion
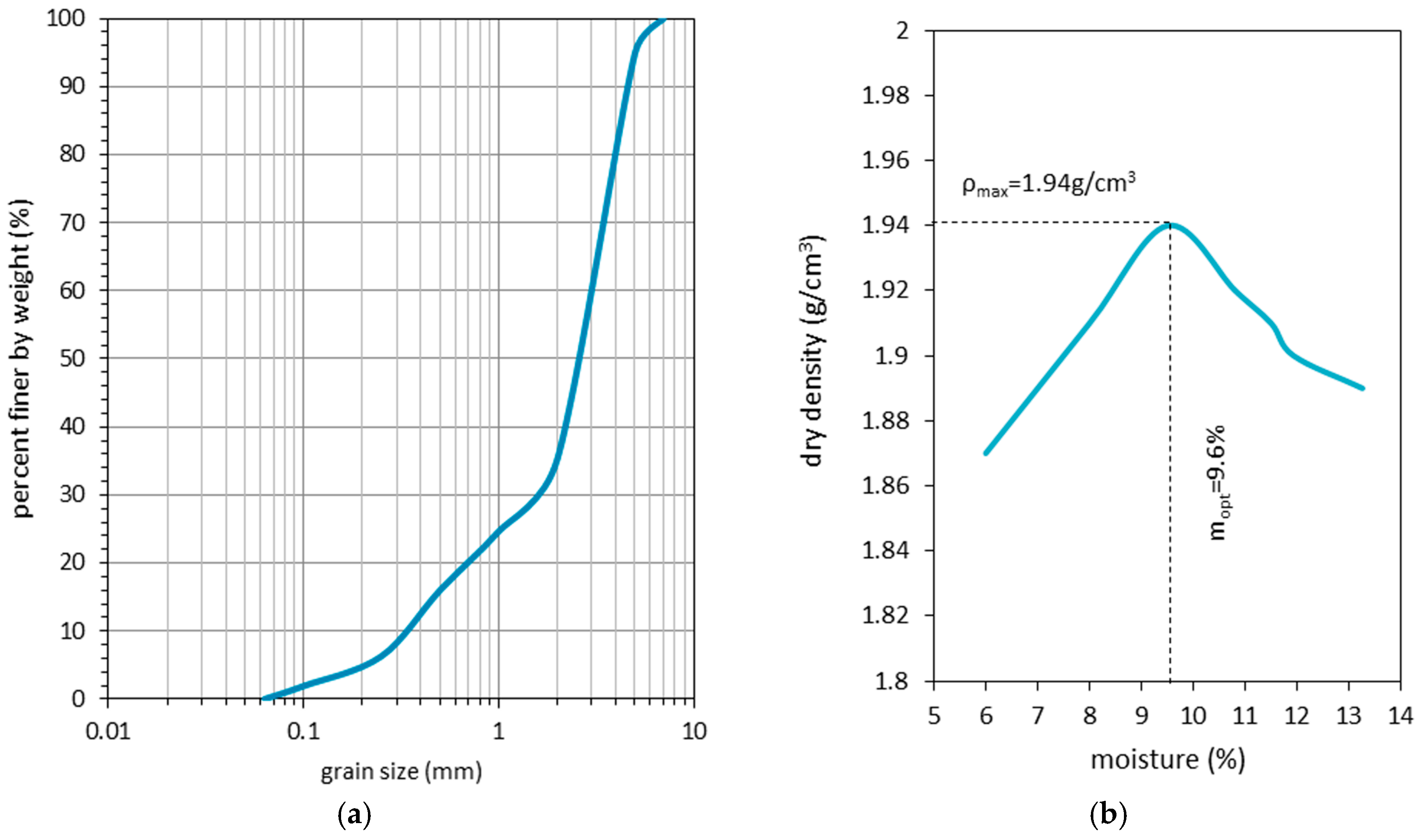
3.1. Results of Physical Tests
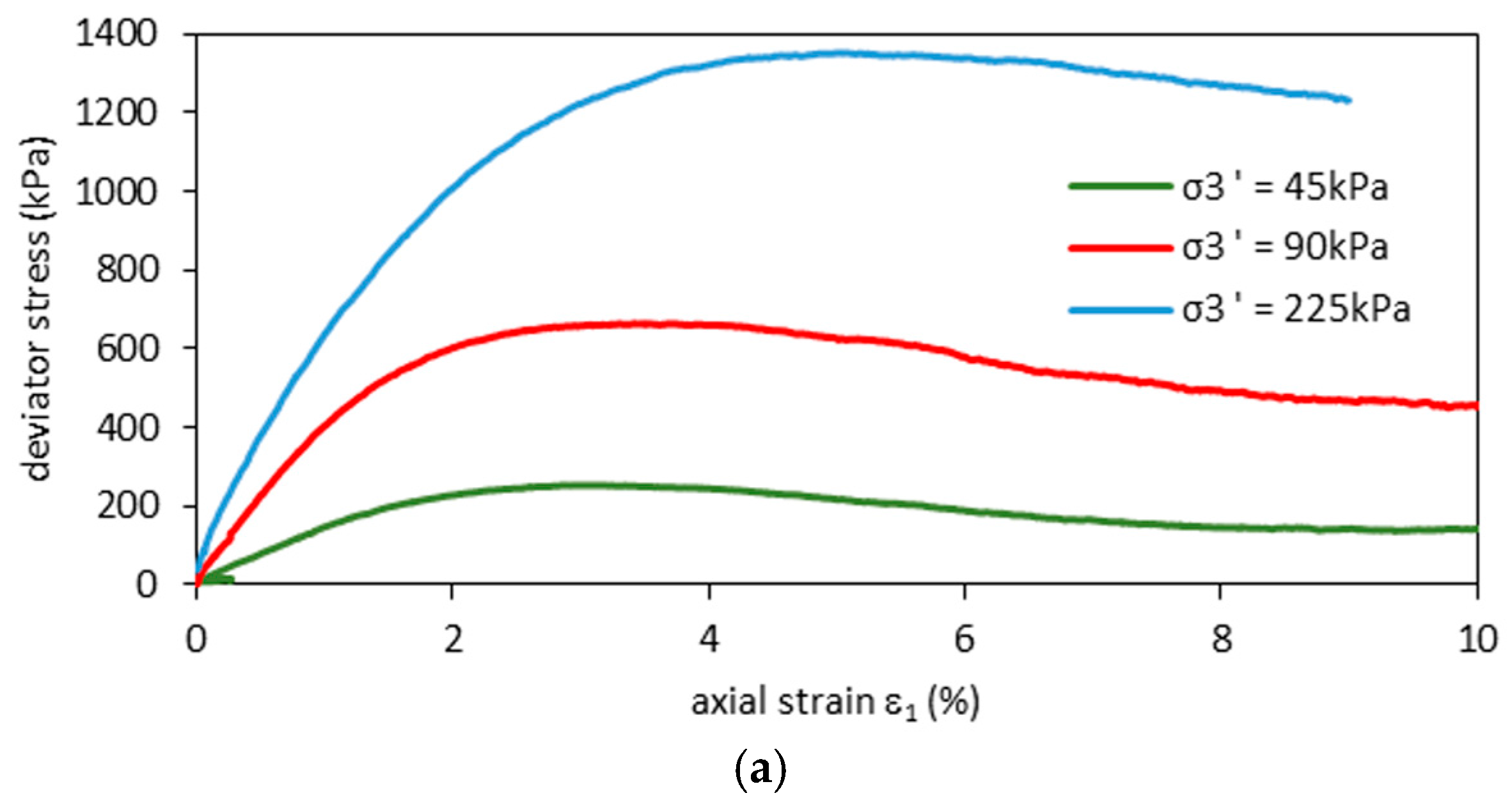
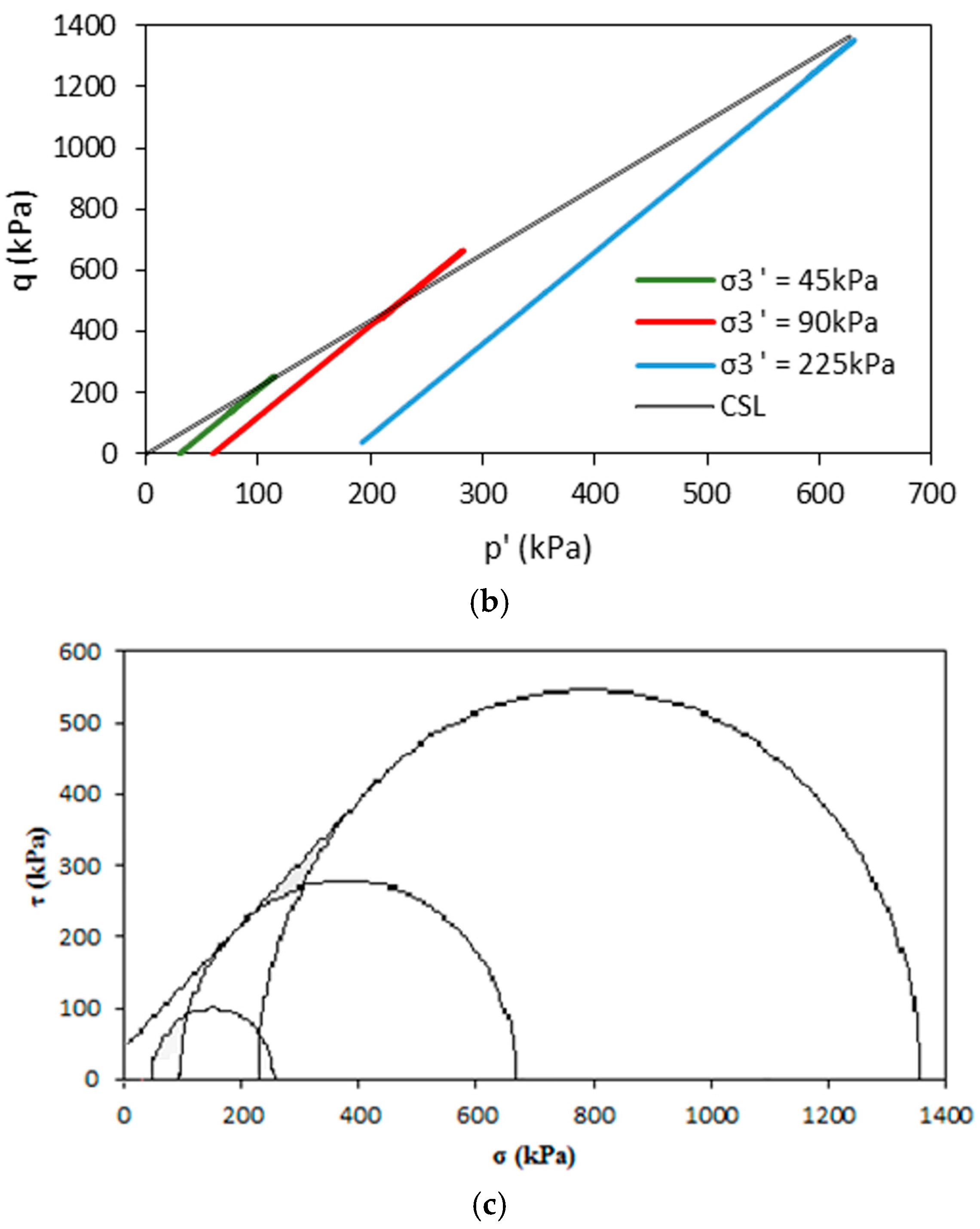
3.2. Results of Static Tests
3.3. Results of Torsional Shear Tests
3.4. Cyclic Triaxial Test Results
4. Conclusions
- CBR test results ranged between 71.7% and 101.5% for a 2.5-mm plunger depth and between 91.3% and 100.4% for 5.00 mm. These results fulfill the standards necessary to classify RCAs as a subbase layer application.
- DSTs allowed an estimation of the friction angle ϕ = 39.5°, while not allowing a proper observation of the cohesion c. Static triaxial test results provided effective friction angle ϕ’ = 42° and apparent cohesion c = 45 kPa. The differences are caused by the RCA structure, which involves high roughness of the grain surface.
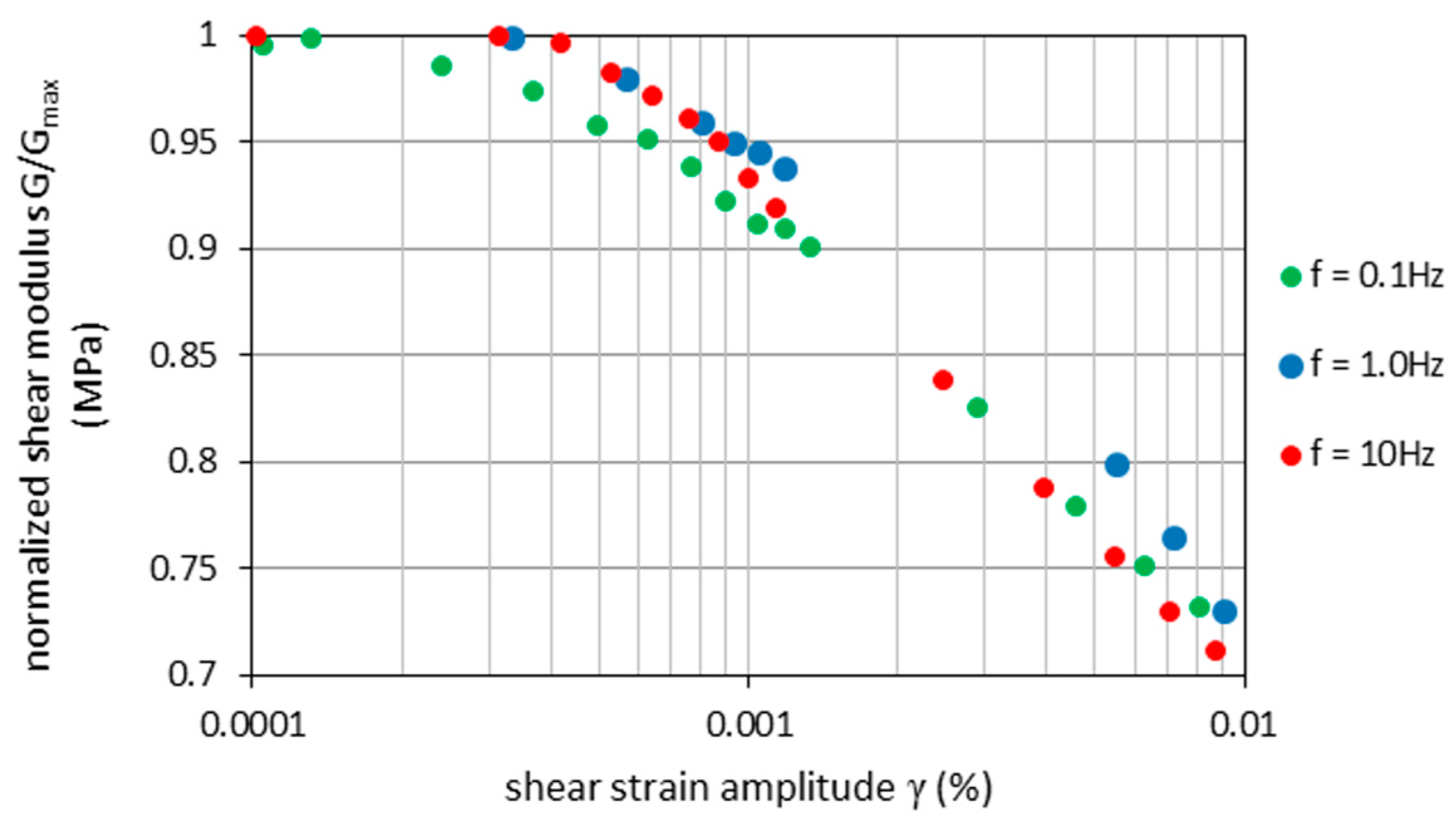
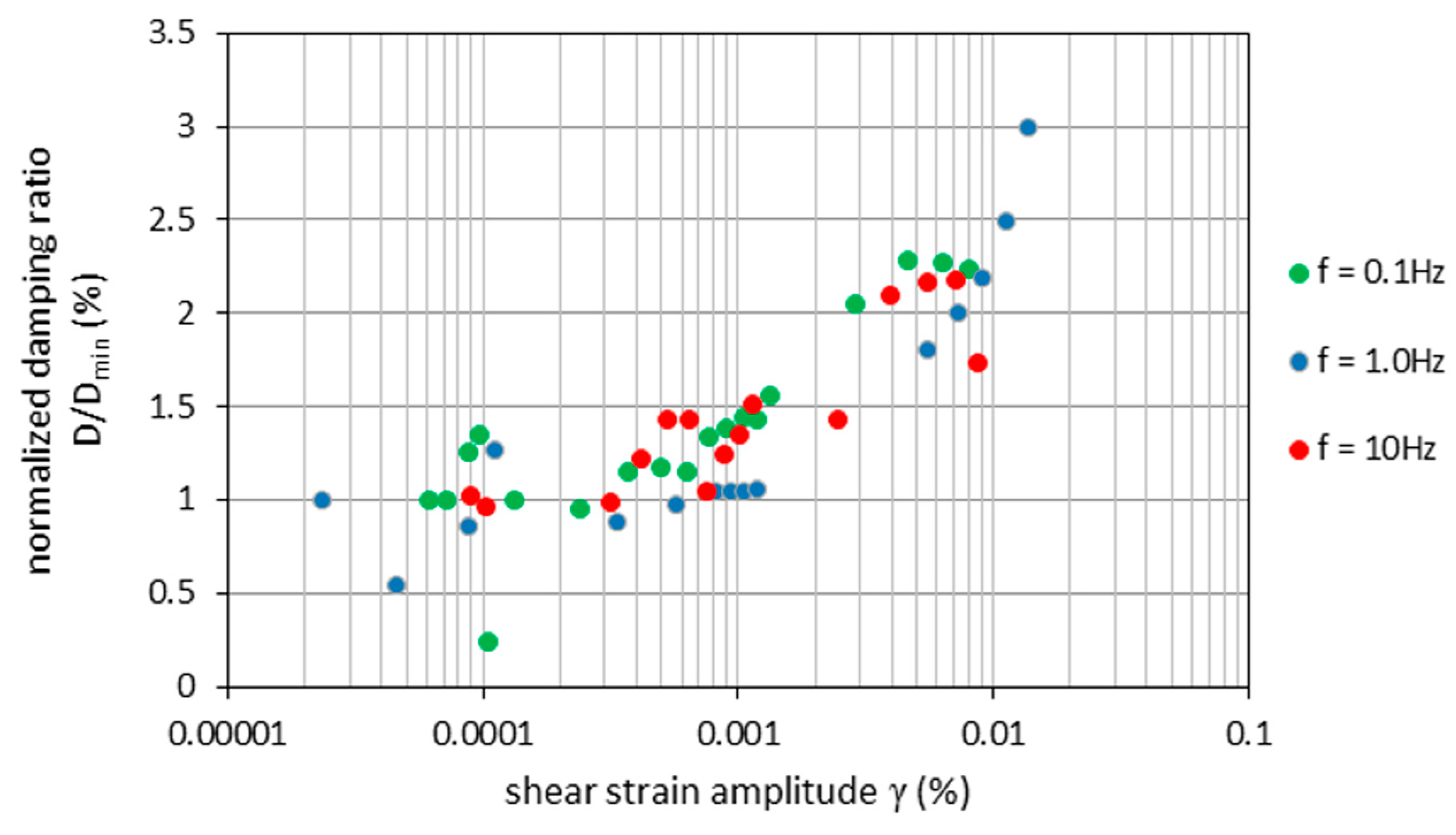
- Torsional shear tests allowed establishing the value of the shear modulus Gmax and damping ratio Dmin for f = 1 Hz at approximately Gmax = 60 MPa and Dmin = 1.83%.
- During the tests, excessive pore water pressures were observed. They started to stabilize after ca. 100 cycles, reaching steady low levels after approximately 1000 cycles.
- During the experiments, a change of the area of the hysteresis loops qx was observed. This was clearly observed during Test 1.1. The resilient modulus Mr also presented a decrease during the test. The decrease of Mr after the plastic hardening process (approximately 102 to 103 cycles) is interpreted as a consequence of the degradation of RCA stiffness. This phenomena was observed in all tests, except Test 2.1. In the latter, the RCA showed hardening even after 3 × 104. The overall maximal obtained Mr was equal to 1715 kPa.
- An empirical formulas (Equations (4)–(7)) for permanent strain development as a function of N, σ'3, qmax and qf max has been established. Predicted permanent strains based on these formulas agree well with the test results.
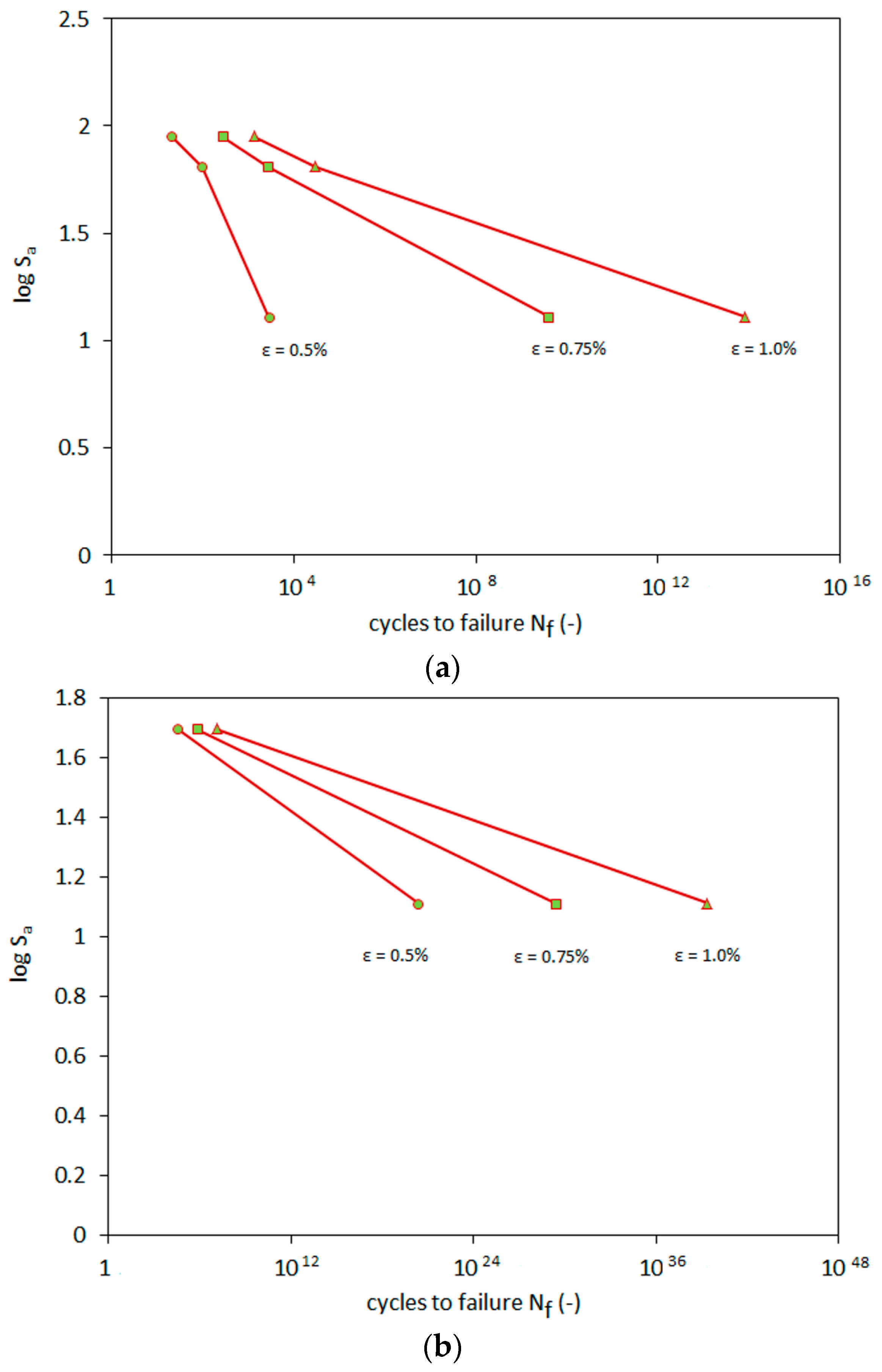
- Results were interpreted based on the stress-life method in the Wohler S-N diagram. The S-N diagram plots the stress amplitude qa versus cycles until the occurrence of the failure Nf. The RCA exhibits behavior in accordance to the Basquin law. The characteristic “knee”, which can be observed in the case of other materials, was not observed during the tests for the RCA.
- Results suggest that the pore pressure development at early stages of cyclic loading is impacted by internal porosity and high water adsorption, which is characteristic for RCAs.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shajarati, A.; Sørensen, K.W.; Nielsen, S.K.; Ibsen, L.B. Behaviour of Cohesionless Soils During Cyclic Loading; DCE Technical Memorandum: Aalborg, Denmark, 2012. [Google Scholar]
- Ishihara, K.; Towhata, I. Cyclic behavior of sand during rotation of principal stress axes. In Mechanics of Granular Material: New Models and Constitutive Equations; Jenkins, J.T., Satake, M., Eds.; Elsevier Science Ltd.: Philadelphia, PA, USA, 1983; pp. 53–73. [Google Scholar]
- Tokimatsu, K.; Yamazaki, T.; Yoshimi, Y. Soil liquefaction evaluations by elastic shear moduli. Soils Found. 1986, 26, 25–35. [Google Scholar] [CrossRef]
- Teachavorasinskun, S.; Tatsuoka, F.; Lo Presti, D.C.F. Effects of the cyclic prestraining on dilatancy characteristics and liquefaction strength of sand. In Proceedings of the Pre-failure Deformation of Geomaterials, Rotterdam, The Netherlands, 12–14 September 1994; pp. 75–80.
- Wichtmann, T.; Niemunis, A.; Triantafyllidis, T. Strain accumulation in sand due to cyclic loading: Drained triaxial tests. Soil Dyn. Earthq. Eng. 2005, 25, 967–979. [Google Scholar] [CrossRef]
- AnhDan, L.Q.; Koseki, J. Effects of large number of cyclic loading on deformation characteristics of dense granular materials. Soils Found. 2004, 44, 115–123. [Google Scholar] [CrossRef]
- Gavin, K.G.; O’Kelly, B.C. Effect of friction fatigue on pile capacity in dense sand. J. Geotech. Geoenviron. Eng. 2007, 133, 63–71. [Google Scholar] [CrossRef]
- Di Benedetto, H.; de La Roche, C.; Baaj, H.; Pronk, A.; Lundstrom, R. Fatigue of bituminous mixtures. Mater. Struct. 2004, 37, 202–216. [Google Scholar] [CrossRef]
- Głuchowski, A. Permanent strain behavior of cyclically loaded cohesive soil in undrained conditions. In Proceedings of the 25th European Young Geotechnical Engineers Conference, Bucharest, Romania, 15–24 June 2016; pp. 53–60.
- Vucetic, M.; Mortezaie, A. Cyclic secant shear modulus versus pore water pressure in sands at small cyclic strains. Soil Dyn. Earthq. Eng. 2015, 70, 60–72. [Google Scholar] [CrossRef]
- Brown, S.F.; Yu, H.S.; Juspi, S.; Wang, J. Validation experiments for lower-bound shakedown theory applied to layered pavement systems. Géotechnique 2012, 62, 923–932. [Google Scholar] [CrossRef]
- Głuchowski, A.; Szymański, A.; Sas, W. Repeated Loading of cohesive soil-shakedown theory in undrained conditions. Stud. Geotech. Mech. 2015, 37, 11–16. [Google Scholar] [CrossRef]
- Tao, M.; Mohammad, L.N.; Nazzal, M.D.; Zhang, Z.; Wu, Z. Application of shakedown theory in characterizing traditional and recycled pavement base materials. J. Transp. Eng. 2010, 136, 214–222. [Google Scholar] [CrossRef]
- Werkmeister, S. Shakedown analysis of unbound granular materials using accelerated pavement test results from New Zealand’s CAPTIF facility. Geotech. Spec. Publ. 2006, 154, 220–228. [Google Scholar]
- Cerfontaine, B.; Collin, F.; Charlier, R. Numerical modelling of transient cyclic vertical loading of suction caissons in sand. Geotechnique 2015, 65. in press. [Google Scholar] [CrossRef]
- Sas, W.; Głuchowski, A.; Soból, E.; Bąkowski, J.; Szymański, A. Analysis of the multistage cyclic loading test on resilient modulus value. Ann. Wars. Univ. Life Sci.–SGGW-Land Reclam. 2016, 48, 53–65. [Google Scholar]
- Soltani-Jigheh, H.; Soroush, A. Cyclic behavior of mixed clayey soils. Int. J. Civ. Eng. 2010, 8, 99–106. [Google Scholar]
- Lee, C.J.; Sheu, S.F. The stiffness degradation and damping ratio evolution of Taipei Silty Clay under cyclic straining. Soil Dyn. Earthq. Eng. 2007, 27, 730–740. [Google Scholar] [CrossRef]
- Rahman, M.A.; Imteaz, M.; Arulrajah, A.; Disfani, M.M. Suitability of recycled construction and demolition aggregates as alternative backfilling materials. J. Clean. Prod. 2014, 66, 75–84. [Google Scholar] [CrossRef]
- Arulrajah, A.; Piratheepan, J.; Ali, M.M.Y.; Bo, M.W. Geotechnical properties of recycled concrete aggregate in pavement sub-base applications. Geotech. Test. J. 2012, 35, 1–9. [Google Scholar] [CrossRef]
- Safiuddin, M.; Jumaat, M.Z.; Salam, M.A.; Islam, M.S.; Hashim, R. Utilization of solid wastes in construction materials. Int. J. Phys. Sci. 2010, 5, 1952–1963. [Google Scholar]
- Arulrajah, A.; Disfani, M.M.; Horpibulsuk, S.; Suksiripattanapong, C.; Prongmanee, N. Physical properties and shear strength responses of recycled construction and demolition materials in unbound pavement base/subbase applications. Constr. Build. Mater. 2014, 58, 245–257. [Google Scholar] [CrossRef]
- Sas, W.; Głuchowski, A.; Szymański, A. Behavior of recycled concrete aggregate improved with lime addition during cyclic loading. Int. J. Geomate 2016, 10, 1662–1669. [Google Scholar] [CrossRef]
- Koenders, E.A.; Pepe, M.; Martinelli, E. Compressive strength and hydration processes of concrete with recycled aggregates. Cem. Concr. Res. 2014, 56, 203–212. [Google Scholar] [CrossRef]
- Pepe, M.; Toledo Filho, R.D.; Koenders, E.A.; Martinelli, E. Alternative processing procedures for recycled aggregates in structural concrete. Constr. Build. Mater. 2014, 69, 124–132. [Google Scholar] [CrossRef]
- Nataatmadja, A.; Tan, Y.L. Resilient response of recycled concrete road aggregates. J. Transp. Eng. 2001, 127, 450–453. [Google Scholar] [CrossRef]
- Poon, C.S.; Qiao, X.C.; Chan, D. The cause and influence of self-cementing properties of fine recycled concrete aggregates on the properties of unbound sub-base. Waste Manag. 2006, 26, 1166–1172. [Google Scholar] [CrossRef]
- Arulrajah, A.; Rahman, M.A.; Piratheepan, J.; Bo, M.W.; Imteaz, M.A. Evaluation of interface shear strength properties of geogrid-reinforced construction and demolition materials using a modified large-scale direct shear testing apparatus. J. Mater. Civ. Eng. 2013, 26, 974–982. [Google Scholar] [CrossRef]
- Van Niekerk, A.A.; Houben, L.J.M.; Molenaar, A.A.A. Estimation of mechanical behavior of unbound road building materials from physical material properties. In Proceedings of the 5th International Conference on the Bearing Capacity of Roads and Airfields, Trondheim, Norway, 6–8 May 1998; pp. 1221–1233.
- Lekarp, F.; Isacsson, U.; Dawson, A. State of the art.II: Premanent strain response of unbound aggregates. J. Transp. Eng. 2000, 126, 76–83. [Google Scholar] [CrossRef]
- Bozyurt, O.; Tinjum, J.M.; Son, Y.H.; Edil, T.B.; Benson, C.H. Resilient modulus of recycled asphalt pavement and recycled concrete aggregate. In Proceedings of the GeoCongress 2012, Oakland, CA, USA, 25–29 March 2012; pp. 3901–3910.
- Stokoe, K.H., II; Isenhower, W.M.; Hsu, J.R. Dynamic properties of offshore silty samples. In Proceedings of the 12th Annual Offshore Technology Conference, Houston, TX, USA, 4–7 May 1980; p. 3771.
- Eurokod 7 Projektowanie Geotechniczne Część 2: Rozpoznawanie i Badanie Podłoża Gruntowego; PN-EN 1997-2:2009; Polish Committee for Standardization: Warsaw, Poland, 2009.
- Badania Geotechniczne-Badania Laboratoryjne Gruntów-Część 4: Oznaczanie Składu Granulometrycznego; Standards PKN-CEN ISO/TS 17892-4:2009; Polish Committee for Standardization: Warsaw, Poland, 2009.
- Adams, C.A.; Apraku, E.; Opoku-Boahen, R. Effect of triaxial geogrid reinforcement on CBR strength of natural gravel soil for road pavements. J. Civ. Eng. Res. 2015, 5, 45–51. [Google Scholar]
- Flora, A.; Lirer, S. Small strain shear modulus of undisturbed gravelly soils during undrained cyclic triaxial tests. Geotechn.Geolog. Eng. 2013, 31, 1107–1122. [Google Scholar] [CrossRef]
- Flora, A.; Lirer, S.; Silvestri, F. Undrained cyclic resistance of undisturbed gravelly soils. Soil Dyn. Earthq. Eng. 2012, 43, 366–379. [Google Scholar] [CrossRef]
- Strahler, A.; Stuedlein, A.W.; Arduino, P.W. Stress-strain response and dilatancy of sandy gravel in triaxial compression and plane strain. J. Geotech. Geoenviron. Eng. 2015, 142, 04015098. [Google Scholar] [CrossRef]
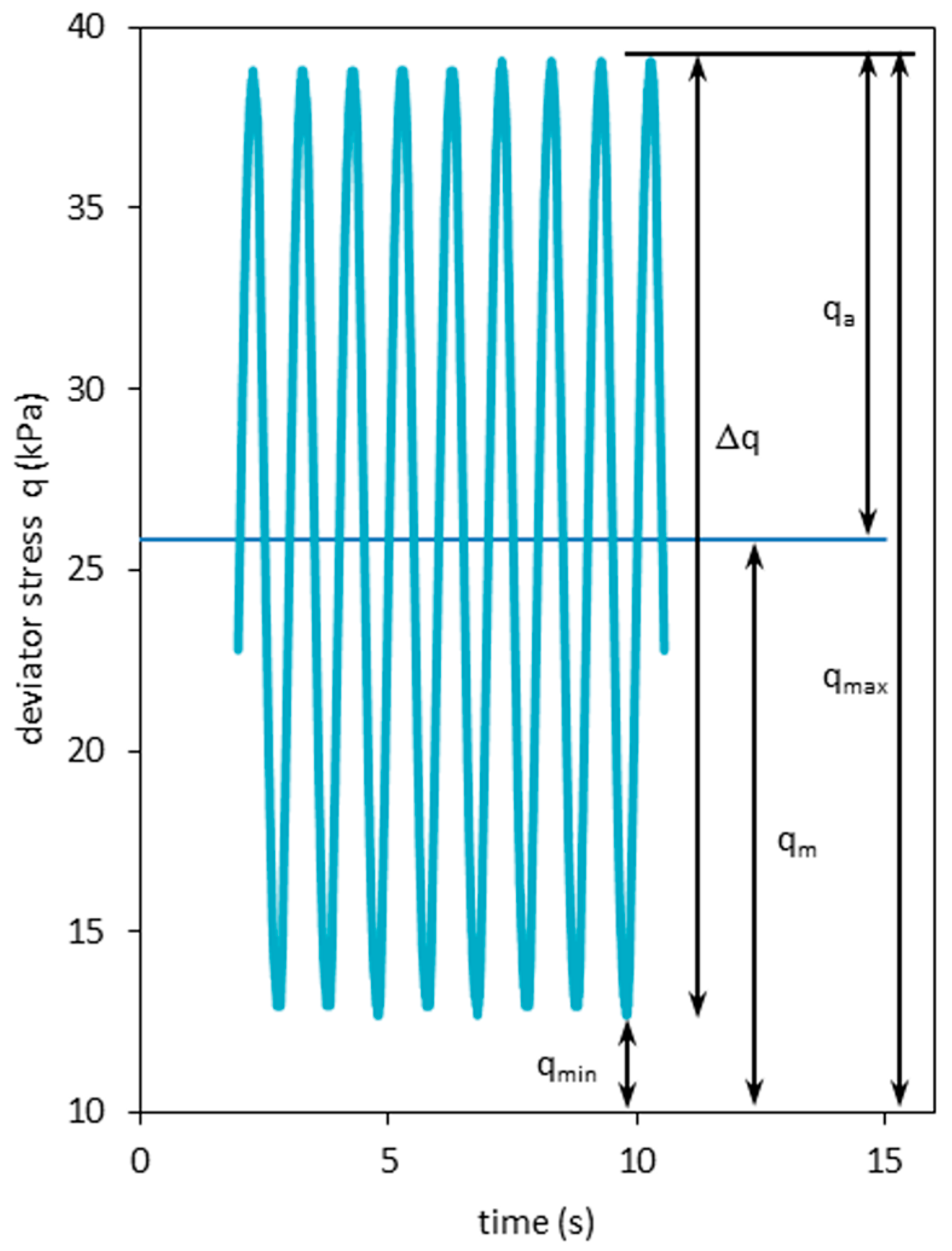

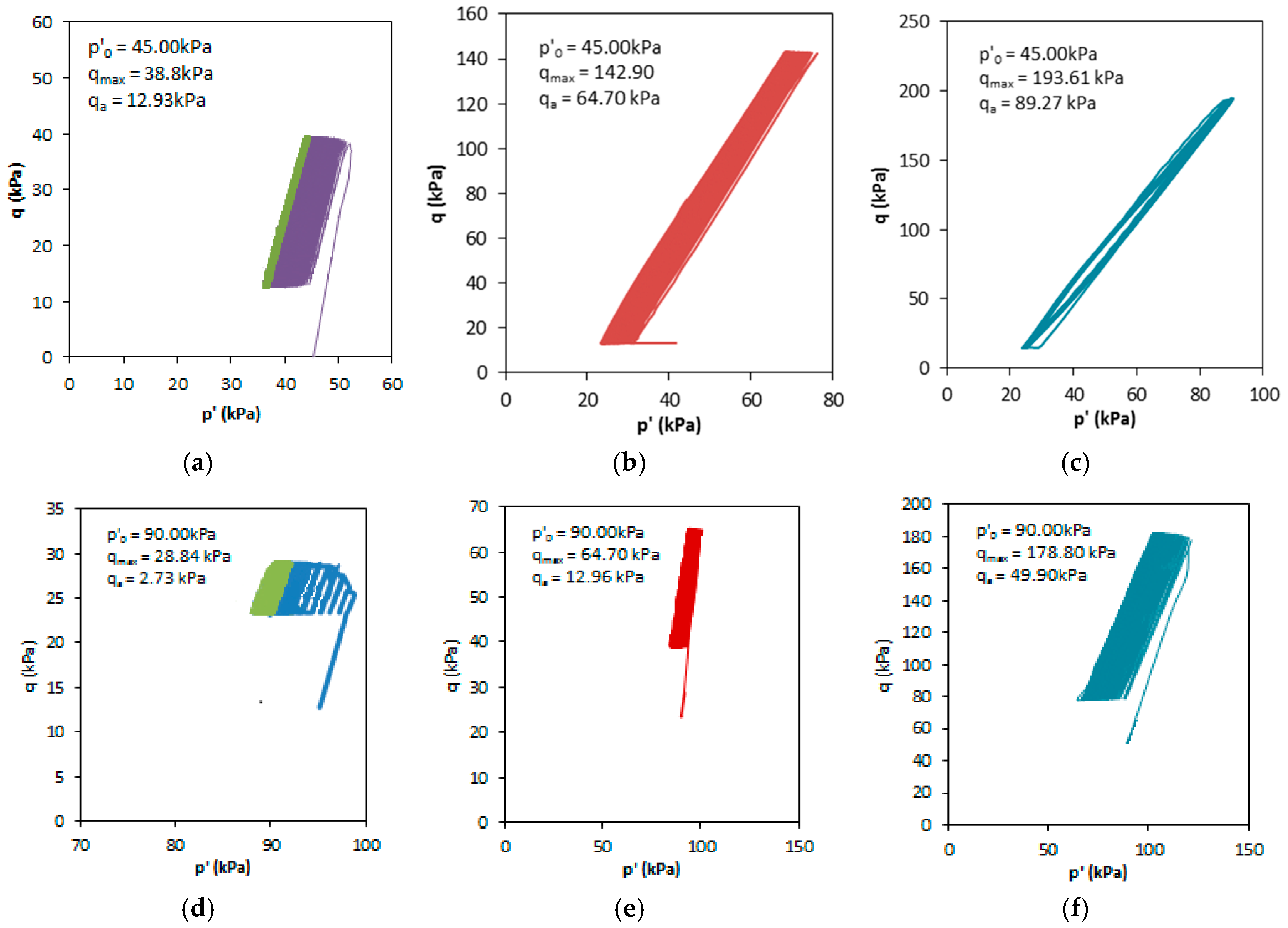

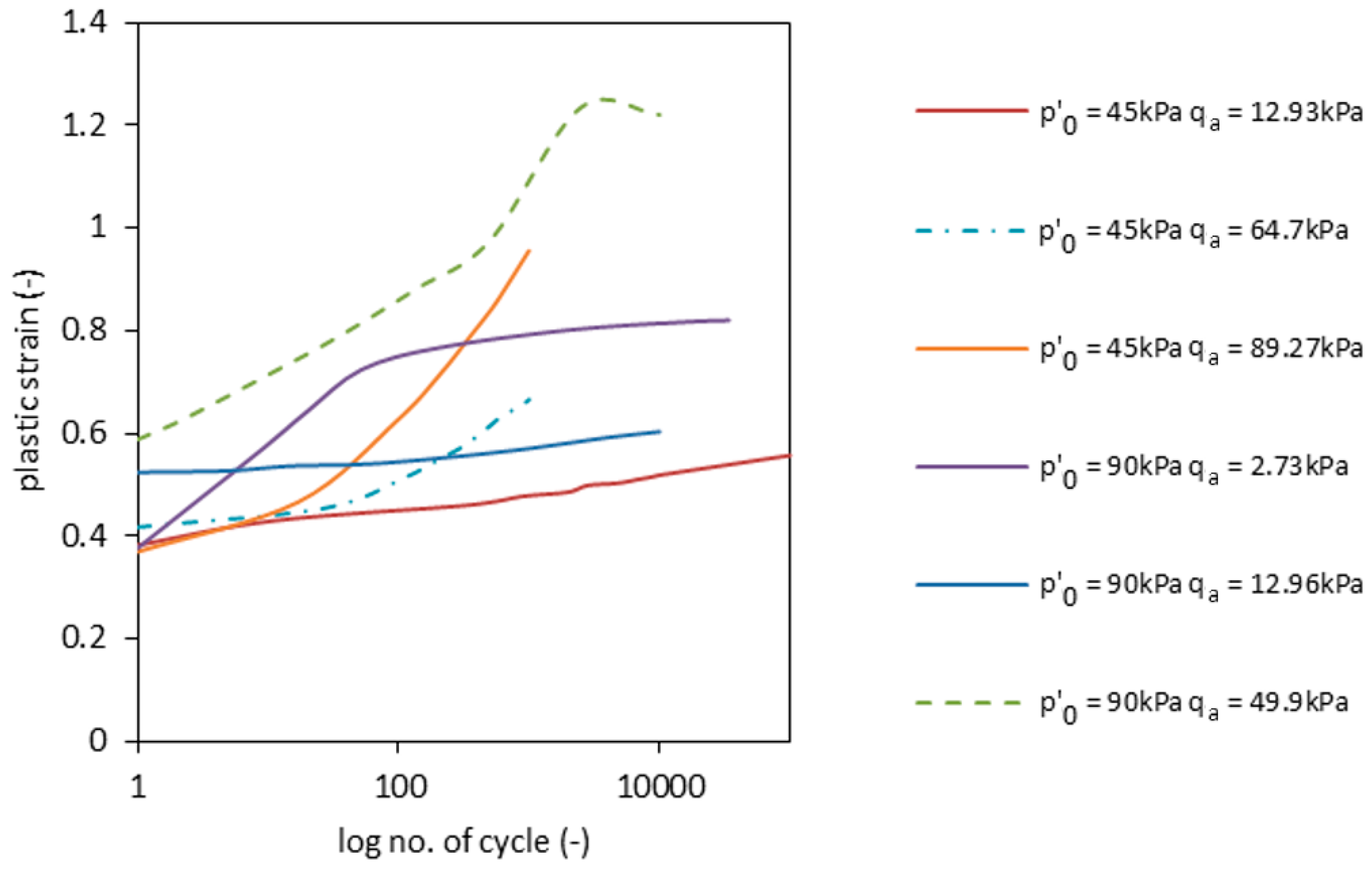
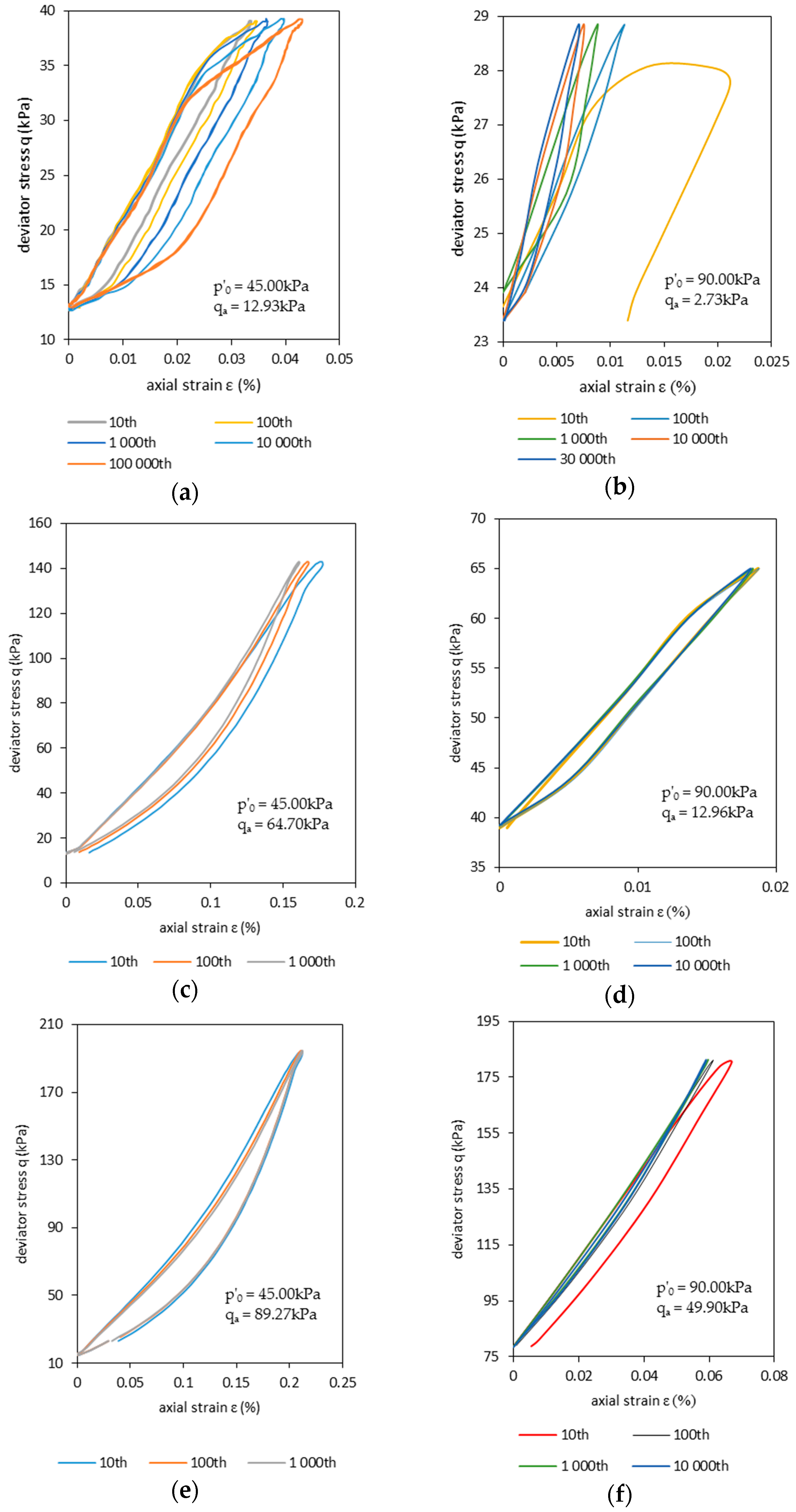


| Caption | Δq (kPa) | qm (kPa) | qmin (kPa) | qmax (kPa) | qa (kPa) |
|---|---|---|---|---|---|
| Test 1.1 | 25.85 | 25.87 | 12.95 | 38.8 | 12.93 |
| Test 1.2 | 129.39 | 78.21 | 13.51 | 142.9 | 64.7 |
| Test 1.3 | 178.54 | 104.34 | 15.07 | 193.61 | 89.27 |
| Test 2.1 | 5.46 | 26.11 | 23.38 | 28.84 | 2.73 |
| Test 2.2 | 25.72 | 51.94 | 38.98 | 64.7 | 12.96 |
| Test 2.3 | 99.78 | 128.91 | 79.01 | 178.79 | 49.9 |
| Test No. | σ3’ Effective Minor Axial Stress Value (kPa) | Deviator Stress at Failure (kPa) |
|---|---|---|
| S.1 | 45.0 | 251.0 |
| S.2 | 90.0 | 661.0 |
| S.3 | 225.0 | 1346.0 |
| Freq. (Hz) | Dmin (%) | Gmax (MPa) |
|---|---|---|
| 0.1 | 1.61 | 55 |
| 1 | 1.83 | 60 |
| 10 | 3.1 | 56 |
| No. of Test/No. of Cycle | 101 | 102 | 103 | 104 | 105 |
|---|---|---|---|---|---|
| 1.1 | 790 | 812 | 744 | 670 | 633 |
| 1.2 | 808 | 823 | 758 | - | - |
| 1.3 | 618 | 652 | 621 | - | - |
| 2.1 | 450 | 483 | 562 | 730 | - |
| 2.2 | 1436 | 1387 | 1410 | 1422 | - |
| 2.3 | 1654 | 1689 | 1715 | 1710 | - |
| Test No. | A | b | R2 |
|---|---|---|---|
| 1.1 | 0.0170 | −0.7890 | 0.992 |
| 1.2 | 0.0686 | −0.3231 | 0.997 |
| 1.3 | 0.1425 | −0.6649 | 0.997 |
| 2.1 | 0.0120 | −0.0489 | 0.982 |
| 2.2 | 0.0119 | −0.0586 | 0.997 |
| 2.3 | 0.0854 | −0.3923 | 0.987 |
| Caption | 45 kPa | 90 kPa | ||
|---|---|---|---|---|
| C | d | C | d | |
| ε = 0.5% | 1.917 | −0.012 | 2.0537 | −0.008 |
| ε = 0.75% | 1.8849 | −0.008 | 2.051 | −0.007 |
| ε = 1.0% | 1.864 | −0.006 | 2.0518 | −0.006 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sas, W.; Głuchowski, A.; Gabryś, K.; Soból, E.; Szymański, A. Deformation Behavior of Recycled Concrete Aggregate during Cyclic and Dynamic Loading Laboratory Tests. Materials 2016, 9, 780. https://doi.org/10.3390/ma9090780
Sas W, Głuchowski A, Gabryś K, Soból E, Szymański A. Deformation Behavior of Recycled Concrete Aggregate during Cyclic and Dynamic Loading Laboratory Tests. Materials. 2016; 9(9):780. https://doi.org/10.3390/ma9090780
Chicago/Turabian StyleSas, Wojciech, Andrzej Głuchowski, Katarzyna Gabryś, Emil Soból, and Alojzy Szymański. 2016. "Deformation Behavior of Recycled Concrete Aggregate during Cyclic and Dynamic Loading Laboratory Tests" Materials 9, no. 9: 780. https://doi.org/10.3390/ma9090780
APA StyleSas, W., Głuchowski, A., Gabryś, K., Soból, E., & Szymański, A. (2016). Deformation Behavior of Recycled Concrete Aggregate during Cyclic and Dynamic Loading Laboratory Tests. Materials, 9(9), 780. https://doi.org/10.3390/ma9090780









