Identification of Material Parameters for the Simulation of Acoustic Absorption of Fouled Sintered Fiber Felts
Abstract
:1. Introduction
2. Fouling Experiment
3. Material Characterization
3.1. Structural Characterization
3.1.1. Initial Material
3.1.2. Fouled Material
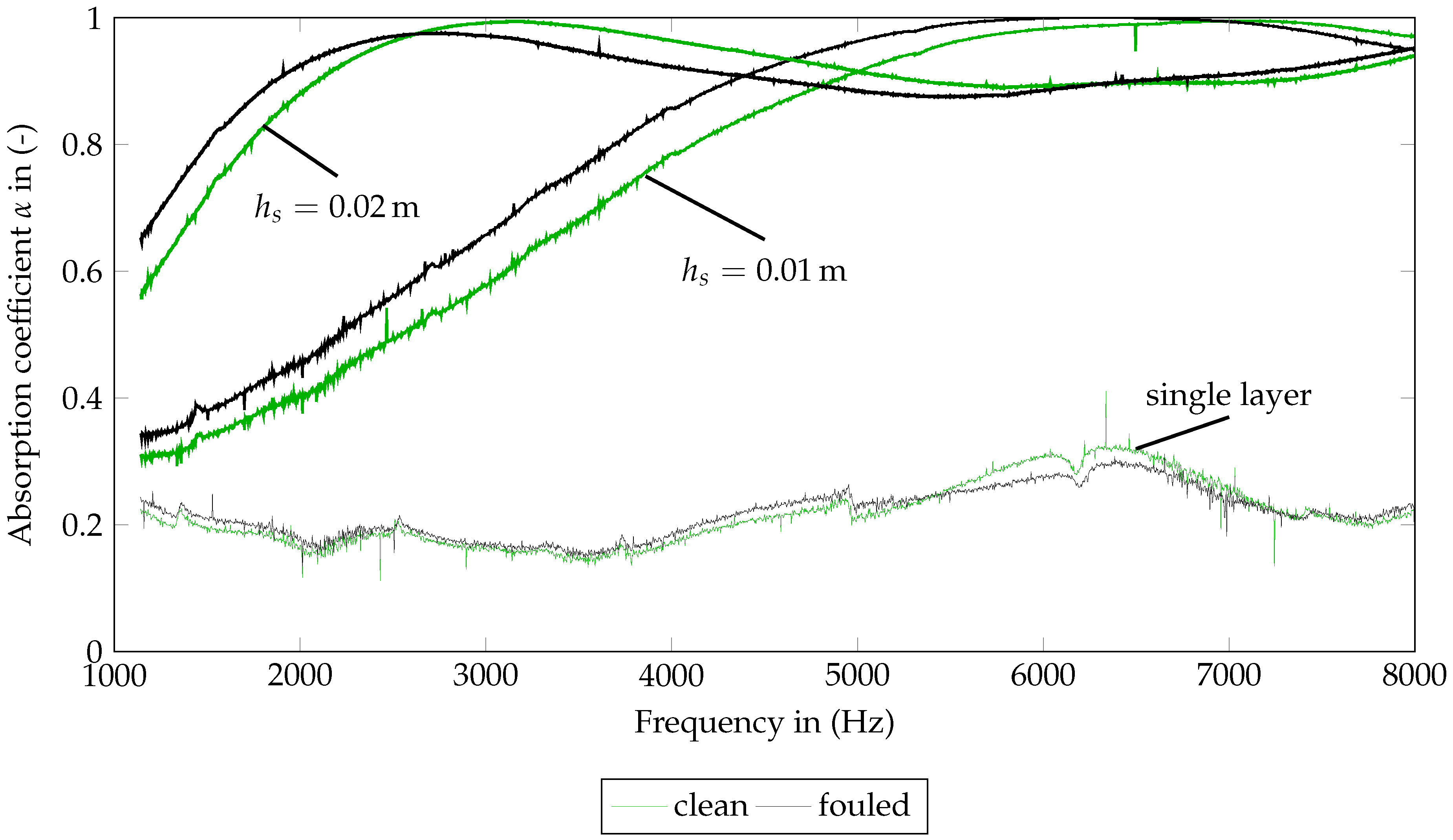
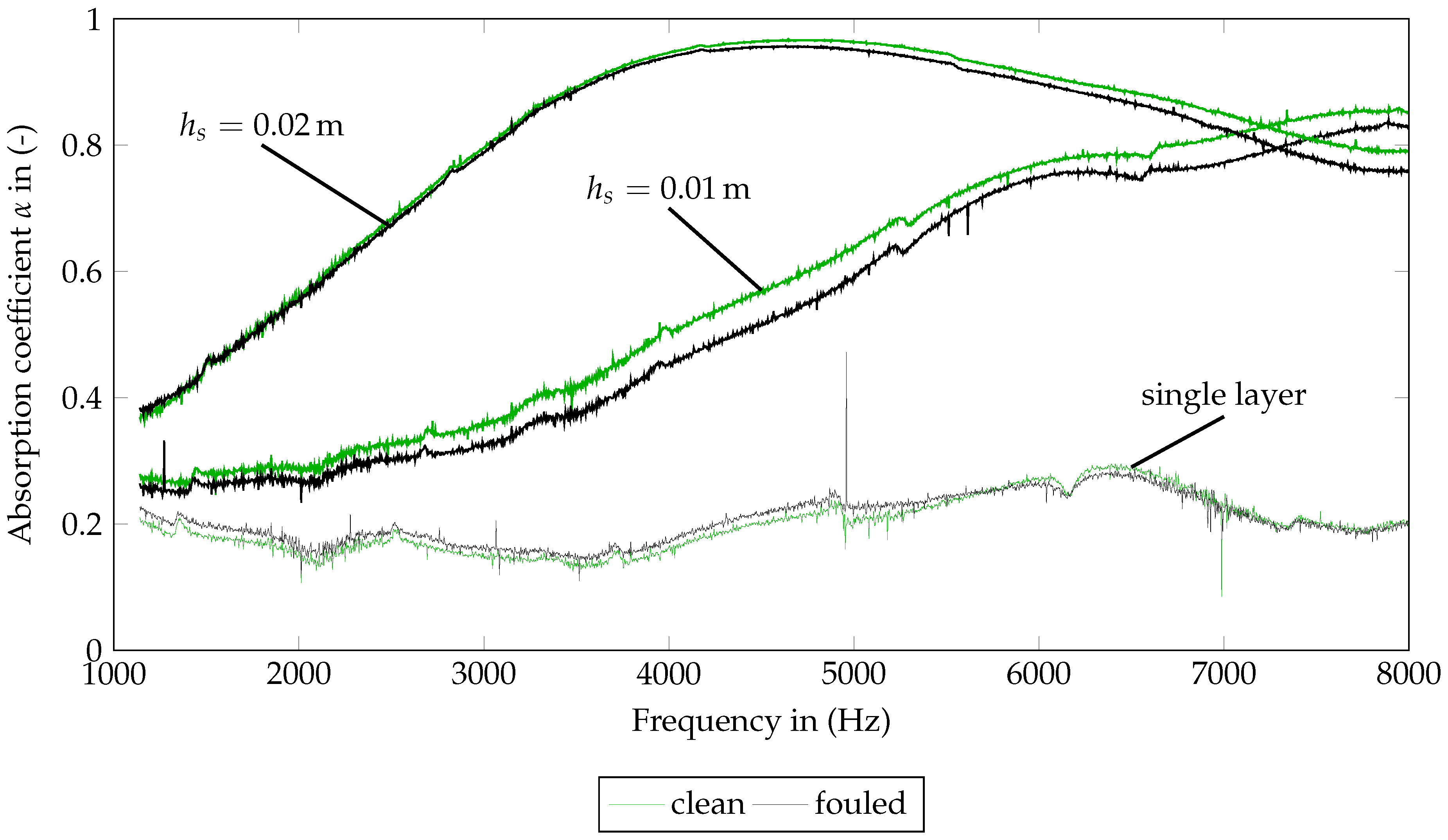
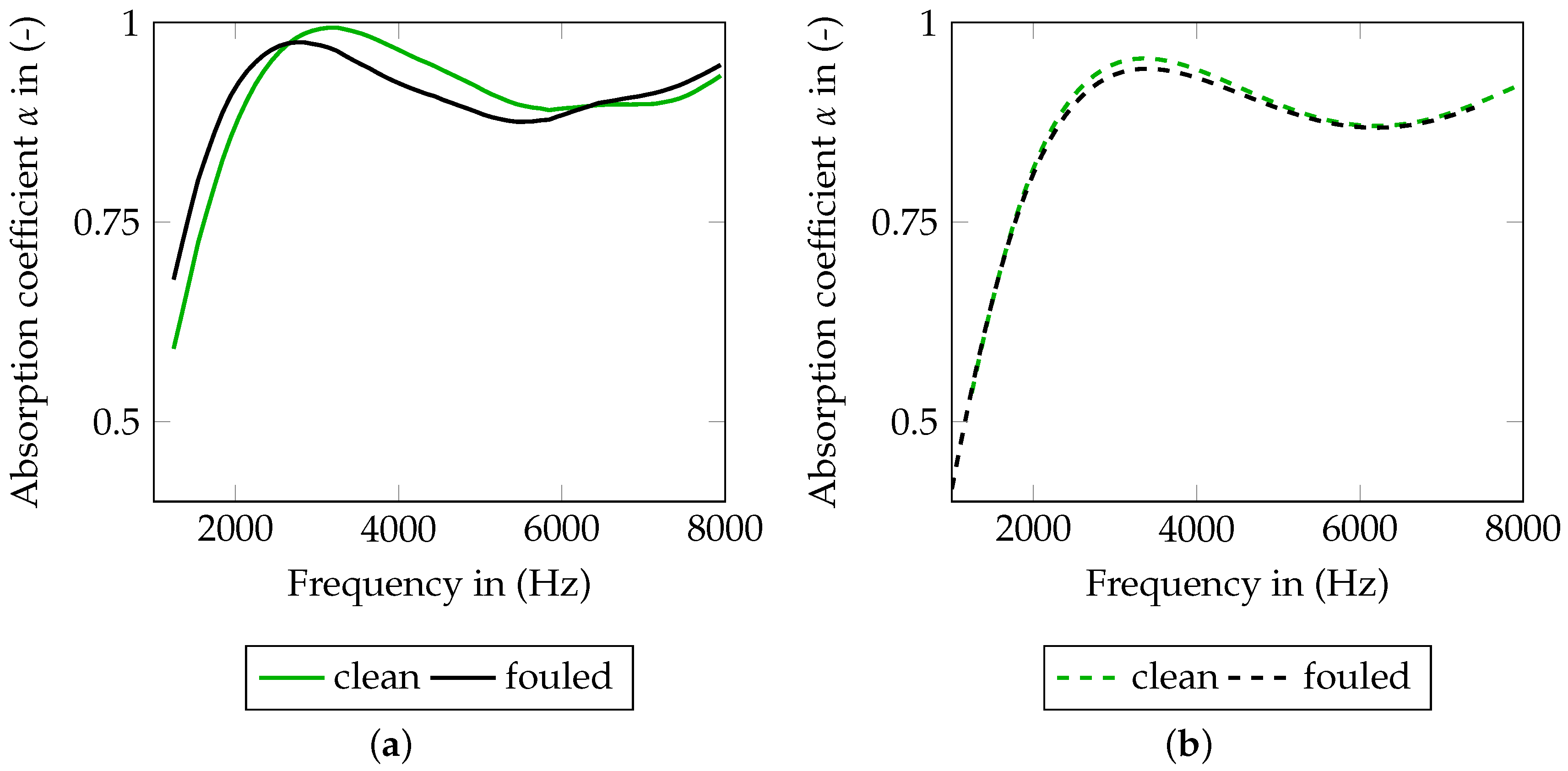
3.2. Acoustic Characterization
4. Numerical Investigation
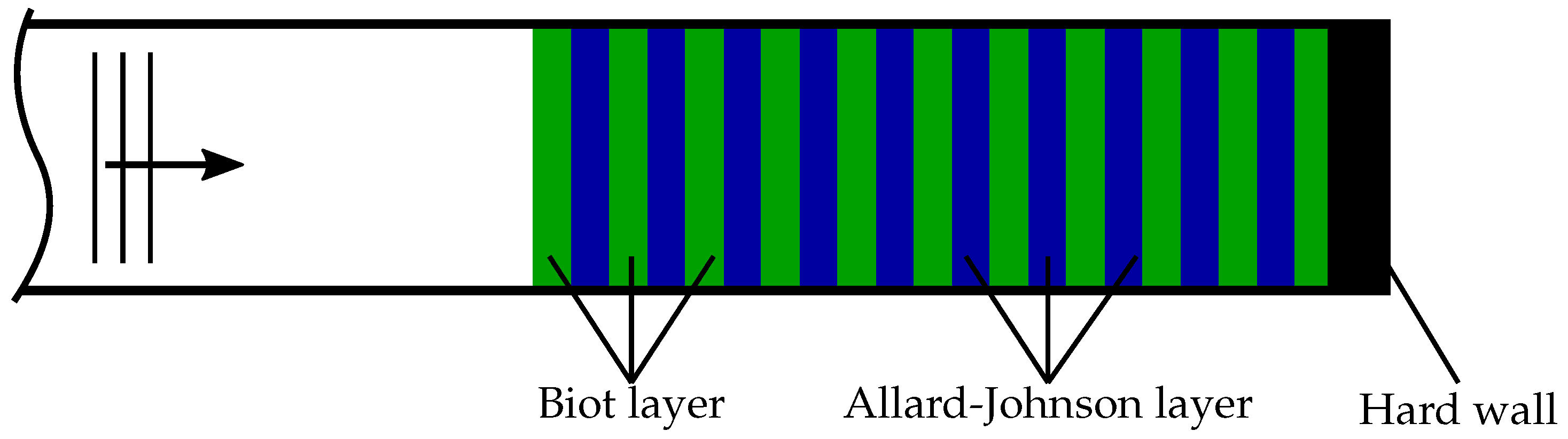
4.1. Modeling of Stapled Sintered Fiber Felts
- Viscous characteristic length Λ is introduced by Johnson et al. as an extension of the hydraulic radius (equal with factor 2 for cylindrical pores) in 1986 [20]. The value is defined as two times the weighted pore’s volume integral divided by the weighted pore wall’s surface integral. The weighting is realised by the fluid’s velocity, respectively, within the volume and on the surface. For common porous materials, the following assumption is taken from literature [21]:where c is an acoustic value describing the pores and η is the dynamic viscosity of air ().
- Thermal characteristic length is defined by Champoux and Allard in 1991 [18] and is used to describe thermal dissipation effects at higher frequencies. equals two times the pore’s volume divided by the pore wall’s surface and influences the bulk modulus of the material layer. For common porous materials, the following assumptions are taken from literature [21]:
4.2. Modeling of Fouling
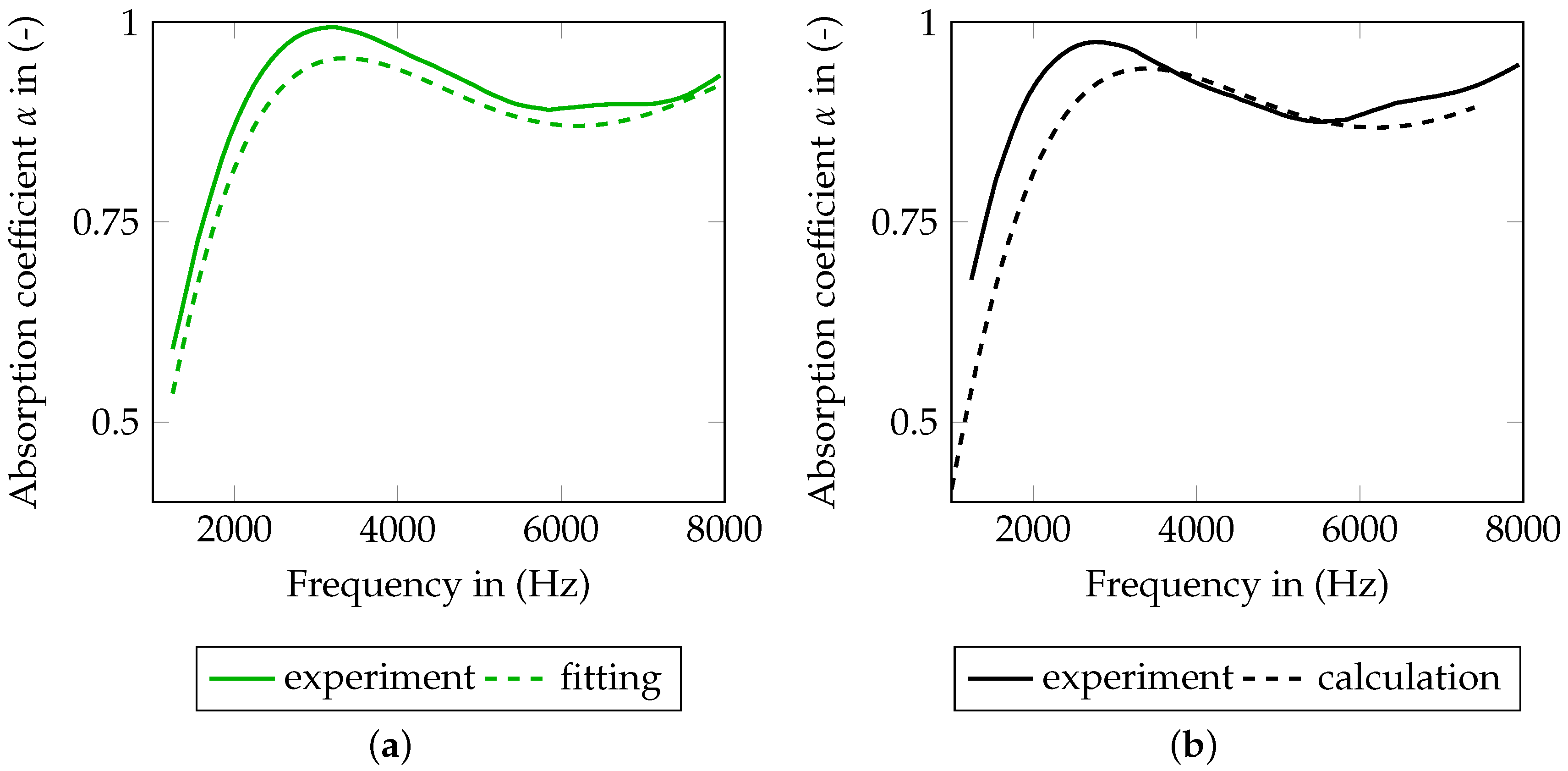
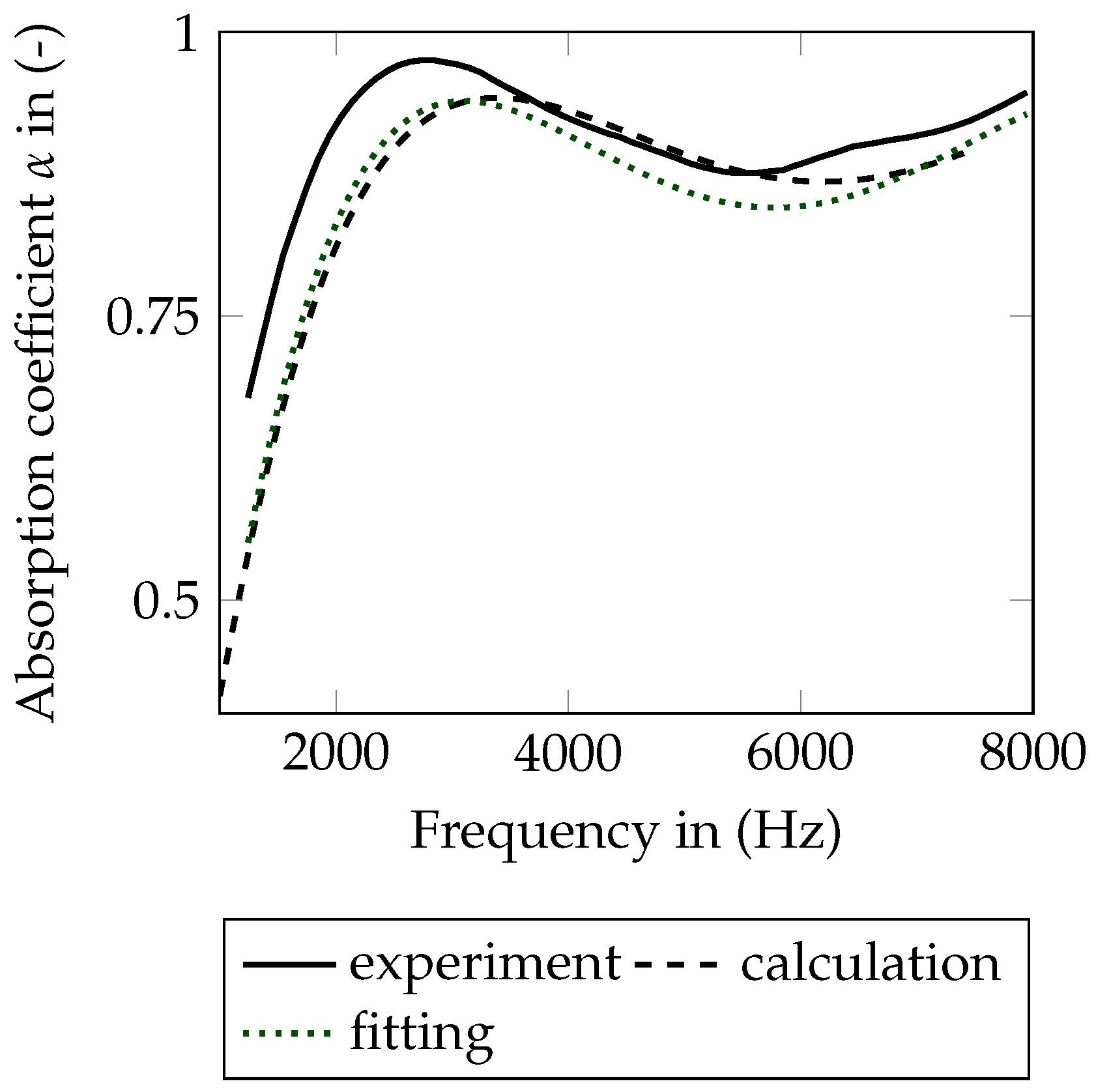
4.3. Inverse Parameter Identification
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CT | Computed Tomography |
| SEM | Scanning Electron Microscope |
| SFF | Sintered Fiber Felt |
| TMM | Transfer Matrix Method |
References
- Revell, J.; Kuntz, H.; Balena, F.; Horne, C.; Storms, B.; Dougherty, R. Trailing-edge flap noise reduction by porous acoustic treatment. In Proceedings of the 3rd AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 12–14 May 1997.
- Herr, M.; Dobrinsky, W. Experimental investigation in low-noise trailing edge design. AIAA J. 2005, 6, 1167–1175. [Google Scholar] [CrossRef]
- Herr, M. Design criteria for low-noise trailing-edges. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference, Rome, Italy, 21–23 May 2007.
- Delfs, J.; Fassmann, B.; Lippitz, N.; Lummer, M.; Mößner, M.; Müller, L.; Rurkowska, K.; Uphoff, S. SFB 880: Aeroacoustic research for low noise take-off and landing. CEAS Aeronaut. J. 2014. [Google Scholar] [CrossRef]
- Herr, M.; Rossignol, K.-S.; Delfs, J.; Mößner, M.; Lippitz, N. Specification of porous materials for low-noise trailing-edge applications. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014.
- Lippitz, N.; Rösler, J. Potential of metal fiber felts as passive absorbers in absorption silencers. Metals 2013, 3, 150–158. [Google Scholar] [CrossRef]
- Lippitz, N.; Hinze, B.; Rösler, J. Characterization of porous materials. In SFB 880 - Fundamentals of High-Lift for Future Commercial Aircraft, Biennial Report; TU Braunschweig, Campus Forschungsflughafen: Braunschweig, Germany, 2013; pp. 29–39. [Google Scholar]
- Blass, E. Geometrische und strömungstechnische untersuchungen an drahtgeweben. Chem. Ing. Tech. 1964, 7, 747–758. [Google Scholar] [CrossRef]
- Armour, J.C.; Cannon, J.N. Fluid through woven screens. AIChE J. 2013, 3, 415–420. [Google Scholar] [CrossRef]
- Müller, M.; Piesche, M. Ähnlichkeitsgesetze zur beschreibung des anfangsdruckverlustes metallischer drahtgewebe bei der filtration nicht-newtonscher fluide. Filtr. Sep. 2013, 5, 284–291. [Google Scholar]
- DIN EN 29053: Akustik. Materialien für Akustische Anwendungen; Deutsches Institut für Normung: Berlin, Germany, 1993.
- Atalla, F.; Panneton, R. Inverse acoustical characterization of open cell porous media using impedance tube measurements. Can. Acoust. 2005, 33, 11–24. [Google Scholar]
- DIN EN ISO 10534-2. Determination of Sound Absorption Coefficient and Acoustic Impedance with the Interferometer; Deutsches Institut für Normung: Berlin, Germany, 2001.
- Lippitz, N. Analyse der Schallabsorptionseigenschaften in Abhängigkeit der Struktur Verschiedener Metallischer Vliese; Studienarbeit, TU Braunschweig: Braunschweig, Germany, 2011. [Google Scholar]
- Brouard, B.; Lafarge, D.; Allard, J.-F. A general method of modelling sound propagation in layered media. J. Sound Vib. 1995. [Google Scholar] [CrossRef]
- Biot, M.A. The theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low frequency range. II. Higher frequency range. J. Acoust. Soc. Am. 1956. [Google Scholar] [CrossRef]
- Johnson, D.L.; Koplik, J.; Dashen, R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. J. Fluid Mech. 1987, 176, 379–402. [Google Scholar] [CrossRef]
- Champoux, Y.; Allard, J.-F. Dynamic tortuosity and bulk modulus in air-saturated porous media. J. Appl. Phys. 1991. [Google Scholar] [CrossRef]
- Allard, J.-F.; Champoux, Y. New empirical equations for sound absorption in rigid frame fibrous materials. J. Acoust. Soc. Am. 1992. [Google Scholar] [CrossRef]
- Johnson, D.L.; Koplik, J.; Schwartz, L.M. New pore size parameter characterizing transport in porous media. Phys. Rev. Lett. 1986. [Google Scholar] [CrossRef] [PubMed]
- Allard, J.-F. Propagation of Sound in Porous Media: Modeling Sound Absorbing Materials; Elsevier Applied Science: New York, NY, USA, 1993. [Google Scholar]
- Lippitz, N.; Rurkowska, K.; Rösler, J.; Langer, S.C. Fouling behavior of porous metals. Proc. Mater. Sci. 2013. [Google Scholar] [CrossRef]




| Material | m) | m) | m) | w m) | m) | ||
|---|---|---|---|---|---|---|---|
| SFF 100 | 0.92 | 430 | 26 | 254 | 432 | 0.69 | 142 |
| SFF 150 | 0.94 | 270 | 24 | 252 | 424 | 0.69 | 140 |
| Parameter | SFF 100 | SFF 150 | ||
|---|---|---|---|---|
| Clean | Fouled | Clean | Fouled | |
| (Ns/m) | ||||
| (m) | ||||
| r (Ns/m) | 119,208 | 129,209 | 56,036 | 57,333 |
| Material | Staple Size (m) | Number of Specimens (-) |
|---|---|---|
| SFF 100 | ||
| SFF 150 |
| Parameter | Symbol | Unit | Functional Layer | Support Grid |
|---|---|---|---|---|
| layer thickness | (m) | |||
| Young’s modulus | E | (N/m2) | - | |
| Poisson ratio | ν | (-) | - | |
| structural density | (kg/m3) | 8000 | - | |
| loss factor | (-) | - | ||
| fluid density | (kg/m3) | |||
| speed of sound | (m/s) | 343 | 343 | |
| porosity | Φ | (-) | ||
| flow resistivity | r | (Ns/m4) | 119,208 | 2610 |
| tortuosity | (-) | 1–1.6 | 1 | |
| viscous length | Λ | (µm) | 409 | |
| thermal length | (µm) | 204 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lippitz, N.; Blech, C.; Langer, S.; Rösler, J. Identification of Material Parameters for the Simulation of Acoustic Absorption of Fouled Sintered Fiber Felts. Materials 2016, 9, 709. https://doi.org/10.3390/ma9080709
Lippitz N, Blech C, Langer S, Rösler J. Identification of Material Parameters for the Simulation of Acoustic Absorption of Fouled Sintered Fiber Felts. Materials. 2016; 9(8):709. https://doi.org/10.3390/ma9080709
Chicago/Turabian StyleLippitz, Nicolas, Christopher Blech, Sabine Langer, and Joachim Rösler. 2016. "Identification of Material Parameters for the Simulation of Acoustic Absorption of Fouled Sintered Fiber Felts" Materials 9, no. 8: 709. https://doi.org/10.3390/ma9080709
APA StyleLippitz, N., Blech, C., Langer, S., & Rösler, J. (2016). Identification of Material Parameters for the Simulation of Acoustic Absorption of Fouled Sintered Fiber Felts. Materials, 9(8), 709. https://doi.org/10.3390/ma9080709





