Removal of Cr(VI) from Water Using a New Reactive Material: Magnesium Oxide Supported Nanoscale Zero-Valent Iron
Abstract
:1. Introduction
2. Results and Discussion
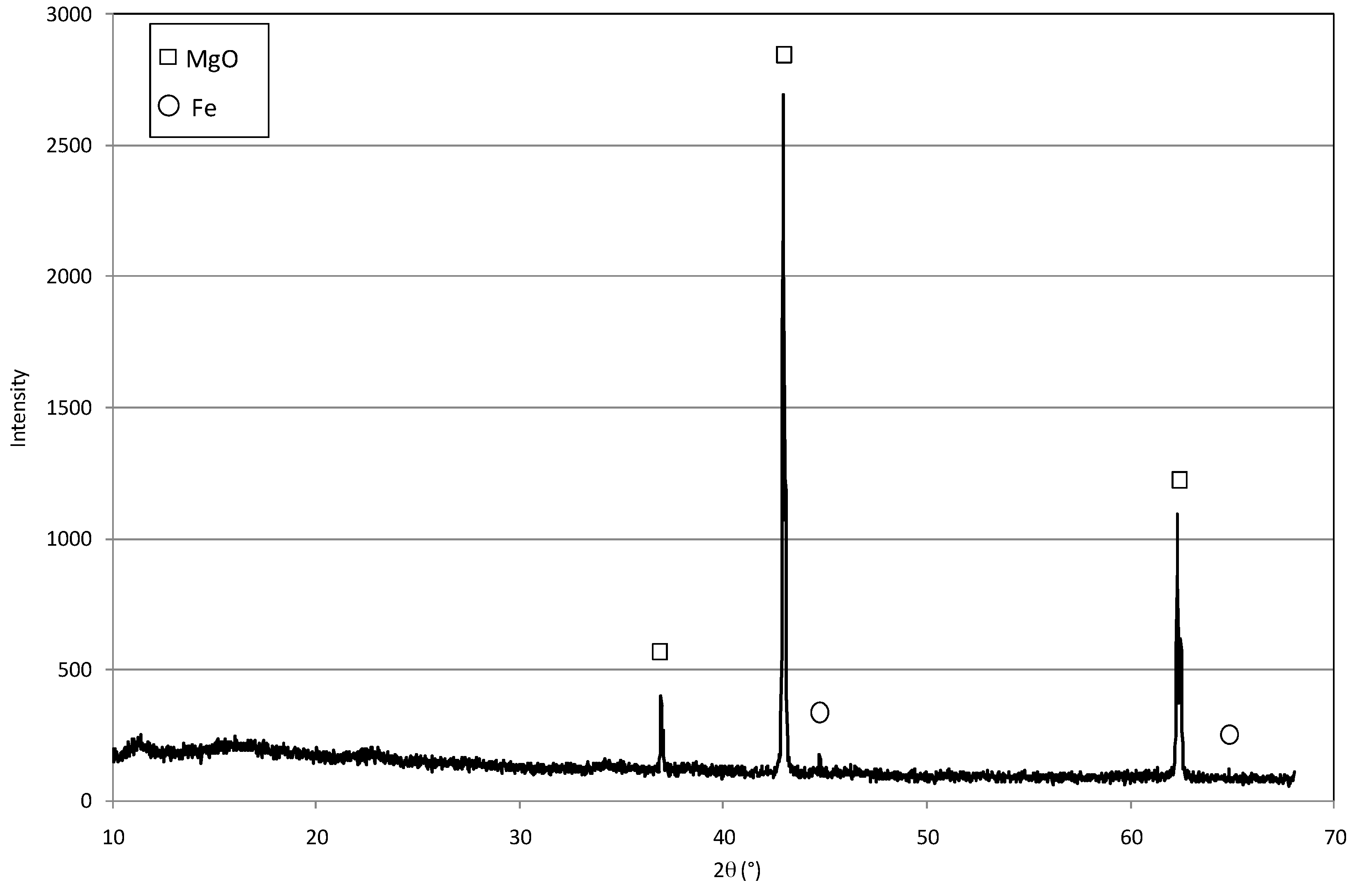
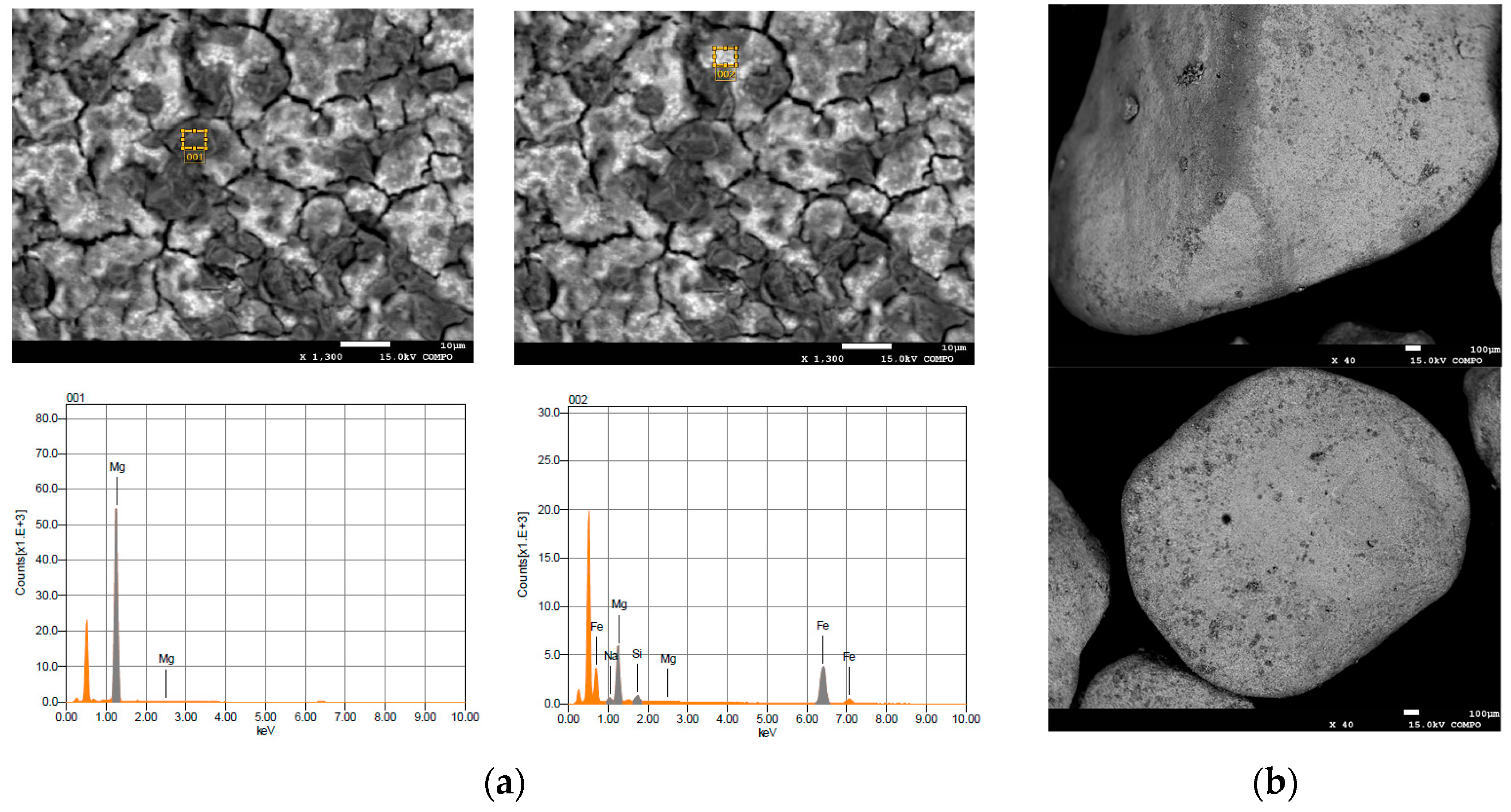
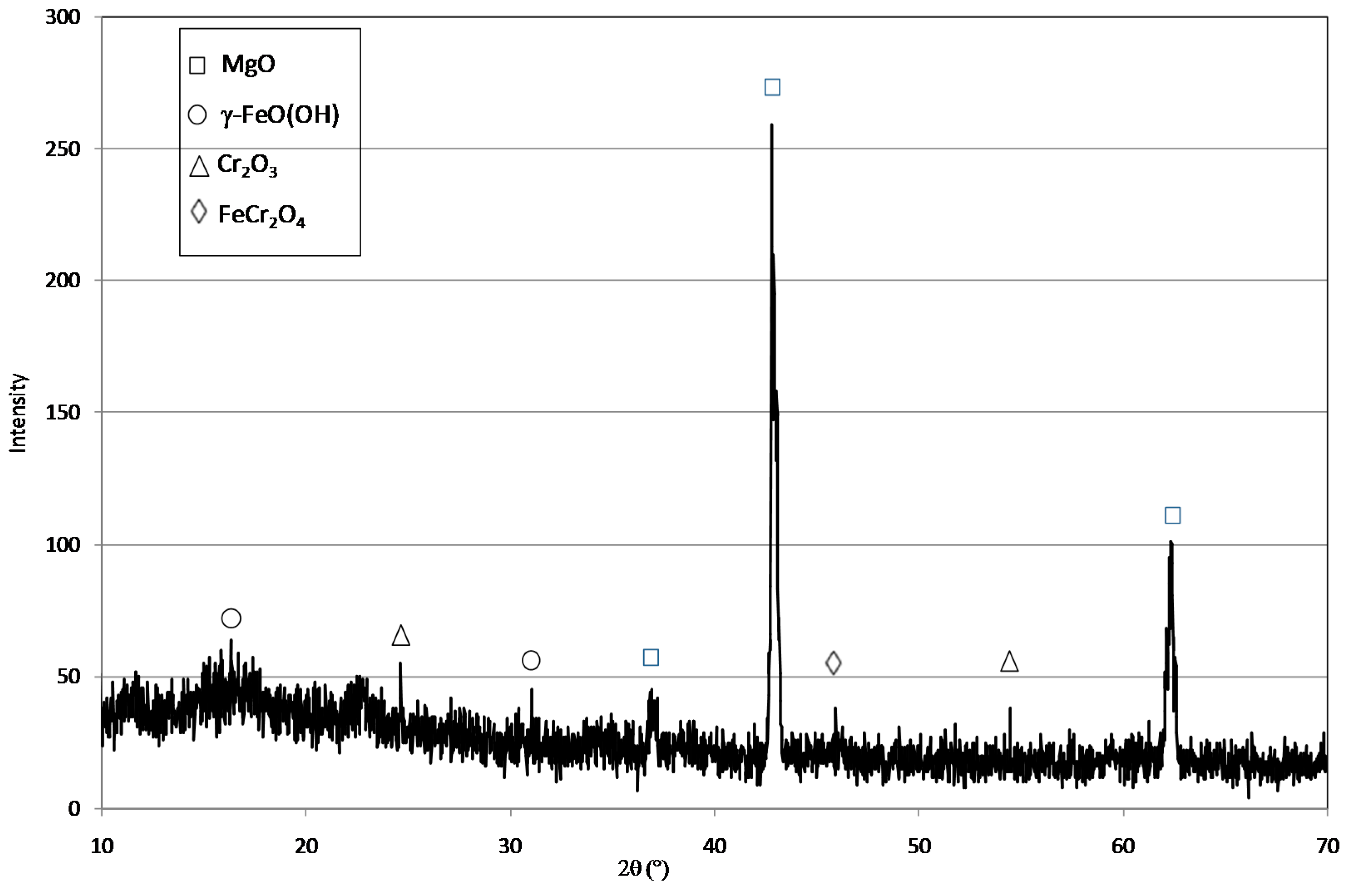
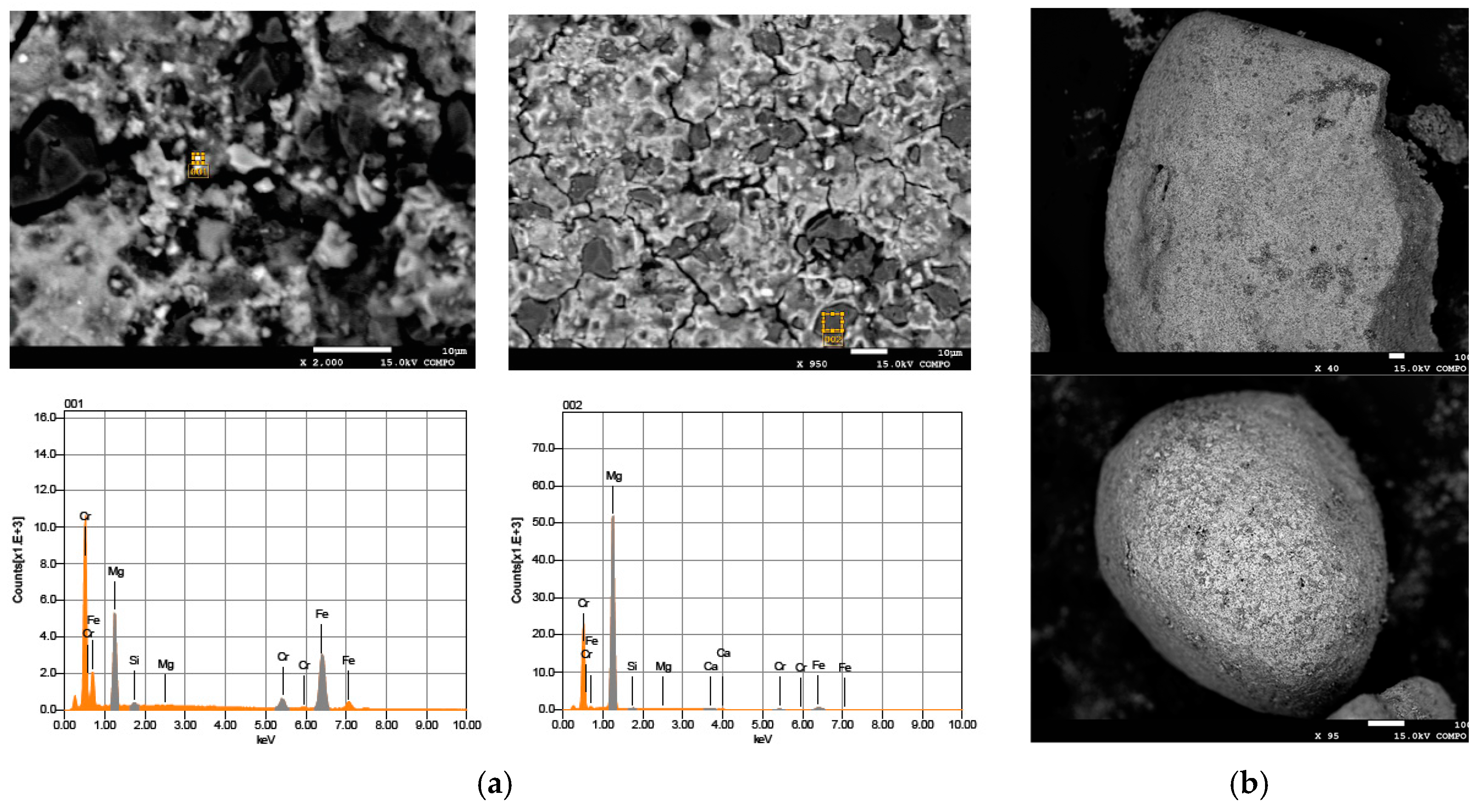
2.1. Reactive Material
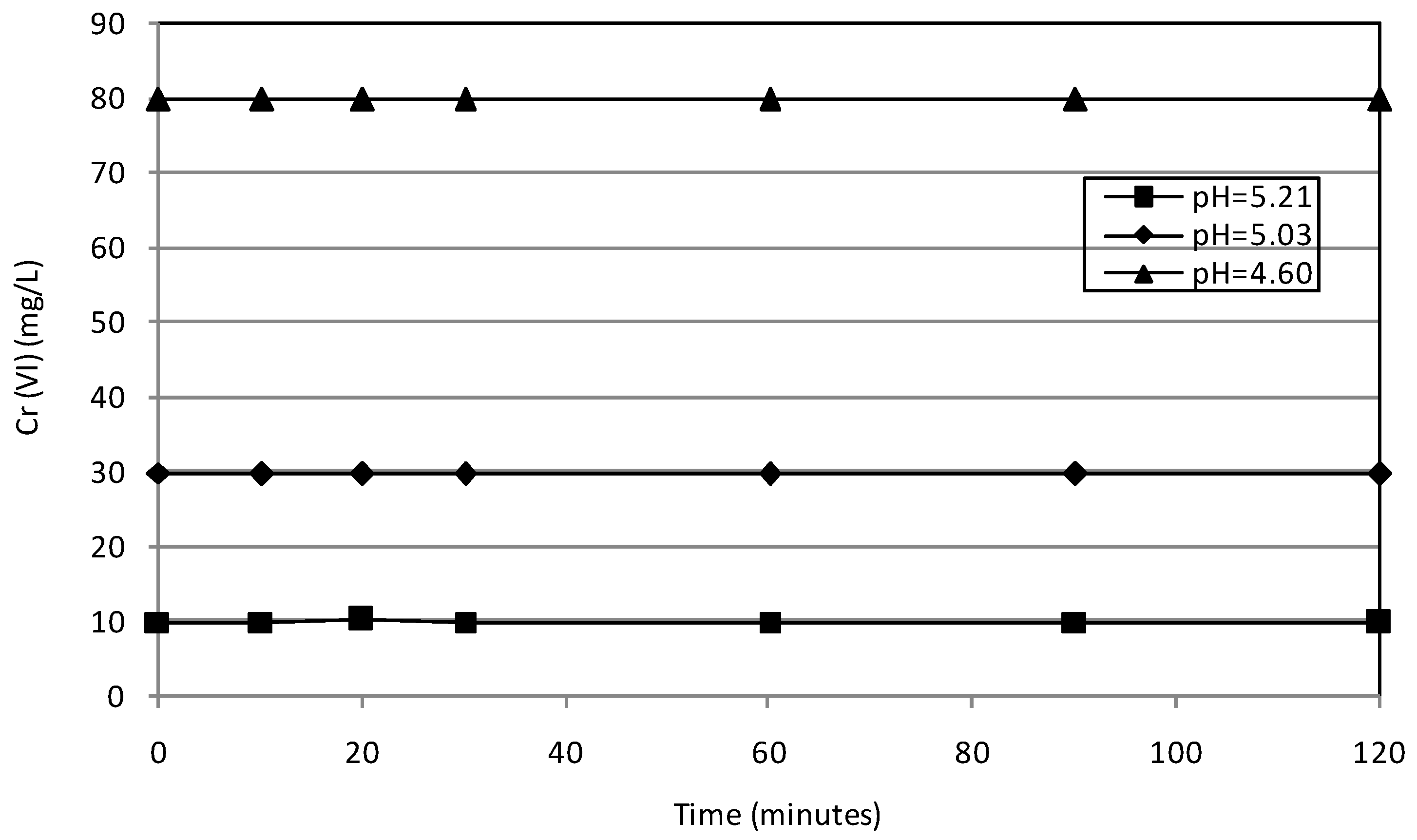
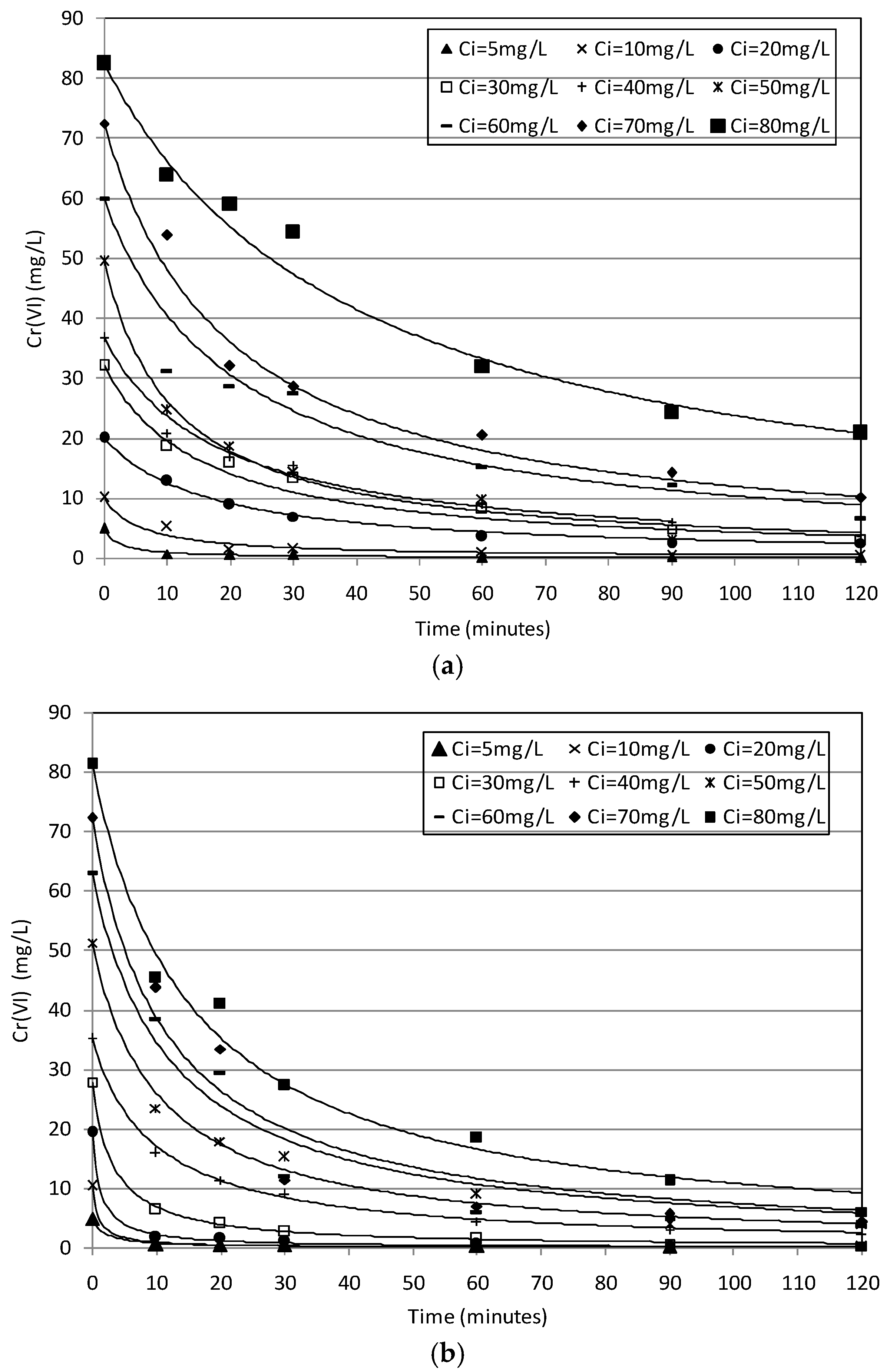
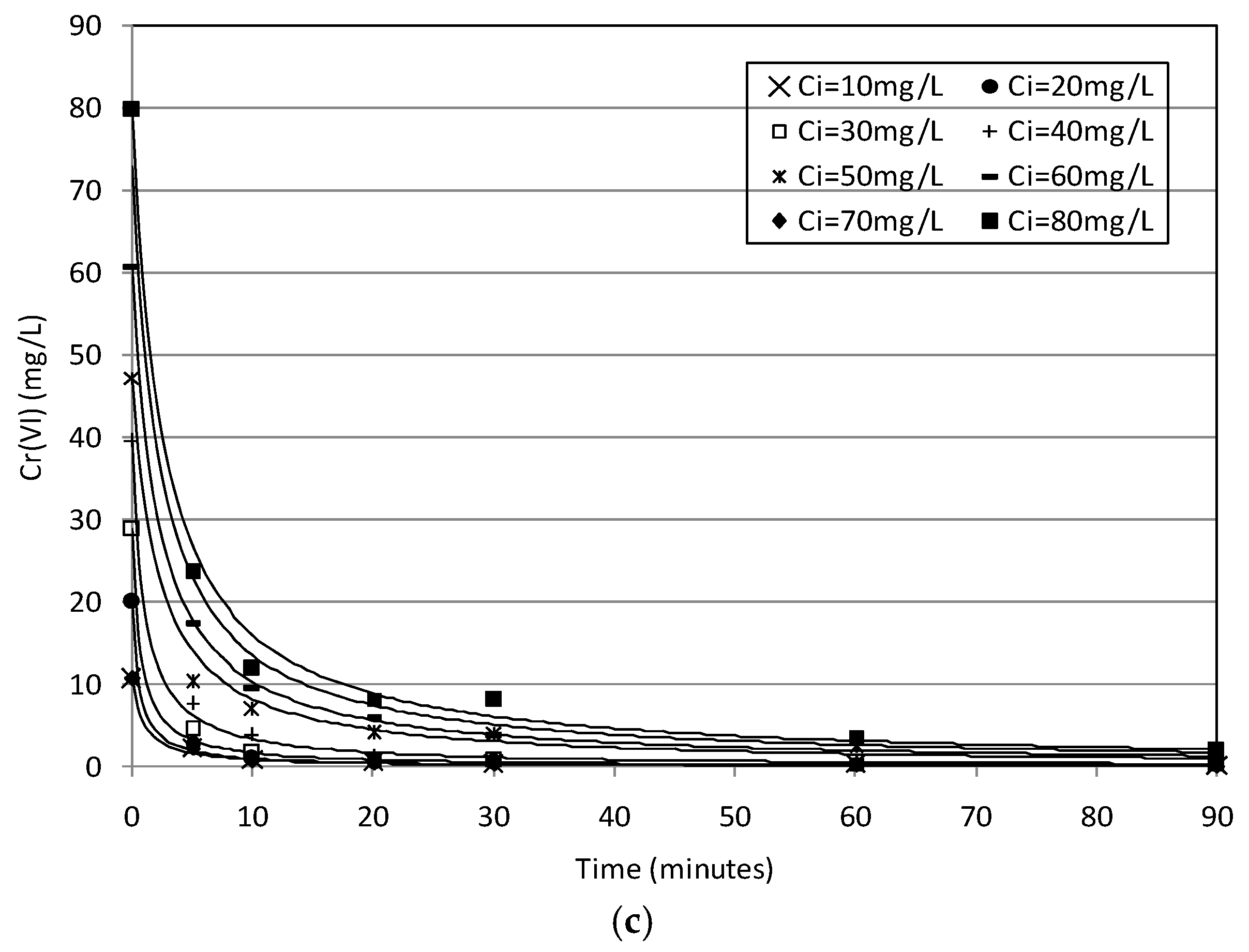
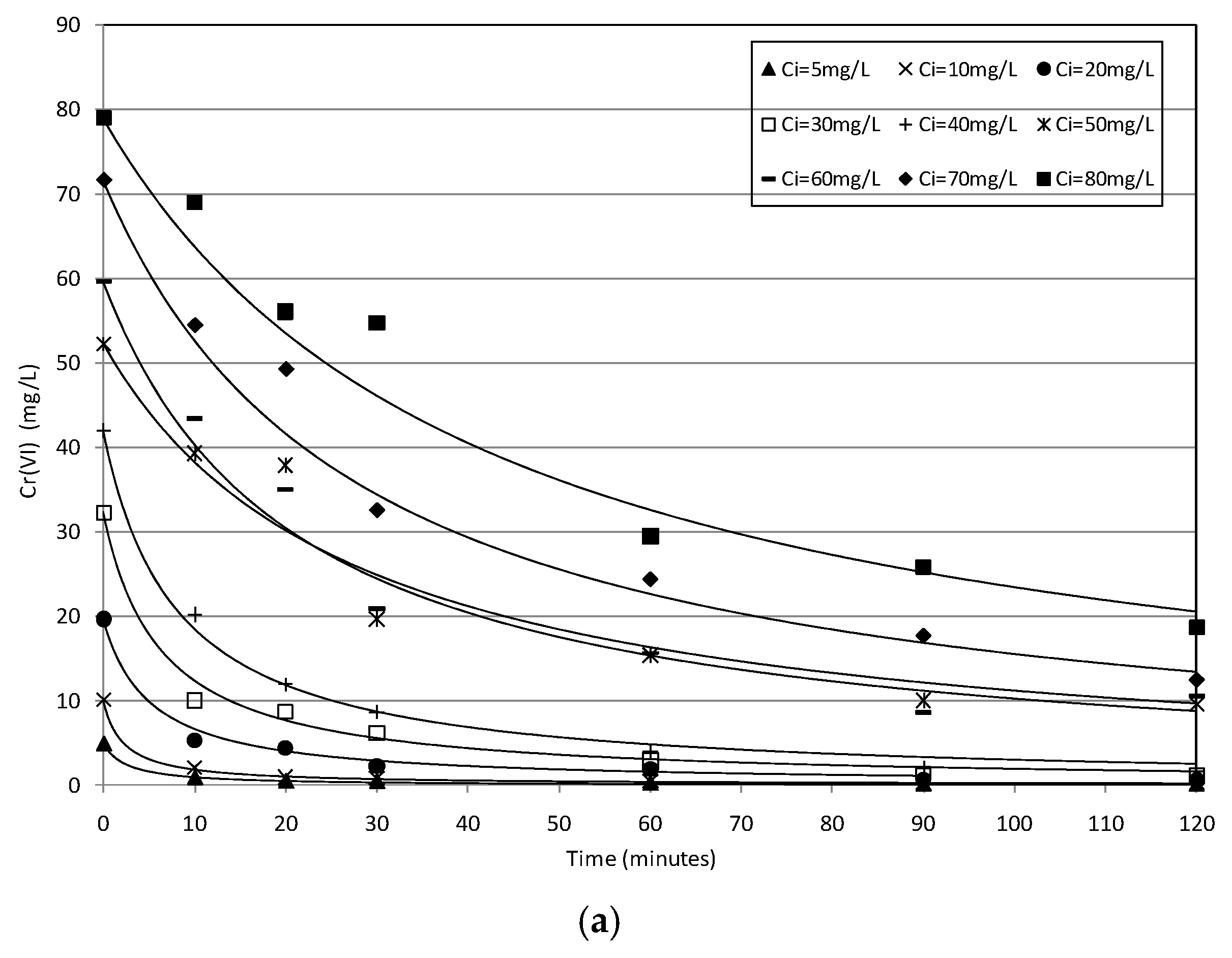
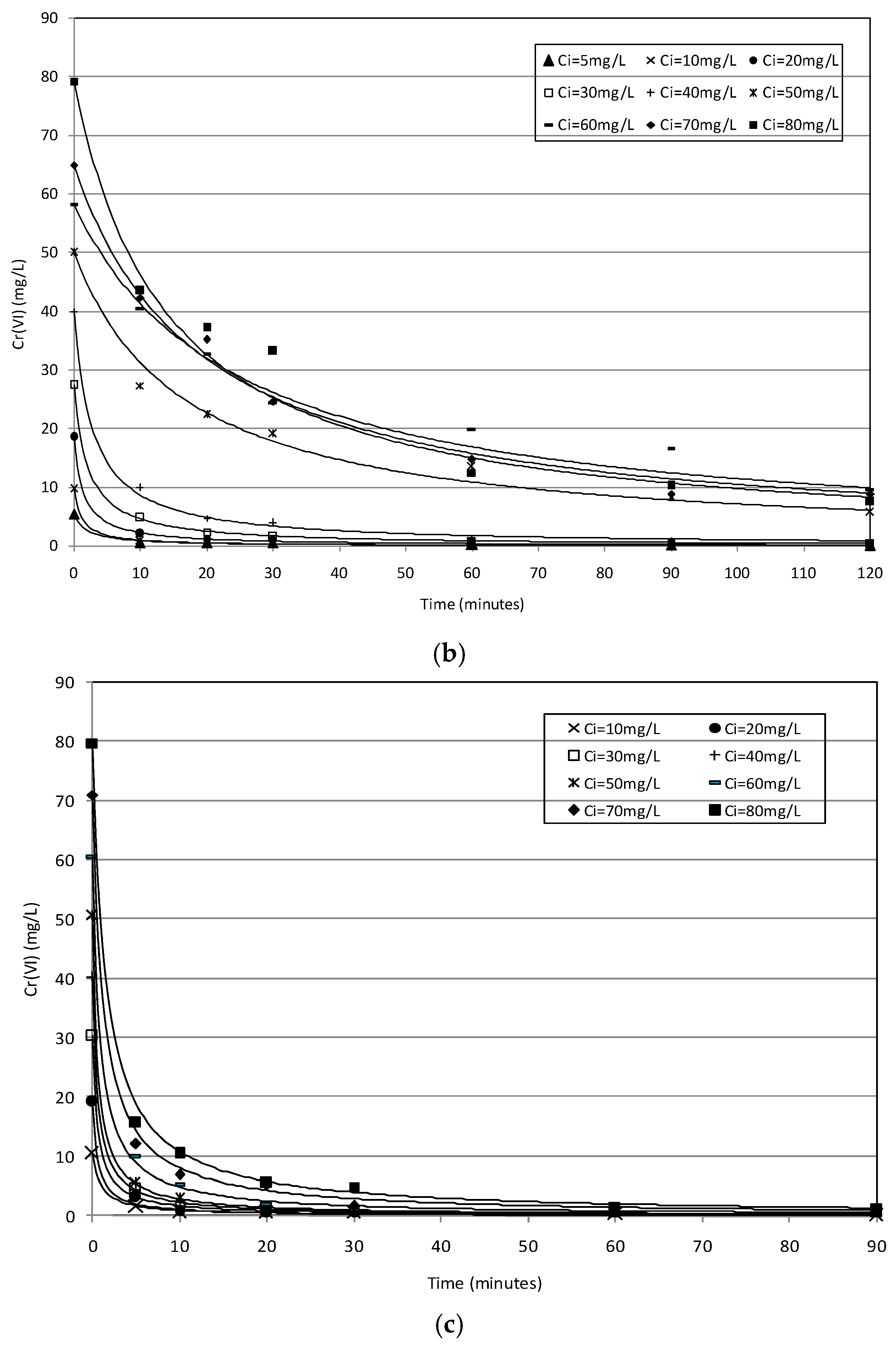
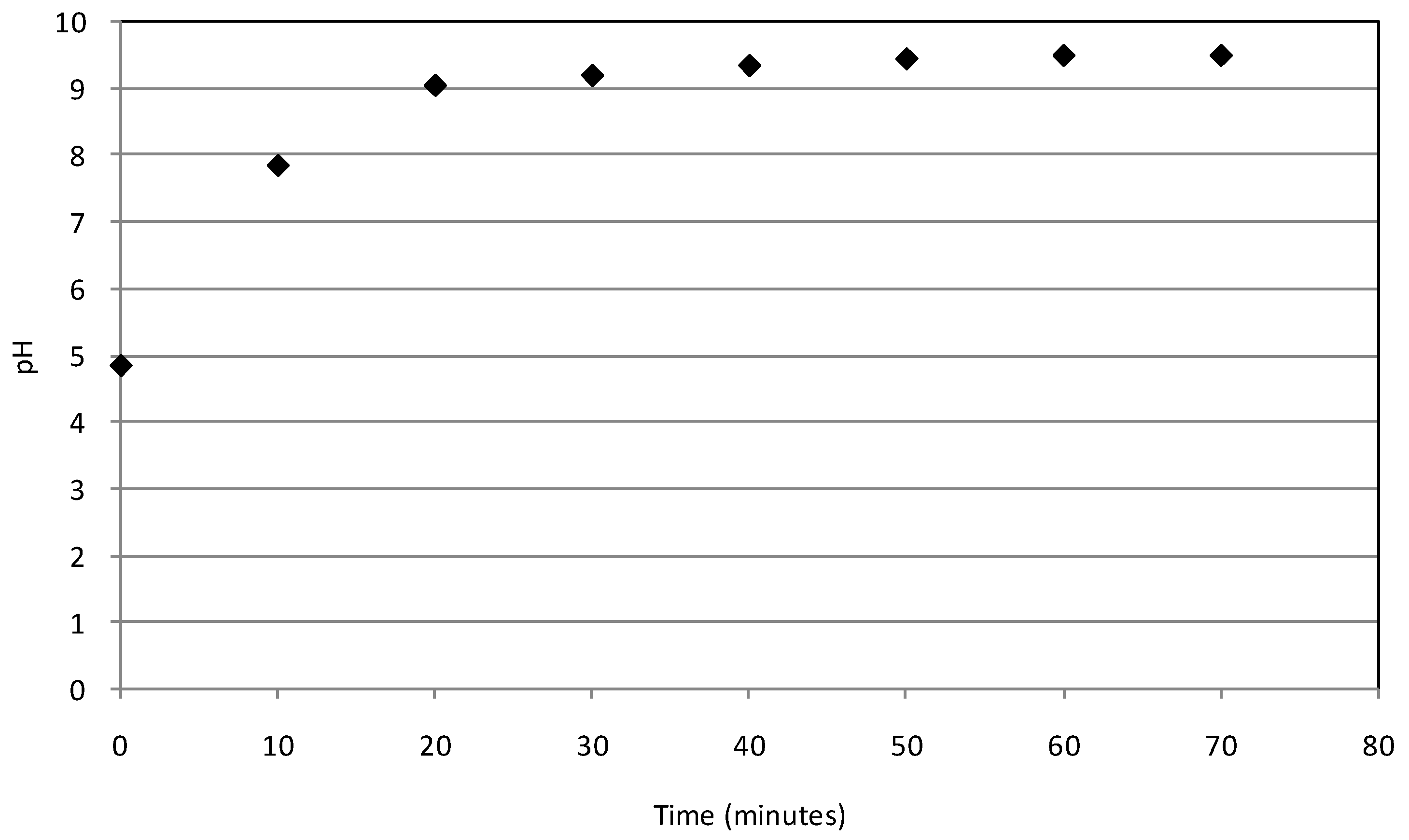
2.2. Batch Tests
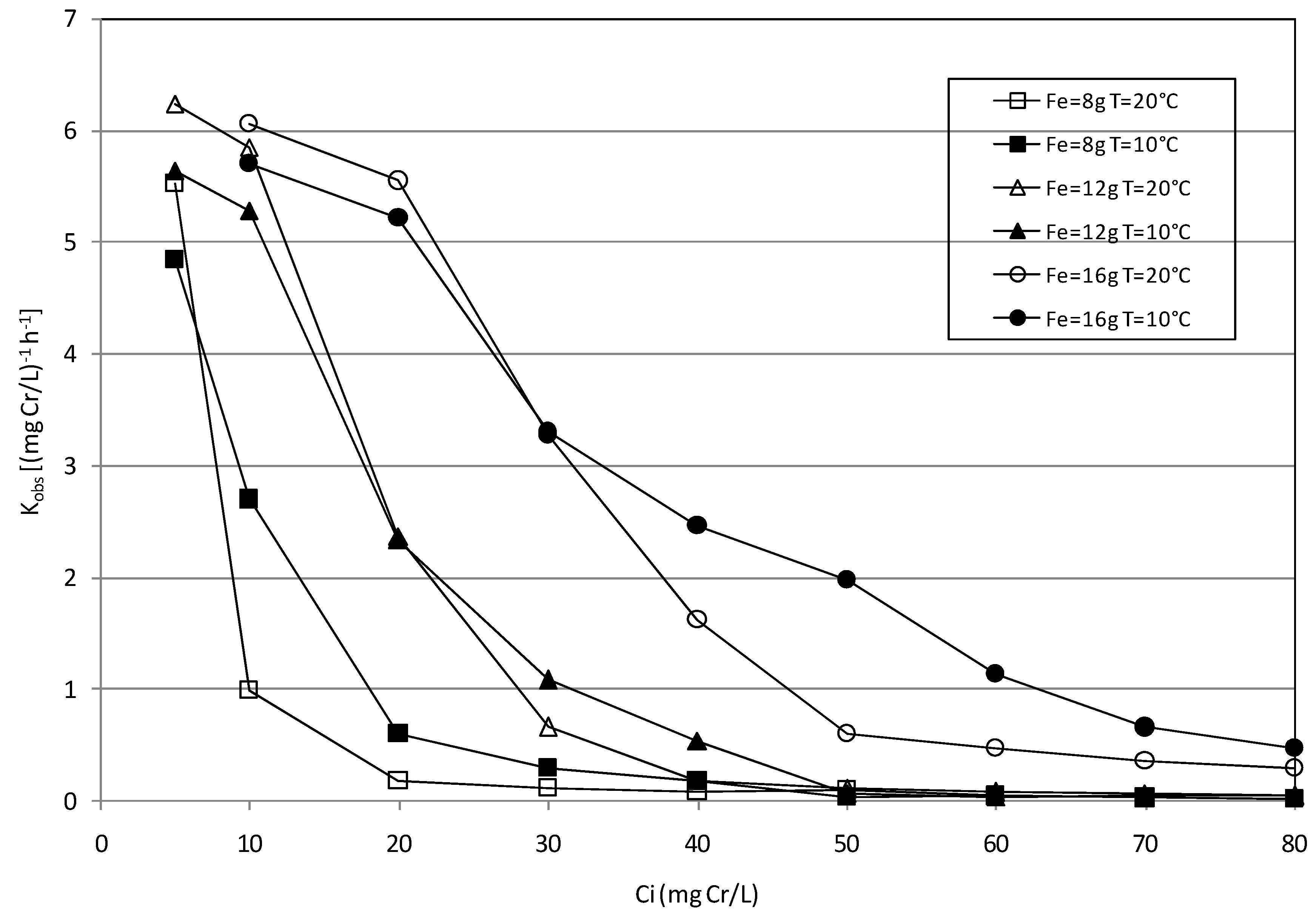
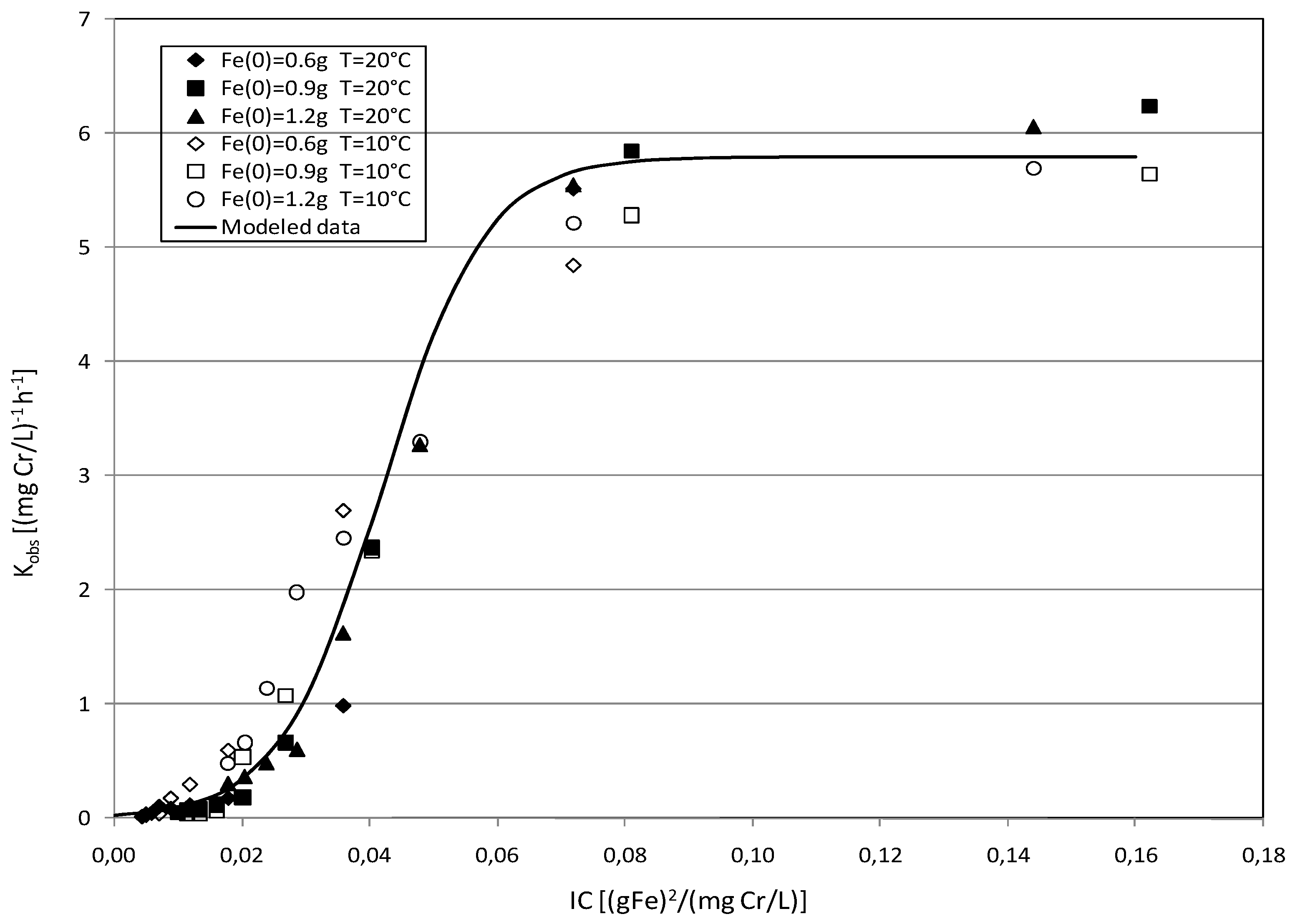
2.3. Kinetic Analysis
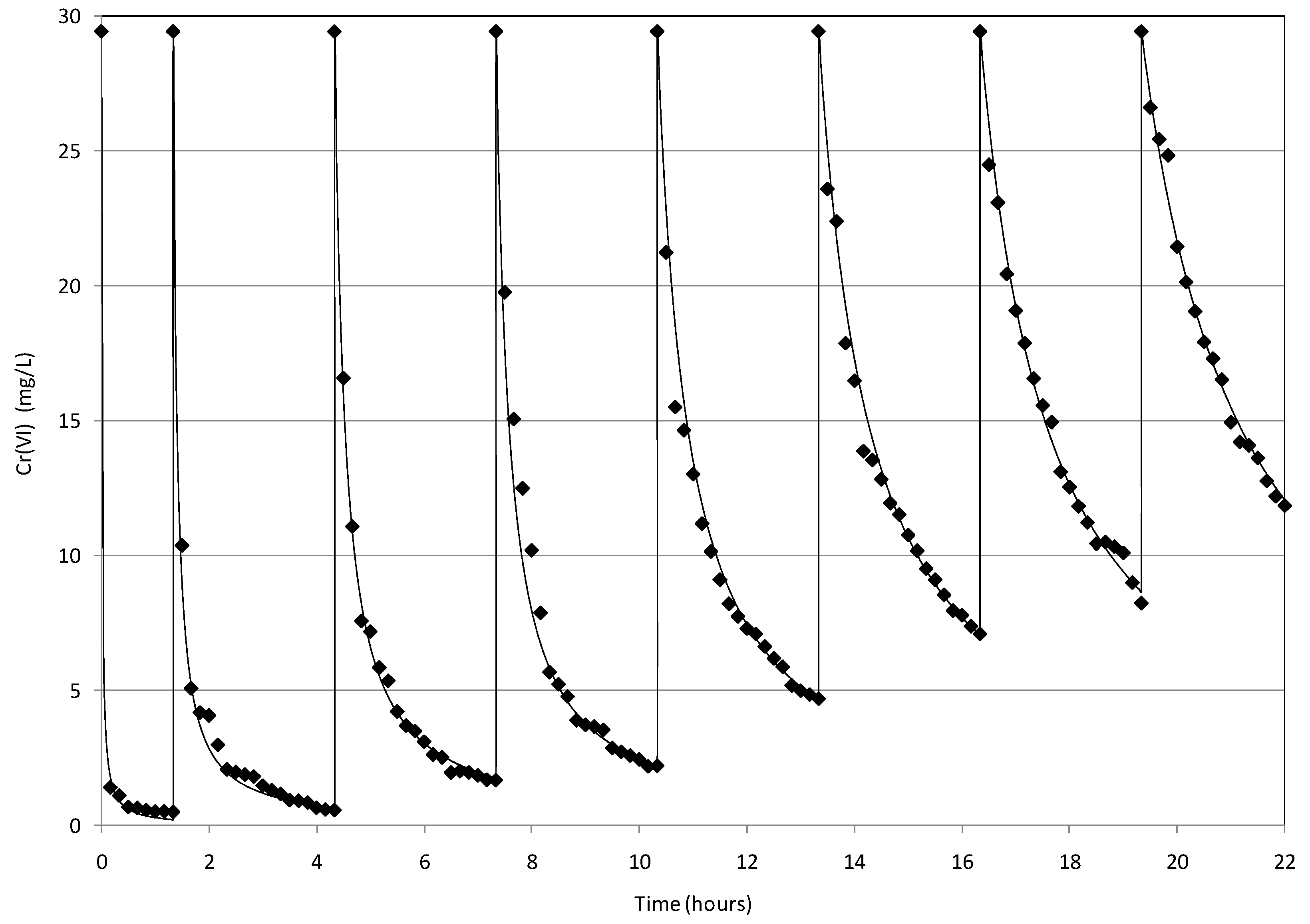
2.4. Reuse of MgO-NZVI
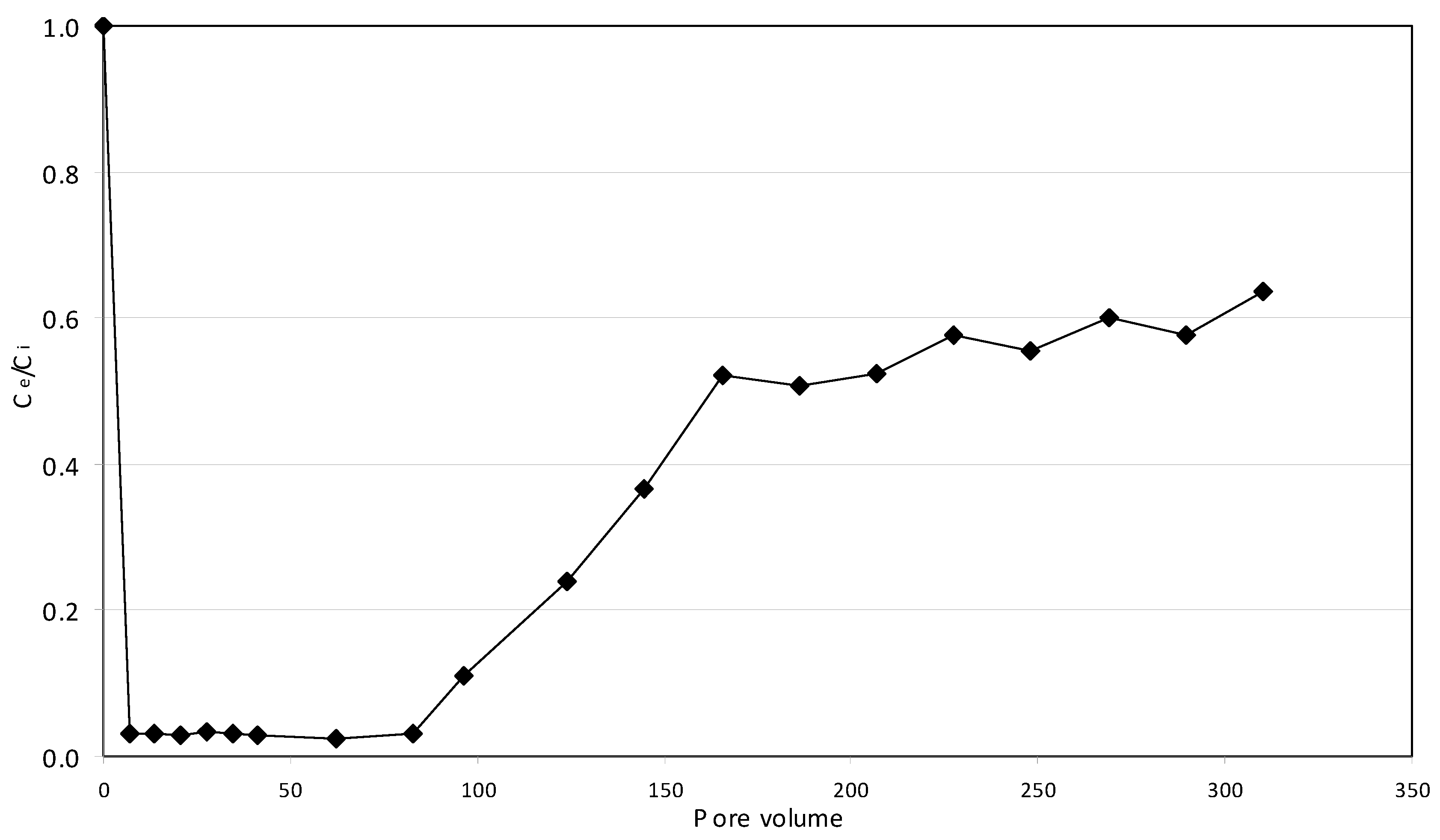
2.5. Continuous Tests
3. Materials and Methods
3.1. Chemicals
3.2. Preparation of Reactive Material
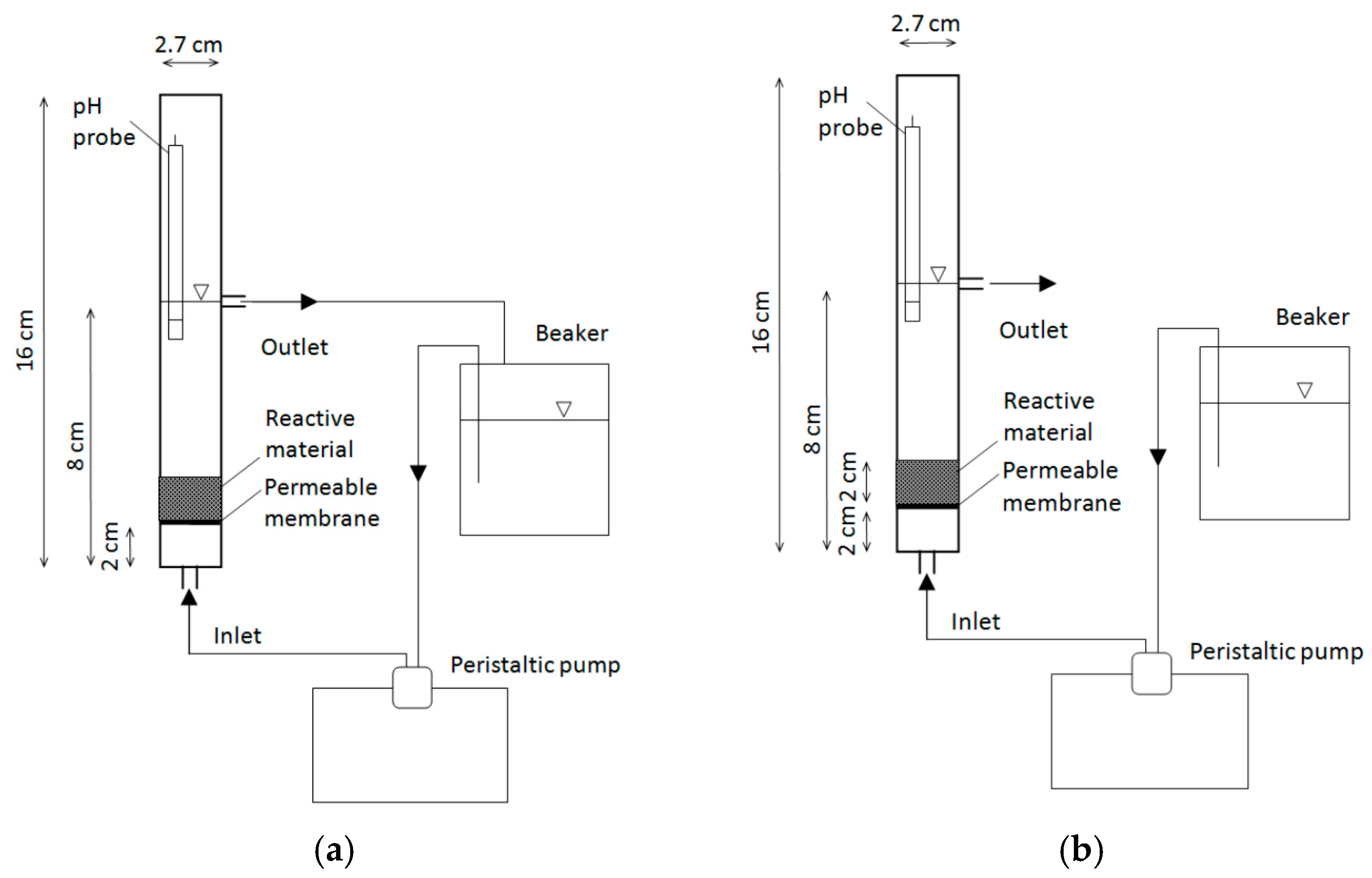
3.3. Column Tests
3.4. Analytical Methods and Presentation of Results
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Li, J.; Zhang, Y. Mechanism insights into enhanced Cr(VI) removal using nanoscale zerovalent iron supported on the pillared bentonite by macroscopic and spectroscopic studies. J. Hazard. Mater. 2012, 227, 211–218. [Google Scholar] [CrossRef] [PubMed]
- Quan, G.; Zhang, J.; Guo, J.; Lan, Y. Removal of Cr(VI) from Aqueous Solution by Nanoscale Zero-Valent Iron Grafted on Acid-Activated Attapulgite. Water Air Soil Pollut. 2014, 225, 1979. [Google Scholar] [CrossRef]
- Wu, P.; Li, S.; Ju, L.; Zhu, N.; Wu, J.; Li, P.; Dang, Z. Mechanism of the reduction of hexavalent chromium by organo-montmorillonite supported iron nanoparticles. J. Hazard. Mater. 2012, 219, 283–288. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.-N.; Zhang, X.; Chen, Z.-L. Removal of Chromium (VI) from wastewater using bentonite-supported nanoscale zero-valent iron. Water Res. 2011, 45, 886–892. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Hong, H.-J.; Jung, J.; Kim, S.-H.; Yang, J.-W. Degradation of trichloroethylene (TCE) by nanoscale zero-valent iron (nZVI) immobilized in alginate bead. J. Hazard. Mater. 2010, 176, 1038–1043. [Google Scholar] [CrossRef] [PubMed]
- Basu, A.; Johnson, T.M. Determination of Hexavalent Chromium Reduction Using Cr Stable Isotopes: Isotopic Fractionation Factors for Permeable Reactive Barrier Materials. Environ. Sci. Technol. 2012, 46, 5353–5360. [Google Scholar] [CrossRef] [PubMed]
- Jeen, S.-W.; Blowes, D.W.; Gillham, R.W. Performance evaluation of granular iron for removing hexavalent chromium under different geochemical conditions. J. Contam. Hydrol. 2008, 95, 76–91. [Google Scholar] [CrossRef] [PubMed]
- Wanner, C.; Eggenberger, U.; Mäder, U. Reactive transport modelling of Cr(VI) treatment by cast iron under fast flow conditions. Appl. Geochem. 2011, 26, 1513–1523. [Google Scholar] [CrossRef]
- Wilkin, R.T.; Su, C.; Ford, R.G.; Paul, C.J. Chromium-Removal Processes during Groundwater Remediation by a Zerovalent Iron Permeable Reactive Barrier. Environ. Sci. Technol. 2005, 39, 4599–4605. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, Y.; Li, J.; Sheng, G.; Zhang, Y.; Zheng, X. Enhanced Cr(VI) removal by using the mixture of pillared bentonite and zero-valent iron. Chem. Eng. J. 2012, 185, 243–249. [Google Scholar] [CrossRef]
- Li, X.-Q.; Elliott, D.-W.; Zhang, W.-X. Zero-Valent Iron Nanoparticles for Abatement of Environmental Pollutants: Materials and Engineering Aspects. Crit. Rev. Sol. State Mater. Sci. 2006, 31, 111–122. [Google Scholar] [CrossRef]
- Cundy, A.B.; Hopkinson, L.; Whitby, R.L.D. Use of iron-based technologies in contaminated land and groundwater remediation: A review. Sci. Total Environ. 2008, 400, 42–51. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, Y.; Meng, Q. Removal of nitrate by zero-valent iron and pillared bentonite. J. Hazard. Mater. 2010, 174, 188–193. [Google Scholar] [CrossRef] [PubMed]
- Alowitz, M.J.; Scherer, M.M. Kinetics of Nitrate, Nitrite, and Cr(VI) Reduction by Iron Metal. Environ. Sci. Technol. 2002, 36, 299–306. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Qin, P.; Shao, J.; Peng, L.; Zeng, Q.; Gu, J.-D. Synthesis of reactive nanoscale zero valent iron using rectorite supports and its application for Orange II removal. Chem. Eng. J. 2013, 223, 1–7. [Google Scholar] [CrossRef]
- Hwang, Y.-H.; Kim, D.-G.; Shin, H.-S. Mechanism study of nitrate reduction by nano zero valent iron. J. Hazard. Mater. 2011, 185, 1513–1521. [Google Scholar] [CrossRef] [PubMed]
- Liou, Y.H.; Lo, S.-L.; Lin, C.-J.; Kuan, W.H.; Weng, S.C. Chemical reduction of an unbuffered nitrate solution using catalyzed and uncatalyzed nanoscale iron particles. J. Hazard. Mater. 2005, 127, 102–110. [Google Scholar] [CrossRef] [PubMed]
- Siciliano, A. Use of nanoscale zero-valent iron (NZVI) particles for chemical denitrification under different operating conditions. Metals 2015, 5, 1507–1519. [Google Scholar] [CrossRef]
- De Rosa, S.; Siciliano, A. A catalytic oxidation process of olive oil mill wastewaters using hydrogen peroxide and copper. Desal. Water Treat. 2010, 23, 187–193. [Google Scholar] [CrossRef]
- Li, X.-Q.; Cao, J.; Zhang, W.-X. Stoichiometry of Cr(VI) Immobilization Using Nanoscale Zerovalent Iron (nZVI): A Study with High-Resolution X-ray Photoelectron Spectroscopy (HR-XPS). Ind. Eng. Chem. Res. 2008, 47, 2131–2139. [Google Scholar] [CrossRef]
- Shi, L.-N.; Lin, Y.-M.; Zhang, X.; Chen, Z.-L. Synthesis, characterization and kinetics of bentonite supported nZVI for the removal of Cr(VI) from aqueous solution. Chem. Eng. J. 2011, 171, 612–617. [Google Scholar] [CrossRef]
- Kim, S.A.; Kamala-Kannan, S.; Lee, K.-J.; Park, Y.-J.; Shea, P.J.; Lee, W.-H.; Kim, H.-M.; Oha, B.-T. Removal of Pb(II) from aqueous solution by a zeolite–nanoscale zero-valent iron composite. Chem. Eng. J. 2013, 217, 54–60. [Google Scholar] [CrossRef]
- Lv, G.; Li, Z.; Jiang, W.-T.; Ackley, C.; Fenske, N.; Demarco, N. Removal of Cr(VI) from water using Fe(II)-modified natural zeolite. Chem. Eng. Res. Des. 2014, 92, 384–390. [Google Scholar] [CrossRef]
- Ponder, S.M.; Darag, J.G.; Mallouk, T.E. Remediation of Cr(VI) and Pb(II) Aqueous Solutions Using Supported, Nanoscale Zero-valent Iron. Environ. Sci. Technol. 2000, 34, 2564–2569. [Google Scholar] [CrossRef]
- Shu, H.-Y.; Chang, M.-C.; Chen, C.-C.; Chen, P.-E. Using resin supported nano zero-valent iron particles for decoloration of Acid Blue 113 azo dye solution. J. Hazard. Mater. 2010, 184, 499–505. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, T.; Jin, Z. Stabilization of Fe0 nanoparticles with silica fume for enhanced transport and remediation of hexavalent chromium in water and soil. J. Environ. Sci. 2011, 23, 1211–1218. [Google Scholar] [CrossRef]
- Fan, M.; Yuan, P.; Zhu, J.; Chen, T.; Yuan, A.; He, H.; Chen, K.; Liu, D. Core–shell structured iron nanoparticles well dispersed on montmorillonite. J. Magn. Magn. Mater. 2009, 321, 3515–3519. [Google Scholar] [CrossRef]
- Li, S.; Wu, P.; Li, H.; Zhu, N.; Li, P.; Wu, J.; Wang, X.; Dang, Z. Synthesis and characterization of organo-montmorillonite supported iron nanoparticles. Appl. Clay Sci. 2010, 50, 330–336. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Li, J.; Hu, L.; Zheng, X. Enhanced removal of nitrate by a novel composite: Nanoscale zero valent iron supported on pillared clay. Chem. Eng. J. 2011, 171, 526–531. [Google Scholar] [CrossRef]
- Frost, R.L.; Xi, Y.; He, H. Synthesis, characterization of palygorskite supported zero-valent iron and its application for methylene blue adsorption. J. Colloid Interface Sci. 2010, 341, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Fu, R.; Yang, Y.; Xu, Z.; Zhang, X.; Guo, X.; Bi, D. The removal of chromium (VI) and lead (II) from groundwater using sepiolite-supported nanoscale zero-valent iron (S-NZVI). Chemosphere 2015, 138, 726–734. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Wang, Z.-L.; Yan, X.; Zhang, B. Removal of mercury (II) and chromium (VI) from wastewater using a new and effective composite: Pumice-supported nanoscale zero-valent iron. Chem. Eng. J. 2014, 245, 34–40. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, S.; Lu, X.-Q.; Chen, Z.-L. Removal of Pb(II) from water using synthesized kaolin supported nanoscale zero-valent iron. Chem. Eng. J. 2010, 163, 243–248. [Google Scholar] [CrossRef]
- Geng, B.; Jin, Z.; Li, T.; Qi, X. Kinetics of hexavalent chromium removal from water by chitosan-Fe0 nanoparticles. Chemosphere 2009, 75, 825–830. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.X.; Gan, B.J.; Zhang, L. Electrochemical deposition of iron nanoneedles on titanium oxide nanotubes. Mater. Lett. 2011, 65, 2992–2994. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, H.; Peng, F.; Wang, H. Facile synthesis of porous hollow iron oxide nanoparticles supported on carbon nanotubes. Mater. Lett. 2012, 67, 245–247. [Google Scholar] [CrossRef]
- Wu, L.; Shamsuzzoha, M.; Ritchie, S.M.C. Preparation of cellulose acetate supported zero-valent iron nanoparticles for the dechlorination of trichloroethylene in water. J. Nanopart. Res. 2005, 7, 469–476. [Google Scholar] [CrossRef]
- Bond, G.; Molloy, K.C.; Stone, F.S. Reduction of MgO-supported iron oxide: Formation and characterization of Fe/MgO catalysts. Sol. State Ion. 1997, 101, 697–705. [Google Scholar] [CrossRef]
- Jung, K.-D.; Joo, O.-S.; Kim, C.-S. Study on the structure of Fe/MgO catalysts for H2S wet oxidation. Catal. Lett. 2002, 84, 53–57. [Google Scholar] [CrossRef]
- Cheng, F.; Muftikian, R.; Fernando, Q.; Korte, N. Reduction of nitrate to ammonia by zero-valent iron. Chemosphere 1997, 35, 2689–2695. [Google Scholar] [CrossRef]
- Gheju, M. Hexavalent chromium reduction with zero-valent iron (ZVI) in aquatic systems. Water Air Soil Pollut. 2011, 222, 103–108. [Google Scholar] [CrossRef]
- Siciliano, A.; De Rosa, S. Experimental formulation of a kinetic model describing the nitrification process in biological aerated filters filled with plastic elements. Environ. Technol. 2015, 36, 293–301. [Google Scholar] [CrossRef] [PubMed]
- Siciliano, A.; Stillitano, M.A.; De Rosa, S. Biogas production from wet olive mill wastes pretreated with hydrogen peroxide in alkaline conditions. Renew. Energy 2016, 85, 903–916. [Google Scholar] [CrossRef]
- American Public Health Association (APHA). Standard Methods for the Examination of Water and Wastewater, 20th ed.; American Public Health Association and Water Environment Federation: Washington, DC, USA, 1998. [Google Scholar]


| Cycle | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Kobs (mgCr/L)−1·h−1 | 3.15 | 0.47 | 0.18 | 0.13 | 0.06 | 0.035 | 0.027 | 0.018 |
| Parameter | Values | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Cr(VI) mg/L | 5 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| pH | 5.29 | 5.21 | 5.12 | 5.03 | 4.94 | 4.85 | 4.77 | 4.69 | 4.60 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siciliano, A. Removal of Cr(VI) from Water Using a New Reactive Material: Magnesium Oxide Supported Nanoscale Zero-Valent Iron. Materials 2016, 9, 666. https://doi.org/10.3390/ma9080666
Siciliano A. Removal of Cr(VI) from Water Using a New Reactive Material: Magnesium Oxide Supported Nanoscale Zero-Valent Iron. Materials. 2016; 9(8):666. https://doi.org/10.3390/ma9080666
Chicago/Turabian StyleSiciliano, Alessio. 2016. "Removal of Cr(VI) from Water Using a New Reactive Material: Magnesium Oxide Supported Nanoscale Zero-Valent Iron" Materials 9, no. 8: 666. https://doi.org/10.3390/ma9080666
APA StyleSiciliano, A. (2016). Removal of Cr(VI) from Water Using a New Reactive Material: Magnesium Oxide Supported Nanoscale Zero-Valent Iron. Materials, 9(8), 666. https://doi.org/10.3390/ma9080666






