Lattice Dynamics Study of Phonon Instability and Thermal Properties of Type-I Clathrate K8Si46 under High Pressure
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
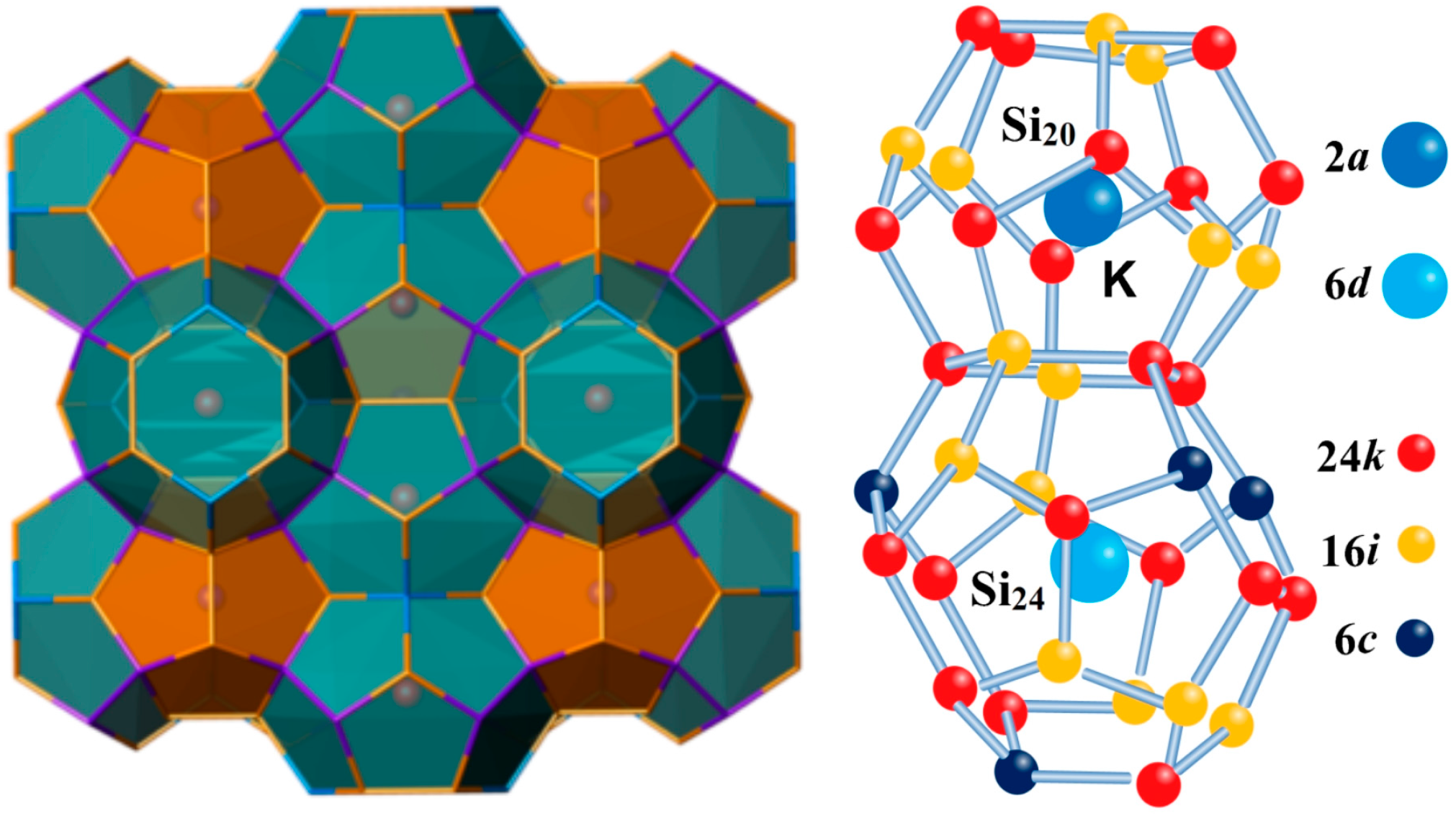
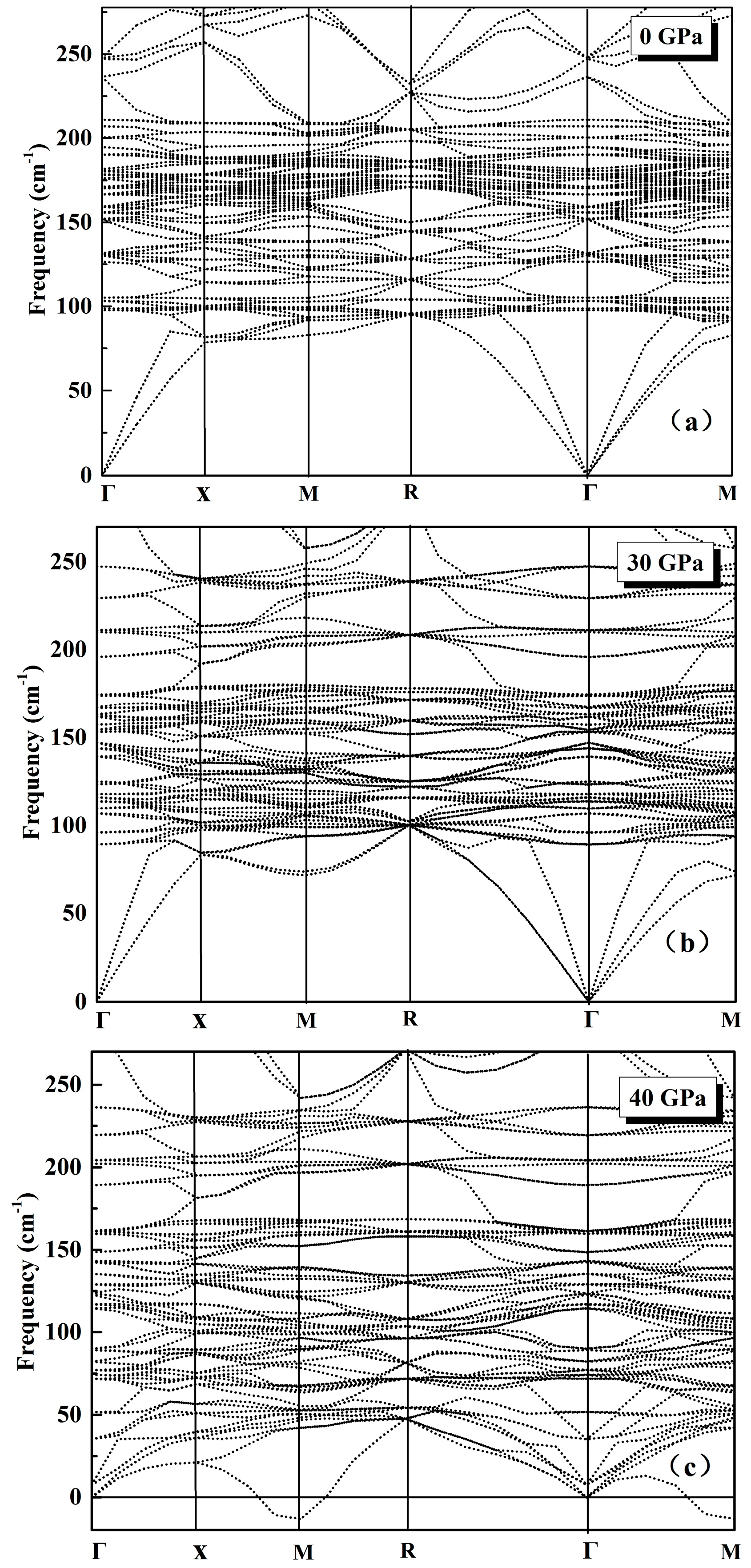
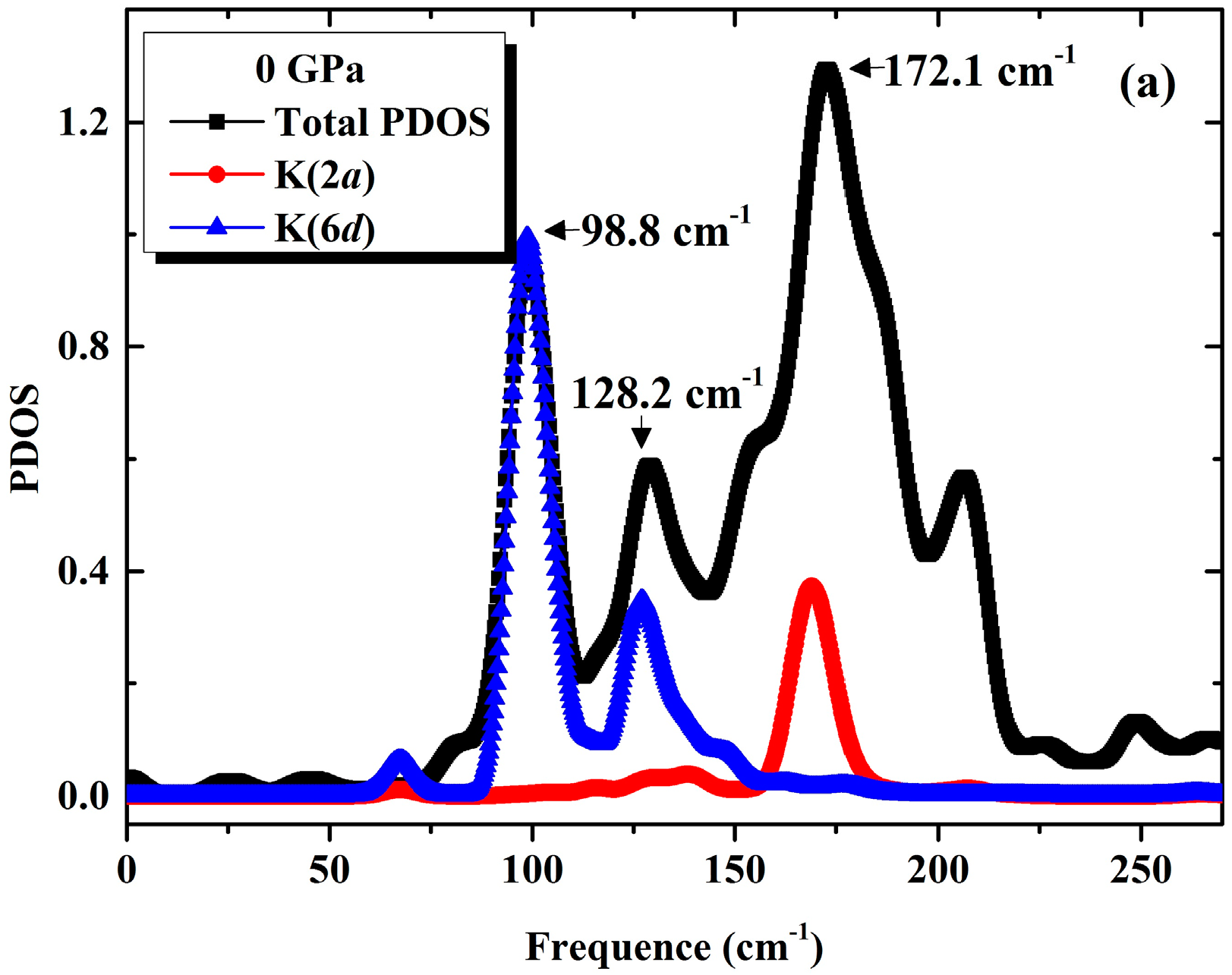
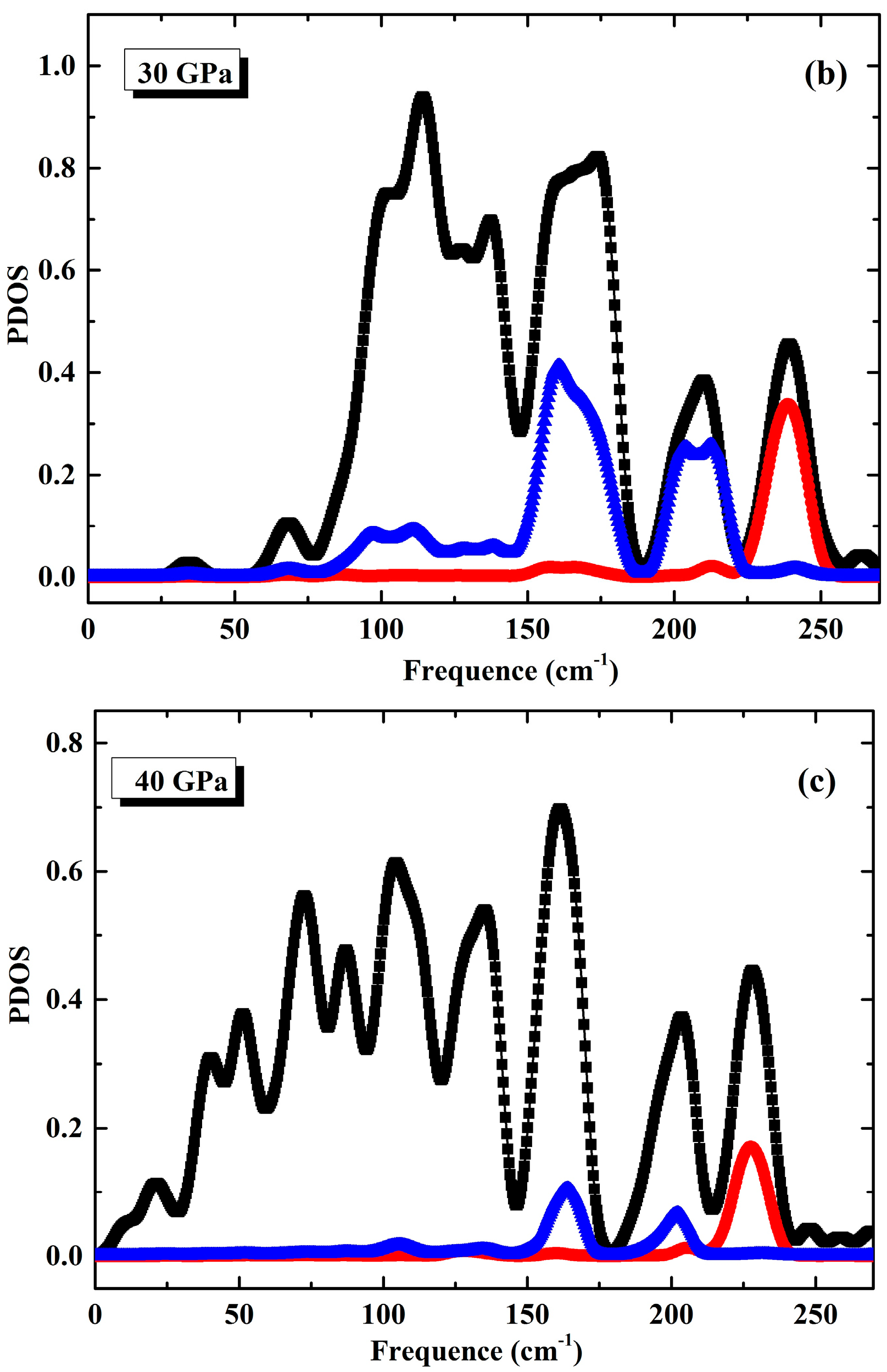
3.1. Phonon Spectra
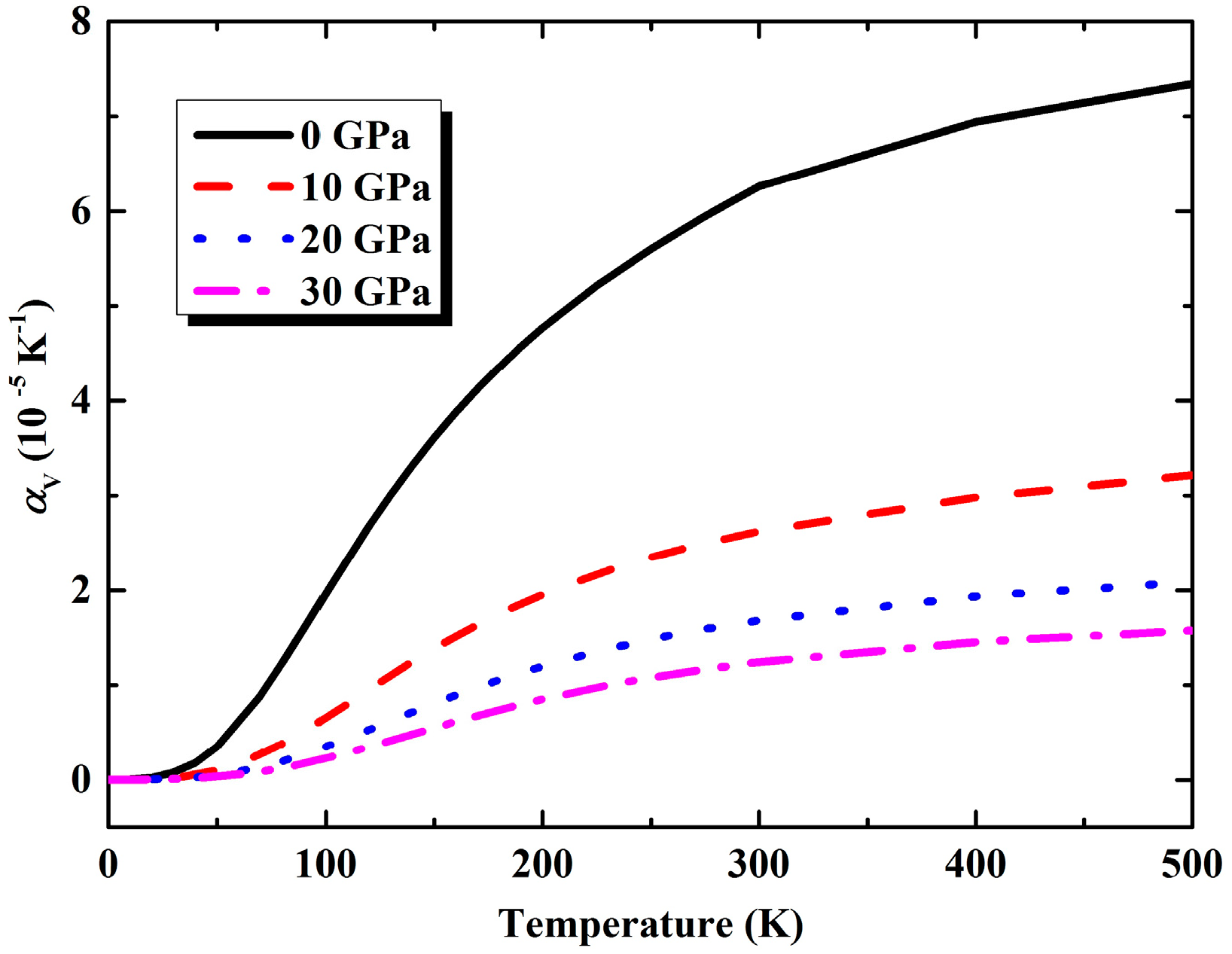
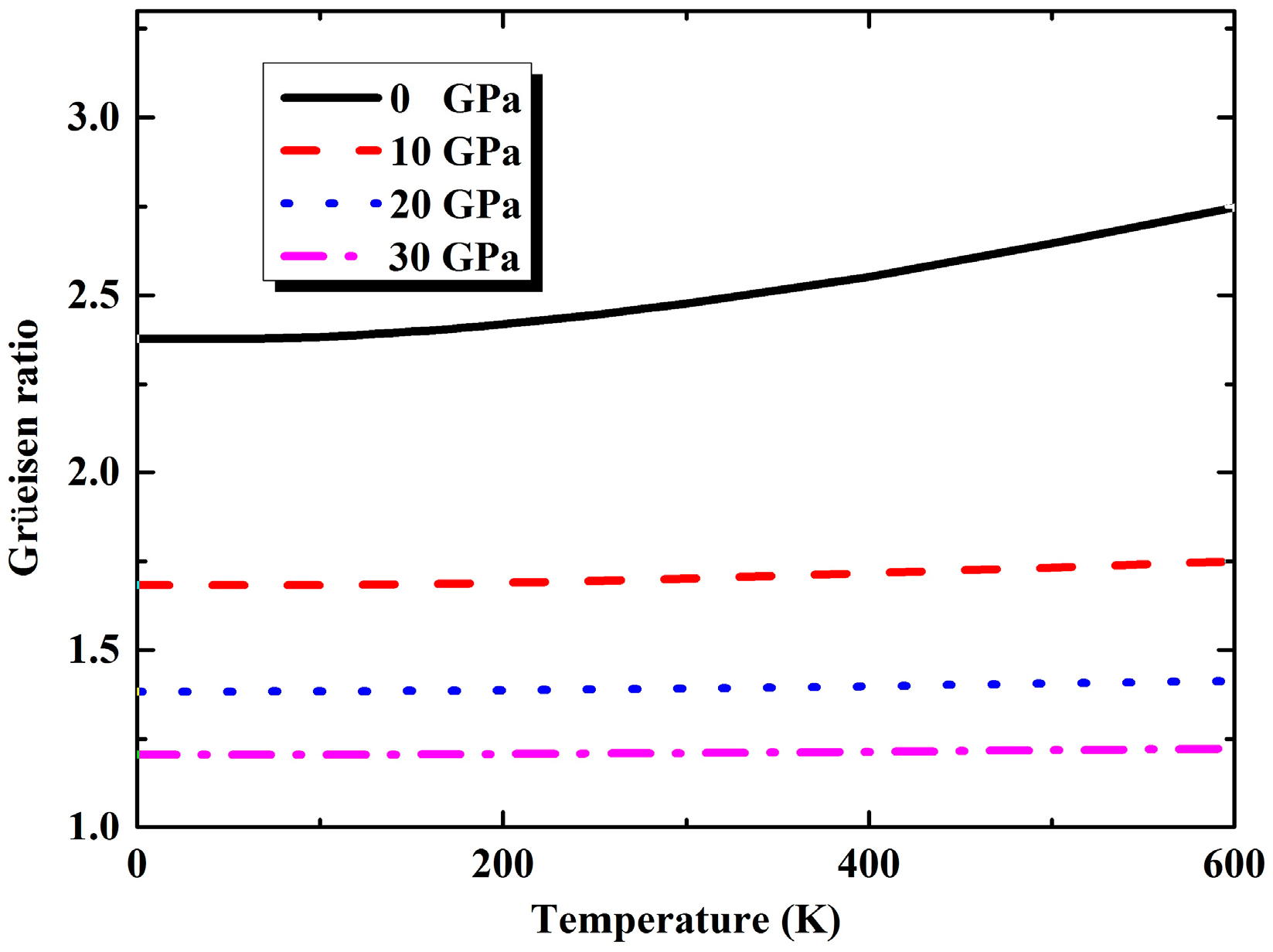
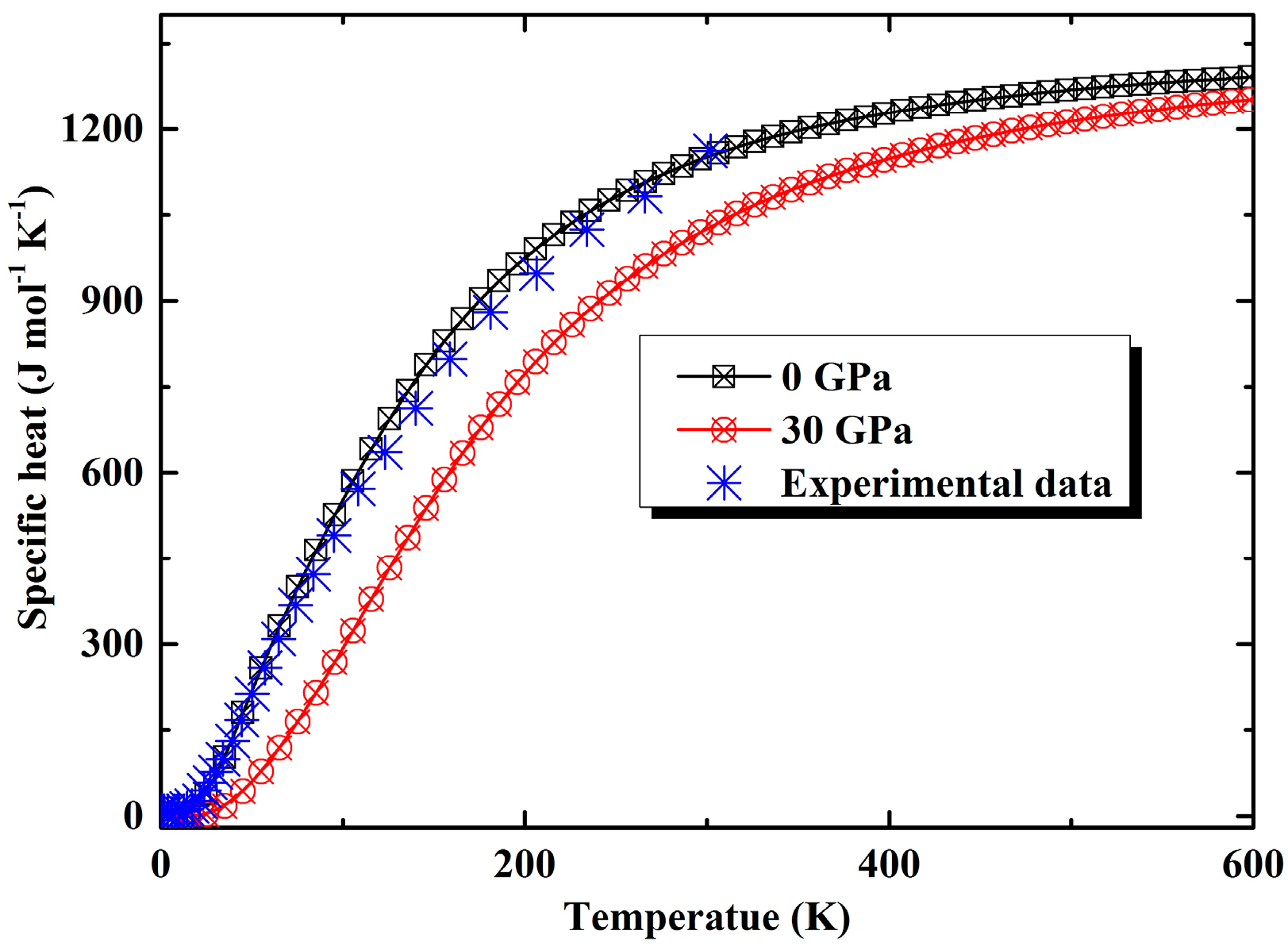
3.2. Thermal Properties from Quasi-Harmonic Approximation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Herrmann, R.F.W.; Tanigaki, K.; Kuroshima, S.; Suematsu, H. Superconductivity in silicon based barium-inclusion clathrates. Chem. Phys. Lett. 1998, 283, 29–32. [Google Scholar] [CrossRef]
- Nolas, G.S.; Cohn, J.L.; Slack, G.A.; Schujman, S.B. Semiconducting Ge clathrates: Promising candidates for thermoelectric applications. Appl. Phys. Lett. 1998, 73, 178–180. [Google Scholar] [CrossRef]
- Menon, M.; Richter, E.; Subbaswamy, K. Structural and vibrational properties of Si clathrates in a generalized tight-binding molecular-dynamics scheme. Phys. Rev. B 1997, 56, 12290–12295. [Google Scholar] [CrossRef]
- Kawaguchi, T.; Tanigaki, K.; Yakusawa, M. Silicon clathrate with an electron system. Phys. Rev. Lett. 2000, 85, 3189–3192. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.; Wang, H.; Nolas, G.S. Optimization of the thermoelectric properties of Ba8Ga16Ge30. Appl. Phys. Lett. 2008, 92, 222110. [Google Scholar] [CrossRef]
- Martinez, A.D.; Krishna, L.; Baranowski, L.L.; Lusk, M.T.; Toberer, E.S.; Tamboli, A.C. Synthesis of Group IV clathrates for photovoltaics. IEEE J. Photovolt. 2013, 3, 1305–1310. [Google Scholar] [CrossRef]
- Yamanaka, S.; Enishi, E.; Fukuoka, H.; Yasukawa, M. High-pressure synthesis of a new silicon clathrate superconductor Ba8Si46. Inorg. Chem. 2000, 39, 56–58. [Google Scholar] [CrossRef] [PubMed]
- Tse, J.S.; Desgreniers, S.; Li, Z.Q.; Ferguson, M.R.; Kawazoe, Y. Structural Stability and Phase Transitions in K8Si46 Clathrate under High Pressure. Phys. Rev. Lett. 2002, 89, 195507. [Google Scholar] [CrossRef] [PubMed]
- Kume, T.; Koda, T.; Sasaki, S.; Shimizu, H.; John, S.T. High-pressure Raman study of the potassium-doped silicon clathrate K8Si46. Phys. Rev. B 2004, 70, 052101. [Google Scholar] [CrossRef]
- San-Miguel, A.; Mélinon, P.; Connétable, D.; Blasé, X.; Tournus, F.; Reny, E.; Itié, J.P. Pressure stability and low compressibility of intercalated cagelike materials: The case of silicon clathrates. Phys. Rev. B 2002, 65, 054109. [Google Scholar] [CrossRef]
- Kume, T.; Fukuoka, H.; Koda, T.; Sasaki, S.; Shimizu, H.; Yamanaka, S. High-pressure Raman study of Ba doped silicon clathrate. Phys. Rev. Lett. 2003, 90, 155503. [Google Scholar] [CrossRef] [PubMed]
- San Miguel, A.; Merlen, A.; Toulemonde, P.; Kume, T.; Le Floch, S.; Aouizerat, A.; Itié, J.P. Pressure-induced homothetic volume collapse in silicon clathrates. Europhys. Lett. 2005, 69, 556. [Google Scholar] [CrossRef]
- Yang, L.; Ma, Y.M.; Iitaka, T.; Tse, J.S.; Stahl, K.; Ohishi, Y.; Jiang, J.Z. Pressure-induced phase transformations in the Ba8Si46 clathrate. Phys. Rev. B 2006, 74, 245209. [Google Scholar] [CrossRef]
- Tse, J.S.; Flacau, R.; Desgreniers, S.; Iitaka, T.; Jiang, J.Z. Electron density topology of high-pressure Ba8Si46 from a combined Rietveld and maximum-entropy analysis. Phys. Rev. B 2007, 76, 17. [Google Scholar] [CrossRef]
- Tse, J.S.; Yang, L.; Zhang, S.J.; Jin, C.Q.; Sahle, C.J.; Sternemann, C.; Nyrow, A.; Giordano, V.; Jiang, J.Z.; Yamanaka, S.; Desgreniers, S. Pressure-induced electron topological transitions in Ba-doped Si clathrate. Phys. Rev. B 2011, 84, 184105. [Google Scholar] [CrossRef]
- San-Miguel, A.; Toulemonde, P. High-pressure properties of group IV clathrates. High. Press. Res. 2005, 25, 159–185. [Google Scholar] [CrossRef]
- Shimizu, H.; Kume, T.; Kuroda, T.; Sasaki, S.; Fukuoka, H.; Yamanaka, S. High-pressure Raman study of the iodine-doped silicon clathrate I8Si44I2. Phys. Rev. B 2003, 68, 212102. [Google Scholar] [CrossRef]
- Machon, D.; Toulemonde, P.; McMillan, P.F.; Amboage, M.; Munoz, A.; Rodríguez-Hernández, P.; San Miguel, A. High-pressure phase transformations, pressure-induced amorphization, and polyamorphic transition of the clathrate Rb6.15Si46. Phys. Rev. B 2009, 79, 184101. [Google Scholar] [CrossRef]
- Zhang, W.; Ge, N.N.; Zou, Y.T.; Zeng, Z.Y.; Cai, L.C. Influence of missing guest and host atoms on the mechanical and electronic properties of type-I clathrate compound Ba8Si46. J. Alloys Compd. 2015, 653, 77–87. [Google Scholar] [CrossRef]
- Iitaka, T. Pressure-induced isostructural phase transition of metal-doped silicon clathrates. Phys. Rev. B 2007, 75, 012106:1–012106:4. [Google Scholar] [CrossRef]
- Blancon, J.C.; Machon, D.; Pischedda, V.; Debord, R.; Toulemonde, P.; Le Floch, S.; San-Miguel, A. Revisiting pressure-induced phase transition in silicon clathrates using Ge substitution. Phys. Rev. B 2016, 93, 134103. [Google Scholar] [CrossRef]
- Parlinski, K.; Li, Z.Q.; Kawazoe, Y. First-principles determination of the soft mode in cubic ZrO2. Phys. Rev. Lett. 1997, 78, 4063. [Google Scholar] [CrossRef]
- Baroni, S.; Giannonzzi, P.; Testa, A. Green’s-function approach to linear response in solids. Phys. Rev. Lett. 1987, 58, 1861. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Gironcoli, S.; Pavone, P.; Baroni, S. Ab initio calculation of phonon dispersions in semiconductors. Phys. Rev. B 1991, 43, 7231. [Google Scholar] [CrossRef]
- Gonze, X.; Allan, D.C.; Teter, M.P. Dielectric tensor, effective charges, and phonons in neutron-diffraction studies of salicylic acid and α-quartz by variational density-functional perturbation theory. Phys. Rev. Lett. 1994, 68, 3603–3606. [Google Scholar] [CrossRef] [PubMed]
- Gonze, X. First-principles responses of solids to atomic displacements and homogeneous electric fields: Implementation of a conjugate-gradient algorithm. Phys. Rev. B 1997, 55, 10337. [Google Scholar] [CrossRef]
- Lin, J.S.; Qteish, A.; Payne, M.C.; Heine, V.; Lin, J.S. Optimized and transferable nonlocal separable ab initio pseudopotentials. Phys. Rev. B 1993, 47, 4174–4180. [Google Scholar] [CrossRef]
- Lee, M.H. Advanced pseudopotentials for large scale electronic structure calculations: With application to a study of weakly ordered material-γ-Al2O3. Ph.D. Thesis, Cambridge University, Cambridge, UK, 1995. [Google Scholar]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 2100–2105. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Crystal structure and pair potentials: A molecular-dynamics study. Phys. Rev. Lett. 1980, 45, 1196–1199. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Fischer, T.H.; Almlof, J. General methods for geometry and wave function optimization. J. Phys. Chem. 1992, 96, 9768–9774. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allen, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef]
- Milman, V.; Winkler, B.; White, J.A.; Packard, C.J.; Payne, M.C.; Akhmatskaya, E.V.; Nobes, R.H. Electronic structure, properties, and phase stability of inorganic crystals: A pseudopotential plane-wave study. Int. J. Quantum Chem. 2000, 77, 895–910. [Google Scholar] [CrossRef]
- Gonze, X.; Lee, C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B 1997, 55, 10355. [Google Scholar] [CrossRef]
- Tse, J.S.; Li, Z.Q.; Uehara, K. Phonon band structures and resonant scattering in Na8Si46 and Cs8Sn46 calthrate. Europhys. Lett. 2001, 56, 261. [Google Scholar] [CrossRef]
- Mélinon, P.; Kéghélian, P.; Perez, A.; Champagnon, B.; Guyot, Y.; Saviot, L.; Dianoux, A.J. Phonon density of states of silicon clathrates: Characteristic width narrowing effect with respect to the diamond phase. Phys. Rev. B 1999, 59, 10099. [Google Scholar]
- Reny, E.; San-Miguel, A.; Guyot, Y.; Masenelli, B.; Mélinon, P.; Saviot, L.; Borowski, M. Vibrational modes in silicon clathrate compounds: A key to understanding superconductivity. Phys. Rev. B 2002, 66, 014532. [Google Scholar] [CrossRef]
- Cohn, J.L.; Nolas, G.S.; Fessatidis, V.; Metcalf, T.H.; Slack, G.A. Glasslike heat conduction in high-mobility crystalline semiconductors. Phys. Rev. Lett. 1999, 82, 779–782. [Google Scholar] [CrossRef]
- Otero-de-la-Roza, A.; Abbasi-Pérez, D.; Luaña, V. Gibbs2: A new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation. Comput. Phys. Commun. 2011, 182, 2232–2248. [Google Scholar] [CrossRef]
- Qiu, L.; White, M.A.; Li, Z.; John, S.T.; Ratcliffe, C.I.; Tulk, C.A.; Sankey, O.F. Thermal and lattice dynamical properties of Na8Si46 clathrate. Phys. Rev. B 2001, 64, 024303. [Google Scholar] [CrossRef]
- Okamoto, N.L.; Nakano, T.; Tanaka, K.; Inui, H. Mechanical and thermal properties of single crystals of the type-I clathrate compounds Ba8Ga16Ge30 and Sr8Ga16Ge30. J. Appl. Phys. 2008, 104, 013529. [Google Scholar] [CrossRef]
- Kaltzoglou, A.; Fässler, T.; Christensen, M.; Johnsen, S.; Iversen, B.B.; Presniakov, I.; Sobolev, A.; Shevelkov, A. Effects of the order-disorder phase transition on the physical properties of A8Sn44□2 (A = Rb, Cs). J. Mater. Chem. 2008, 18, 5630–5637. [Google Scholar] [CrossRef]
- Lortz, R.; Viennois, R.; Petrovic, A.; Wang, Y.; Toulemonde, P.; Meingast, C.; Koza, M.M.; Mutka, H.; Bossak, A.; San Miguel, A. Phonon density of states, anharmonicity, electron-phonon coupling, and possible multigap superconductivity in the clathrate superconductors Ba8Si46 and Ba24Si100: Factors behind large difference in Tc. Phys. Rev. B 2008, 77, 224507. [Google Scholar] [CrossRef]
- Falmbigl, M.; Rogl, G.; Rogl, P.; Kriegisch, M.; Müller, H.; Bauer, E.; Reinecker, M.; Schranz, W. Thermal expansion of thermoelectric type-I-clathrates. J. Appl. Phys. 2010, 108, 043529. [Google Scholar] [CrossRef]
- Stefanoski, S. Synthesis and Physical Properties of Group 14 Intermetallic Clathrates. Ph.D Theses, University of South Florida, Gainesville, FL, USA, 2012. [Google Scholar]
- Zhang, W.; Chen, Q.Y.; Li, B.; Zeng, Z.Y.; Cai, L.C. First-principles calculations for thermodynamic properties of type-I silicon clathrate intercalated by sodium atoms. Mod. Phys. Lett. B 2015, 29, 1550166. [Google Scholar] [CrossRef]
- Nolas, G.S. The Physics and Chemistry of Inorganic Clathrates; Springer Science+Business Media: Dordrecht, The Netherlands, 2014. [Google Scholar]
- White, A.M. Properties of Materials; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Anderson, O.L. A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zeng, Z.Y.; Ge, N.N.; Li, Z.G. Lattice Dynamics Study of Phonon Instability and Thermal Properties of Type-I Clathrate K8Si46 under High Pressure. Materials 2016, 9, 616. https://doi.org/10.3390/ma9080616
Zhang W, Zeng ZY, Ge NN, Li ZG. Lattice Dynamics Study of Phonon Instability and Thermal Properties of Type-I Clathrate K8Si46 under High Pressure. Materials. 2016; 9(8):616. https://doi.org/10.3390/ma9080616
Chicago/Turabian StyleZhang, Wei, Zhao Yi Zeng, Ni Na Ge, and Zhi Guo Li. 2016. "Lattice Dynamics Study of Phonon Instability and Thermal Properties of Type-I Clathrate K8Si46 under High Pressure" Materials 9, no. 8: 616. https://doi.org/10.3390/ma9080616
APA StyleZhang, W., Zeng, Z. Y., Ge, N. N., & Li, Z. G. (2016). Lattice Dynamics Study of Phonon Instability and Thermal Properties of Type-I Clathrate K8Si46 under High Pressure. Materials, 9(8), 616. https://doi.org/10.3390/ma9080616





